Entropic Steering Criteria: Applications to Bipartite and Tripartite Systems
Abstract
1. Introduction
2. Steering
3. Entropies and Entropic Uncertainty Relations
3.1. Entropies
- The entropies and are positive and they are zero if and only if the probability distribution is concentrated at one value (k), i.e., .
- In the limit of and , the Tsallis and Rényi entropies converge to the Shannon entropy, and both decrease monotonically in q and r.
- The Rényi entropy is a monotonous function of the Tsallis entropy:
- Shannon and Tsallis entropy are concave functions in , i.e., they obey the relationwhere for Shannon entropy, and for Tsallis entropy. The Rényi entropy is concave if , and for other values of r it is neither convex nor concave.
- In the limit of , the Rényi entropy is known as min-entropy
- For two independent distributions, and , Shannon and Rényi entropies are additive, i.e.,whereas Tsallis entropy is pseudo-additive, i.e.,
3.2. Relative Entropies
3.3. Entropic Uncertainty Relations
4. Entropic Steering Criteria
4.1. Entropic Steering Criteria for Shannon Entropy
4.2. Entropic Steering Criteria for Generalized Entropies
4.2.1. Tsallis Entropy
4.2.2. Rényi Entropy
5. Connection to Existing Entanglement Criteria
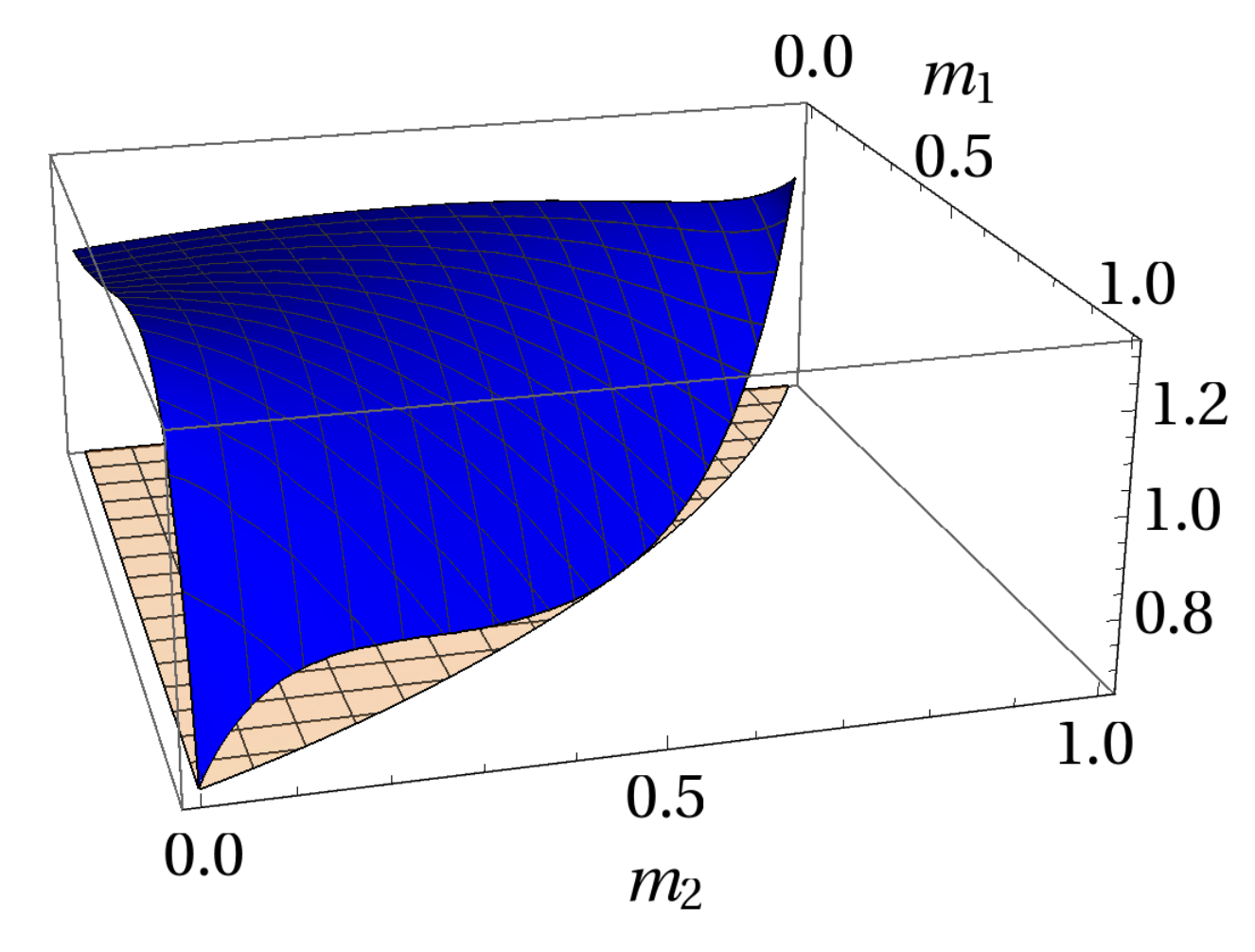
6. Applications
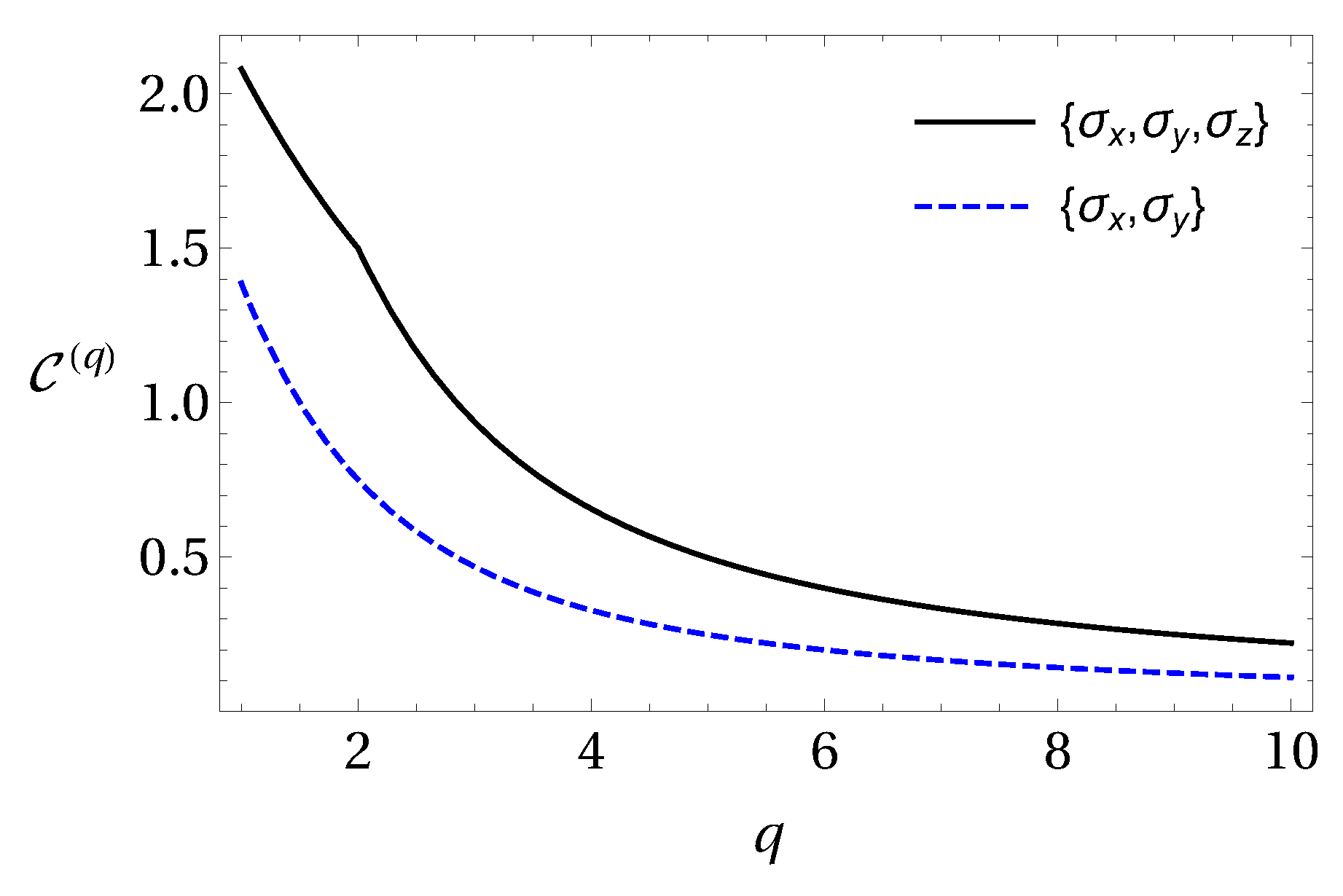
6.1. Optimal Values of q and r for Steering Detection
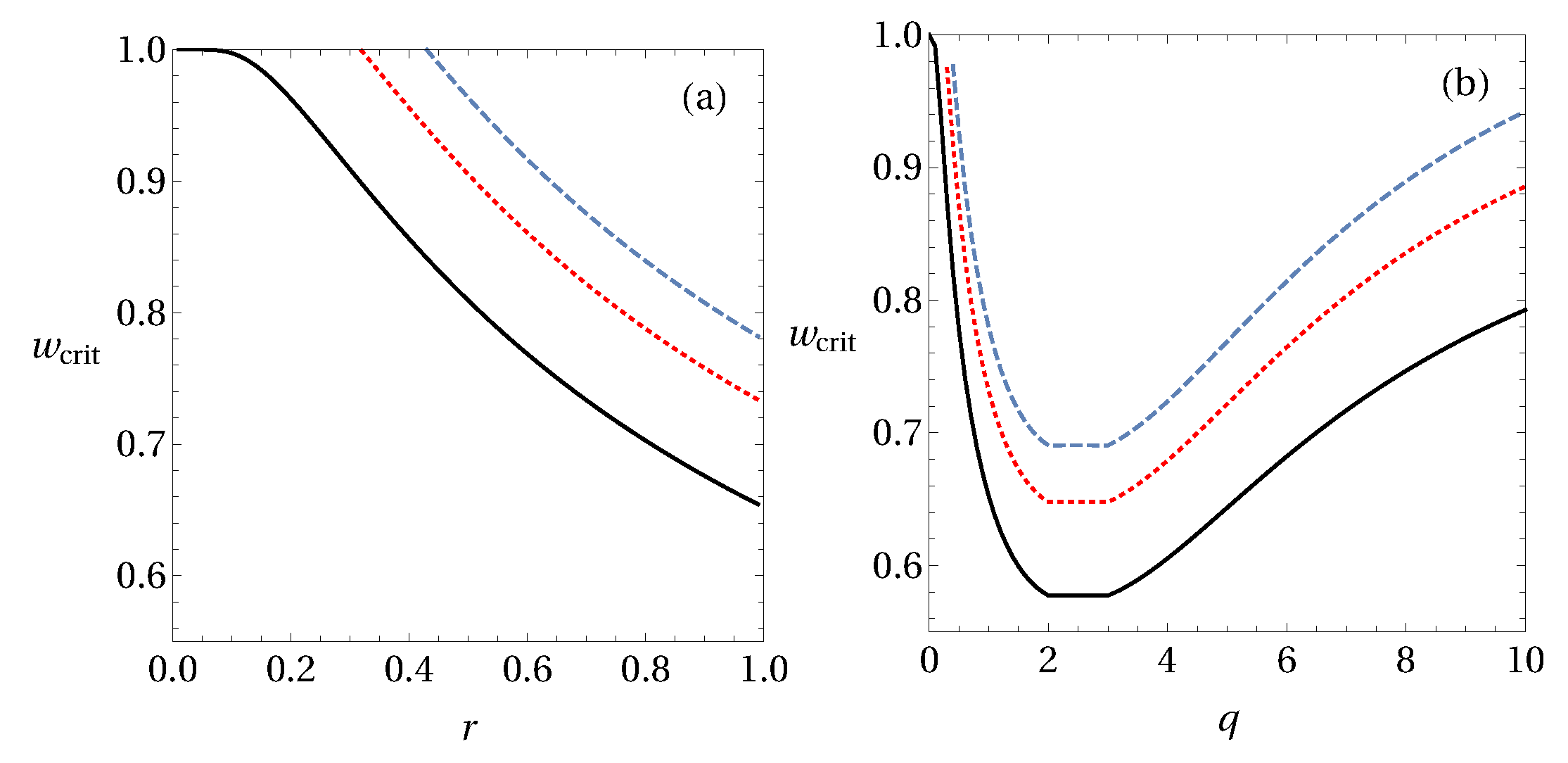
6.2. Isotropic States
6.3. General Two-Qubit States
6.4. One-Way Steerable States
6.5. Bound Entangled States
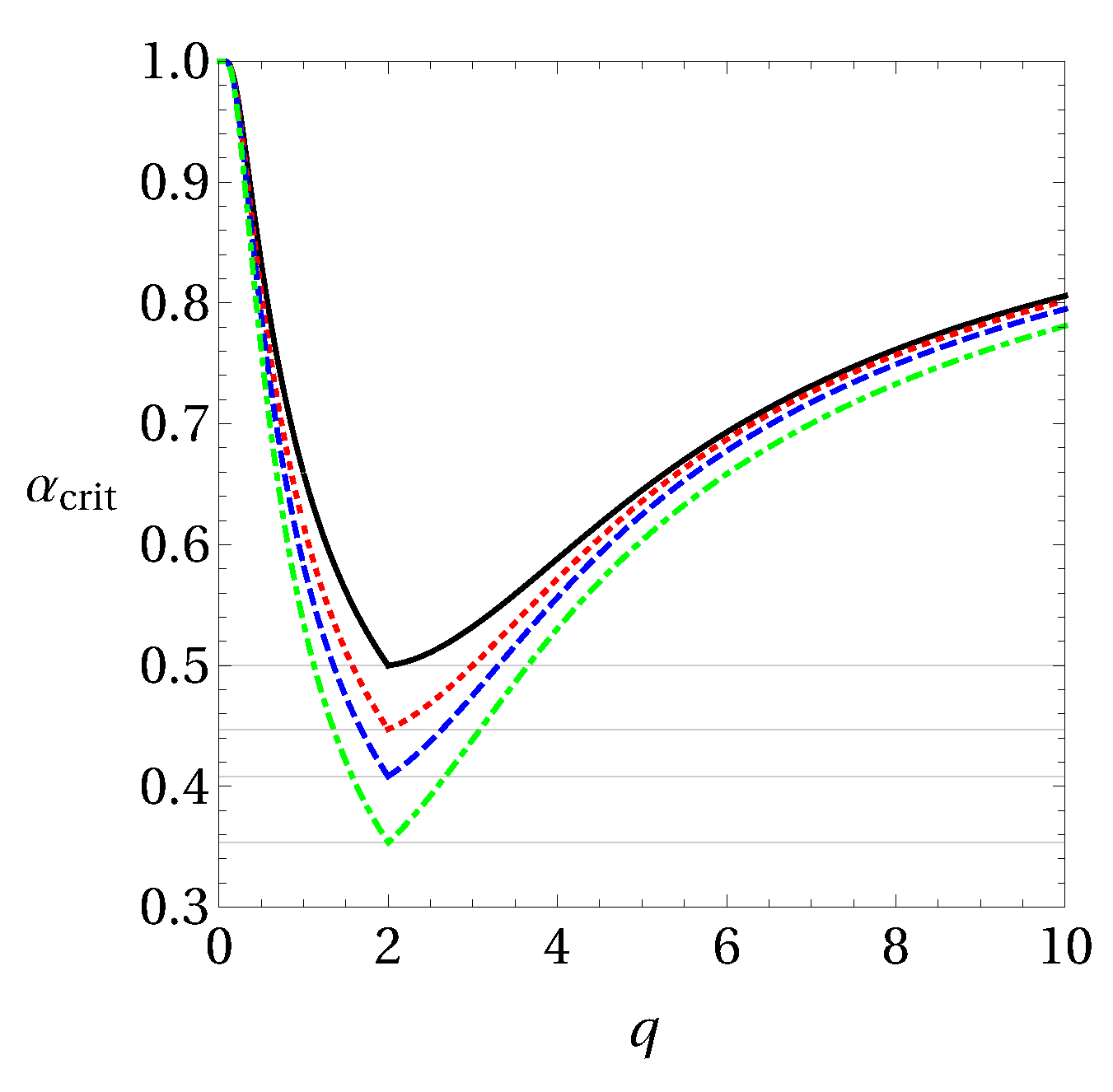
7. Multipartite Scenario
7.1. Steering from Alice to Bob and Charlie
7.2. Steering from Alice and Bob to Charlie
7.3. Applications
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schrödinger, E. Eine Entdeckung Von Ganz Außerordentlicher Tragweite; Springer: Berlin, Germany, 2011; p. 551. [Google Scholar]
- Wiseman, H.M.; Jones, S.J.; Doherty, A.C. Steering, Entanglement, Nonlocality, and the Einstein-Podolsky-Rosen Paradox. Phys. Rev. Lett. 2007, 98, 140402. [Google Scholar] [CrossRef] [PubMed]
- Branciard, C.; Cavalcanti, E.G.; Walborn, S.P.; Scarani, V.; Wiseman, H.M. One-sided device-independent quantum key distribution: Security, feasibility, and the connection with steering. Phys. Rev. A 2012, 85, 010301. [Google Scholar] [CrossRef]
- Piani, M.; Watrous, J. Necessary and Sufficient Quantum Information Characterization of Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 2015, 114, 060404. [Google Scholar] [CrossRef] [PubMed]
- Law, Y.Z.; Thinh, L.P.; Bancal, J.-D.; Scarani, V. Quantum randomness extraction for various levels of characterization of the devices. J. Phys. A 2014, 47, 424028. [Google Scholar] [CrossRef]
- Moroder, T.; Gittsovich, O.; Huber, M.; Gühne, O. Steering Bound Entangled States: A Counterexample to the Stronger Peres Conjecture. Phys. Rev. Lett. 2014, 113, 050404. [Google Scholar] [CrossRef] [PubMed]
- Vertési, T.; Brunner, N. Disproving the Peres conjecture by showing Bell nonlocality from bound entanglement. Nat. Commun. 2014, 5, 5297. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Oh, C.H. Family of nonlocal bound entangled states. Phys. Rev. A 2017, 95, 032111. [Google Scholar] [CrossRef]
- Quintino, M.T.; Vértesi, T.; Brunner, N. Joint Measurability, Einstein-Podolsky-Rosen Steering, and Bell Nonlocality. Phys. Rev. Lett. 2014, 113, 160402. [Google Scholar] [CrossRef] [PubMed]
- Uola, R.; Moroder, T.; Gühne, O. Joint Measurability of Generalized Measurements Implies Classicality. Phys. Rev. Lett. 2014, 113, 160403. [Google Scholar] [CrossRef] [PubMed]
- Uola, R.; Budroni, C.; Gühne, O.; Pellonpää, J.-P. One-to-One Mapping between Steering and Joint Measurability Problems. Phys. Rev. Lett. 2015, 115, 230402. [Google Scholar] [CrossRef] [PubMed]
- Uola, R.; Lever, F.; Gühne, O.; Pellonpää, J.-P. Unified picture for spatial, temporal, and channel steering. Phys. Rev. A 2018, 97, 032301. [Google Scholar] [CrossRef]
- Kiukas, J.; Budroni, C.; Uola, R.; Pellonpää, J.-P. Continuous-variable steering and incompatibility via state-channel duality. Phys. Rev. A 2017, 96, 042331. [Google Scholar] [CrossRef]
- He, Q.Y.; Drummond, P.D.; Reid, M.D. Entanglement, EPR steering, and Bell-nonlocality criteria for multipartite higher-spin systems. Phys. Rev. A 2011, 83, 032120. [Google Scholar] [CrossRef]
- Cavalcanti, E.G.; He, Q.Y.; Reid, M.D.; Wiseman, H.M. Unified criteria for multipartite quantum nonlocality. Phys. Rev. A 2011, 84, 032115. [Google Scholar] [CrossRef]
- He, Q.Y.; Reid, M.D. Genuine Multipartite Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 2013, 111, 250403. [Google Scholar] [CrossRef] [PubMed]
- Cavalcanti, D.; Skrzypczyk, P.; Aguilar, G.H.; Nery, R.V.; Souto Ribeiro, P.H.; Walborn, S.P. Detection of entanglement in asymmetric quantum networks and multipartite quantum steering. Nat. Commun. 2015, 6, 7941. [Google Scholar] [CrossRef] [PubMed]
- Riccardi, A.; Macchiavello, C.; Maccone, L. Multipartite steering inequalities based on entropic uncertainty relations. Phys. Rev. A 2018, 97, 052307. [Google Scholar] [CrossRef]
- Pusey, M.F. Negativity and steering: A stronger Peres conjecture. Phys. Rev. A 2013, 88, 032313. [Google Scholar] [CrossRef]
- Cavalcanti, D.; Skrzypczyk, P. Quantum steering: A review with focus on semidefinite programming. Rep. Prog. Phys. 2017, 80, 024001. [Google Scholar] [CrossRef] [PubMed]
- Kogias, I.; Skrzypczyk, P.; Cavalcanti, D.; Acín, A.; Adesso, G. Hierarchy of Steering Criteria Based on Moments for All Bipartite Quantum Systems. Phys. Rev. Lett. 2015, 115, 210401. [Google Scholar] [CrossRef] [PubMed]
- Fillettaz, M.; Hirsch, F.; Designolle, S.; Brunner, N. Algorithmic construction of local models for entangled quantum states: Optimization for two-qubit states. arXiv, 2018; arXiv:1804.07576. [Google Scholar] [CrossRef]
- Hirsch, F.; Quintino, M.T.; Vértesi, T.; Pusey, M.F.; Brunner, N. Algorithmic Construction of Local Hidden Variable Models for Entangled Quantum States. Phys. Rev. Lett. 2016, 117, 190402. [Google Scholar] [CrossRef] [PubMed]
- Cavalcanti, D.; Guerini, L.; Rabelo, R.; Skrzypczyk, P. General Method for Constructing Local Hidden Variable Models for Entangled Quantum States. Phys. Rev. Lett. 2016, 117, 190401. [Google Scholar] [CrossRef] [PubMed]
- Cavalcanti, E.G.; Foster, C.J.; Fuwa, M.; Wiseman, H.M. Analog of the Clauser–Horne–Shimony–Holt inequality for steering. J. Opt. Soc. Am. B 2015, 32, A74–A81. [Google Scholar] [CrossRef]
- Jevtic, S.; Pusey, M.; Jennings, D.; Rudolph, T. Quantum Steering Ellipsoids. Phys. Rev. Lett. 2014, 113, 020402. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.C.; Vu, T. Necessary and sufficient condition for steerability of two-qubit states by the geometry of steering outcomes. Europhys. Lett. 2016, 115, 10003. [Google Scholar] [CrossRef]
- Bowles, J.; Hirsch, F.; Quintino, M.T.; Brunner, N. Sufficient criterion for guaranteeing that a two-qubit state is unsteerable. Phys. Rev. A 2016, 93, 022121. [Google Scholar] [CrossRef]
- Moroder, T.; Gittsovich, O.; Huber, M.; Uola, R.; Gühne, O. Steering Maps and Their Application to Dimension-Bounded Steering. Phys. Rev. Lett. 2016, 116, 090403. [Google Scholar] [CrossRef] [PubMed]
- Costa, A.C.S.; Uola, R.; Gühne, O. Steering criteria from general entropic uncertainty relations. arXiv, 2017; arXiv:1710.04541. [Google Scholar]
- Walborn, S.P.; Salles, A.; Gomes, R.M.; Toscano, F.; Souto Ribeiro, P.H. Revealing Hidden Einstein-Podolsky-Rosen Nonlocality. Phys. Rev. Lett. 2011, 106, 130402. [Google Scholar] [CrossRef] [PubMed]
- Schneeloch, J.; Broadbent, C.J.; Walborn, S.P.; Cavalcanti, E.G.; Howell, J.C. Einstein-Podolsky-Rosen steering inequalities from entropic uncertainty relations. Phys. Rev. A 2013, 87, 062103. [Google Scholar] [CrossRef]
- Kriváchy, T.; Fröwis, F.; Brunner, N. Tight steering inequalities from generalized entropic uncertainty relations. arXiv, 2018; arXiv:1807.09603. [Google Scholar]
- Quintino, M.T.; Brunner, N.; Huber, M. Superactivation of quantum steering. Phys. Rev. A 2016, 94, 062123. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2006; ISBN 0471241954. [Google Scholar]
- Havrda, J.; Charvát, F. Quantification method of classification processes. Concept of structural α-entropy. Kybernetika 1967, 3, 30. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479. [Google Scholar] [CrossRef]
- Rényi, A. Valószínüségszámítás; Tankönyvkiadó: Budapest, Hungary, 1966; (English Translation: Probability Theory (North-Holland, Amsterdam, 1970)). [Google Scholar]
- Tsallis, C. Generalized entropy-based criterion for consistent testing. Phys. Rev. E 1998, 58, 1442. [Google Scholar] [CrossRef]
- Furuichi, S.; Yanagi, K.; Kuriyama, K. Fundamental properties of Tsallis relative entropy. J. Math. Phys. 2004, 45, 4868. [Google Scholar] [CrossRef]
- Van Erven, T.; Harremoës, P. Rényi Divergence and Kullback-Leibler Divergence. IEEE Trans. Inf. Theory 2014, 60, 3797. [Google Scholar] [CrossRef]
- Deutsch, D. Uncertainty in Quantum Measurements. Phys. Rev. Lett. 1983, 50, 631. [Google Scholar] [CrossRef]
- Maassen, H.; Uffink, J.B.M. Generalized entropic uncertainty relations. Phys. Rev. Lett. 1988, 60, 1103. [Google Scholar] [CrossRef] [PubMed]
- Durt, T.; Englert, B.-G.; Bengtsson, I.; Życzkowski, K. On mutually unbiased bases. Int. J. Quant. Inf. 2010, 8, 535. [Google Scholar] [CrossRef]
- Bengtsson, I.; Bruzda, W.; Ericsson, Å.; Larsson, J.-Å.; Tadej, W.; Życzkowski, K. Mutually unbiased bases and Hadamard matrices of order six. J. Math. Phys. 2007, 48, 052106. [Google Scholar] [CrossRef]
- Sanchez-Ruiz, J. Improved bounds in the entropic uncertainty and certainty relations for complementary observables. Phys. Lett. 1995, 201, 125. [Google Scholar] [CrossRef]
- Wu, S.; Yu, S.; Mølner, K. Entropic uncertainty relation for mutually unbiased bases. Phys. Rev. A 2009, 79, 022104. [Google Scholar] [CrossRef]
- Haapasalo, E. Robustness of incompatibility for quantum devices. J. Phys. A 2015, 48, 255303. [Google Scholar] [CrossRef]
- Uola, R.; Luoma, K.; Moroder, T.; Heinosaari, T. Adaptive strategy for joint measurements. Phys. Rev. A 2016, 94, 022109. [Google Scholar] [CrossRef]
- Designolle, S.; Skrzypczyk, P.; Fröwis, F.; Brunner, N. Quantifying measurement incompatibility of mutually unbiased bases. arXiv, 2018; arXiv:1805.09609. [Google Scholar]
- Schwonnek, R. Additivity of entropic uncertainty relations. Quantum 2018, 2, 59. [Google Scholar] [CrossRef]
- Rastegin, A.E. Uncertainty relations for MUBs and SIC-POVMs in terms of generalized entropies. Eur. Phys. J. D 2013, 67, 269. [Google Scholar] [CrossRef]
- Gühne, O.; Lewenstein, M. Entropic uncertainty relations and entanglement. Phys. Rev. A 2004, 70, 022316. [Google Scholar] [CrossRef]
- Furuichi, S. Information theoretical properties of Tsallis entropies. J. Math. Phys. 2006, 47, 023302. [Google Scholar] [CrossRef]
- Fehr, S.; Berens, S. On the Conditional Rényi Entropy. IEEE Trans. Inf. Theory 2014, 60, 6801. [Google Scholar] [CrossRef]
- Huang, Y. Entanglement criteria via concave-function uncertainty relations. Phys. Rev. A 2010, 82, 012335. [Google Scholar] [CrossRef]
- Gühne, O. Characterizing Entanglement via Uncertainty Relations. Phys. Rev. Lett. 2004, 92, 117903. [Google Scholar] [CrossRef] [PubMed]
- Zhen, Y.-Z.; Zheng, Y.-L.; Cao, W.-F.; Li, L.; Chen, Z.-B.; Liu, N.-L.; Chen, K. Certifying Einstein-Podolsky-Rosen steering via the local uncertainty principle. Phys. Rev. A 2016, 93, 012108. [Google Scholar] [CrossRef]
- Cavalcanti, E.G.; Jones, S.J.; Wiseman, H.M.; Reid, M.D. Experimental criteria for steering and the Einstein-Podolsky-Rosen paradox. Phys. Rev. A 2009, 80, 032112. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P. Reduction criterion of separability and limits for a class of distillation protocols. Phys. Rev. A 1999, 59, 4206. [Google Scholar] [CrossRef]
- Werner, R.F. Quantum states with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40, 4277. [Google Scholar] [CrossRef]
- Skrzypczyk, P.; Cavalcanti, D. Loss-tolerant Einstein-Podolsky-Rosen steering for arbitrary-dimensional states: Joint measurability and unbounded violations under losses. Phys. Rev. A 2015, 92, 022354. [Google Scholar] [CrossRef]
- Bavaresco, J.; Quintino, M.T.; Guerini, L.; Maciel, T.O.; Cavalcanti, D.; Cunha, M.T. Most incompatible measurements for robust steering tests. Phys. Rev. A 2017, 96, 022110. [Google Scholar] [CrossRef]
- Costa, A.C.S.; Angelo, R.M. Quantification of Einstein-Podolski-Rosen steering for two-qubit states. Phys. Rev. A 2016, 93, 020103(R). [Google Scholar] [CrossRef]
- Życzkowski, K.; Penson, K.A.; Nechita, I.; Collins, B. Generating random density matrices. J. Math. Phys. 2011, 52, 062201. [Google Scholar] [CrossRef]
- Xiao, Y.; Ye, X.-J.; Sun, K.; Xu, J.-S.; Li, C.-F.; Guo, G.-C. Demonstration of Multisetting One-Way Einstein-Podolsky-Rosen Steering in Two-Qubit Systems. Phys. Rev. Lett. 2017, 118, 140404. [Google Scholar] [CrossRef] [PubMed]
- Peres, A. All the Bell Inequalities. Found. Phys. 1999, 29, 589. [Google Scholar] [CrossRef]
- Skrzypczyk, P.; Navascués, M.; Cavalcanti, D. Quantifying Einstein-Podolsky-Rosen Steering. Phys. Rev. Lett. 2014, 112, 180404. [Google Scholar] [CrossRef] [PubMed]
- Bronzan, J.B. Parametrization of SU(3). Phys. Rev. D 1988, 38, 1994. [Google Scholar] [CrossRef]
- Schack, R.; Caves, C.M. Explicit product ensembles for separable quantum states. J. Mod. Opt. 2000, 47, 387. [Google Scholar] [CrossRef]
- Dür, W.; Cirac, J.I. Classification of multiqubit mixed states: Separability and distillability properties. Phys. Rev. A 2000, 61, 42314. [Google Scholar] [CrossRef]
- Gruca, J.; Laskowski, W.; Żukowski, M.; Kiesel, N.; Wieczorek, W.; Schmid, C.; Weinfurter, H. Nonclassicality thresholds for multiqubit states: Numerical analysis. Phys. Rev. A 2010, 82, 012118. [Google Scholar] [CrossRef]
- Chen, Z.-H.; Ma, Z.-H.; Gühne, O.; Severini, S. Estimating Entanglement Monotones with a Generalization of the Wootters Formula. Phys. Rev. Lett. 2012, 109, 200503. [Google Scholar] [CrossRef] [PubMed]
- Berta, M.; Christandl, M.; Colbeck, R.; Renes, J.M.; Renner, R. The uncertainty principle in the presence of quantum memory. Nat. Phys. 2010, 6, 659. [Google Scholar] [CrossRef]
- Barchielli, A.; Gregoratti, M.; Toigo, A. Measurement uncertainty relations for discrete observables: Relative entropy formulation. Commun. Math. Phys. 2018, 357, 1253. [Google Scholar] [CrossRef]
- Schneeloch, J.; Howland, G.A. Quantifying high-dimensional entanglement with Einstein-Podolsky-Rosen correlations. Phys. Rev. A 2018, 97, 042338. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, A.C.S.; Uola, R.; Gühne, O. Entropic Steering Criteria: Applications to Bipartite and Tripartite Systems. Entropy 2018, 20, 763. https://doi.org/10.3390/e20100763
Costa ACS, Uola R, Gühne O. Entropic Steering Criteria: Applications to Bipartite and Tripartite Systems. Entropy. 2018; 20(10):763. https://doi.org/10.3390/e20100763
Chicago/Turabian StyleCosta, Ana C. S., Roope Uola, and Otfried Gühne. 2018. "Entropic Steering Criteria: Applications to Bipartite and Tripartite Systems" Entropy 20, no. 10: 763. https://doi.org/10.3390/e20100763
APA StyleCosta, A. C. S., Uola, R., & Gühne, O. (2018). Entropic Steering Criteria: Applications to Bipartite and Tripartite Systems. Entropy, 20(10), 763. https://doi.org/10.3390/e20100763