Entropy Generation Rates in Two-Dimensional Rayleigh–Taylor Turbulence Mixing
Abstract
:1. Introduction
2. Macroscopic Dynamics Equation of Thermal Fluid and Lattice Boltzmann Method
2.1. Macroscopic Dynamics Equation of Thermal Fluid
2.2. Double Distribution Lattice Boltzmann Method
3. Some Numerical Results and Discussions
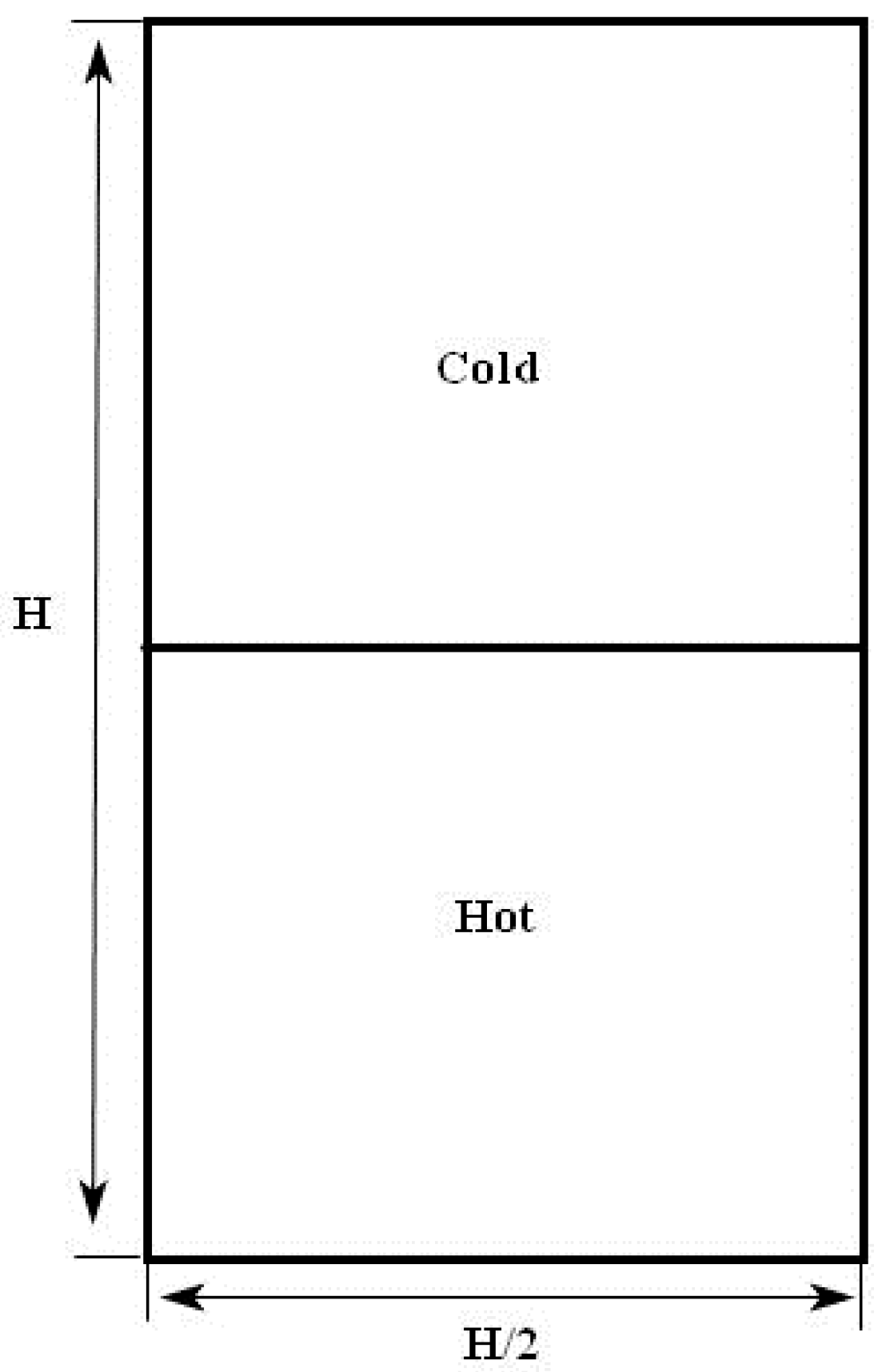
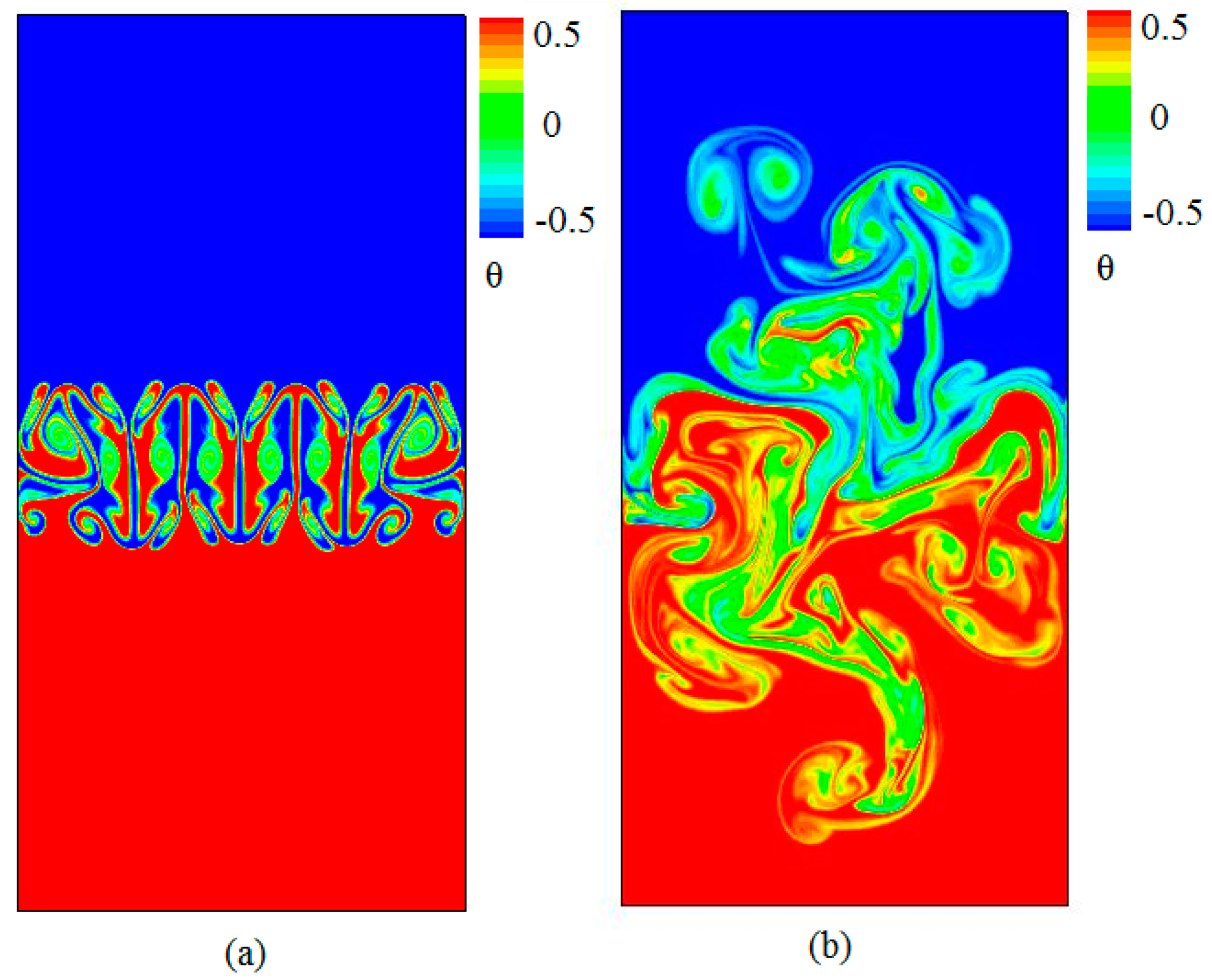
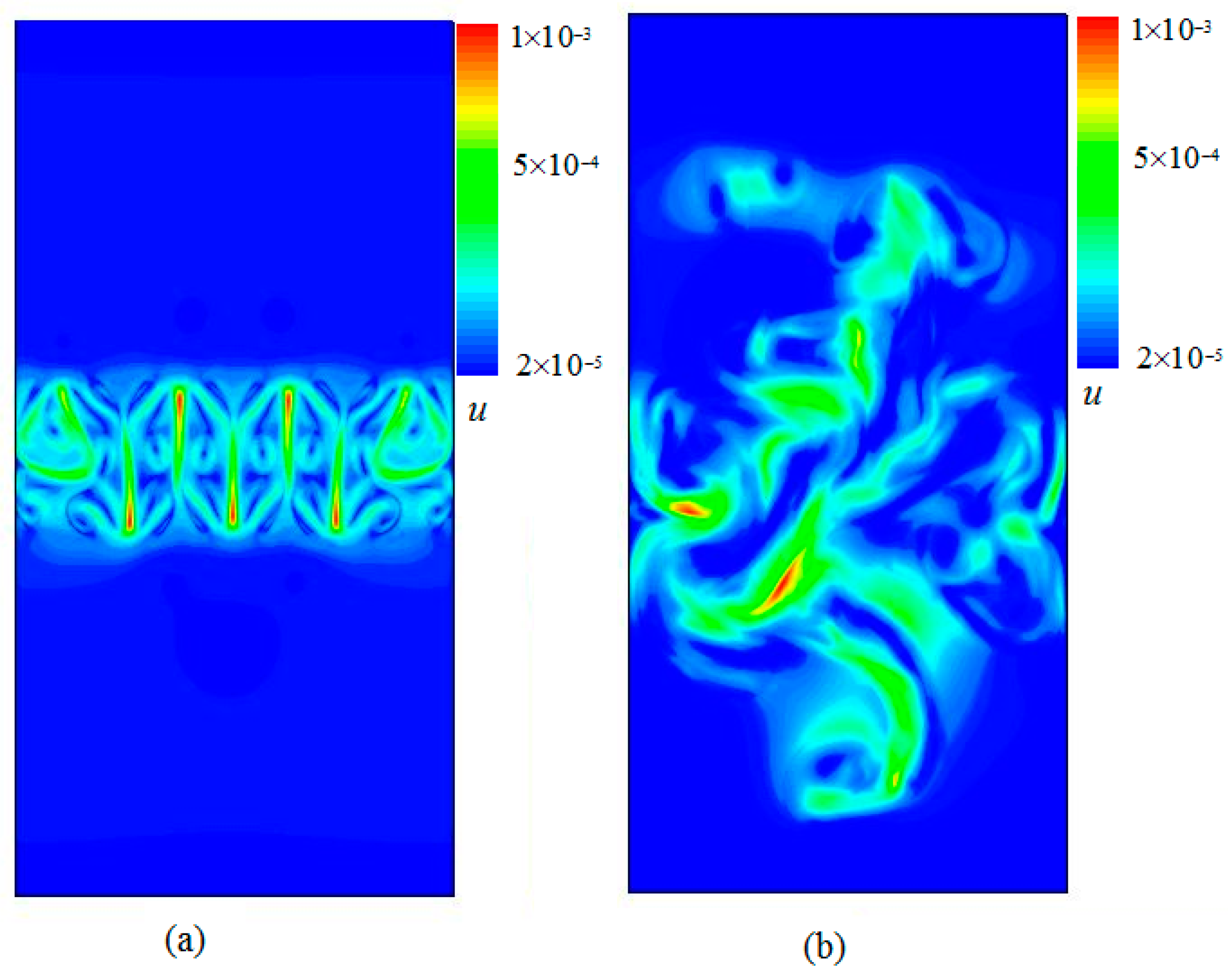
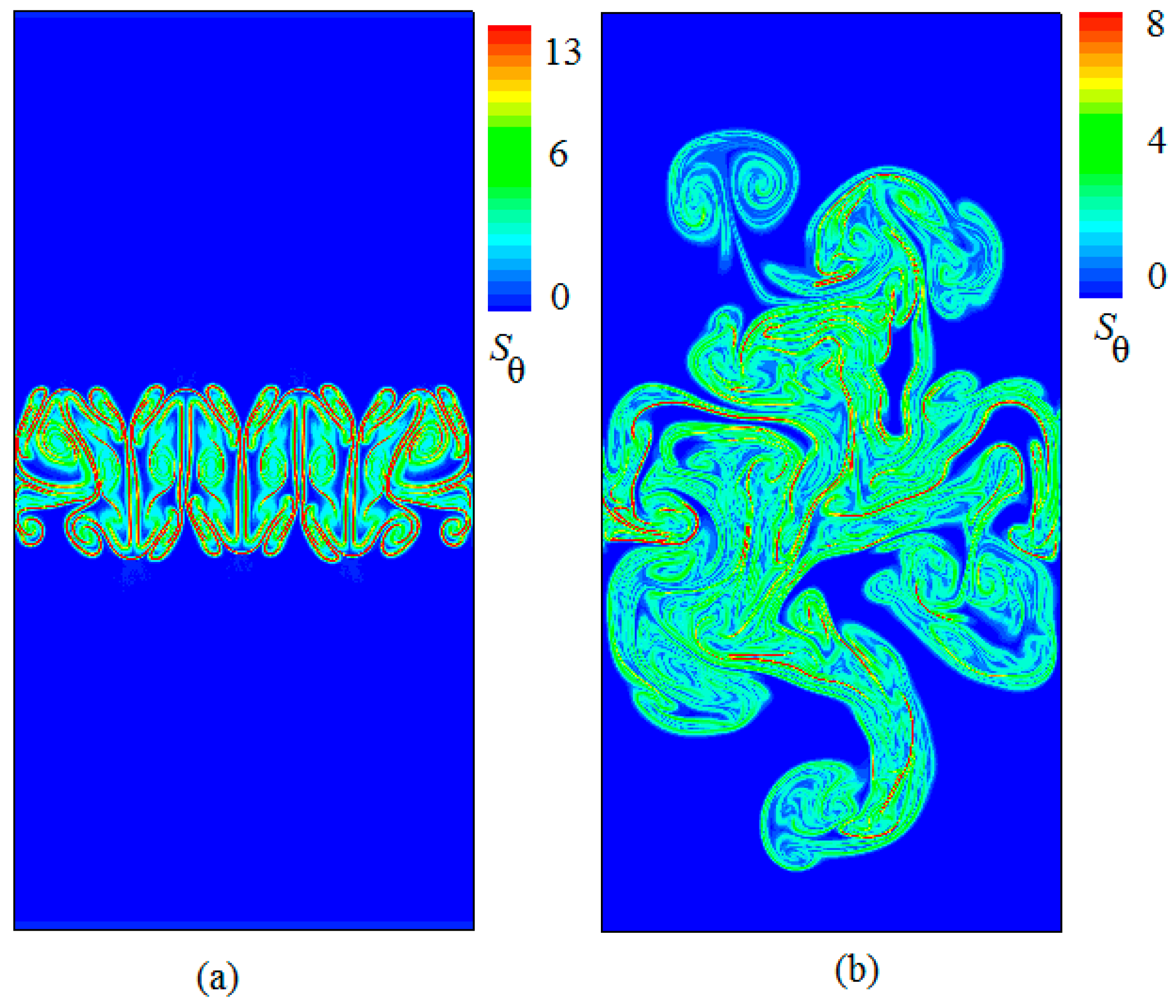
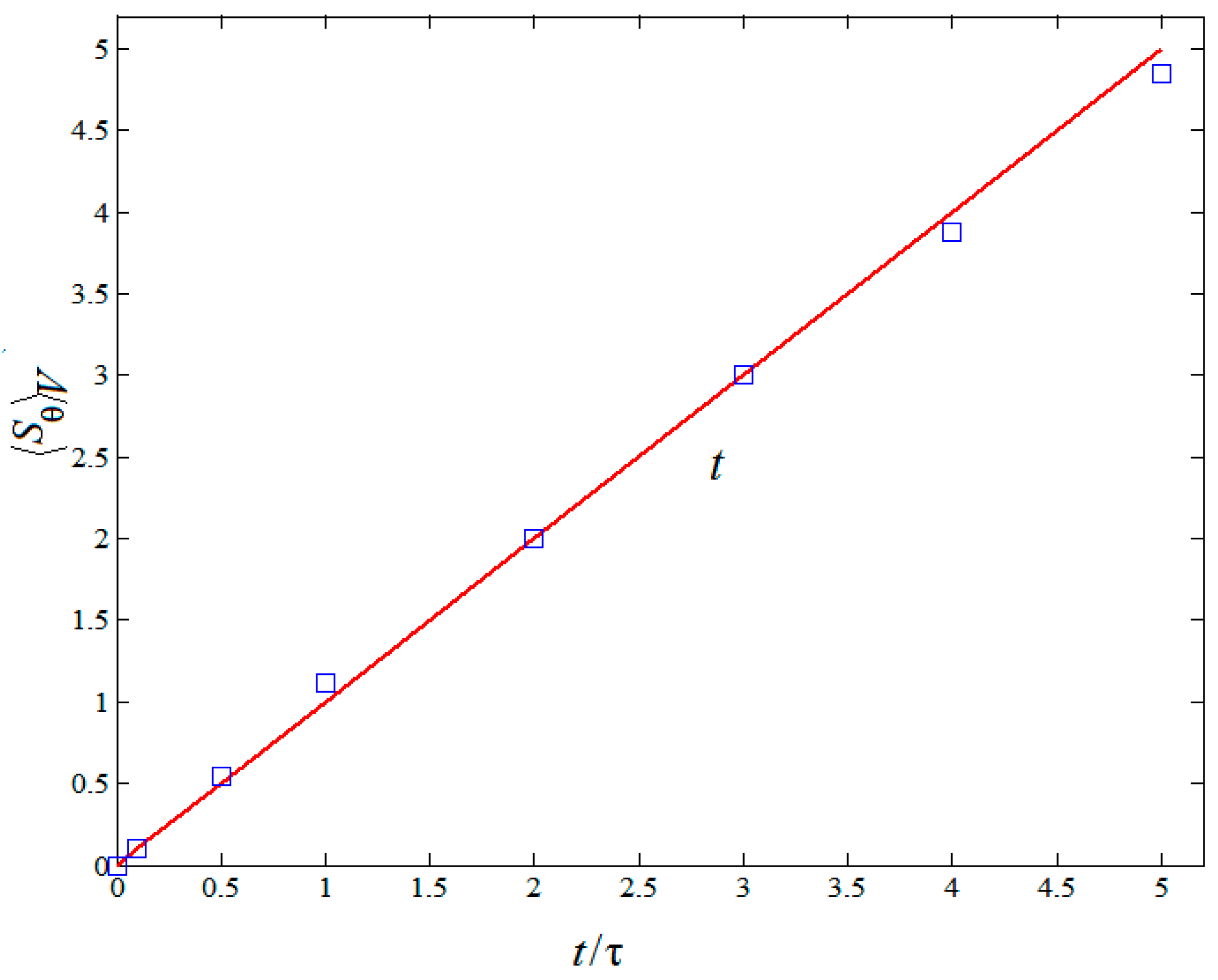
3.1. Analysis of Flow and Temperature Field
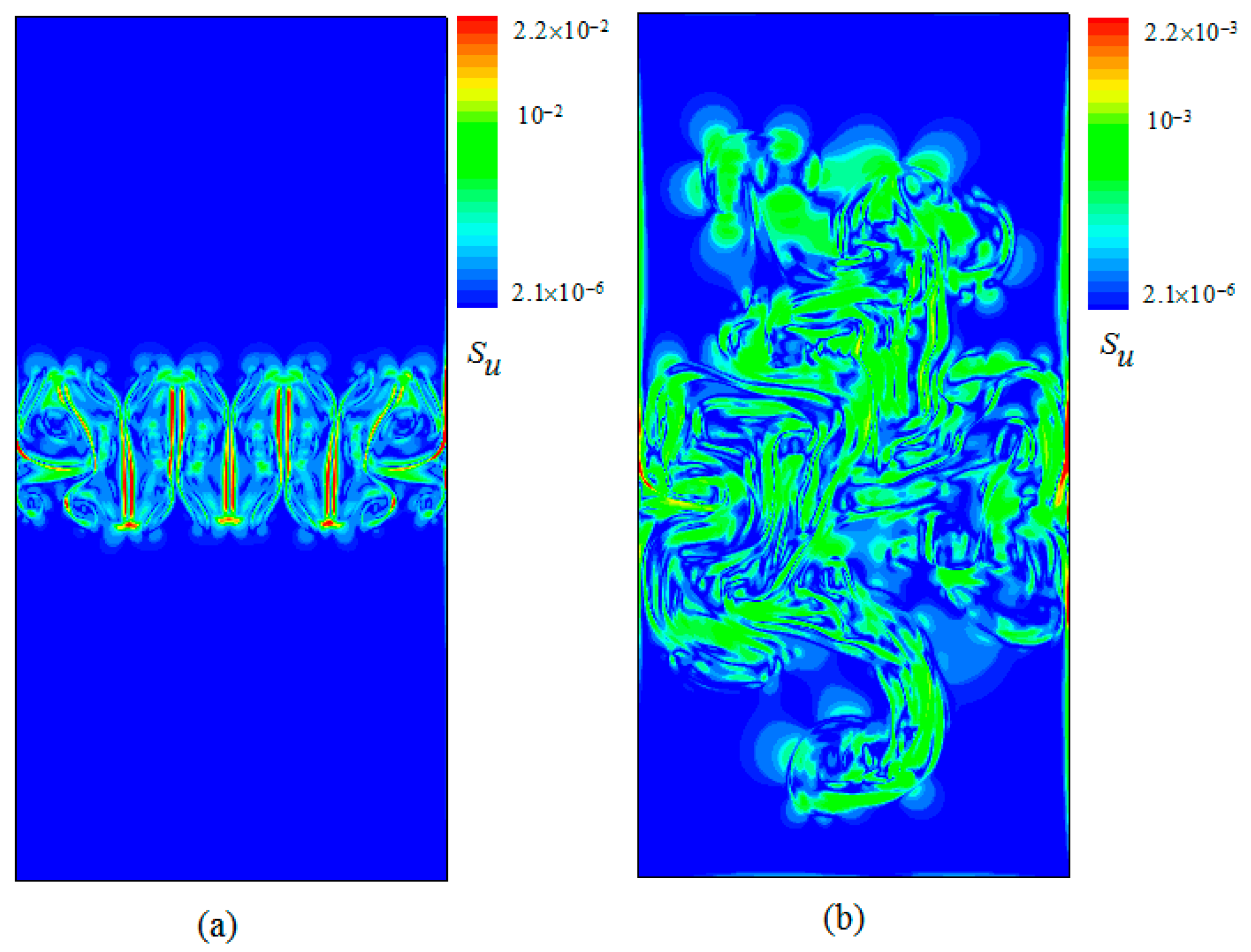
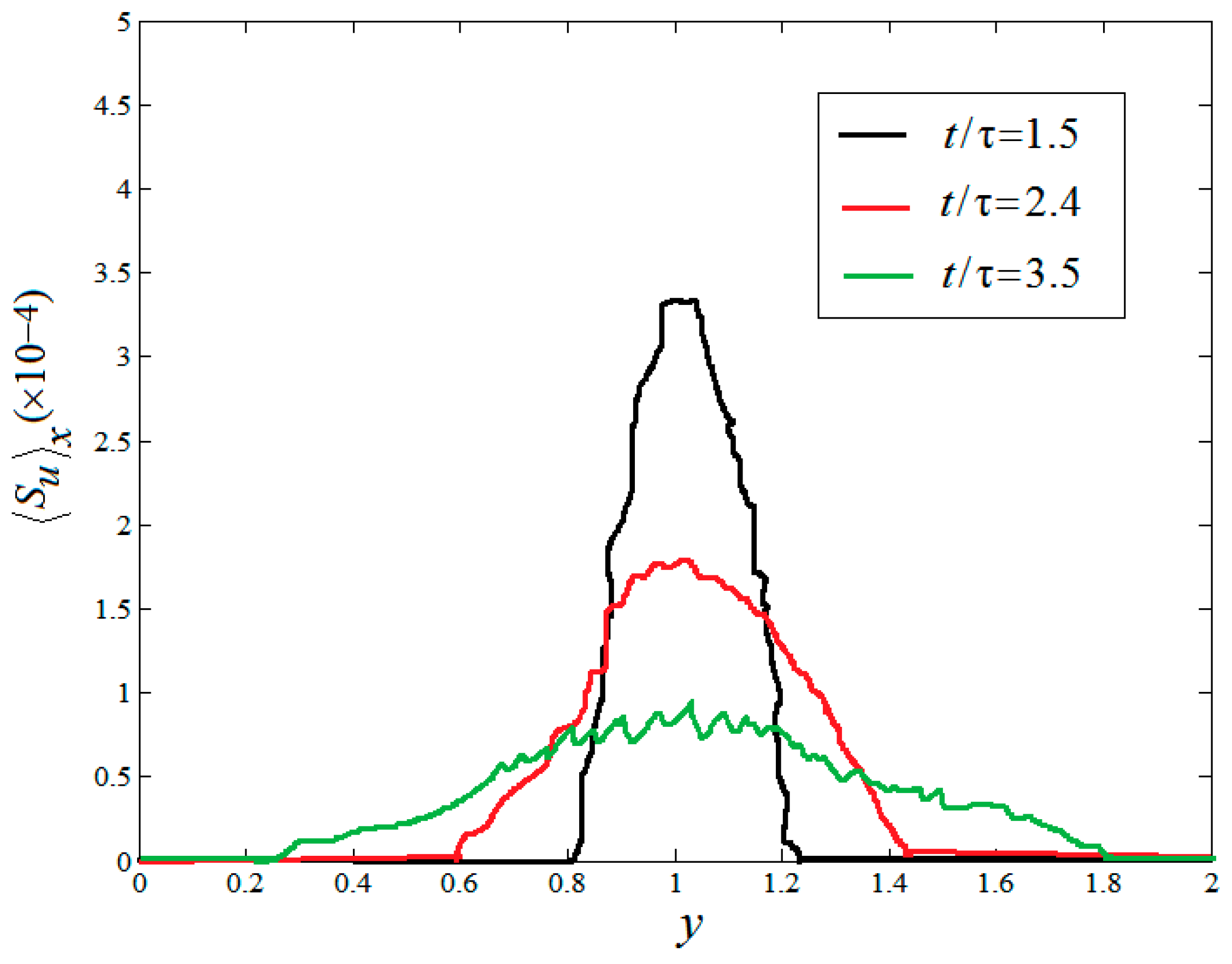
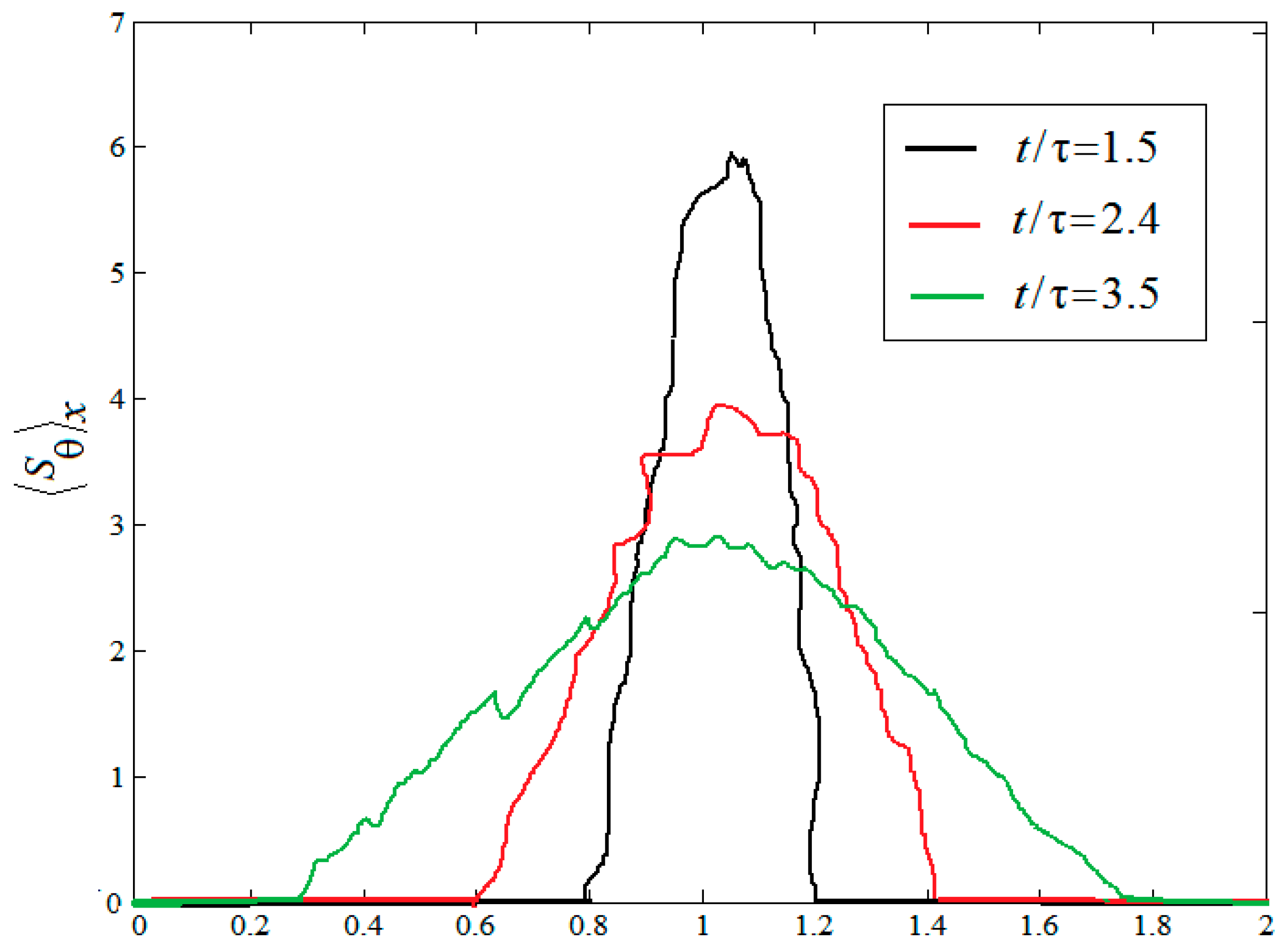
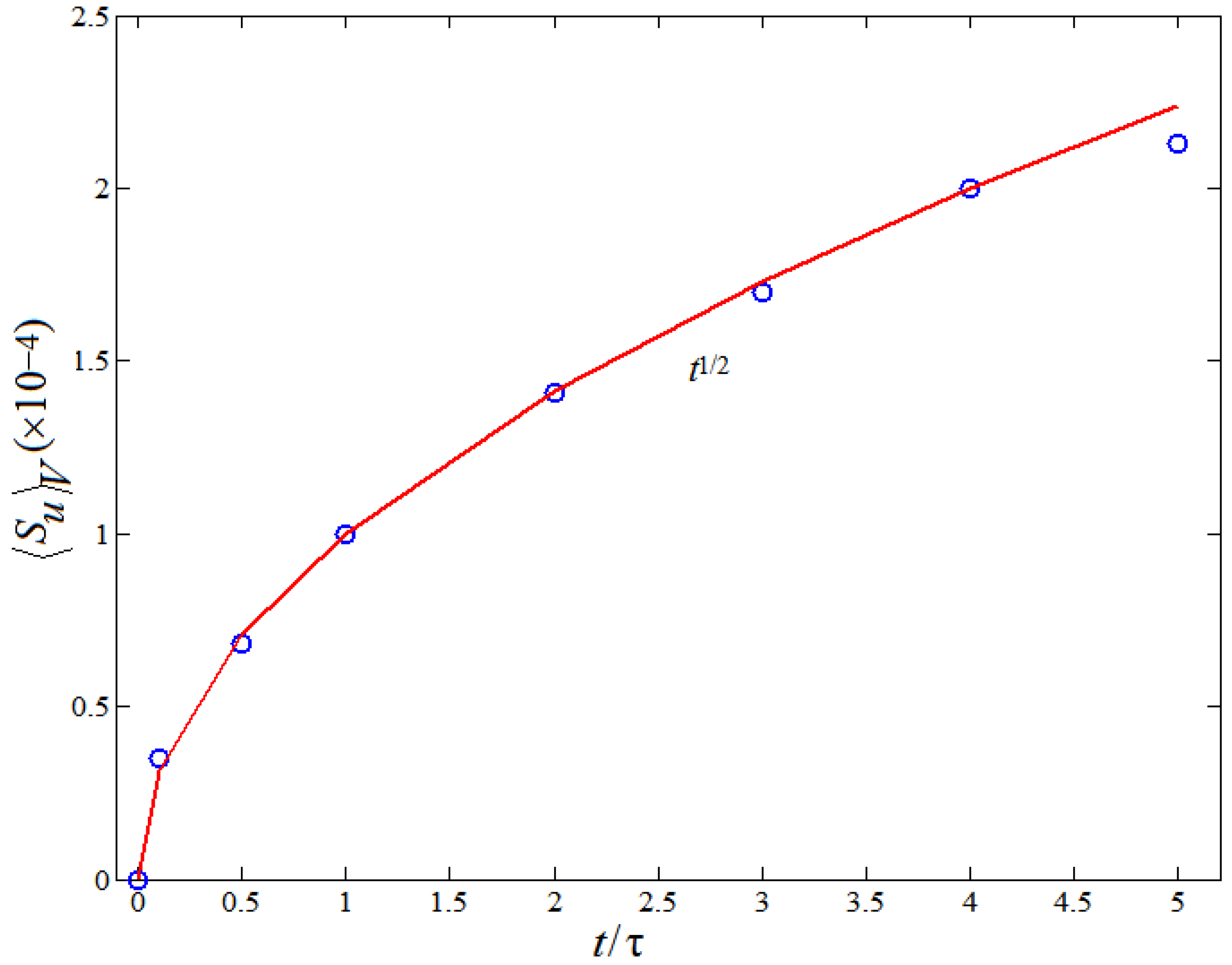
3.2. Analysis of and in RT Turbulence Mixing
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lohse, D.; Xia, K.Q. Small-scale properties of turbulent Rayleigh-Bénard convection. Annu. Rev. Fluid Mech. 2010, 42, 335–364. [Google Scholar] [CrossRef]
- Grea, B.J. The rapid acceleration model and the growth rate of a turbulent mixing zone induced by Rayleigh-Taylor instability. Phys. Fluids 2013, 25, 015118. [Google Scholar] [CrossRef]
- Abarzhi, S.I. Review of theoretical modelling approaches of Rayleigh–Taylor instabilities and turbulent mixing. Philos. Trans. R. Soc. A 2010, 368, 1809–1828. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Q.; Jiang, L.F. Kinetic and thermal energy dissipation rates in two-dimensional Rayleigh-Taylor turbulence. Phys. Fluids 2016, 28, 045109. [Google Scholar] [CrossRef]
- Zhou, Y. A scaling analysis of turbulent flows driven by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Phys. Fluids 2001, 13, 538–543. [Google Scholar] [CrossRef]
- Abarzhi, S.I. On fundamentals of Rayleigh-Taylor turbulent mixing. Europhys. Lett. 2010, 91, 35001–35006. [Google Scholar] [CrossRef]
- Rejane, D.C.; Mario, H.; Copetti, J.B. Entropy generation and natural convection in rectangular cavities. Appl. Ther. Eng. 2009, 29, 1417–1425. [Google Scholar]
- Sheremet, M.A.; Oztop, H.F.; Pop, I.; Hamdeh, N.A. Analysis of entropy generation in natural convection of nanofluid inside a square cavity having hot solid block: Tiwari and Das’ model. Entropy 2016, 18, 9. [Google Scholar] [CrossRef]
- Qing, J.; Bhatti, M.M.; Abbas, M.A.; Rashidi, M.M.; Ali, M.S. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface. Entropy 2016, 18, 123. [Google Scholar] [CrossRef]
- Abbas, M.A.; Bai, Y.; Rashidi, M.M.; Bhatti, M.M. Analysis of entropy generation in the flow of peristaltic nanofluids in channels with compliant walls. Entropy 2016, 18, 90. [Google Scholar] [CrossRef]
- Yang, H.; Wei, Y.K.; Zhu, Z.C.; Dou, H.S. Statistics of Heat Transfer in Two-Dimensional Turbulent Rayleigh-Bénard Convection at Various Prandtl Number. Entropy 2018, 20, 582. [Google Scholar] [CrossRef]
- Pizzolato, A.; Sciacovelli, A.; Verda, V. Transient local entropy generation analysis for the design improvement of a thermocline thermal energy storage. Appl. Ther. Eng. 2016, 101, 622–629. [Google Scholar] [CrossRef] [Green Version]
- Mahian, O.; Kianifar, A.; Pop, I. A review on entropy generation in nanofluid flow. Int. J. Heat Mass Transf. 2013, 65, 514–532. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M.; Ali, M.E.; Yang, Z.G. Entropy generation on MHD Eyring–Powell nanofluid through a permeable stretching surface. Entropy 2016, 18, 224. [Google Scholar] [CrossRef]
- Bhatti, M.M.; RashidiM, M. Entropy generation with nonlinear thermal radiation in MHD boundary layer flow over a permeable shrinking/stretching sheet: Numerical solution. J. Nanofluids 2016, 5, 543–554. [Google Scholar] [CrossRef]
- Zahmatkesh, I. On the importance of thermal boundary conditions in heat transfer and entropy generation for natural convection inside a porous enclosure. Int. J. Therm. Sci. 2008, 47, 339–346. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Natural convection and entropy generation of nanofluid filled cavity having different shaped obstacles under the influence of magnetic field and internal heat generation. J. Taiwan Inst. Chem. Eng. 2015, 56, 42–56. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Verda, V.; Sciubba, E. Entropy generation analysis as a design tool—A review. Renew. Sustain. Energy Rev. 2015, 43, 1167–1181. [Google Scholar] [CrossRef]
- Wei, Y.K.; Wang, Z.D.; Qian, Y.H. A numerical study on entropy generation in two-dimensional Rayleigh-Bénard convection at different Prandtl number. Entropy 2017, 19, 443. [Google Scholar] [CrossRef]
- Wang, Z.D.; Wei, Y.K.; Qian, Y.H. Numerical study on entropy generation in thermal convection with differentially discrete heat boundary conditions. Entropy 2018, 20, 351. [Google Scholar] [CrossRef]
- Jin, Y. Second-law analysis: A powerful tool for analyzing Computational Fluid Dynamics results. Entropy 2017, 19, 679. [Google Scholar] [CrossRef]
- Liu, H.H.; ValocchA, J.; Zhang, Y.H.; Kang, Q.J. Lattice Boltzmann phase-field modeling of thermocapillary flows in a confined microchannel. J. Comput. Phys. 2014, 256, 334–356. [Google Scholar] [CrossRef] [Green Version]
- Shan, X. Simulation of Rayleigh-Bénard convection using a lattice Boltzmann method. Phys. Rev. E 1997, 55, 2780–2788. [Google Scholar] [CrossRef] [Green Version]
- Liang, H.; Shi, B.C.; Chai, Z.H. An efficient phase-field-based multiple-relaxation-time lattice Boltzmann model for three-dimensional multiphase flows. Comput. Math. Appl. 2017, 73, 1524–1538. [Google Scholar] [CrossRef]
- Wei, Y.K.; Wang, Z.D.; Yang, J.F.; Dou, H.S.; Qian, Y.H. Simulations of natural convection heat transfer in an enclosure at different Rayleigh number using lattice Boltzmann method. Comput. Fluids 2016, 124, 30–38. [Google Scholar] [CrossRef]
- Wei, Y.K.; Wang, Z.D.; Dou, H.S.; Qian, Y.H. A novel two-dimensional coupled lattice Boltzmann model for incompressible flow in application of turbulence Rayleigh–Taylor instability. Comput. Fluids 2017, 156, 97–102. [Google Scholar] [CrossRef]
- Chen, S.Y.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Liang, H.; Shi, B.C.; Chai, Z.H. Lattice Boltzmann simulation of three-dimensional Rayleigh-Taylor instability. Phys. Rev. E 2016, 93, 033113. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.H.; D’Humieres, D.; Lallemand, P. Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Xu, H.; Malaspinas, O.; Sagaut, P. Sensitivity analysis and determination of free relaxation parameters for the weakly-compressible MRT–LBM schemes. J. Comput. Phys. 2012, 231, 7335–7367. [Google Scholar] [CrossRef] [Green Version]
- Xu, H.; Sagaut, P. Optimal low-dispersion low-dissipation LBM schemes for computational aeroacoustics. J. Comput. Phys. 2011, 230, 5353–5382. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.W.; Hu, X.Q.; Lei, X.C. Adaptive operation strategy for voltage stability enhancement in active DMFCs. Energy Convers. Manag. 2018, 168, 11–20. [Google Scholar] [CrossRef] [Green Version]
| Mesh | 500 × 1000 | 1000 × 2000 | 2056 × 4112 | 2200 × 4400 | (Nu-Ra) Theoretical Value [4] |
|---|---|---|---|---|---|
| Nu | 96,573.33 | 98,089.26 | 98,993.76 | 98,993.75 | 98,994.95 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; He, H.; Xu, J.; Wei, Y.; Zhang, H. Entropy Generation Rates in Two-Dimensional Rayleigh–Taylor Turbulence Mixing. Entropy 2018, 20, 738. https://doi.org/10.3390/e20100738
Yang X, He H, Xu J, Wei Y, Zhang H. Entropy Generation Rates in Two-Dimensional Rayleigh–Taylor Turbulence Mixing. Entropy. 2018; 20(10):738. https://doi.org/10.3390/e20100738
Chicago/Turabian StyleYang, Xinyu, Haijiang He, Jun Xu, Yikun Wei, and Hua Zhang. 2018. "Entropy Generation Rates in Two-Dimensional Rayleigh–Taylor Turbulence Mixing" Entropy 20, no. 10: 738. https://doi.org/10.3390/e20100738
APA StyleYang, X., He, H., Xu, J., Wei, Y., & Zhang, H. (2018). Entropy Generation Rates in Two-Dimensional Rayleigh–Taylor Turbulence Mixing. Entropy, 20(10), 738. https://doi.org/10.3390/e20100738




