The Stochastic Complexity of Spin Models: Are Pairwise Models Really Simple?
Abstract
1. Introduction
1.1. The Exponential Family of Spin Models (With Interactions of Arbitrary Order)
1.2. Stochastic Complexity
2. Results
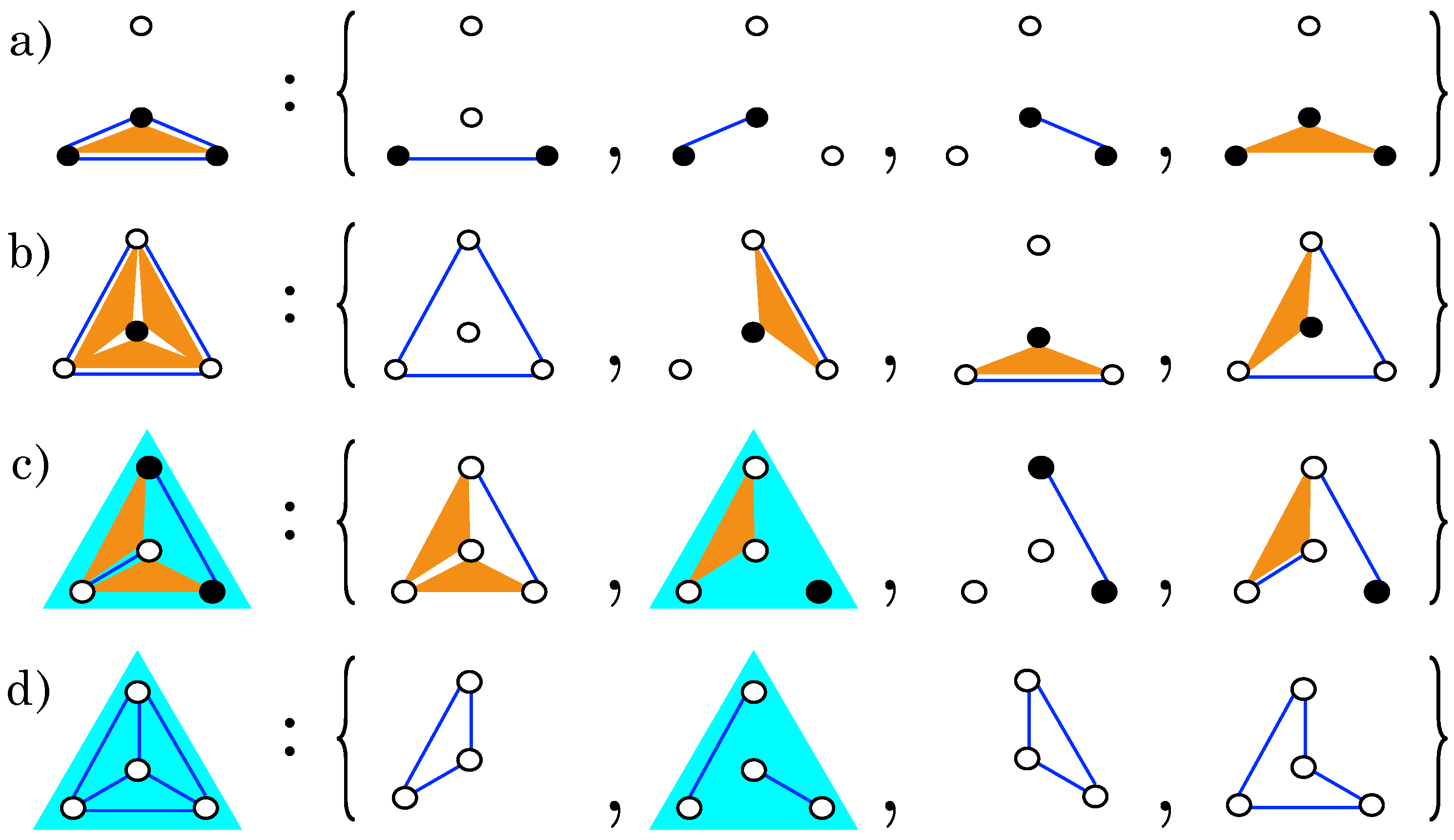
2.1. Gauge Transformations
2.2. Complexity Classes
3. Discussion: How Do Simple Models Look Like?
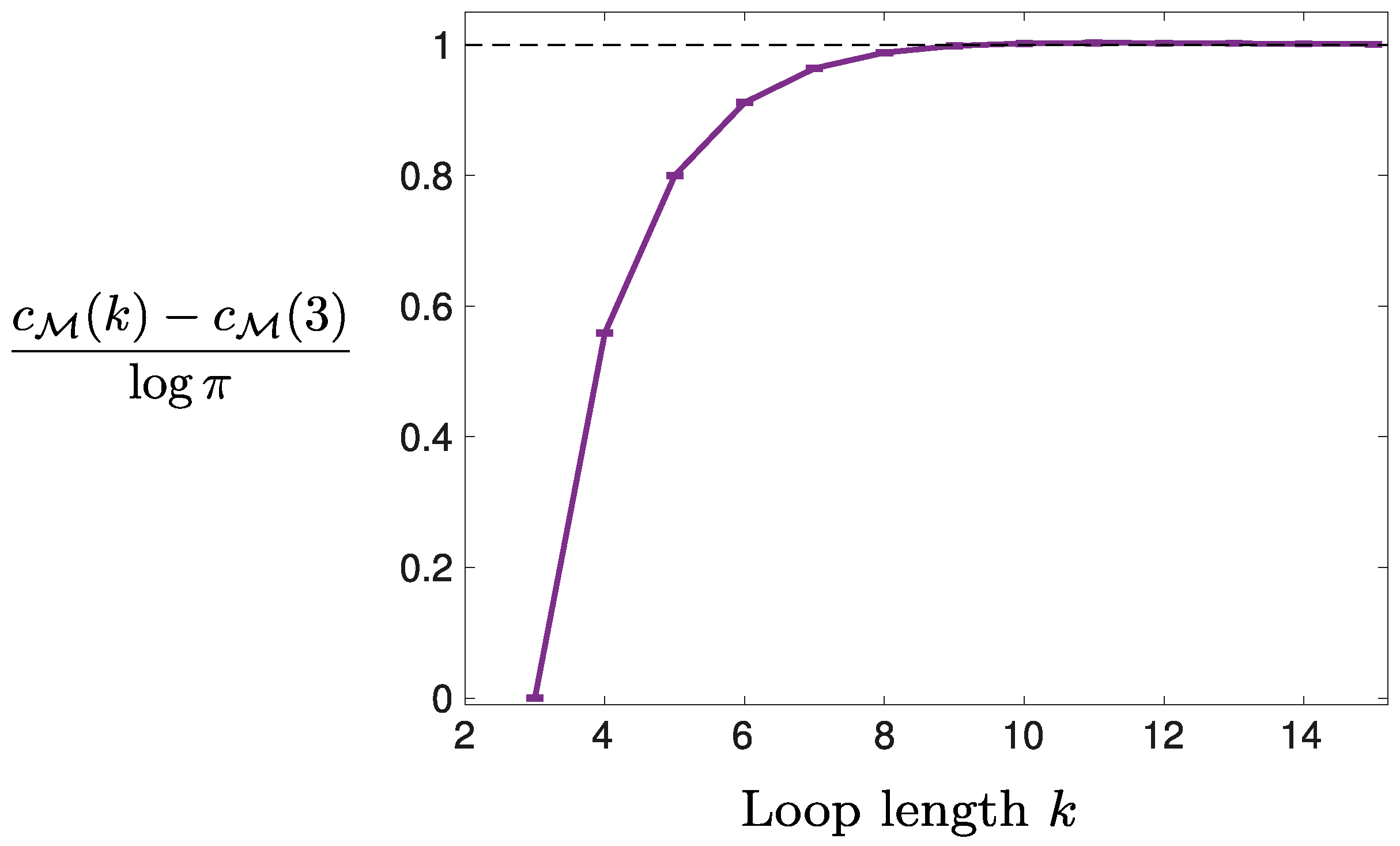
3.1. Fewer Independent Operators, Shorter Loops
3.2. Complete and Sub-Complete Models
3.3. Maximally Overlapping Loops
3.4. Summary
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References and Notes
- Mayer-Schonberger, V.; Cukier, K. Big Data: A Revolution That Will Transform How We Live, Work and Think; John Murray Publishers: London, UK, 2013. [Google Scholar]
- Anderson, C. The End of Theory: The Data Deluge Makes the Scientific Method Obsolete, 2008. Wired. Available online: https://www.wired.com/2008/06/pb-theory/ (accessed on 20 September 2018).
- Cristianini, N. Are we there yet? Neural Netw. 2010, 23, 466–470. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Kavukcuoglu, K.; Farabet, C. Convolutional networks and applications in vision. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems, Paris, France, 30 May–2 June 2010; pp. 253–256. [Google Scholar]
- Hannun, A.; Case, C.; Casper, J.; Catanzaro, B.; Diamos, G.; Elsen, E.; Prenge, R.; Satheesh, S.; Sengupta, S.; Coates, A.; Ng, A. Deep Speech: Scaling up end-to-end speech recognition. arXiv, 2014; arXiv:cs.CL/1412.5567. [Google Scholar]
- Bishop, C. Pattern Recognition and Machine Learning; (Information Science and Statistics); Springer-Verlag: New York, NY, USA, 2006. [Google Scholar]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 20 September 2018).
- Popper, K. The Logic of Scientific Discovery (Routledge Classics); Taylor & Francis: London, UK, 2002. [Google Scholar]
- Chater, N.; Vitányi, P. Simplicity: A unifying principle in cognitive science? Trends Cogn. Sci. 2003, 7, 19–22. [Google Scholar] [CrossRef]
- Rissanen, J. Stochastic complexity in learning. J. Comput. Syst. Sci. 1997, 55, 89–95. [Google Scholar] [CrossRef]
- Rissanen, J. Modeling by shortest data description. Automatic 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Grünwald, P. The Minimum Description Length Principle; (Adaptive Computation and Machine Learning); MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Chau Nguyen, H.; Zecchina, R.; Berg, J. Inverse statistical problems: From the inverse Ising problem to data science. arXiv, 2017; arXiv:cond-mat.dis-nn/1702.01522. [Google Scholar]
- Margolin, A.; Wang, K.; Califano, A.; Nemenman, I. Multivariate dependence and genetic networks inference. IET Syst. Biol. 2010, 4, 428–440. [Google Scholar] [CrossRef] [PubMed]
- Merchan, L.; Nemenman, I. On the Sufficiency of Pairwise Interactions in Maximum Entropy Models of Networks. J. Stat. Phys. 2016, 162, 1294–1308. [Google Scholar] [CrossRef]
- Ravikumar, P.; Wainwright, M.J.; Lafferty, J.D. High-dimensional Ising model selection using ℓ1-regularized logistic regression. Ann. Stat. 2010, 38, 1287–1319. [Google Scholar] [CrossRef]
- Bulso, N.; Marsili, M.; Roudi, Y. Sparse model selection in the highly under-sampled regime. J. Stat. Mech. Theor. Exp. 2016, 2016, 093404. [Google Scholar] [CrossRef]
- Balasubramanian, V. Statistical inference, Occam’s razor, and statistical mechanics on the space of probability distributions. Neural Comput. 1997, 9, 349–368. [Google Scholar] [CrossRef]
- There is a broader class of models, where subsets ⊆ of operators have the same parameter, i.e., gμ = g for all μ ∈ or gμ are subject to linear constrains. These degenerate models are rarely considered in the inference literature. Here we confine our discussion to non-degenerate models and refer the reader to Section SM-7 of the Supplementary Material for more discussion.
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Tikochinsky, Y.; Tishby, N.Z.; Levine, R.D. Alternative approach to maximum-entropy inference. Phys. Rev. A 1984, 30, 2638–2644. [Google Scholar] [CrossRef]
- Rissanen, J.J. Fisher information and stochastic complexity. IEEE Trans. Inf. Theory 1996, 42, 40–47. [Google Scholar] [CrossRef]
- Rissanen, J. Strong optimality of the normalized ML models as universal codes and information in data. IEEE Trans. Inf. Theo. 2001, 47, 1712–1717. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Myung, I.J.; Balasubramanian, V.; Pitt, M.A. Counting probability distributions: Differential geometry and model selection. Proc. Natl. Acad. Sci. USA 2000, 97, 11170–11175. [Google Scholar] [CrossRef] [PubMed]
- Jeffreys, H. An Invariant Form for the Prior Probability in Estimation Problems. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1946, 186, 453–461. [Google Scholar] [CrossRef]
- Amari, S. Information Geometry and Its Applications; (Applied Mathematical Sciences); Springer: Tokyo, Japan, 2016. [Google Scholar]
- Kass, R.E.; Wasserman, L. The selection of prior distributions by formal rules. J. Am. Stat. Assoc. 1996, 91, 1343–1370. [Google Scholar] [CrossRef]
- A simplicial complex [31], in our notation, is a model such that, for any interaction μ ∈ , any interaction that involves any subset ν ⊆ μ of spins is also contained in the model (i.e., ν ∈ ).
- Courtney, O.T.; Bianconi, G. Generalized network structures: The configuration model and the canonical ensemble of simplicial complexes. Phys. Rev. E 2016, 93, 062311. [Google Scholar] [CrossRef] [PubMed]
- Landau, L.; Lifshitz, E. Statistical Physics, 3rd ed.; Elsevier Science: London, UK, 2013. [Google Scholar]
- Kramers, H.A.; Wannier, G.H. Statistics of the Two-Dimensional Ferromagnet. Part II. Phys. Rev. 1941, 60, 263–276. [Google Scholar] [CrossRef]
- Pelizzola, A. Cluster variation method in statistical Physics and probabilistic graphical models. J. Phys. A Math. Gen. 2005, 38, R309–R339. [Google Scholar] [CrossRef]
- The symmetric difference of two sets ℓ1 and ℓ2 is defined as the set that contains the elements that occur in ℓ1 but not in ℓ2 and viceversa: ℓ1 ⊕ ℓ2 = (ℓ1 ∪ ℓ2) \ (ℓ1 ∩ ℓ2). It corresponds to the XOR operator between the operators of the two loops.
- Amari, S.; Nagaoka, H. Methods of Information Geometry; (Translations of mathematical monographs); American Mathematical Society: Providence, RI, USA, 2007. [Google Scholar]
- Wainwright, M.J.; Jordan, M.I. Graphical Models, Exponential Families, and Variational Inference. Found. Trends® Mach. Learn. 2008, 1, 1–305. [Google Scholar] [CrossRef]
- Wainwright, M.J.; Jordan, M.I. Variational inference in graphical models: The view from the marginal polytope. In Proceedings of the Forty-First Annual Allerton Conference on Communication, Control, and Computing, Monticello, NY, USA, 1–3 October 2003; Volume 41, pp. 961–971. [Google Scholar]
- Mastromatteo, I. On the typical properties of inverse problems in statistical mechanics. arXiv, 2013; arXiv:cond-mat.stat-mech/1311.0190. [Google Scholar]
- In information geometry [28,36], a model defines a manifold in the space of probability distributions. For exponential models (1), the natural metric, in the coordinates gμ, is given by the Fisher Information (5), and the stochastic complexity (4) is the volume of the manifold [26].
- Gresele, L.; Marsili, M. On maximum entropy and inference. Entropy 2017, 19, 642. [Google Scholar] [CrossRef]
- Wigner, E.P. The unreasonable effectiveness of mathematics in the natural sciences. Commun. Pure Appl. Math. 1960, 13, 1–14. [Google Scholar] [CrossRef]
- In his response to Reference [2] on edge.org, W.D. Willis observes that “Models are interesting precisely because they can take us beyond the data”.
- Schneidman, E.; Berry, M.J., II; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.; Broedersz, C.; Bialek, W. Statistical mechanics of the US Supreme Court. J. Stat. Phys. 2015, 160, 275–301. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
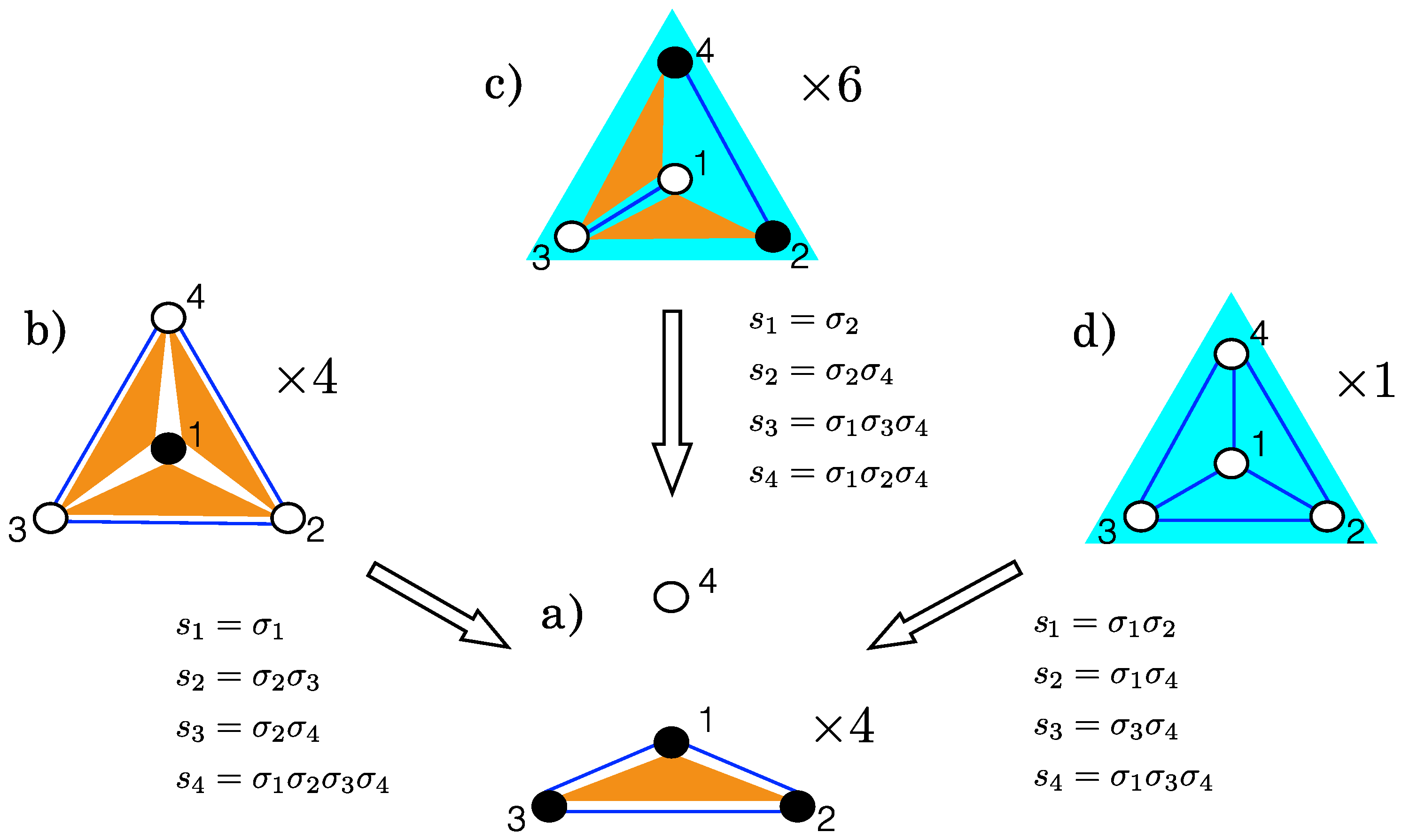

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beretta, A.; Battistin, C.; De Mulatier, C.; Mastromatteo, I.; Marsili, M. The Stochastic Complexity of Spin Models: Are Pairwise Models Really Simple? Entropy 2018, 20, 739. https://doi.org/10.3390/e20100739
Beretta A, Battistin C, De Mulatier C, Mastromatteo I, Marsili M. The Stochastic Complexity of Spin Models: Are Pairwise Models Really Simple? Entropy. 2018; 20(10):739. https://doi.org/10.3390/e20100739
Chicago/Turabian StyleBeretta, Alberto, Claudia Battistin, Clélia De Mulatier, Iacopo Mastromatteo, and Matteo Marsili. 2018. "The Stochastic Complexity of Spin Models: Are Pairwise Models Really Simple?" Entropy 20, no. 10: 739. https://doi.org/10.3390/e20100739
APA StyleBeretta, A., Battistin, C., De Mulatier, C., Mastromatteo, I., & Marsili, M. (2018). The Stochastic Complexity of Spin Models: Are Pairwise Models Really Simple? Entropy, 20(10), 739. https://doi.org/10.3390/e20100739




