Analytic Study of Complex Fractional Tsallis’ Entropy with Applications in CNNs
Abstract
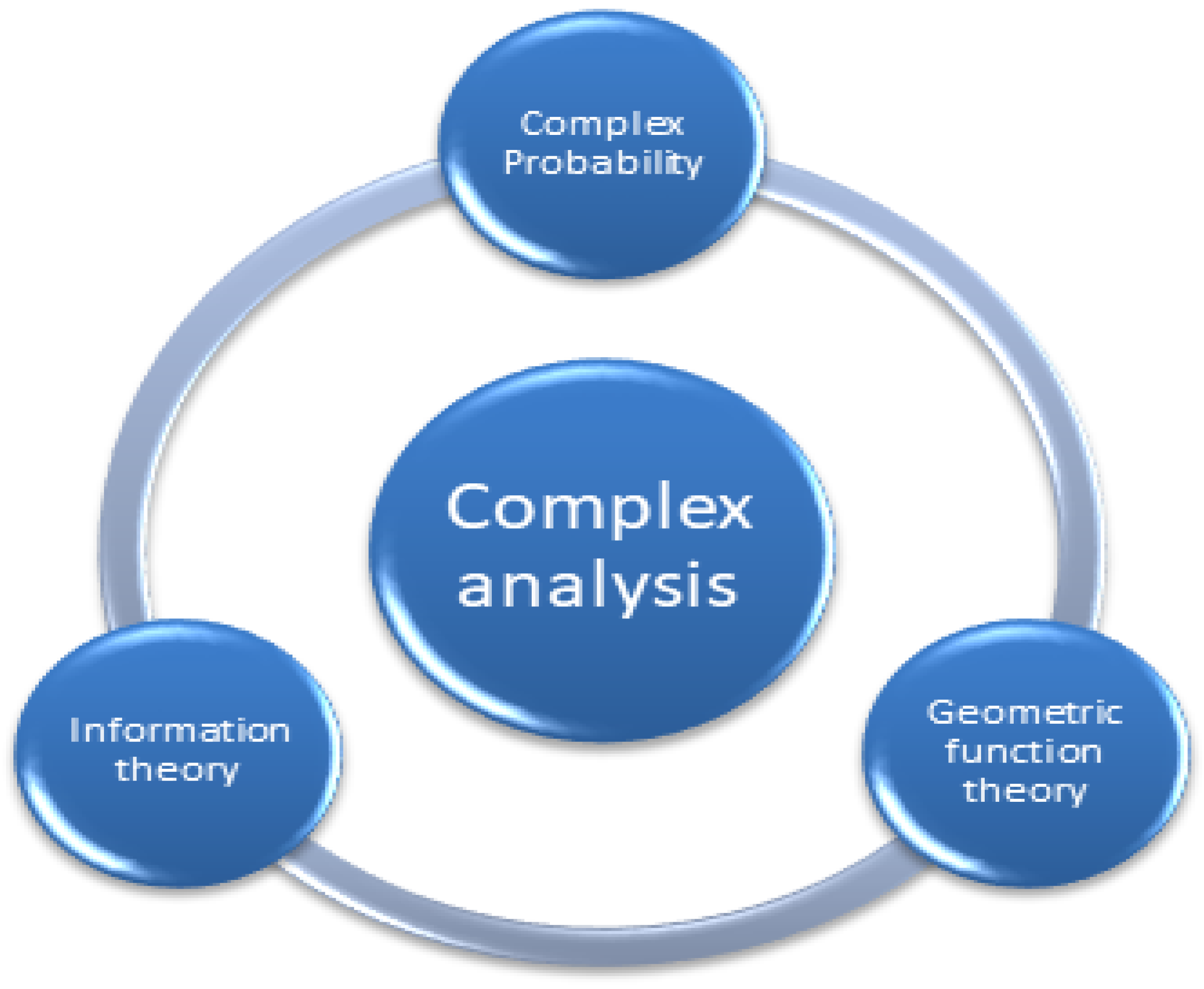
1. Introduction
2. Results
2.1. Bernoulli Function
2.2. Gaussian Function
2.3. Fractional Sigmoid Function FSF
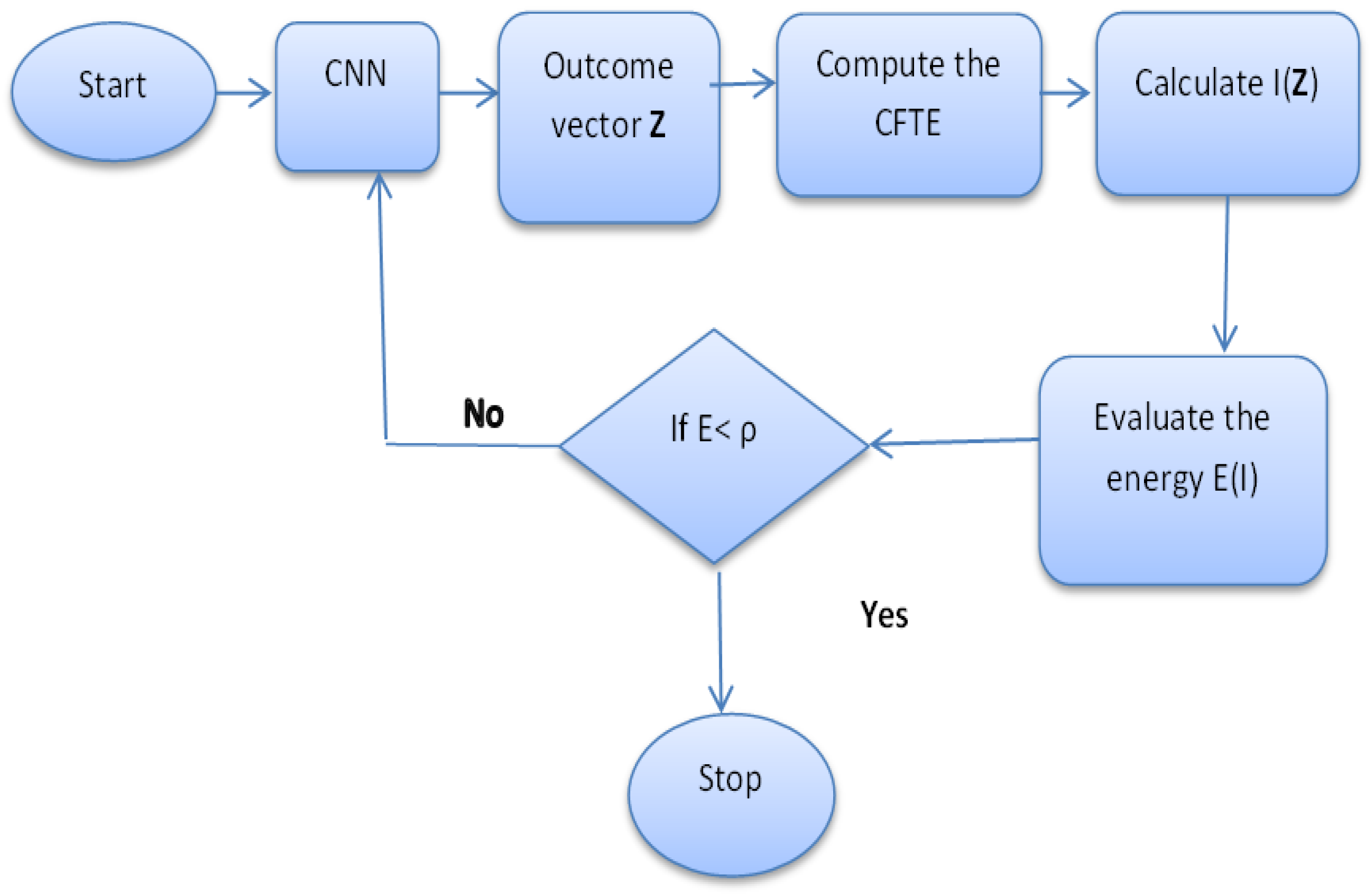
3. Complex-Valued Neural Networks
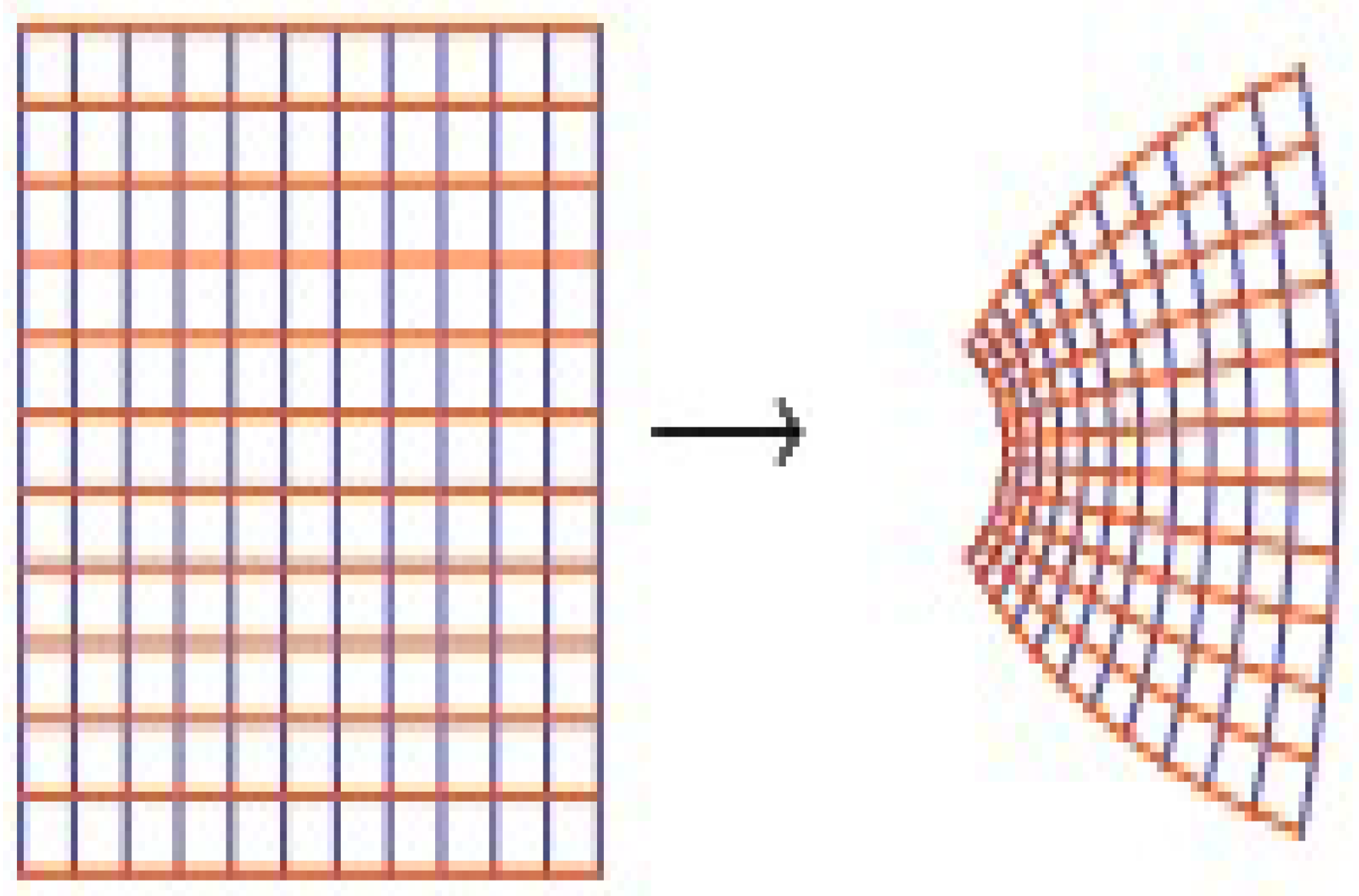
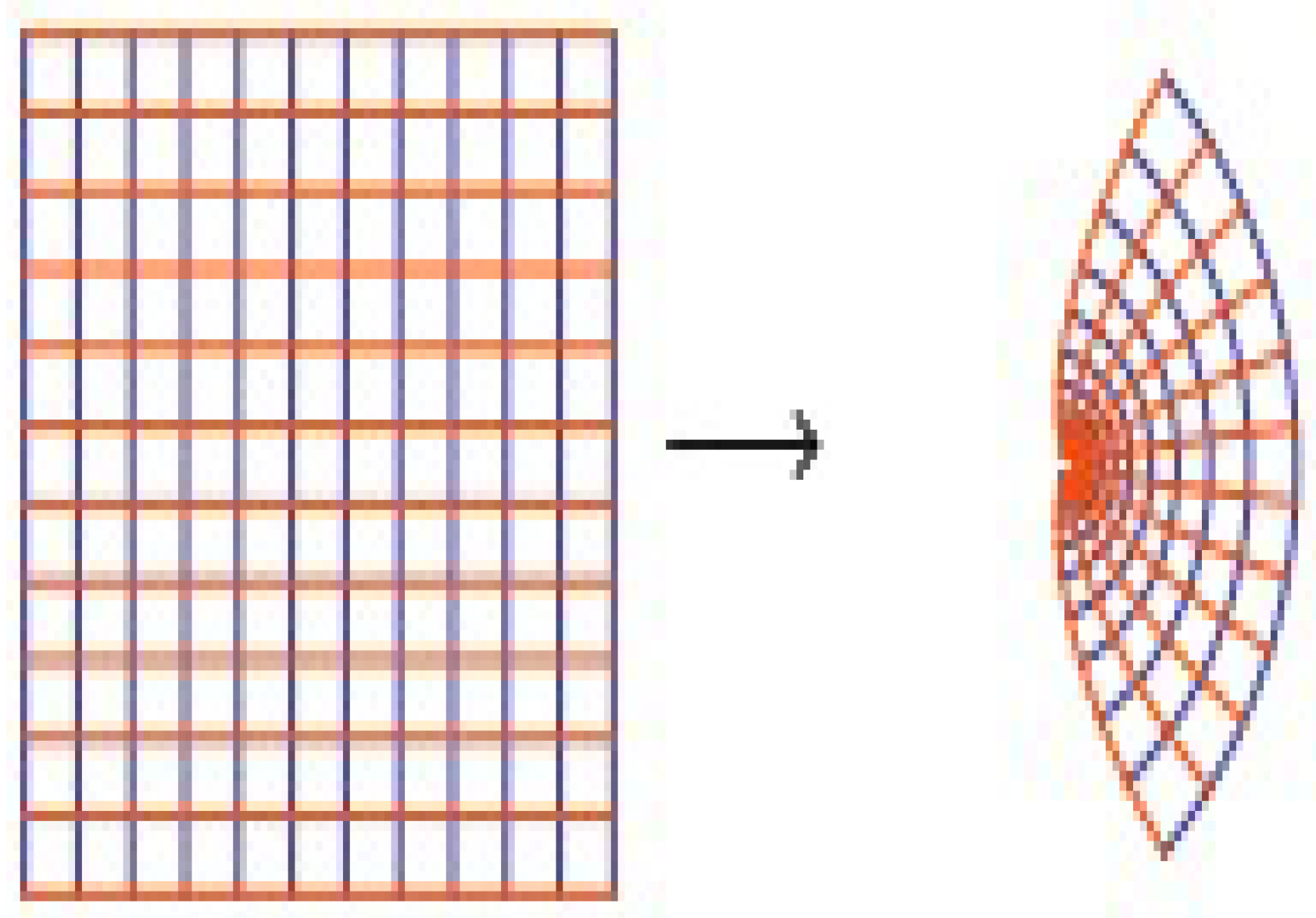
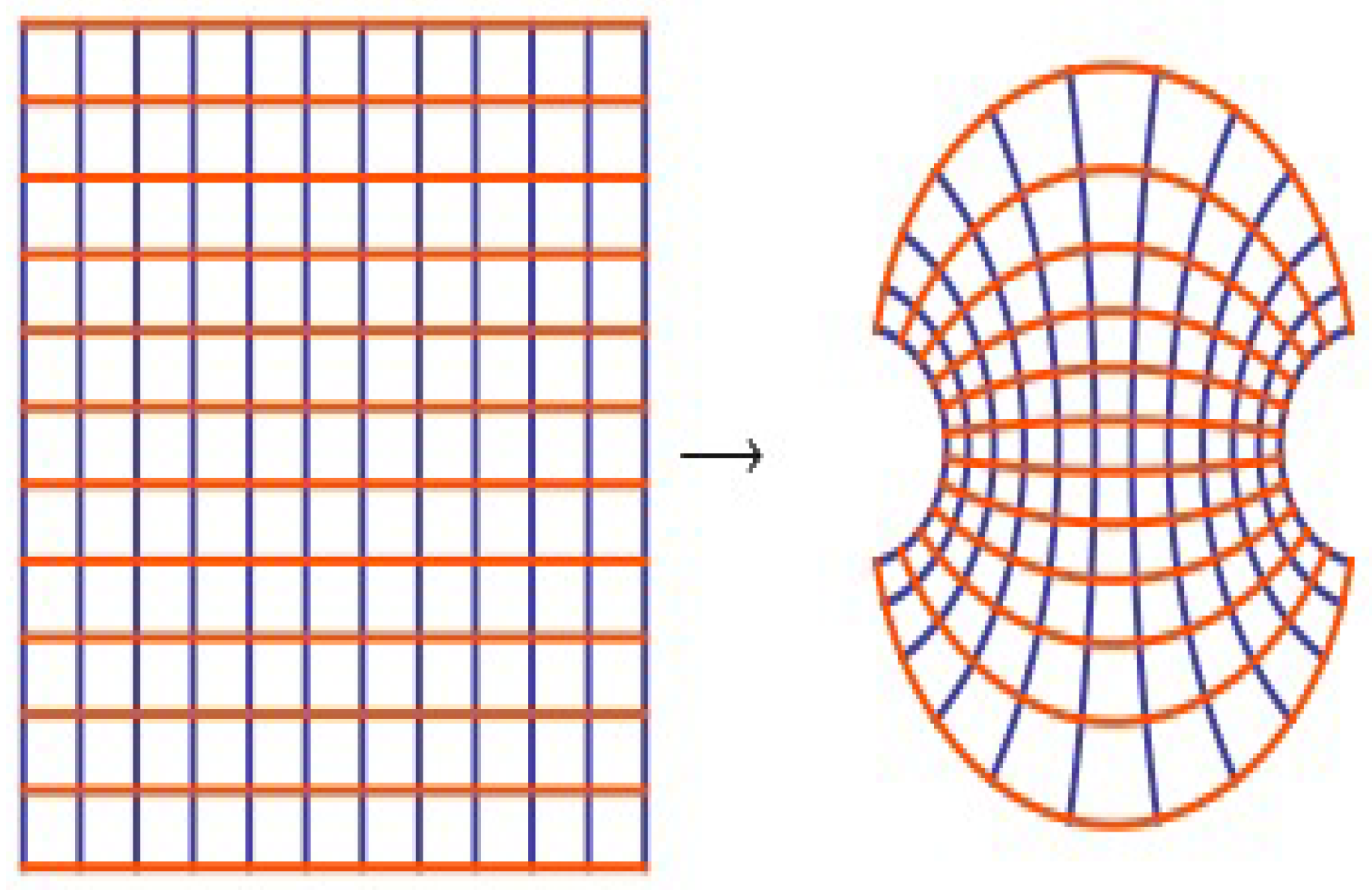
Numerical Examples
4. Discussion
- Equation (10) refers to the amount of information in the complex system, which is given in the CNN. The advantage is that CNN does not depend on the number of neurons to get full training of the system (see [11,12,13,14,15,26]). Furthermore, the complex value of the output converges to the stability state faster than the real value. All the complex value outputs are given in the open unit disk where (see [16]). In this case, we may use the properties of geometry function theory (GFT). For example, the sigmoid function of the complex value is studied widely in view of GFT. The convexity and other geometric representations of this function have been studied by many authors (see [27]).
- The parameter from is: the simplest non-trivial perturbation of any unperturbed complex system; the complex system (CNN) in which obvious necessary and sufficient conditions are recognized for a small divisor problem is stable.
- The output may cause a complex-valued function incited by the set In this situation, the stability comes from the first derivative of with respect to z. This type of stability is called Lyapunov stability. At a fixed point :At a periodic point of period ℘, the first derivative of a function:is usually given by and represented by the multiplier or the Lyapunov characteristic number. It applies to checking the stability of periodic points, as well as fixed points ().
- At a non-periodic point, the derivative, can be iterated by:
- The above derivative can be replaced by any derivative for a complex variable such as the Schwarzian derivative. We may suggest this as a future work.
- Derivative with respect to (parametric derivative): This type of derivative is called the distance estimation method. In this case, CNN has one output in the set , and it is fixed. Therefore, we suggest to use the parameter plane collecting information. This occurs as follows: On the parameter plane: is a variable, and is constant. The first derivative of with respect to is given by the relation:This derivative can be defined by the following iteration:and then replacing at every consecutive step:
5. Conclusions and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| parameter | |
| diffusion constant | |
| z | complex number |
| complex probability | |
| real set of events | |
| imaginary set of events | |
| probability in the real set | |
| probability in the imaginary set | |
| U | the open unit disk |
| the degree of our knowledge of the random experiment; it is the square of the norm of z | |
| CFTE | |
| the real part of CFTE | |
| Gaussian function | |
| gamma function | |
| total information | |
| the energy | |
| the upper bound of energy |
References
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. The nonadditive entropy Sq and its applications in physics and elsewhere: Some remarks. Entropy 2011, 13, 1765–1804. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Jalab, H.A. Existence of entropy solutions for nonsymmetric fractional systems. Entropy 2014, 16, 4911–4922. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Jalab, H.A. Existence of Ulam stability for iterative fractional differential equations based on fractional entropy. Entropy 2015, 17, 3172–3181. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Jalab, H.A.; Gani, A. Cloud entropy management system involving a fractional power. Entropy 2015, 18, 14. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Jalab, H.A.; Gani, A. Perturbation of fractional multi-agent systems in cloud entropy computing. Entropy 2016, 18, 31. [Google Scholar] [CrossRef]
- Jalab, H.A.; Ibrahim, R.W.; Amr, A. Image denoising algorithm based on the convolution of fractional Tsallis entropy with the Riesz fractional derivative. Neural Comput. Appl. 2017, 28, 217–223. [Google Scholar] [CrossRef]
- Ibrahim, R.W. The maximum principle of Tsallis entropy in a complex domain. Ital. J. Pure Appl. Math. 2017, 601–606. [Google Scholar]
- Ibrahim, R.W. On new classes of analytic functions imposed via the fractional entropy integral operator. Facta Univ. Ser. Math. Inform. 2017, 32, 293–302. [Google Scholar] [CrossRef]
- Al-Shamasneh, A.A.R.; Jalab, H.A.; Palaiahnakote, S.; Obaidellah, U.H.; Ibrahim, R.W.; El-Melegy, M.T. A new local fractional entropy-based model for kidney MRI image enhancement. Entropy 2018, 20, 344. [Google Scholar] [CrossRef]
- Rubio, J.D.J.; Lughofer, E.; Plamen, A.; Novoa, J.F.; Meda-Campaña, J.A. A novel algorithm for the modeling of complex processes. Kybernetika 2018, 54, 79–95. [Google Scholar] [CrossRef]
- Meda, C.; Jesus, A. On the estimation and control of nonlinear systems with parametric uncertainties and noisy outputs. IEEE Access 2018, 6, 31968–31973. [Google Scholar] [CrossRef]
- Rubio, J. Error convergence analysis of the SUFIN and CSUFIN. Appl. Soft Comput. 2018, in press. [Google Scholar]
- Meda, C.; Jesus, A. Estimation of complex systems with parametric uncertainties using a JSSF heuristically adjusted. IEEE Lat. Am. Trans. 2018, 16, 350–357. [Google Scholar] [CrossRef]
- De Jesús Rubio, J.; Lughofer, E.; Meda-Campaña, J.A.; Páramo, L.A.; Novoa, J.F.; Pacheco, J. Neural network updating via argument Kalman filter for modeling of Takagi-Sugeno fuzzy models. J. Intell. Fuzzy Syst. 2018, 35, 2585–2596. [Google Scholar] [CrossRef]
- Abou Jaoude, A. The paradigm of complex probability and Chebyshev’s inequality. Syst. Sci. Control Eng. 2016, 4, 99–137. [Google Scholar] [CrossRef]
- Youssef, S. Quantum mechanics as Bayesian complex probability theory. Mod. Phys. Lett. A 1994, 9, 2571–2586. [Google Scholar] [CrossRef]
- Abou Jaoude, A. The paradigm of complex probability and Claude Shannon’s information theory. Syst. Sci. Control Eng. 2017, 5, 380–425. [Google Scholar] [CrossRef]
- Abou Jaoude, A.; El-Tawil, K.; Seifedine, K. Prediction in complex dimension using Kolmogorov’s set of axioms. J. Math. Stat. 2010, 6, 116–124. [Google Scholar] [CrossRef]
- Abou Jaoude, A. The complex probability paradigm and analytic linear prognostic for vehicle suspension systems. Am. J. Eng. Appl. Sci. 2015, 8, 147. [Google Scholar] [CrossRef]
- Wilk, G.; Włodarczyk, Z. Tsallis distribution with complex nonextensivity parameter q. Phys. A Stat. Mech. Its Appl. 2014, 413, 53–58. [Google Scholar] [CrossRef]
- Mocanu, P.T. Convexity of some particular functions. Studia Univ. Babes-Bolyai Math. 1984, 29, 70–73. [Google Scholar]
- Ruscheweyh, S. Convolutions in Geometric Function Theory; Presses de l’Université de Montréal: Montréal, QC, Canada, 1982. [Google Scholar]
- Miller, S.S.; Mocanu, P.T. Differential Subordinations: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Kaslik, E.; Ileana, R.R. Dynamics of complex-valued fractional-order neural networks. Neural Netw. 2017, 89, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, R.W. The fractional differential polynomial neural network for approximation of functions. Entropy 2013, 15, 4188–4198. [Google Scholar] [CrossRef]
- Ezeafulukwe, U.A.; Darus, M.; Olubunmi, A. On analytic properties of a sigmoid function. Int. J. Math. Comput. Sci. 2018, 13, 171–178. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, R.W.; Darus, M. Analytic Study of Complex Fractional Tsallis’ Entropy with Applications in CNNs. Entropy 2018, 20, 722. https://doi.org/10.3390/e20100722
Ibrahim RW, Darus M. Analytic Study of Complex Fractional Tsallis’ Entropy with Applications in CNNs. Entropy. 2018; 20(10):722. https://doi.org/10.3390/e20100722
Chicago/Turabian StyleIbrahim, Rabha W., and Maslina Darus. 2018. "Analytic Study of Complex Fractional Tsallis’ Entropy with Applications in CNNs" Entropy 20, no. 10: 722. https://doi.org/10.3390/e20100722
APA StyleIbrahim, R. W., & Darus, M. (2018). Analytic Study of Complex Fractional Tsallis’ Entropy with Applications in CNNs. Entropy, 20(10), 722. https://doi.org/10.3390/e20100722




