1. Introduction
In his book on fractal geometry, Falconer characterizes a set
as a fractal if it has some of the following properties [
1] (p. xxviii):
has a fine structure, i.e., there is detail on arbitrarily small scales
does not admit a description in traditional geometrical language, neither locally nor globally; it is irregular in some sense
has some form of self-similarity, at least approximate or statistical
The fractal dimension of exceeds its topological dimension
is defined in a simple, often recursive way
In this work, we investigate whether polar codes and Reed–Muller are fractal in above sense. For a blocklength of
, these codes are based on the
n-fold Kronecker product
, where
i.e., on a simple, recursive operation. Based on this, it has long been suspected that Kronecker product-based codes possess a fractal nature. For example, the authors of [
2] observed that
, when converted to a picture, resembles the Sierpinski triangle. In a personal communication [
3], Abbe expressed his suspicion that the set of “good” polarized channels is fractal. Nevertheless, to the best of the author’s knowledge, a definite statement regarding this fractal nature has not been presented yet.
A rate-
Kronecker product-based code is uniquely defined by a set
of
K indices: Its generator matrix is the submatrix of
consisting of the rows indexed by
. Letting
index the
K rows of
with the largest Hamming weight defines a Reed–Muller code. Alternatively, one can fix the
order r of a Reed–Muller code, which defines
as the index set of all rows with a Hamming weight at least as large as
r (see
Section 4). For polar codes, the rows of
can be interpreted as a communication channels. Then, a rate-
polar code is defined by the set
indexing the
K channels with the lowest Bhattacharyya parameters [
4] (the “good” channels, see
Section 2).
Although the sets
are important for the construction of polar and Reed–Muller codes, surprisingly little is known about their fractal properties. Recently, Renes, Sutter, and Hassani stated conditions under which the good (bad) channels derived from one binary-input memoryless channel are also good (bad) for another channel [
5]. Moreover, the authors of [
6,
7] observed the self-similar structure of
by showing that polar and Reed–Muller codes are decreasing monomial codes.
In this paper, we analyze the fractal properties of
for polar codes (
Section 3) and Reed–Muller codes (
Section 5). In contrast to [
6,
7], we study the properties of
for infinite blocklengths, i.e., for
. Specifically, we compute the Hausdorff dimension of
, show that it is self-similar, and that it has detail on arbitrarily small scales (e.g.,
is symmetric and dense in some well-defined containing set). Each of these results is relatively easy to obtain once appropriate definitions have been put in place. Taken as a whole, however, they paint an interesting picture and make a convincing point for the claim that polar and Reed–Muller codes are fractal.
The presented results will improve our understanding of polar and Reed–Muller codes, even though we have to admit that their practical implication (e.g., in code construction) still eludes us. Nevertheless, our results may apply in areas beyond channel coding: Arıkan’s polarization technique was used to polarize Rényi information dimension [
8] and to construct high-girth matrices [
9]. Moreover, Nasser showed that a sufficient and necessary condition for a binary operation to be polarizing is that it is uniformity preserving and that its inverse is strongly ergodic [
10,
11]. We are convinced that fractality carries over to these applications as well and that an analysis similar to ours can deepen understanding.
Since we consider the case
, the set
indexes a subset of
, the set of infinite binary sequences. We let
and abbreviate
. Let
where
. Let furthermore
be a probability space with
the Borel field generated by the cylinder sets
and
a probability measure satisfying
. In the following, we represent every infinite binary sequence
by a point in the unit interval
. The mapping between
and
is given by
Lemma 1 ([
12] (Exercises 7–10, p. 80)).
Let be the Borel σ-algebra on and let λ be the Lebesgue measure. Let furthermore denote the set of dyadic rationals in the unit interval. Then, the function in (
2)
satisfies the following properties:- 1.
f is measurable
- 2.
f is bijective on
- 3.
for all ,
Example 1. Lemma 1 states that f is not injective in general. The reason is that dyadic rationals have a non-unique binary expansion. For example, f maps both and to , where we call the latter binary expansion terminating.
2. Preliminaries for Polar Codes
Let
be a binary-input memoryless channel with finite output alphabet
, (symmetric) capacity
, and with Bhattacharyya parameter
It can be shown using [
13] (Proposition 1) that
and
. We say that the channel
W is
symmetric if there exists a permutation
such that
and, for every
,
.
Arıkan’s polarization technique [
13]
combines and splits two channel uses of
W into one use of a “worse” channel
and one use of a “better” channel
where
and
. The combining operation encodes two input bits by
F in (
1); transmitting them via two channel uses of
W creates a vector channel. This vector channel can then be split into the two virtual binary-input memoryless channels indicated in (
4) and (
5). The better (worse) channel obtained by polarization has a larger (smaller) capacity than the original channel
W, i.e.,
—the inequalities are strict if
. The sum capacity equals two times the capacity of the original channel, i.e.,
[
13] (Proposition 4). Similarly, polarization has an effect on the Bhattacharyya parameter:
Lemma 2 (Bounds on the Bhattacharyya Parameter).
with equality in if W is a binary erasure channel (BEC). Proof. The equality and inequality in (
6) follow from [
13] (Proposition 7) and the fact that
, respectively. The inequalities in (7) follow from the fact that
, from [
14] (Lemma 20), and from [
13] (Proposition 7). The last inequality becomes an equality if
W is a BEC [
13] (Proposition 7). ☐
For larger blocklengths
,
, we apply the polarization procedure recursively and obtain, for
,
where
and
denote the sequences of zeros and ones obtained by appending 0 and 1 to
, respectively. Note that the functions
,
, and
from Lemma 2 are non-negative and non-decreasing and map the unit interval onto itself. Hence, the inequalities in (7) are preserved under composition:
where
.
Applying this recursive polarization infinitely often leads to a situation in which almost all channels are either perfect or useless, i.e., either or for . This is the assertion of Arıkan’s polarization theorem:
Proposition 1 ([
13] (Proposition 10)).
With probability one, the limit RV takes values in the set : and . If we stop the polarization procedure at a finite blocklength
for
n large enough, then still most of the resulting
channels are either almost perfect or almost useless (i.e., the channel capacities are close to one or to zero). The idea of polar coding is to transmit data only on those channels that are almost perfect. The generator matrix of a blocklength-
polar code is thus the submatrix of
consisting of rows indexed by
, where
contains the indices corresponding to the
K virtual channels with the largest capacities. Determining this set
is inherently difficult, since (whenever
W is not a BEC) the cardinality of the output alphabet increases exponentially in
[
15] (Chapter 3.3), [
16] (p. 36). Tal and Vardy proposed an approximate construction method based on reducing the output alphabet and showing that the resulting channels are either upgraded or degraded w.r.t. the channel of interest [
17] (see also Korada’s PhD thesis [
16] (Definition 1.7 & Lemma 1.8)). These upgrading/degrading properties are important tools in our proofs.
Definition 1 (Channel Upgrading and Degrading).
A channel is degraded
w.r.t. the channel W (short: ) if there exists a channel such that A channel is upgraded
w.r.t. the channel W (short: ) if there exists a channel such that Moreover, if and only if .
Upgraded (degraded) channels remains upgraded (degraded) during polarization:
Lemma 3 ([
16] (Lemma 4.7) & [
17] (Lemmas 3 & 5)).
Suppose that . Then, Lemma 4 ([
15] (p. 9) & [
6] (Lemma 3)).
. If W is symmetric, then . Proof. By choosing
one can show that
. To show that also
for symmetric channels, take [
6] (Lemma 3)
☐
3. Fractal Properties of the Sets of Good and Bad Channels
We next investigate the behavior of the set
as we let the blocklength tend to infinity, i.e., as
. This set indexes all sequences
b for which we obtain
. With the help of (
2), we map these sequences to a subset of the unit interval, which we will call the set of
good channels.
Definition 2 (The Good and the Bad Channels).
Let denote the set of good channels, i.e., Let denote the set of bad channels, i.e., If , then all polarized channels are useless and we have . Similarly, if , then all polarized channels are perfect and we have . We hence assume throughout this section that the channel W is nontrivial, i.e., that .
Proposition 2 (Denseness).
, i.e., the good and bad channels are dense in the unit interval. Moreover, and are dense in .
It is not really surprising that
and
are not disjoint; this is a direct consequence of the fact that
f is not injective. It is not obvious, however, that the intersection exhausts the set on which
f is non-injective. A consequence of this proposition is that there is no interval that contains only good channels. This has implications for code construction techniques. Indeed, the authors of [
18,
19] suggest that, for a polar code of a given blocklength, one may stop polarizing channels at shorter blocklengths and use copies of these channels rather than their polarization. For example, they suggest to use the channels
rather than the channels
if
is sufficiently large. Such a procedure can be justified if further polarizing
to the desired blocklength will lead to including all channels polarized from
in the code. Such a justification can never appear for polar codes with unbounded blocklength: Stopping polarizing at a given blocklength
for a given polarization sequence and using copies of the resulting channel
is equivalent to including a dyadic interval in the index set. This dyadic interval contains, by Proposition 2, bad channels, which shows that this choice is suboptimal.
Proposition 3 (Symmetry).
There exists a function ϑ, defined for almost all values in , that is independent of W and satisfies and . Let be such that is defined. Then, implies . If W is a BEC, then implies .
Proposition 3 has two implications. The first implication concerns the
alignment of the sets
and
for two different channels
W and
. Specifically, it is connected to the question whether
implies
. In general, the answer is negative [
5]. Indeed, it may happen that for some
, we have
despite
, i.e., that the polarized channel turns out to be good even though the sufficient condition from Proposition 3 is not fulfilled. Such a situation cannot occur for BECs, as Proposition 3 shows. Hence, the set of good channels for a BEC is also good for any binary-input memoryless channel with a smaller Bhattacharyya parameter [
20].
The second implication is that, at least for BECs, the sets
and
are symmetric. Indeed, if
, then
implies
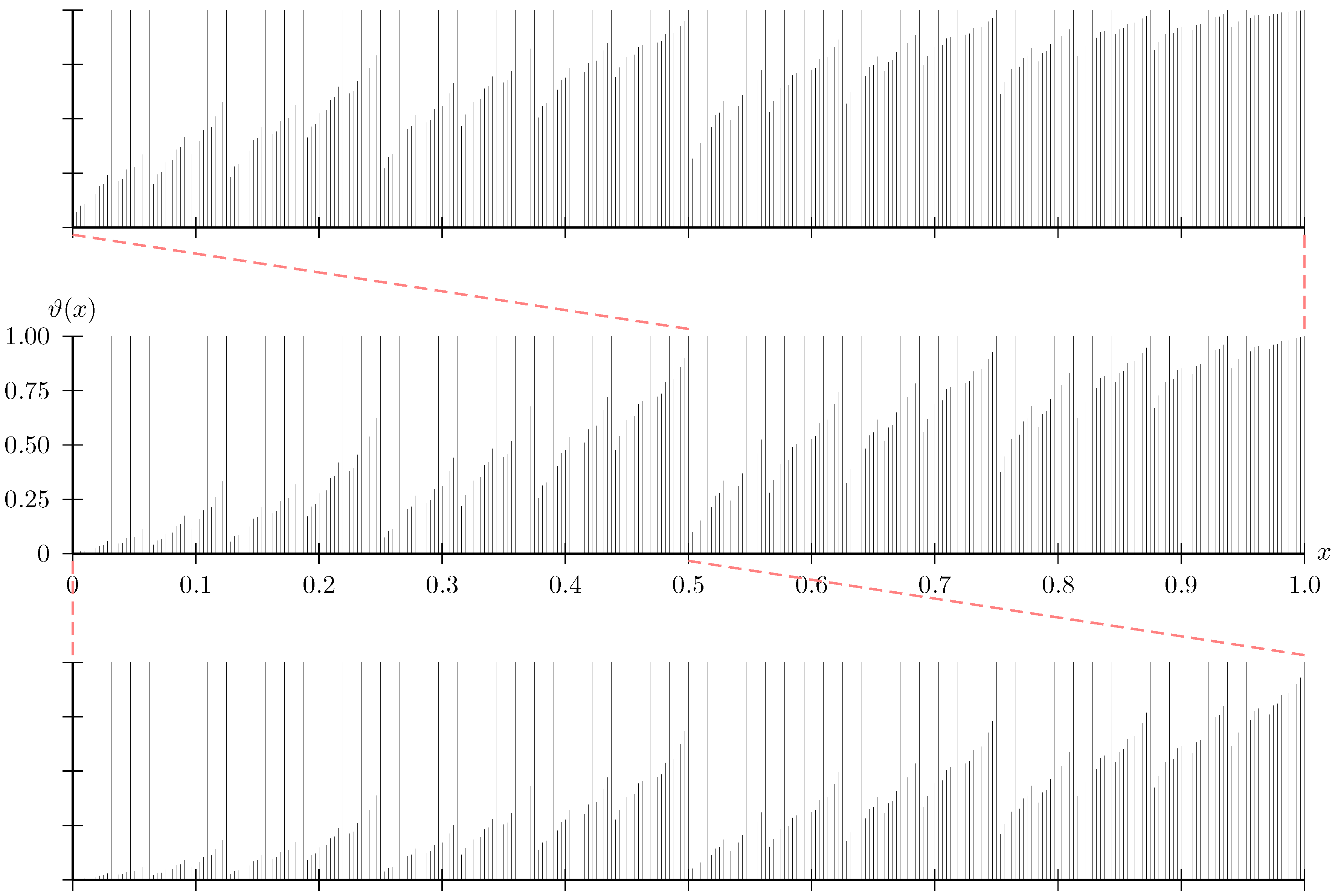
. This symmetry is visible in the polar fractal that we display in
Figure 1.
It is possible to define for . We know from Proposition 2 that dyadic rationals are both good and bad, hence setting for every leads to . (The fact that also is not captured by nor in conflict with this setting.) The question whether the function can be defined for is more interesting. In this case, the binary expansion is unique and recurring, i.e., there is a length-k sequence such that for some . It is straightforward to show that for every non-trivial sequence (i.e., contains zeros and ones), is from to , non-negative, and non-decreasing with vanishing derivatives at 0 and 1. Since this ensures that for z close to zero and for z close to one, the operation constitutes an iterated function system with attracting fixed points at and . Note further that, since corresponds to the recurring part of the binary expansion of x, will be bounded from above by the value to which this iterated function system converges after being initialized with . To show that Proposition 3 holds for requires showing that intersects the identity function only once on , i.e., that there is no attracting fixed point on this open interval. We leave this problem for future investigation.
Example 2. Let , hence . We determine the fixed points of the iterated function system corresponding to one period of the recurring sequence, i.e, the fixed points of . These are given by the roots of , which are , , and . One of these latter nontrivial roots lies outside and is hence irrelevant. The remaining root determines the threshold, .
Now suppose that W is a BEC with Bhattacharyya parameter . Since is a fixed point, we get . This illustrates that Proposition 1 holds only almost surely.
Proposition 4 (Lebesgue Measure & Hausdorff Dimension).
is a Borel set and has Lebesgue measure . is a Borel set and has Lebesgue measure . Therefore, the Hausdorff dimensions of and satisfy .
Loosely speaking, the Lebesgue measure of is the asymptotic equivalent of the rate of the “infinite-blocklength” polar code for the channel W. The fact that states that the rate approaches the symmetric capacity of W. A positive Lebesgue measure and a Hausdorff dimension equal to one are not indicators of fractality.
The last fractal property we consider is self-similarity. As Falconer notes [
1] (p. xxviii), self-similarity often occurs only approximately. What we show in the following proposition is that the set
is
quasi self-similar. Along the same lines, the quasi self-similarity of
can be shown.
Proposition 5 (Self-Similarity).
Let for . is quasi self-similar
in the sense that, for all n and all k, is quasi self-similar to its right half: If W is symmetric, is quasi self-similar: In other words, at least for a symmetric channel,
is composed of two similar copies of itself (see
Figure 1). The self-similarity is closely related to the fact that polar codes are decreasing monomial codes [
6] (Theorem 1).
Example 3. We want to determine whether for a given BEC W. This question translates the questions whether and whether . Along the lines of Example 2, we obtain , , and , i.e., . Since W is a BEC, we can connect this with Proposition 3 and thus obtain the inclusion indicated in Proposition 5.
4. Preliminaries for Reed–Muller Codes
An order-
r, length-
Reed–Muller code is defined by having a generator matrix
composed of all length-
sequences with a Hamming weight larger than
. For example, we have
, while
is a single row vector containing only ones (length-
repetition code). To make this more precise, let
be the
Hamming weight of
and let
be the
i-th row of
. Then, the generator matrix
of an order-
r, length-
Reed–Muller code consists of the rows of
indexed by [
4]
To analyze the effect of doubling the block length, note that
Assume that we indicate the rows of
by a sequence of binary numbers, i.e., let the
i-th row be indexed by
. Furthermore, let
and
denote the sequences of zeros and ones obtained by prepending 0 and 1 to
, respectively. Clearly,
and
. Combining this with (
21) yields
Defining
, we thus get
and
In
Section 5, we will analyze the properties of
in the limit as
n tends to infinity. An important ingredient in our proofs is the concept of
normal numbers.
Definition 3 (Normal Numbers).
A number is called simply normal to base 2
() if and only if In general, a number is simply normal to base M if the fraction of its digits used in its M-ary expansion is . A number is called normal if this property not only holds for digits, but also for subsequences: a number is normal in base M if, for each , the fraction of each length-k sequences used in its M-ary expansion is . It immediately follows that a normal number is simply normal. The converse is in general not true:
Example 4. Let , hence . x is simply normal to base 2, but not normal (since the sequences 00 and 11 never occur). Let , hence . x is neither normal nor simply normal. Let , hence b is either terminating () or non-terminating (). Dyadic rationals are not simply normal.
Lemma 5 (Borel’s Law of Large Numbers, cf. [
21] (Corollary 8.1, p. 70)).
Almost all numbers in are simply normal, i.e., Despite this result, there are uncountably many numbers in the unit interval which are not normal. Moreover, the set of numbers that are not normal is
superfractal, i.e., it has a Hausdorff dimension equal to one although it has zero Lebesgue measure [
22].
5. Fractal Properties of the Set of Heavy Codewords
If we let
n tend to infinity, the definition of
in (
23) becomes problematic. Rather than looking at order-
r, length-
Reed–Muller codes, we investigate order-
, length-
codes, where we assume that
is integer. In other words, we assume that the threshold for the Hamming weight increases linearly with the blocklength. This gives rise to the definition of
heavy codewords:
Definition 4 (The Heavy Codewords).
Let denote the set of ρ-heavy codewords, i.e., Loosely speaking, the set of heavy codewords corresponds to those rows of that asymptotically have a fractional Hamming weight larger than a given threshold.
Example 5. . This follows from the fact that 1 is the only number in the unit interval with a binary expansion consisting only of ones. . This follows from the fact that .
Proposition 6 (Denseness).
For all , . Moreover, for , and its complement are dense in .
Similarly as for polar codes, also Reed–Muller codes are such that no interval is contained in either
or its complement (unless in the trivial cases
and
). This is again in contrast with the intuition one obtains for Reed–Muller code with finite blocklength. Suppose we fix
n to be even and set
, i.e., we require that at least one half of the bits in
are one. The matrix
resembles a Sierpinski triangle, as depicted in [
2] (Figure 2). In our notation, the set
indexes none of the first
rows of
, since they cannot have sufficient Hamming weight. Consequently, the transition as
creates complications that are not present for finite
n, and one needs to depart from intuition based on these finite-blocklength considerations.
Proposition 7 (Lebesgue Measure & Hausdorff Dimension).
is Lebesgue measurable and has Lebesgue measureThe Hausdorff dimension satisfieswhere . Loosely speaking, the Lebesgue measure of is the asymptotic equivalent of the rate of the fractional order- Reed–Muller code. As we showed in Proposition 4, the Lebesgue measure of is equal to the symmetric capacity of W. In contrast, the set does not depend on W. Rather, Proposition 7 suggests that the order parameter induces a phase transition for the rate of Reed–Muller codes: If , the “infinite-blocklength” Reed–Muller code consists of almost all (in the sense of Lebesgue measure) possible binary sequences. In contrast, if , the “infinite-blocklength” Reed–Muller code consists of almost no codewords (again, in the sense of Lebesgue measure).
Let us briefly consider the case . For this case, Proposition 7 states that is a Lebesgue null set that has a Hausdorff dimension equal to 1. Thus, the set is a superfractal. Unfortunately, we were not able to give an exact expression for the Hausdorff dimension of for . While the set of all non-normal numbers is superfractal, we are not sure if this holds also for the specific proper subset .
The sets
and
exhibit self-similarity, i.e., detailed structure on every scale (cf.
Figure 1). We next show that also
is self-similar. At least for
and
(cf. Example 5) this is as trivial as the self-similarity of a point or a line. For
this self-similarity is more interesting, and related to the fact that Reed–Muller codes are decreasing monomial codes [
6] (Proposition 2).
Proposition 8 (Self-Similarity).
Let for . is quasi self-similar
in the sense that, for all n and all k, is quasi self-similar: 6. Discussion and Outlook
That Kronecker product-based codes possess fractal properties has long been suspected. The present manuscript contains several results that back this suspicion with solid mathematical analyses. Specifically, we assumed that the blocklength tends to infinity and investigated the properties of the set
of virtual channels that are perfect and the set
of codewords that have a fractional Hamming weight no less than
. Since both polar codes and Reed–Muller codes are obtained by a simple, recursive procedure, it remains to investigate whether the sets
and
satisfy any of the following properties [
1] (p. xxviii):
The set has a fine structure, i.e., there is detail on arbitrarily small scales;
It does not admit a description in traditional geometrical language, neither locally nor globally; it is irregular in some sense;
It has some form of self-similarity, at least approximate or statistical;
The fractal dimension of the set exceeds its topological dimension.
Indeed, the sets and possess a fine structure in the sense that they are dense in the unit interval, but that also their complements are dense in the unit interval (cf. Propositions 2 and 6). Therefore, at an arbitrarily small scale, the sets and admit no simple description in geometrical language. Both of these sets are self-similar in a specific sense, as we outlined in Propositions 5 and 8. Finally, while has a fractal dimension of one (cf. Proposition 4), the set has, for a certain range of , a positive (fractional?) Hausdorff dimension despite being a Lebesgue null set. This result, which we proved in Proposition 7, is one of the defining properties of a fractal set.
One reviewer pointed out that our definition of can be complemented by a different one. Specifically, while indexes the codewords with a fractional Hamming weight not smaller than , one could define a set indexing the codewords of a Reed–Muller code with rate R. In other words, while is parameterized via the fractional order of the code, is parameterized via its rate. We expect that the Lebesgue measure of the (adequately defined) set should be R and that, thus, its Hausdorff dimension equals one. An appropriate definition of is tied to the set of a rate-R, length- Reed–Muller code (such as is our Definition 4). Since finding such a definition has so far eluded us, we postpone this investigation to future work.
Another obvious extension of our work are non-binary polar and Reed–Muller codes. For example, consider an
matrix with entries from
, where
q is prime. One can show that this matrix is polarizing as long as it is not upper-triangular [
15] (Theorem 5.2). We believe that our analysis can be replicated by considering the
ℓ-ary expansion of real numbers in
. Along the same lines, it would be interesting to examine the properties of
q-ary Reed–Muller codes, e.g., [
23,
24].