Approach to a Quantitative Description of Social Systems Based on Thermodynamic Formalism

Abstract

Certain statistical aspects of social systems are described by appropriately defined quantities named social potentials. Relations between social potentials are postulated by drawing an analogy with thermodynamics relations between thermodynamic potentials, thus obtaining a toy model of some of the statistical properties of social systems. Within this model, an interpretation of a socially relevant acting (acting as opposed to action, see ref. [1]) that does not invoke structural changes in social systems, is given in terms of social po-tentials.

Introduction

Study of social systems requires the application of statistical methods to their description and gives results of social system research in terms of statistical data. The existence of rich statistics usually, but not necessarily, implies some underlying structure or even dynamics. Bearing in mind the very concept of social systems, it is reasonable to assume the existence of some sort of dynamics describing social systems that leads to the observed statistics. The present level of knowledge of a quantitative descrip-tion of social systems [2] implies that the formulation of complete and consistent theory is a formidable task.

In this paper we concentrate on certain characteristics of social systems and present a toy model that makes possible their quantitative description. This model is mainly formed by drawing an analogy with thermodynamic formalism. In this model we use only selected concepts of thermodynamic formalism and apply them to suitably defined characteristics of social systems. In forming the model, our intention is to give a coherent description of at least some aspects of social systems. This necessarily requires the toy model to be rather abstract, perhaps not directly applicable. One may argue that a better under-standing at the abstract level of the toy model may, through its refinements, lead to useful implementa-tions.

In order to establish a connection between social systems and thermodynamic formalism as clearly as possible, we present only selected parts of social systems theory and thermodynamics. The article is organized as follows: in the following section we extract the necessary aspects of social systems, while in the third section we present some characteristics of thermodynamics. In the fourth section we de-scribe social potentials using the analogy between thermodynamical concepts and theory of social sys-tems. This analogy is used as a starting point in forming a quantitative scheme for describing social sys-tems. The last section contains conclusions and lines of future development.

Aspects of Social Systems Relevant to a Quantitative Approach

Social systems represent objects of permanent interest and work in science, philosophy, politics and, in some aspects, even in theology, from the early beginning of these human disciplines. According to one of the most general definitions stated by T. Parsons “social system is a mode of organization of ac-tion elements relative to the persistence or ordered processes of change of the interactive patterns of a plurality of individual actors” [1].

These systems may differ in size, structure, and influence. They are engaged in different activities at different technological development levels, use different communication systems between their actors, and can function in different socio-political systems. Within social systems, different formal (laws) and informal (customs) sets of rules can dominate. Regardless of all these characteristics, social systems are permanent entities of human civilization, possessing their own dynamical structure, formation develop-ment and deformation processes including disappearance [3]. Despite this variety, as emphasized by T. Parsons [1, 3], social systems have some common characteristics like social acting and individual actor general inputs, which may be used for mutual comparison of various social systems.

In a scientific approach to society as a social system, social sciences, particularly sociology, social anthropology, and social psychology have probably reached the highest level. On the other hand, sys-tematic application of all results obtained is probably most thoroughly used in demography, political, and economic sciences, and by institutions of socialization such as preeducational, educational, relig-ious, military, and off-time institutions.

Large efforts are made for further development of description and explanation of social systems. The scientific exactness of these efforts is connected with an analysis of the exactness of both scientific methodology and objects of research in social sciences. However, both of these are significantly con-fined by ethical and technical factors, extreme complexity of objects of investigation, an extremely large number of influences and other confinements. Because of all that, social sciences are in a considerably worse position regarding the exactness of scientific methodology and objects of exploration, in relation to natural sciences. A possible way of improving the exactness of social phenomena exploration seems to be inclusion of formal modeling originating from natural sciences. The origins of a number of social science theories were concepts taken from natural sciences [3, 4]. Here we do not want to review the existing extensive literature, but try to formulate a possible approach to this relationship in more detail.

For this reason in this article we extract and discuss part of possible foundations for further social systems modeling, based on thermodynamics. This is done by relating several consequences of the basic assumptions about social systems to results of thermodynamic formalism. These assumptions are not the traditional ones made for social systems, but those that extract a possible basis for thermodynamic for-malism incorporation.

First we assume that a scale of achievable values can be attributed to each observable system char-acteristic. Generally, some of the system characteristics are redundant with respect to the quantity of information they contain. The least set of characteristics necessary and sufficient for explanation and description of all relevant system phenomena is called a basis in this paper.

The second assumption is that principles governing system time development exist and can, in princi-ple, be formulated, regardless of their complexity. The combination of an estimate of initial values of basis characteristics and the laws of time development maximizes the reliability of the prediction of the values of basis characteristics at some future time. At this stage, we do not assume anything about the possibility of measuring various characteristics.

In order to determine the basis correctly and to establish the proper form of laws, quantitative meth-ods should be introduced. It seems opportune to look for possible models of complex systems in other disciplines where this kind of approach has been used. Such a discipline is physics with a number of system models having a rather low number of parameters. The two branches particularly suitable are thermodynamics and statistical physics. The basic motivation that lead to the models was to describe the dynamics of systems with a large number of degrees of freedom. The transfer of modeling from physics to complex systems has already taken place in evolutionary biology, ecosystem modeling and in model-ing of financial and other markets. Many models seem suitable for particular social situations, or for a smaller number of them. However, in physics, where these models originated, their foundation has been thoroughly evaluated. We think that assumptions leading to models relevant to social context should also be thoroughly analyzed.

A particular situation covered is the evaluation of the ability of a social system to perform a socially relevant acting without an important change in structure.

Basics of Thermodynamic Formalism

In thermodynamics, systems consisting of a very large number of entities are described [5]. These entities are many times identified as particles of some kind, although this is not necessarily so. The vari-ables describing the system are divided into thermodynamic coordinates (TC) and thermodynamic forces (TF). Examples of TC are entropy S, number of particles N, gas volume, and other quantities (like specimen magnetization or polarization) that will be generally denoted by x_i. Examples of TF are tem-perature T, chemical potential μ, gas pressure and other external quantities (like the magnetic or the electric field) that will be generally denoted by f_i. Combinations of these variables used for determining the present and predicting the future system states are called thermodynamic potentials (TP), and to these belong internal energy U, Helmholtz energy F, enthalpy, and Gibbs potential G, as well as grand-canonical potential Ω. One of the relations among these is [5]

(1)

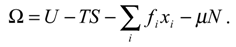
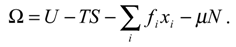
Historically, the proper identification of the variables and TP listed above made possible a highly symmetrical mathematical description of their relationship. Usually, TC are chosen among the extensive and TF among the intensive variables. The state of the system is determined by values of system vari-ables. Each variable does not have to be independently measured, because, in many cases, variables are functionally related.

The time during which the state of the system is being examined is called observation time. It has to be much larger than the characteristic time of fluctuations and the thermalization time (which is the time the system needs to come close to the observed state) and simultaneously much shorter than the equili-bration time of combination consisting of the observed system and its environment [6, 7].

The description of thermodynamic systems is possible using several variables, although they contain a large number of entities. This means that there is a great reduction in the number of variables needed for description of the system, compared with the number of variables needed for description of the same number of independent entities. However, there are fluctuations in the values of variables around their averages.

The special state of the system is the state of thermodynamic equilibrium (TE). For states close enough to TE, the system spontaneously evolves into TE. The usual statement describing this evolution is that the entropy is nondecreasing in time, i.e., it is maximal for a system in thermodynamic equilib-rium. Parameters describing the system evolution unambiguously, generally having the property of not decreasing in time, are called Lyapunov exponents. Changes in some of TP appropriately chosen for a particular system are connected with the system evolution [7, 8]. Historically, thermodynamics was de-veloped mostly through description of the system in states close enough to TE. In recent decades, em-phasis has been put on other states, especially stationary nonequilibrium states. These states are possible for systems having exchange with the environment in some of their degrees of freedom. The evolution of nonequilibrium states is generally unknown, its entropy does not have to be monotonically increasing in time, the appropriate Lyapunov coefficients are unknown and, even asymptotically, system states are unknown. For these states, the problem is to define variables and TP as functions/functionals of entity characteristics, identify TF, and determine their connection. Therefore, nonequilibrium states are un-knowns even in the traditional thermodynamics. Realistically, systems in the state of equilibrium are just idealizations the correctness of which depends on the observation time [6, 7].

Application of Thermodynamic Formalism to Social Systems Theory

The formal approach to social systems is the objective of the general system theory. In it, knowledge originating from various natural and technical sciences was the starting point for a unified description of various and diverse systems. Although of large potential, this theory has not been able to take explicitly into account all diversity of social systems and provide its satisfactory description [2]. Our approach differs from that of the general system theory in that we tend to achieve a quantitative formulation of particular aspects of social systems. In this way, we do not intend to give a complete description of all social systems and we do not restrict the possible extension of thermodynamic formalism.

The first step in an efficient description of social systems is the extraction and description of its vari-ables [3]. Following this, we try to identify some variables that have not all been common to the tradi-tional sociological description of social systems, but are common to thermodynamics and statistical physics [8]. Among various variables, the entropy is the easiest quantity to apply to social systems if it is considered to be a measure of system (dis)order [4, 9, 10].

The initial step of this attempt is to establish analogies between some of thermodynamic variables and some of social systems characteristics. A thermodynamic variable that we start with is the internal en-ergy of a thermodynamic system. We now introduce an analogous quantity that we call the internal en-ergy of a social system, $\tilde{U}$. The internal energy of a social system $\tilde{U}$ is appropriate, yet at this stage unknown, combination of actor characteristics. Relevant actor characteristics, among the others, are material assets, acquired knowledge, skills, and psycho-physical characteristics. In social systems, $\tilde{U}$ can be interpreted as a measure of total resources of the system, determined according to some set of generally accepted social standards. One can also invoke an analogous quantity $\tilde{u}$ for each actor of the system, according to the same standards. However, straightforward summing of all $\tilde{u}$’s does not amount to $\tilde{U}$. The difference is a consequence of interactions between the actors. Still, having established $\tilde{U}$, one can determine the average internal energy per actor, $\overline{u}$, as the ratio of $\tilde{U}$ to the total number of actors. This average internal energy also includes the average interaction between the actors, i.e., the interaction of an actor with the rest of the system if fluctuations in the number of actors are negligible compared with its average.

There are two components of the internal energy of a social system $\tilde{U}$. The first one comprises the ability of the system to perform socially relevant acting. We denote it by $\tilde{F}$. The second component comprises the amount of resources required to achieve and maintain the social system welfare. This component can be seen as part of internal energy bound in the social system as a “price” of creating its structure. It contains details of the system structure and we express it as a product of two quantities; $\tilde{T}$·$\tilde{S}$. We call the quantities $\tilde{T}$ and $\tilde{S}$ temperature and entropy of the social system, respectively.

Let us discuss these quantities in some detail. We can define the entropy of the social system $\tilde{S}$ as a monotonic function of a number of possibilities for the system structure for given $\tilde{U}$. It counts the number of ways that the system can exist in, with a given amount of resources. Generally, the number of accessible system structure possibilities grows with time, which is correlated with constant scientific, technological and cultural progress. The applicability of the previous statements depends crucially on the size of social system resources. The larger are the resources, the less likely are the large fluctuations which might result in decrease of the number of possibilities. For example, knowledge may influence social system entropy. In larger systems it is unlikely that some part of knowledge is lost, whereas in smaller ones some knowledge can be simply forgotten. The entropy of the social system introduced in this way resembles the traditional thermodynamic entropy in several important respects. In both cases, the entropy grows monotonically with time and the likelihood of fluctuations decreases with the size of the system. It can be argued that the number of system structure realizations depends on the number of actors, technological level and social norms that can be legislative or informal, etc. Some of these fac-tors increase the entropy, whereas others reduce it.

In order to elaborate the concept of temperature of a social system we start from the difference be-tween the accessibility and realizability of particular possibilities of the system structure. Namely, all accessible possibilities do not have to be realized. The quantity that measures how efficiently one social system uses its realizations we call the temperature of the social system. In systems with relatively high $\tilde{T}$, most of the options are realized, whereas in the systems with relatively low $\tilde{T}$ we have the opposite situation.

From the very nature of the quantities discussed it is clear that we should not consider them inde-pendent, that is, some additional relations between them may exist. For example, it is plausible that re-sources influence the number of possibilities and the efficiency of their use for a given social system. The form of mutual dependence of variables is the consequence of internal social system dynamics.

The above considerations lead us to the equation

(2)

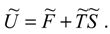
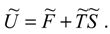
This relation brings about some fundamental difference compared with thermodynamics. The basic measurable quantities are $\tilde{F}$, $\tilde{T}$, and $\tilde{S}$, while the measurement of $\tilde{U}$ is, in principle, more difficult. The reason is that $\tilde{F}$, $\tilde{T}$, and $\tilde{S}$ are quantities that are easier to detect in social systems owing to their more specific definitions. This is to be compared with the thermodynamics where $\tilde{U}$ is more pro-nounced because of its figuration in the first law of thermodynamics. Here, the analogue of the first law is more difficult to discuss because it involves the transfer of resources through the system boundary, which is an additional problem.

However, in most of the situations, a social system cannot be considered separated from the envi-ronment. The surroundings of the system brings about external factors which are, in general, time de-pendent and independent of social system characteristics. We assume that the characteristic time scale of changes of these factors is much larger than the time the system needs to adapt itself to environ-mental changes (the analogue of thermalization time). In such a system, the analogues of thermody-namic potentials retain their applicability. The analogue of this type of social system is an open thermo-dynamic system.

In such a system, along with the mentioned limits of the amount of internal energy that can be trans-formed into social acting, there are limits imposed by the system environment. Let us consider the ex-ternal factors ${\tilde{f}}_{\text{i}}$, which influence some of the social system characteristics ${\tilde{x}}_i$, upon which the internal energy $\tilde{U}$ depends. The ${\tilde{f}}_{\text{i}}$’s denote the external influence on the number of actors of the system, so their recognition depends on the system characteristics. Depending on it, it could be possible for some influences to be treated either as external or as internal, and thereby put them into ${\tilde{f}}_{\text{i}}$’s or include in $\tilde{S}$, respectively. In order to achieve and maintain the level ${\tilde{x}}_i$ of each characteristic, the social system has to act against external influences. This action requires a certain amount of total system resources, which comes from $\tilde{F}$, so we have:

(3)

(4)

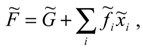
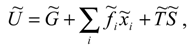where we call $\tilde{G}$ the Gibbs potential of the social system, in analogy with thermodynamics. Examples of ${\tilde{f}}_{\text{i}}$’s are found among influences as different as are atmospheric conditions, taxes, and other external influences, while examples of characteristics, respectively. ${\tilde{x}}_i$’s are the amounts of agricultural production, total income and other characteristics, respectively.

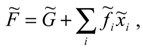
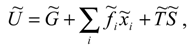
In this simplified example, the possibility of a change in the available system energy by changing its number of actors is not considered. For social systems in which changes of the number of actors are connected with additional changes in resources this factor is important. We present the change in re-sources as $\tilde{\mu }·\tilde{N}$, where $\tilde{N}$ is the number of actors and $\tilde{\mu }$; the energy change which corresponds to a change in the number of actors by one. It is realized through perturbations among actors after one actor entered or left the system. This perturbation also invokes the change of $\tilde{F}$, thereby making natural the introduction of another quantity $\tilde{\Omega }$, which leads to

(5)

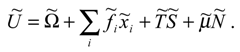
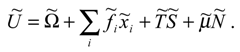
From the above considerations, we see that depending on whether (2), (4), or (5) is relevant for the system, $\tilde{F}$, $\tilde{F}$, or $\tilde{\Omega }$, respectively, describe the ability to perform socially relevant acting.

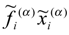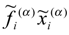Here we did not consider the problem whether ${\tilde{f}}_{\text{i}}·{\tilde{x}}_i$ can be obtained by summing analogous quanti-ties for individual actors, , where α denotes the individual actor, or whether these quantities are predominantly of collective origin. The answer to this questions cannot be given generally from a preliminary analysis, but depends on the particular social system and character of each and every exter-nal influence.

We have introduced several quantities relevant to social systems as analogues of thermodynamic po-tentials. It seems plausible to call them social potentials since, for the moment, we have heuristically demonstrated their similarity with thermodynamic potentials. The analogy would be more complete if a set of units for the quantities introduced were established. For this purpose one would need a set of reference measures. We may think of the equations listed to be scaled using these reference measures.

The procedure of measuring social potentials, including the determination of reference measures, is a separate problem. In principle, one of the ways that these quantities could be measured is through the process of polling on a sample representative for each social system [11, 12]. It is also possible to adopt some other methods from psychology, economy, or demography to give an operational meaning to so-cial potentials.

All of the social systems characteristics of the basis defined in the introductory section are, by no means, included in these considerations. Only those that are most relevant to the statistical behavior of social systems are comprised by the model.

However, the formalism presented is just of heuristic value and its suitability for a particular social system could be shown a posteriori, that is, through the results obtained. A number of problems emerge from the foregoing presentation. The first is that all characteristics on which the introduced social po-tentials depend should be identified. The second is that the functional dependence of social potentials on the characteristics identified should be modeled appropriately. A separate problem is the determination of the character of the social system state, i.e., whether the state of the system is in nonequilibrium or not. As the fourth problem, characteristic times for system dynamic observation should be carefully cho-sen. The fifth problem is to see which combination of identified variables and external influences make possible characterization of present and the prediction of future system states. As the sixth problem, special situations in which values of some of the functions used are constant should be considered in more detail. The seventh problem is the evaluation of relative fluctuations in order to clarify state definiteness. As the eighth problem, one should consider the equivalence of states, i.e., whether all states having the same energy are equally accessible to all actors. This problem questions the very foun-dation of the traditional thermodynamics and statistical physics analogues in the new context and could lead to a more simplified quantitative description in the case of affirmative answer to the eighth prob-lem. Then the analogies between thermodynamics and social systems would be more directly estab-lished. The ninth in this list is the problem of required number of actors and the size of the social system. An additional problem is the influence of the social system environment and a border between it and the social system. All these problems are obviously mutually interconnected, and are not listed here ac-cording to their importance.

Conclusions

In this paper we have presented a toy model that made possible interpretation of certain characteris-tics of social systems. The established level of analogy between certain characteristics of social systems and part of thermodynamic formalism in the simplified model encourages one to assume that even deeper analogies might be drawn to construct more complete and detailed models of social systems. One may argue that the social system quantities defined in this paper seem to be a good starting point for such an attempt. On the other hand, in our opinion, the refinement of the model may be applied in empirical research to specific social systems in future interdisciplinary work.