When does robust latching, as a model of spontaneous sequence generation, occur? We address this question with extensive computer simulations, mostly focused on latching between randomly correlated patterns. We consider first the slowly adapting regime () in which active states () adapt slower than activity propagation to other units (), while inhibitory feedback is restricted to an even slower timescale, . Next, we contrast with it the fast adapting regime () in which, instead, inhibitory feedback is immediate, relative to the other two time scales.
3.1. Slowly Adapting Regime
In the slowly adapting regime, over a (short) time of order
the network, if suitably cued, may reach one of the global attractors, and stay there for a while; whereupon, after an adaptation time of order
, it may latch to another attractor, or else activity may die [
25]. However, how distinct is the convergence to the new attractor? One may assess this as the difference between the two highest overlaps the network activity has, at time
t, with any of the memory patterns,
: ideally,
and
is small, so their difference approaches unity. A summary measure of memory pattern discrimination can be defined as
, where, of course, the identity of patterns 1 and 2 changes over the sequence.
As discussed in [
25], by looking at the latching length, how long a simulation runs before, if ever, the network falls into the global quiescent state, one can distinguish several “phases”. Depending on the parameters, the dynamics exhibit finite or infinite latching behaviour, or no latching at all. Typically, when increasing the storage load
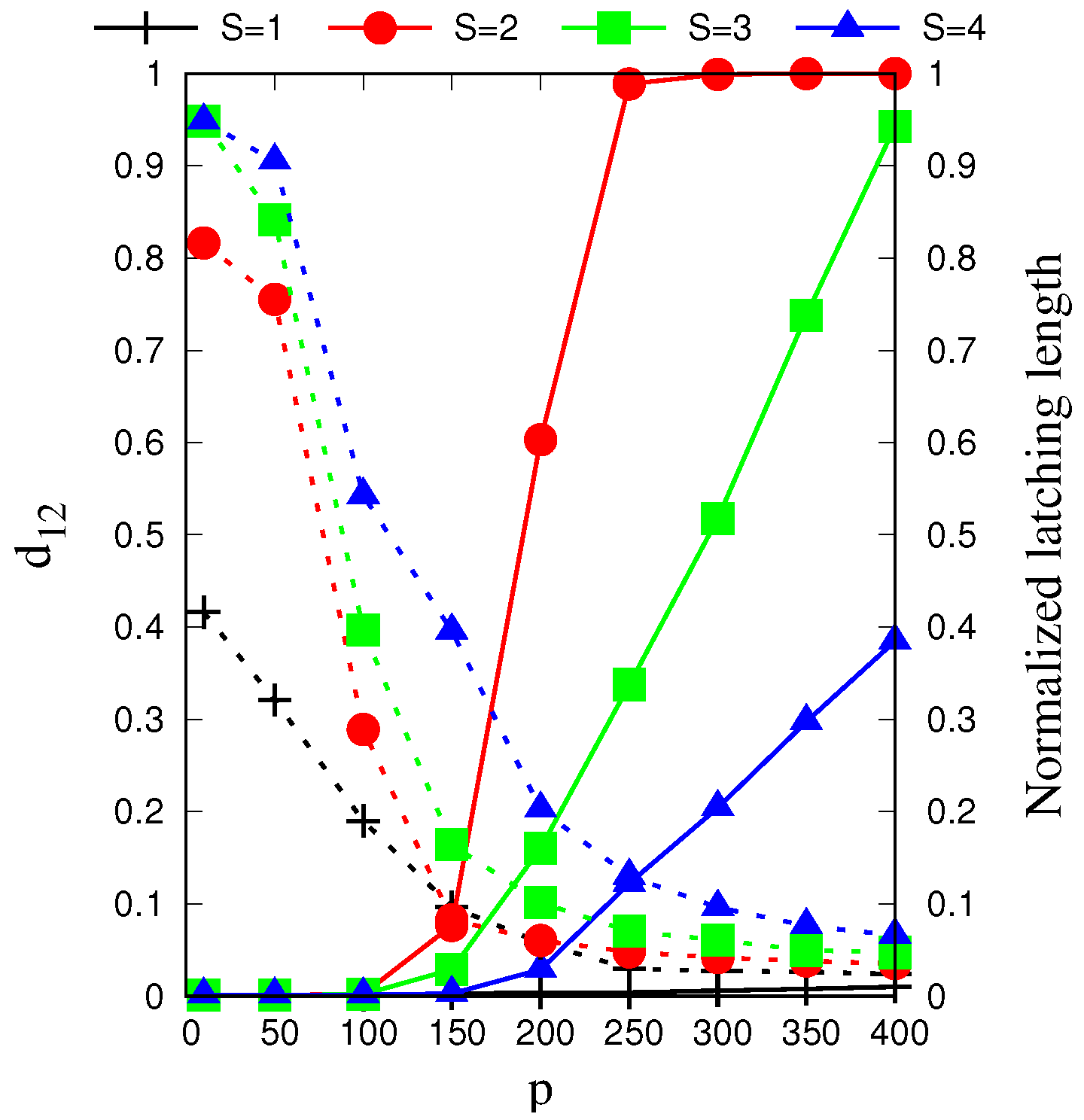
p, the latching sequence is prolonged and eventually extends indefinitely, but, at the same time, its distinctiveness decreases, since memory patterns cannot be individually retrieved beyond the storage capacity; and, even before, each acquires neighbouring patterns, in the finite and more crowded pattern space, with which it is too correlated to be well discriminated.
In
Figure 2, we see that, for each
S = (2, 3, 4), as
p is increased beyond a certain value, latching dynamics rapidly picks up and extends eventually through the whole simulation, but, in parallel, its discriminative ability decreases and almost vanishes—the
p-range where
is large is in fact when there is no latching, and
only measures the quality of the initial cued retrieval. For
no significant latching sequence is seen, whereas for higher values, at fixed
p, its distinctiveness increases with
S, but its length decreases from the peak value at
.
Since the latching length l is not itself sufficient to characterize latching and has to be complemented by discriminative ability, we find it convenient to quantify the overall quality of latching.
With a new quantity
Q defined as
where
is introduced to exclude cases in which the network gets stuck in the initial cued pattern, so that no latching occurs; however, high
and
l are:
Q is therefore a positive real number between 0 and 1, and we report its color-coded value to delineate the relevant phases in phase space.
Thus,
low quality latching with small
Q may result from either small
or short
l, or both. The parameters that determine
Q which we focus on are
S,
C and
p, after having suitably chosen all the other parameters, which are kept fixed. Their default values in the slowly adapting regime are
,
,
,
,
,
,
,
, unless explicitly noted otherwise. If activity does not die out before, simulations are terminated after
= 6 × 10
steps, the total number of updates of the entire Potts network, and are repeated with different cued patterns. Re the values of
S,
C and
p, we use the following notation, for simplicity:
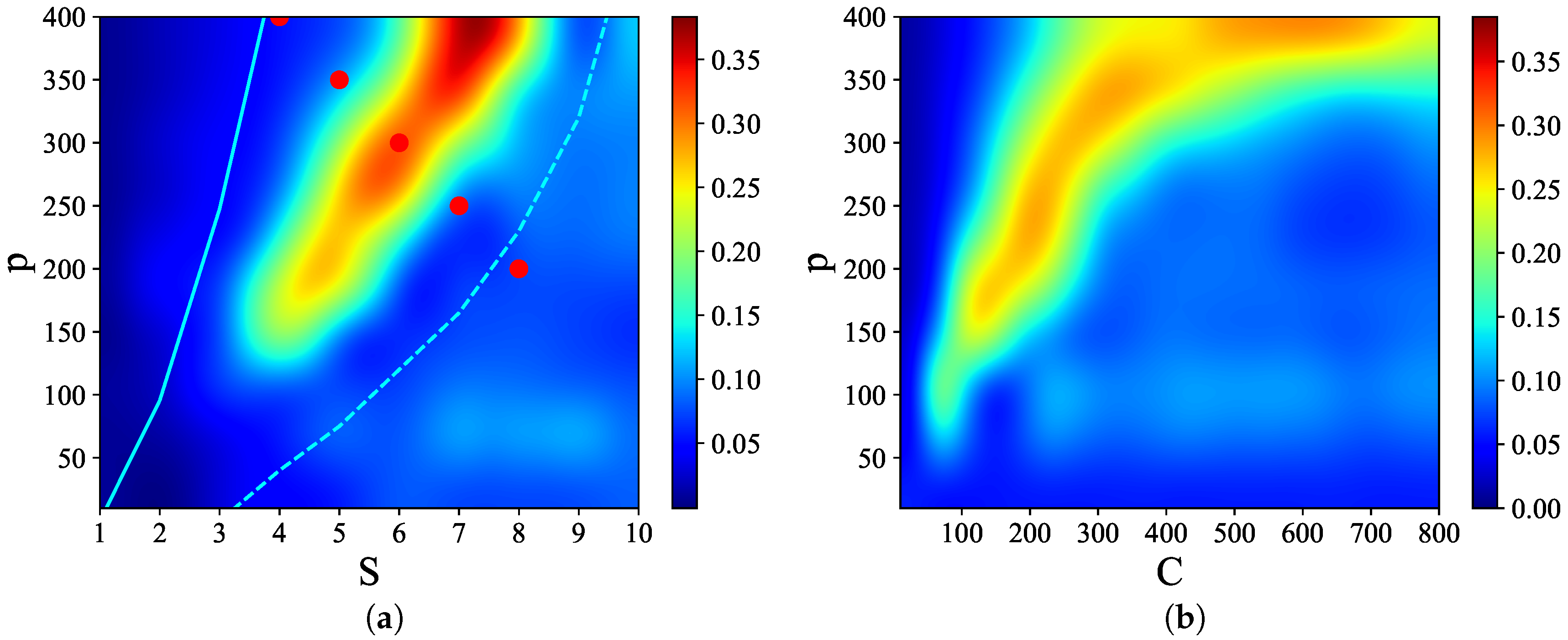
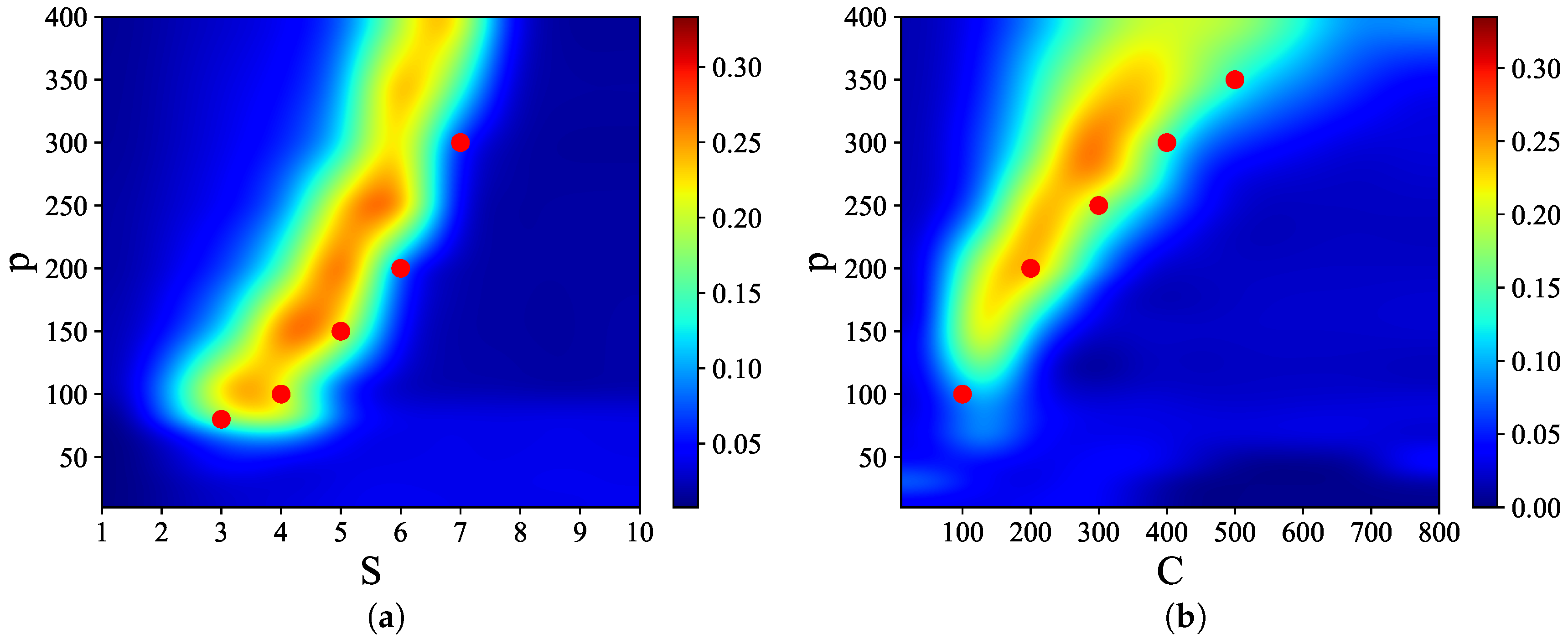
Figure 3 shows that there are narrow regions in the
S–
p and
C–
p planes, which we call
, where relatively
high quality latching occurs. The values of
p with the “best” latching scale almost quadratically in
S, and sublinearly in
C. Moreover, one notices that, below certain values of
S and
C, no latching is seen, i.e., the band effectively ends at
,
in
Figure 3a and at
,
in
Figure 3b. Importantly, the band in
Figure 3a is confined in the area delimited by the cyan solid and dashed curves above and below it. The dashed curve is for the onset of latching, i.e., the phase transition to finite latching [
25], while the solid curve above is the storage capacity curve in a diluted network, given by the approximate relation beyond which retrieval fails [
25]. It should also be noted that overall
Q values are not large, in fact well below 0.5 throughout both
S–
p and
C–
p planes. The reason is, again, in the conflicting requirements of persistent latching, favoured by dense storage, high
p, and good retrieval, allowed instead only at low storage loads (in practice, relatively low
and
values):
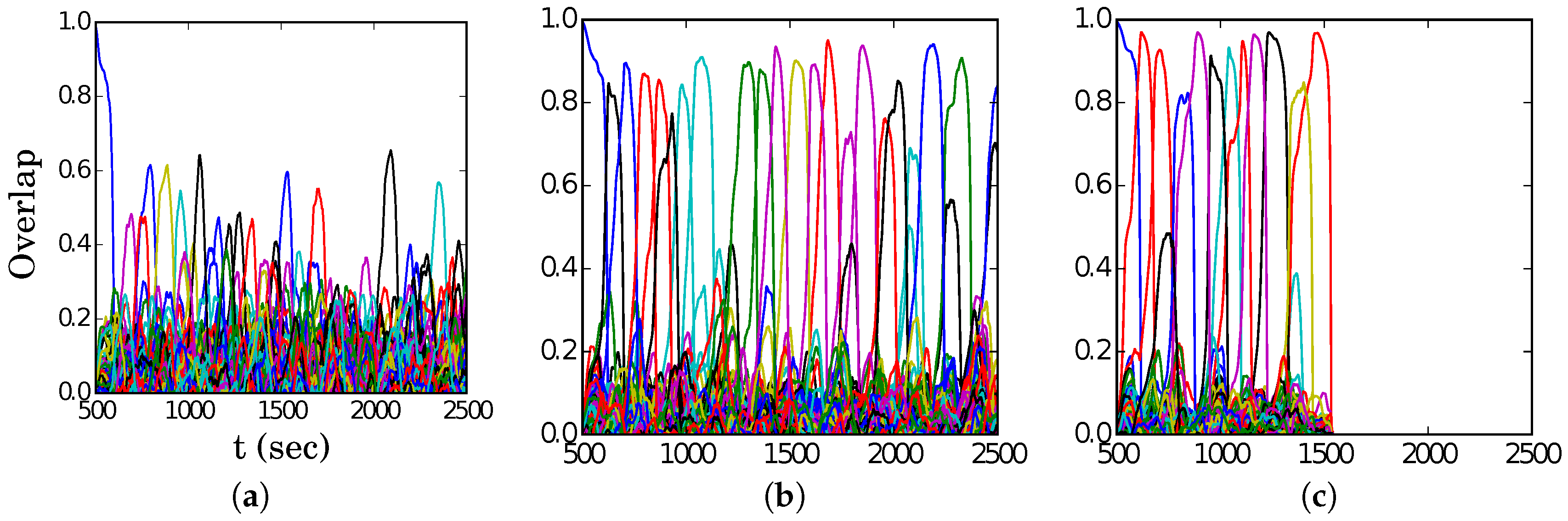
In
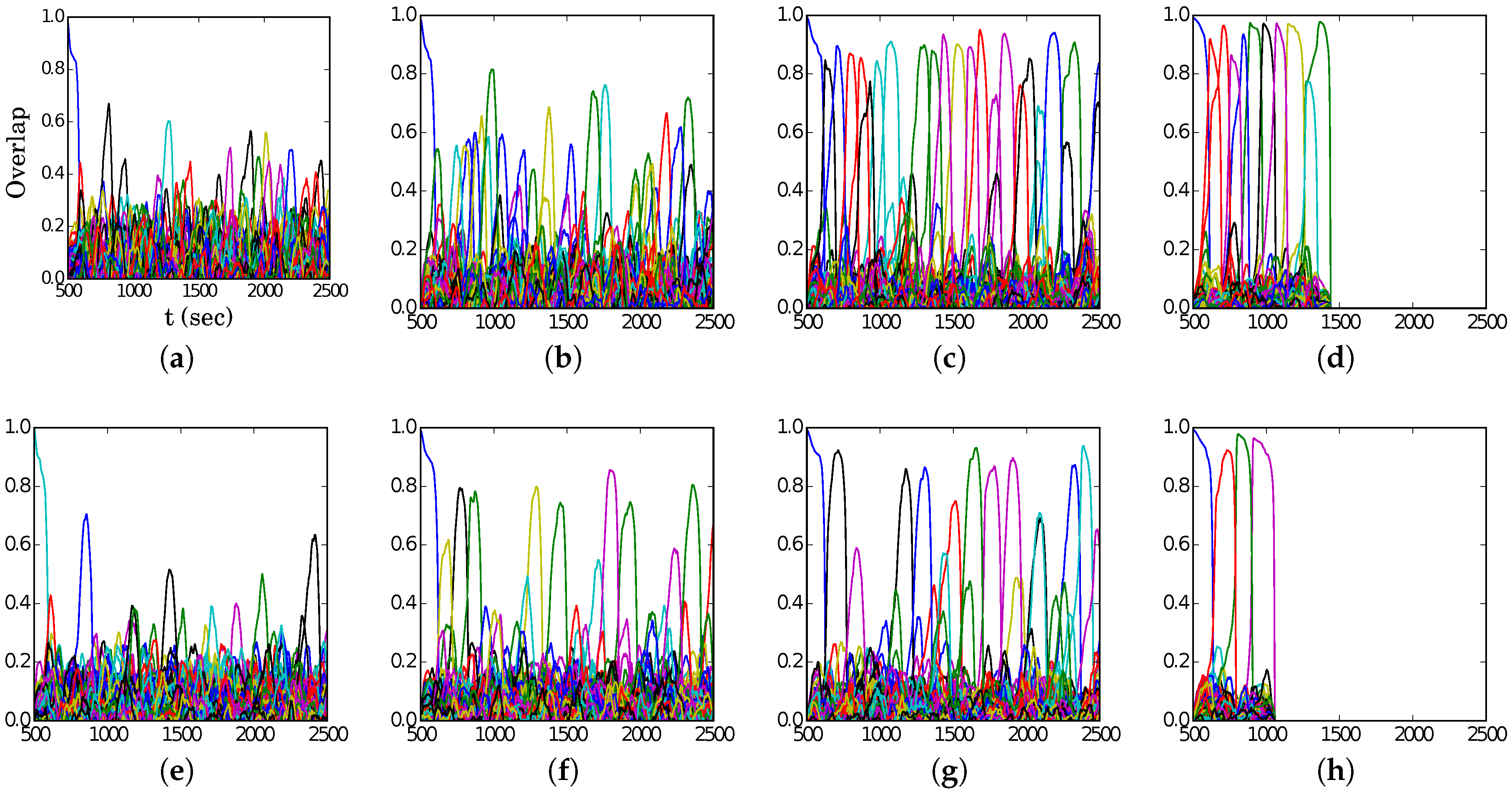
Figure 4, we show representative latching dynamics at three selected points in the
plane, in terms of the time evolution of the overlap of the states with the stored activity patterns (see Equation (
8)). The three points, marked in red, span across the band in
Figure 3a, and we see that latching is indefinite but noisy in the example at (5, 250), which is apparently too close to storage capacity, while memory retrieval is good at (7, 150), but the sequence of states ends abruptly, as the network is in the phase of finite latching [
25]. The two trends are representative of the two sides of the band, while in the middle, at (6, 200), one finds a reasonable trade-off, with relatively good retrieval combined with protracted latching.
We use two statistical measures, the
asymmetry of the transition probability matrix and Shannon’s
information entropy [
33,
36,
37] to characterize the essential features of the dynamics in different parameter regions. For that, we take all five red points from
Figure 3a, such that they cut across the latching band in the
S–
p plane, and extend further upwards. We first compile a transition probability (or rather, frequency) matrix
M from all distinct transitions observed along many latching sequences generated with the
same set of stored patterns, as in [
33]. The dimension of the matrix
M is
, as it includes all possible transitions between
p patterns
the global quiescent state.
M is constructed from the transitions between states having both overlaps above a given threshold value, e.g., 0.5, in a data set of 1000 latching sequences, by accumulating their frequency between any two patterns into each element of the matrix and then normalizing to 1 row by row, so that
reflects the probability of a transition from pattern
to
.
A, the degree of asymmetry of
M, is defined as
where
is the transpose matrix of
M and
. Note that
A is small for unconstrained bi-directional dynamics and large for simpler stereotyped flows among global patterns, attaining its maximum value
for strictly uni-directional transitions. Note also that if the average had been taken over
different realizations of the memory patterns, given sufficient statistics
A would obviously vanish.
Another measure we apply to the transition matrix
M is Shannon’s information entropy, defined as
takes positive real values from 0 (deterministic, all transitions from one state are to a single other state) to 1 (completely random), since it is normalized by , which corresponds to a completely random case.
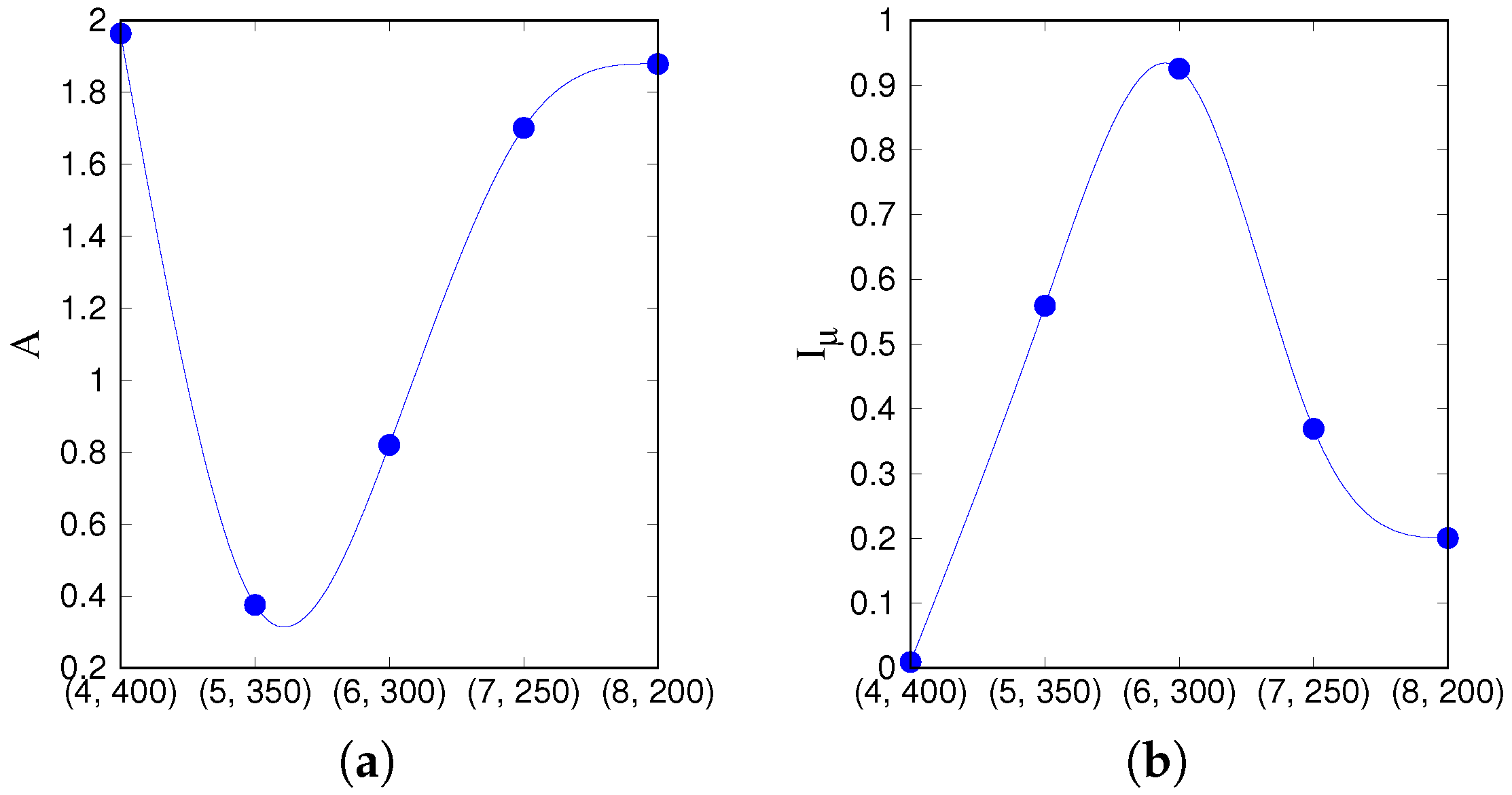
We use these two measures,
A and
, on the points, marked red in
Figure 3a.
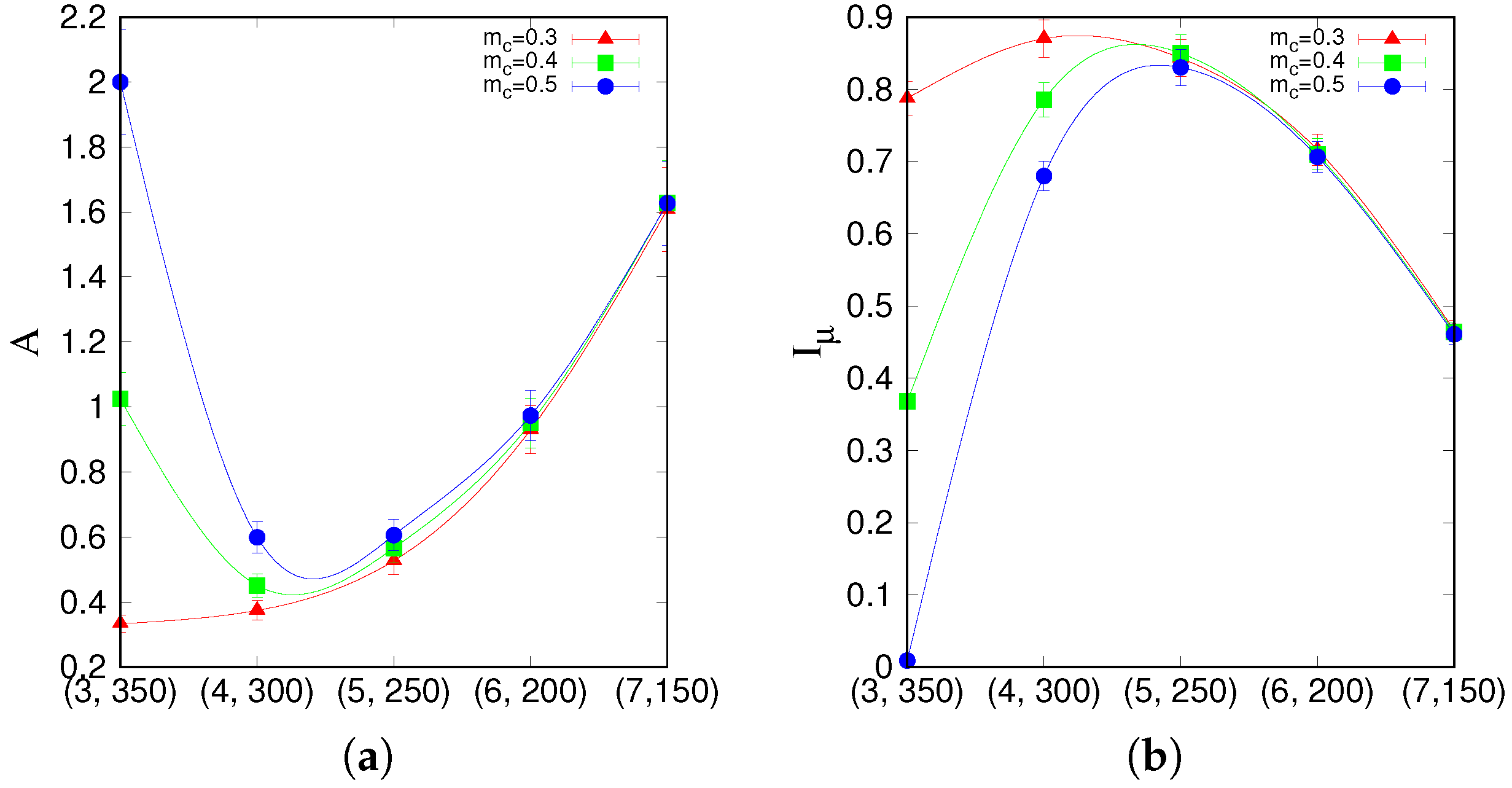
that lie on a segment going through the latching band observed in the slowly adapting regime. If we focus on transitions between states reaching at least a threshold overlap of 0.5,
Figure 5 appears to show two complementary, almost opposite U-shaped curves as the two measures, asymmetry and entropy, are applied to the five points along the segment. One branch of each U shape extends over the range that includes the high-
Q latching band: these are the right branches of the two curves, in which asymmetry decreases from a large value
at (7, 150) to a smaller one
at (5, 250), while concurrently the entropy increases from
at (7, 150) to
at (5, 250). As
Figure 4 indicates, at (7, 150), latching sequences are distinct but very short, and few entries are filled in the transition matrix: generally either
or
, so that asymmetry is high and entropy relatively low. This holds irrespective of the number of sequences that are averaged over. The opposite happens at (5, 250), where many transitions are observed, and in filling the transition matrix they approach the random limit. The point with the highest
Q-value, (6, 200), is characterized by intermediate values of asymmetry and entropy which, we have previously observed, may be seen as a signature of complex dynamics [
33]. Extending the range upwards, it seems as if the asymmetry, with threshold 0.5, were to eventually increase again, reaching its maximum
at (3, 350), with a decreasing entropy, vanishing at the same point (3, 350). These left branches are, however, dependent on the threshold values used, as
Figure 5 shows, and do not imply that transitions become more deterministic because, in this region, there are simply fewer and fewer distinct transitions discernible above the noise (
Figure 4). The left branches merely reflect the increasing arbitrariness with which one can identify significant correlations with memory states in the rambling dynamics observed at higher storage loads.
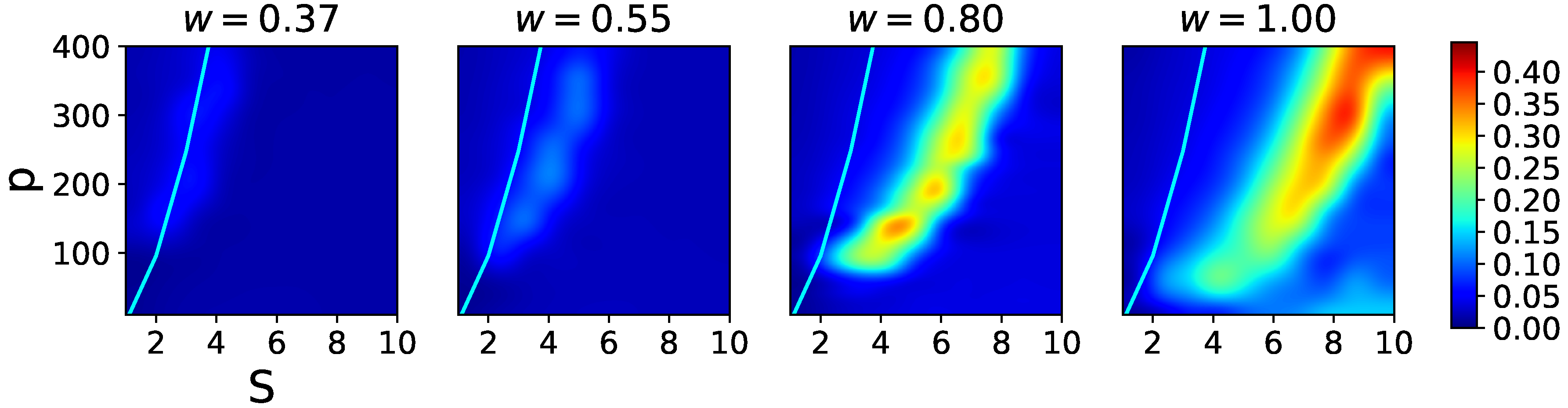
In
Figure 6, we see that the effect of the local feedback term,
w, is first to enable latching sequences of reasonable quality, and then to also shift the latching band to higher values of
S, effectively pushing this behaviour away from the storage capacity curve representing the retrieval capability of the Potts associative network. Hence, if one were to regard
S as a structural parameter of the network, and
w as a parameter that can be tuned, there is an optimal range of
w values that allows good quality latching for higher storage. This argument has to be revised, however, by considering also the threshold
U, since increasing
w can be shown to be functionally equivalent, in terms of storage capacity, to decreasing
U [
32]. Also for
U, in fact, one can find an optimal range for associative retrieval to occur, in the simple Potts network with no adaptation and with
[
23]. This near equivalence between
U and
does not hold anymore in the fast adapting regime, to which we turn next.
3.2. Fast Adapting Regime
We characterize the fast adapting regime by the alternative ordering of time scales
, such that the mean activity in each Potts unit is rapidly regulated by fast inhibition, at the time scale
. Equation (
6) stipulates that
, the total activity of each unit, is followed almost immediately, or more precisely at speed
, by the generic threshold
. Extensive simulations, with the same parameters as for the slowly adapting regime, except for
,
,
and
, show that, similarly to the slowly adapting regime, there are latching bands in the
and
planes (see
Figure 7). With these parameters, in particular, the larger value chosen for the feedback term
w, the bands occupy a similar position as in the slowly adapting regime. Again, they appear to vanish below certain values of
S and
C, more precisely around
,
in
Figure 7a and around
,
in
Figure 7b, and to scale subquadratically in
S and sublinearly in
C. The band in the
S–
p plane is again confined by the storage capacity (solid cyan curve) and by the onset of (finite) latching (dashed curve). The storage capacity curve, which is independent of threshold adaptation, follows the same Equation (
13).
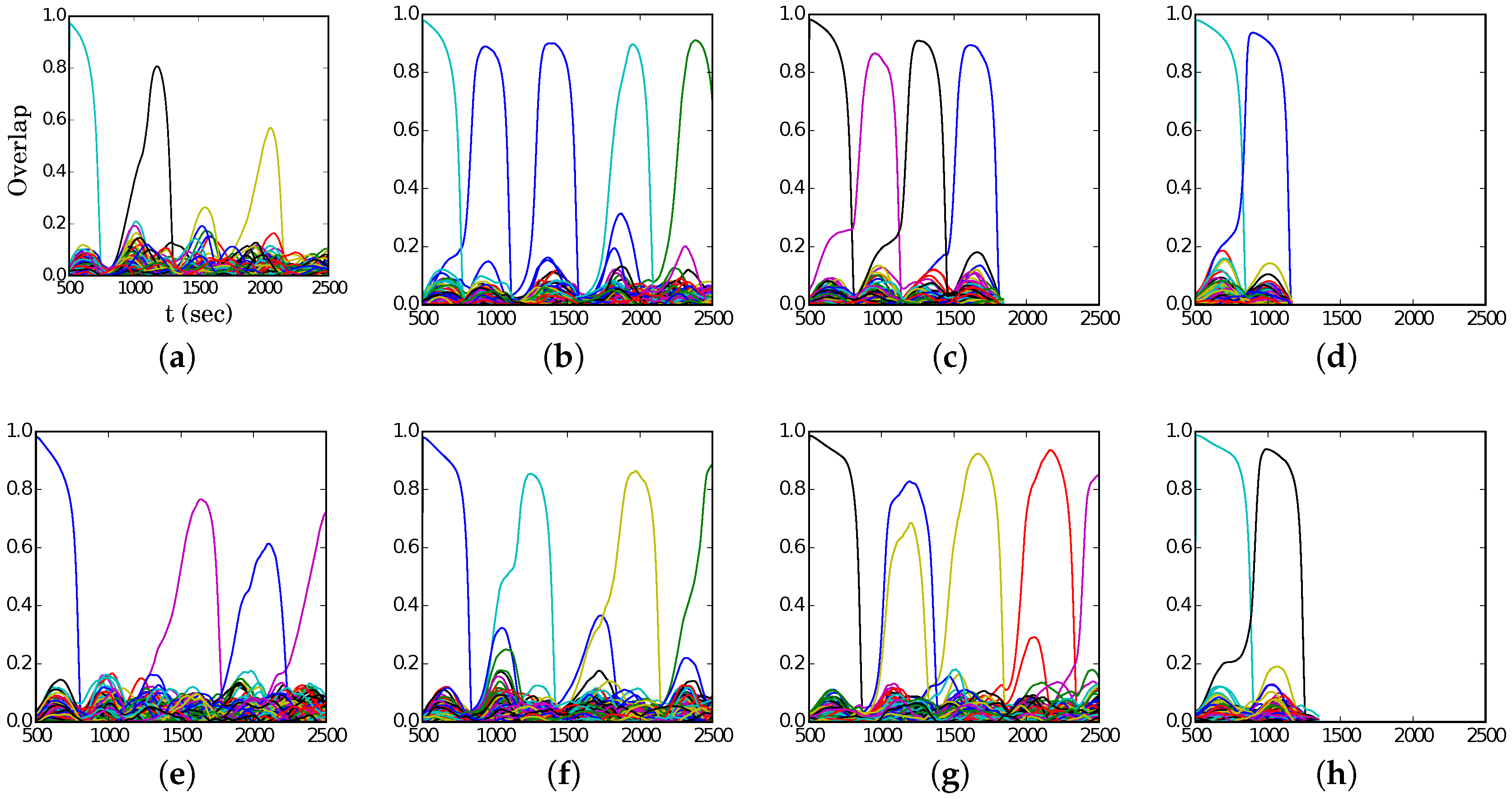
Examples of latching behaviour outside and inside the band are presented in
Figure 8, at the same values for
S but shifted by
, i.e., at the “red” points (5, 350), (6, 300), and (7, 250) in the
S–
p plane. Again, we see from
Figure 7a that (5, 350) lies just above the band, while (6, 300) is right on the centre. To the right of the band, e.g., at (7, 250), the transitions are distinct but latching dies out very soon, while on the left, e.g., at (5, 350), the progressively reduced overlaps are a manifestation of increasingly noisy retrieval dynamics. In all three examples, we observe that latching steps proceed slowly, even slower than the doubled time scale
would have led to predict. This appears to be because often a significant time elapses between the decay of the overlap of the network with one pattern and the emergence of a new one.
Figure 9 shows the asymmetry and entropy measures,
A and
, along the points
in
Figure 7a, where, again, we have chosen a series shifted by
upwards in order to centre it better on the high quality latching band. Only an overlap threshold of 0.5 is considered. What one can see, in contrast with the slowly adapting regime, is that now the two measures are not quite complementary. The point (6, 300) that lies inside the band, very much at its quality peak, shows again an intermediate value for the asymmetry, but the highest value, given the overlap threshold, for the entropy. The discrepancy may be ascribed to the different prevailing type of latching transition observed in the fast adapting regime,
Figure 8. As discussed in [
24], in a Potts network latching transitions with a high cross-over, which can only occur between memory patterns with a certain degree of correlation, can be distinguished from those with a vanishing cross-over, which are much more random. In the fast adapting regime, as indicated by the examples in
Figure 8, all transitions tend to be of the latter type. A more careful analysis indicates, in fact, that they are quasi-random, in that they avoid a memory pattern in which largely the same Potts units are active as in the preceding pattern. In fact, the value of the entropy at (6, 300) implies that on average from each of the 300 memory patterns there are transitions to at least 190 other patterns (to 190 if they were equiprobable, in practice many more); therefore, only the few patterns that happen to be more (spatially) correlated are avoided.
Towards the left, the curves do not vary much depending on the threshold chosen for the overlaps, but the asymmetry eventually becomes maximal and the entropy vanishes simply because sequences of robustly retrieved patterns do not last long, so, in this particular case, it would take more than 1000 sequences to accumulate sufficient statistics.
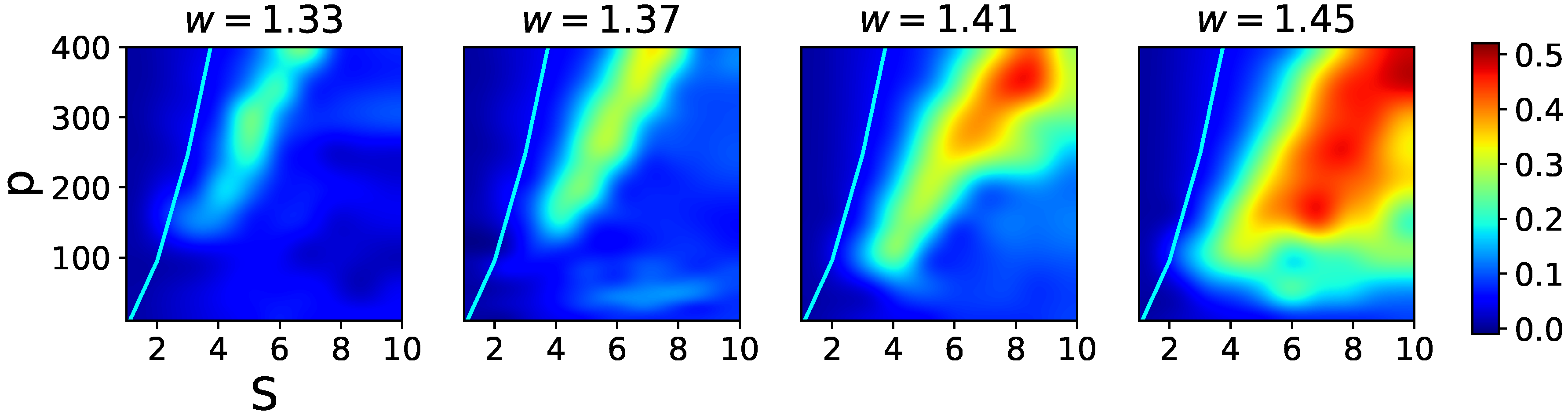
The effects of increasing the
w term in the fast adapting regime are shown in
Figure 10, where one notices two main features. First, there is heightened sensitivity to the exact value of
w, so that relatively close data points at
w = 1.33, 1.37, 1.41, and 1.45 yield rather different pictures. Second, although again increasing
w shifts the latching band rightward, by far the main effect is a widening of the band itself. This is because in the presence of rapid feedback inhibition a larger
w term ceases to be functionally similar to a lower threshold, which in the slowly adapting regime was leading in turn to noisier dynamics and eventually indiscernible transitions. In the fast adapting regime, the increased positive feedback can be rapidly compensated by inhibitory feedback, so that in the high-storage region overlaps remain large, until they are suppressed by storage capacity constraints (the cyan curve, which remains at approximately the same distance from the larger and larger latching band).
We now turn to more explicit comparison of the transition dynamics in two regimes.
3.3. Comparison of Two Regimes
To look more closely at latching dynamics in the slowly and fast adapting regimes, we take the following points from
Figure 3a and
Figure 7a, which allow us to cut through the bands at two different storage levels
Figure 11 shows in different colors the overlaps of the state of the network with the global patterns, for sample sequences along the points (
16), in the slowly adapting regime. For both
and 400, latching length is observed to decrease with
S, unlike the discrimination between patterns, as measured by
, in agreement with
Figure 2. Note that the two rows in the figure are similar, indicating that the shift
is approximately compensated by the rightward shift
.
The fast adapting regime shows the same trends, again one sees in
Figure 12 the approximate compensation between the two shifts
and
, but latching appears in general less noisy.
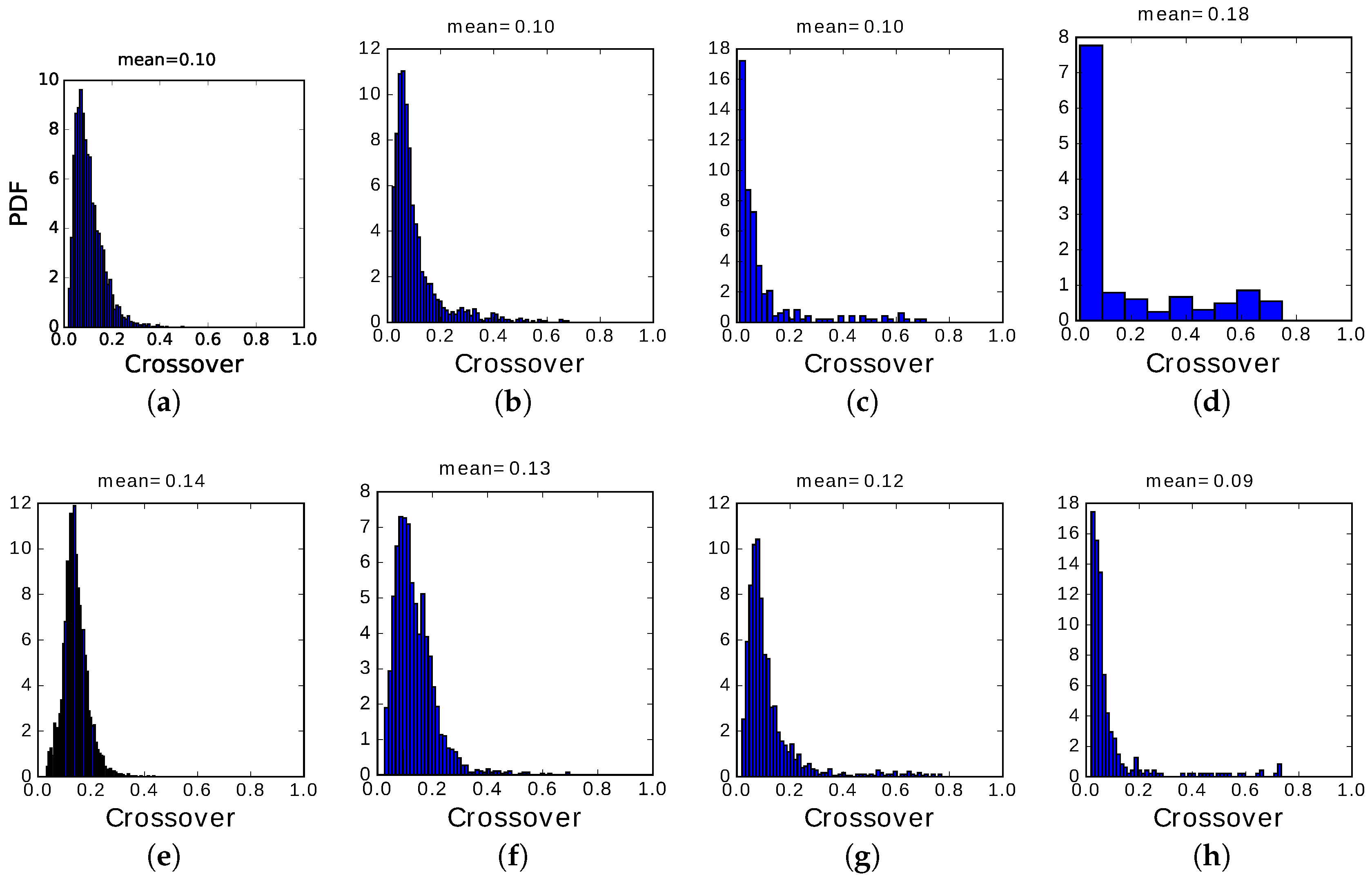
The main difference between the two regimes, however, is in the distribution of crossover values, those when the network has equal overlap with the preceding and the following pattern: their distribution (PDF, or probability density function) is shown in
Figure 13 and
Figure 14.
We see that, in the fast adapting regime, most transitions occur at very low crossover, i.e., the correlation with the preceding memory has to decay almost to zero before the next memory pattern can be activated. Only in regions of the plane where latching sequences are very short, a few transitions only, we begin to see a small fraction of them with crossover values above 0.2. In most cases, the inhibitory feedback conveyed by the variable is so fast as not to allow transitions to be carried through by positive correlations, i.e., by the subset of Potts units which are in the same active state in the preceding and successive pattern. The choice of the next pattern is not completely random, as indicated by the relative entropy values still below unity, but is determined essentially by negative selection, as mentioned above: the next pattern tends to have few active Potts units that coincide with those active in the preceding pattern.
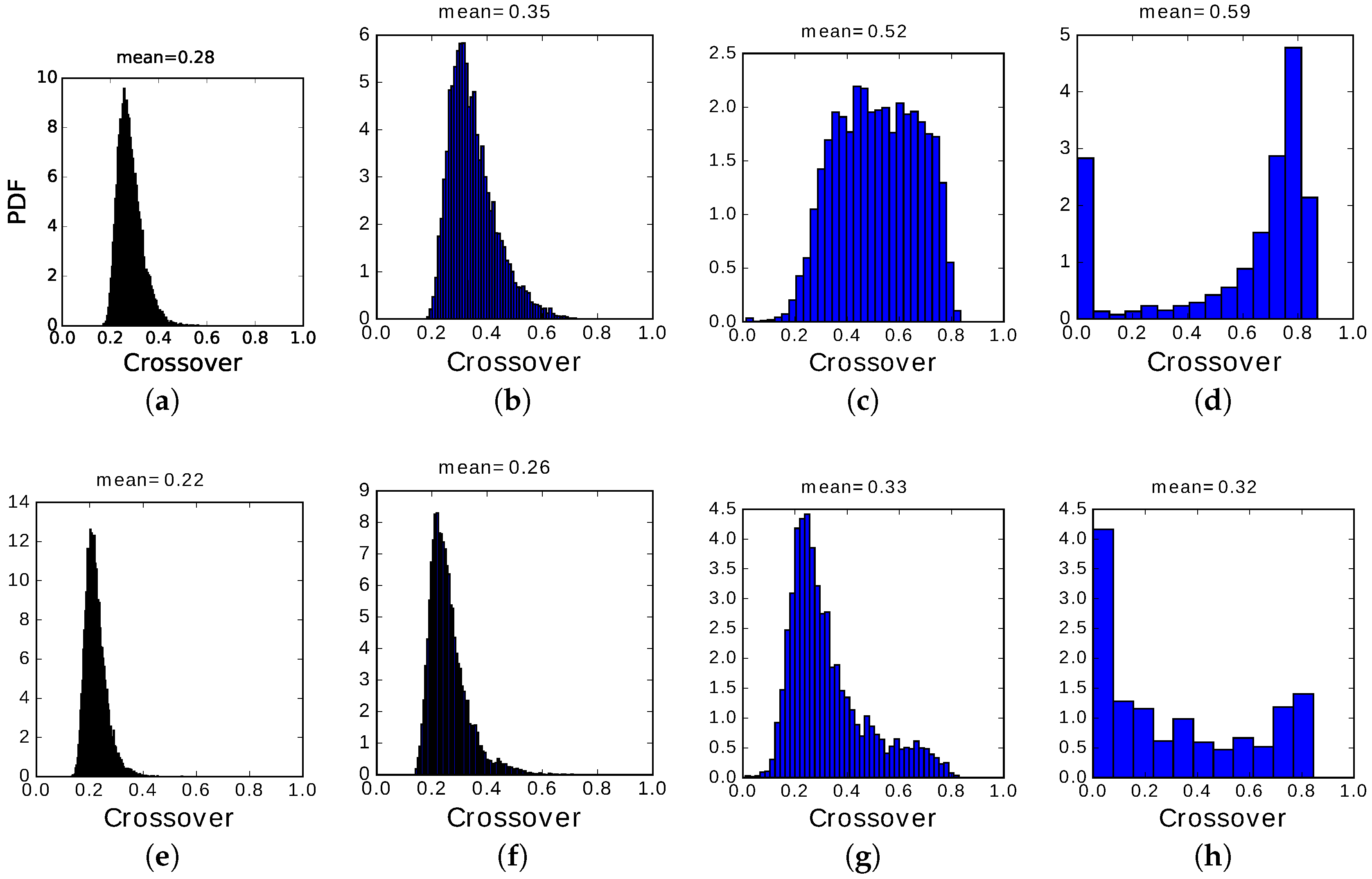
In the slowly adapting regime, instead, due to the slow variation of the non-specific threshold, active Potts units can remain active, but they are
encouraged by the variables
to switch between active states if they have been in the same for too long. This can produce, particularly in the center of the latching band, sequences of patterns succeeding each other at high crossover, as shown by the distribution in
Figure 13c. Even when latching is very noisy and approaches randomness, as in panels
Figure 13a,e, crossover values are consistently above 0.2, indicating a preference for patterns insisting on the same set of active Potts units, unlike the fast adapting regime. Finally, when the number of states
S is too large or, equivalently, that of patterns
p too low, we observe some transitions with minimal crossover and a majority with very large crossover, as if occurring only with those patterns that were already partially retrieved when the network had still the largest overlap with the preceding pattern, but the main observation is that there are very few transitions at all, so that to plot a probability density distribution we need to used wide bins, in panels
Figure 13d,h (and in
Figure 14d).
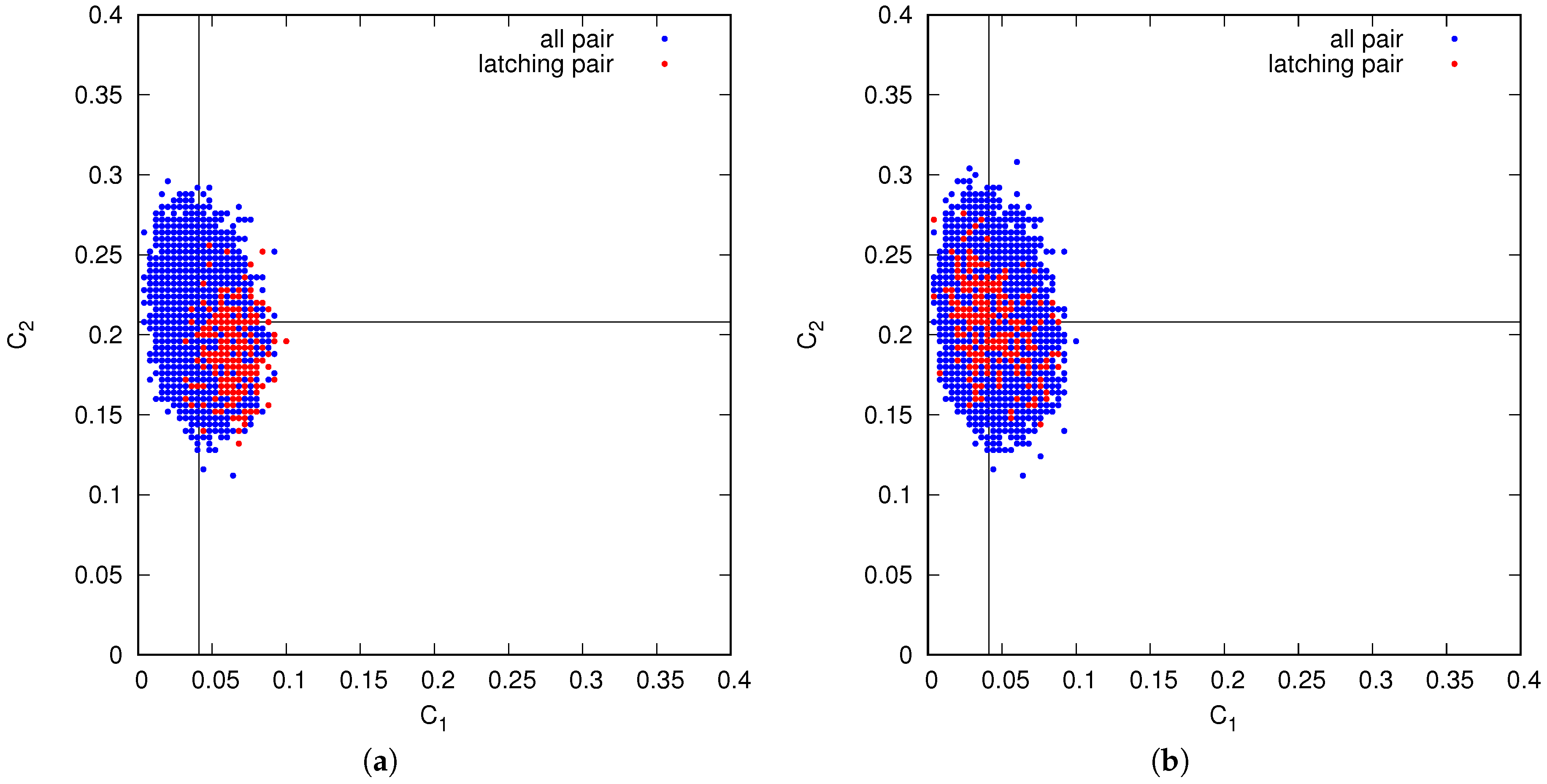
This difference between the two regimes is confirmed by an analysis of the correlations between successive patterns in latching sequences. In the Potts network, at least two types of spatial correlation between patterns are relevant: how many active Potts units the two patterns share, and how many of these units are active and in the same state. We quantify them with , the fraction of the units active in one pattern that are active also in the other, and in the same state; and with , the fraction that are also active, but in a different state. In a large set of randomly determined patterns, the mean values are and . The full distribution, among all pairs, is scattered around these mean values. However, do transitions occur between any pair of patterns?
Figure 15 shows that relative to the full distribution, in blue, transitions tend to occur, in the slowly adapting regime on the left, only between patterns with
above and
below (or at most around) their average values. Thus, when the network has retrieved a memory representation, it looks for correlated ones, as it were, where to jump. In the fast adapting regime, this is not the case: transitions are almost random, except there appears to be a slight tendency to avoid those with
well above its mean value. Note that the values of
p and
w are different in the two panels, and are chosen so as to be in roughly equivalent positions within the respective latching bands.
The analysis of the crossover points, therefore, affords insight into the rather different transition dynamics prevailing in the fast and slowly adapting regimes, in particular in the center of their latching bands, suggesting that in a more realistic cortical model, which combines both types of activity regulation, there should still be a significant component of “slow adaptation” for interesting sequences of correlated patterns to emerge. The preceding simulations, however, were all carried out with randomly correlated patterns, in which the occasional high or low correlation of a pair is merely the result of a statistical fluctuation. Does the insight carry over to a more stuctured model of the correlations among memory patterns? This is what we ask next.
3.4. Analysis with Correlated Patterns
Correlated patterns were generated according to the algorithm mentioned by [
22] and discussed in detail in [
35]. The multi-parent pattern generation algorithm works in three stages. In the first step, a total set of
random patterns are generated to act as parents. In the second step, each of the total set of parents are assigned to
randomly chosen children. Then, a “child” pattern is generated: each pattern, receiving the influence of its parents with a probability
, aligns itself, unit by unit, in the direction of the largest field. In the third and final step, a fraction
a of the units with the highest fields is set to become active. In this way, child patterns with a sparsity
a are generated. In addition, another parameter
can be defined, according to which the field received by a child pattern is weighted with a factor
where the index
k runs through all parents. This is meant to express a non-homogeneous input from parents.
It is clear that such patterns, however, cannot be considered as independent and identically distributed, as in Equation (
9), because their activity is drawn from a common pool of parents. In fact, they are correlated, in the sense that those children receiving congruent input from a larger number of common parents will tend to be more similar. All of these observations are studied in more detail in [
35], and here we only focus on how correlations affect the phase diagrams. In the following simulations, the parameters pertaining to the patterns are
,
,
while
, the probability that a pattern be influenced by a parent is kept constant at
.
Simulations with correlated patterns were carried out across the same
S–
p and
C–
p planes in phase space, in the slowly adapting regime, as shown in
Figure 16. We focused on the slowly adapting regime based on the results of the crossover analysis. All other simulation parameters were kept at the values used with randomly correlated patterns.
We see from the figure that the presence of non-random correlations among the memory patterns, albeit weak, shifts the bands to the left and upward in phase space, keeping approximately the dependence of the viable storage load p on S and C, but at somewhat higher values. It is as if more memories could “fit”, if correlated, into the same latching dynamics.
Figure 17 shows the
S–
p plane cut along
, to better compare the cases with correlated (blue) and random (red) patterns. It is apparent that there is a leftward shift, in the case of correlated patterns, from the red curve applying to the random case, but the dependence on
S remains very similar.