Entropies of Weighted Sums in Cyclic Groups and an Application to Polar Codes
Abstract
:1. Introduction
According to [29], Conway denied having conjectured the patently false statement about equality; apparently his original conjecture was that always has at least as many elements as . However, that is not always the case. In 1969, Marica [30] showed that the conjecture is false by exhibiting the set , for which has 30 elements and has 29 elements. Such a set is called an MSTD (more-sums-than-differences) set. According to Nathanson [31], Conway himself had already found the MSTD set in the late 1960s, thus disproving his own conjecture. Subsequently, Stein [32] showed that one can construct sets A for which the ratio is as close to zero or as large as we please; apart from his own proof, he observed that such constructions also follow by adapting arguments in an earlier work of Piccard [33] that focused on the Lebesgue measure of and for subsets A of . A stream of recent papers aims to quantify how rare or frequent MSTD sets are (see, e.g., [34,35] for work on the integers and [36] for finite abelian groups more generally) or try to provide denser constructions of infinite families of MSTD sets (see, e.g., [37,38]); however, these are not directions we will explore in this note.“Let be a finite set of integers, and define and . Prove that always has more members than , unless A is symmetric about 0.”
2. Comparing Entropies of Sums and Differences
2.1. Basic Examples
- For Conway’s MSTD set , we have and . Let be independent random variables uniformly distributed on A. Straightforward calculations show that:
- The second example is based on the set with . Let be independent random variables uniformly distributed on A. Then, we have:
- The group is the smallest cyclic group that contains an MSTD set. Let . It is easy to check that A is an MSTD set since and . We let be independent random variables uniformly distributed on A. Then, we have:
2.2. Achievable Differences
2.3. Entropy Analogue of the Freiman–Pigarev Inequality
3. Weighted Sums and Polar Codes
3.1. Polar Codes: Introduction
3.2. Polar Martingale
3.3. Kernels with Maximal Spread
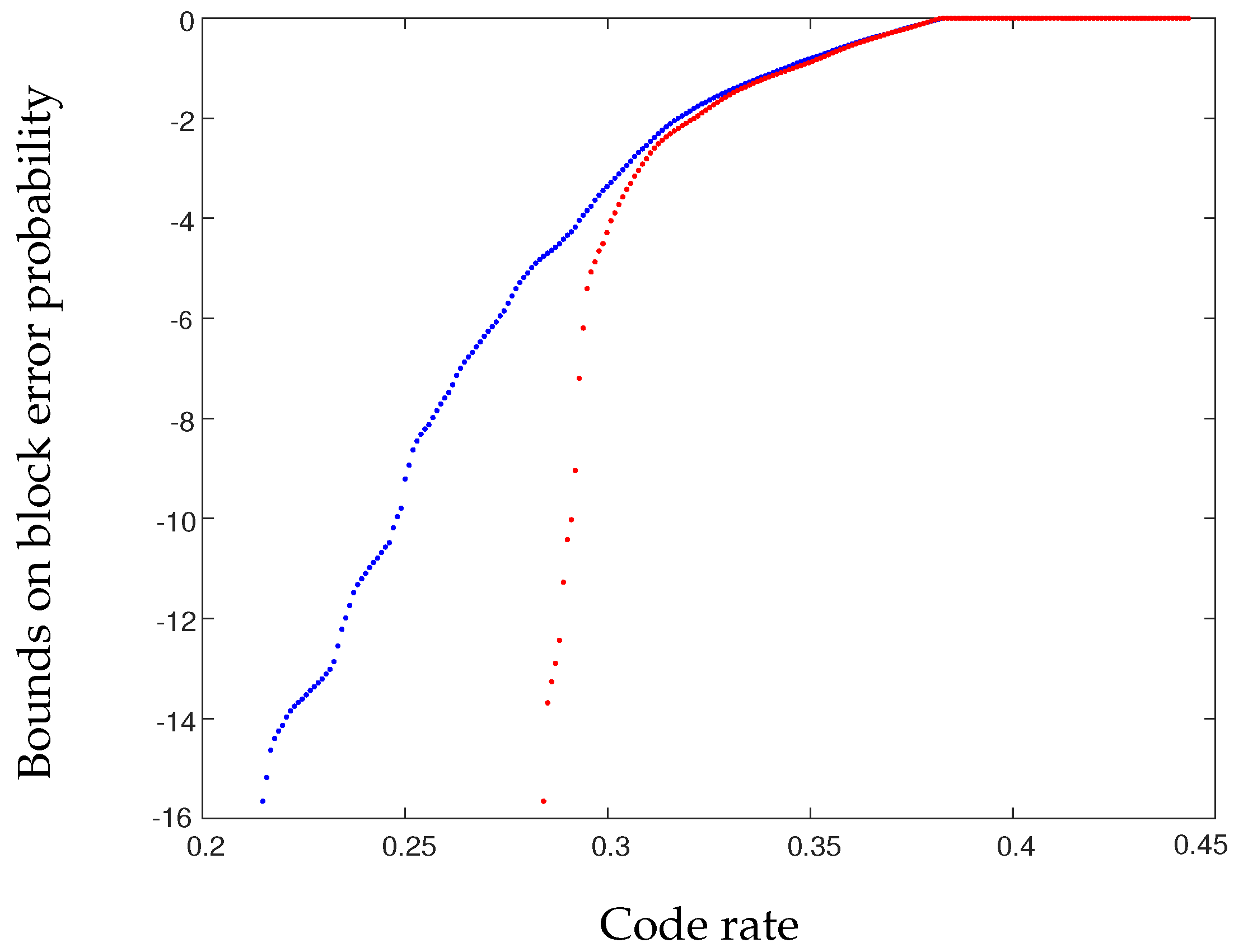
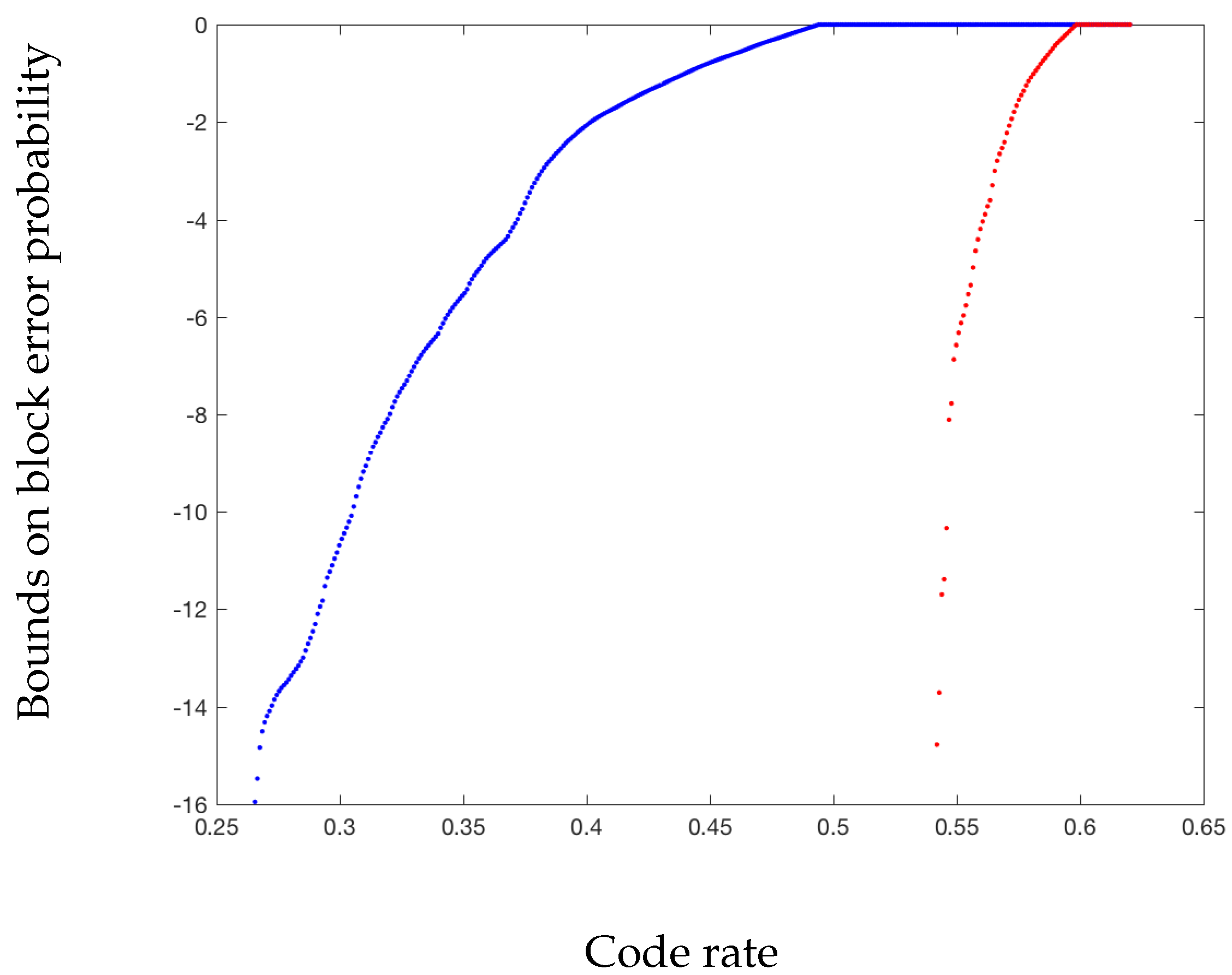
- Let over be such that . Picking , one obtains and , and (39) is verified. In this case, using can only provide a strictly smaller spread since it will not set . It is hence better to use the two-optimal kernel rather than the original kernel . As illustrated in Figure 3, this leads to significant improvements in the error probability at finite block length. Also note that a channel with noise satisfying (39) has positive zero-error capacity, which is captured by the two-optimal kernel as shown with the rapid drop of the error probability (it is zero at low enough rates since half of the synthesized channels have noise entropy exactly zero). If is close to a distribution satisfying (39), the error probability can also be significantly improved with respect to the original kernel .
- Over general , let . If , we can see that will satisfy (39).
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Madiman, M.; Tetali, P. Information inequalities for joint distributions, with interpretations and applications. IEEE Trans. Inf. Theory 2010, 56, 2699–2713. [Google Scholar] [CrossRef]
- Tao, T.; Vu, V. Additive combinatorics. In Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 2006; Volume 105, xviii, 512. [Google Scholar]
- Ruzsa, I.Z. Sumsets and Entropy. Random Struct. Algoritms 2009, 34, 1–10. [Google Scholar] [CrossRef]
- Madiman, M.; Marcus, A.; Tetali, P. Information-theoretic inequalities in additive combinatorics. In Proceedings of the 2010 IEEE Information Theory Workshop on Information Theory, Cairo, Egypt, 6–8 January 2010. [Google Scholar]
- Madiman, M.; Marcus, A.; Tetali, P. Entropy and set cardinality inequalities for partition-determined functions. Random Struct. Algoritms 2012, 40, 399–424. [Google Scholar]
- Tao, T. Sumset and inverse sumset theory for Shannon entropy. Comb. Probab. Comput. 2010, 19, 603–639. [Google Scholar] [CrossRef]
- Haghighatshoar, S.; Abbe, E.; Telatar, E. A new entropy power inequality for integer-valued random variables. IEEE Trans. Inf. Theory 2014, 60, 3787–3796. [Google Scholar] [CrossRef]
- Jog, V.; Anantharam, V. The entropy power inequality and Mrs. Gerber’s lemma for groups of order 2n. IEEE Trans. Inf. Theory 2014, 60, 3773–3786. [Google Scholar] [CrossRef]
- Wang, L.; Woo, J.O.; Madiman, M. A lower bound on the Rényi entropy of convolutions in the integers. In Proceedings of the 2014 IEEE International Symposium on Information Theory (ISIT), Honolulu, HI, USA, 29 June–4 July 2014; pp. 2829–2833. [Google Scholar]
- Woo, J.O.; Madiman, M. A discrete entropy power inequality for uniform distributions. In Proceedings of the 2015 IEEE International Symposium on Information Theory (ISIT), Hongkong, China, 14–19 June 2015. [Google Scholar]
- Madiman, M.; Kontoyiannis, I. The Entropies of the Sum and the Difference of Two IID Random Variables are Not Too Different. In Proceedings of the 2010 IEEE International Symposium on Information Theory Proceedings (ISIT), Austin, TX, USA, 13–18 June 2010. [Google Scholar]
- Lapidoth, A.; Pete, G. On the Entropy of the Sum and of the Difference of Two Independent Random Variables. In Proceedings of the IEEE 25th Convention of Electrical and Electronics Engineers in Israel, Eilat, Israel, 3–5 December 2008. [Google Scholar]
- Madiman, M. On the entropy of sums. In Proceedings of the 2008 IEEE Information Theory Workshop, Porto, Portugal, 5–9 May 2008; pp. 303–307. [Google Scholar]
- Cohen, A.S.; Zamir, R. Entropy amplification property and the loss for writing on dirty paper. IEEE Trans. Inf. Theory 2008, 54, 1477–1487. [Google Scholar] [CrossRef]
- Etkin, R.H.; Ordentlich, E. The degrees-of-freedom of the K-user Gaussian interference channel is discontinuous at rational channel coefficients. IEEE Trans. Inf. Theory 2009, 55, 4932–4946. [Google Scholar]
- Wu, Y.; Shamai, S.S.; Verdú, S. Information dimension and the degrees of freedom of the interference channel. IEEE Trans. Inf. Theory 2015, 61, 256–279. [Google Scholar] [CrossRef]
- Stotz, D.; Bölcskei, H. Degrees of freedom in vector interference channels. IEEE Trans. Inf. Theory 2016, 62, 4172–4197. [Google Scholar] [CrossRef]
- Kontoyiannis, I.; Madiman, M. Sumset and Inverse Sumset Inequalities for Differential Entropy and Mutual Information. IEEE Trans. Inf. Theory 2014, 60, 4503–4514. [Google Scholar] [CrossRef]
- Madiman, M.; Kontoyiannis, I. Entropy bounds on abelian groups and the Ruzsa divergence. arXiv 2015. [Google Scholar]
- Bobkov, S.; Madiman, M. Dimensional behaviour of entropy and information. C. R. Math. 2011, 349, 201–204. [Google Scholar] [CrossRef]
- Madiman, M.; Melbourne, J.; Xu, P. Forward and reverse entropy power inequalities in convex geometry. arXiv 2016. [Google Scholar]
- Madiman, M.; Ghassemi, F. Combinatorial entropy power inequalities: A preliminary study of the Stam region. arXiv 2017. [Google Scholar]
- Fradelizi, M.; Madiman, M.; Marsiglietti, A.; Zvavitch, A. On the monotonicity of Minkowski sums towards convexity. arXiv 2017. [Google Scholar]
- Harremoës, P.; Johnson, O.; Kontoyiannis, I. Thinning, entropy, and the law of thin numbers. IEEE Trans. Inf. Theory 2010, 56, 4228–4244. [Google Scholar] [CrossRef]
- Johnson, O.; Yu, Y. Monotonicity, thinning, and discrete versions of the entropy power inequality. IEEE Trans. Inf. Theory 2010, 56, 5387–5395. [Google Scholar] [CrossRef]
- Barbour, A.D.; Johnson, O.; Kontoyiannis, I.; Madiman, M. Compound Poisson approximation via information functionals. Electron. J. Probab. 2010, 15, 1344–1368. [Google Scholar]
- Johnson, O.; Kontoyiannis, I.; Madiman, M. Log-concavity, ultra-log-concavity, and a maximum entropy property of discrete compound Poisson measures. Discret. Appl. Math. 2013, 161, 1232–1250. [Google Scholar] [CrossRef]
- Croft, H.T. Research Problems; Mimeographed Notes: Cambridge, UK, August 1967. [Google Scholar]
- Macdonald, S.O.; Street, A.P. On Conway’s conjecture for integer sets. Bull. Aust. Math. Soc. 1973, 8, 355–358. [Google Scholar] [CrossRef]
- Marica, J. On a conjecture of Conway. Can. Math. Bull. 1969, 12, 233–234. [Google Scholar] [CrossRef]
- Nathanson, M.B. Problems in additive number theory. I. In Additive Combinatorics, CRM Proceedings Lecture Notes; American Mathematical Society: Providence, RI, USA, 2007; Volume 43, pp. 263–270. [Google Scholar]
- Stein, S.K. The cardinalities of A + A and A − A. Can. Math. Bull. 1973, 16, 343–345. [Google Scholar] [CrossRef]
- Piccard, S. Sur des Ensembles Parfaits; Mém. Univ. Neuchâtel; Secrétariat de l’Université: Neuchâtel, Switzerland, 1942; Volume 16, p. 172. (In French) [Google Scholar]
- Martin, G.; O’Bryant, K. Many sets have more sums than differences. In Additive Combinatorics, CRM Proceedings Lecture Notes; American Mathematical Society: Providence, RI, USA, 2007; Volume 43, pp. 287–305. [Google Scholar]
- Hegarty, P.; Miller, S.J. When almost all sets are difference dominated. Random Struct. Algoritms 2009, 35, 118–136. [Google Scholar] [CrossRef]
- Zhao, Y. Counting MSTD sets in finite abelian groups. J. Number Theory 2010, 130, 2308–2322. [Google Scholar] [CrossRef]
- Mossel, E. Gaussian bounds for noise correlation of functions. Geom. Funct. Anal. 2010, 19, 1713–1756. [Google Scholar] [CrossRef]
- Zhao, Y. Constructing MSTD sets using bidirectional ballot sequences. J. Number Theory 2010, 130, 1212–1220. [Google Scholar] [CrossRef]
- Stein, E.M.; Shakarchi, R. Fourier Analysis: An Introduction Princeton Lectures in Analysis; Princeton University Press: Princeton, NJ, USA, 2003; Volume 1, xvi, 311. [Google Scholar]
- Hegarty, P.V. Some explicit constructions of sets with more sums than differences. Acta Arith. 2007, 130, 61–77. [Google Scholar]
- Ruzsa, I.Z. On the number of sums and differences. Acta Math. Hung. 1992, 59, 439–447. [Google Scholar] [CrossRef]
- Nathanson, M.B. Sets with more sums than differences. Integers 2007, 7, 1–24. [Google Scholar]
- Li, J.; Madiman, M. A combinatorial approach to small ball inequalities for sums and differences. arXiv 2016. [Google Scholar]
- Ruzsa, I.Z. On the cardinality of A + A and A − A. In Combinatorics (Proc. Fifth Hungarian Colloq., Keszthely, 1976), Vol. II; János Bolyai Mathematical Society: Amsterdam, The Netherlands, 1978; Volume 18, pp. 933–938. [Google Scholar]
- Pigarev, V.P.; Freĭman, G.A. The Relation between the Invariants R and T. In Number-Theoretic Studies in the Markov Spectrum and in the Structural Theory of Set Addition (Russian); Kalinin Gos. University: Moscow, Russian, 1973; pp. 172–174. [Google Scholar]
- Arıkan, E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels. IEEE Trans. Inf. Theory 2009, 55, 3051–3073. [Google Scholar] [CrossRef] [Green Version]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006; xxiv, 748. [Google Scholar]
- Roth, R.M. Introduction to Coding Theory; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Park, W.; Barg, A. Polar codes for q-ary channels, q = 2r. IEEE Trans. Inf. Theory 2013, 59, 955–969. [Google Scholar] [CrossRef]
- Sahebi, A.G.; Pradhan, S.S. Multilevel channel polarization for arbitrary discrete memoryless channels. IEEE Trans. Inf. Theory 2013, 59, 7839–7857. [Google Scholar] [CrossRef]
- Mori, R.; Tanaka, T. Non-Binary Polar Codes using Reed-Solomon Codes and Algebraic Geometry Codes. In Proceedings of the 2010 IEEE Information Theory Workshop (ITW 2010), Dublin, Ireland, 30 August–3 September 2010. [Google Scholar]
- Arıkan, E. Source polarization. In Proceedings of the 2010 IEEE International Symposium on Information Theory Proceedings (ISIT), Austin, TX, USA, 13–18 June 2010; pp. 899–903. [Google Scholar]
- Abbe, E. Randomness and dependencies extraction via polarization. In Proceedings of the 2011 Information Theory and Applications Workshop (ITA), La Jolla, CA, USA, 6–11 February 2011; pp. 1–7. [Google Scholar]
- Arıkan, E.; Telatar, E. On the rate of channel polarization. In Proceedings of the 2009 IEEE International Symposium on Information Theory (ISIT 2009), Seoul, Korea, 28 June–3 July 2009; pp. 1493–1495. [Google Scholar]
- Abbe, E. Polar martingale of maximal spread. In Proceedings of the International Zurich Seminar, Zurich, Switzerland, 29 February–2 March 2012. [Google Scholar]
- Hassani, S.H.; Alishahi, K.; Urbanke, R.L. Finite-length scaling for polar codes. IEEE Trans. Inf. Theory 2014, 60, 5875–5898. [Google Scholar] [CrossRef]
- Mondelli, M.; Hassani, S.H.; Urbanke, R.L. Unified Scaling of Polar Codes: Error Exponent, Scaling Exponent, Moderate Deviations, and Error Floors. IEEE Trans. Inf. Theory 2016, 62, 6698–6712. [Google Scholar] [CrossRef]
- Hassani, H. Polarization and Spatial Coupling: Two Techniques to Boost Performance. Ph.D. Thesis, École Polytechnique Fédérale de Lausanne, Lausanne, Switzerland, 2013. [Google Scholar]
- Korada, S.B.; Şaşoğlu, E.; Urbanke, R. Polar codes: Characterization of exponent, bounds, and constructions. Trans. Inf. Theory 2010, 56, 6253–6264. [Google Scholar]
- Fazeli, A.; Vardy, A. On the Scaling Exponent of Binary Polarization Kernels. In Proceedings of the 2014 IEEE 52nd Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 30 September–3 October 2014; pp. 797–804. [Google Scholar]
- Pfister, H.D.; Urbanke, R. Near-Optimal Finite-Length Scaling for Polar Codes over Large Alphabets. In Proceedings of the 2016 IEEE International Symposium on Information Theory (ISIT), Barcelona, Spain, 10–15 July 2016; pp. 215–219. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbe, E.; Li, J.; Madiman, M. Entropies of Weighted Sums in Cyclic Groups and an Application to Polar Codes. Entropy 2017, 19, 235. https://doi.org/10.3390/e19090235
Abbe E, Li J, Madiman M. Entropies of Weighted Sums in Cyclic Groups and an Application to Polar Codes. Entropy. 2017; 19(9):235. https://doi.org/10.3390/e19090235
Chicago/Turabian StyleAbbe, Emmanuel, Jiange Li, and Mokshay Madiman. 2017. "Entropies of Weighted Sums in Cyclic Groups and an Application to Polar Codes" Entropy 19, no. 9: 235. https://doi.org/10.3390/e19090235
APA StyleAbbe, E., Li, J., & Madiman, M. (2017). Entropies of Weighted Sums in Cyclic Groups and an Application to Polar Codes. Entropy, 19(9), 235. https://doi.org/10.3390/e19090235




