The Emergence of Hyperchaos and Synchronization in Networks with Discrete Periodic Oscillators
Abstract
:1. Introduction
2. Complex Dynamical Networks
3. Emergence of Hyperchaos with Coupled Periodic Oscillators
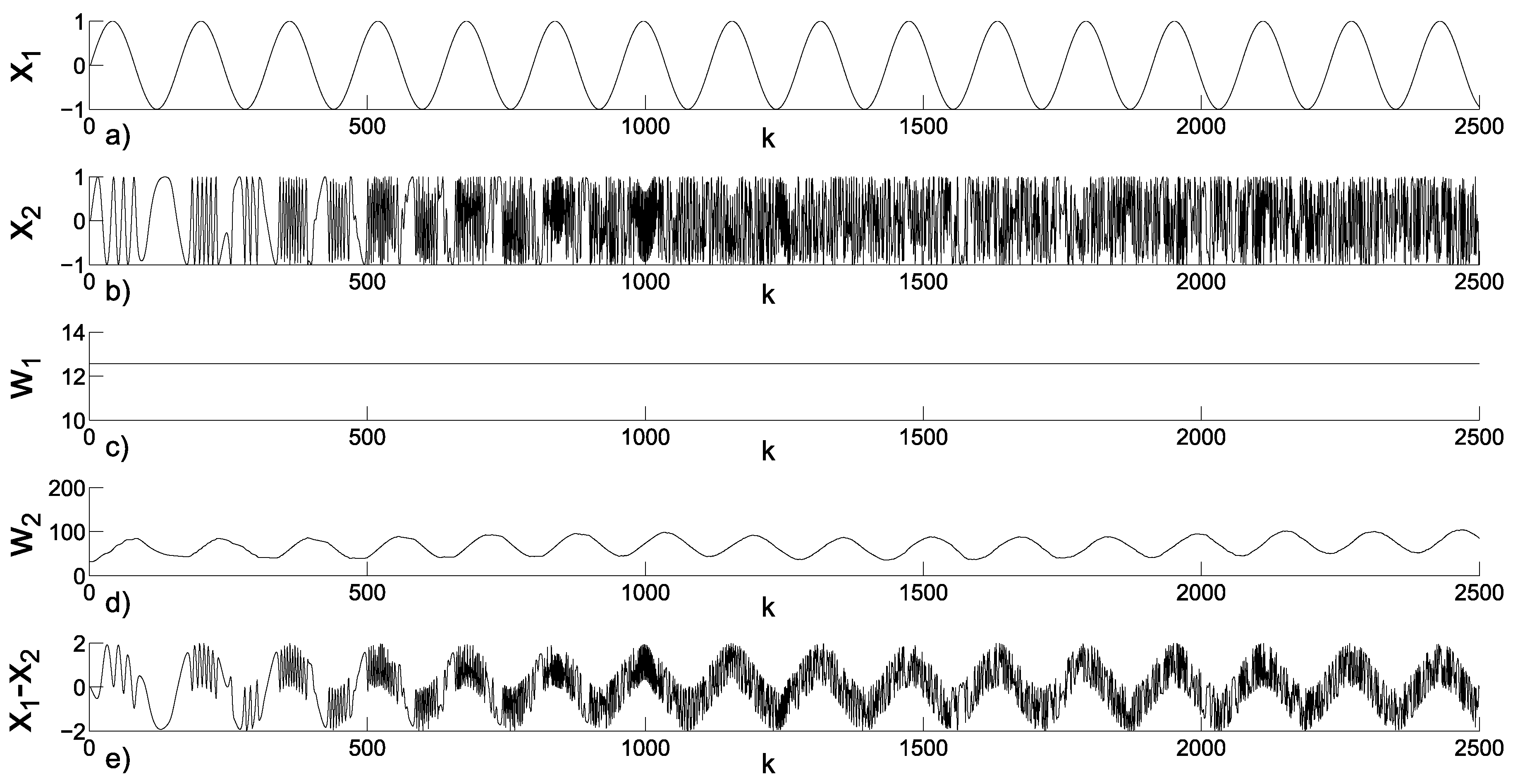
3.1. Uncoupled Periodic Oscillators
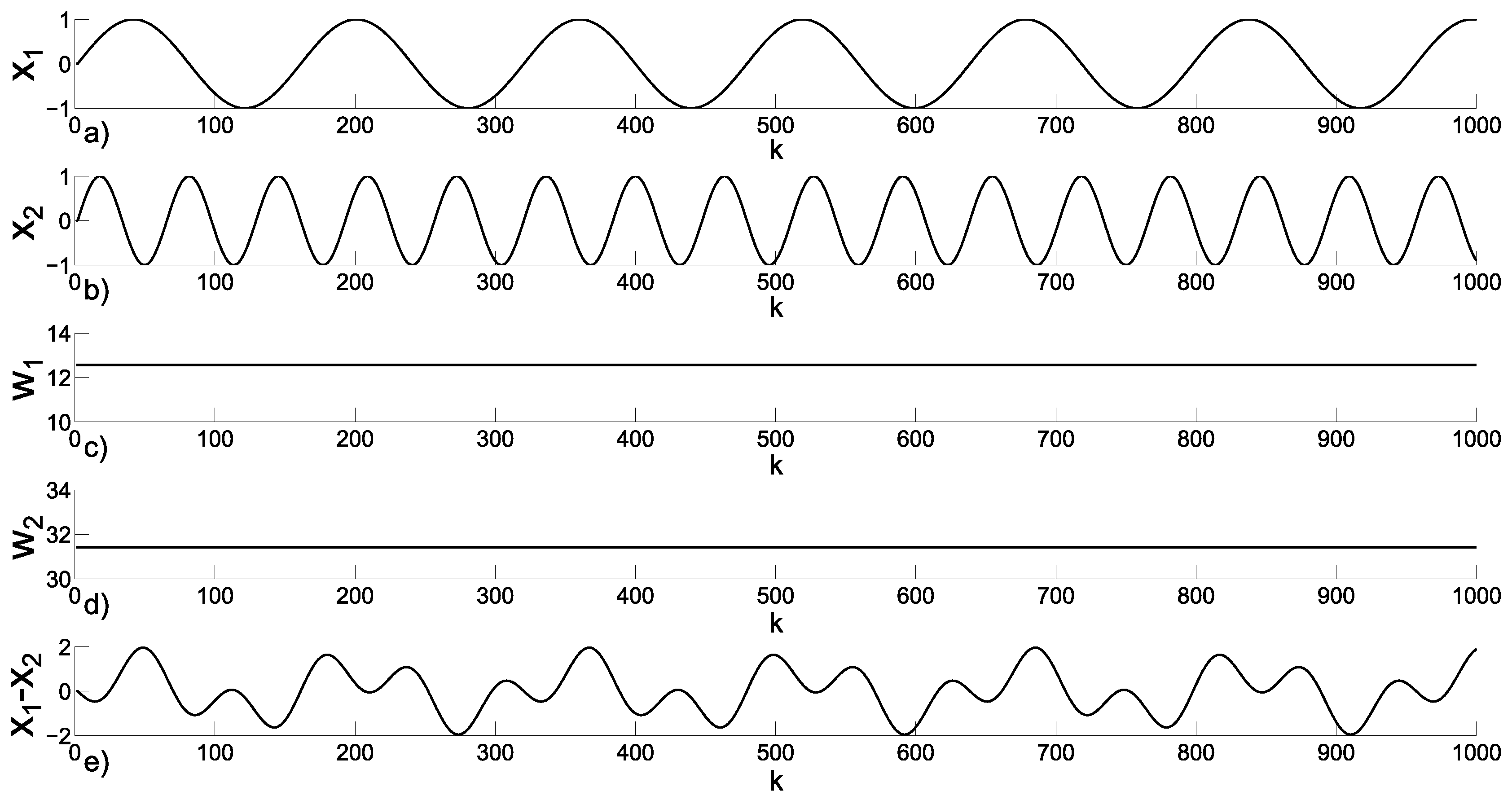
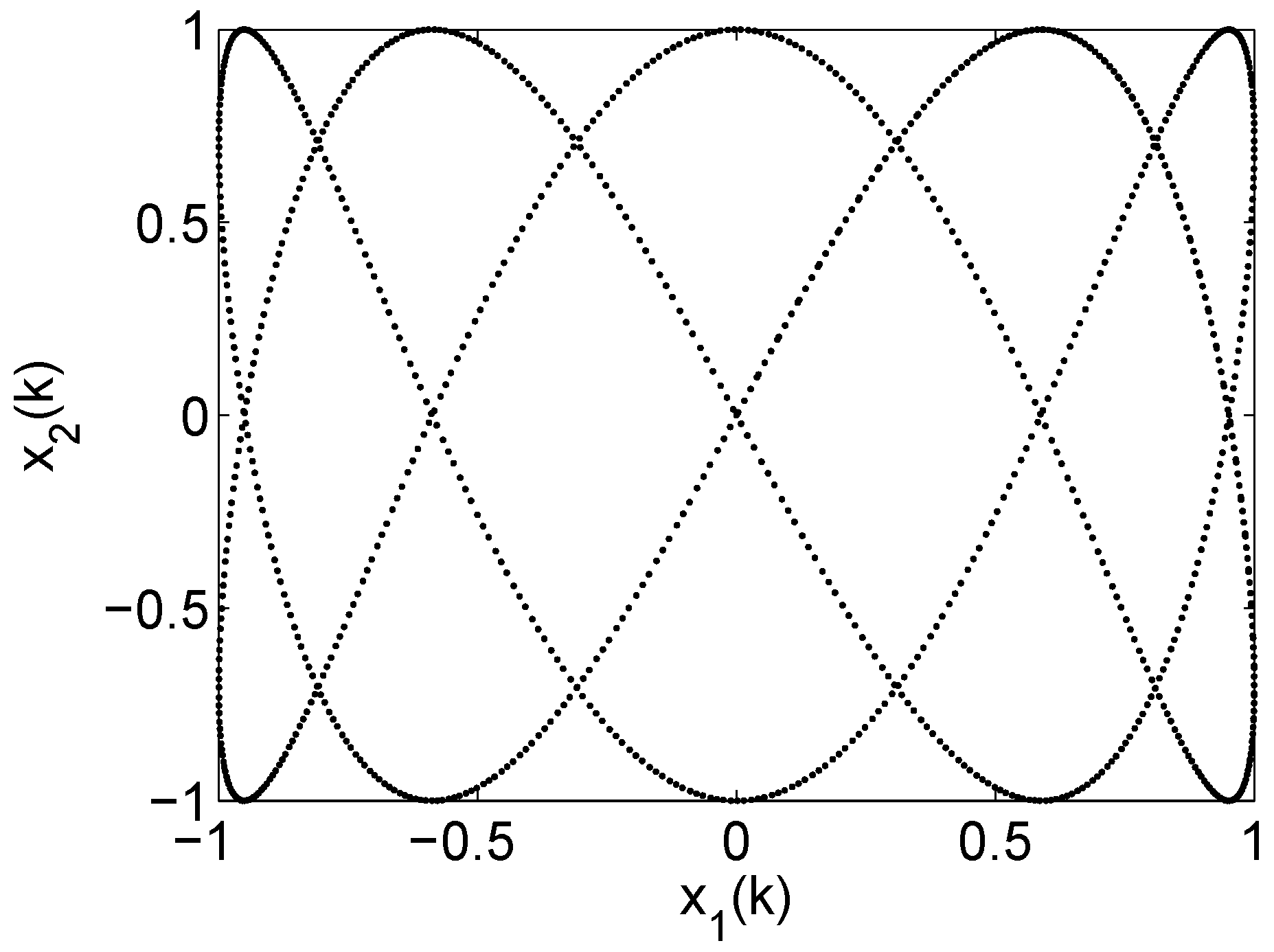
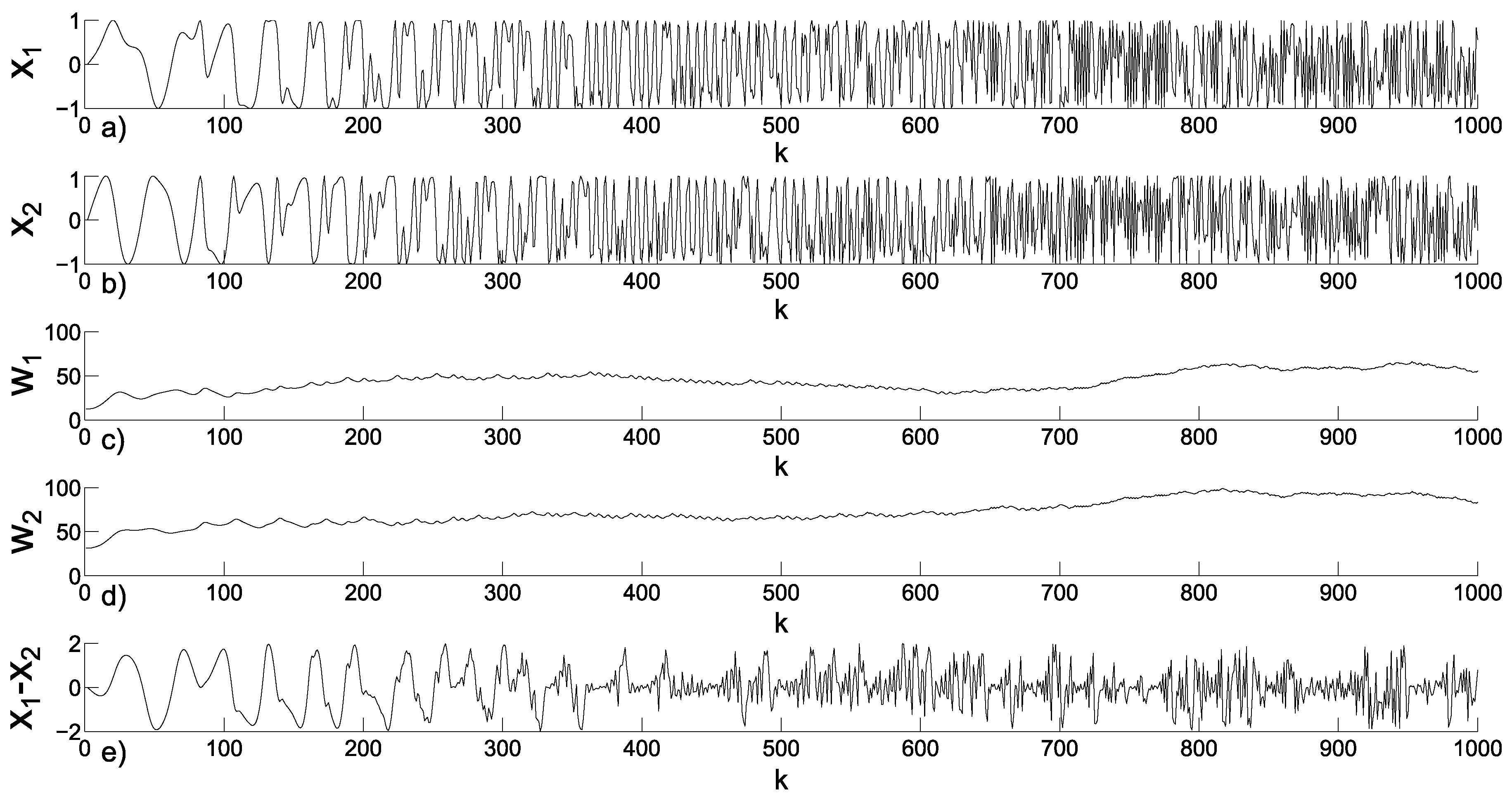
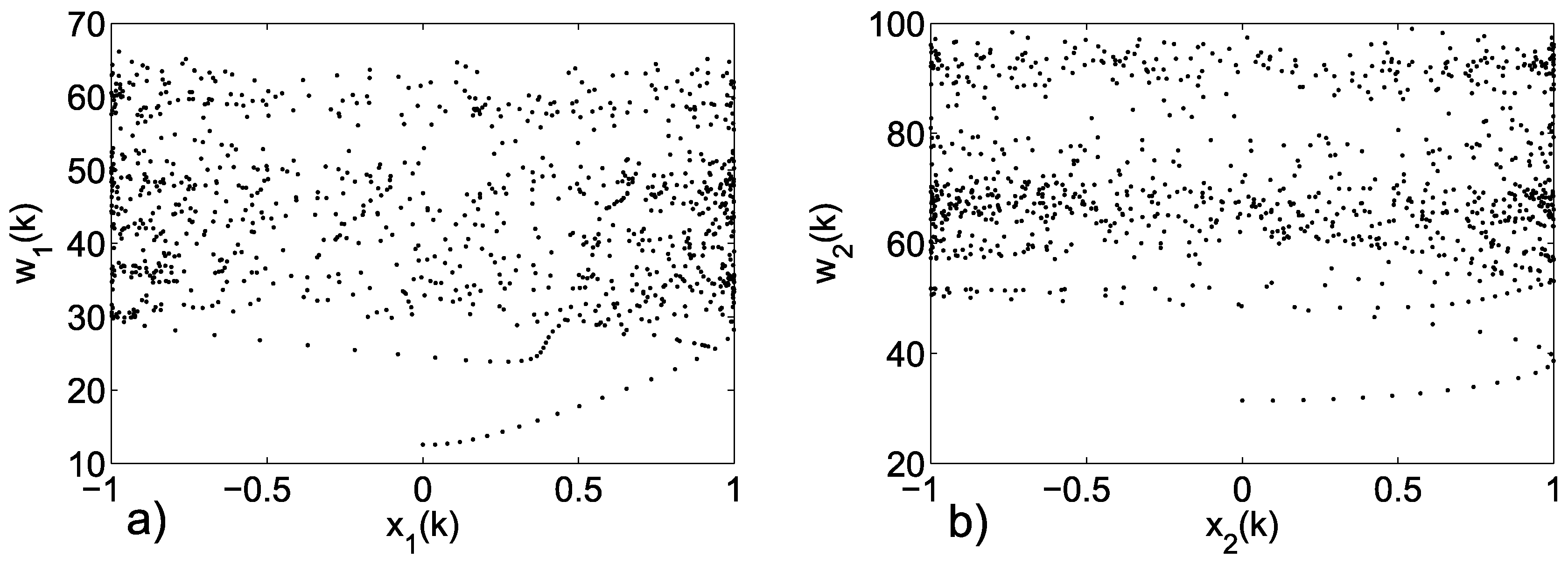
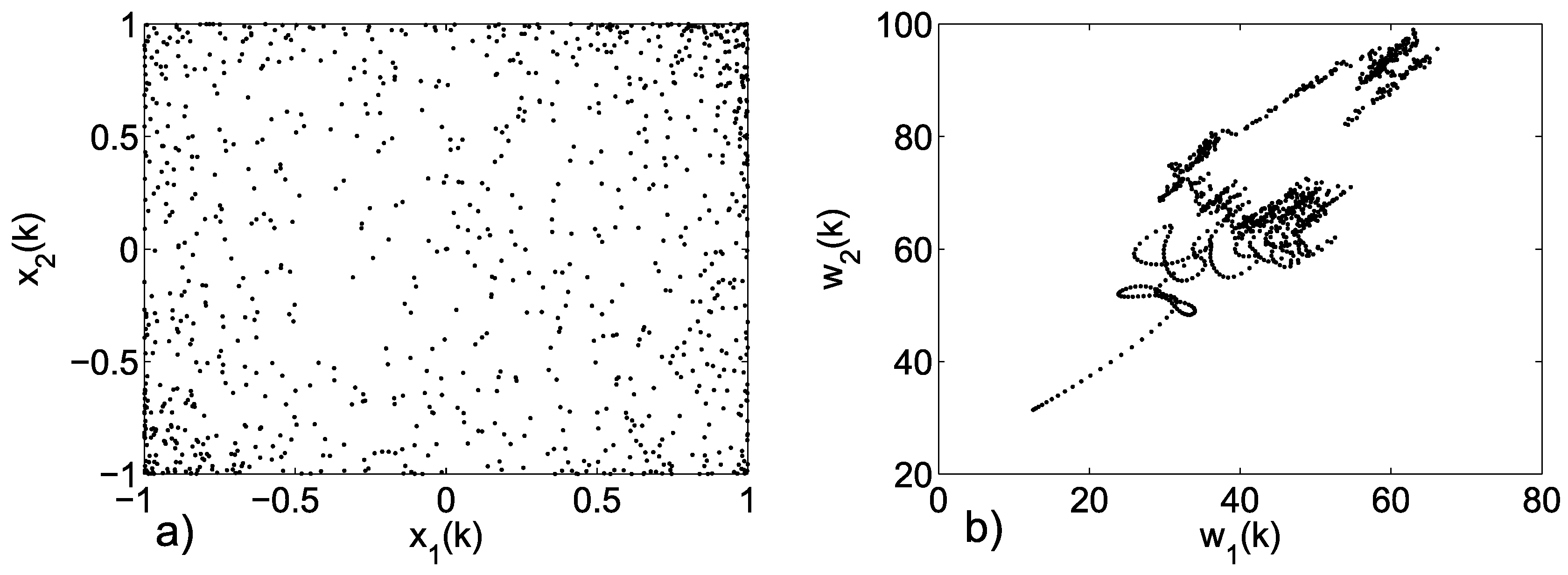
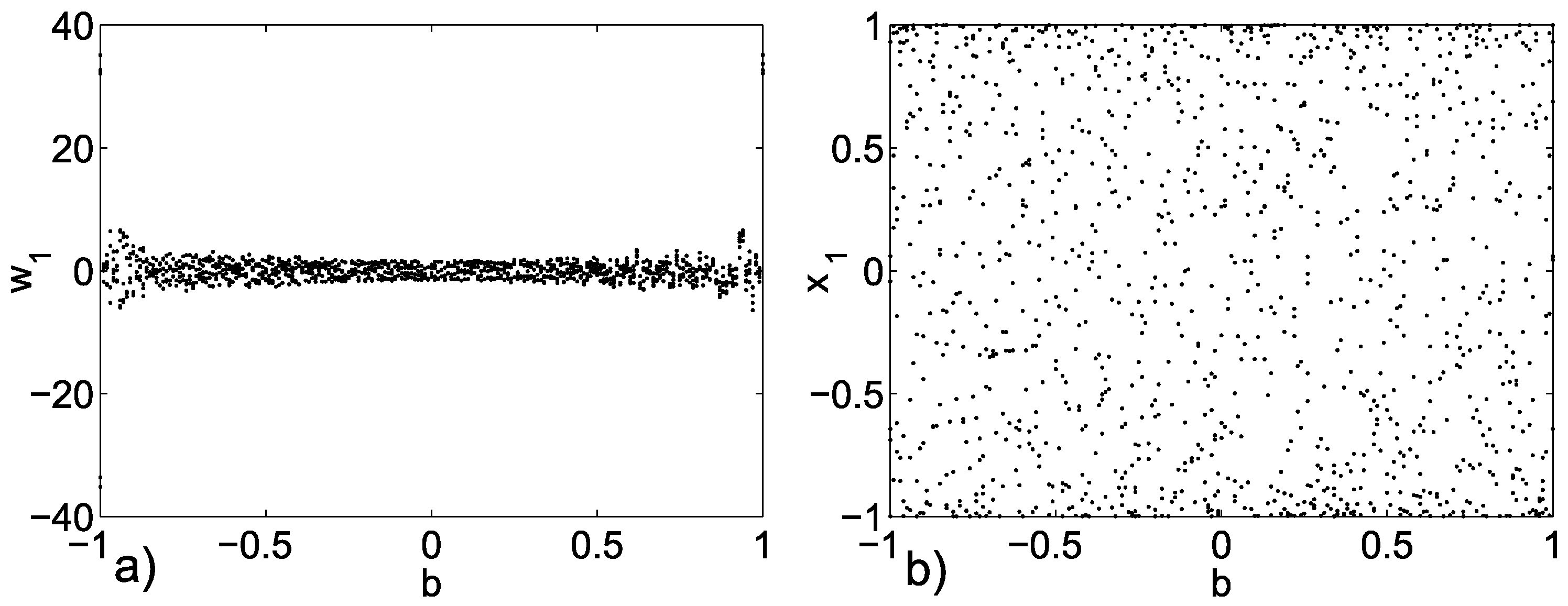
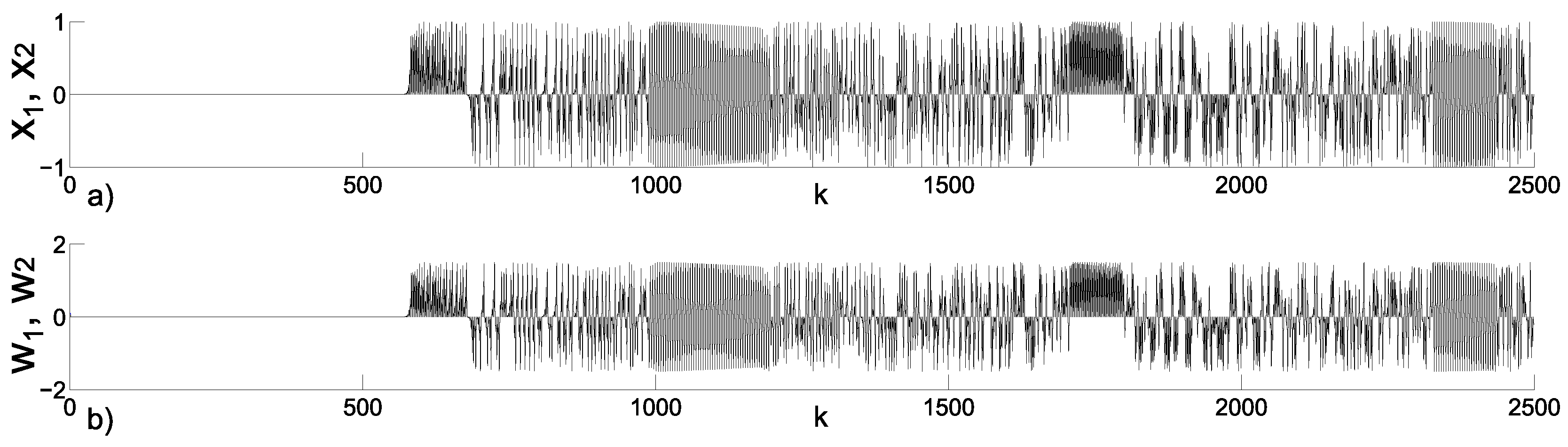
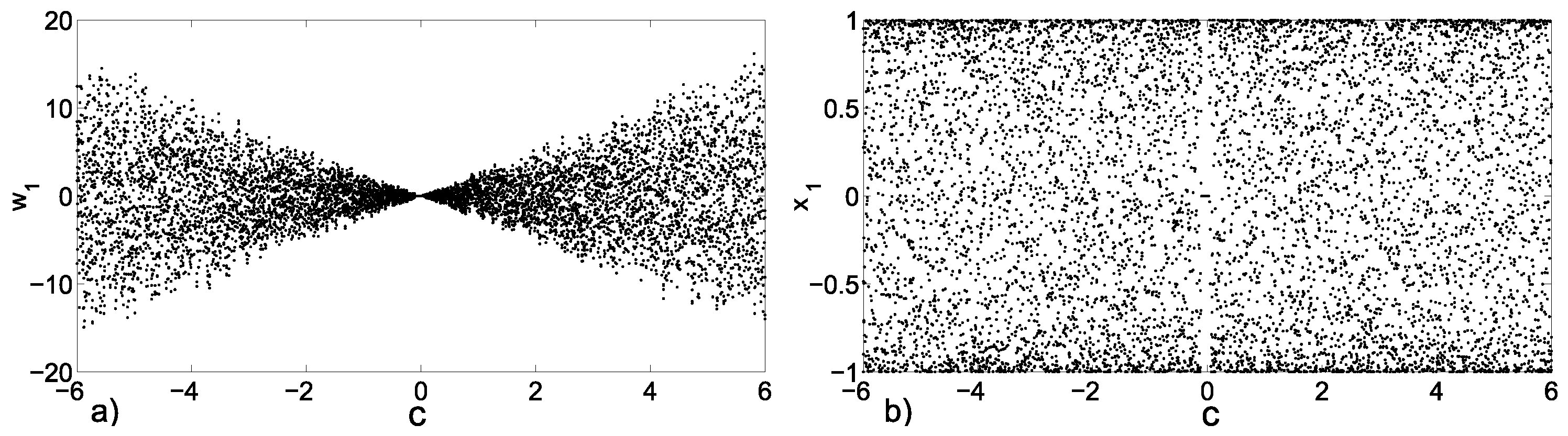
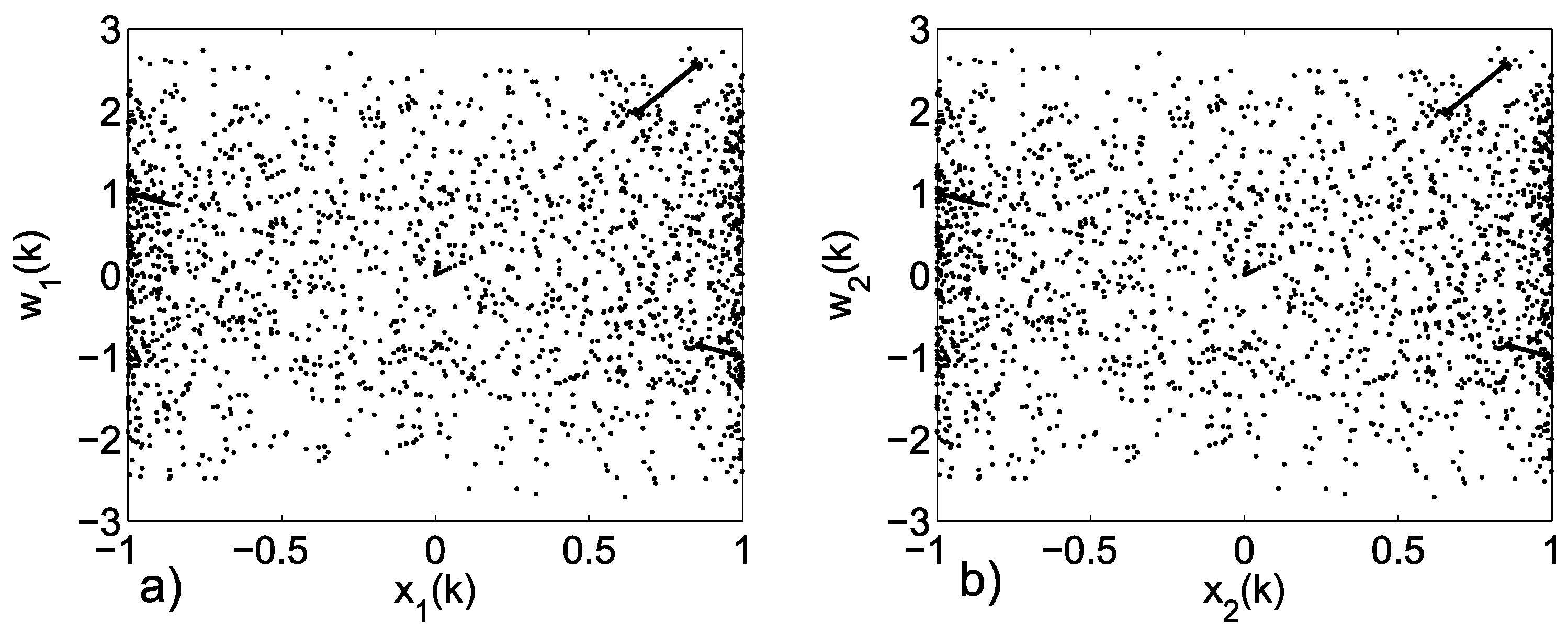
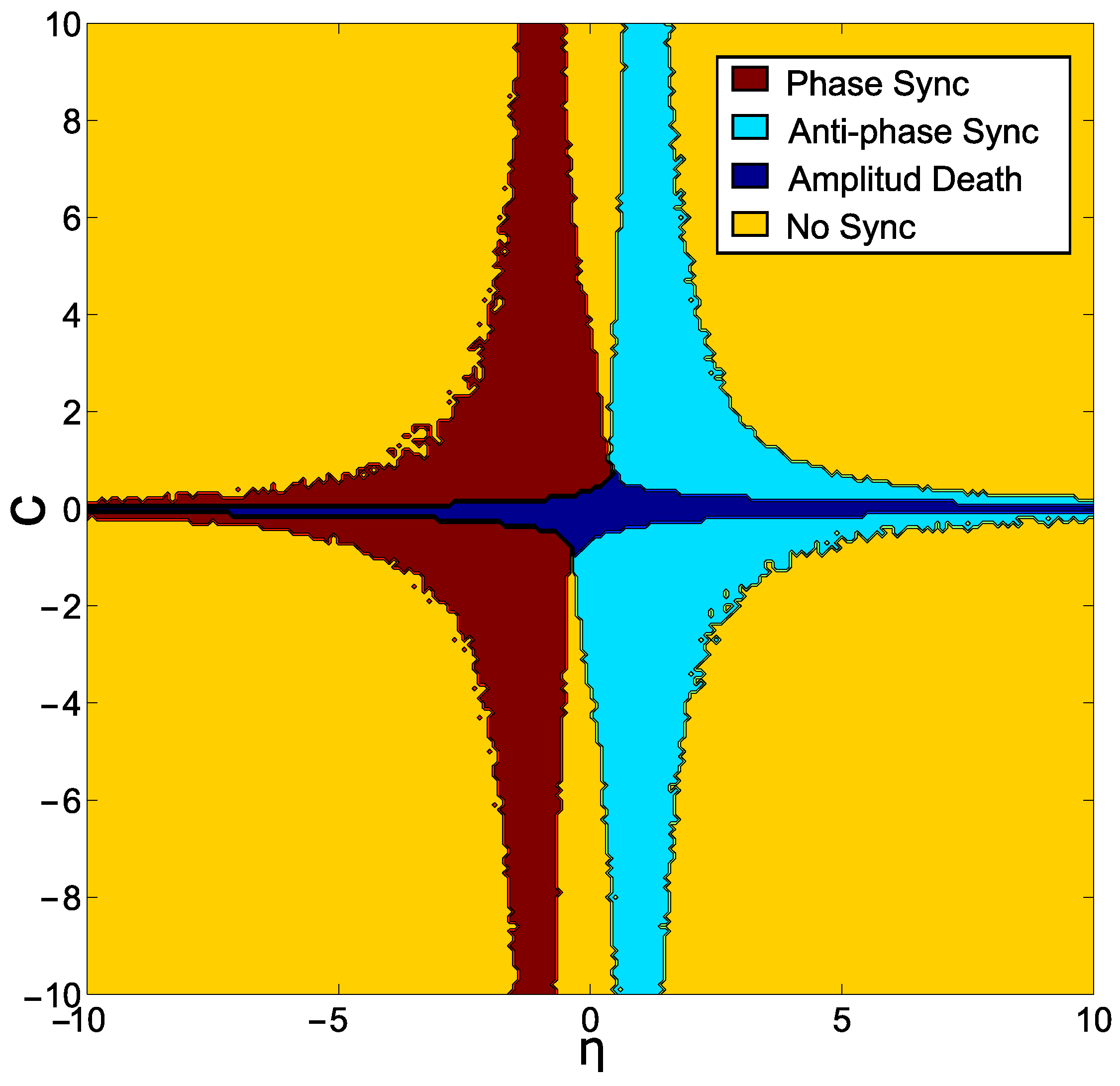
3.2. Emerging Hyperchaos with Two Coupled Periodic Oscillators
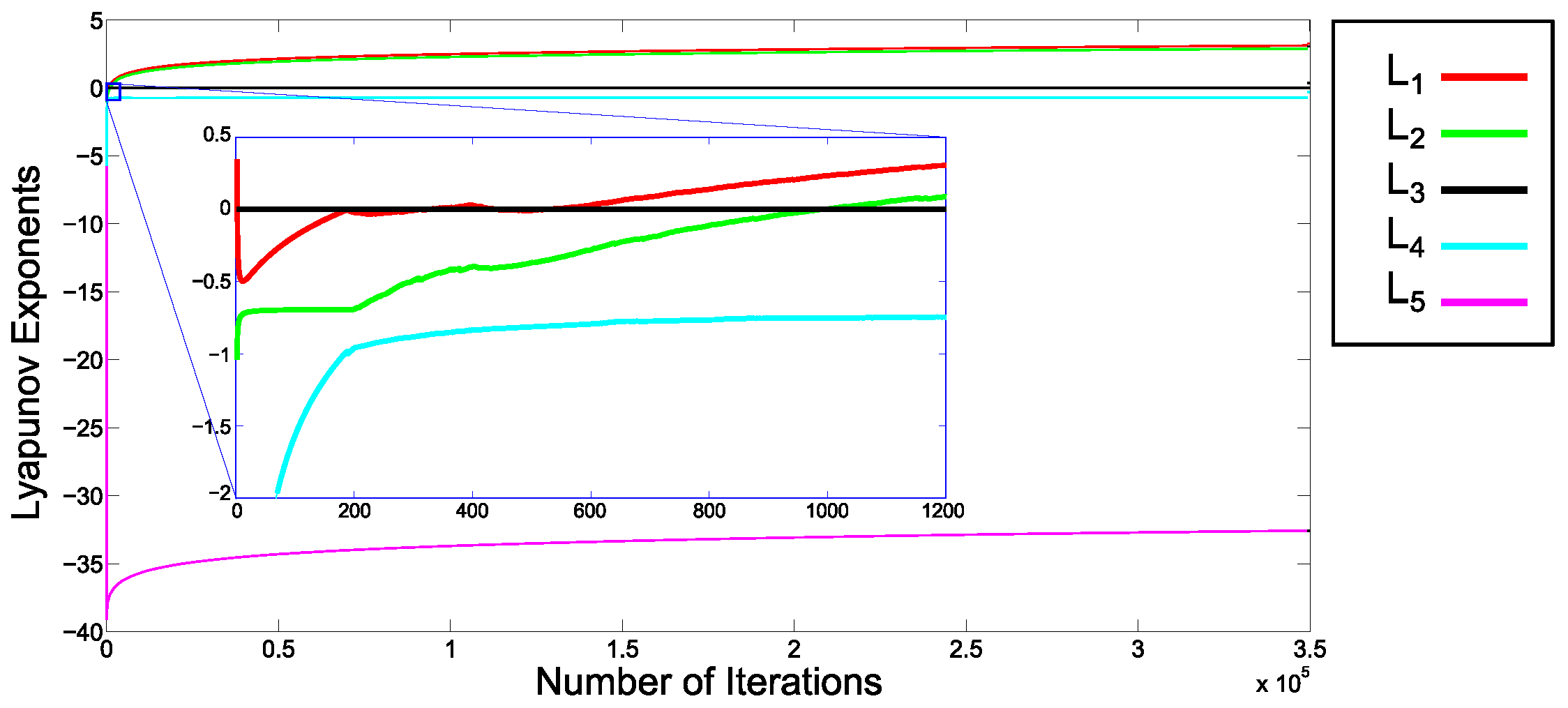
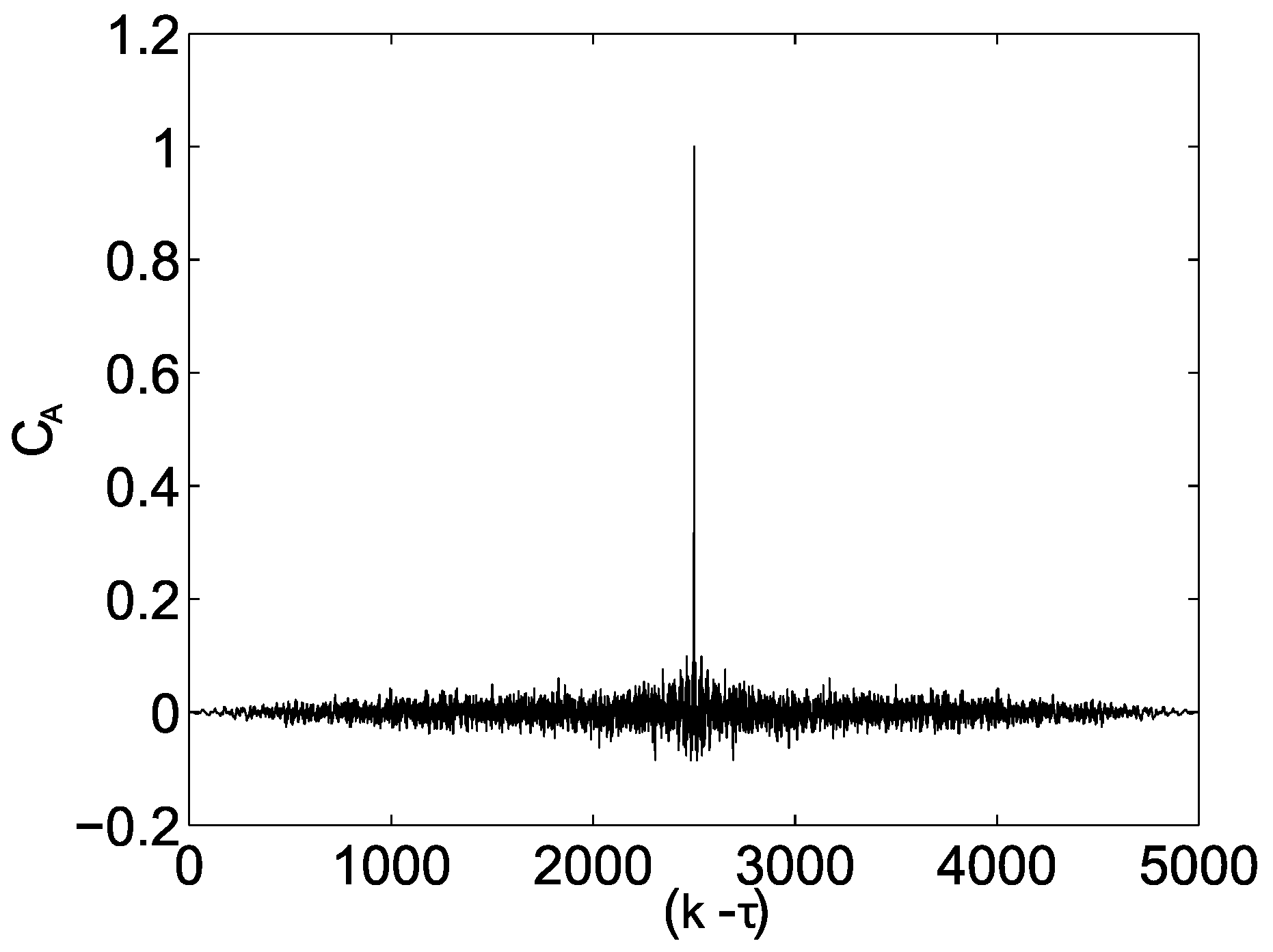
4. Confirmation of Collective Hyperchaotic Behavior
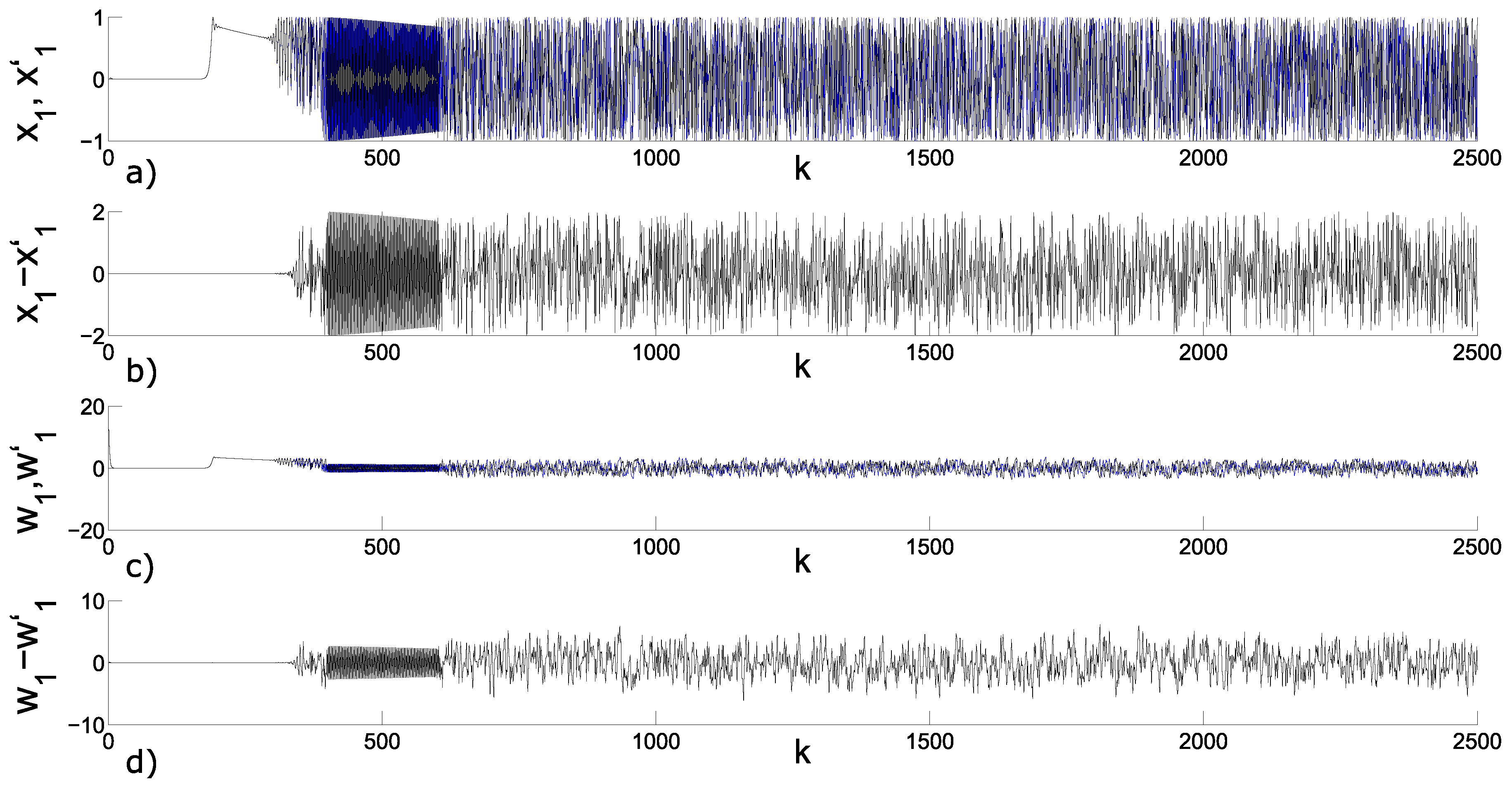
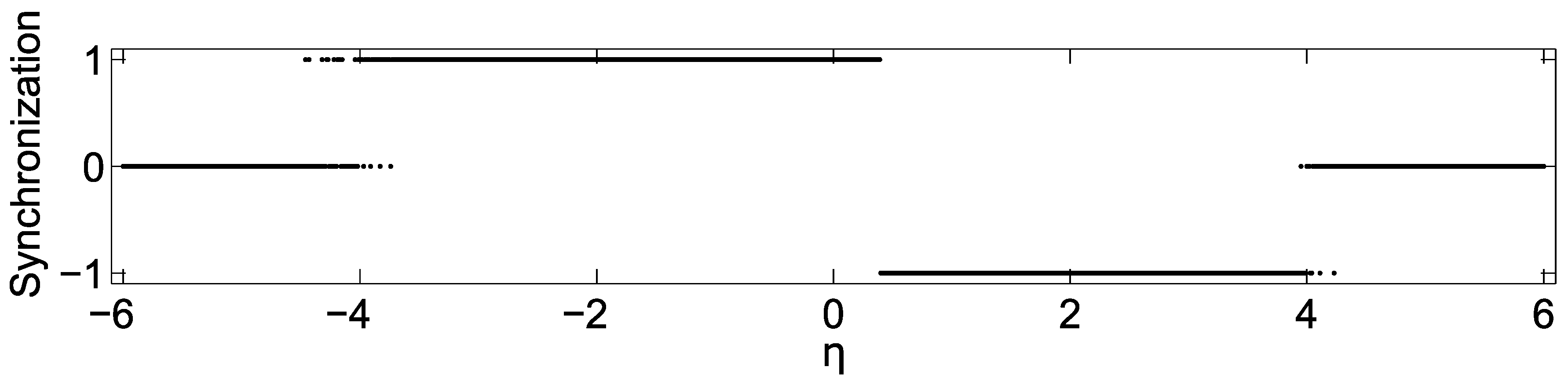
5. Hyperchaotic Network Synchronization of Two Oscillators
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chun-Ni, W.; Ma, J.; Liu, Y.; Huang, L. Chaos control, spiral wave formation, and the emergence of spatiotemporal chaos in networked Chua circuits. Nonlinear Dyn. 2012, 67, 139–146. [Google Scholar]
- Courbage, M.; Kazantsev, V.B.; Nekorkin, V.I.; Senneret, M. Emergence of chaotic attractor and anti-synchronization for two coupled monostable neurons. Chaos 2004, 14, 1148–1156. [Google Scholar] [CrossRef] [PubMed]
- Awrejcewicz, J. Bifurcation and Chaos in Coupled Oscillators; World Scientific Publishing: Teaneck, NJ, USA, 1991. [Google Scholar]
- Ulrichs, H.; Mann, A.; Parlitz, U. Synchronization and chaotic dynamics of coupled mechanical metronomes. Chaos 2009, 19, 043120. [Google Scholar] [CrossRef] [PubMed]
- Kanter, I. Emergence of Chaos in Asymmetric Networks. Phys. Rev. Lett. 1996, 77, 4844–4847. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.F.; Wu, R.X.; Fu, X.C. The emergence of chaos in complex dynamical networks. Chaos Solitons Fractals 2006, 28, 472–479. [Google Scholar] [CrossRef]
- Yuan, W.J.; Luo, X.S.; Jiang, P.Q.; Wang, B.H.; Fang, J.Q. Transition to chaos in small-world dynamical network. Chaos Solitons Fractals 2008, 37, 799–806. [Google Scholar] [CrossRef]
- Xiang, L.; Guanrong, C.; King-Tim, K. Transition to chaos in complex dynamical networks. Physica A 2008, 338, 367–378. [Google Scholar]
- Perlikowski, P.; Yanchuk, S.; Wolfrum, M.; Stefanski, A.; Mosiolek, P.; Kapitaniak, T. Routes to complex dynamics in a ring of unidirectionally coupled systems. Chaos 2010, 20, 013111. [Google Scholar] [CrossRef] [PubMed]
- Arroyo-Almanza, D.A.; Pisarchik, A.N.; Ruiz-Oliveras, F.R. Route to chaos in a ring of three unidirectionally-coupled semiconductor Lasers. IEEE Photonics Technol. Lett. 2012, 24, 605–607. [Google Scholar] [CrossRef]
- Arellano-Delgado, A.; López-Gutiérrez, R.M.; Cruz-Hernández, C.; Posadas-Castillo, C.; Cardoza-Avendaño, L.; Serrano-Guerrero, H. Experimental network synchronization via plastic optical fiber. Opt. Fiber Technol. 2013, 19, 93–108. [Google Scholar] [CrossRef]
- Posadas-Castillo, C.; Cruz-Hernández, C.; López-Gutiérrez, R.M. Experimental realization of synchronization in complex networks with Chua’s circuits like nodes. Chaos Solitons Fractals 2007, 40, 1963–1975. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, L. Network synchronization and application of chaotic Lur’e systems based on event-triggered mechanism. Nonlinear Dyn. 2016, 83, 2497–2507. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, R.; Ma, X.; Liu, S. Chaotic synchronization and anti-synchronization for a novel class of multiple chaotic systems via a sliding mode control scheme. Nonlinear Dyn. 2012, 69, 35–55. [Google Scholar] [CrossRef]
- Mirollo, R.E.; Strogatz, S.H. Synchronization of pulse-coupled biological oscillators. SIAM J. Appl. Math. 1990, 50, 1645–1662. [Google Scholar] [CrossRef]
- Strogatz, S.H. Spontaneous Synchronization in nature. In Proceedings of the International Frequency Control Symposium, Orlando, FL, USA, 30 May 1997. [Google Scholar]
- Lewis, F.L.; Zhang, H.; Hengster-Movric, K.; Das, A. Cooperative Control of Multi-Agent Systems Optimal and Adaptive Design Approaches; Springer: London, UK, 2013. [Google Scholar]
- Arellano-Delgado, A.; Cruz-Hernández, C.; López-Gutiérrez, R.M.; Posadas-Castillo, C. Outer synchronization of simple firefly discrete models in coupled networks. Math. Probl. Eng. 2015, 2015, 895379. [Google Scholar] [CrossRef]
- Chen, B.S.; Hsieh, C.Y.; Ho, S.J. System Entropy Measurement of Stochastic Partial Differential Systems. Entropy 2016, 18, 99. [Google Scholar] [CrossRef]
- Garbaczewski, P. Differential entropy and time. Entropy 2005, 7, 253–299. [Google Scholar] [CrossRef]
- Harremoës, P.; Topsøe, F. Maximum Entropy Fundamentals. Entropy 2001, 3, 191–226. [Google Scholar] [CrossRef]
- Gao, J.; Liu, F.; Zhang, J.; Hu, J.; Cao, Y. Information Entropy As a Basic Building Block of Complexity Theory. Entropy 2013, 15, 3396–3418. [Google Scholar] [CrossRef]
- Cruz-Hernández, C.; López-Gutiérrez, R.M.; Aguilar-Bustos, A.Y.; Posadas-Castillo, C. Communicating encrypted information based on synchronized hyperchaotic maps. Int. J. Nonlinear Sci. Numer. 2010, 11, 337–349. [Google Scholar] [CrossRef]
- Cruz-Hernández, C.; Aguilar-Bustos, A.Y. Synchronization of discrete-time hyperchaotic systems. CSF 2009, 41, 1301–1310. [Google Scholar]
- Song, C.; Qiao, Y. A Novel Image Encryption Algorithm Based on DNA Encoding and Spatiotemporal Chaos. Entropy 2015, 17, 6954–6968. [Google Scholar] [CrossRef]
- Méndez-Ramírez, R.; Arellano-Delgado, A.; Cruz-Hernández, C.; Martínez-Clark, R. A new simple chaotic Lorenz-type system and its digital realization using a TFT touch-screen display embedded system. Complexity 2017, 2017, 6820492. [Google Scholar] [CrossRef]
- Wang, X.; Chen, G. Synchronization in small-world dynamical networks. Int. J. Bifurc. Chaos 2002, 12, 187–192. [Google Scholar] [CrossRef]
- Wang, X. Complex networks: Topology, dynamics and synchronization. Int. J. Bifurc. Chaos 2002, 12, 885–916. [Google Scholar] [CrossRef]
- Gottwald, G.A.; Melbourne, I. A new test for chaos in a deterministic system. Proc. R. Soc. A 2004, 460, 603–611. [Google Scholar] [CrossRef]
- Farmer, J.D.; Ott, E.; Yorke, J.A. The dimension of chaotic attractors. Physica D 1983, 7, 153–180. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov Exponents from a Time Series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Theiler, J. Efficient algorithm for estimating the correlation dimension from a set of discrete points. Phys. Rev. A 1987, 36, 4456–4462. [Google Scholar] [CrossRef]

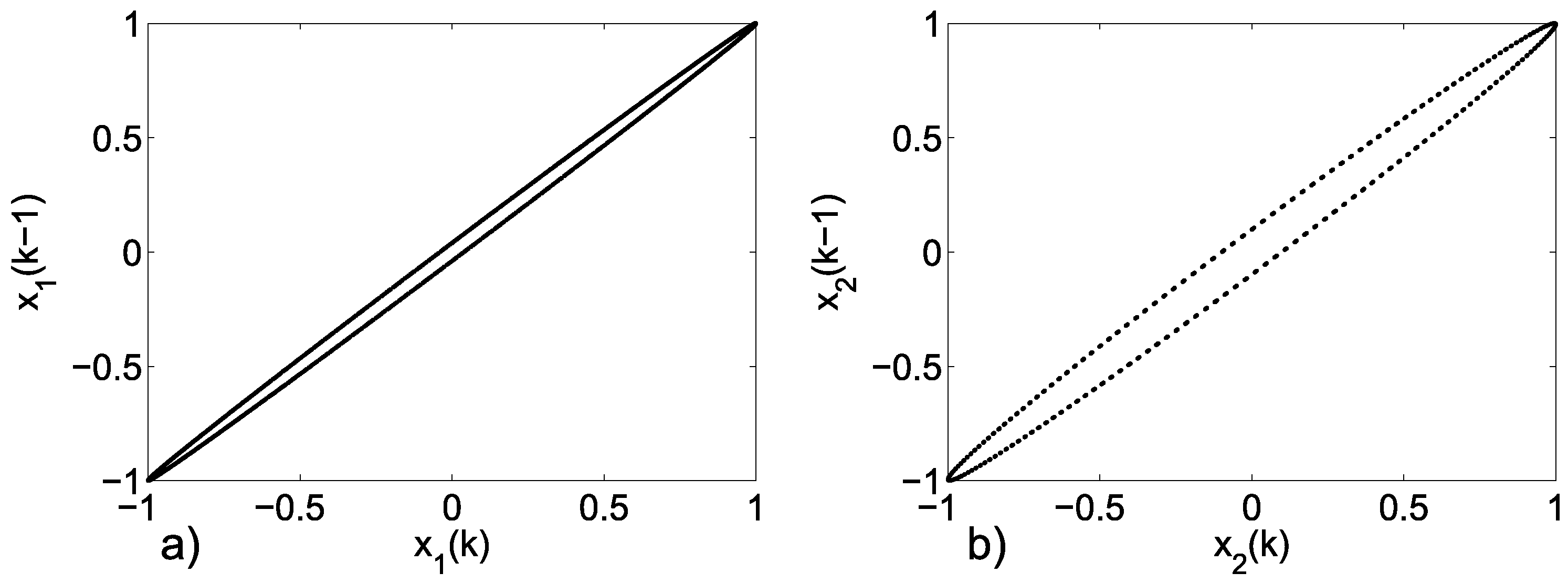
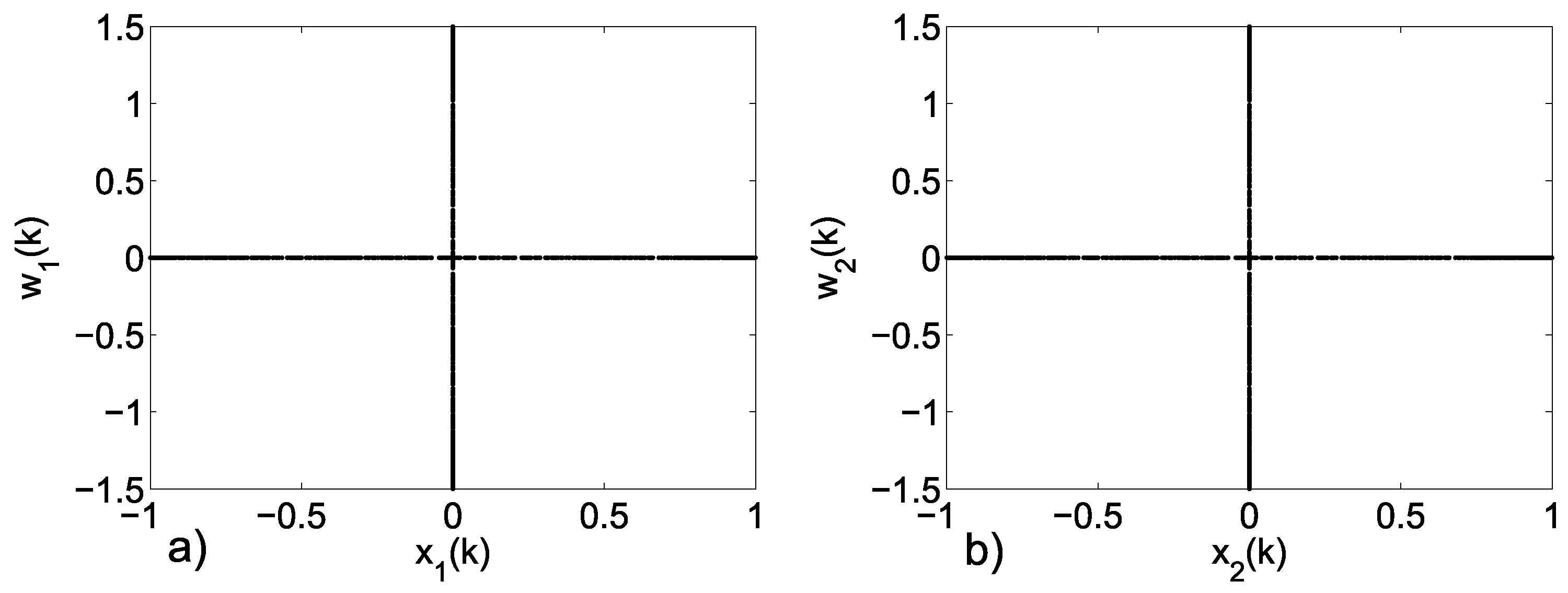
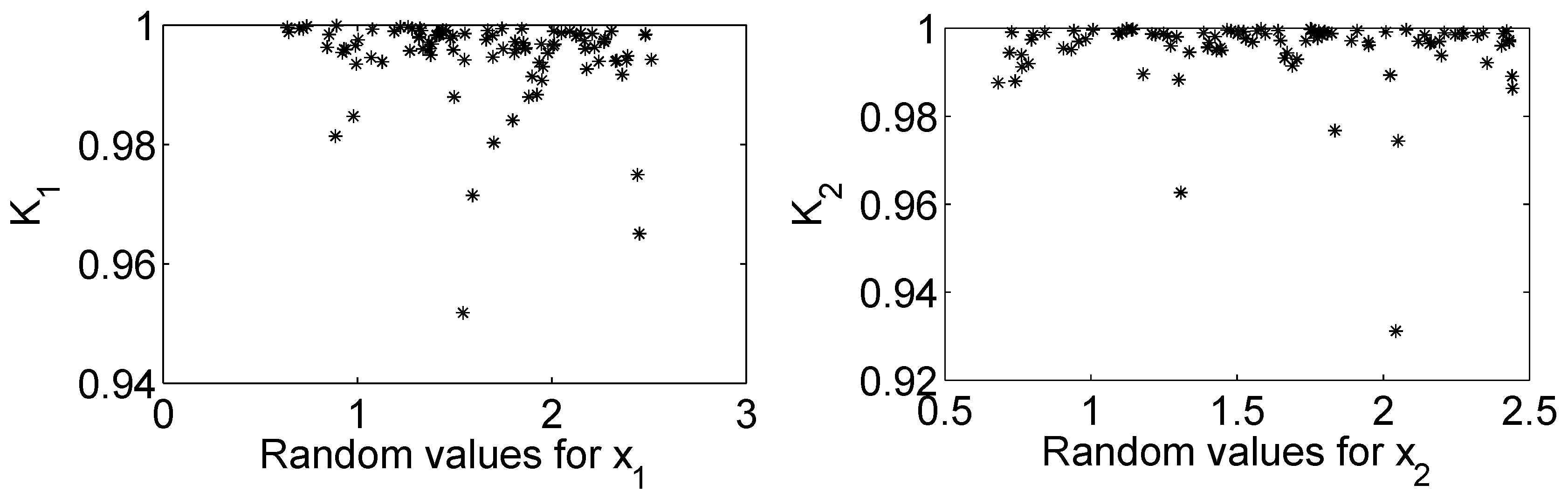


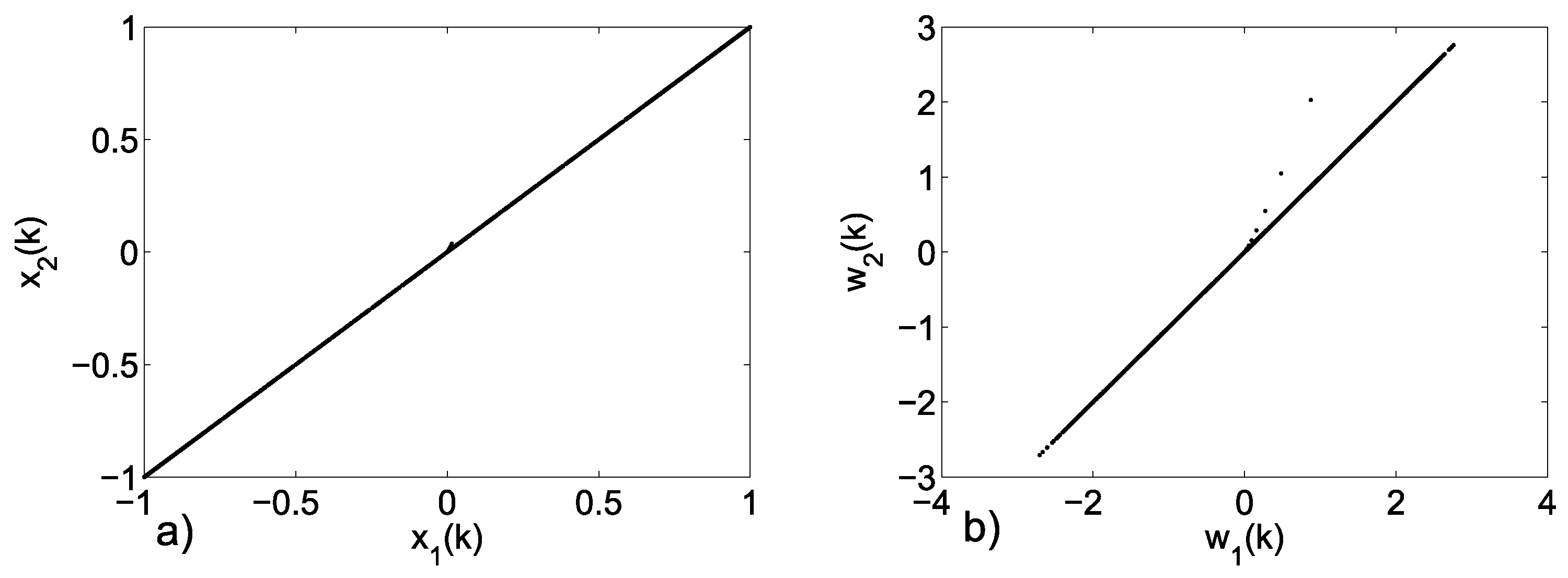
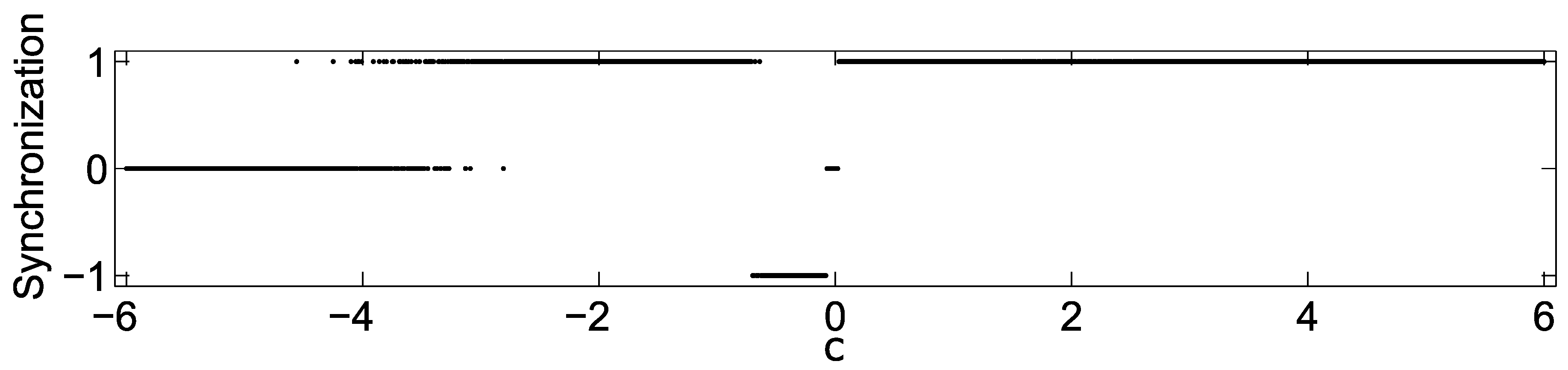
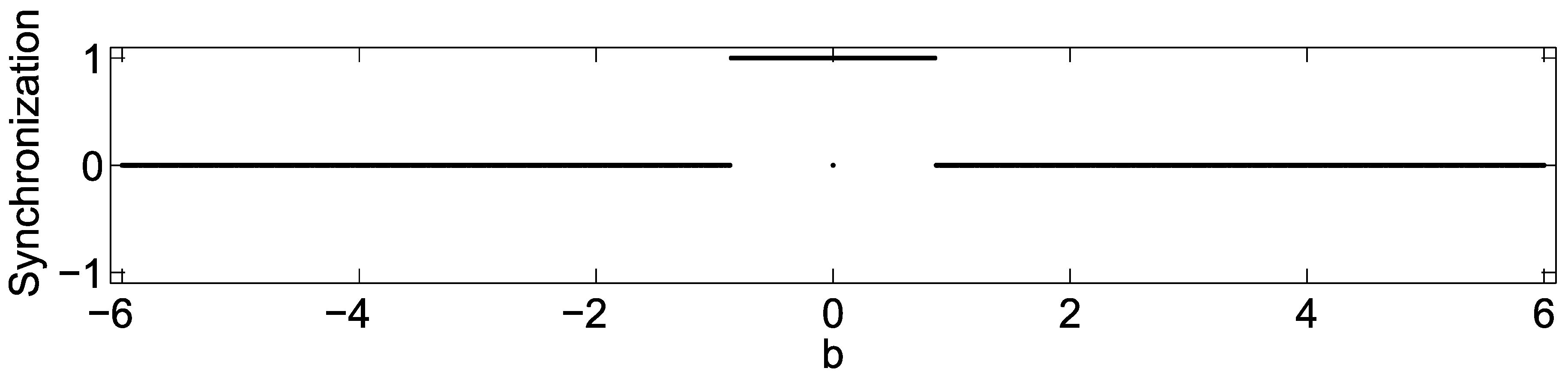
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arellano-Delgado, A.; López-Gutiérrez, R.M.; Murillo-Escobar, M.A.; Cardoza-Avendaño, L.; Cruz-Hernández, C. The Emergence of Hyperchaos and Synchronization in Networks with Discrete Periodic Oscillators. Entropy 2017, 19, 413. https://doi.org/10.3390/e19080413
Arellano-Delgado A, López-Gutiérrez RM, Murillo-Escobar MA, Cardoza-Avendaño L, Cruz-Hernández C. The Emergence of Hyperchaos and Synchronization in Networks with Discrete Periodic Oscillators. Entropy. 2017; 19(8):413. https://doi.org/10.3390/e19080413
Chicago/Turabian StyleArellano-Delgado, Adrian, Rosa Martha López-Gutiérrez, Miguel Angel Murillo-Escobar, Liliana Cardoza-Avendaño, and César Cruz-Hernández. 2017. "The Emergence of Hyperchaos and Synchronization in Networks with Discrete Periodic Oscillators" Entropy 19, no. 8: 413. https://doi.org/10.3390/e19080413
APA StyleArellano-Delgado, A., López-Gutiérrez, R. M., Murillo-Escobar, M. A., Cardoza-Avendaño, L., & Cruz-Hernández, C. (2017). The Emergence of Hyperchaos and Synchronization in Networks with Discrete Periodic Oscillators. Entropy, 19(8), 413. https://doi.org/10.3390/e19080413