Self-Organized Supercriticality and Oscillations in Networks of Stochastic Spiking Neurons
Abstract
1. Introduction
2. The Model
3. Mean-Field Calculations
4. Results
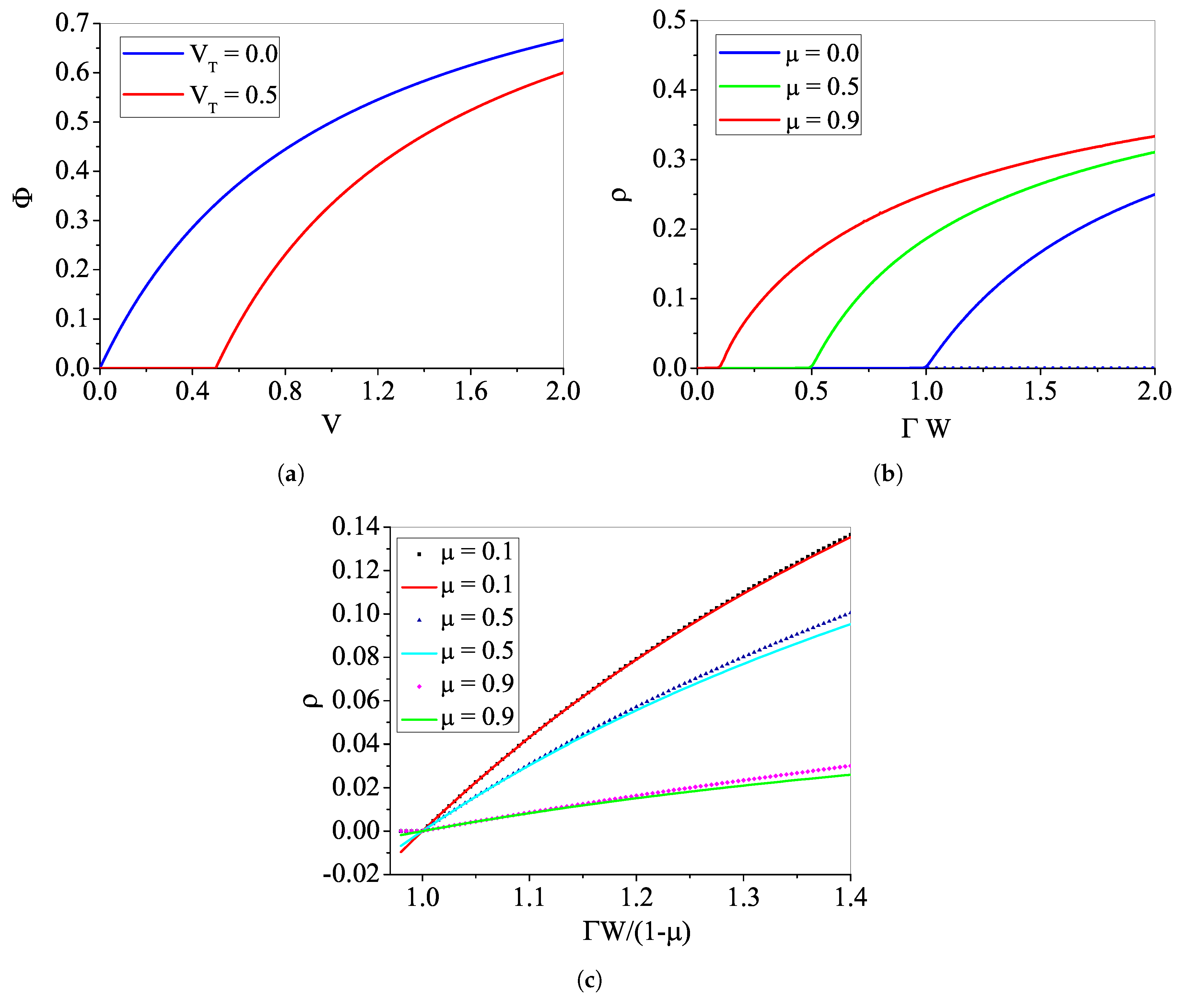
4.1. Phase Transitions for the Rational
4.1.1. The Case with
4.1.2. Analytic Results for
4.1.3. The Case with : Continuous Transition
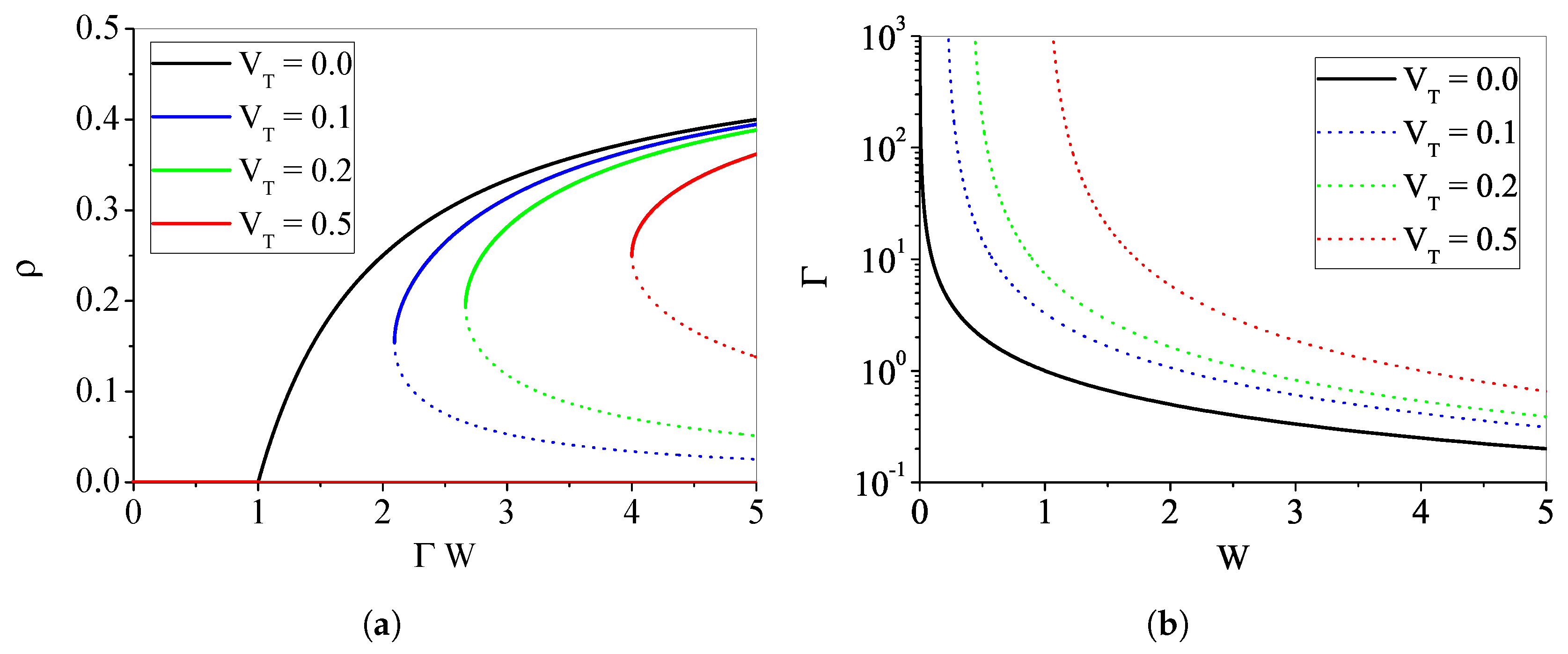
4.1.4. The Case with : Discontinuous Transition
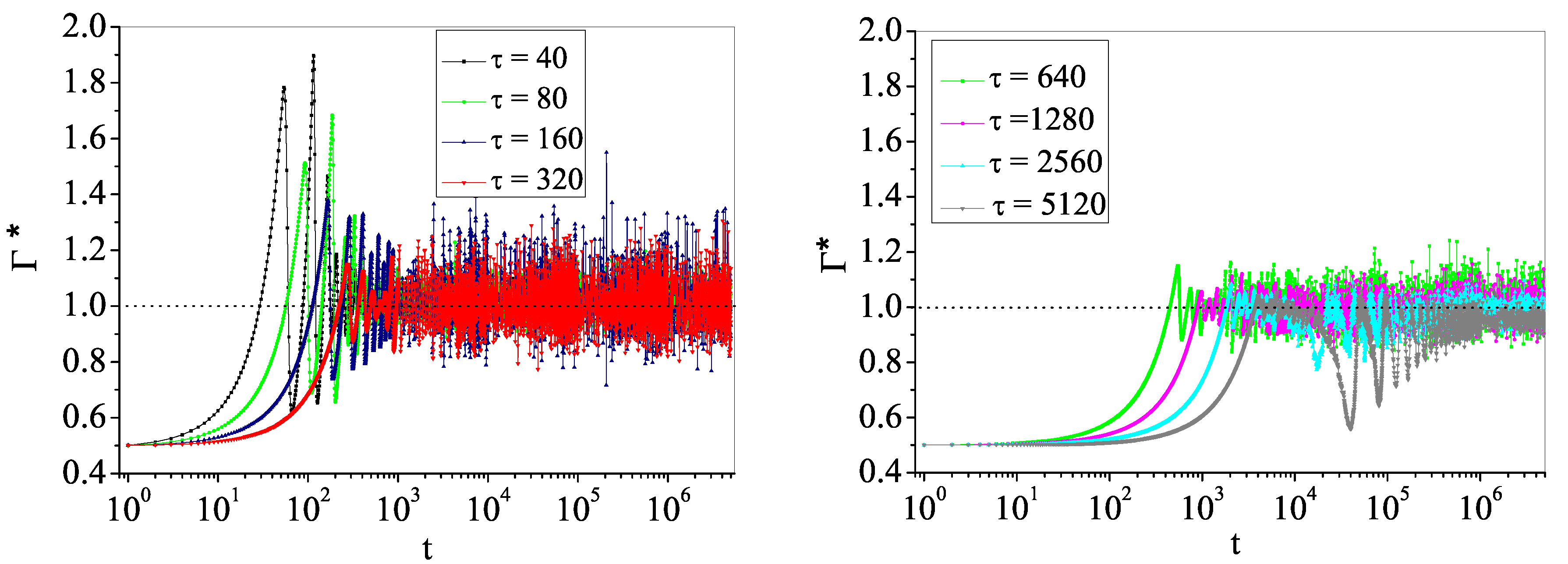
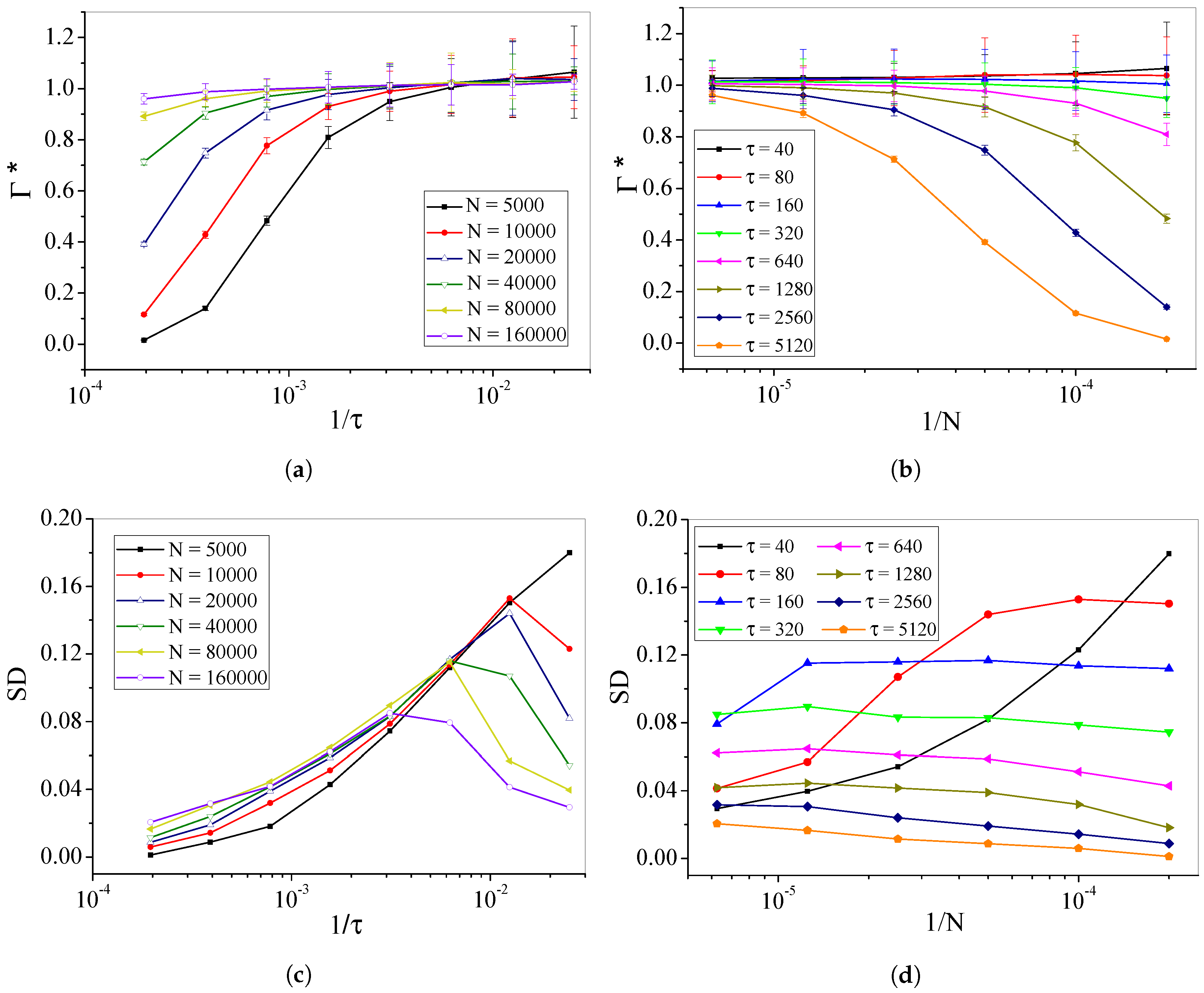
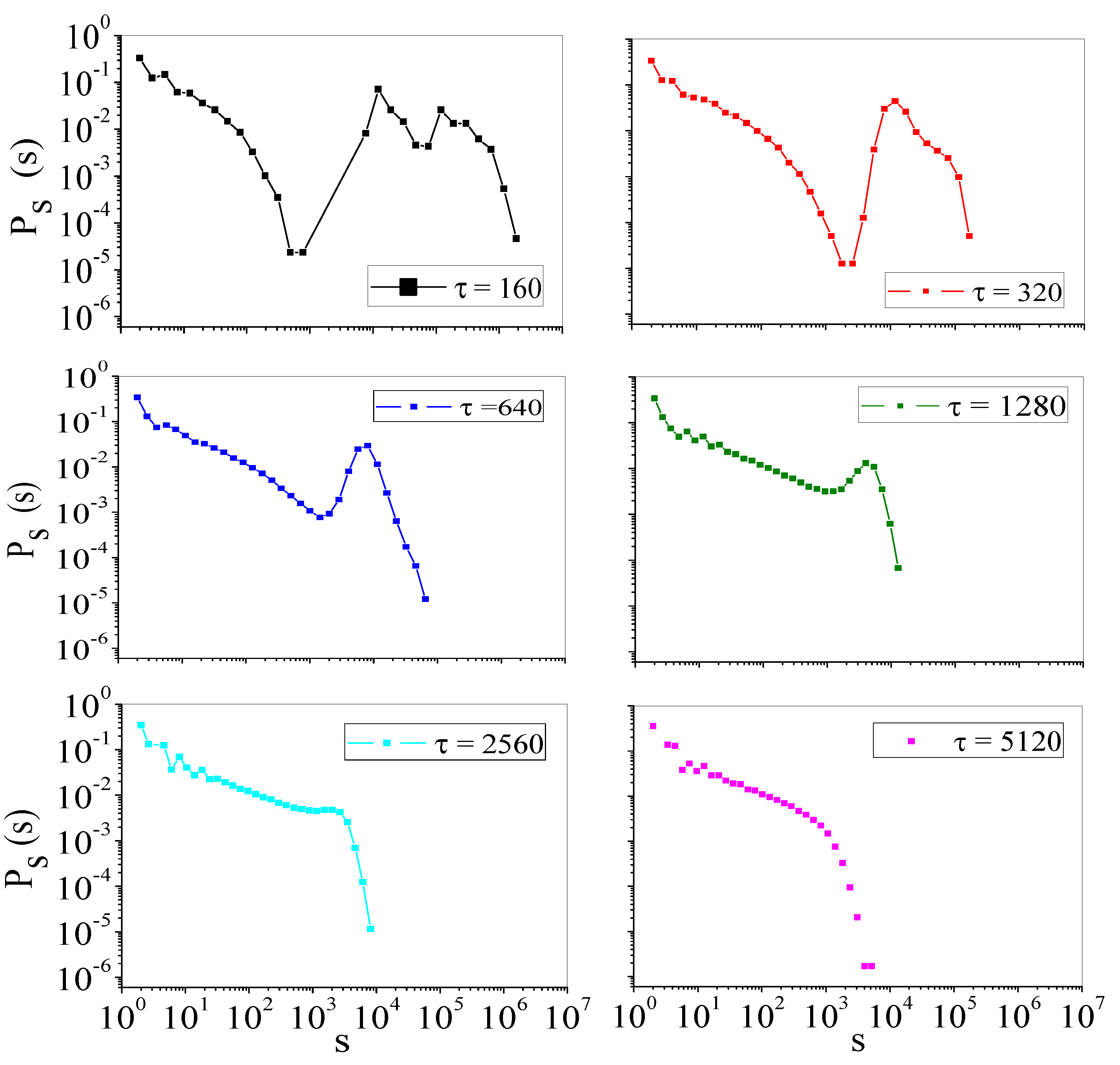
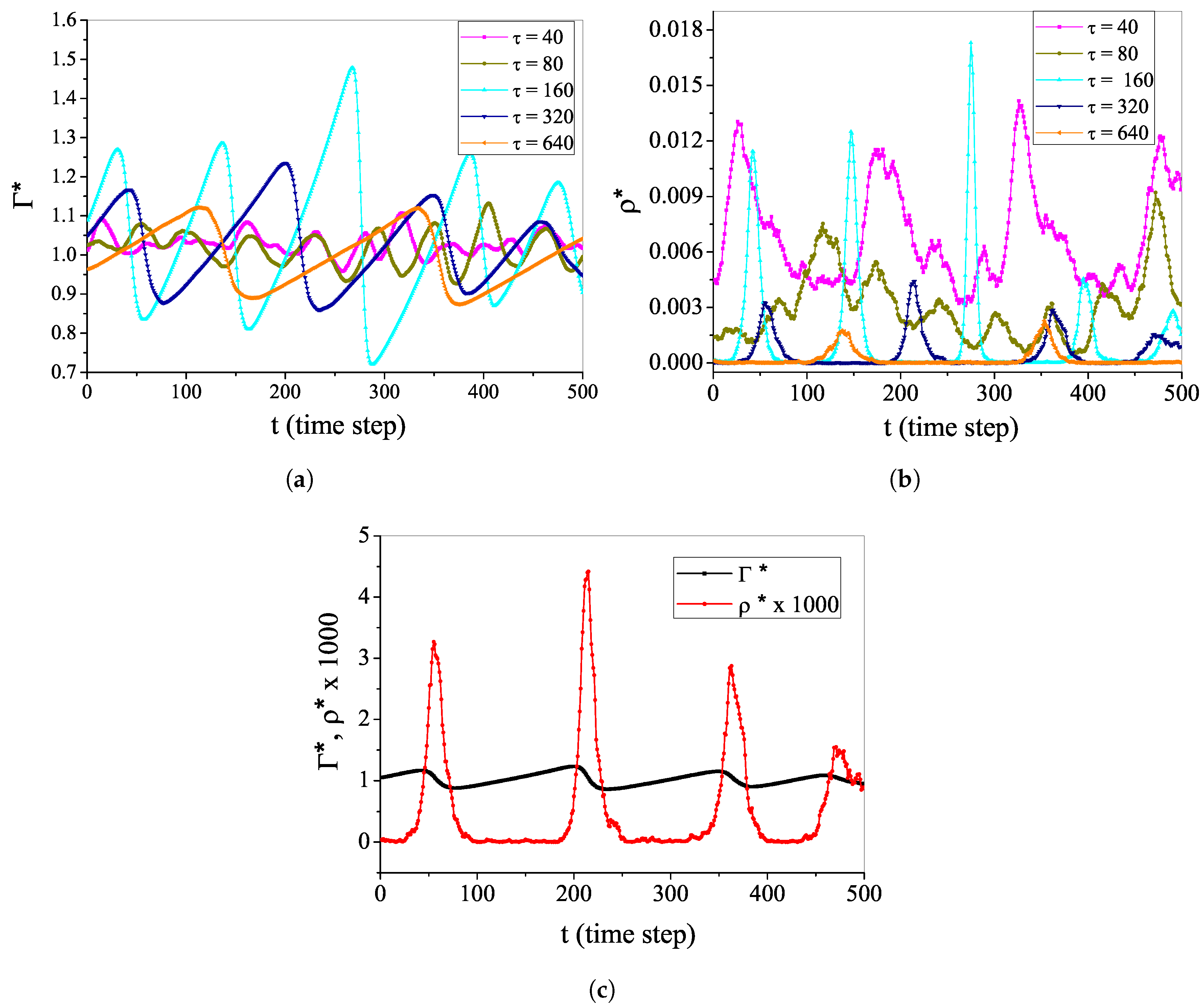
4.2. Self-Organized Supercriticality through Dynamic Gains with , ,
5. Discussion
6. Materials and Methods
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
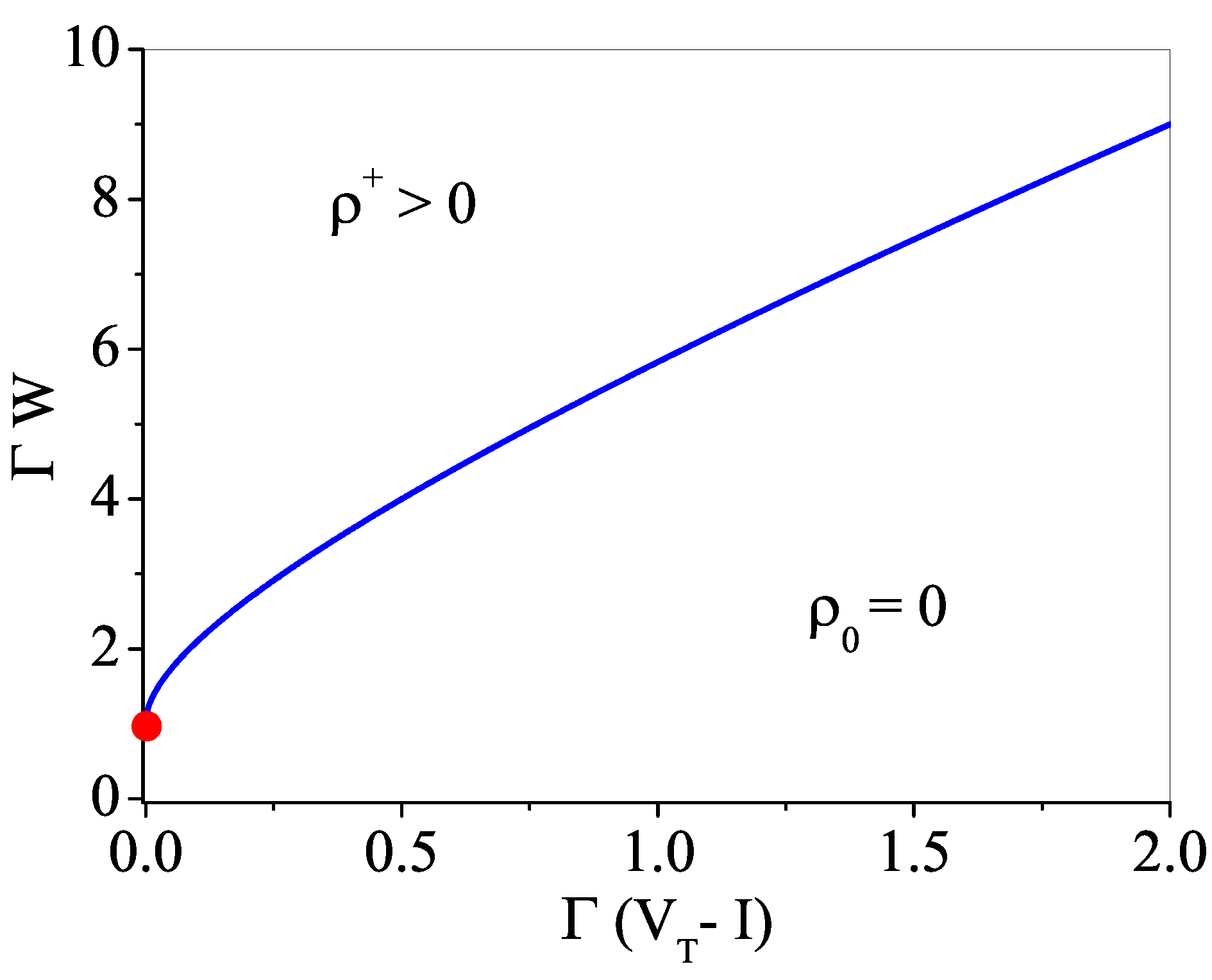
Appendix A. Phase Transition for μ > 0, VT = 0
References
- Herz, A.V.; Hopfield, J.J. Earthquake cycles and neural reverberations: Collective oscillations in systems with pulse-coupled threshold elements. Phys. Rev. Lett. 1995, 75, 1222. [Google Scholar] [CrossRef] [PubMed]
- Beggs, J.M.; Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 2003, 23, 11167–11177. [Google Scholar] [PubMed]
- Kinouchi, O.; Copelli, M. Optimal dynamical range of excitable networks at criticality. Nat. Phys. 2006, 2, 348–351. [Google Scholar] [CrossRef]
- Chialvo, D.R. Emergent complex neural dynamics. Nat. Phys. 2010, 6, 744–750. [Google Scholar] [CrossRef]
- Marković, D.; Gros, C. Power laws and self-organized criticality in theory and nature. Phys. Rep. 2014, 536, 41–74. [Google Scholar] [CrossRef]
- Hesse, J.; Gross, T. Self-organized criticality as a fundamental property of neural systems. Front. Syst. Neurosci. 2014, 8. [Google Scholar] [CrossRef] [PubMed]
- Cocchi, L.; Gollo, L.L.; Zalesky, A.; Breakspear, M. Criticality in the brain: A synthesis of neurobiology, models and cognition. Prog. Neurobiol. 2017, in press. [Google Scholar] [CrossRef] [PubMed]
- Beggs, J.M. The criticality hypothesis: How local cortical networks might optimize information processing. Philos. Trans. R. Soc. A 2008, 366, 329–343. [Google Scholar] [CrossRef] [PubMed]
- Shew, W.L.; Yang, H.; Petermann, T.; Roy, R.; Plenz, D. Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J. Neurosci. 2009, 29, 15595–15600. [Google Scholar] [CrossRef] [PubMed]
- Massobrio, P.; de Arcangelis, L.; Pasquale, V.; Jensen, H.J.; Plenz, D. Criticality as a signature of healthy neural systems. Front. Syst. Neurosci. 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- De Arcangelis, L.; Perrone-Capano, C.; Herrmann, H.J. Self-organized criticality model for brain plasticity. Phys. Rev. Lett. 2006, 96, 028107. [Google Scholar] [CrossRef] [PubMed]
- Pellegrini, G.L.; de Arcangelis, L.; Herrmann, H.J.; Perrone-Capano, C. Activity-dependent neural network model on scale-free networks. Phys. Rev. E 2007, 76, 016107. [Google Scholar] [CrossRef] [PubMed]
- De Arcangelis, L.; Herrmann, H.J. Learning as a phenomenon occurring in a critical state. Proc. Natl. Acad. Sci. USA 2010, 107, 3977–3981. [Google Scholar] [CrossRef] [PubMed]
- De Arcangelis, L. Are dragon-king neuronal avalanches dungeons for self-organized brain activity? Eur. Phys. J. Spec. Top. 2012, 205, 243–257. [Google Scholar] [CrossRef]
- De Arcangelis, L.; Herrmann, H. Activity-Dependent Neuronal Model on Complex Networks. Front. Physiol. 2012, 3. [Google Scholar] [CrossRef] [PubMed]
- Van Kessenich, L.M.; de Arcangelis, L.; Herrmann, H. Synaptic plasticity and neuronal refractory time cause scaling behaviour of neuronal avalanches. Sci. Rep. 2016, 6, 32071. [Google Scholar] [CrossRef] [PubMed]
- Levina, A.; Herrmann, J.M.; Geisel, T. Dynamical synapses causing self-organized criticality in neural networks. Nat. Phys. 2007, 3, 857–860. [Google Scholar] [CrossRef]
- Levina, A.; Herrmann, J.M.; Geisel, T. Phase transitions towards criticality in a neural system with adaptive interactions. Phys. Rev. Lett. 2009, 102, 118110. [Google Scholar] [CrossRef] [PubMed]
- Bonachela, J.A.; De Franciscis, S.; Torres, J.J.; Muñoz, M.A. Self-organization without conservation: Are neuronal avalanches generically critical? J. Stat. Mech. Theory Exp. 2010, 2010, P02015. [Google Scholar] [CrossRef]
- Costa, A.A.; Copelli, M.; Kinouchi, O. Can dynamical synapses produce true self-organized criticality? J. Stat. Mech. Theory Exp. 2015, 2015, P06004. [Google Scholar] [CrossRef]
- Campos, J.G.F.; Costa, A.A.; Copelli, M.; Kinouchi, O. Correlations induced by depressing synapses in critically self-organized networks with quenched dynamics. Phys. Rev. E 2017, 95, 042303. [Google Scholar] [CrossRef] [PubMed]
- Tsodyks, M.; Markram, H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc. Natl. Acad. Sci. USA 1997, 94, 719–723. [Google Scholar] [CrossRef] [PubMed]
- Tsodyks, M.; Pawelzik, K.; Markram, H. Neural networks with dynamic synapses. Neural Comput. 1998, 10, 821–835. [Google Scholar] [CrossRef] [PubMed]
- Kole, M.H.; Stuart, G.J. Signal processing in the axon initial segment. Neuron 2012, 73, 235–247. [Google Scholar] [CrossRef] [PubMed]
- Ermentrout, B.; Pascal, M.; Gutkin, B. The effects of spike frequency adaptation and negative feedback on the synchronization of neural oscillators. Neural Comput. 2001, 13, 1285–1310. [Google Scholar] [CrossRef] [PubMed]
- Benda, J.; Herz, A.V. A universal model for spike-frequency adaptation. Neural Comput. 2003, 15, 2523–2564. [Google Scholar] [CrossRef] [PubMed]
- Buonocore, A.; Caputo, L.; Pirozzi, E.; Carfora, M.F. A leaky integrate-and-fire model with adaptation for the generation of a spike train. Math. Biosci. Eng. 2016, 13, 483–493. [Google Scholar] [PubMed]
- Brochini, L.; Costa, A.A.; Abadi, M.; Roque, A.C.; Stolfi, J.; Kinouchi, O. Phase transitions and self-organized criticality in networks of stochastic spiking neurons. Sci. Rep. 2016, 6, 35831. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Nyengaard, J.R.; De Groot, D.M.; Gundersen, H.J.G. Total regional and global number of synapses in the human brain neocortex. Synapse 2001, 41, 258–273. [Google Scholar] [CrossRef] [PubMed]
- Gerstner, W.; van Hemmen, J.L. Associative memory in a network of ’spiking’ neurons. Netw. Comput. Neural Syst. 1992, 3, 139–164. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W.M. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Galves, A.; Löcherbach, E. Infinite Systems of Interacting Chains with Memory of Variable Length—A Stochastic Model for Biological Neural Nets. J. Stat. Phys. 2013, 151, 896–921. [Google Scholar] [CrossRef]
- Larremore, D.B.; Shew, W.L.; Ott, E.; Sorrentino, F.; Restrepo, J.G. Inhibition causes ceaseless dynamics in networks of excitable nodes. Phys. Rev. Lett. 2014, 112, 138103. [Google Scholar] [CrossRef] [PubMed]
- De Masi, A.; Galves, A.; Löcherbach, E.; Presutti, E. Hydrodynamic limit for interacting neurons. J. Stat. Phys. 2015, 158, 866–902. [Google Scholar] [CrossRef]
- Duarte, A.; Ost, G. A model for neural activity in the absence of external stimuli. Markov Process. Relat. Fields 2016, 22, 37–52. [Google Scholar]
- Duarte, A.; Ost, G.; Rodríguez, A.A. Hydrodynamic Limit for Spatially Structured Interacting Neurons. J. Stat. Phys. 2015, 161, 1163–1202. [Google Scholar] [CrossRef]
- Galves, A.; Löcherbach, E. Modeling networks of spiking neurons as interacting processes with memory of variable length. J. Soc. Fr. Stat. 2016, 157, 17–32. [Google Scholar]
- Hinrichsen, H. Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 2000, 49, 815–958. [Google Scholar] [CrossRef]
- Friedman, N.; Ito, S.; Brinkman, B.A.; Shimono, M.; DeVille, R.L.; Dahmen, K.A.; Beggs, J.M.; Butler, T.C. Universal critical dynamics in high resolution neuronal avalanche data. Phys. Rev. Lett. 2012, 108, 208102. [Google Scholar] [CrossRef] [PubMed]
- Scott, G.; Fagerholm, E.D.; Mutoh, H.; Leech, R.; Sharp, D.J.; Shew, W.L.; Knöpfel, T. Voltage imaging of waking mouse cortex reveals emergence of critical neuronal dynamics. J. Neurosci. 2014, 34, 16611–16620. [Google Scholar] [CrossRef] [PubMed]
- Priesemann, V.; Munk, M.H.; Wibral, M. Subsampling effects in neuronal avalanche distributions recorded in vivo. BMC Neurosci. 2009, 10. [Google Scholar] [CrossRef] [PubMed]
- Girardi-Schappo, M.; Tragtenberg, M.; Kinouchi, O. A brief history of excitable map-based neurons and neural networks. J. Neurosci. Methods 2013, 220, 116–130. [Google Scholar] [CrossRef] [PubMed]
- Levina, A.; Priesemann, V. Subsampling scaling. Nat. Commun. 2017, 8, 15140. [Google Scholar] [CrossRef] [PubMed]
- Sornette, D.; Ouillon, G. Dragon-kings: Mechanisms, statistical methods and empirical evidence. Eur. Phys. J. Spec. Top. 2012, 205, 1–26. [Google Scholar] [CrossRef]
- Lin, Y.; Burghardt, K.; Rohden, M.; Noël, P.A.; D’Souza, R.M. The Self-Organization of Dragon Kings. arXiv, 2017; arXiv:1705.10831. [Google Scholar]
- Hobbs, J.P.; Smith, J.L.; Beggs, J.M. Aberrant neuronal avalanches in cortical tissue removed from juvenile epilepsy patients. J. Clin. Neurophysiol. 2010, 27, 380–386. [Google Scholar] [CrossRef] [PubMed]
- Meisel, C.; Storch, A.; Hallmeyer-Elgner, S.; Bullmore, E.; Gross, T. Failure of adaptive self-organized criticality during epileptic seizure attacks. PLoS Comput. Biol. 2012, 8, e1002312. [Google Scholar] [CrossRef] [PubMed]
- Haldeman, C.; Beggs, J.M. Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys. Rev. Lett. 2005, 94, 058101. [Google Scholar] [CrossRef] [PubMed]
- Gireesh, E.D.; Plenz, D. Neuronal avalanches organize as nested theta-and beta/gamma-oscillations during development of cortical layer 2/3. Proc. Natl. Acad. Sci. USA 2008, 105, 7576–7581. [Google Scholar] [CrossRef] [PubMed]
- Poil, S.S.; Hardstone, R.; Mansvelder, H.D.; Linkenkaer-Hansen, K. Critical-state dynamics of avalanches and oscillations jointly emerge from balanced excitation/inhibition in neuronal networks. J. Neurosci. 2012, 32, 9817–9823. [Google Scholar] [CrossRef] [PubMed]
- Bedard, C.; Kroeger, H.; Destexhe, A. Does the 1/f frequency scaling of brain signals reflect self-organized critical states? Phys. Rev. Lett. 2006, 97, 118102. [Google Scholar] [CrossRef] [PubMed]
- Tetzlaff, C.; Okujeni, S.; Egert, U.; Wörgötter, F.; Butz, M. Self-organized criticality in developing neuronal networks. PLoS Comput. Biol. 2010, 6, e1001013. [Google Scholar] [CrossRef] [PubMed]
- Priesemann, V.; Wibral, M.; Valderrama, M.; Pröpper, R.; Le Van Quyen, M.; Geisel, T.; Triesch, J.; Nikolić, D.; Munk, M.H. Spike avalanches in vivo suggest a driven, slightly subcritical brain state. Front. Syst. Neurosci. 2014, 8. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, A.A.; Brochini, L.; Kinouchi, O. Self-Organized Supercriticality and Oscillations in Networks of Stochastic Spiking Neurons. Entropy 2017, 19, 399. https://doi.org/10.3390/e19080399
Costa AA, Brochini L, Kinouchi O. Self-Organized Supercriticality and Oscillations in Networks of Stochastic Spiking Neurons. Entropy. 2017; 19(8):399. https://doi.org/10.3390/e19080399
Chicago/Turabian StyleCosta, Ariadne A., Ludmila Brochini, and Osame Kinouchi. 2017. "Self-Organized Supercriticality and Oscillations in Networks of Stochastic Spiking Neurons" Entropy 19, no. 8: 399. https://doi.org/10.3390/e19080399
APA StyleCosta, A. A., Brochini, L., & Kinouchi, O. (2017). Self-Organized Supercriticality and Oscillations in Networks of Stochastic Spiking Neurons. Entropy, 19(8), 399. https://doi.org/10.3390/e19080399




