Abstract
The origin of the long-range memory in non-equilibrium systems is still an open problem as the phenomenon can be reproduced using models based on Markov processes. In these cases, the notion of spurious memory is introduced. A good example of Markov processes with spurious memory is a stochastic process driven by a non-linear stochastic differential equation (SDE). This example is at odds with models built using fractional Brownian motion (fBm). We analyze the differences between these two cases seeking to establish possible empirical tests of the origin of the observed long-range memory. We investigate probability density functions (PDFs) of burst and inter-burst duration in numerically-obtained time series and compare with the results of fBm. Our analysis confirms that the characteristic feature of the processes described by a one-dimensional SDE is the power-law exponent of the burst or inter-burst duration PDF. This property of stochastic processes might be used to detect spurious memory in various non-equilibrium systems, where observed macroscopic behavior can be derived from the imitative interactions of agents.
1. Introduction
The application of statistical physics to diverse fields such as social sciences and economics, biology and population genetics, medicine, information technology, computer science and others [1,2,3,4] is making this interdisciplinary research very universal. Though the number of agents is usually incomparable with the number of particles in physical systems, the understanding of the macroscopic behavior of social and biological systems naturally invokes methods of statistical physics with very simplified interactions of individuals. Humans and biological entities are themselves complex systems with unknown detailed behavior, and any attempt to reproduce microscopic interactions of agents might appear to be unrealistic. Thus, the probabilistic description of agent interactions in social systems seems to be the most appropriate and natural. Even in very simplified models of agent interactions, the collective behavior may lead to the ordered or disordered states. How the disordered interactions of agents create order in macroscopic behavior is a very interesting question; nevertheless, the cases when non-equilibrium fluctuations do not disappear in the system are of high importance, as well [5].
There is a limited number of solvable and mathematically-tractable models of many-body systems. The Ising model is among the most fundamental and well-known examples of such models [6,7]. Being a very popular tool for the investigation of transition from order and disorder states, the Ising model in a one-dimensional case with local interactions of spins can be simplified by Glauber dynamics [4] and gives motivation to many other applications of statistical mechanics. It is possible to simplify pairwise interactions of agents in the way, which leads to the solvable cases of many body systems in more spatial dimensions or topologies. The voter model is a good example of such a social system widely used in modeling of opinion dynamics and population genetics [8,9,10,11]. In the one-dimensional case, the voter model coincides with one-dimensional Glauber dynamics, while in other dimensions, various topologies can be solved, as well. The standard voter model converges to the consensus of opinions, and this is related to two circumstances: the local nature of interactions and the imitation of neighbor opinion without idiosyncratic decision making [11]. From our point of view, the case of global agent interactions or a system running on the randomly-generated network, including idiosyncratic switching of opinions, is of great importance as it exhibits continuing stochastic fluctuations in collective behavior [5,12]. The evolution of such a system can be described using the Fokker–Planck equation or as a non-linear SDE for population evolution and can be seen as a special case of the voter model [13,14], Moran model [2] or the Kirman model [5,15]. The continuing fluctuations in such a non-equilibrium system with imitative behavior of agents exhibit very general power-law scaling properties, including spurious memory applicable to social [16,17], financial [18,19,20] or biological [2] systems.
Here, we investigate the long-range memory property, which might originate from the true long-range memory process, one with correlated increments, such as the fractional Brownian motion (fBm) [21,22,23,24]; while the long-range memory might be also obtained from the stochastic processes with non-stationary uncorrelated increments [23,24,25,26]. Note that both stochastic processes are one-dimensional unlike in other known cases of spurious memory [27]. There is a fundamental problem to find out which of the possible alternatives, fBm or diffusive processes with non-stationary increments, is the origin of the observed long-range memory. Here, we employ the dependence of the first passage time PDF on Hurst parameter H for the fBm [28,29] and apparently different behavior for the non-linear diffusive processes [10,30,31]. This explains that the long-range memory present in social, financial and biological systems could arise from non-linear agent interactions, as well as from the implicit non-linear transformations of the latent variables [32].
2. Non-Equilibrium Stochastic Fluctuations Arising from the Imitative Behavior of Agents
One agent (particle) jump Markov processes have become an efficient tool in modeling of physical, biological and social systems [2,16,33]. The microscopic behavior of the agent is replaced by continuous time Markov processes with specified transition rates. In the system with a large number of agents N and two possible states (choices of opinion), e.g., , there are two possible one-step transitions: (a) the number of agents n in State 1 increases (birth) or (b) decreases (death). Such a simple, but general enough definition of opinion or population dynamics can be specified by two system-wide one-step transition rates:
In the above, are per-agent transition rates to a state given by index i, which in general might take many different forms dependent on n and N [16]. For the sake of notational simplicity, we will drop the explicit statement of this dependence and use shorthand, i.e., further in this paper, . We will postpone assigning an explicit form for the until it will be necessary.
The system-wide rates define the master equation for PDF of the macroscopic state evolution :
In the limit of large N values, one can introduce the normalized system state variable and write down the following Fokker–Planck equation:
which corresponds to the following SDE in the Ito sense:
where W is the standard Wiener noise. One gets the very well-known result, the Kirman model on complete or random (Erdos–Renyi) graph, when per-agent transition rates are defined as follows [5,12,15]:
In the above, describe idiosyncratic transition rates to state i normalized by the imitation parameter and time scale on which fluctuations occur, in the literature denoted as h. The same equations describe the behavior of the noisy voter model on a complete graph; see the discussion in [17]. In this paper, we refer to this model, defined by Equation (5), and its later generalizations as an imitative behavior model, because model’s per-agent transition rates to a given state depend on the number of agents already in that state. One could see this as agents copying the state (opinion) of the agents in the other state (of other opinion). In other papers, this feature is often described using a different, yet synonymous, term: herding behavior [5,12,18,34].
This model leads to a very general case in opinion and population dynamics retaining the perpetual fluctuations in system state variable x even in the limit . This is ensured by the same form of the imitation term in both system-wide transition rates and its linear dependence on N. In this case, the drift term in the corresponding SDE does not depend on the imitation term, while idiosyncratic terms vanish in the diffusion term. If this dependence were sub-linear, then the model would instead converge to some fixed value of x [5,12].
This model can be generalized introducing the non-linear dependence of time scale on system state variable x, as was proposed in a few financial market models to account for the intrinsic variability of trading activity [35,36,37]. Such additional non-linearity of the system probably is a common feature of the real world. From our point of view, this might be considered as a source of spurious memory, which has to be identified from the empirical data of real social, biological or physical systems, e.g., see [19] and the references there. Let us generalize per-agent transition rates by introducing non-linear inter-agent interaction time scale variability dependent on system state variable x (non-linearity is controlled by a parameter ),
Certainly, there are other choices for how to introduce this variability, e.g., [19,37]. In this paper, we have chosen this one as it is symmetric with respect to x. This feature allows us to consider the burst durations to be statistically equivalent to the inter-burst durations and retains symmetry regarding the new variable y introduced below. In this paper, we use , as it seems to be the most appropriate value in the modeling of return in financial markets [19], while other positive values of could be also considered as appropriate for the modeling of social systems with inherent imitative behavior. The stationary distribution of x in the generalized imitative behavior model is the beta distribution, with parameter values equal to and ,
In earlier works [18,19,20,37], it was shown that the Kirman model is suitable to model return in financial markets, with return defined to be proportional to . For this reason, we are more interested in the properties of the time series of y instead of x. Though other non-linear transformations of x, leading to very big fluctuations in the transformed time series, might reproduce similar properties, as well.
Using the Ito lemma [38], we can derive SDE for y, assuming that x time series are generated by SDE (4) with per-agent transition rates given by Equation (6),
Note that being derived from SDE symmetric with respect to x (x and are statistically equivalent), this SDE for y also has symmetry with respect to y. Namely, y and are equivalent in their statistical properties. This is important as we seek to retain the symmetry in burst and inter-burst duration statistics and in the definition of y.
Note that SDE (8) does not satisfy the Lipschitz condition. In order to satisfy the Lipschitz condition and to avoid over-flow problems in numerical simulations, we introduce the reflective boundary condition for very large values of y. The exact choice of the y value to place boundaries does not influence the results discussed in this paper; yet, for the sake of completeness, we would like to note that we have placed boundaries at and . Numerically, we solve this SDE using the Euler–Maruyama method, but using variable time steps. For more details, see earlier works, e.g., [19,37,39], in which similar equations were solved numerically.
As can be seen from the previous discussion, agent-based models with non-linear interactions can lead to the macroscopic description by non-linear SDEs, which represent a class of Markov processes. Note that if we take only the highest powers of y in SDE (8), we would obtain an SDE of a well-known form [40]:
where new parameters and are related to the previously-used parameters as:
SDEs having a form similar to SDE (9) were considered in numerous earlier papers, and it was shown that they generate the time series with the power-law statistical properties, namely PDF and power-spectral density (PSD), [40,41]:
In Figure 1, we demonstrate an excerpt of the model time series (a), its stationary PDF (b) and PSD (c). Note that diffusion here is restricted in the region , and PSD is . Only after non-linear transformation of the time series (see Figure 2), PSD becomes and stationary PDF has the power-law tail as given by Equation (11).
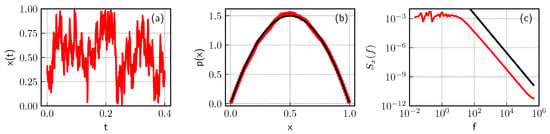
Figure 1.
Excerpt of a time series (a), obtained by solving SDE (4) with given by Equation (6); (b) PDF and (c) PSD of the same time series (red curves). Black curves in (b,c) represent theoretical fits: (b) beta distribution with parameter values two and two; (c) trend line. Parameter set used in numerical simulation: , .
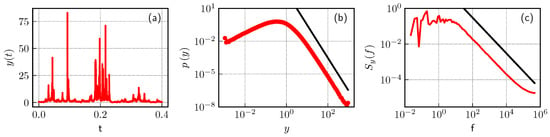
Figure 2.
Excerpt of the transformed time series (a), where the time series is the same as in Figure 1; (b) PDF and (c) PSD of the same transformed time series (red curves). Black curves in (b,c) represent theoretical fits: (b) trend line and (c) trend line.
From our point of view, spurious long-range memory might originate in many social systems with the imitative behavior of agents, where the long-term stochastic agent population or opinion fluctuations do not disappear. First of all, such an approach has to be considered as an explanation of observed long-range memory in financial markets [20,37,39]. In the next section, we investigate the PDF of the first passage times seeking to demonstrate that such a long-range memory property is different from the one observed in the case of fBm.
3. PDFs of Burst and Inter-Burst Duration in the Stochastic Model of Imitative Behavior
The class of SDEs, defined by Equation (9), describes multifractal stochastic processes [37] with non-stationary increments [23,24], power-law PSD and related auto-correlation (11); thus, unlike for processes with correlated increments such as fBm, this class can be considered as having spurious memory. Here, we will demonstrate a clear distinction between these two different models with correlated (fBm) and uncorrelated (non-linear SDE) increments. The idea of such a distinction is based on the PDF of the first return times of stochastic processes with the absorbing boundary at some threshold level . Ding and Yang have considered the problem for fBm as the first return time in [28].
To our knowledge, we make the first attempt to discriminate between these two one-dimensional stochastic processes. Other models of spurious memory are qualitatively different and usually related to double stochasticity [27]. The exponent of the PDF for the first passage times in one-dimensional Markov processes is a characteristic feature [10,30,31], when deviations from this law are a characteristic feature of fBm [28,29].
In this paper, we consider two distinct threshold passage events: one describes return to the threshold from above, while the other describes return to the threshold from below. We consider burst duration as the amount of time the series spent above the threshold. In Figure 3, the burst period lasts from the threshold passage at time until the next threshold passage at time . Hence, burst duration, in this case, is given by . Evidently, it is the same as the first return time, but with the restriction that the return was made from above the threshold. In Figure 3, the inter-burst period lasts from the threshold passage at time until the next threshold passage at time . Hence, inter-burst duration, in this case, is given by . Evidently, it is the same as the first return time, but with the restriction that the return was made from below the threshold.
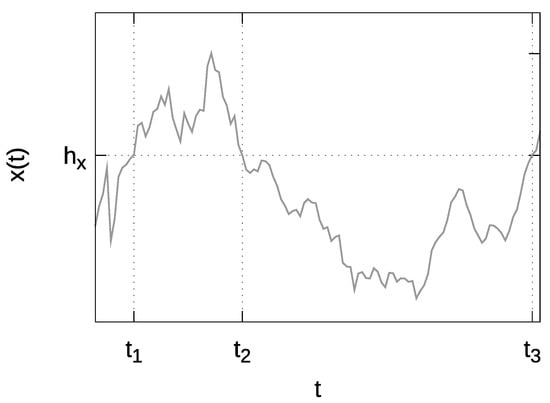
Figure 3.
Excerpt of a generic time series. Three threshold, , passage events, , are shown. Thus burst duration T can be defined as , and inter-burst duration can be defined as .
While these definitions might seem puzzling from the purely theoretical point of view, they make better sense from the empirical point of view. When analyzing generated, numerically or extracted from empirical data, time series, each first return time, obtained after each threshold passage event, is always either the burst duration or the inter-burst duration. Furthermore, almost surely after each burst period comes the inter-burst period and vice versa. Furthermore, as will be shown later in this paper, the distribution of burst and inter-burst duration coincide (actually, it also coincides with first return time distribution) if the model is symmetric with respect to the selected threshold.
Due to symmetry, for all real thresholds of one-dimensional fBm, its PDFs of burst and inter-burst duration coincide and can be written as [28,29]:
The Hurst parameter H, defining the exponent of the power-law PDF , coincides with the corresponding exponent for other one-dimensional Markov processes only when [10,30,38,42]. When fBm is biased, the PDF of T has exponential cutoff [28]:
where is defined by the mean and standard deviation of increments and Hurst parameter H. Note that for biased fBm, PDFs of burst and inter-burst duration will no longer coincide. In this paper, we generate biased fBm time series by solving the following iterative equation:
In the above, is the damping coefficient, while is the fractional Gaussian noise with Hurst exponent H. Fractional Gaussian noise, in this case, is generated by using the approximate circulant method introduced in [22].
Analytically, only burst duration of SDE (9) was considered in previous work [31]. Namely, in [31], we have shown that SDE (9) can be transformed into the Bessel process. This was used to obtain the approximation of burst duration PDF, as some formulas for the distribution of the first passage time of the Bessel process are well known. The asymptotic behavior of the obtained burst duration PDF is given by:
Here, , and is the first zero of a Bessel function of the first kind. The power-law behavior with exponent in Equation (15) is consistent with the general theory of the first passage times in one-dimensional stochastic processes [10,30].
As we have discussed in earlier sections, the PDF and PSD of the time series change significantly with non-linear transformations of system state variables. Yet, the distribution of the first return time remains invariant under the considered transformations, as a long threshold is also appropriately transformed. This may serve us as a criterion for how to identify from empirical data which model of the time series is better suited to describe a real system exhibiting observed long-range memory properties, as any deviation of the PDF exponent from other than the cutoff in the region of extremely long duration would be proof that true long-range memory is present. Thus, we investigate here the statistical properties of time series generated by non-linear transformations of SDE (4) with transition rates Equation (6), which give SDE (8).
We demonstrate in Figure 4 this clear distinction of fBm and SDE by numerical comparison of signal PSD and PDF of T. As can be seen in Sub-figures (a) and (b), we have selected parameters of both models, so that we obtain similar PSDs (with the same exponents ). Yet, PDFs of the burst duration are different for the considered models (Sub-figures (c) and (d)). While the burst duration PDFs are the power-law in both cases, the exponent differs. For the case of SDE (8), we have the same exponent for all cases, constant at , as predicted by Equation (15); while for the fBm case, we have differing exponents, which coincide with predictions, , by Equation (12). Exponential cutoffs are present in both cases, as models are mean reverting. Thus, the statistical analysis of burst and inter-burst duration in empirical time series could reveal whether empirical time series contain true long-range memory or spurious memory, which originates from non-linear Markov stochastic processes.
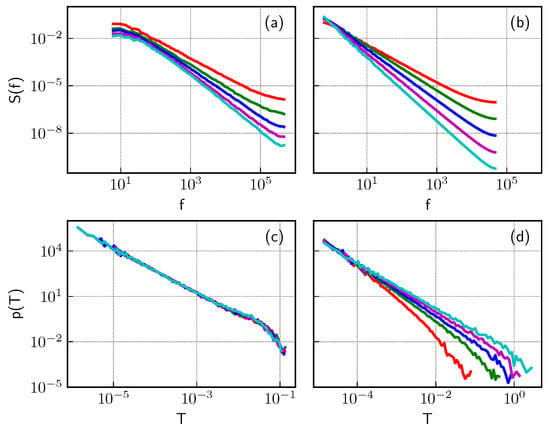
Figure 4.
Comparison of PSD (a,b) and burst duration PDF (c,d) of the time series generated by numerically solving Equation (8) (a,c) with the ones obtained from fractional Brownian motion (fBm) with the relaxation time series, obtained by solving Equation (14) (b,d). fBm parameter sets: (all cases), (red curve), (green curve), (blue curve), (magenta curve), (cyan curve). Parameters of Equation (8) are selected to give values of the same as for fBm: , (red curve), (green curve), (blue curve), (magenta curve), 3 (cyan curve).
It is worth defining more precisely the statistical properties of burst and inter-burst duration in the described agent system with imitative behavior as potentially recoverable in real social systems [20].
In Figure 5, we present numerical calculations of the PDF for burst T and inter-burst durations with different values of the threshold . Our numerical simulations confirm the symmetry of the model for the statistics of burst and inter-burst durations regarding the values of threshold on both sides of mid-point , where PDFs of T and coincide. Note that fundamental power-law is retained for all values of the threshold, but burst and inter-burst durations have different positions of the power-law cutoff. More precise analyses confirm that the cutoff of the PDF for burst duration T is well described by the previously-derived exponential form Equation (12). The cutoff of inter-burst duration has a similar exponential form, but the location is shifted proportionally to the deviation from the mid-point.
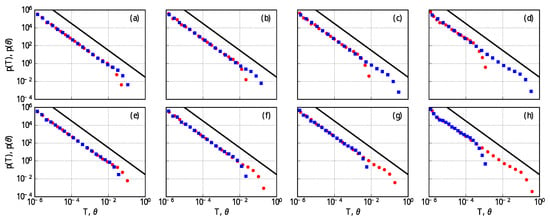
Figure 5.
PDFs of burst (red circles) and inter-burst (blue squares) durations of time series, obtained by solving SDE (4) with given by Equation (6), for various thresholds: (a), (b), (c), (d), (e), (f), (g) and (h). Parameter set used in numerical simulation: , . Solid black lines guide the eye according the power-law .
Observed power-law properties of this model of imitative behavior arise from the power-law properties of non-linear SDEs Equation (9) extensively studied elsewhere [26,40,43]. Note that these properties are in close relation with rapidly developing ideas of non-extensive statistical mechanics and the generalized concept of entropy [44,45].
4. Conclusions
It is widely accepted that fluctuations of volatility and trading activity in the financial markets exhibit slowly-decaying auto-correlations and so-called noise [46,47,48,49]. The discussion whether this slow decay corresponds to long-range memory is still ongoing. The statistical analysis in general is not able to provide a definite answer concerning the presence or absence of long-range memory in finance [50,51,52]. From our point of view, the heterogeneous agent dynamics has to be employed seeking to explain the statistical properties of financial time series [19,20,53]. Certainly, such a complex system as finance [20] is not the best starting point for conceptual consideration of the long-range memory problem in other social systems. Thus, in this contribution, we consider a much more abstract definition of an agent system with imitative behavior leading to the continuing non-equilibrium stochastic fluctuations. Derived SDEs driven by Wiener noise describe Markov processes and cannot be treated as suitable to model long-range memory with correlated stochastic increments. Such modeling by stochastic agent systems becomes an alternative to the stochastic processes driven by fBm. Thus, the choice between these two possibilities is the fundamental question for the understanding of the observed long-range memory property in many other complex systems.
The model we investigate here is the generalized version of the Kirman model with pairwise global interaction of agents and is directly related to the voter model, as well. The introduced additional feedback of the macroscopic state on the time scale of interactions lets us to adjust the multiplicativity of SDE, defining the properties of PSD for the ratio . The retained symmetry of generalized equations makes this choice preferable among other possible alternatives. From our point of view, such modeling first of all is applicable to financial systems, but is general enough and analytically tractable for other systems with heterogeneous agents.
Here, we prove analytically and numerically that the PDF of the burst and inter-burst duration of stochastic variable y is a power-law with exponential cut-off for extremely long durations. We consider this property as very valuable being very different from the fBm process, where the PDF of the first passage time is dependent on H, [28,29]. Thus, a detailed empirical analysis of burst and inter-burst duration may serve as a criterion to distinguish two different origins of noise and the long-range memory property. Empirical evidence of the power-law exponent should be considered as a case of spurious memory, when deviations from this exponent should witness the presence of real long-rage correlations. From our point of view, the financial markets have to be considered as a social system with imitative behavior and spurious memory arising from the non-linear stochastic dynamics [19,20,54].
Author Contributions
V.G. designed and wrote the draft text of paper. A.K. performed all calculations and prepared the illustrations. V.G. and A.K. discussed and prepared the final version of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SDE | Stochastic differential equation |
| fBm | fractional Brownian motion |
| Probability density function | |
| PSD | Power spectral density |
References
- Ausloos, M.; Vandewalle, N.; Boveroux, P.; Minguet, A.; Ivanova, K. Applications of statistical physics to economic and financial topics. Physica A 1999, 274, 229–240. [Google Scholar] [CrossRef]
- Blythe, R.A.; McKane, A.J. Stochastic models of evolution in genetics, ecology and linguistics. J. Stat. Mech. 2007, 2007. [Google Scholar] [CrossRef]
- Nishimori, H. Statistical Physics of Spin Glasses and Information Processing: An Introduction; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Castellano, C.; Fortunato, S.; Loreto, V. Statistical physics of social dynamics. Rev. Mod. Phys. 2009, 81, 591–646. [Google Scholar] [CrossRef]
- Alfarano, S.; Milakovic, M. Network structure and N-dependence in agent-based herding models. J. Econ. Dyn. Control 2009, 33, 78–92. [Google Scholar] [CrossRef]
- Onsager, L. Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition. Phys. Rev. 1944, 65, 117–149. [Google Scholar] [CrossRef]
- Glauber, R.J. Time-Dependent Statistics of the Ising Model. J. Math. Phys. 1963, 4, 294–307. [Google Scholar] [CrossRef]
- Clifford, P.; Sudbury, A. A model for spatial conflict. Biometrica 1973, 60, 581–588. [Google Scholar] [CrossRef]
- Holley, R.A.; Liggett, T.M. Ergodic theorems for weakly interacting infinite systems and the voter model. Ann. Probab. 1975, 3, 643–663. [Google Scholar] [CrossRef]
- Redner, S. A Guide to First-Passage Processes; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Slanina, F. Essentials of Econophysics Modelling; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Kononovicius, A.; Ruseckas, J. Continuous transition from the extensive to the non-extensive statistics in an agent-based herding model. Eur. Phys. J. B 2014, 87. [Google Scholar] [CrossRef][Green Version]
- Liggett, T. Stochastic Interacting Systems: Contact, Voter, and Exclusion Processes; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Fernandez-Gracia, J.; Suchecki, K.; Ramasco, J.J.; San Miguel, M.; Eguiluz, V.M. Is the voter model a model for voters? Phys. Rev. Lett. 2014, 112, 158701. [Google Scholar] [CrossRef] [PubMed]
- Kirman, A.P. Ants, rationality and recruitment. Q. J. Econ. 1993, 108, 137–156. [Google Scholar] [CrossRef]
- Aoki, M.; Yoshikawa, H. Reconstructing Macroeconomics: A Perspektive from Statistical Physics and Combinatorial Stochastic Processes; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Kononovicius, A. Empirical analysis and agent-based modeling of Lithuanian parliamentary elections. arXiv, 2017; arXiv:1704.02101v1. [Google Scholar]
- Alfarano, S.; Lux, T.; Wagner, F. Estimation of Agent-Based Models: The Case of an Asymmetric Herding Model. Comput. Econ. 2005, 26, 19–49. [Google Scholar] [CrossRef]
- Gontis, V.; Kononovicius, A. Consentaneous agent-based and stochastic model of the financial markets. PLoS ONE 2014, 9, e102201. [Google Scholar] [CrossRef] [PubMed]
- Gontis, V.; Havlin, S.; Kononovicius, A.; Podobnik, B.; Stanley, E. Stochastic model of financial markets reproducing scaling and memory in volatility return intervals. Physica A 2016, 462, 1091–1102. [Google Scholar] [CrossRef]
- Mandelbrot, B.; Ness, V. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Dieker, A.B.; Mandjes, M. On Spectral Simulation of Fractional Brownian Motion. Probab. Eng. Inf. Sci. 2003, 17, 417–434. [Google Scholar] [CrossRef]
- Bassler, K.E.; Gunaratne, G.H.; McCauley, J.L. Markov processes, Hurst exponents, and nonlinear diffusion equations: With application to finance. Physica A 2006, 369, 343–353. [Google Scholar] [CrossRef]
- McCauley, J.L.; Gunaratne, G.H.; Bassler, K.E. Hurst exponents, Markov processes, and fractional Brownian motion. Physica A 2007, 379, 1–9. [Google Scholar] [CrossRef]
- Gontis, V.; Kaulakys, B. Modeling financial markets by the multiplicative sequence of trades. Physica A 2004, 344, 128–133. [Google Scholar] [CrossRef][Green Version]
- Ruseckas, J.; Kaulakys, B. Tsallis distributions and 1/f noise from nonlinear stochastic differential equations. Phys. Rev. E 2011, 84, 051125. [Google Scholar] [CrossRef] [PubMed]
- Lanouar, C. A Varieties of Spurious Long Memory Process. Int. J. Bus. Soc. Sci. 2011, 2, 52–66. [Google Scholar]
- Ding, M.; Yang, W. Distribution of the first return time in fractional Brownian motion and its application to the study of on-off intermittency. Phys. Rev. E 1995, 52, 207–213. [Google Scholar] [CrossRef]
- Metzler, R.; Oshanin, G.; Redner, S. (Eds.) First-Passage Phenomena and Their Applications; World Scientific: Singapore, 2014; p. 608. [Google Scholar]
- Jeanblanc, M.; Yor, M.; Chesney, M. Mathematical Methods for Financial Markets; Springer: London, UK, 2009. [Google Scholar]
- Gontis, V.; Kononovicius, A.; Reimann, S. The class of nonlinear stochastic models as a background for the bursty behavior in financial markets. ACS 2012, 15, 1250071. [Google Scholar] [CrossRef]
- Kaulakys, B.; Alaburda, M.; Ruseckas, J. 1/f noise from the nonlinear transformations of the variables. Mod. Phys. Lett. B 2015, 29, 1550223. [Google Scholar] [CrossRef]
- Risken, H. The Fokker–Planck Equation: Methods of Solutions and Applications, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Carro, A.; Toral, R.; San Miguel, M. Markets, Herding and Response to External Information. PLoS ONE 2015, 10, e0133287. [Google Scholar] [CrossRef] [PubMed]
- Gontis, V.; Kaulakys, B. Long-range memory model of trading activity and volatility. J. Stat. Mech. 2006, 2006. [Google Scholar] [CrossRef]
- Gontis, V.; Kaulakys, B. Modeling long-range memory trading activity by stochastic differential equatios. Physica A 2007, 382, 114–120. [Google Scholar] [CrossRef]
- Kononovicius, A.; Gontis, V. Agent based reasoning for the non-linear stochastic models of long-range memory. Physica A 2012, 391, 1309–1314. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Methods; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Gontis, V.; Ruseckas, J.; Kononovicius, A. A long-range memory stochastic model of the return in financial markets. Physica A 2010, 389, 100–106. [Google Scholar] [CrossRef]
- Ruseckas, J.; Kaulakys, B. Scaling properties of signals as origin of 1/f noise. J. Stat. Mech. 2014, 2014. [Google Scholar] [CrossRef]
- Kaulakys, B.; Gontis, V.; Alaburda, M. Point process model of 1/f noise vs a sum of Lorentzians. Phys. Rev. E 2005, 71, 051105. [Google Scholar]
- Borodin, A.N.; Salminen, P. Handbook of Brownian Motion, 2nd ed.; Birkhauser: Basel, Switzerland, 2002. [Google Scholar]
- Ruseckas, J.; Kaulakys, B. 1/f noise from nonlinear stochastic differential equations. Phys. Rev. E 2010, 81, 031105. [Google Scholar] [CrossRef] [PubMed]
- Ausloos, M.; Ivanova, K. Dynamical model and nonextensive statistical mechanics of a market index on large time windows. Phys. Rev. E 2003, 68, 046122. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Engle, R.; Patton, A. What good is a volatility model? Quant. Financ. 2001, 1, 237–245. [Google Scholar] [CrossRef]
- Plerou, V.; Gopikrishnan, P.; Gabaix, X.; Amaral, L.; Stanley, H. Price fluctuations, market activity and trading volume. Quant. Financ. 2001, 1, 262–269. [Google Scholar] [CrossRef]
- Gabaix, X.; Gopikrishnan, P.; Plerou, V.; Stanley, H.E. A theory of power law distributions in financial market fluctuations. Nature 2003, 423, 267–270. [Google Scholar] [CrossRef] [PubMed]
- Rangarajan, G.; Ding, M. (Eds.) Processes with Long-Range Correlations: Theory and Applications; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2003; pp. XVIII, 398. [Google Scholar]
- Lo, A.W. Long-Term memory in stock market prices. Econometrica 1991, 59, 1279–1313. [Google Scholar] [CrossRef]
- Willinger, W.; Taqqu, M.S.; Teverovsky, V. Stock market prices and long-range dependence. Financ. Stoch. 1999, 3, 1–13. [Google Scholar] [CrossRef]
- Mikosch, T.; Starica, C. Long-range dependence effects and ARCH modeling. In Theory and Applications of Long-Range Dependence; Birkhauser: Boston, MA, USA, 2003; pp. 439–459. [Google Scholar]
- Kononovicius, A.; Gontis, V. Three state herding model of the financial markets. EPL 2013, 101, 28001. [Google Scholar] [CrossRef]
- Gontis, V.; Kononovicius, A. Burst and inter-burst duration statistics as empirical test of long-range memory in the financial markets. Physica A 2017, 483, 266–272. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).