Reliable Approximation of Long Relaxation Timescales in Molecular Dynamics
Abstract
:1. Introduction
2. Diffusion Process and the Associated Operators
3. Galerkin Approximation of the Eigenvalues of the Generator
3.1. Some General Results
3.2. Finite Dimensional Subspaces
- 1.
- Write and let . Then problem (15) is equivalent to the generalized matrix eigenproblem,where are matrices whose entries are given by,
- 2.
- Let be the smallest eigenvalues of problem (24) and,be the orthonormal eigenvector corresponding to such that . Define , then we have,where , are the eigenvalues and the eigenfunctions of the operator , respectively.
- 3.
- Let be the orthogonal projection operator from H to , and φ be an eigenfunction of the operator corresponding to the eigenvalue λ. Define constants,and suppose that . Then there is an eigenvalue of problem (24) such that,
3.3. Infinite Dimensional Subspace: Effective Dynamics
- 1.
- For where , we have,
- 2.
- Let and be the normalized eigenfunctions of the operators and corresponding to eigenvalues and , respectively. We have,
- 3.
- Let φ be the normalized eigenfunction of the operator corresponding to the eigenvalue λ. Define constants,and suppose . Then there is an eigenvalue of the problem (34), such that,
4. Variational Approach to Generator Eigenproblem
4.1. Variational Principle
- For the lower bound, we consider the optimization problem,Next, we introduce the Lagrange multipliers for , and consider the auxiliary functional,Applying calculus of variation, we conclude that the minimizer of (44) satisfies,Multiplying for some in the first equation of (46) and integrating, we obtain . In the same way we could also obtain . Using the fact that is self-adjoint and for , we conclude that,and (46) reduces to an eigenproblem,Therefore, the minimizer of (44) is given by the orthonormal eigenfunctions. Applying Lemma 1, we can further conclude that the lower bound is obtained when , with value,
- For the upper bound, similarly to the proof of Theorem 1, direct computation gives,where we have used the fact that and , since both are normalized functions.
4.2. Optimization Problem
5. Numerical Algorithms
5.1. Computing Coefficient Matrices Using Effective Dynamics
5.2. Algorithms for Simulating the Effective Dynamics
5.2.1. Algorithm 1
- At step , starting from , generate N trajectories of length of the (unconstrained) full dynamics by discretizing (1). Compute the coefficients by,where .
- Compute from by matrix decomposition. Update by,where are independent standard Gaussian variables, .
5.2.2. Algorithm 2
- Compute from by matrix decomposition. Update the state according to,where are independent standard Gaussian variables, .
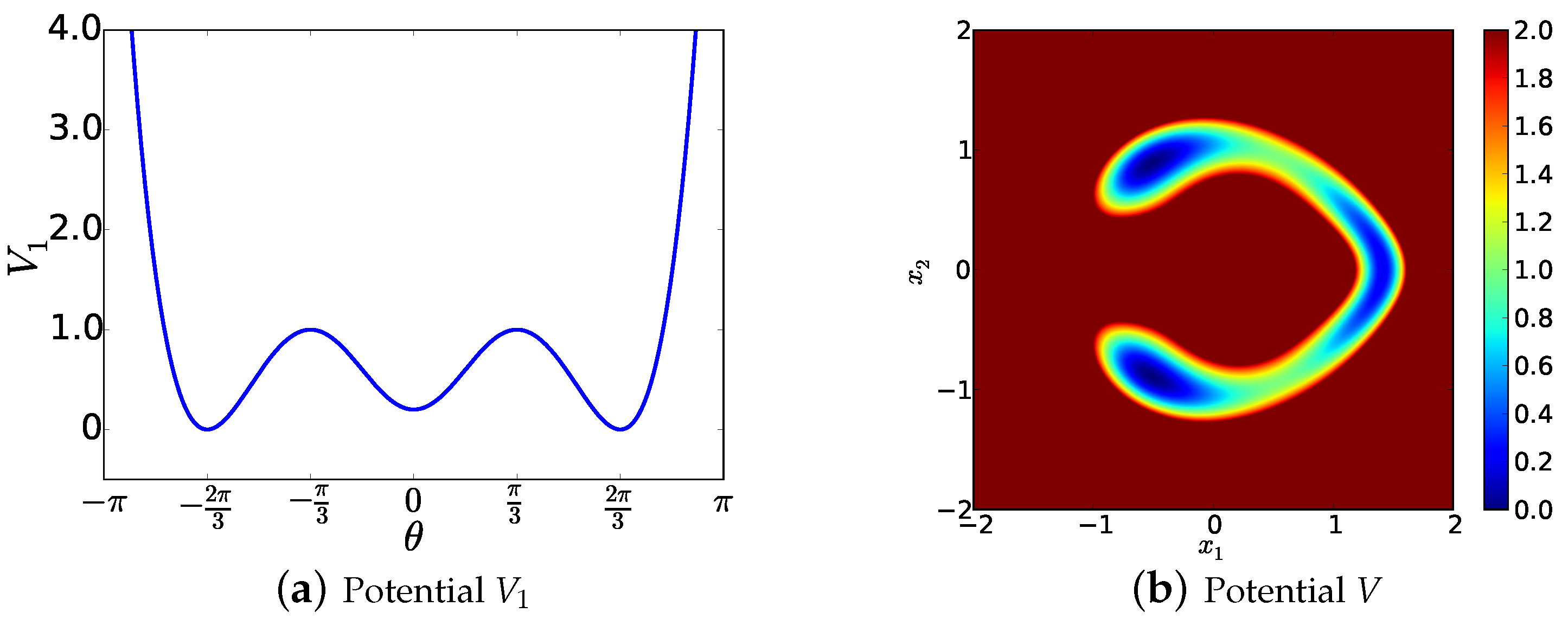
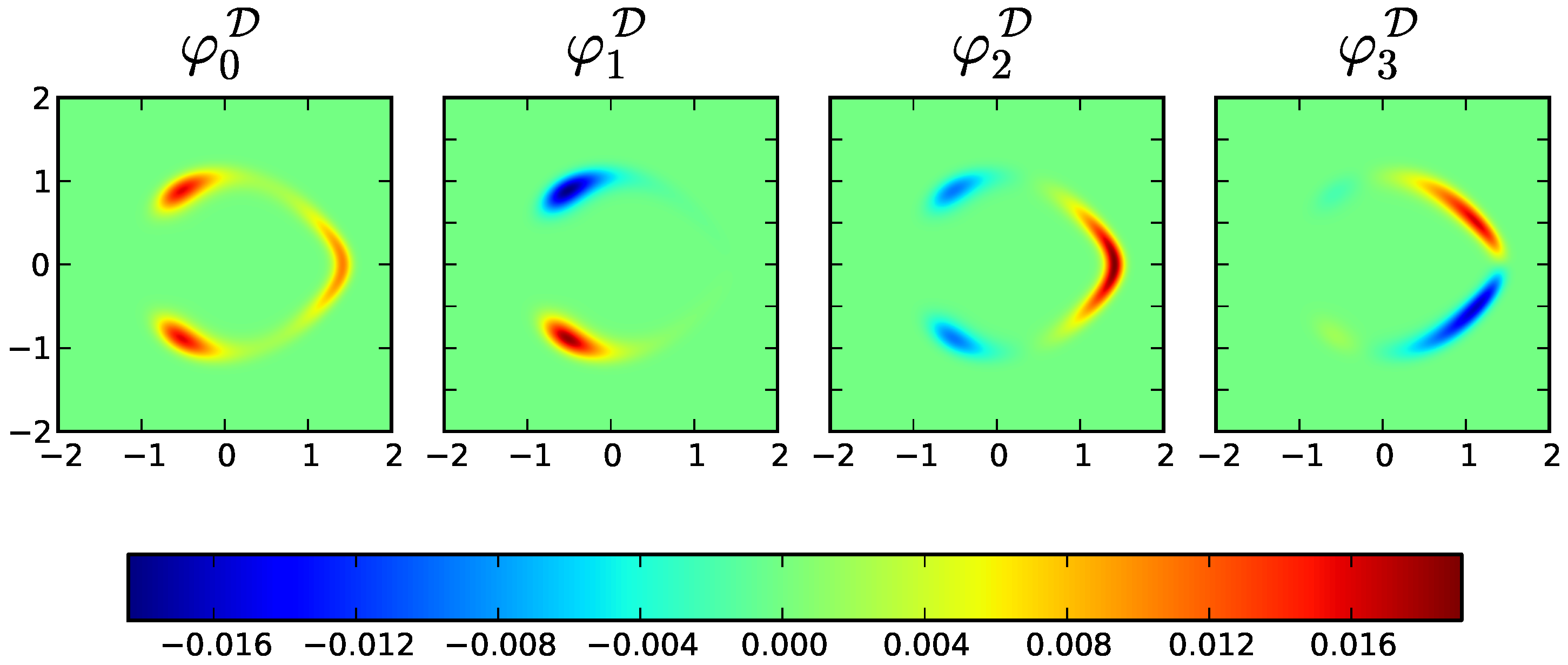
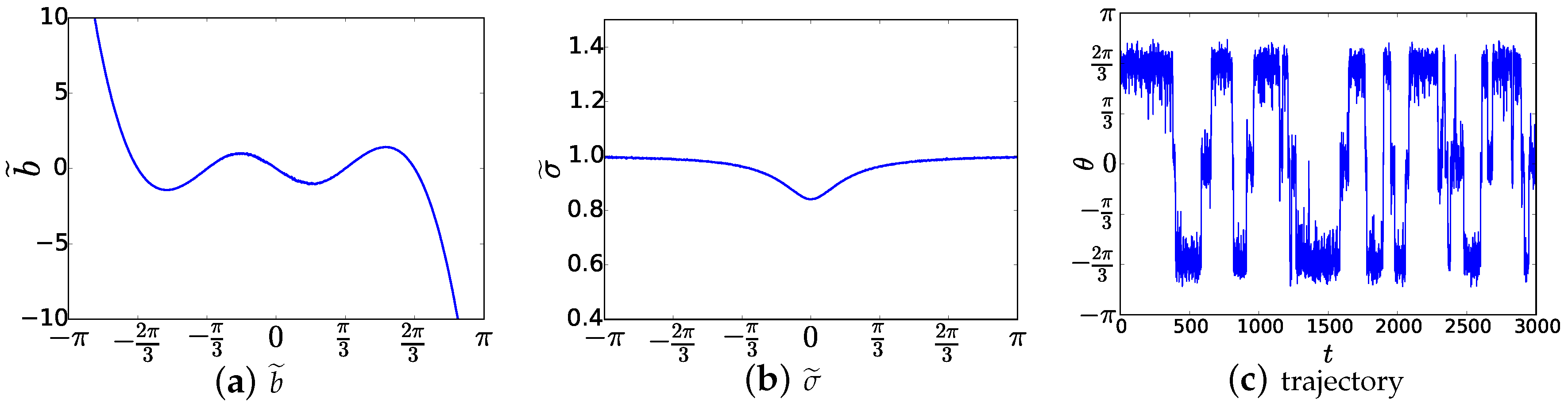
6. Illustrative Example
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Schütte, C.; Fischer, A.; Huisinga, W.; Deuflhard, P. A direct approach to conformational dynamics based on hybrid Monte Carlo. J. Comput. Phys. 1999, 151, 146–168. [Google Scholar]
- Pande, V.S.; Beauchamp, K.; Bowman, G.R. Everything you wanted to know about Markov state models but were afraid to ask. Methods 2010, 52, 99–105. [Google Scholar]
- Pérez-Hernández, G.; Paul, F.; Giorgino, T.; De Fabritiis, G.; Noé, F. Identification of slow molecular order parameters for Markov model construction. J. Chem. Phys. 2013, 139, 015102. [Google Scholar]
- Nüske, F.; Schneider, R.; Vitalini, F.; Noé, F. Variational tensor approach for approximating the rare-event kinetics of macromolecular systems. J. Chem. Phys. 2016, 144, 054105. [Google Scholar]
- Noé, F.; Schütte, C.; Vanden-Eijnden, E.; Reich, L.; Weikl, T.R. Constructing the full ensemble of folding pathways from short off-equilibrium simulations. Proc. Natl. Acad. Sci. USA 2009, 106, 19011–19016. [Google Scholar]
- Bowman, G.R.; Pande, V.S.; Noé, F. (Eds.) Advances in Experimental Medicine and Biology. In An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation; Springer: Dordrecht, The Netherlands, 2014; Volume 797. [Google Scholar]
- Noé, F.; Nüske, F. A variational approach to modeling slow processes in stochastic dynamical systems. Multiscale Model. Simul. 2013, 11, 635–655. [Google Scholar]
- Nüske, F.; Keller, B.G.; Pérez-Hernández, G.; Mey, A.; Noé, F. Variational approach to molecular kinetics. J. Chem. Theory Comput. 2014, 10, 1739–1752. [Google Scholar]
- Schütte, C.; Sarich, M. Metastability and Markov State Models in Molecular Dynamics: Modeling, Analysis, Algorithmic Approaches; Courant Lecture Notes; American Mathematical Society/Courant Institute of Mathematical Science: New York, NY, USA, 2014. [Google Scholar]
- Schütte, C.; Noé, F.; Lu, J.; Sarich, M.; Vanden-Eijnden, E. Markov state models based on milestoning. J. Chem. Phys. 2011, 134, 204105. [Google Scholar]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar]
- Laio, A.; Gervasio, F.L. Metadynamics: A method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar]
- Ciccotti, G.; Kapral, R.; Vanden-Eijnden, E. Blue moon sampling, vectorial eeaction coordinates, and unbiased constrained dynamics. ChemPhysChem 2005, 6, 1809–1814. [Google Scholar]
- Darve, E.; Rodríguez-Gömez, D.; Pohorille, A. Adaptive biasing force method for scalar and vector free energy calculations. J. Chem. Phys. 2008, 128, 144120. [Google Scholar]
- Maragliano, L.; Vanden-Eijnden, E. A temperature accelerated method for sampling free energy and determining reaction pathways in rare events simulations. Chem. Phys. Lett. 2006, 426, 168–175. [Google Scholar]
- Faradjian, A.K.; Elber, R. Computing time scales from reaction coordinates by milestoning. J. Chem. Phys. 2004, 120, 10880–10889. [Google Scholar]
- Moroni, D.; van Erp, T.; Bolhuis, P. Investigating rare events by transition interface sampling. Physica A 2004, 340, 395–401. [Google Scholar]
- Becker, N.B.; Allen, R.J.; ten Wolde, P.R. Non-stationary forward flux sampling. J. Chem. Phys. 2012, 136, 174118. [Google Scholar]
- Legoll, F.; Lelièvre, T. Effective dynamics using conditional expectations. Nonlinearity 2010, 23, 2131–2163. [Google Scholar]
- Froyland, G.; Gottwald, G.A.; Hammerlindl, A. A computational method to extract macroscopic variables and their dynamics in multiscale systems. SIAM J. Appl. Dyn. Syst. 2014, 13, 1816–1846. [Google Scholar]
- Zhang, W.; Hartmann, C.; Schutte, C. Effective dynamics along given reaction coordinates, and reaction rate theory. Faraday Discuss. 2016, 195, 365–394. [Google Scholar]
- Kevrekidis, I.G.; Gear, C.W.; Hummer, G. Equation-free: The computer-aided analysis of complex multiscale systems. AIChE J. 2004, 50, 1346–1355. [Google Scholar]
- Kevrekidis, I.G.; Samaey, G. Equation-free multiscale computation: Algorithms and applications. Annu. Rev. Phys. Chem. 2009, 60, 321–344. [Google Scholar]
- Kevrekidis, I.G.; Gear, C.W.; Hyman, J.M.; Kevrekidid, P.G.; Runborg, O.; Theodoropoulos, C. Equation-free, coarse-grained multiscale computation: Enabling mocroscopic simulators to perform system-level analysis. Commun. Math. Sci. 2003, 1, 715–762. [Google Scholar]
- Prinz, J.H.; Wu, H.; Sarich, M.; Keller, B.; Senne, M.; Held, M.; Chodera, J.D.; Schütte, C.; Noé, F. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 2011, 134, 174105. [Google Scholar]
- Djurdjevac, N.; Sarich, M.; Schütte, C. Estimating the eigenvalue error of Markov state models. Multiscale Model. Simul. 2012, 10, 61–81. [Google Scholar]
- Sarich, M.; Noé, F.; Schütte, C. On the approximation quality of Markov state models. Multiscale Model. Simul. 2010, 8, 1154–1177. [Google Scholar]
- Sarich, M.; Schütte, C. Approximating selected non-dominant timescales by Markov state models. Comm. Math. Sci. 2012, 10, 1001–1013. [Google Scholar]
- Mattingly, J.C.; Stuart, A.M.; Higham, D.J. Ergodicity for SDEs and approximations: locally Lipschitz vector fields and degenerate noise. Stoch. Proc. Appl. 2002, 101, 185–232. [Google Scholar] [Green Version]
- Schütte, C.; Huisinga, W.; Deuflhard, P. Transfer operator approach to conformational dynamics in biomolecular systems. In Ergodic Theory, Analysis, and Efficient Simulation of Dynamical Systems; Fiedler, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 191–223. [Google Scholar]
- Gyöngy, I. Mimicking the one-dimensional marginal distributions of processes having an Ito differential. Probab. Theory Relat. Fields 1986, 71, 501–516. [Google Scholar]
- Ciccotti, G.; Lelièvre, T.; Vanden-Eijnden, E. Projection of diffusions on submanifolds: Application to mean force computation. Commun. Pure Appl. Math. 2008, 61, 371–408. [Google Scholar]
- Lelièvre, T.; Rousset, M.; Stoltz, G. Langevin dynamics with constraints and computation of free energy differences. Math. Comput. 2012, 81, 2071–2125. [Google Scholar]
- Hernandez, V.; Roman, J.E.; Vidal, V. SLEPc: A scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 2005, 31, 351–362. [Google Scholar]
- Hartmann, C.; Schütte, C.; Zhang, W. Model reduction algorithms for optimal control and importance sampling of diffusions. Nonlinearity 2016, 29, 2298–2326. [Google Scholar]
- Rohrdanz, M.A.; Zheng, W.; Maggioni, M.; Clementi, C. Determination of reaction coordinates via locally scaled diffusion map. J. Chem. Phys. 2011, 134, 124116. [Google Scholar]
- Bittracher, A.; Koltai, P.; Klus, S.; Banisch, R.; Dellnitz, M.; Schütte, C. Transition manifolds of complex metastable systems: Theory and data-driven computation of effective dynamics. J. Nonlinear Sci. 2017, submitted. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Schütte, C. Reliable Approximation of Long Relaxation Timescales in Molecular Dynamics. Entropy 2017, 19, 367. https://doi.org/10.3390/e19070367
Zhang W, Schütte C. Reliable Approximation of Long Relaxation Timescales in Molecular Dynamics. Entropy. 2017; 19(7):367. https://doi.org/10.3390/e19070367
Chicago/Turabian StyleZhang, Wei, and Christof Schütte. 2017. "Reliable Approximation of Long Relaxation Timescales in Molecular Dynamics" Entropy 19, no. 7: 367. https://doi.org/10.3390/e19070367
APA StyleZhang, W., & Schütte, C. (2017). Reliable Approximation of Long Relaxation Timescales in Molecular Dynamics. Entropy, 19(7), 367. https://doi.org/10.3390/e19070367



