An Exploration Algorithm for Stochastic Simulators Driven by Energy Gradients
Abstract
:1. Introduction
2. Diffusion Maps and the iMapD Algorithm
2.1. Diffusion Maps in Statistical Mechanics
2.2. Overview of the iMapD Method
3. Algorithmic Building Blocks
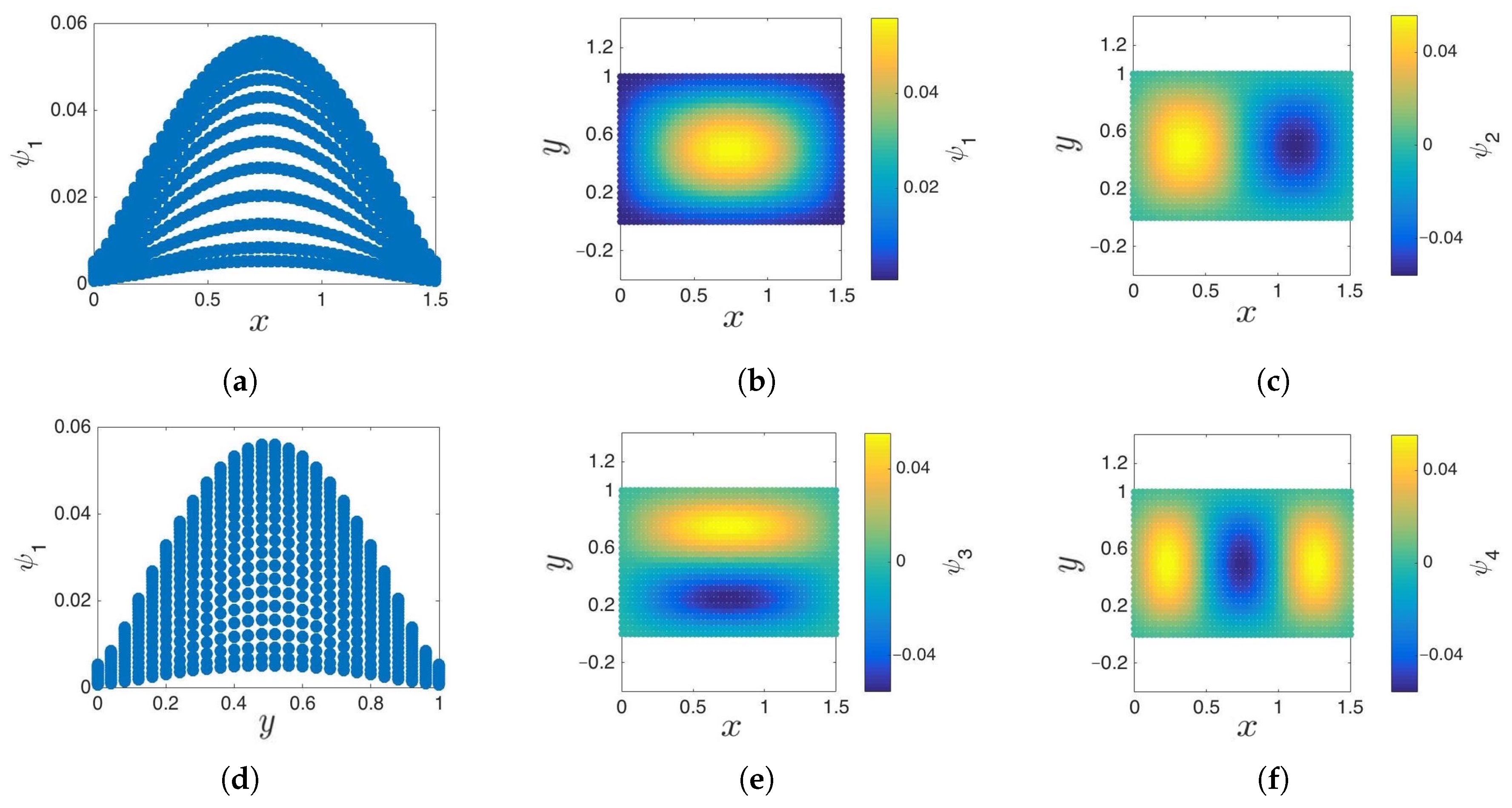
3.1. Cosine and Sine-Diffusion Maps
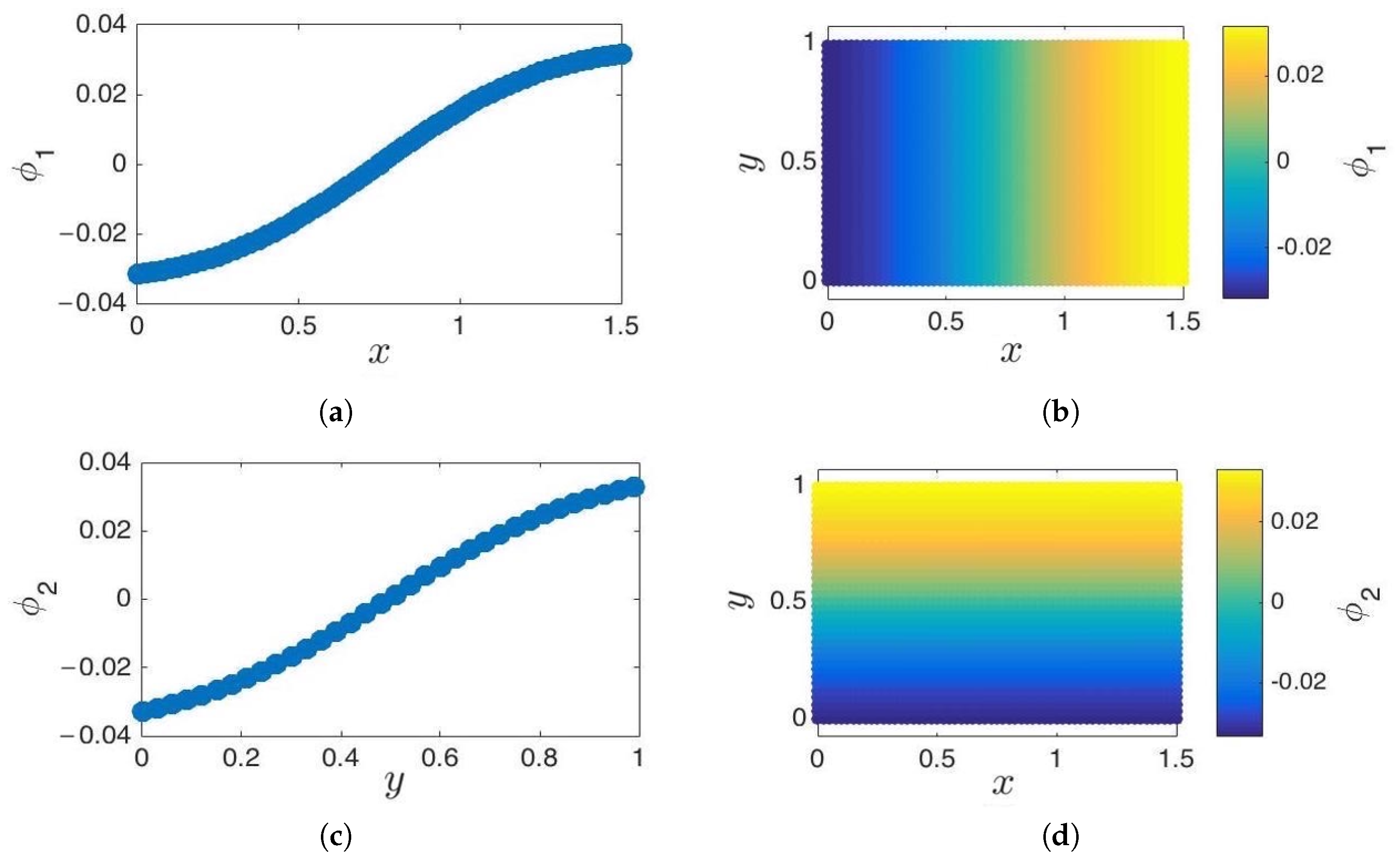
3.2. Local Principal Component Analysis
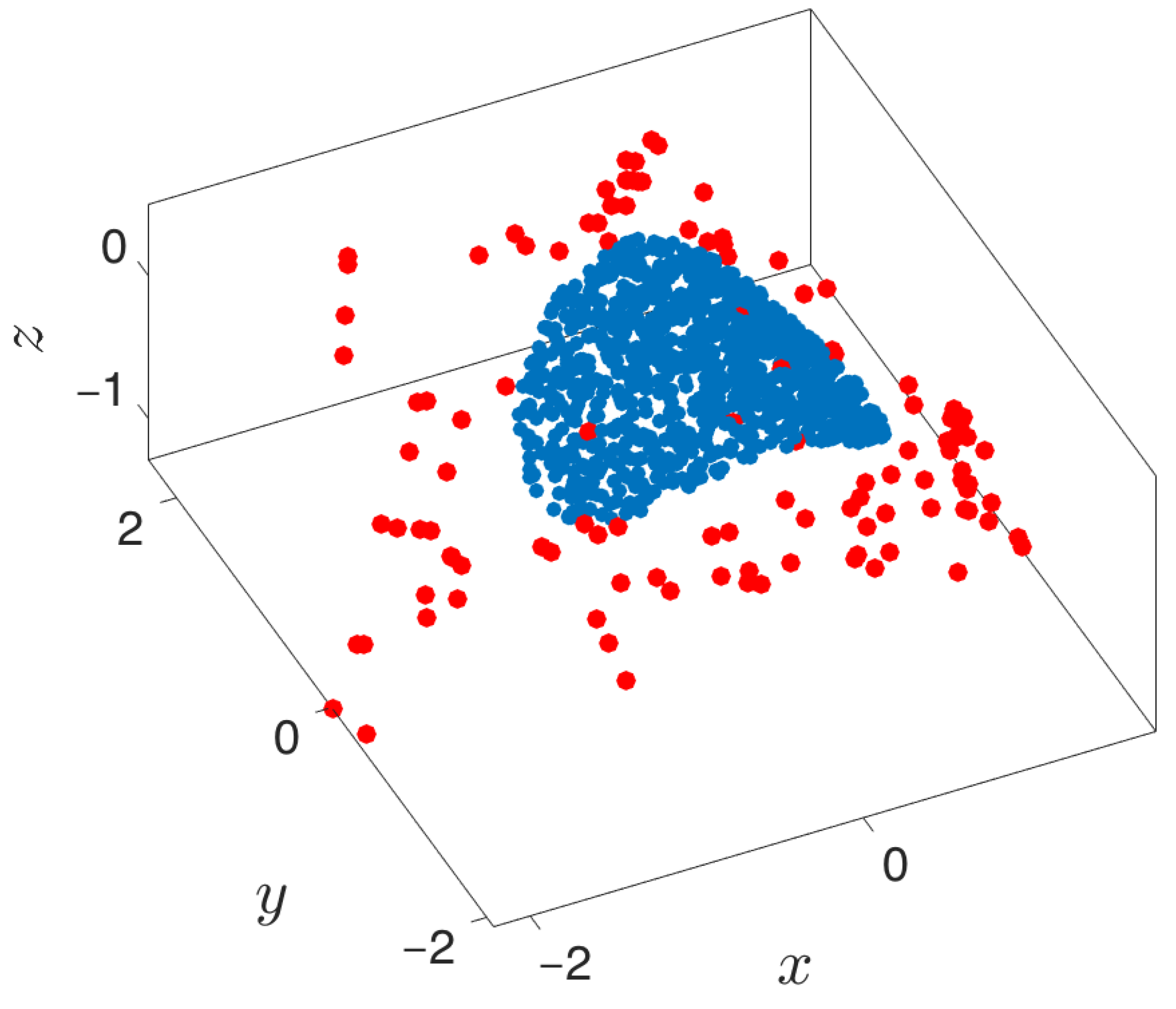
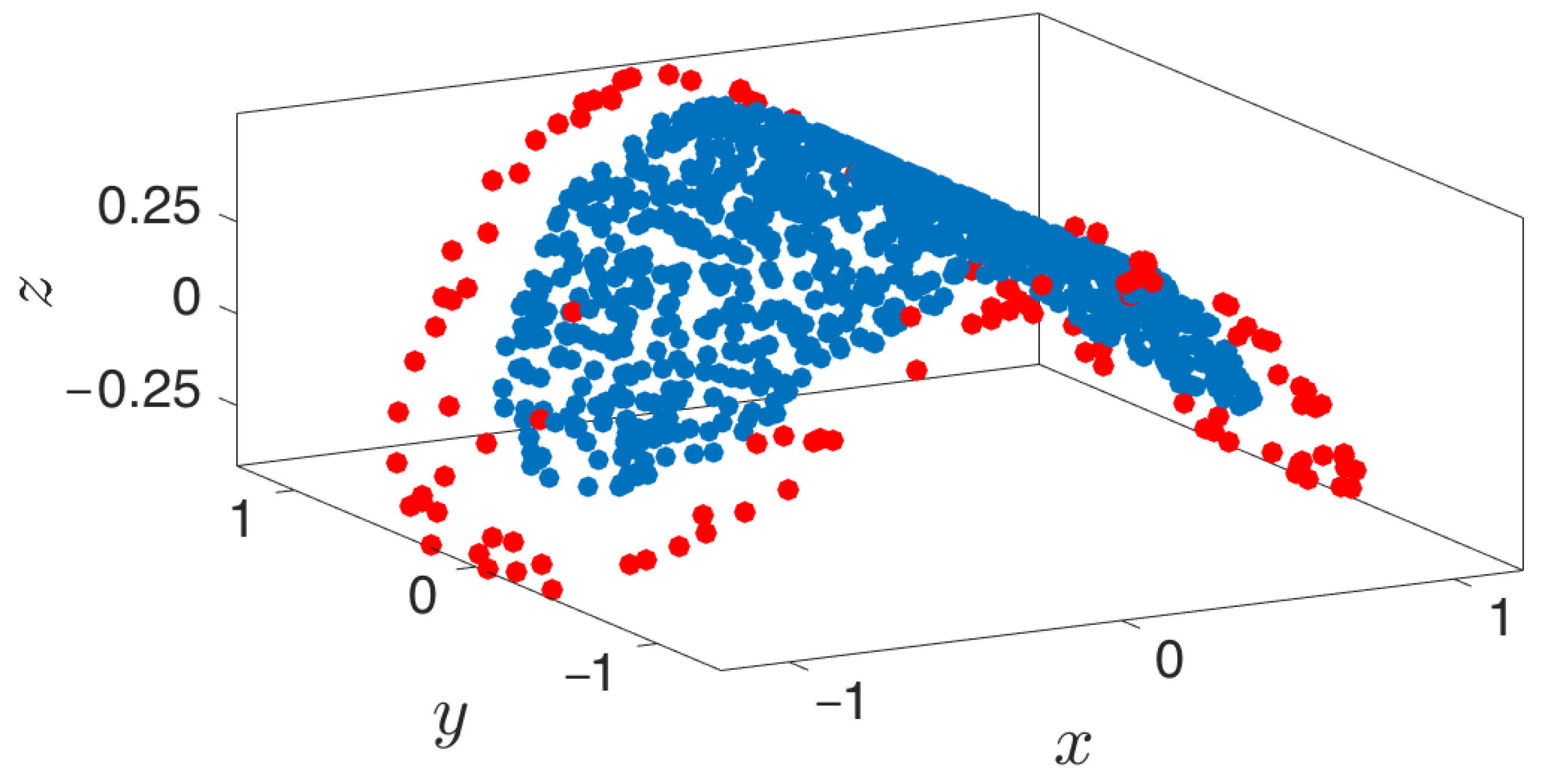
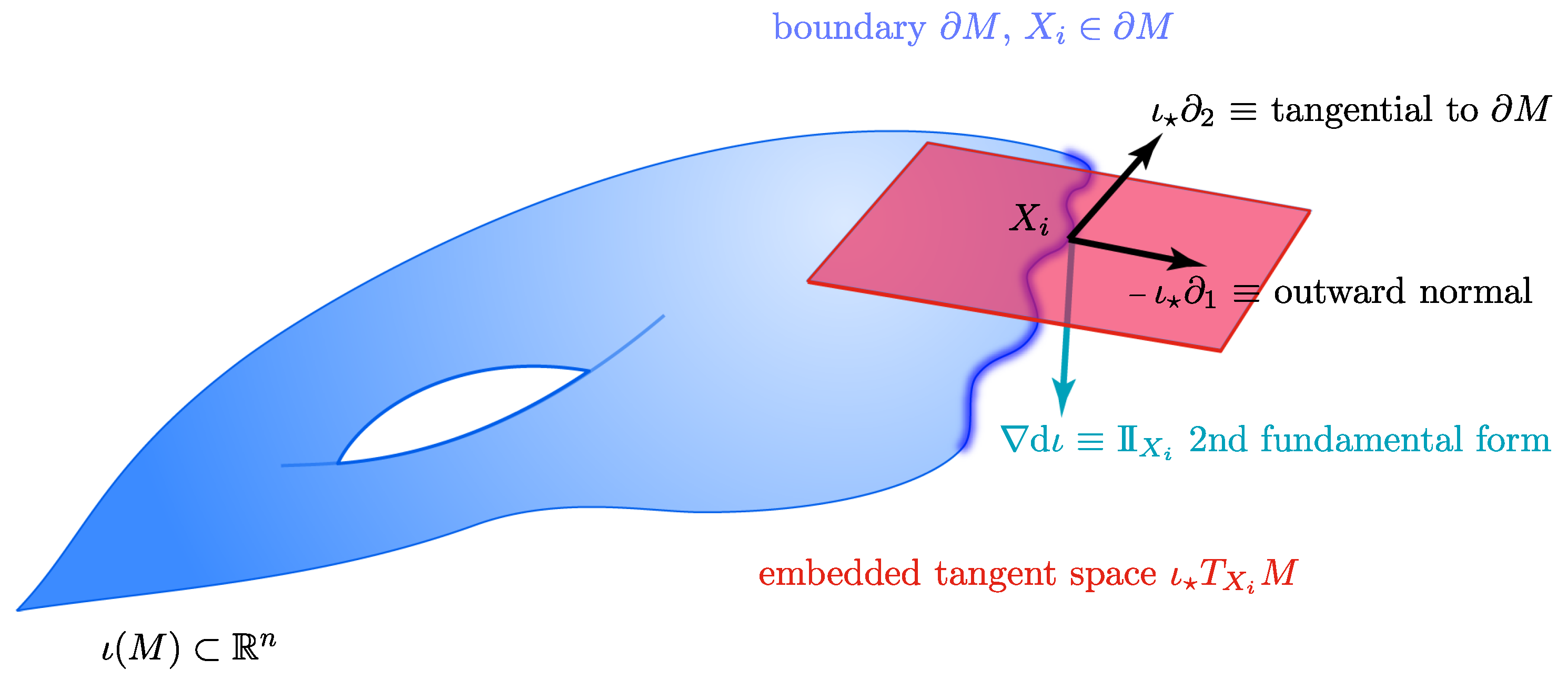
3.3. Boundary Detection
3.4. Outward Extension across the Boundary of a Manifold
3.5. Geometric Harmonics
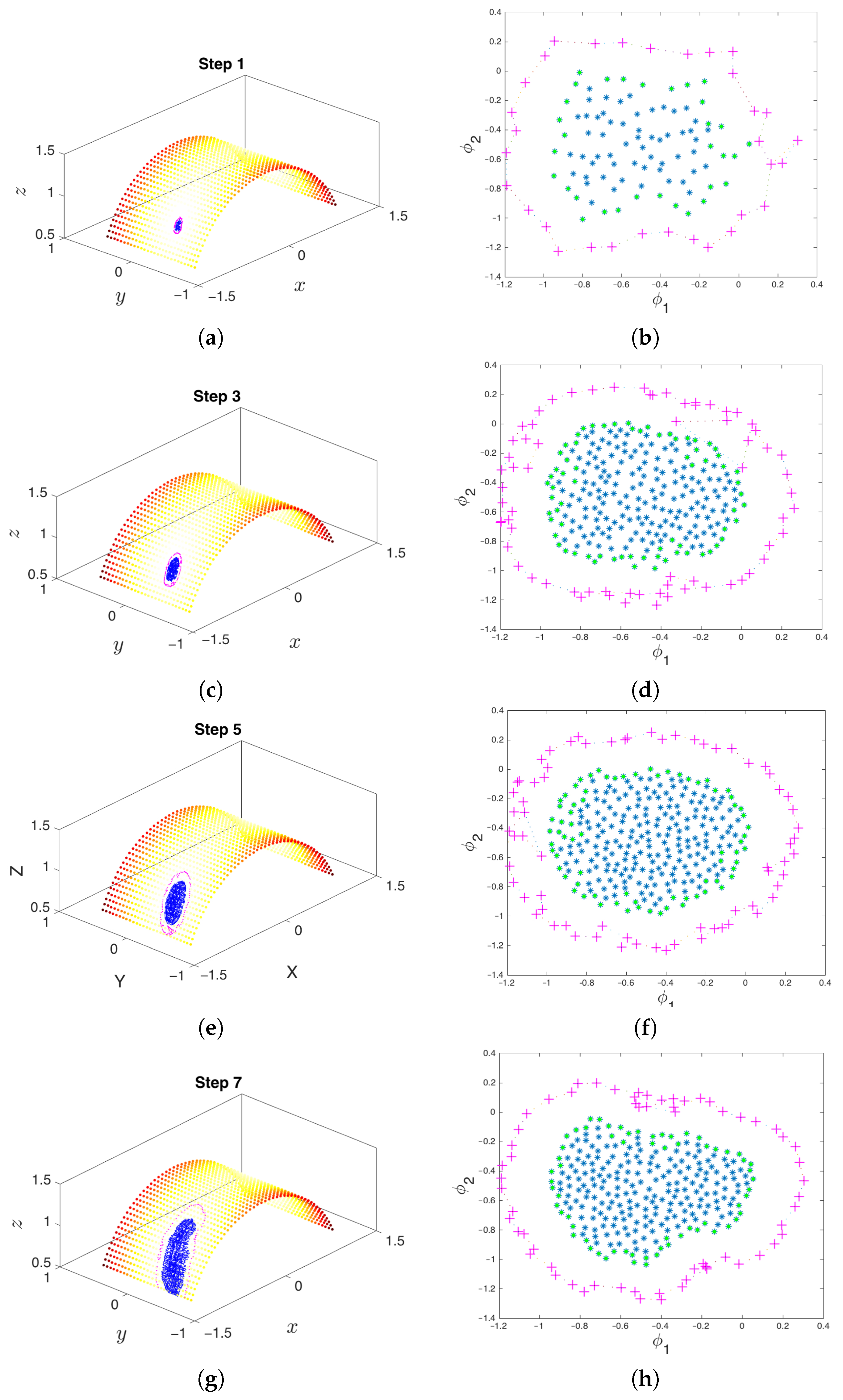
3.6. iMapD Algorithm
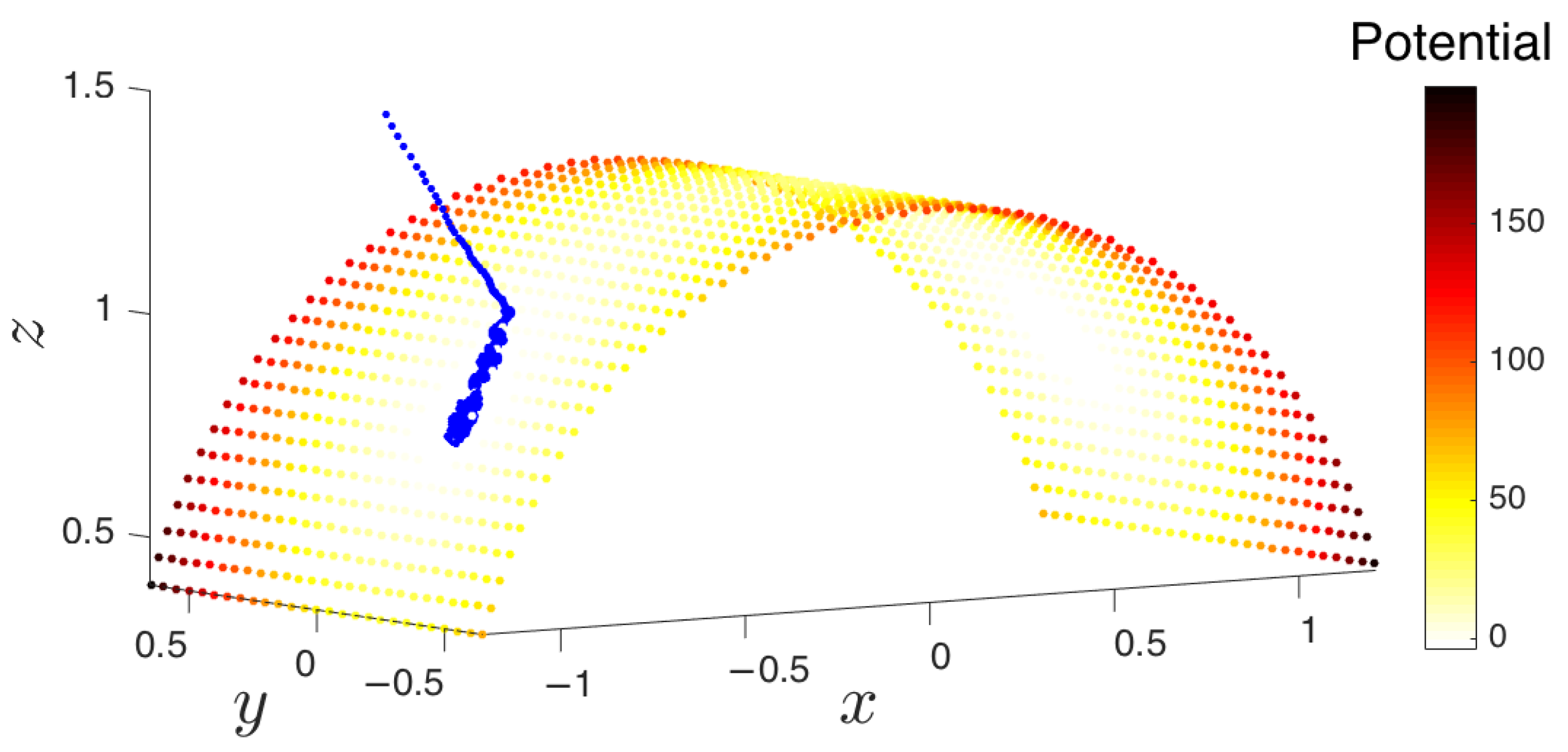
- Collection of an initial set of samples: The molecular system is initialized and evolved long enough so that it arrives at some basin of attraction. After removing the initial points that quickly arrive at the attracting manifold, the remaining data points constitute the initial set of samples (point cloud) on the manifold. These samples will be used in the subsequent steps of the method.
- Parameterization of point cloud in lower dimensions: Using the set of samples from the previous step, we extract an optimal (and typically low-dimensional) set of coarse variables using DMAPS (for example, with cosine-diffusion maps). This process yields a parameterization of the local geometry of the free energy landscape around the region being currently visited by our system. All of our points are then mapped to the new set of coarse variables, thereby reducing the dimensionality of the system.
- Outward extrapolation in low-dimensional space: After identifying the current generation of boundary points in the space of coarse variables (for example, via the alpha-shapes algorithm), we obtain additional points by extrapolating in the direction normal to the boundary.
- Lifting of points from the (local) space of coarse variables to the conformational space: In order to continue the simulation, we must obtain a realization in conformational space of the newly-extended points in DMAP (or other reduced) space. In other words, we need a sufficient number of points in conformational space that are consistent with the DMAP (reduced) coordinates of the newly-extrapolated points. In the present paper, we use geometric harmonics, but in general, this task can be accomplished using biasing potentials, such as those available in PLUMED [96] or Colvars [97].
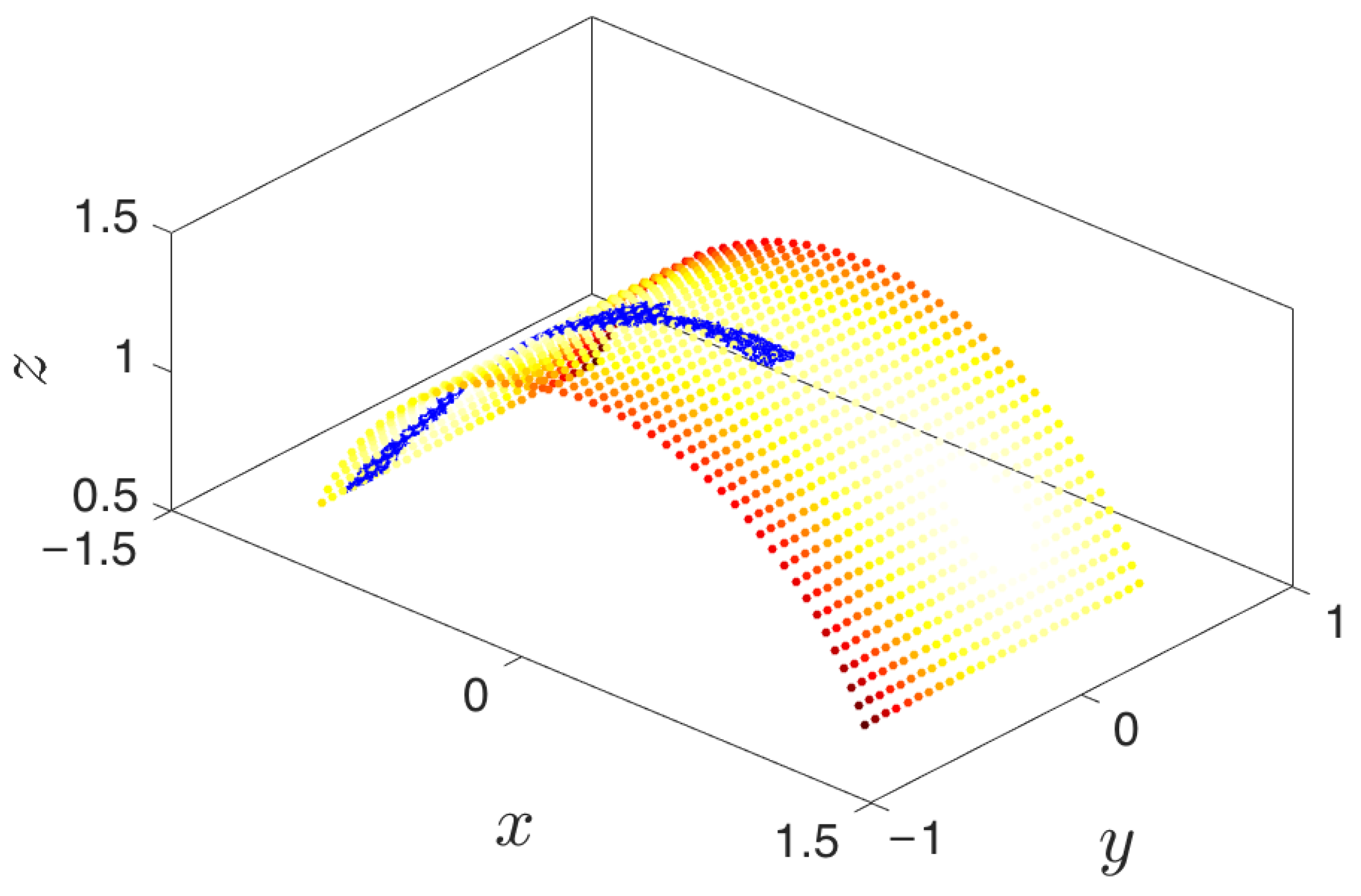
- Repetition until the landscape is sufficiently explored: The lifted points serve as guesses for regions of the manifold that are yet to be probed. The system is reinitialized at these points (usually by running new parallel simulations), and the unexplored space is progressively discovered. This process is then repeated, effectively growing the set of sampled points on the free energy landscape.
- Simulation run time: Though system dependent, simulations should be run until (a) the trajectory enters a region already explored, or (b) a new basin is discovered, or (c) a reasonable amount of time has passed for the trajectory to have explored “new ground” within the current basin. These conditions can be tested by detecting if the trajectory remains within a certain radius for a given amount of time (it has most likely found a potential well) or if the trajectory has a nontrivial amount of nearest neighbors from already explored regions.
- Selection of trajectory points: Only “on manifold” points that belong to the basin of attraction should be collected. We implement this by removing a fixed number of points early in the trajectory that correspond to the initial approach to the attracting manifold. Discarding them will have the beneficial effect of preventing the exploration in directions orthogonal to the attractor. The exploration among the remaining points will lead to better sampling of basins and around saddle points within the attracting manifold.
- Memory storage of data points: Observe that the samples gathered throughout the exploration process need not be kept in memory and can instead be stored in the hard drive. In principle, the file system or an appropriate database can be used to keep the corresponding files, but if storage space becomes an issue, then it is possible to randomly prune points whenever a (user-specified) maximum number of data points is exceeded. Note that if, between random pruning and preprocessing the data, distinct patches of explored regions appear, each sample of the manifold must be expanded separately so as not to discard samples that may have potentially reached new metastable states.
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shaw, D.E.; Grossman, J.; Bank, J.A.; Batson, B.; Butts, J.A.; Chao, J.C.; Deneroff, M.M.; Dror, R.O.; Even, A.; Fenton, C.H.; et al. Anton 2: Raising the Bar for Performance and Programmability in a Special-Purpose Molecular Dynamics Supercomputer. In Proceedings of the SC14: International Conference for High Performance Computing, Networking, Storage and Analysis, New Orleans, LA, USA, 16–21 November 2014; pp. 41–53. [Google Scholar]
- Demir, O.; Ieong, P.U.; Amaro, R.E. Full-length p53 tetramer bound to DNA and its quaternary dynamics. Oncogene 2017, 36, 1451–1460. [Google Scholar] [CrossRef] [PubMed]
- Leimkuhler, B.; Matthews, C. Molecular Dynamics; Interdisciplinary Applied Mathematics; Springer International Publishing: Cham, Switzerland, 2015; Volume 39, pp. 1–88. [Google Scholar]
- Bryngelson, J.D.; Onuchic, J.N.; Socci, N.D.; Wolynes, P.G. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins 1995, 21, 167–195. [Google Scholar] [CrossRef] [PubMed]
- Wales, D. Energy Landscapes; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [Google Scholar] [CrossRef] [PubMed]
- Darve, E.; Rodríguez-Gómez, D.; Pohorille, A. Adaptive biasing force method for scalar and vector free energy calculations. J. Chem. Phys. 2008, 128, 144120. [Google Scholar] [CrossRef] [PubMed]
- Hénin, J.; Fiorin, G.; Chipot, C.; Klein, M.L. Exploring multidimensional free energy landscapes using time-dependent biases on collective variables. J. Chem. Theory Comput. 2010, 6, 35–47. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.J.; Valeriani, C.; Rein Ten Wolde, P. Forward flux sampling for rare event simulations. J. Phys. Condens. 2009, 21, 463102. [Google Scholar] [CrossRef] [PubMed]
- Roitberg, A.; Elber, R. Modeling side chains in peptides and proteins: Application of the locally enhanced sampling and the simulated annealing methods to find minimum energy conformations. J. Chem. Phys. 1991, 95, 9277–9287. [Google Scholar] [CrossRef]
- Krivov, S.V.; Karplus, M. Hidden complexity of free energy surfaces for peptide (protein) folding. Proc. Natl. Acad. Sci. USA 2004, 101, 14766–14770. [Google Scholar] [CrossRef] [PubMed]
- Schultheis, V.; Hirschberger, T.; Carstens, H.; Tavan, P. Extracting Markov Models of Peptide Conformational Dynamics from Simulation Data. J. Chem. Theory Comput. 2005, 1, 515–526. [Google Scholar] [CrossRef] [PubMed]
- Muff, S.; Caflisch, A. Kinetic analysis of molecular dynamics simulations reveals changes in the denatured state and switch of folding pathways upon single-point mutation of a β-sheet miniprotein. Proteins Struct. Funct. Bioinform. 2007, 70, 1185–1195. [Google Scholar] [CrossRef] [PubMed]
- Pan, A.C.; Roux, B. Building Markov state models along pathways to determine free energies and rates of transitions. J. Chem. Phys. 2008, 129, 064107. [Google Scholar] [CrossRef] [PubMed]
- Schütte, C.; Sarich, M. Metastability and Markov State Models in Molecular Dynamics: Courant Lecture Notes; American Mathematical Society: Providence, RI, USA, 2013; Volume 24. [Google Scholar]
- Laio, A.; Gervasio, F.L. Metadynamics: A method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar] [CrossRef]
- Valsson, O.; Tiwary, P.; Parrinello, M. Enhancing Important Fluctuations: Rare Events and Metadynamics from a Conceptual Viewpoint. Ann. Rev. Phys. Chem. 2016, 67, 159–184. [Google Scholar] [CrossRef] [PubMed]
- Faradjian, A.K.; Elber, R. Computing time scales from reaction coordinates by milestoning. J. Chem. Phys. 2004, 120, 10880–10889. [Google Scholar] [CrossRef] [PubMed]
- Bello-Rivas, J.M.; Elber, R. Exact milestoning. J. Chem. Phys. 2015, 142, 094102. [Google Scholar] [CrossRef] [PubMed]
- Jónsson, H.; Mills, G.; Jacobsen, K.W. Nudged elastic band method for finding minimum energy paths of transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations; World Scientific: Singapore, 1998; pp. 385–404. [Google Scholar]
- Mills, G.; Jónsson, H.; Schenter, G.K. Reversible work transition state theory: Application to dissociative adsorption of hydrogen. Surf. Sci. 1995, 324, 305–337. [Google Scholar] [CrossRef]
- Mills, G.; Jónsson, H. Quantum and thermal effects in H2 dissociative adsorption: Evaluation of free energy barriers in multidimensional quantum systems. Phys. Rev. Lett. 1994, 72, 1124–1127. [Google Scholar] [CrossRef] [PubMed]
- Sugita, Y.; Okamoto, Y. Replica-exchange molecular dynamics method for protein folding. Chem. Phys. Lett. 1999, 314, 141–151. [Google Scholar] [CrossRef]
- Lyubartsev, A.P.; Martsinovski, A.A.; Shevkunov, S.V.; Vorontsov-Velyaminov, P.N. New approach to Monte Carlo calculation of the free energy: Method of expanded ensembles. J. Chem. Phys. 1992, 96, 1776–1783. [Google Scholar] [CrossRef]
- Marinari, E.; Parisi, G. Simulated Tempering: A New Monte Carlo Scheme. Europhys. Lett. 1992, 19, 451–458. [Google Scholar] [CrossRef]
- Izrailev, S.; Stepaniants, S.; Isralewitz, B.; Kosztin, D.; Lu, H.; Molnar, F.; Wriggers, W.; Schulten, K. Steered Molecular Dynamics. In Computational Molecular Dynamics: Challenges, Methods, Ideas; Deuflhard, P., Hermans, J., Leimkuhler, B., Mark, A.E., Reich, S., Skeel, R.D., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 39–65. [Google Scholar]
- Weinan, E.; Ren, W.; Vanden-Eijnden, E. String method for the study of rare events. Phys. Rev. B 2002, 66, 052301. [Google Scholar]
- Maragliano, L.; Fischer, A.; Vanden-Eijnden, E.; Ciccotti, G. String method in collective variables: Minimum free energy paths and isocommittor surfaces. J. Chem. Phys. 2006, 125, 024106. [Google Scholar] [CrossRef] [PubMed]
- Dellago, C.; Bolhuis, P.G.; Chandler, D. Efficient transition path sampling: Application to Lennard-Jones cluster rearrangements. J. Chem. Phys. 1998, 108, 9236–9245. [Google Scholar] [CrossRef]
- Bolhuis, P.G.; Chandler, D.; Dellago, C.; Geissler, P.L. Transition path sampling: Throwing ropes over rough nountain passes, in the dark. Ann. Rev. Phys. Chem. 2002, 53, 291–318. [Google Scholar] [CrossRef] [PubMed]
- Van Erp, T.S.; Moroni, D.; Bolhuis, P.G. A novel path sampling method for the calculation of rate constants. J. Chem. Phys. 2003, 118, 7762–7774. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Monte Carlo free energy estimates using non-Boltzmann sampling: Application to the sub-critical Lennard-Jones fluid. Chem. Phys. Lett. 1974, 28, 578–581. [Google Scholar] [CrossRef]
- Kästner, J. Umbrella sampling. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 932–942. [Google Scholar] [CrossRef]
- Huber, G.; Kim, S. Weighted-ensemble Brownian dynamics simulations for protein association reactions. Biophys. J. 1996, 70, 97–110. [Google Scholar] [CrossRef]
- Suárez, E.; Pratt, A.J.; Chong, L.T.; Zuckerman, D.M. Estimating first-passage time distributions from weighted ensemble simulations and non-Markovian analyses. Protein Sci. 2016, 25, 67–78. [Google Scholar] [CrossRef] [PubMed]
- Bernardi, R.C.; Melo, M.C.; Schulten, K. Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Biophys. Acta 2015, 1850, 872–877. [Google Scholar] [CrossRef] [PubMed]
- Elber, R. Perspective: Computer simulations of long time dynamics. J. Chem. Phys. 2016, 144, 060901. [Google Scholar] [CrossRef] [PubMed]
- Peters, B. Reaction Coordinates and Mechanistic Hypothesis Tests. Annu. Rev. Phys. Chem. 2016, 67, 669–690. [Google Scholar] [CrossRef] [PubMed]
- Du, R.; Pande, V.S.; Grosberg, A.Y.; Tanaka, T.; Shakhnovich, E.S. On the transition coordinate for protein folding. J. Chem. Phys. 1998, 108, 334–350. [Google Scholar] [CrossRef]
- Geissler, P.L.; Dellago, C.; Chandler, D. Kinetic Pathways of Ion Pair Dissociation in Water. J. Phys. Chem. B 1999, 103, 3706–3710. [Google Scholar] [CrossRef]
- Peters, B. Using the histogram test to quantify reaction coordinate error. J. Chem. Phys. 2006, 125, 241101. [Google Scholar] [CrossRef] [PubMed]
- Krivov, S.V. On Reaction Coordinate Optimality. J. Chem. Theory Comput. 2013, 9, 135–146. [Google Scholar] [CrossRef] [PubMed]
- Van Erp, T.S.; Moqadam, M.; Riccardi, E.; Lervik, A. Analyzing Complex Reaction Mechanisms Using Path Sampling. J. Chem. Theory Comput. 2016, 12, 5398–5410. [Google Scholar] [CrossRef] [PubMed]
- Socci, N.D.; Onuchic, J.N.; Wolynes, P.G.; Introduction, I. Diffusive dynamics of the reaction coordinate for protein folding funnels. J. Chem. Phys. 1996, 104, 5860. [Google Scholar] [CrossRef]
- Best, R.B.; Hummer, G. Coordinate-dependent diffusion in protein folding. Proc. Natl. Acad. Sci. USA 2010, 107, 1088–1093. [Google Scholar] [CrossRef] [PubMed]
- Zwanzig, R. Nonequilibrium Statistical Mechanics; Oxford University Press: New York, NY, USA, 2001. [Google Scholar]
- Lei, H.; Baker, N.; Li, X. Data-driven parameterization of the generalized Langevin equation. Proc. Natl. Acad. Sci. USA 2016, 113, 14183–14188. [Google Scholar] [CrossRef] [PubMed]
- Hijón, C.; Español, P.; Vanden-Eijnden, E.; Delgado-Buscalioni, R. Mori–Zwanzig formalism as a practical computational tool. Faraday Discuss. 2010, 144, 301–322. [Google Scholar] [CrossRef] [PubMed]
- Chiavazzo, E.; Covino, R.; Coifman, R.R.; Gear, C.W.; Georgiou, A.S.; Hummer, G.; Kevrekidis, I.G. Intrinsic Map Dynamics exploration for uncharted effective free-energy landscapes. Proc. Natl. Acad. Sci. USA 2017, in press. [Google Scholar] [CrossRef]
- Wales, D.J. Perspective: Insight into reaction coordinates and dynamics from the potential energy landscape. J. Chem. Phys. 2015, 142, 130901. [Google Scholar] [CrossRef] [PubMed]
- Karatzas, I.; Shreve, S.E. Brownian Motion and Stochastic Calculus: Graduate Texts in Mathematics; Springer: New York, NY, USA, 1998; Volume 113. [Google Scholar]
- Gardiner, C. Stochastic Methods, 4th ed.; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany, 2009; p. xviii+447. [Google Scholar]
- Risken, H. The Fokker-Planck Equation, 2nd ed.; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany, 1989; Volume 18, p. xiv+472. [Google Scholar]
- Coifman, R.R.; Kevrekidis, I.G.; Lafon, S.; Maggioni, M.; Nadler, B. Diffusion Maps, Reduction Coordinates, and Low Dimensional Representation of Stochastic Systems. Multiscale Model. Simul. 2008, 7, 842–864. [Google Scholar] [CrossRef]
- Brenner, S.C.; Scott, L.R. The Mathematical Theory of Finite Element Methods; Vol. 15, Texts in Applied Mathematics; Springer: New York, NY, USA, 2008. [Google Scholar]
- Singer, A. From graph to manifold Laplacian: The convergence rate. Appl. Comput. Harmon. Anal. 2006, 21, 128–134. [Google Scholar] [CrossRef]
- Singer, A.; Coifman, R.R. Non-linear independent component analysis with diffusion maps. Appl. Comput. Harmon. Anal. 2008, 25, 226–239. [Google Scholar] [CrossRef]
- Dsilva, C.J.; Talmon, R.; Coifman, R.R.; Kevrekidis, I.G. Parsimonious representation of nonlinear dynamical systems through manifold learning: A chemotaxis case study. Appl. Comput. Harmon. Anal. 2015, 1, 1–15. [Google Scholar] [CrossRef]
- Chung, F.R.K. Spectral Graph Theory; CBMS Regional Conference Series in Mathematics, Published for the Conference Board of the Mathematical Sciences; American Mathematical Society: Providence, RI, USA, 1997; Volume 92, p. xii+207. [Google Scholar]
- Nadler, B.; Lafon, S.; Coifman, R.R.; Kevrekidis, I.G. Diffusion maps, spectral clustering and reaction coordinates of dynamical systems. Appl. Comput. Harmon. Anal. 2006, 21, 113–127. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Matthews, C. Rational Construction of Stochastic Numerical Methods for Molecular Sampling. Appl. Math. Res. Express 2013, 2013, 34–56. [Google Scholar] [CrossRef]
- Parton, D.L.; Grinaway, P.B.; Hanson, S.M.; Beauchamp, K.A.; Chodera, J.D. Ensembler: Enabling high-throughput molecular simulations at the superfamily scale. PLoS Comput. Biol. 2016, 12, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.; Hanson, S. Microsecond Molecular Dynamics Simulation of Kinase Domain of The Human Tyrosine Kinase ABL1. Available online: https://figshare.com/articles/Microsecond_molecular_dynamics_simulation_of_kinase_domain_of_the_human_tyrosine_kinase_ABL1/4496795 (accessed on 9 May 2017).
- Beberg, A.L.; Ensign, D.L.; Jayachandran, G.; Khaliq, S.; Pande, V.S. Folding@home: Lessons from eight years of volunteer distributed computing. In Proceedings of the 2009 IEEE International Symposium on Parallel & Distributed Processing Symposium, Rome, Italy, 23–29 May 2009; pp. 1–8. [Google Scholar]
- Eastman, P.; Swails, J.; Chodera, J.D.; McGibbon, R.T.; Zhao, Y.; Beauchamp, K.A.; Wang, L.P.; Simmonett, A.C.; Harrigan, M.P.; Brooks, B.R.; et al. OpenMM 7: Rapid Development of High Performance Algorithms for Molecular Dynamics. bioRxiv 2016. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins Struct. Funct. Bioinform. 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Skeel, R.D.; Izaguirre, J.A. An impulse integrator for Langevin dynamics. Mol. Phys. 2002, 100, 3885–3891. [Google Scholar] [CrossRef]
- Melchionna, S. Design of quasisymplectic propagators for Langevin dynamics. J. Chem. Phys. 2007, 127, 044108. [Google Scholar] [CrossRef] [PubMed]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577. [Google Scholar] [CrossRef]
- Chow, K.H.; Ferguson, D.M. Isothermal-isobaric molecular dynamics simulations with Monte Carlo volume sampling. Comput. Phys. Commun. 1995, 91, 283–289. [Google Scholar] [CrossRef]
- Åqvist, J.; Wennerström, P.; Nervall, M.; Bjelic, S.; Brandsdal, B.O. Molecular dynamics simulations of water and biomolecules with a Monte Carlo constant pressure algorithm. Chem. Phys. Lett. 2004, 384, 288–294. [Google Scholar] [CrossRef]
- Milstein, G.N.; Tretyakov, M.V. Stochastic Numerics for Mathematical Physics; Scientific Computation; Springer: Berlin/Heidelberg, Germany, 2004; p. xx+594. [Google Scholar]
- Coifman, R.R.; Lafon, S.; Lee, A.B.; Maggioni, M.; Nadler, B.; Warner, F.; Zucker, S.W. Geometric diffusions as a tool for harmonic analysis and structure definition of data: diffusion maps. Proc. Natl. Acad. Sci. USA 2005, 102, 7426–7431. [Google Scholar] [CrossRef] [PubMed]
- Belkin, M.; Que, Q.; Wang, Y.; Zhou, X. Toward understanding complex spaces: Graph Laplacians on manifolds with singularities and boundaries. arXiv, 2012; arXiv:1211.6727. [Google Scholar]
- Chiavazzo, E.; Gear, C.W.; Dsilva, C.; Rabin, N.; Kevrekidis, I. Reduced Models in Chemical Kinetics via Nonlinear Data-Mining. Processes 2014, 2, 112–140. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2002; p. xxx+487. [Google Scholar]
- Trefethen, L.; Bau, D. Numerical Linear Algebra; Number 50; Society for Industrial Mathematics: Philadelphia, PA, USA, 1997. [Google Scholar]
- Kutz, J.N. Data-Driven Modeling & Scientific Computation: Methods for Complex Systems & Big Data; Oxford University Press, Inc.: New York, NY, USA, 2013. [Google Scholar]
- Singer, A.; Wu, H.T. Vector diffusion maps and the connection Laplacian. Commun. Pure Appl. Math. 2012, 65, 1067–1144. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.Y.; Wu, H.T. Local Linear Regression on Manifolds and Its Geometric Interpretation. J. Am. Stat. Assoc. 2013, 108, 1421–1434. [Google Scholar] [CrossRef]
- Hashemian, B.; Millán, D.; Arroyo, M. Charting molecular free-energy landscapes with an atlas of collective variables. J. Chem. Phys. 2016, 145, 174109. [Google Scholar] [CrossRef] [PubMed]
- Galton, A.; Duckham, M. What is the region occupied by a set of points? In Geographic Information Science: Proceedings of the 4th International Conference, GIScience 2006, Münster, Germany, 20–23 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 81–98. [Google Scholar]
- Moreira, A.; Santos, M.Y. Concave Hull: A k-Nearest Neighbours Approach for the Computation of the Region Occupied by a Set of Points. In Proceedings of the 2nd International Conference on Computer Graphics Theory and Applications (GRAPP 2007), Barcelona, Spain, 8–11 March 2007; pp. 61–68. [Google Scholar]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Mücke, E.P. Three-dimensional alpha shapes. ACM Trans. Graph. 1994, 13, 43–72. [Google Scholar] [CrossRef]
- Edelsbrunner, H. Surface Reconstruction by Wrapping Finite Sets in Space. In Discrete & Computational Geometry; Springer: New York, NY, USA, 2003; Volume 25, pp. 379–404. [Google Scholar]
- The MathWorks. MATLAB Documentation (R2015b). Alpha Shape; The MathWorks Inc.: Natick, MA, USA, 2015. [Google Scholar]
- Xia, C.; Hsu, W.; Lee, M.L.; Ooi, B.C. BORDER: Efficient computation of boundary points. IEEE Trans. Knowl. Data Eng. 2006, 18, 289–303. [Google Scholar]
- Qiu, B.Z.; Yue, F.; Shen, J.Y. BRIM: An Efficient Boundary Points Detecting Algorithm. In Advances in Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2007; pp. 761–768. [Google Scholar]
- Qiu, B.; Wang, S. A boundary detection algorithm of clusters based on dual threshold segmentation. In Proceedings of the 2011 Seventh International Conference on Computational Intelligence and Security, Sanya, China, 3–4 December 2011; pp. 1246–1250. [Google Scholar]
- Gear, C.W.; Chiavazzo, E.; Kevrekidis, I.G. Manifolds defined by points: Parameterizing and boundary detection (extended abstract). AIP Conf. Proc. 2016, 1738, 020005. [Google Scholar]
- Do Carmo, M.P. Riemannian Geometry; Mathematics: Theory & Applications; Birkhäuser Boston, Inc.: Boston, MA, USA, 1992; p. xiv+300. [Google Scholar]
- Coifman, R.R.; Lafon, S. Geometric harmonics: A novel tool for multiscale out-of-sample extension of empirical functions. Appl. Comput. Harmon. Anal. 2006, 21, 31–52. [Google Scholar] [CrossRef]
- Wendland, H. Scattered Data Approximation (Cambridge Monographs on Applied and Computational Mathematics); Cambridge University Press: Cambridge, UK, 2005; Volume 17, p. x+336. [Google Scholar]
- Tribello, G.A.; Bonomi, M.; Branduardi, D.; Camilloni, C.; Bussi, G. PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 2014, 185, 604–613. [Google Scholar] [CrossRef]
- Fiorin, G.; Klein, M.L.; Hénin, J. Using collective variables to drive molecular dynamics simulations. Mol. Phys. 2013, 111, 3345–3362. [Google Scholar] [CrossRef]
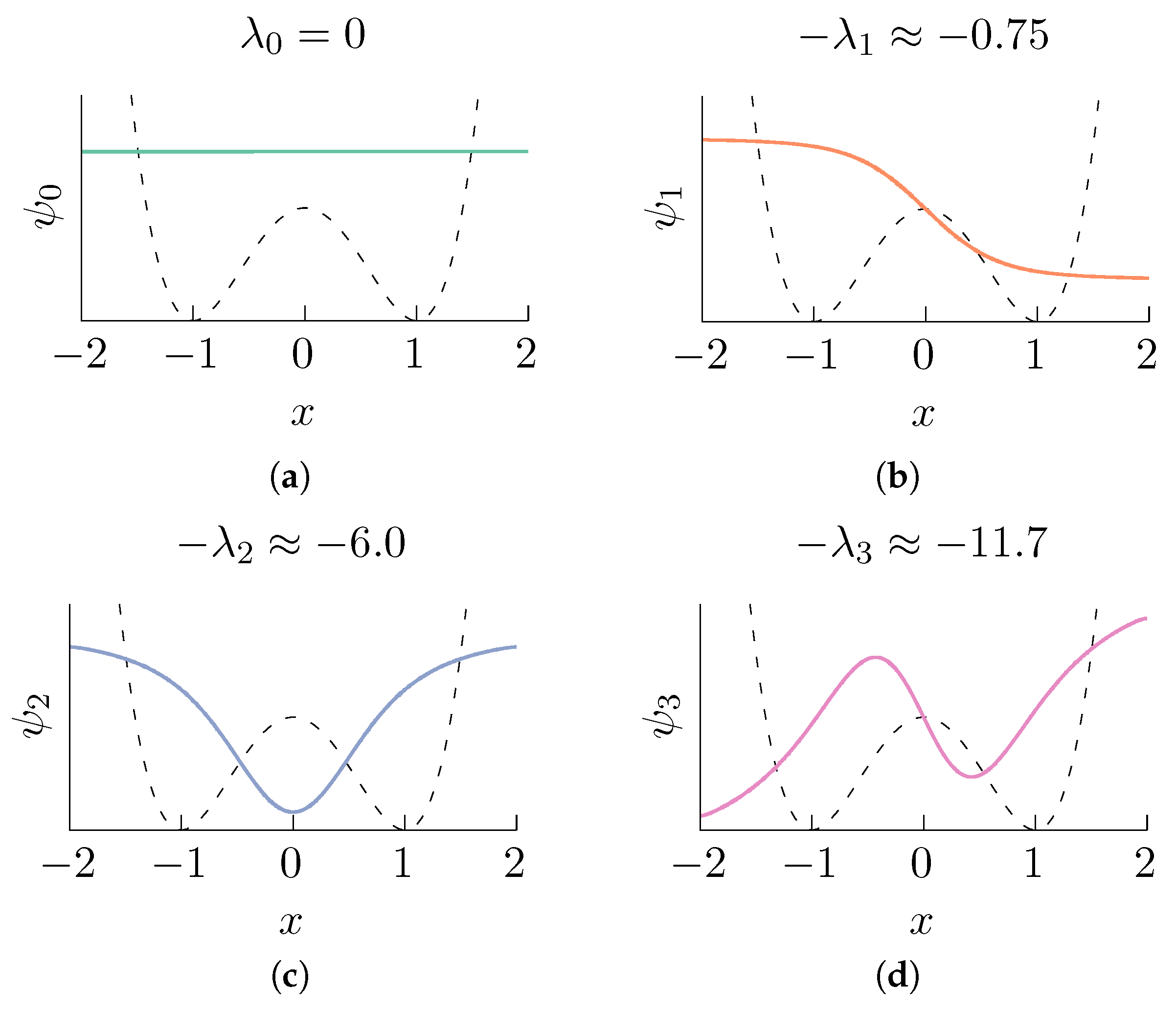
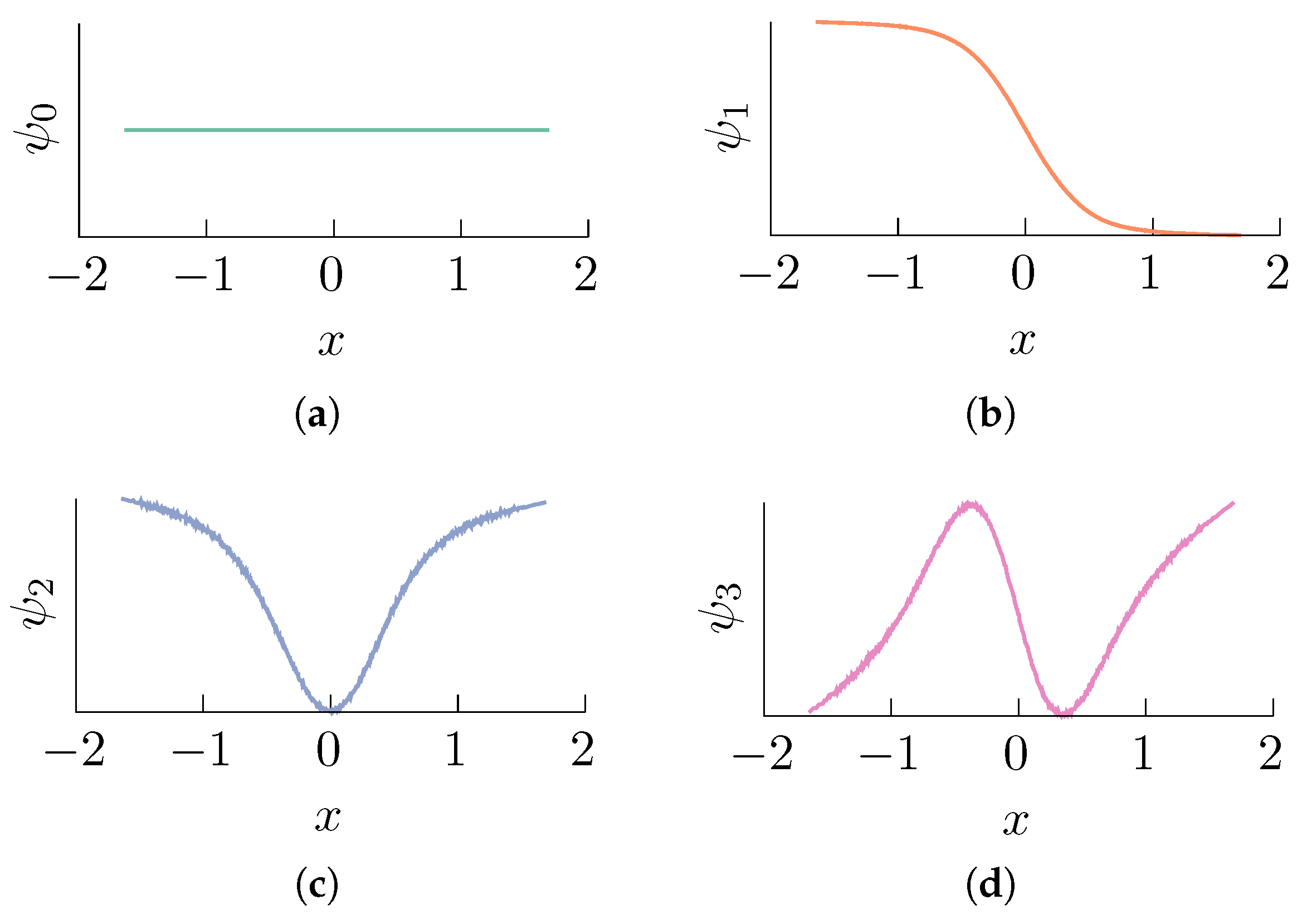
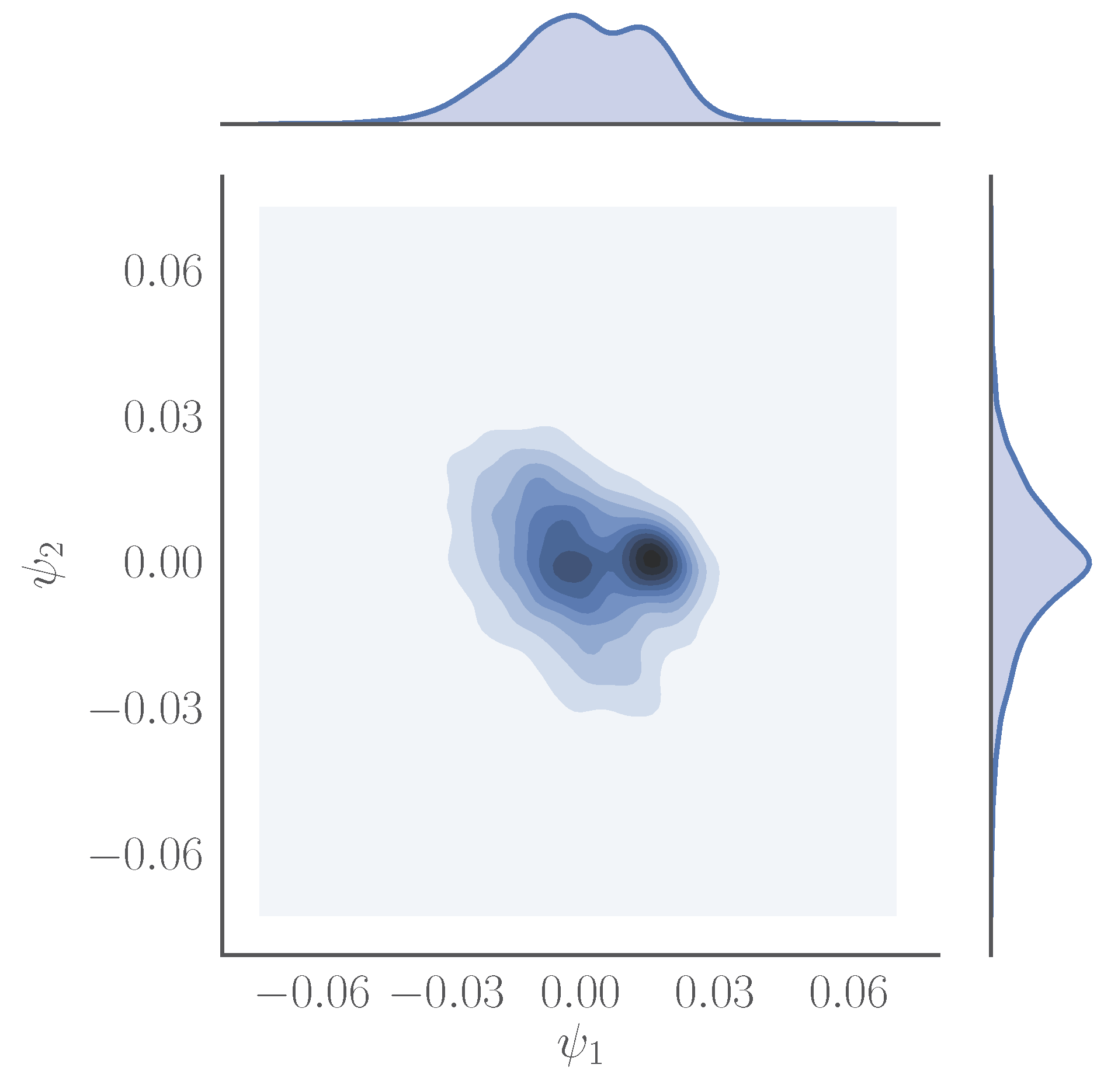
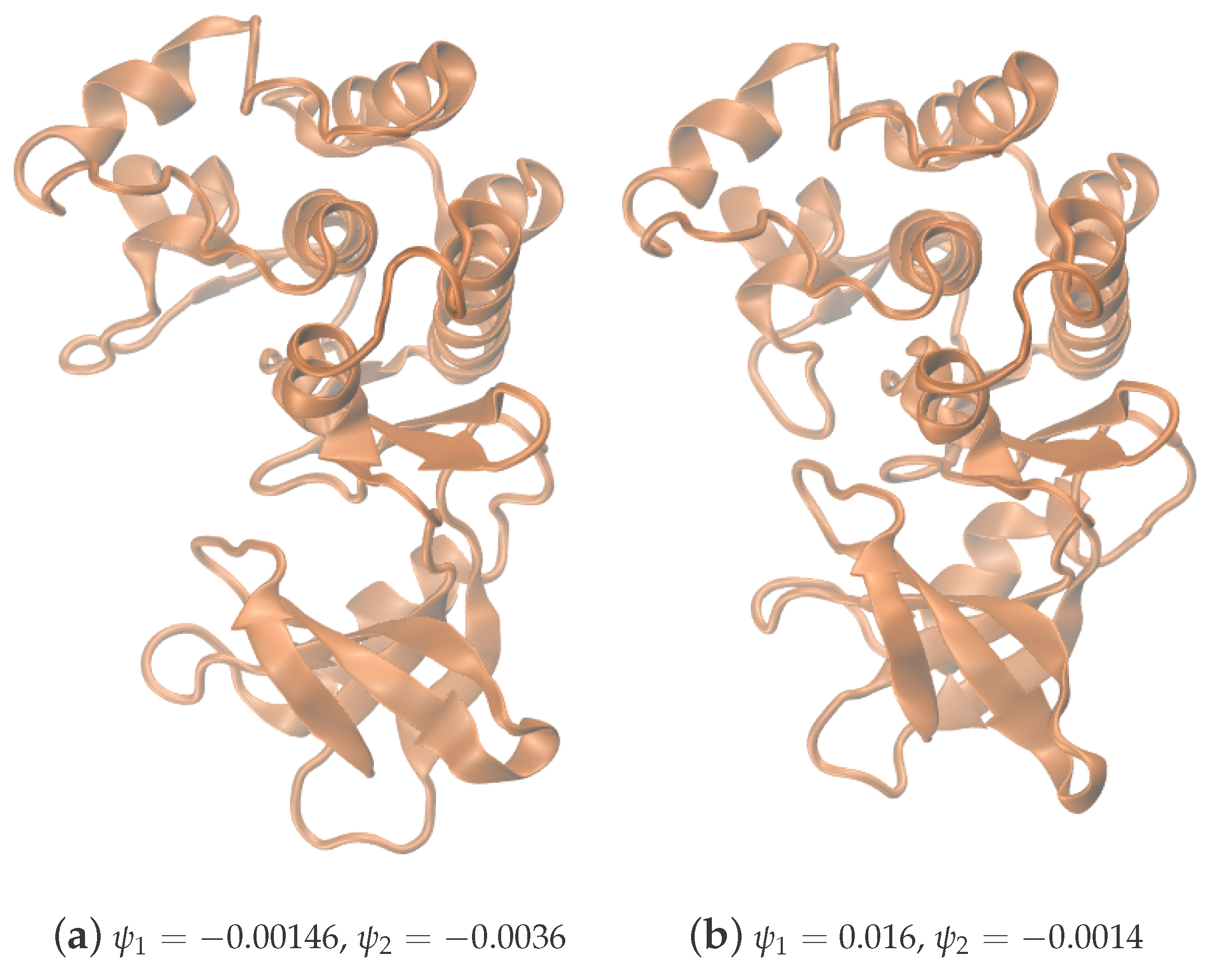
| Iteration | |
|---|---|
| 0 | 0.36 |
| 1 | 0.55 |
| 2 | 0.75 |
| 3 | 0.99 |
| 4 | 1.21 |
| 5 | 1.49 |
| 6 | 1.76 |
| 7 | 2.00 |
| 8 | 2.25 |
| 9 | 2.60 |
| 10 | 2.95 |
| 11 | 3.33 |
| 12 | 3.49 |
| 13 | 3.98 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Georgiou, A.S.; Bello-Rivas, J.M.; Gear, C.W.; Wu, H.-T.; Chiavazzo, E.; Kevrekidis, I.G. An Exploration Algorithm for Stochastic Simulators Driven by Energy Gradients. Entropy 2017, 19, 294. https://doi.org/10.3390/e19070294
Georgiou AS, Bello-Rivas JM, Gear CW, Wu H-T, Chiavazzo E, Kevrekidis IG. An Exploration Algorithm for Stochastic Simulators Driven by Energy Gradients. Entropy. 2017; 19(7):294. https://doi.org/10.3390/e19070294
Chicago/Turabian StyleGeorgiou, Anastasia S., Juan M. Bello-Rivas, Charles William Gear, Hau-Tieng Wu, Eliodoro Chiavazzo, and Ioannis G. Kevrekidis. 2017. "An Exploration Algorithm for Stochastic Simulators Driven by Energy Gradients" Entropy 19, no. 7: 294. https://doi.org/10.3390/e19070294
APA StyleGeorgiou, A. S., Bello-Rivas, J. M., Gear, C. W., Wu, H.-T., Chiavazzo, E., & Kevrekidis, I. G. (2017). An Exploration Algorithm for Stochastic Simulators Driven by Energy Gradients. Entropy, 19(7), 294. https://doi.org/10.3390/e19070294







