A Quantized Kernel Learning Algorithm Using a Minimum Kernel Risk-Sensitive Loss Criterion and Bilateral Gradient Technique
Abstract
:1. Introduction
2. Backgrounds
2.1. The Kernel Risk-Sensitive Loss (KRSL) Algorithm
2.2. Minimum Kernel Risk-Sensitive Loss (MKRSL) Algorithm
| Algorithm 1 The minimum kernel risk-sensitive loss (MKRSL) algorithm. |
| Initialization: |
| Choose parameters , , and . |
| , . |
| Computation: |
| while is available do |
| (1) ; |
| (2) ; |
| (3) ; |
| (4) ; |
| (5) . |
| end while |
3. The Proposed Algorithm
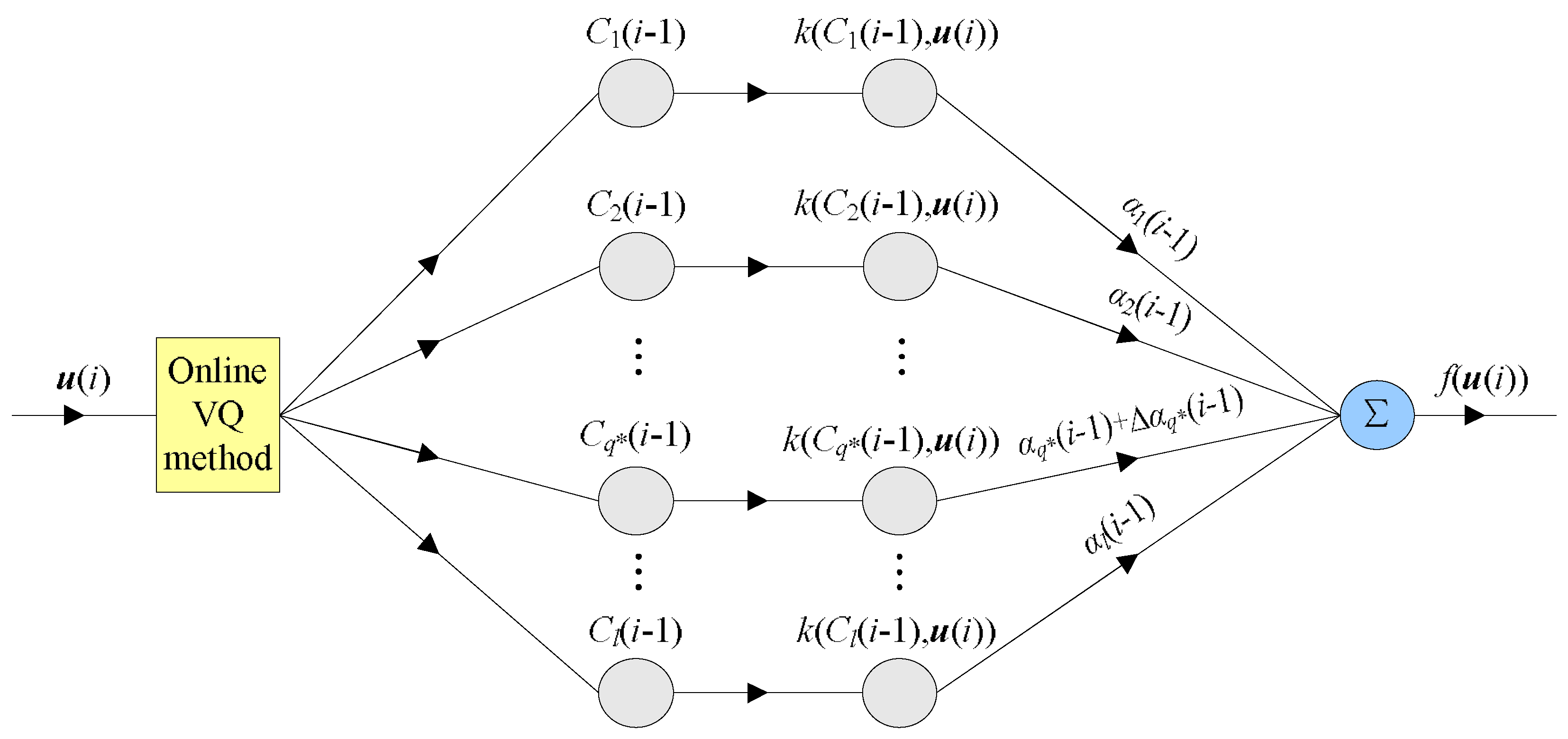
3.1. The Quantized MKRSL (QMKRSL) Algorithm
| Algorithm 2 The quantized minimum kernel risk-sensitive loss (QMKRSL) algorithm. |
| Initialization: |
| Choose parameters , , and , . |
| , . |
| Computation: |
| while is available do |
| (1) ; |
| (2) ; |
| (3) ; |
| // compute the distance between and |
| (4) if |
| ; |
| , |
| where ; |
| (5) else |
| ; |
| ; |
| (6) . |
| end while |
3.2. The QMKRSL Using Bilateral Gradient Technique (QMKRSL_BG)
| Algorithm 3 Quantized MKRSL using the bilateral gradient technique (QMKRSL_BG) algorithm. |
| Initialization: |
| Choose parameters , , , and , . |
| , , . |
| Computation: |
| while is available do |
| (1) ; |
| (2) ; |
| (3) ; |
| // compute the distance between and |
| (4) if |
| ; |
| ; |
| ; |
| , |
| where ; |
| (5) else |
| ; |
| ; |
| (6) . |
| end while |
3.3. Complexity Analysis
4. Simulation Results and Discussion
4.1. Dataset and Metric
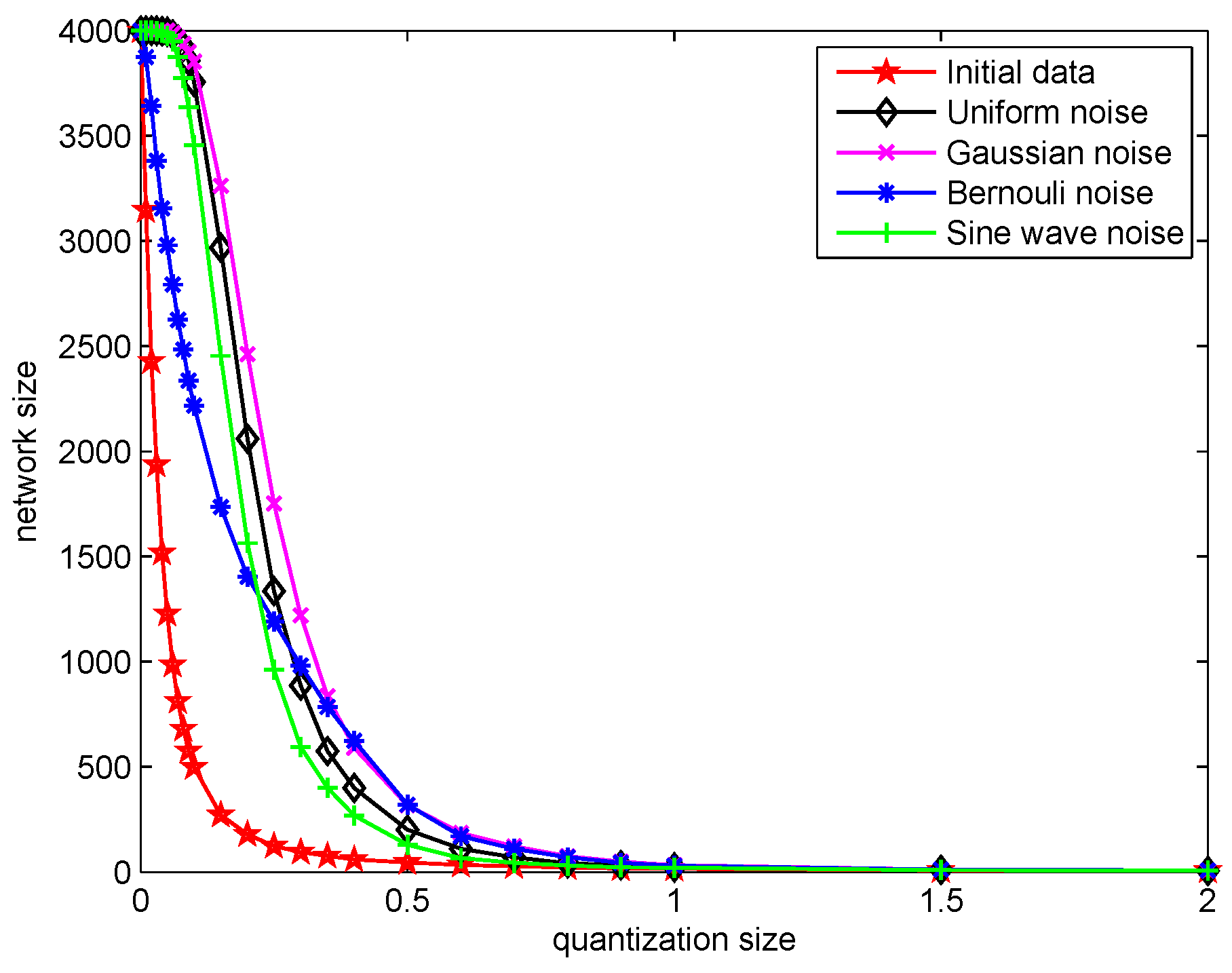
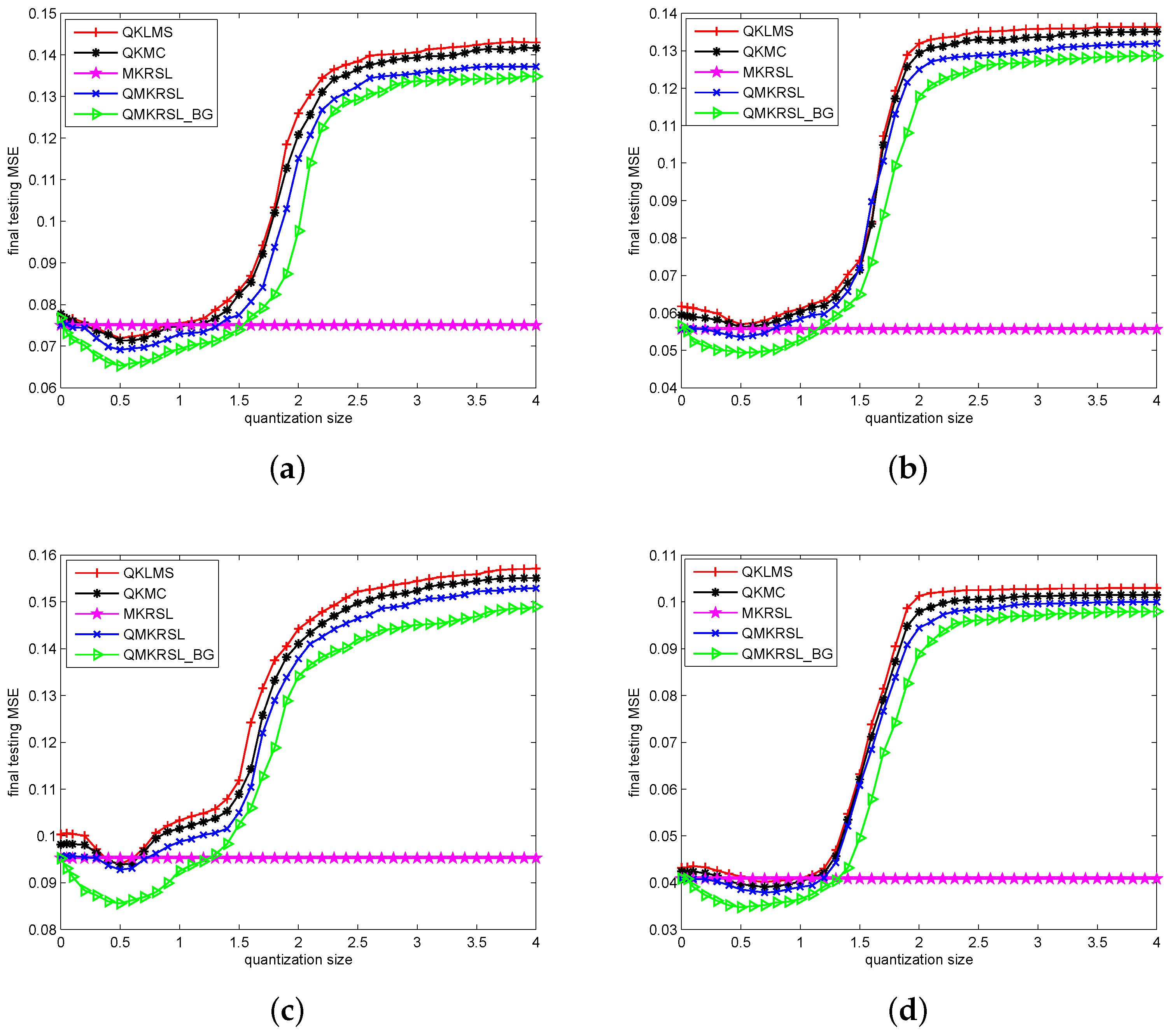
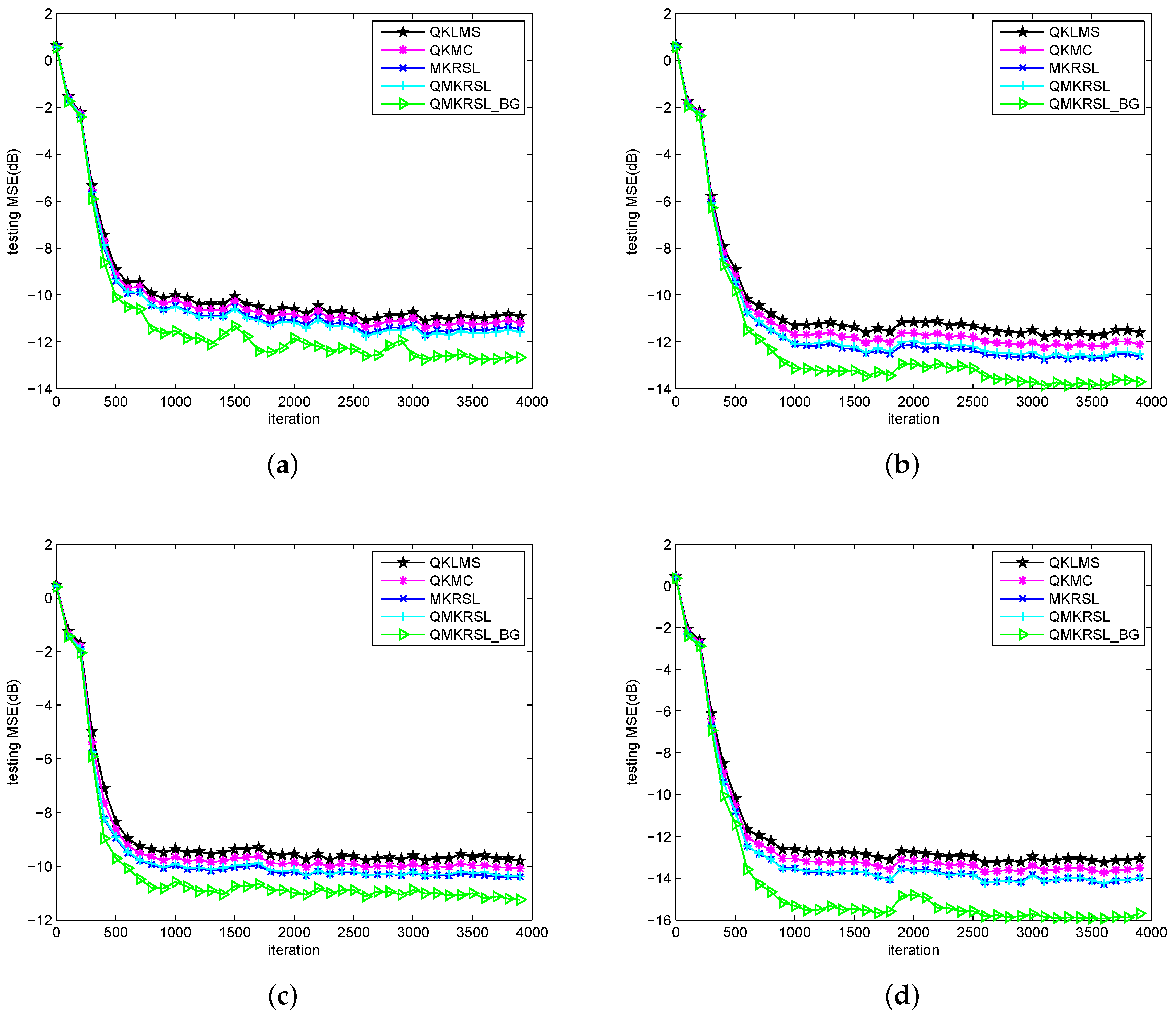
4.2. Simulation Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kivinen, J.; Smola, A.J.; Williamson, R.C. Online learning with kernels. IEEE Trans. Signal Process. 2004, 52, 2165–2176. [Google Scholar] [CrossRef]
- Gao, W.; Huang, J.G.; Han, J. Online nonlinear adaptive filtering based on multi-kernel learning algorithm. Syst. Eng. Electron. 2014, 36, 1473–1477. [Google Scholar]
- Fan, H.J.; Song, Q.; Yang, X.L.; Xu, Z. Kernel online learning algorithm with state feedbacks. Knowl. Based Syst. 2015, 89, 173–180. [Google Scholar] [CrossRef]
- Lu, J.; Hoi, S.C.H.; Wang, J.L.; Zhao, P.L.; Liu, Z.Y. Large scale online kernel learning. J. Mach. Learn. Res. 2016, 17, 1–43. [Google Scholar]
- Luo, X.; Zhang, D.D.; Yang, L.T.; Liu, J.; Chang, X.H.; Ning, H.S. A kernel machine-based secure data sensing and fusion scheme in wireless sensor networks for the cyber-physical systems. Future Gener. Comput. Syst. 2016, 61, 85–96. [Google Scholar] [CrossRef]
- Liu, W.F.; Príncipe, J.C.; Haykin, S. Kernel Adaptive Filtering; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Chen, B.D.; Li, L.; Liu, W.F.; Príncipe, J.C. Nonlinear adaptive filtering in kernel spaces. In Springer Handbook of Bio-/Neuroinformatics; Springer: Berlin, Germany, 2014; pp. 715–734. [Google Scholar]
- Burges, C.J.C. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Li, Y.S.; Jin, Z.; Wang, Y.Y.; Yang, R. A robust sparse adaptive filtering algorithm with a correntropy induced metric constraint for broadband multi-path channel estimation. Entropy 2016, 18, 380. [Google Scholar] [CrossRef]
- Nakajima, Y.; Yukawa, M. Nonlinear channel equalization by multi-kernel adaptive filter. In Proceedings of the IEEE 13th International Workshop on Signal Processing Advances in Wireless Communications, Cesme, Turkey, 17–20 June 2012; pp. 384–388. [Google Scholar]
- Dixit, S.; Nagaria, D. Design and analysis of cascaded LMS adaptive filters for noise cancellation. Circ. Syst. Signal Process. 2017, 36, 742–766. [Google Scholar] [CrossRef]
- Luo, X.; Liu, J.; Zhang, D.D.; Chang, X.H. A large-scale web QoS prediction scheme for the industrial Internet of Things based on a kernel machine learning algorithm. Comput. Networks 2016, 101, 81–89. [Google Scholar] [CrossRef]
- Jiang, S.Y.; Gu, Y.T. Block-sparsity-induced adaptive filter for multi-clustering system identification. IEEE Trans. Signal Process. 2015, 63, 5318–5330. [Google Scholar] [CrossRef]
- Liu, W.F.; Príncipe, P.P.; Principe, J.C. The kernel least mean square algorithm. IEEE Trans. Signal Process. 2008, 56, 543–554. [Google Scholar] [CrossRef]
- Liu, W.F.; Príncipe, J.C. Kernel affine projection algorithms. EURASIP J. Adv. Signal Process. 2007, 2008, 1–12. [Google Scholar]
- Engel, Y.; Mannor, S.; Meir, R. The kernel recursive least-squares algorithm. IEEE Trans. Signal Process. 2004, 52, 2275–2285. [Google Scholar] [CrossRef]
- Chen, B.D.; Zhao, S.L.; Zhu, P.P.; Príncipe, J.C. Quantized kernel least mean square algorithm. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 22–32. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.D.; Zhao, S.L.; Zhu, P.P.; Príncipe, J.C. Quantized kernel recursive least squares algorithm. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1484–1491. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.L.; Chen, B.D.; Príncipe, J.C. Fixed budget quantized kernel least mean square algorithm. Signal Process. 2013, 93, 2759–2770. [Google Scholar] [CrossRef]
- Zhao, S.L.; Chen, B.D.; Cao, Z.; Zhu, P.P.; Príncipe, J.C. Self-organizing kernel adaptive filtering. EURASIP J. Adv. Signal Process. 2016, 2016, 106. [Google Scholar] [CrossRef]
- Luo, X.; Liu, J.; Zhang, D.D.; Wang, W.P.; Zhu, Y.Q. An entropy-based kernel learning scheme toward efficient data prediction in cloud-assisted network environments. Entropy 2016, 18, 274. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, X.; Wang, W.P.; Zhao, W.B. Efficient DV-HOP localization for wireless cyber-physical social sensing system: A correntropy-based neural network learning scheme. Sensors 2017, 17, 135. [Google Scholar] [CrossRef] [PubMed]
- He, R.; Tan, T.; Wang, L. Robust recovery of corrupted low-rank matrix by implicit regularizers. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 770–783. [Google Scholar] [CrossRef] [PubMed]
- Príncipe, J.C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; Springer: New York, NY, USA, 2010. [Google Scholar]
- Fan, H.J.; Song, Q.; Xu, Z. An information theoretic sparse kernel algorithm for online learning. Expert Syst. Appl. 2014, 41, 4349–4359. [Google Scholar] [CrossRef]
- Erdogmus, D.; Príncipe, J.C. Generalized information potential criterion for adaptive system training. IEEE Trans. Neural Netw. 2002, 13, 1035–1044. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.Z.; Shi, J.H.; Zhang, X.; Ma, W.T.; Chen, B.D. Kernel recursive maximum correntropy. Signal Process. 2015, 117, 11–16. [Google Scholar] [CrossRef]
- Sra, S.; Nowozin, S.; Wright, S.J. Optimization for Machine Learning; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Bertsimas, D.; Sim, M. The price of robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Büsing, C.; D’Andreagiovanni, F. New results about multi-band uncertainty in robust optimization. Lect. Notes Comput. Sci. 2012, 7276, 63–74. [Google Scholar]
- Santamaria, I.; Pokharel, P.P.; Príncipe, J.C. Generalized correlation function: Definition, properties, and application to blind equalization. IEEE Trans. Signal Process. 2006, 54, 2187–2197. [Google Scholar] [CrossRef]
- Liu, W.F.; Pokharel, P.P.; Príncipe, J.C. Correntropy: Properties and applications in non-Gaussian signal processing. IEEE Trans. Signal Process. 2007, 55, 5286–5298. [Google Scholar] [CrossRef]
- Liu, X.; Qu, H.; Zhao, J.H.; Yue, P.C.; Wang, M. Maximum correntropy unscented kalman filter for spacecraft relative state estimation. Sensors 2016, 16, 1530. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.P.; Wang, J.J.; Zhang, M.M.; Cai, Q.; Gong, Y.H. Correntropy-based level set method for medical image segmentation and bias correction. Neurocomputing 2017, 234, 216–229. [Google Scholar] [CrossRef]
- Lu, L.; Zhao, H.Q. Active impulsive noise control using maximum correntropy with adaptive kernel size. Mech. Syst. Signal Process. 2017, 87, 180–191. [Google Scholar] [CrossRef]
- Zhao, S.L.; Chen, B.D.; Príncipe, J.C. Kernel adaptive filtering with maximum correntropy criterion. In Proceedings of the International Joint Conference on Neural Network, San Jose, CA, USA, 31 July–5 August 2011; pp. 2012–2017. [Google Scholar]
- Chen, B.D.; Xing, L.; Xu, B.; Zhao, H.Q.; Zheng, N.N.; Príncipe, J.C. Kernel risk-sensitive loss: Definition, properties and application to robust adaptive filtering. IEEE Trans. Signal Process. 2017, 65, 2888–2901. [Google Scholar] [CrossRef]
- Liu, W.F.; Park, I.; Príncipe, J.C. An information theoretic approach of designing sparse kernel adaptive filters. IEEE Trans. Neural Netw. 2009, 20, 1950–1961. [Google Scholar] [CrossRef] [PubMed]
- Platt, J. A resource-allocating network for function interpolation. Neural Comput. 1991, 3, 213–225. [Google Scholar] [CrossRef]
- Richard, C.; Bermudez, J.C.M.; Honeine, P. Online prediction of time series data with kernels. IEEE Trans. Signal Process. 2009, 57, 1058–1067. [Google Scholar] [CrossRef]
- Wang, S.Y.; Zheng, Y.F.; Duan, S.K.; Wang, L.D.; Tan, H.T. Quantized kernel maximum correntropy and its mean square convergence analysis. Dig. Signal Process. 2017, 63, 164–176. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, J.H. Correntropy kernel learning for nonlinear system identification with outliers. Ind. Eng. Chem. Res. 2013, 53, 5248–5260. [Google Scholar] [CrossRef]
- Wu, Z.Z.; Peng, S.Y.; Chen, B.D.; Zhao, H.Q. Robust Hammerstein adaptive filtering under maximum correntropy criterion. Entropy 2015, 17, 7149–7166. [Google Scholar] [CrossRef]
- Liu, W.F.; Park, I.; Wang, Y.W.; Príncipe, J.C. Extended kernel recursive least squares algorithm. IEEE Trans. Signal Process. 2009, 57, 3801–3814. [Google Scholar]

| Noise | QKLMS | QKMC | MKRSL | QMKRSL | QMKRSL_BG |
|---|---|---|---|---|---|
| Gaussian | |||||
| Uniform | |||||
| Bernouli | |||||
| Sine wave |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, X.; Deng, J.; Wang, W.; Wang, J.-H.; Zhao, W. A Quantized Kernel Learning Algorithm Using a Minimum Kernel Risk-Sensitive Loss Criterion and Bilateral Gradient Technique. Entropy 2017, 19, 365. https://doi.org/10.3390/e19070365
Luo X, Deng J, Wang W, Wang J-H, Zhao W. A Quantized Kernel Learning Algorithm Using a Minimum Kernel Risk-Sensitive Loss Criterion and Bilateral Gradient Technique. Entropy. 2017; 19(7):365. https://doi.org/10.3390/e19070365
Chicago/Turabian StyleLuo, Xiong, Jing Deng, Weiping Wang, Jenq-Haur Wang, and Wenbing Zhao. 2017. "A Quantized Kernel Learning Algorithm Using a Minimum Kernel Risk-Sensitive Loss Criterion and Bilateral Gradient Technique" Entropy 19, no. 7: 365. https://doi.org/10.3390/e19070365
APA StyleLuo, X., Deng, J., Wang, W., Wang, J.-H., & Zhao, W. (2017). A Quantized Kernel Learning Algorithm Using a Minimum Kernel Risk-Sensitive Loss Criterion and Bilateral Gradient Technique. Entropy, 19(7), 365. https://doi.org/10.3390/e19070365








