Chaos Synchronization of Nonlinear Fractional Discrete Dynamical Systems via Linear Control
Abstract
:1. Introduction
2. Preliminaries
3. A Synchronization Scheme of Nonlinear Fractional Discrete Dynamical Systems
4. Application to the Fractional Discrete Dynamical Income Change System
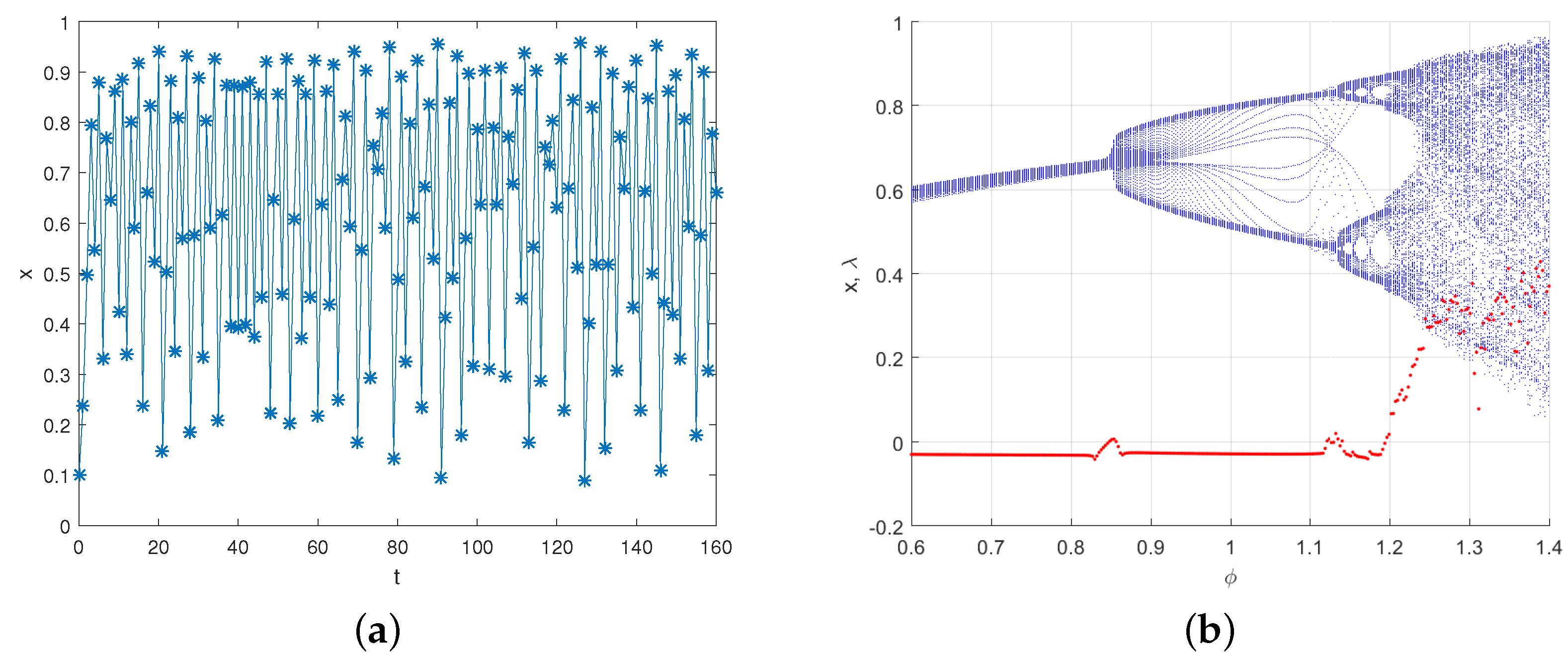
4.1. A Fractional Discrete Dynamical Income Change System
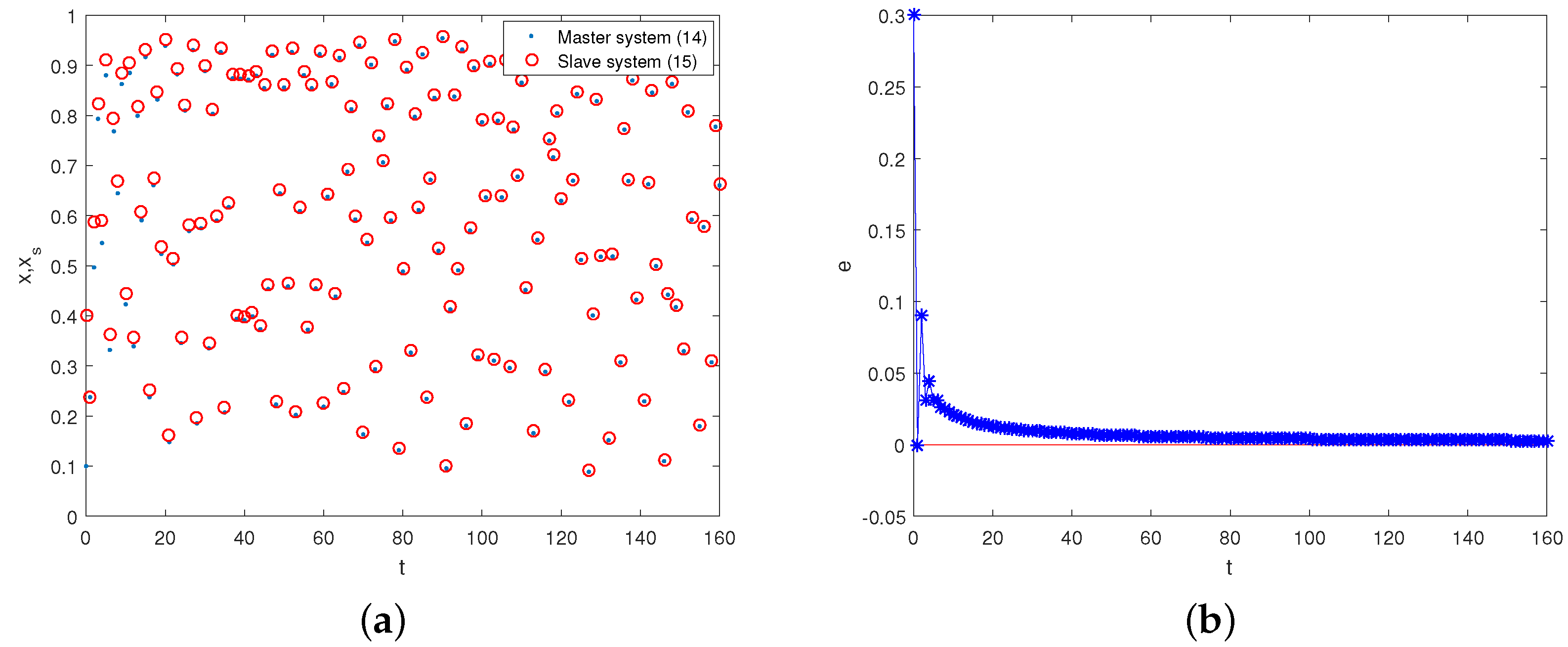
4.2. A Synchronization Scheme of Fractional Discrete Dynamical Income Change Systems
5. Application to the Novel Three-Dimensional Fractional Discrete Dynamical System
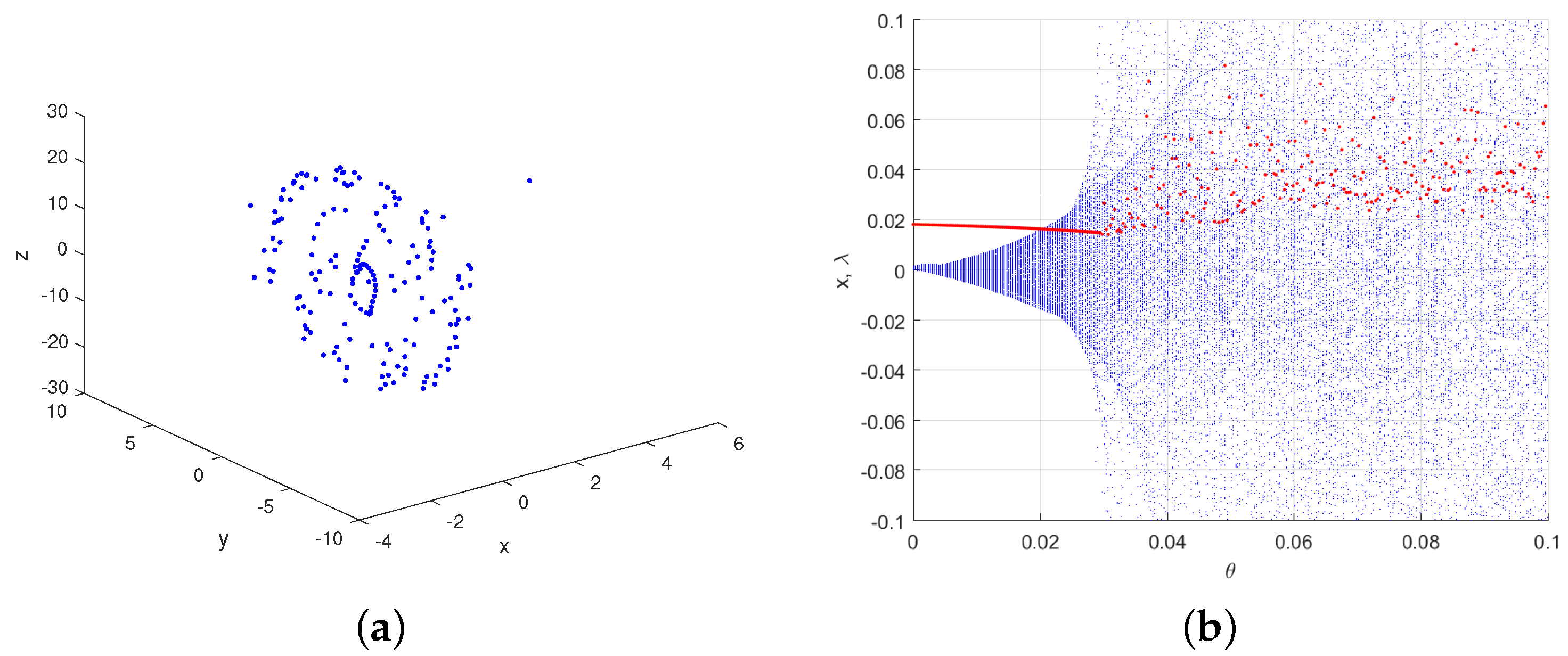
5.1. A Novel Three-Dimensional Fractional Discrete Dynamical System
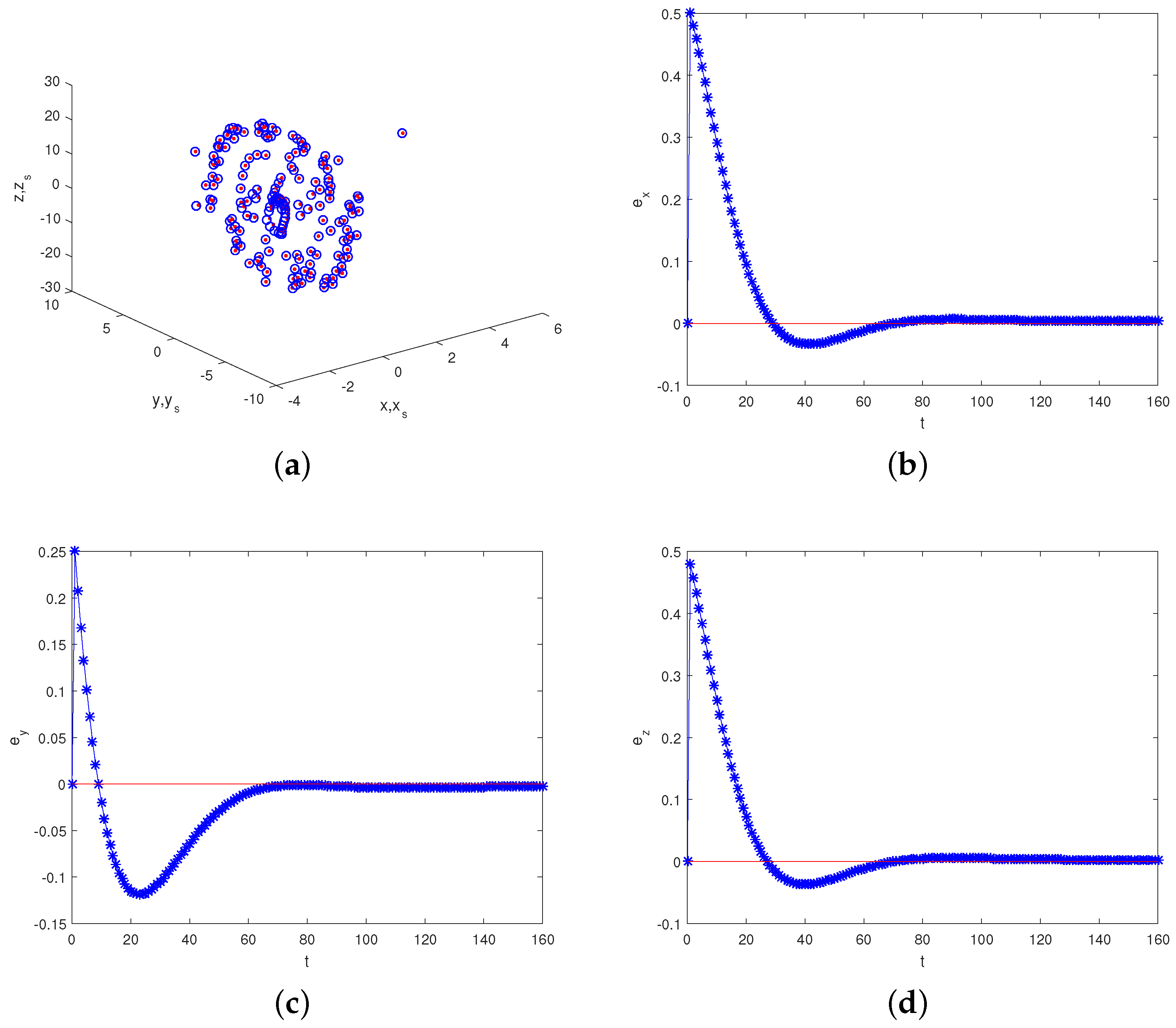
5.2. A Synchronization Scheme of the Novel Three-Dimensional Fractional Discrete Dynamical Systems
6. Conclusions
- The proposed 1-D fractional discrete income change system and a kind of novel 3-D fractional chaotic discrete system are employed to implement some interesting numerical simulations, which coincide well with the mentioned results.
- The proposed chaos synchronization scheme via the linear feedback control technique is very robust and easy to implement efficiently, and should have additional interesting applications in the future, such as secure communications, information storage, message identification, encryption and decryption.
- It is necessary for us to employ other control techniques, such as active control, sliding mode control, and pinning control, to achieve chaos synchronization of nonlinear fractional discrete dynamical systems.
- It will be challenging and interesting to expand the mentioned results to study the anti-synchronization or finite-time synchronization of the fractional discrete dynamic systems via the linear feedback control technique or others.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Craiem, D.; Magin, R. Fractional order models of viscoelasticity as an alternative in the analysis of red blood cell (RBC) membrane mechanics. Phys. Biol. 2010, 7, 013001. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Qi, H.; Xu, H.; Jiang, X. Transient electroosmotic slip flow of fractional Oldroyd-B fluids. Microfluid. Nanofluid. 2017, 21, 7. [Google Scholar] [CrossRef]
- Xu, H.; Jiang, X. Creep constitutive models for viscoelastic materials based on fractional derivatives. Comput. Math. Appl. 2017, 73, 1377–1384. [Google Scholar] [CrossRef]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2014. [Google Scholar]
- Xin, B.; Zhang, J. Finite-time stabilizing a fractional-order chaotic financial system with market confidence. Nonlinear Dyn. 2015, 79, 1399–1409. [Google Scholar] [CrossRef]
- Atici, F.; Eloe, P. Initial value problems in discrete fractional calculus. Proc. Am. Math. Soc. 2009, 137, 981–989. [Google Scholar] [CrossRef]
- Abu-Saris, R.; Al-Mdallal, Q. On the asymptotic stability of linear system of fractional-order difference equations. Fract. Calc. Appl. Anal. 2013, 16, 613–629. [Google Scholar] [CrossRef]
- Wu, G.; Baleanu, D.; Xie, H.; Chen, F. Chaos synchronization of fractional chaotic maps based on the stability condition. Physica A 2016, 460, 374–383. [Google Scholar] [CrossRef]
- Wyrwas, M.; Mozyrska, D.; Girejko, E. Stability of discrete fractional-order nonlinear systems with the nabla Caputo difference. IFAC Proc. Vol. 2013, 46, 167–171. [Google Scholar] [CrossRef]
- Mozyrska, D.; Wyrwas, M. Explicit criteria for stability of fractional h-difference two-dimensional systems. Int. J. Dyn. Control 2016, 2016, 1–6. [Google Scholar] [CrossRef]
- Mohan, J.; Deekshitulu, G. Fractional order difference equations. Int. J. Differ. Equ. 2012, 2012, 1–11. [Google Scholar] [CrossRef]
- Dassios, I. Stability and robustness of singular systems of fractional nabla difference equations. Circuits Syst. Signal Process. 2017, 36, 49–64. [Google Scholar] [CrossRef]
- Diblík, J.; Fečkan, M.; Pospíšil, M. Nonexistence of periodic solutions and S-asymptotically periodic solutions in fractional difference equations. Appl. Math. Comput. 2015, 257, 230–240. [Google Scholar] [CrossRef]
- Atıcı, F.M.; Şengl, S. Modeling with fractional difference equations. J. Math. Anal. Appl. 2010, 369, 1–9. [Google Scholar] [CrossRef]
- Hu, T. Discrete Chaos in Fractional Henon Map. Appl. Math. 2014, 5, 2243–2248. [Google Scholar] [CrossRef]
- Wu, G.; Baleanu, D. Discrete fractional logistic map and its chaos. Nonlinear Dyn. 2014, 75, 283–287. [Google Scholar] [CrossRef]
- Chen, D.; Zhao, W.; Sprott, J.; Ma, X. Application of Takagi–Sugeno fuzzy model to a class of chaotic synchronization and anti-synchronization. Nonlinear Dyn. 2013, 73, 1495–1505. [Google Scholar] [CrossRef]
- Chen, D.; Shi, L.; Chen, H.; Ma, X. Analysis and control of a hyperchaotic system with only one nonlinear term. Nonlinear Dyn. 2012, 67, 1745–1752. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, R.; Sprott, J.; Ma, X. Synchronization between integer-order chaotic systems and a class of fractional-order chaotic system based on fuzzy sliding mode control. Nonlinear Dyn. 2012, 70, 1549–1561. [Google Scholar] [CrossRef]
- Odibat, Z.; Corson, N.; Aziz-Alaoui, M.; Bertelle, C. Synchronization of chaotic fractional-order systems via linear control. Int. J. Bifurc. Chaos 2010, 20, 81–97. [Google Scholar] [CrossRef]
- Shao, S.; Chen, M.; Yan, X. Adaptive sliding mode synchronization for a class of fractional-order chaotic systems with disturbance. Nonlinear Dyn. 2016, 83, 1855–1866. [Google Scholar] [CrossRef]
- Li, C.; Zhang, M.; Zhou, F.; Yang, X. Projective synchronization for a fractional-order chaotic system via single sinusoidal coupling. Opt. Int. J. Light Electron Opt. 2016, 127, 2830–2836. [Google Scholar]
- Ouannas, A.; Azar, A.; Vaidyanathan, S. A robust method for new fractional hybrid chaos synchronization. Math. Methods Appl. Sci. 2017, 40, 1804–1812. [Google Scholar] [CrossRef]
- Wang, X.; Song, J. Synchronization of the fractional order hyperchaos Lorenz systems with activation feedback control. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3351–3357. [Google Scholar] [CrossRef]
- Lu, J. Synchronization of a class of fractional-order chaotic systems via a scalar transmitted signal. Chaos Solitons Fract. 2006, 27, 519–525. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, S. Adaptive synchronization of fractional-order chaotic systems via a single driving variable. Nonlinear Dyn. 2011, 66, 831–837. [Google Scholar] [CrossRef]
- Pan, L.; Zhou, W.; Fang, J.; Li, D. Synchronization and anti-synchronization of new uncertain fractional-order modified unified chaotic systems via novel active pinning control. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 3754–3762. [Google Scholar] [CrossRef]
- Wu, G.; Baleanu, D. Chaos synchronization of the discrete fractional logistic map. Signal Process. 2014, 102, 96–99. [Google Scholar] [CrossRef]
- Liu, Y. Chaotic synchronization between linearly coupled discrete fractional Hénon maps. Indian J. Phys. 2016, 90, 313–317. [Google Scholar] [CrossRef]
- Kassim, S.; Hamiche, H.; Djennoune, S.; Bettayeb, M. A novel secure image transmission scheme based on synchronization of fractional-order discrete-time hyperchaotic systems. Nonlinear Dyn. 2017, 88, 2473. [Google Scholar] [CrossRef]
- Wu, X.; Chen, G.; Cai, J. Chaos synchronization of the master-slave generalized Lorenz systems via linear state error feedback control. Physica D 2007, 229, 52–80. [Google Scholar] [CrossRef]
- Xin, B.; Wu, Z. Projective synchronization of chaotic discrete dynamical systems via linear state error feedback control. Entropy 2015, 17, 2677–2687. [Google Scholar] [CrossRef]
- Xin, B.; Chen, T.; Liu, Y. Projective synchronization of chaotic fractional-order energy resources demand–supply systems via linear control. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4479–4486. [Google Scholar] [CrossRef]
- Xin, B.; Chen, T.; Liu, Y. Synchronization of chaotic fractional-order WINDMI systems via linear state error feedback control. Math. Probl. Eng. 2010, 2010, 1–10. [Google Scholar] [CrossRef]
- Xin, B.; Chen, T. Projective synchronization of N-dimensional chaotic fractional-order systems via linear state error feedback control. Discret. Dyn. Nat. Soc. 2012, 2012, 1–10. [Google Scholar] [CrossRef]
- Abdeljawad, T. On Riemann and Caputo fractional differences. Comput. Math. Appl. 2011, 62, 1602–1611. [Google Scholar] [CrossRef]
- Chen, F.; Luo, X.; Zhou, Y. Existence Results for Nonlinear Fractional Difference Equation. Adv. Differ. Equ. 2011, 2011, 713201. [Google Scholar] [CrossRef]
- Baleanu, D.; Wu, G.; Bai, Y.; Chen, F. Stability analysis of Caputo–Like discrete fractional systems. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 520–530. [Google Scholar] [CrossRef]
- Puu, T.; Sushko, I. A business cycle model with cubic nonlinearity. Chaos Solitons Fract. 2004, 19, 597–612. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xin, B.; Liu, L.; Hou, G.; Ma, Y. Chaos Synchronization of Nonlinear Fractional Discrete Dynamical Systems via Linear Control. Entropy 2017, 19, 351. https://doi.org/10.3390/e19070351
Xin B, Liu L, Hou G, Ma Y. Chaos Synchronization of Nonlinear Fractional Discrete Dynamical Systems via Linear Control. Entropy. 2017; 19(7):351. https://doi.org/10.3390/e19070351
Chicago/Turabian StyleXin, Baogui, Li Liu, Guisheng Hou, and Yuan Ma. 2017. "Chaos Synchronization of Nonlinear Fractional Discrete Dynamical Systems via Linear Control" Entropy 19, no. 7: 351. https://doi.org/10.3390/e19070351
APA StyleXin, B., Liu, L., Hou, G., & Ma, Y. (2017). Chaos Synchronization of Nonlinear Fractional Discrete Dynamical Systems via Linear Control. Entropy, 19(7), 351. https://doi.org/10.3390/e19070351