1. Introduction
Classical susceptible-infectious-removed (SIR) epidemic models with bilinear incidence rate typically have at most one endemic equilibrium; the disease will die out when the basic reproduction number is less than unity and will persist otherwise [
1,
2,
3,
4]. However, in practice, many infectious diseases exhibit multiple peaks or periodic oscillations during the outbreak. Therefore, various nonlinear incidence rates have been proposed recently due to the fact that they can produce rich dynamics for the epidemic models.
Liu et al. [
5] used the following form of nonlinear saturated incidence rate to incorporate the effect of behavioral changes
where
measures the infection force of the disease,
describes the inhibition effect from the behavioral change of the susceptible individuals when the number of infectious individuals increases,
are positive constants and
is non-negative constant [
6,
7]. The nonlinear function
given in (
1) has three types, for details one can see [
7]. Capasso and Serio [
8] used the case when
, i.e.,
, to represent a “crowding effect” or “protection measure” in investigating the cholera epidemic in Bari in 1973. Due to the nonlinearity and saturation property of these incidence rates, SIR epidemic models usually possess multiple endemic equilibria and rich nonlinear dynamics [
5,
6,
7,
8,
9,
10,
11,
12]. Furthermore, a compartmental model with nonlinear incidence rate is usually used to explore the impact of intervention strategies on the transmission dynamics of infectious diseases. Therefore, it is essential to investigate the dynamics of this type of epidemic model to prevent and control the spread of infectious diseases.
On the other hand, the resources of health system availability to the public determines how well the diseases are controlled. Particularly, the capacity of the hospital settings and effectiveness and efficiency of the treatment may influence the recovery rate [
13]. In classical epidemic models, the recovery rate is usually assumed to be proportional to the number of infected, which means that the resources of the health system are quite sufficient for the infectious disease [
1]. In fact, the number of health care workers and the facilities of the hospital including medical apparatus and equipment, the number of hospital beds and medicines available to the public are limited, especially during the outbreak of the disease. For instance, during the severe acute respiratory syndrome (SARS) outbreaks in 2003, the Chinese government had to create the first and only SARS hospital, Beijing Xiaotangshan Hospital, to treat the larger number of SARS patients, as the normal public-health system and capacity in Beijing City were unable to cope with the rapidly increasing number of SARS cases [
9,
14]. Hence, the capacity of the health care system from both a modeling and analysis of the view should be considered.
Based on the World Health Organization (WHO) Statistical Information System, hospital bed-population ratio (HBPR), the number of available hospital beds per 10,000 population, is used by health planners as a method of estimating resource availability to the public [
13,
15]. To study the impact of HBPR, Shan and Zhu [
13] proposed the following nonlinear recovery rate function of the number of hospital beds per 10,000 population
b and the number of infective individuals
I
where
,
(
are, respectively, the minimum and maximum per capita recovery rates. Parameter
b is considered as a measure of available hospital resource. Their study showed that the SIR model with standard saturate incidence and recovery rate (
2) has rich and interesting dynamics such as backward bifurcation, saddle-node bifurcation, Hopf bifurcation and cusp type of Bogdanov–Takens bifurcation of codimension 3. Recently, Abdelrazec et al. [
16] applied the recovery rate (
2) to investigate the impact of available resources of the health system on the spread and control of dengue fever, which could be helpful for public health authorities in their planning of a proper resource allocation for the control of dengue transmission.
Motivated by these points, our model thus incorporates both nonlinear incidence rate and recovery rate to well control the emerging infectious. In other words, the combined effects of government intervention and hospitalization condition are considered to prevent an outbreak. However, it is more natural to consider perturbations of contagion coefficients through the Wiener process or treat them directly as random variables since the transmission coefficients are usually unknown in practice (see, for example, [
17,
18] and references therein). Here, we focus on the deterministic epidemic model and leave the consideration of randomness in epidemiological model as our future work. Therefore, in this paper, we investigate the following deterministic epidemic model with a nonlinear incidence rate and recovery rate:
with
defined in (
2). In system (
3),
and
are the numbers of susceptible, infectious and recovered individuals at time
t, respectively;
is the recruitment rate of the population;
is the per capital natural death rate of the population;
is the per capita disease-induced death rate;
is the per capita recovery rate of infectious individuals incorporating the impact of the capacity and limited resources of the health care system, and
is the number of available hospital beds per 10,000 population.
The organization of this paper is as follows. In the next section, we investigate the existence and classification of the equilibria for system (
3). In
Section 3, we analyze the nonlinear dynamics for system (
3) such as forward bifurcation, backward bifurcation, saddle-node bifurcation and Hopf bifurcation. In
Section 4, the numerical simulations are obtained to verify our results. A brief discussion is then presented and conclusions are presented in the final section.
4. Bifurcation Diagram and Simulation
The theoretical results in previous sections show that the dynamics of system (
4) depend on the expressions of
and
. Therefore, in the following, we first analyze these expressions in the
plane.
From the expression of the basic reproduction number
, we know that
defines a straight line
in
plane
defines a hyperbola
in
plane
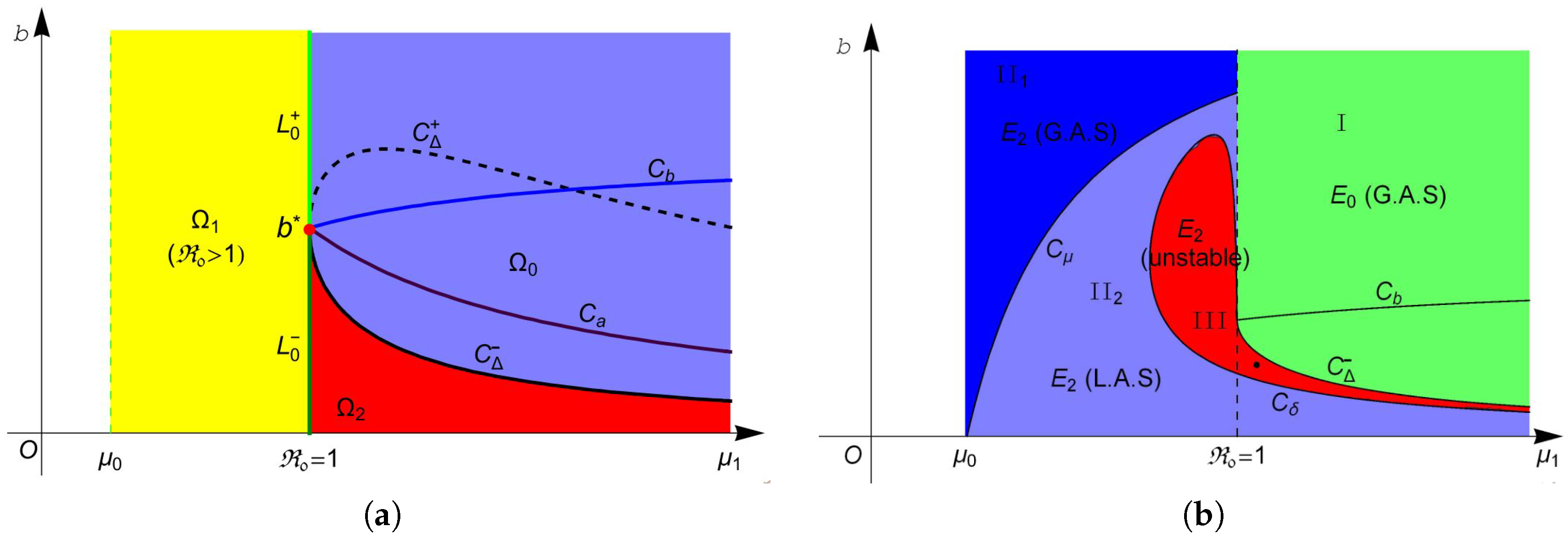
One can easily verify that hyperbola and line intersects at point , and is a decreasing convex function of with a horizontal asymptote .
If
, we obtain the curves
by solving
b in term of
, where
A straightforward calculation leads to
and
, which suggests that
is tangent to the curve
at the point
. Furthermore, for any
, we have
and
Therefore, the curve
under the curve
is convex and decreasing with the asymptote
.
determines a curve
where
are given in (
23). Furthermore, we define
which will be used later.
Based on the above discussions and Theorem 1, let
Then, system (
4) has no endemic equilibrium in region
, one endemic equilibrium
in region
and two equilibria
and
in region
. The two equilibria in
coalesce into one equilibrium
on curve
. For more intuitive observation, one can see
Figure 1a.
The stability of these equilibria can be observed in
Figure 1b. According to Theorem 2, the disease-free equilibrium
always exists, and it is locally asymptotically stable (L.A.S) in region
and unstable in region
. Furthermore, Theorem 4 suggests that
is globally asymptotically stable (G.A.S) in region I (green region in
Figure 1b). From Theorem 3, we know that
is always unstable whenever it exists, and
is unstable in region II (red region in
Figure 1b) and is L.A.S. in region II
(light blue region in
Figure 1b). Moreover, Theorem 4 implies that
is G.A.S in region II
(blue region in
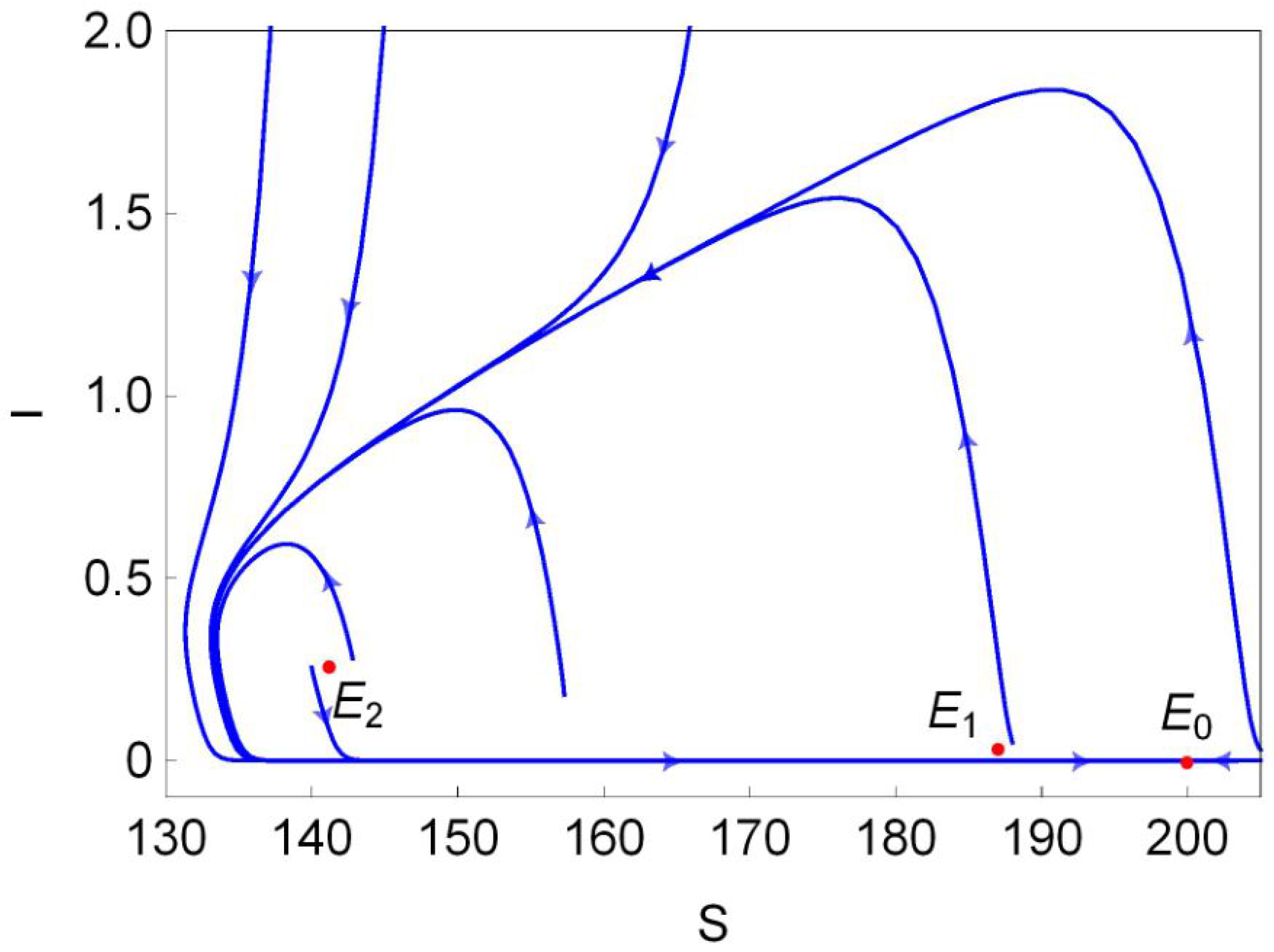
Figure 1b). Finally, we choose a point (marked in black dot in
Figure 1b) in the region III and plot its phase portrait in
Figure 2. It is clear that the disease-free equilibrium
and two endemic equilibria
and
coexist, and
is L.A.S,
is a saddle and
is unstable.
According to Theorem 5, system (
4) undergoes forward bifurcation on
, backward bifurcation on
, pitchfork bifurcation when transversally passing through the line
at point
and saddle-node (SN) bifurcation on the curve
when the two endemic equilibria coalesce into one endemic equilibrium
. Hopf bifurcation occurs on the curve
as proved in Theorem 7.
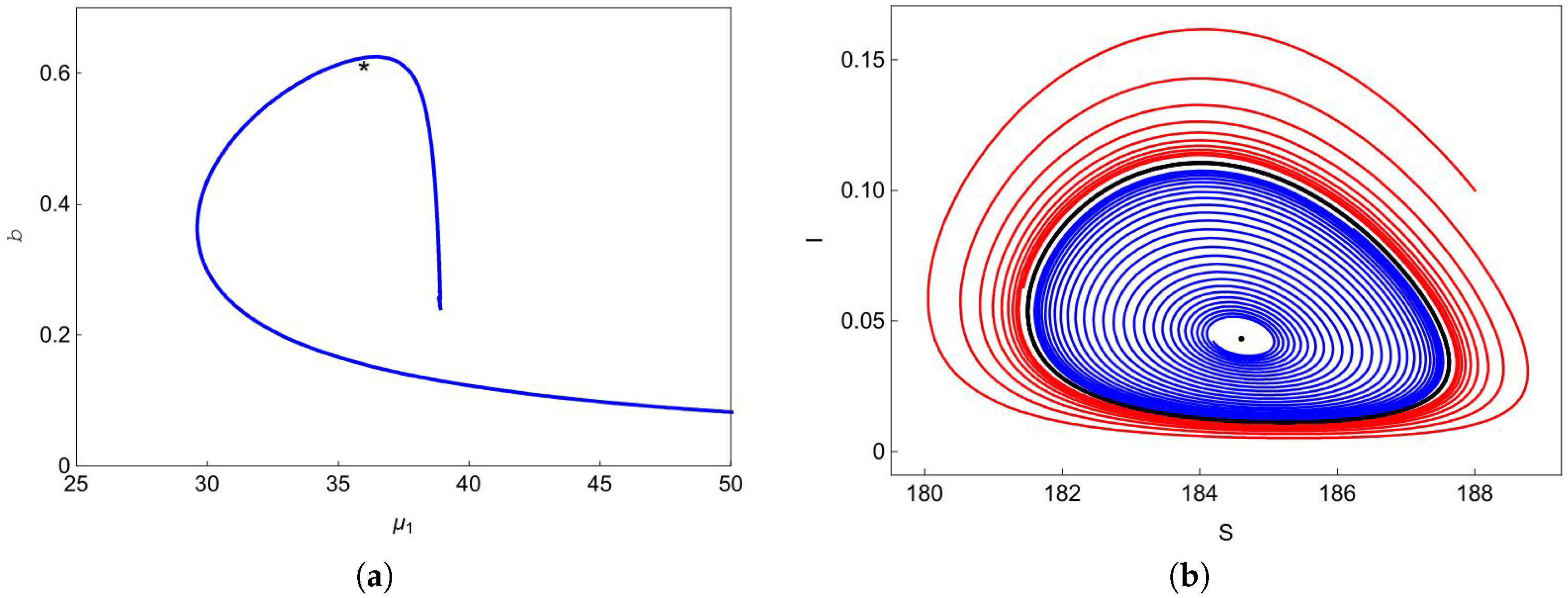
Figure 3a shows the Hopf bifurcation curve in the
plane. We choose one point
marked with a black asterisk below the blue curve in
Figure 3a, and plot the phase portrait at this point in
Figure 3b. We can observe from
Figure 3b that the trajectory (blue curve) starting at
spirals outward to the stable limit curve (black curve) and the trajectory (red curve) starting at
spirals inward to the stable limit curve. At point
, one can easily obtain that
does not exist and
exists, but it is unstable. Therefore, system (
4) has a stable limit curve that enriches the unstable equilibrium
.
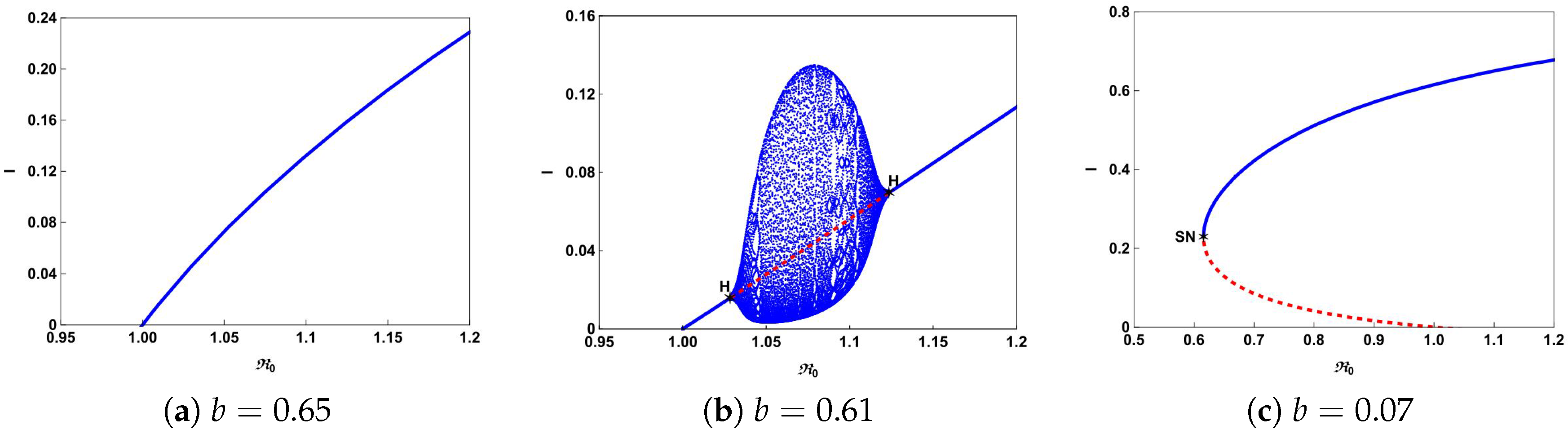
The typical bifurcation diagrams in
plane can be seen in
Figure 4.
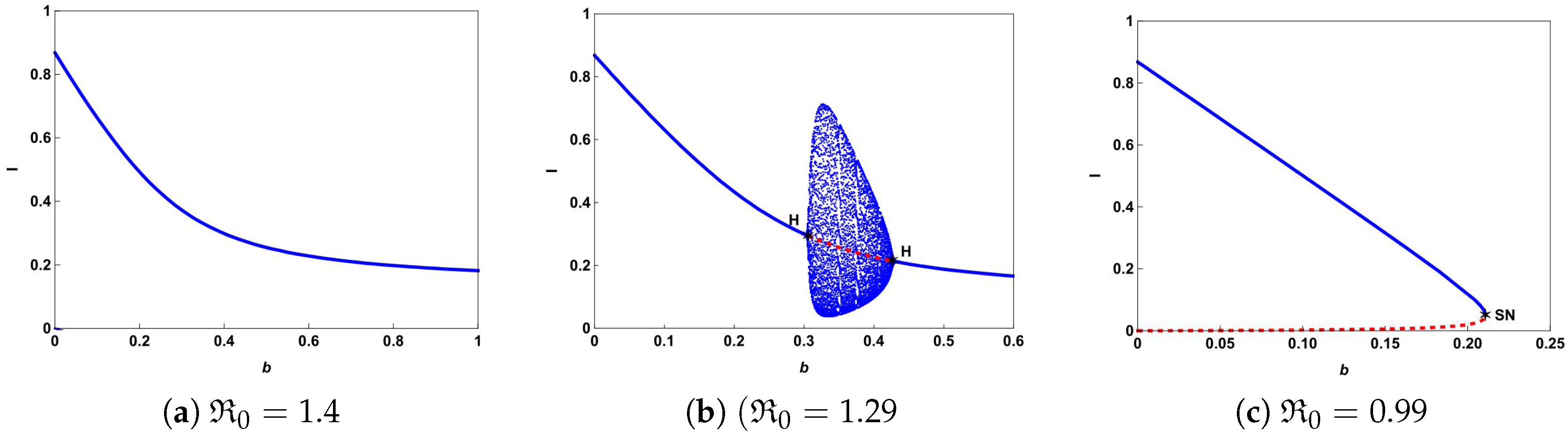
Figure 4a shows that there is a forward bifurcation at
from disease-free equilibrium
to a unique endemic equilibrium
when
. If we decrease
b from 0.65 to 0.61, system (
4) not only undergoes forward bifurcation but also undergoes Hopf bifurcation as shown in
Figure 4b. In this case, a stable limit cycle bifurcated from forward Hopf bifurcation and disappears from the backward Hopf bifurcation. If we further decrease
b to 0.07, we can observe from
Figure 4c that the backward bifurcation and saddle-node bifurcation occur. This illustrates that the number of hospital beds plays an important role in controlling an infectious disease.
To further explore the impact of the number of hospital beds, we also present the possible bifurcation diagrams in
plane by fixing all the parameters except
b.
Figure 5 depicts some typical bifurcation diagrams in
plane with different
. If
, one can see from
Figure 5a,b that increasing the beds can reduce the number of infectious individuals but can not eliminate the disease. Especially in the case of
, Hopf bifurcation occurs and a stable limit cycle bifurcated from forward Hopf bifurcation disappears from backward bifurcation. If
, backward bifurcation and saddle-node bifurcation may occur and the disease dies out when the value of
b is above the curve
based on Theorem 4 and
Figure 1.
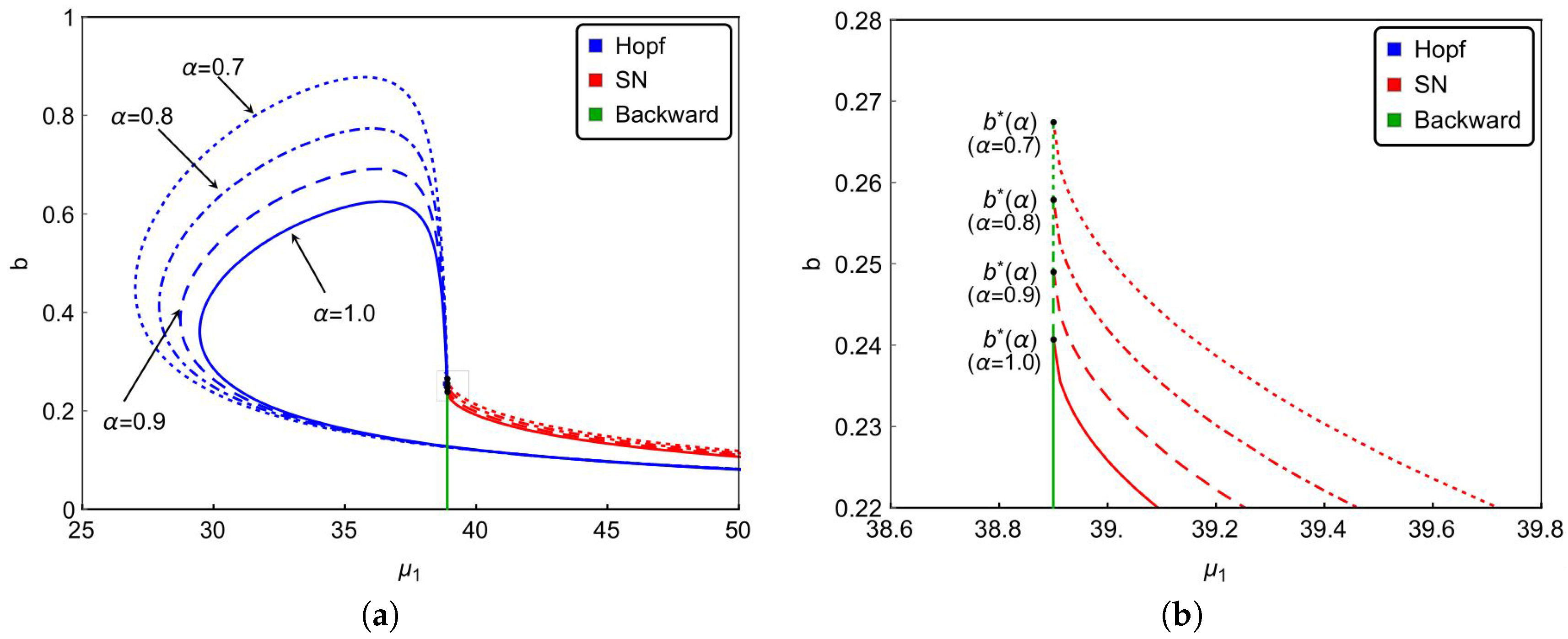
Finally, we investigate the effect of the nonlinear incidence rate. For the nonlinear saturate incidence rate
, it is known that larger
reflects stronger inhibition effect caused by the infective individuals. Although the increasing of
cannot reduce the basic reproduction number
, it does affect the dynamical behaviors of the system. Based on previous results, we can see from
Figure 6a that backward bifurcation occurs on green lines, saddle-node bifurcation occurs on red curves and Hopf bifurcation happens on blue curves.
Figure 6a and the magnified diagram
Figure 6b also illustrate that the occurrence of backward bifurcation, saddle-node bifurcation and Hopf bifurcation shrink with increasing
. That is to say, the strong inhibition effect will lower the complexity of the transmission of the infectious diseases. In other words, enhancing the public’s defensive “crowding effect” through education or medium is beneficial to control and prevent the spread of the infectious diseases. Furthermore,
Figure 6 also implies that the stronger inhibition effect of the lower number of hospital beds will be needed to eliminate the diseases. It reveals that strengthened public defensive “crowding effect” can mitigate the demand for hospital beds in controlling the spread of the disease during an outbreak.
5. Discussion
Due to the important biological significance of hospital beds, in this paper, we have investigated an SIR epidemic model to simulate the impact of a limited health care system in terms of the number of hospital beds. Theoretical analysis and numerical simulations illustrated that system (
4) has at most three equilibria and possesses complex nonlinear dynamics. From Theorems 5–7 and
Figure 4 and
Figure 5, we have shown that system (
4) can undergo backward bifurcation, saddle-node bifurcation and Hopf bifurcation due to the insufficient number of hospital beds.
If
, it follows from Theorem 3 and
Figure 1b that
is the unique endemic equilibrium, and it is stable if
b is sufficiently large such that the values of
b are all above the curve
. Since
and
, then
is a monotone decreasing function of
b and
trends to some positive constant as
b to infinity. That is, increasing the number of hospital beds can only reduce the number of the infectious, but cannot eliminate the infectious disease (see
Figure 5a,b). If
, it follows from Theorem 3 and
Figure 1b that the disease can be eliminated when the value of
b above the curve is
. This means that the basic reproduction number is not the only evaluation standard for the control and elimination of the disease. It also depends on the resources of the health care system such as the number of hospital beds.
The bifurcation analysis is carried out through reducing the three dimension model (
3) to the planar system (
4). The typical bifurcation curves and diagrams are shown in
Section 4, and all of the results reveal that system (
3) possesses complex dynamics such as forward bifurcation, backward bifurcation, saddle-node bifurcation and Hopf bifurcation. Contrasting to the results for the classic SIR epidemic models, we also find that the nonlinearity of incidence rate and recovery rate are important factors that lead to very rich dynamics. Moreover, we find that the dynamical behavior of system (
3) not only depends on
but also relies on the number of hospital beds and the inhibition effect caused by the infective individuals. Therefore, the public health makers should consider the combined effects of the government intervention strategies (such as education and medium) and hospitalization conditions to make guidelines in controlling the spread of infectious diseases. Hopefully, in the future, we can explore more theoretical results to control and eliminate infectious diseases, especially in the outbreak of diseases.