Because of its fundamental importance in the communications theory, Shannon entropy will be used to develop the communications based model used in this paper. While Shannon entropy shares some structural similarities with the Thermodynamic Entropy there are some important differences. Ben-Naim [
9] discusses these differences in detail. One important distinction relevant for this paper is the fact that Shannon entropy can change over time whereas the Thermodynamic Entropy of a closed system does not. As will be shown the growth of Shannon entropy in the entropic yield curve represents the loss of information in the economy.
The loss of information or the growth of entropy in the economy is assumed to arise from two primary sources. These sources are the natural decay of the current set of information about the economy over time and a non-zero error in the processing of that current information set. This interplay of information diffusion and processing errors determines the total entropy of an economy. The entropic yield curve defines the average growth rate of entropy at any time t.
If all information is perfectly incorporated into prices with no error, prices will evolve identically with information Ross [
10]. However physical limits on information processing make perfect contemporaneous reflection of all information in prices impossible Sims [
11]. Instantaneous and perfect utilization of all economic information would imply economic agents with infinite bandwidth and faster than light communication and processing. There will always be at least a non-zero time lag in information processing and arguably some error in that processing. The time lag ultimately results in a trade off in terms of completeness of information collection and processing speed.
2.1. Entropic Yield Curve Initial Derivation
The zero rate curve is also known as the yield curve since it is the yield of a zero-coupon bond with maturity
t, where
r =
r(0,
t) is the zero rate between time 0 and
t (see Stefanica [
12]). In this section a new yield curve will be developed based on entopic arguments. To help facilitate the derivation, the finding of Theorem 2 from Ross [
10] will be assumed. Specifically, Ross utilized a martingale no-arbitrage approach to prove that the variance of price change must equal the variance of information flow or else arbitrage would be possible. Ross additionally proved with Theorem 2 that price and information changes are perfectly correlated.
Information and bond price will be assumed to be driven by the Brownian motion type processes below respectively:
Solving for
and equating both expressions results in the ratio below:
Bond growth and information diffusion assumptions:
An interest rate
r is defined by the typical relationship between intertemporal prices:
Substituting
and
into the ratio (2) yields:
Therefore with errorless and instantaneous processing:
The assumption of perfect price and information correlation will now be relaxed to allow for the introduction of errors in the price response. Assume a computational error or processing lag affects the price response as seen below. Depending on the value of the error term
price diffusion could be magnified or suppressed:
The equation above represents the total time averaged loss of information by the economy through time period t. A more precise description of the entropic yield curve follows from the perspective of a weighted Kullback–Leibler divergence follows.
2.2. Entropic Yield Curve, Kullback–Leibler Divergence, and the Implied Information Processing Rate
The Shannon entropy is intimately related to another fundamental quantity from information theory, the Kullback–Leibler divergence. In fact the Shannon entropy can be easily represented in the form of Kullback–Leibler divergence. Despite this equivalence, the Kullback–Leibler provides another informative perspective from which to analyze the entropic yield curve.
The relative entropy
D(
p‖
q) is a measure of the inefficiency of utilizing distribution
q instead of the true distribution of
p Cover [
13]:
Use of the approximate distribution q implies H(x) + D(p‖q) bits instead of H(x) bits on average to describe a random variable. In other words, information in the amount of D(p‖q) bits is being lost as entropy increases through this inefficiency.
Information is lost as it is collected, modeled and communicated through time in a fashion similar to the more familiar concept of information loss as it is communicated through space as studied by Shannon [
14] and Burnashev [
15]. In the equation above
p represents the probability of an error and also serves as the weighting in the Kullback–Leibler divergence.
In the extreme if there is perfect information processing without error or time lag then
p = 0% and
r is only determined by the diffusion of information:
In the converse if information processing is completely flawed then
p = 100%:
Further developing the metaphor, the communication of information in the economy will be modeled as a discrete memory less channel (DMC) with feedback. This system will utilize variable length codes to transmit information. This description is motivated by both in the realism and practicality.
The assumption of this structure is based on the fact that DMC’s with feedback are ubiquitous in computer and communication networks and thus ultimately a major component our economic system’s communication structure Polyanskiy et al. [
16]. DMC’s use feedback to reduce error in transmissions. If a transmission has been received with an error, the receiver can request that the transmitter resend the message. Alternatively the transmitter may await confirmation that the message has been received without error before sending the next message. If this confirmation is not received within a specified time the message is automatically resent.
The practicality of the DMC model in this context results from the fortunate availability of a precise computational tool to estimate the reliability of such communication. In 1976 Burnashev [
15] published the groundbreaking result of being able to characterize the reliability of a (DMC) with feedback utilizing variable length codes (see also Polyanskiy et al. [
16] and Berlin et al. [
17]). This reliability can be precisely computed at all rates of transmission with a relatively simple formula:
where
R is a transmitted message and
C is the channel capacity of the transmitter.
The Burnashev error exponent is used to represent
p or probability of error in the entropic yield curve. The rate of interest as modeled by the entropic yield curve is the average rate of entropy growth or information loss over the time period
t:
The Implied Information Processing Rate (IIPR) or (
R/C) can be estimated by matching the entropic yield curve to the observed yields in the markets and then solving for IIPR. Despite their seemingly disparate theoretical origins, the entropic yield curve and the popular Nelson–Siegel [
18,
19] model share deep similarities as seen in the next section.
2.3. The Entropic Yield Curve vs. the Nelson–Siegel Specification
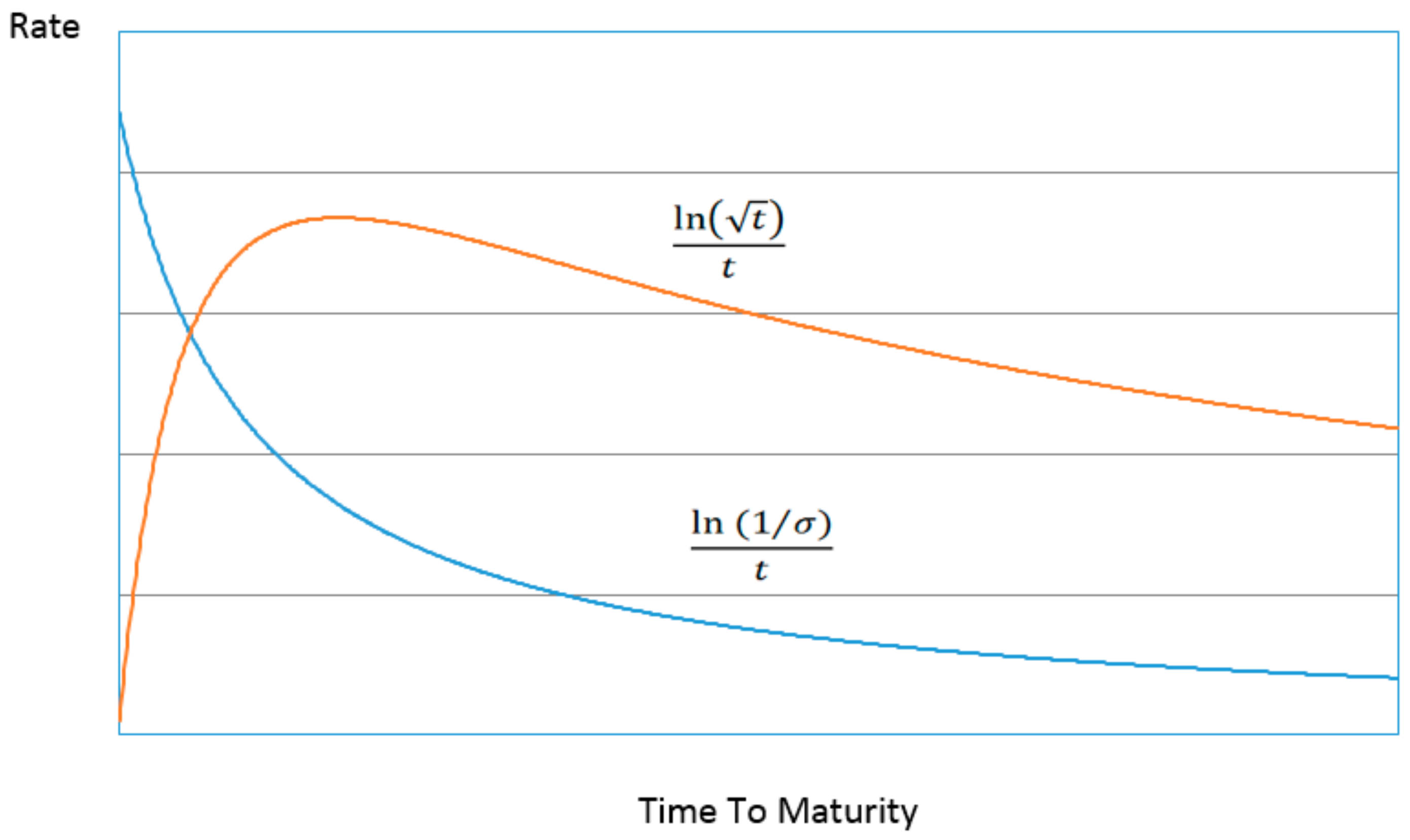
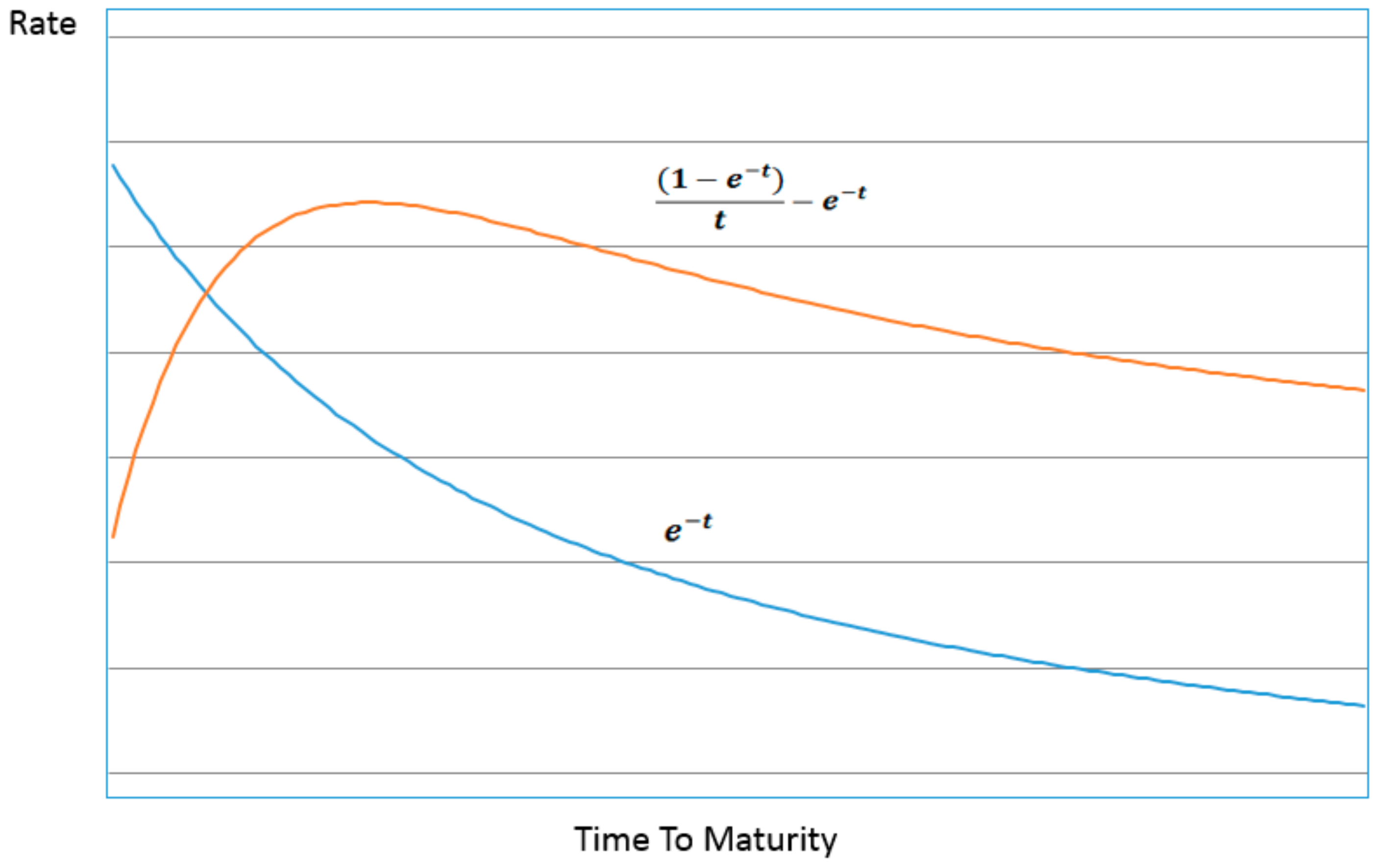
Figure 1 and
Figure 2 below illustrates the contribution of the two main terms to the structure of the entropic yield curve (ignoring for now the
p factor) compared to the Nelson–Siegel specification. The structures bear a striking resemblance to one another despite their different derivations. Just as with the Nelson–Siegel specification almost any conceivable structure of the yield curve can be constructed with the appropriate parameterization and combination of the two decomposed curves making up the entropic yield curve.
Nelson and Siegel [
18,
19] derived a popular and parsimonious technique for modeling the yield curve. Nelson–Siegel first modeled forward rate curves as the solutions to ordinary differential equations. Their yield curve could be then modeled as an average of these forward rate curves. They further used simulations to drop extra parameters and develop a final efficient form. The parameters of their model are ultimately “initial conditions” empirically derived to adjust the shape of their yield curve to fit reality. The parameters have no traditional economic or financial meaning. Although less theoretically rigorous in its construction than other methods, the Nelson Siegel model has proven to be more accurate than other yield curve modeling methods subsequently developed by academics.
Nelson and Siegel [
18,
19] demonstrated that a transformation of their yield curve by manipulation of the parameter
a (or -
β2) produced most of the typical shapes of the yield curve as seen in the reproduction below. This parameter had no true economic, financial or other interpretation, other than its demonstrated utility in adjusting the curve to fit those observed in reality.
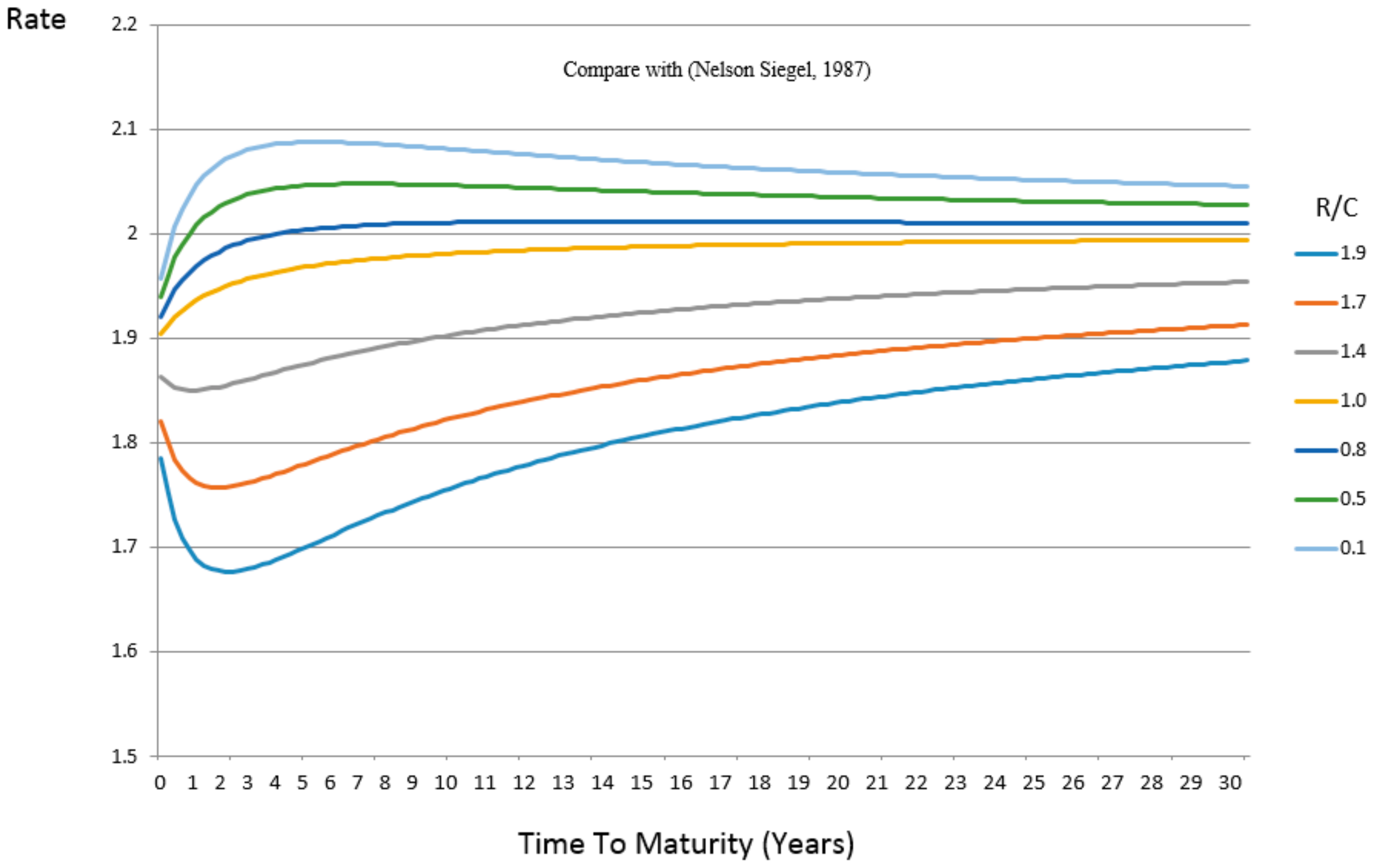
The Nelson–Siegel parameter
a (or -
β2) has an equivalent representation (in terms of function) in the Entropic Yield Curve. This equivalent parameter is the ratio at the heart of this paper
R/C. As the values of
R/C vary from 1.9 to 0.1 (bottom to top) the resulting curves appear nearly identical to the variety and style produced by varying Nelson–Siegel’s nondescript parameter as seen below in
Figure 3 using the parameter settings in
Table 1:
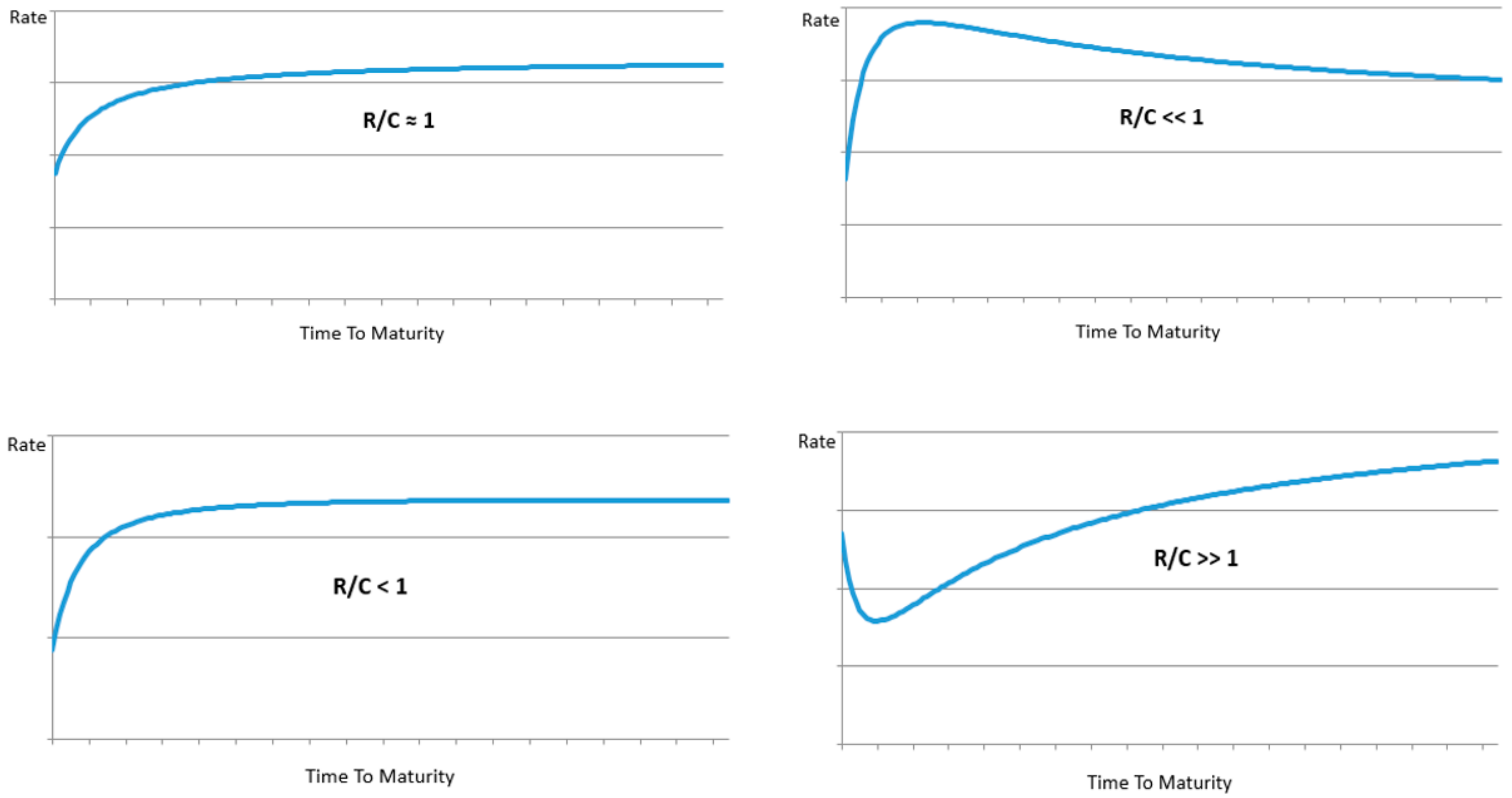
However unlike the Nelson–Siegel specification, in the Entropic Yield Curve the various shapes are generated by a variable with an intuitive origin. The normal upward sloping yield curve is generated in an environment where the information arrival and processing rates are approximately equal as seen in the center curve (R/C ≈ 1). When R/C >> 1 or << 1 information is either arriving much faster or much slower than it can be processed in the economy resulting in the curves at the bottom and top of the chart respectively.
Currency in economy that cannot process current information efficiency is inherently less valuable than that of an economy accurately processing all arriving information. The amount of interest needed to separate currency holders from their money when R/C >> 1, is significantly less than when R/C ≈ 1. Alternatively when an economy is able to absorb all information the value of its currency will likely rise and the associated interest needed to separate the fortunate currency holder from her money will rise.
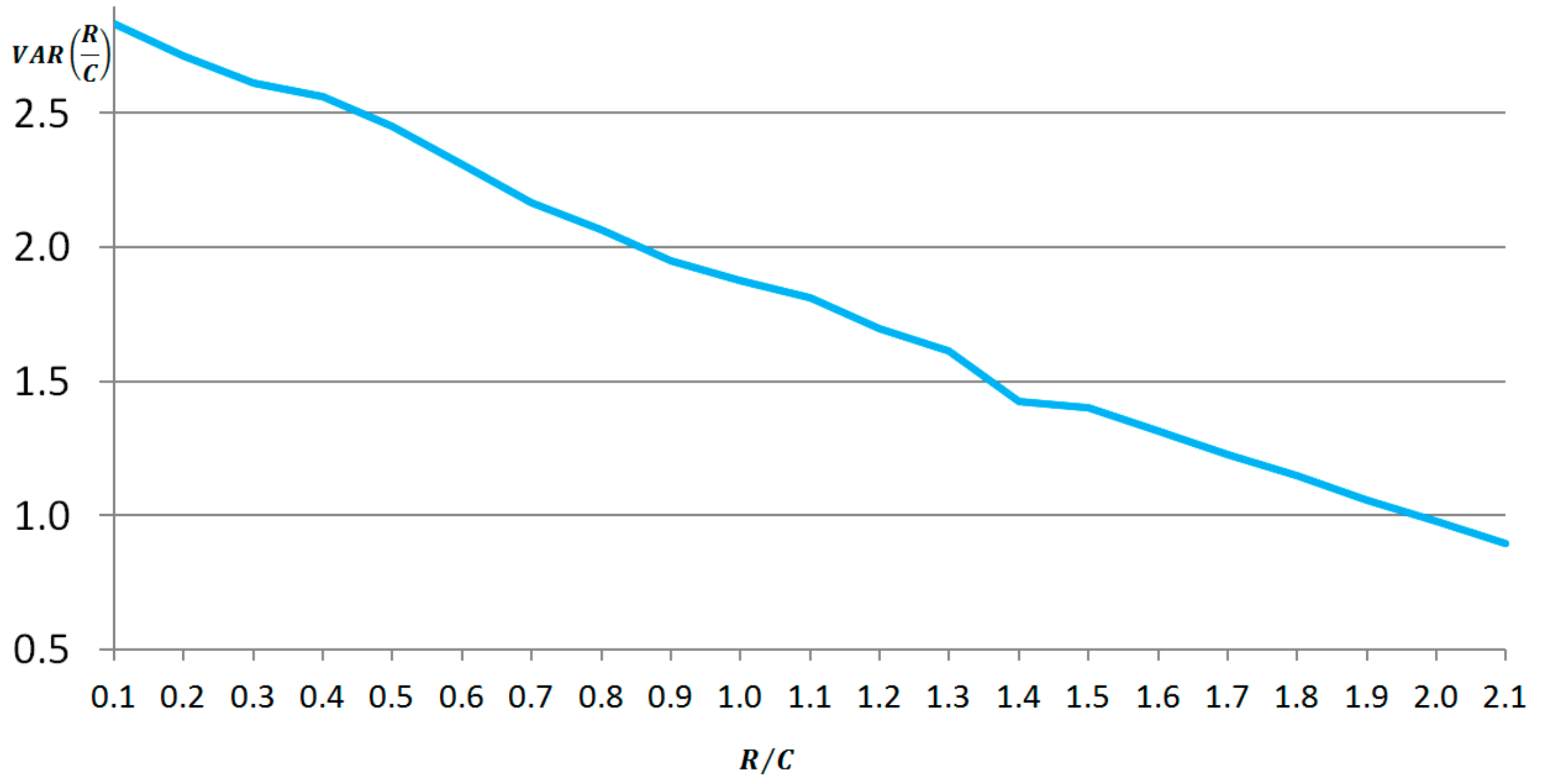
2.5. Simulation: Level of R/C vs. Variance of R/C
Next a simulation was run to better understand the dynamics of the R/C. Specifically the variance of R/C over different levels of R/C varied was examined. To isolate the relationship between the R/C level and variance, the variance of interest rates was held constant throughout.
The variance of
R/C was modified by the adjustment of a multiplier
M as seen in the equation below.
M is multiplied by a variable which is
. At each mean value of
R/C from 0.1 to 2.1,
M was adjusted such that the average variance of the rates
r(
t) remained constant at each level of
R/C. This simplifying assumption highlights the relationship between the level and variance of
R/C without the confounding effect of interest rate variability changes:
The level of the average variance of the solved interest rates was held constant by solving for a multiplier
M at each
R/C
where:
The results of the simulation are presented in
Figure 5 below. There is an inverse relationship between the level and variance of
R/C. The potential causes and implications of changes in the variance of
R/C are presented in the next section.
2.6. Harbinger of the Bears
Next the ratio
R/C will be used to elucidate a new entropic linkage between the bond and equity markets. Parker [
8] demonstrated:
…that ratio of these rates R/C or (CCA/CCL) can determine different regimes of normal and “anomalous” behaviors for security returns”. As this ratio evolves over a continuum of values, security returns can be expected to go through phase transitions between different types of behavior. These dramatic phase transitions can occur even when the underlying information generation mechanism is unchanged. Additionally when the information arrival and processing rates are assumed to fluctuate independently and normally, the resulting ratio (CCA/CCL) is shown to be Cauchy distributed and thus fat tailed…
For more information on the Cauchy distribution as the ratio of Normal variables see Marsaglia [
20].
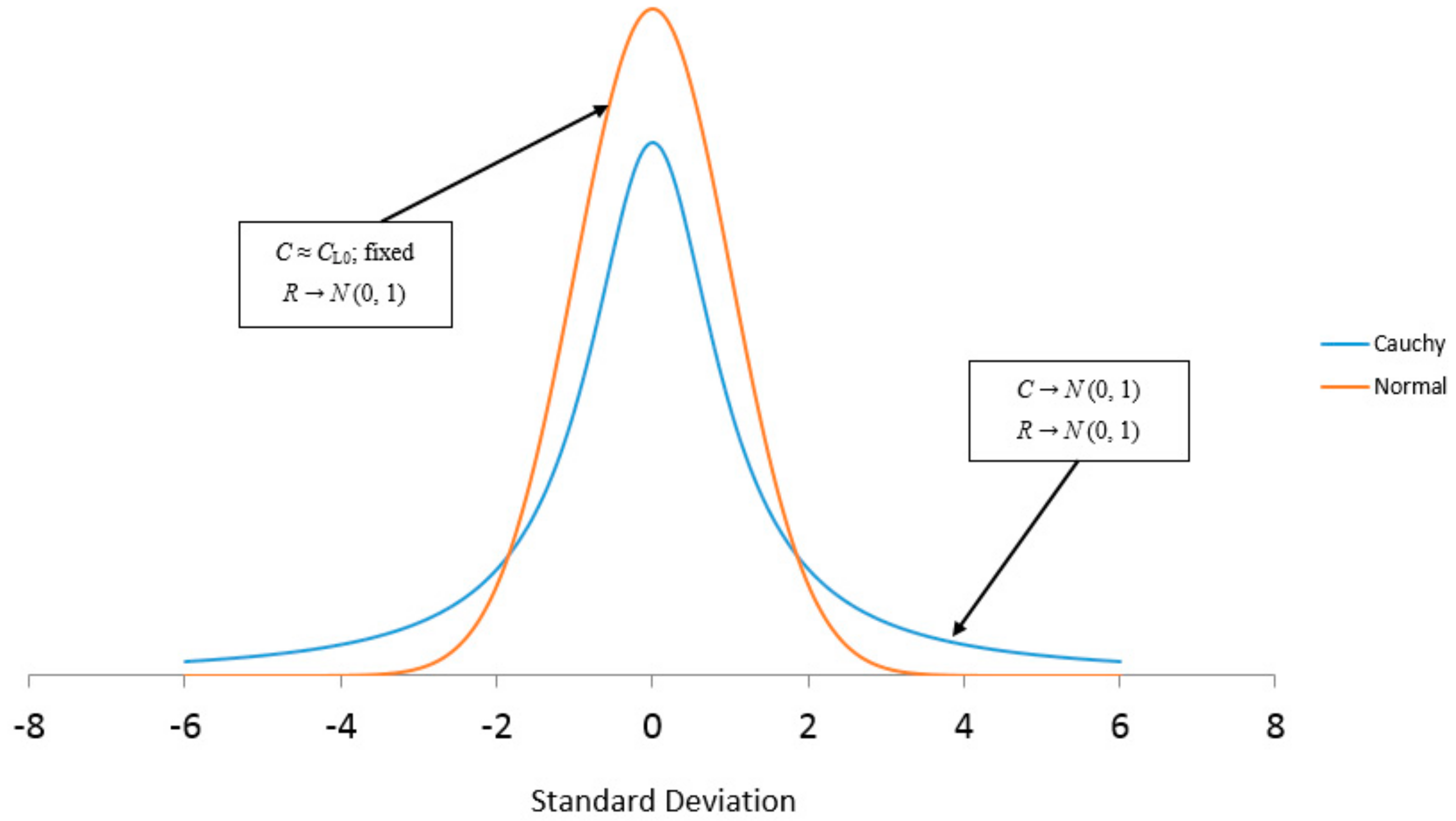
Parker [
8] also showed how an increase in the variance of
C could lead to a similar outcome as a simple increase in the level of
C. If initially
R is assumed to be
N ~ (0, 1) and
C constant, then the ratio
R/C is also normally distributed. However when both
R and
C are normally distributed it can be shown that the ratio
R/C will then be Cauchy Distributed. Cauchy distributions actually have nonfinite (or undefined) means and variances. This results in fatter tails which cause extreme events to occur much more frequently compared to a process modeled with the normal distribution. The transformation of
R/C from a normal to a Cauchy type distribution resulting from a change in
C from constant to
N ~ (0, 1) is illustrated in
Figure 6 below.
The transformation of the relative information processing ration
R/C from a normal to Cauchy distribution leads to unpredictable explosions and collapses in the amount of unprocessed information in the economy. Companies cannot efficiently process information and massive information loss (or entropy growth) occurs relative to periods of more stable information and information processing growth. Additionally future information processing resource allocation and planning cannot be reliably made during such unstable periods. These factors ultimately lead to a collapse in economic growth and to the stock market collapses Parker [
8], and by similar reasoning the emergence of bear markets.