On the Simplification of Statistical Mechanics for Space Plasmas
Abstract
:1. Introduction
2. Tsallis Entropy and Ordinary/Escort Formalism
3. The Entropy Maximization in the Framework of Non-Extensive Statistical Mechanics
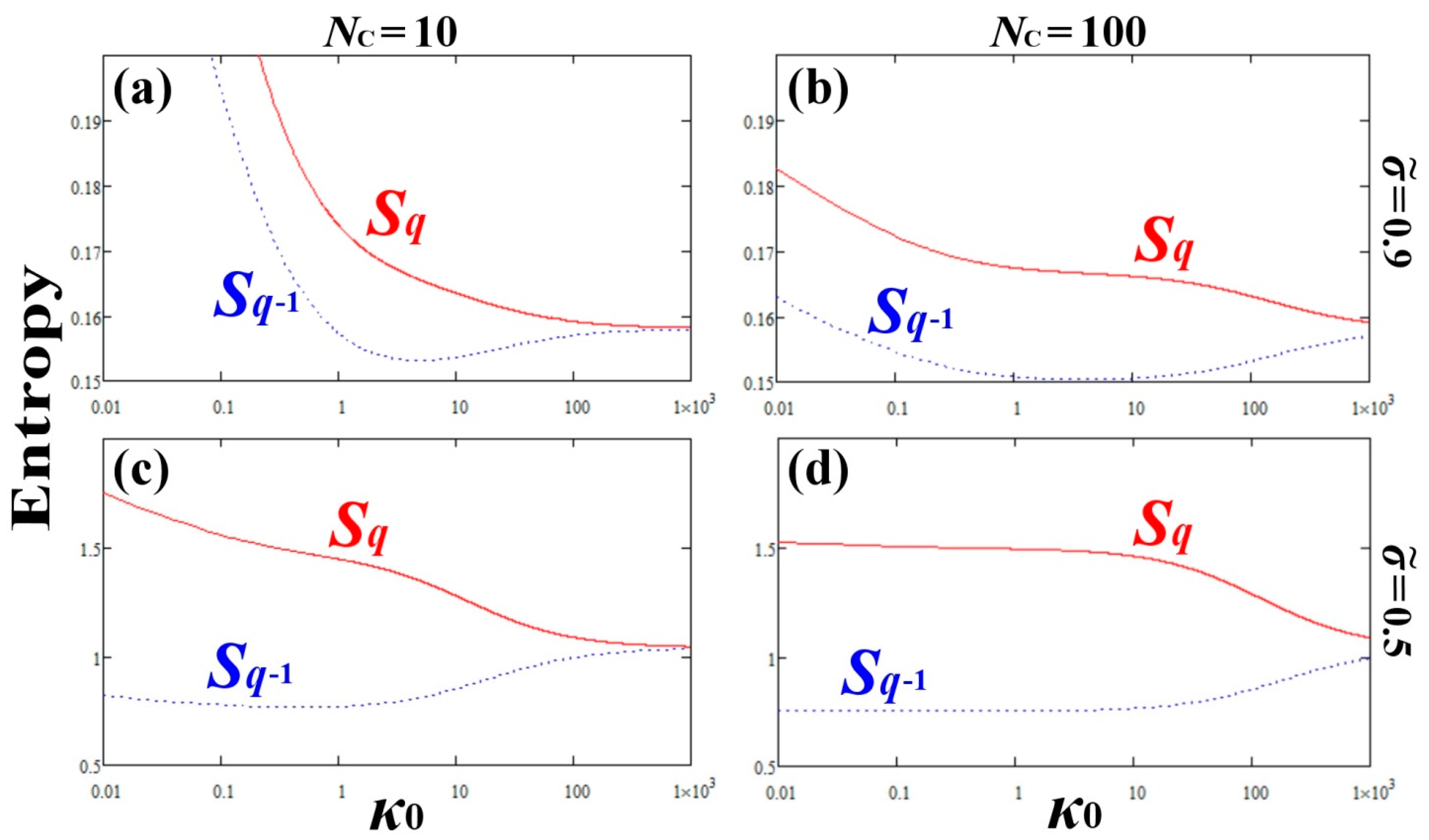
4. Avoiding Ordinary/Escort Formalism
5. Connection to Thermodynamics
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Maksimovic, M.; Pierrard, V.; Lemaire, J. A kinetic model of the solar wind with Kappa distributions in the corona. Astron. Astrophys. 1997, 324, 725–734. [Google Scholar]
- Pierrard, V.; Maksimovic, M.; Lemaire, J. Electron velocity distribution function from the solar wind to the corona. J. Geophys. Res. 1999, 104, 17021–17032. [Google Scholar] [CrossRef]
- Mann, G.; Classen, H.T.; Keppler, E.; Roelof, E.C. On electron acceleration at CIR related shock waves. Astron. Astrophys. 2002, 391, 749–756. [Google Scholar] [CrossRef]
- Marsch, E. Kinetic physics of the solar corona and solar wind. Living Rev. Sol. Phys. 2006, 3, 1. [Google Scholar] [CrossRef]
- Zouganelis, I. Measuring suprathermal electron parameters in space plasmas: Implementation of the quasi-thermal noise spectroscopy with kappa distributions using in situ Ulysses/URAP radio measurements in the solar wind. J. Geophys. Res. 2008. [Google Scholar] [CrossRef]
- Štverák, S.; Maksimovic, M.; Travnicek, P.M.; Marsch, E.; Fazakerley, A.N.; Scime, E.E. Radial evolution of nonthermal electron populations in the low-latitude solar wind: Helios, Cluster, and Ulysses Observations. J. Geophys. Res. 2009. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Exploring transitions of space plasmas out of equilibrium. Astrophys. J. 2010, 714, 971. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. The influence of pick-up ions on space plasma distributions. Astrophys. J. 2011, 738, 64. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Understanding kappa distributions: A toolbox for space science and astrophysics. Space Sci. Rev. 2013, 75, 183–214. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Near-equilibrium heliosphere-Far-equilibrium heliosheath. In Proceedings of the 13th International Solar Wind Conference, Big Island, HI, USA, 17–22 June 2012; pp. 344–347. [Google Scholar]
- Yoon, P.H. Electron kappa distribution and quasi-thermal noise. J. Geophys. Res. 2014, 119, 7074. [Google Scholar] [CrossRef]
- Pierrard, V.; Pieters, M. Coronal heating and solar wind acceleration for electrons, protons, and minor ions, obtained from kinetic models based on kappa distributions. J. Geophys. Res. 2015, 119, 9441. [Google Scholar] [CrossRef]
- Pavlos, G.P.; Malandraki, O.E.; Pavlos, E.G.; Iliopoulos, A.C.; Karakatsanis, L.P. Non-extensive statistical analysis of magnetic field during the March 2012 ICME event using a multi-spacecraft approach. Phys. A Stat. Mech. Appl. 2016, 464, 149–181. [Google Scholar] [CrossRef]
- Dzifčáková, E.; Dudík, J. H to Zn ionization equilibrium for the non-Maxwellian electron κ-distributions: Updated calculations. Astrophys. J. Suppl. Ser. 2013, 206, 6. [Google Scholar] [CrossRef]
- Dzifčáková, E.; Dudík, J.; Kotrč, P.; Fárník, F.; Zemanová, A. KAPPA: A package for synthesis of optically thin spectra for the non-Maxwellian κ-distributions based on the Chianti database. Astrophys. J. Suppl. Ser. 2015, 217, 14. [Google Scholar] [CrossRef]
- Owocki, S.P.; Scudder, J.D. The effect of a non-Maxwellian electron distribution on oxygen and iron ionization balances in the solar corona. Astrophys. J. 1983, 270, 758–768. [Google Scholar] [CrossRef]
- Vocks, C.; Mann, G.; Rausche, G. Formation of suprathermal electron distributions in the quiet solar corona. Astron. Astrophys. 2008, 480, 527–536. [Google Scholar] [CrossRef]
- Lee, E.; Williams, D.R.; Lapenta, G. Spectroscopic indication of suprathermal ions in the solar corona. arXiv 2013. [Google Scholar]
- Cranmer, S.R. Suprathermal electrons in the solar corona: Can nonlocal transport explain heliospheric charge states? Astrophys. J. Lett. 2014. [Google Scholar] [CrossRef]
- Xiao, F.; Shen, C.; Wang, Y.; Zheng, H.; Whang, S. Energetic electron distributions fitted with a kappa-type function at geosynchronous orbit. J. Geophys. Res. 2008. [Google Scholar] [CrossRef]
- Laming, J.M.; Moses, J.D.; Ko, Y.K.; Ng, C.K.; Rakowski, C.E.; Tylka, A.J. On the remote detection of suprathermal ions in the solar corona and their role as seeds for solar energetic particle production. Astrophys. J. 2013, 770, 73. [Google Scholar] [CrossRef]
- Chotoo, K.; Schwadron, N.A.; Mason, G.M.; Zurbuchen, T.H.; Gloeckler, G.; Posner, A.; Fisk, L.A.; Galvin, A.B.; Hamilton, D.C.; Collier, M.R. The suprathermal seed population for corotaing interaction region ions at 1AU deduced from composition and spectra of H+, He++, and He+ observed by Wind. J. Geophys. Res. 2000, 105, 23107–23122. [Google Scholar] [CrossRef]
- Mann, G.; Warmuth, A.; Aurass, H. Generation of highly energetic electrons at reconnection outflow shocks during solar flares. Astron. Astrophys. 2009, 494, 669–675. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Evidence of large scale phase space quantization in plasmas. Entropy 2013, 15, 1118–1132. [Google Scholar] [CrossRef]
- Bian, N.; Emslie, G.A.; Stackhouse, D.J.; Kontar, E.P. The formation of a kappa-distribution accelerated electron populations in solar flares. Astrophys. J. 2014, 796, 142. [Google Scholar] [CrossRef]
- Jeffrey, N.L.S.; Fletcher, L.; Labrosse, N. First evidence of non-Gaussian solar flare EUV spectral line profiles and accelerated non-thermal ion motion. Astron. Astrophys. 2016, 590, 99. [Google Scholar] [CrossRef]
- Formisano, V.; Moreno, G.; Palmiotto, F.; Hedgecock, P.C. Solar Wind Interaction with the Earth’s Magnetic Field 1. Magnetosheath. J. Geophys. Res. 1973, 78, 3714–3730. [Google Scholar] [CrossRef]
- Ogasawara, K.; Angelopoulos, V.; Dayeh, M.A.; Fuselier, S.A.; Livadiotis, G.; McComas, D.J.; McFadden, J.P. Characterizing the dayside magnetosheath using ENAs: IBEX and THEMIS observations. J. Geophys. Res. 2013, 118, 3126–3137. [Google Scholar] [CrossRef]
- Ogasawara, K.; Dayeh, M.A.; Funsten, H.O.; Fuselier, S.A.; Livadiotis, G.; McComas, D.J. Interplanetary magnetic field dependence of the suprathermal energetic neutral atoms originated in subsolar magnetopause. J. Geophys. Res. 2015, 120, 964–972. [Google Scholar] [CrossRef]
- Grabbe, C. Generation of broadband electrostatic waves in Earth’s magnetotail. Phys. Rev. Lett. 2000, 84, 3614. [Google Scholar] [CrossRef] [PubMed]
- Pisarenko, N.F.; Budnik, E.Y.; Ermolaev, Y.I.; Kirpichev, I.P.; Lutsenko, V.N.; Morozova, E.I.; Antonova, E.E. The ion differential spectra in outer boundary of the ring current: November 17, 1995 case study. J. Atm. Sol.-Terr. Phys. 2002, 64, 573–583. [Google Scholar] [CrossRef]
- Christon, S.P. A comparison of the Mercury and earth magnetospheres: electron measurements and substorm time scales. Icarus 1987, 71, 448–471. [Google Scholar] [CrossRef]
- Wang, C.-P.; Lyons, L.R.; Chen, M.W.; Wolf, R.A.; Toffoletto, F.R. Modeling the inner plasma sheet protons and magnetic field under enhanced convection. J. Geophys. Res. 2003, 108, 1074. [Google Scholar] [CrossRef]
- Kletzing, C.A.; Scudder, J.D.; Dors, E.E.; Curto, C. Auroral source region: Plasma properties of the high latitude plasma sheet. J. Geophys. Res. 2003, 108, 1360. [Google Scholar] [CrossRef]
- Ogasawara, K.; Livadiotis, G.; Grubbs, G.A.; Jahn, J.-M.; Michell, R.; Samara, M.; Sharber, J.R.; Winningham, J.D. Properties of suprathermal electrons associated with discrete auroral arcs. Geophys. Res. Lett. 2017, in press. [Google Scholar]
- Hapgood, M.; Perry, C.; Davies, J.; Denton, M. The role of suprathermal particle measurements in CrossScale studies of collisionless plasma processes. Planet. Space Sci. 2011, 59, 618–629. [Google Scholar] [CrossRef]
- Collier, M.R.; Hamilton, D.C. The relationship between kappa and temperature in the energetic ion spectra at Jupiter. Geophys. Res. Lett. 1995, 22, 303–306. [Google Scholar] [CrossRef]
- Mauk, B.H.; Mitchell, D.G.; McEntire, R.W.; Paranicas, C.P.; Roelof, E.C.; Williams, D.J.; Krimigis, S.M.; Lagg, A. Energetic ion characteristics and neutral gas interactions in Jupiter’s magnetosphere. J. Geophys. Res. 2004. [Google Scholar] [CrossRef]
- Dialynas, K.; Krimigis, S.M.; Mitchell, D.G.; Hamilton, D.C.; Krupp, N.; Brandt, P.C. Energetic ion spectral characteristics in the Saturnian magnetosphere using Cassini/MIMI measurements. J. Geophys. Res. 2009. [Google Scholar] [CrossRef]
- Livi, R.; Goldstein, J.; Burch, J.L.; Crary, F.; Rymer, A.M.; Mitchell, D.G.; Persoon, A.M. Multi-instrument analysis of plasma parameters in Saturn’s equatorial, inner magnetosphere using corrections for spacecraft potential and penetrating background radiation. J. Geophys. Res. 2014, 119, 3683. [Google Scholar] [CrossRef]
- Carbary, J.F.; Kane, M.; Mauk, B.H.; Krimigis, S.M. Using the kappa function to investigate hot plasma in the magnetospheres of the giant planets. J. Geophys. Res. 2014, 119, 8426–8447. [Google Scholar] [CrossRef]
- Mauk, B.H.; Krimigis, S.M.; Keath, E.P.; Cheng, A.F.; Armstrong, T.P.; Lanzerotti, L.G.; Gloeckler, G.; Hamilton, D.C. The hot plasma and radiation environment of the Uranian magnetosphere. J. Geophys. Res. 1987, 92, 15283–15308. [Google Scholar] [CrossRef]
- Krimigis, S.M.; Armstrong, T.P.; Axford, W.I.; Bostrom, C.O.; Cheng, A.F.; Gloeckler, G.; Hamilton, D.C.; Keath, E.P.; Lanzerotri, L.J.; Mauk, B.H.; et al. Hot plasma and energetic particles in Neptune’s magnetosphere. Science 1989, 246, 1483. [Google Scholar] [CrossRef] [PubMed]
- Moncuquet, M.; Bagenal, F.; Meyer-Vernet, N. Latitudinal structure of the outer Io plasma torus. J. Geophys. Res. 2002, 108, 1260. [Google Scholar] [CrossRef]
- Jurac, S.; McGrath, M.A.; Johnson, R.E.; Richardson, J.D.; Vasyliunas, V.M.; Eviatar, A. Saturn: Search for a missing water source. Geophys. Res. Lett. 2002, 29, 2172. [Google Scholar]
- Broiles, T.W.; Livadiotis, G.; Burch, J.L.; Chae, K.; Clark, G.; Cravens, T.E.; Davidson, R.; Eriksson, A.; Frahm, R.A.; Fuselier, S.A.; et al. Characterizing cometary electrons with kappa distributions. J. Geophys. Res. 2016, 121, 7407–7422. [Google Scholar] [CrossRef]
- Broiles, T.W.; Burch, J.L.; Chae, K.; Cravens, T.E.; Eriksson, A.; Fuselier, S.F.; Frahm, R.F.; Gasc, S.; Goldstein, R.; Henri, P.; et al. Statistical analysis of suprathermal electron drivers at 67P/Churyumov-Gerasimenko. Mon. Not. R. Astron. Soc. 2016, 462, 312–322. [Google Scholar] [CrossRef]
- Decker, R.B.; Krimigis, S.M. Voyager observations of low-energy ions during solar cycle 23. Adv. Space Res. 2003, 32, 597–602. [Google Scholar] [CrossRef]
- Decker, R.B.; Krimigis, S.M.; Roelof, E.C.; Hill, M.E.; Armstrong, T.P.; Gloeckler, G.; Hamilton, D.C.; Lanzerotti, L.J. Voyager 1 in the foreshock, termination shock, and heliosheath. Science 2005, 309, 2020–2024. [Google Scholar] [CrossRef] [PubMed]
- Heerikhuisen, J.; Pogorelov, N.V.; Florinski, V.; Zank, G.P.; le Roux, J.A. The effects of a 𝜅-distribution in the heliosheath on the global heliosphere and ENA flux at 1 AU. Astrophys. J. 2008, 682, 679–689. [Google Scholar] [CrossRef]
- Heerikhuisen, J.; Zirnstein, E.; Pogorelov, N. 𝜅-distributed protons in the solar wind and their charge-exchange coupling to energetic hydrogen. J. Geophys. Res. 2015, 120, 1516–1525. [Google Scholar] [CrossRef]
- Zank, G.P.; Heerikhuisen, J.; Pogorelov, N.V.; Burrows, R.; McComas, D.J. Microstructure of the heliospheric termination shock: implications for energetic neutral atom observations. Astrophys. J. 2010, 708, 1092. [Google Scholar] [CrossRef]
- Livadiotis, G. Lagrangian temperature: Derivation and physical meaning for systems described by kappa distributions. Entropy 2014, 16, 4290–4308. [Google Scholar] [CrossRef]
- Livadiotis, G. Curie law for systems described by kappa distributions. Europhys. Lett. 2016, 113, 10003. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Invariant kappa distribution in space plasmas out of equilibrium. Astrophys. J. 2011, 741, 88. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Non-equilibrium thermodynamic processes: Space plasmas and the inner heliosheath. Astrophys. J. 2012, 749, 11. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Dayeh, M.A.; Funsten, H.O.; Schwadron, N.A. First sky map of the inner heliosheath temperature using IBEX spectra. Astrophys. J. 2011, 734, 1. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Randol, M.B.; Funsten, H.O.; Möbius, E.S.; Schwadron, N.A.; Dayeh, M.A.; Zank, G.P.; Frisch, P.C. Pick-up ion distributions and their influence on ENA spectral curvature. Astrophys. J. 2012, 751, 64. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J.; Schwadron, N.A.; Funsten, H.O.; Fuselier, S.A. Pressure of the proton plasma in the inner heliosheath. Astrophys. J. 2013, 762, 134. [Google Scholar] [CrossRef]
- Fuselier, S.A.; Allegrini, F.; Bzowski, M.; Dayeh, M.A.; Desai, M.; Funsten, H.O.; Galli, A.; Heirtzler, D.; Janzen, P.; Kubiak, M.A.; et al. Low energy neutral atoms from the heliosheath. Astrophys. J. 2014, 784, 89. [Google Scholar] [CrossRef]
- Zirnstein, E.J.; McComas, D.J. Using kappa functions to characterize outer heliosphere proton distributions in the presence of charge-exchange. Astrophys. J. 2015, 815, 31. [Google Scholar] [CrossRef]
- Zank, G.P. Faltering steps into the galaxy: The boundary regions of the heliosphere. Ann. Rev. Astron. Astrophys. 2015, 53, 449–500. [Google Scholar] [CrossRef]
- Nicholls, D.C.; Dopita, M.A.; Sutherland, R.S. Resolving the electron temperature discrepancies in h ii regions and planetary nebulae: Κ-distributed electrons. Astrophys. J. 2012, 752, 148. [Google Scholar] [CrossRef]
- Nicholls, D.C.; Dopita, M.A.; Sutherland, R.S.; Kewley, L.J.; Palay, E. Measuring nebular temperatures: the effect of new collision strengths with equilibrium and κ-distributed electron energies. Astrophys. J. Supp. Ser. 2013, 207, 21. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.-W.; Zhang, B. HI free-bound emission of planetary nebulae with large abundance discrepancies: Two-component models versus κ-distributed electrons. Astrophys. J. 2014, 780, 93. [Google Scholar] [CrossRef]
- Raymond, J.C.; Winkler, P.F.; Blair, W.P.; Lee, J.-J.; Park, S. Non-Maxwellian Hα profiles in Tycho’s supernova remnant. Astrophys. J. 2010, 712, 901. [Google Scholar] [CrossRef]
- Milovanov, A.V.; Zelenyi, L.M. Functional background of the Tsallis entropy: “Coarse-grained” systems and “kappa” distribution functions. Nonlinear Process. Geophys. 2000, 7, 211–221. [Google Scholar] [CrossRef]
- Saito, S.; Forme, F.R.E.; Buchert, S.C.; Nozawa, S.; Fujii, R. Effects of a kappa distribution function of electrons on incoherent scatter spectra. Ann. Geophys. 2000, 18, 1216–1223. [Google Scholar] [CrossRef]
- Du, J. The nonextensive parameter and Tsallis distribution for self-gravitating systems. Europhys. Lett. 2004, 67, 893–899. [Google Scholar]
- Yoon, P.H.; Rhee, T.; Ryu, C.M. Self-consistent formation of electron κ distribution: 1. Theory. J. Geophys. Res. 2006, 111, 09106. [Google Scholar] [CrossRef]
- Raadu, M.A.; Shafiq, M. Test charge response for a dusty plasma with both grain size distribution and dynamical charging. Phys. Plasmas 2007, 14, 012105. [Google Scholar] [CrossRef]
- Livadiotis, G. Approach on Tsallis statistical interpretation of hydrogen-atom by adopting the generalized radial distribution function. J. Math. Chem. 2009, 45, 930–939. [Google Scholar] [CrossRef]
- Livadiotis, G. Kappa distribution in the presence of a potential energy. J. Geophys. Res. 2015, 120, 880–903. [Google Scholar] [CrossRef]
- Livadiotis, G. Kappa and q indices: Dependence on the degrees of freedom. Entropy 2015, 17, 2062–2081. [Google Scholar] [CrossRef]
- Tribeche, M.; Mayout, S.; Amour, R. Effect of ion suprathermality on arbitrary amplitude dust acoustic waves in a charge varying dusty plasma. Phys. Plasmas 2009, 16, 043706. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Measure of the departure of the q-metastable stationary states from equilibrium. Phys. Scr. 2010, 82, 035003. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Electrostatic shielding in plasmas and the physical meaning of the Debye length. J. Plasma Phys. 2014, 80, 341–378. [Google Scholar] [CrossRef]
- Baluku, T.K.; Hellberg, M.A.; Kourakis, I.; Saini, N.S. Dust ion acoustic solitons in a plasma with kappa-distributed electrons. Phys. Plasmas 2010, 17, 053702. [Google Scholar] [CrossRef]
- Le Roux, J.A.; Webb, G.M.; Shalchi, A.; Zank, G.P. A generalized nonlinear guiding center theory for the collisionless anomalous perpendicular diffusion of cosmic rays. Astrophys. J. 2010, 716, 671–692. [Google Scholar] [CrossRef]
- Eslami, P.; Mottaghizadeh, M.; Pakzad, H.R. Nonplanar dust acoustic solitary waves in dusty plasmas with ions and electrons following a q-nonextensive distribution. Phys. Plasmas 2011, 18, 102303. [Google Scholar] [CrossRef]
- Kourakis, I.; Sultana, S.; Hellberg, M.A. Dynamical characteristics of solitary waves, shocks and envelope modes in kappa-distributed non-thermal plasmas: An overview. Plasma Phys. Control. Fusion 2012, 54, 124001. [Google Scholar] [CrossRef]
- Randol, B.M.; Christian, E.R. Coupling of charged particles via Coulombic interactions: Numerical simulations and resultant kappa-like velocity space distribution functions. J. Geophys. Res. 2016, 121, 1907–1919. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Study of the temporal correlations in the magnitude time series before major earthquakes in Japan. J. Geophys. Res. 2014, 119, 9192–9206. [Google Scholar] [CrossRef]
- Nicolaou, G.; Livadiotis, G.; Moussas, X. Long term variability of the polytropic Index of solar wind protons at 1AU. Sol. Phys. 2014, 289, 1371–1378. [Google Scholar] [CrossRef]
- Fisk, L.A.; Gloeckler, G. The case for a common spectrum of particles accelerated in the heliosphere: Observations and theory. J. Geophys. Res. 2014, 119, 8733–8749. [Google Scholar] [CrossRef]
- Viñas, A.F.; Moya, P.S.; Navarro, R.E.; Valdivia, J.A.; Araneda, J.A.; Muñoz, V. Electromagnetic fluctuations of the whistler-cyclotron and firehose instabilities in a Maxwellian and Tsallis-kappa-like plasma. J. Geophys. Res. 2015, 120, 3307–3317. [Google Scholar] [CrossRef]
- Livadiotis, G. Shock strength in space and astrophysical plasmas. Astrophys. J. 2015, 809, 111. [Google Scholar] [CrossRef]
- Dos Santos, M.S.; Ziebell, L.F.; Gaelzer, R. Ion firehose instability in a dusty plasma considering product-bi-kappa distributions for the plasma particles. Phys. Plasmas 2016, 23, 013705. [Google Scholar] [CrossRef]
- Nicolaou, G.; Livadiotis, G. Misestimation of temperature when applying Maxwellian distributions to space plasmas described by kappa distributions. Astrophys. Space Sci. 2016. [Google Scholar] [CrossRef]
- Sarri, G.; Dieckmann, M.E.; Brown, C.R.D.; Cecchetti, C.A.; Hoarty, D.J. Observation and characterization of laser-driven phase space electron holes. Phys. Plasmas 2010. [Google Scholar] [CrossRef]
- Hammond, C.M.; Feldman, W.C.; Phillips, J.L.; Goldstein, B.E.; Balogh, A. Solar wind double ion beams and the heliospheric current sheet. J. Geophys. Res. 1996, 100, 7881–7889. [Google Scholar] [CrossRef]
- Treumann, R.A. Theory of superdiffusion for the magnetopause. Geophys. Res. Lett. 1997, 24, 1727–1730. [Google Scholar] [CrossRef]
- Leubner, M.P. A nonextensive entropy approach to kappa distributions. Astrophys. Space Sci. 2002, 282, 573–579. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Beyond kappa distributions: Exploiting Tsallis statistical mechanics in space plasmas. J. Geophys. Res. 2009. [Google Scholar] [CrossRef]
- Livadiotis, G. Statistical background and properties of kappa distributions in space plasmas. J. Geophys. Res. 2015, 120, 1607–1619. [Google Scholar] [CrossRef]
- Livadiotis, G. Kappa Distribution: Theory and Applications in Plasmas, 1st ed.; Elsevier: New York, NY, USA, 2017. [Google Scholar]
- Silva, R.; Plastino, A.R.; Lima, J.A.S. A Maxwellian path to the q-nonextensive velocity distribution function. Phys. Lett. A 1998, 249, 401–408. [Google Scholar] [CrossRef]
- Yamano, T. Some properties of q-logarithmic and q-exponential functions in Tsallis statistics. Phys. A Stat. Mech. Appl. 2002, 305, 486–496. [Google Scholar] [CrossRef]
- Beck, C.; Schlögl, F. Thermodynamics of Chaotic Systems; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Abe, S. Correlation induced by Tsallis’ nonextensivity. Phys. A Stat. Mech. Appl. 1999, 269, 403–409. [Google Scholar] [CrossRef]
- Abe, S. Heat and entropy in nonextensive thermodynamics: Transmutation from Tsallis theory to Renyi-entropy-based theory. Phys. A Stat. Mech. Appl. 2001, 300, 417–423. [Google Scholar] [CrossRef]
- Rama, S.K. Tsallis statistics: Averages and a physical interpretation of the Lagrange multiplier β. Phys. Lett. A 2000, 276, 103–108. [Google Scholar] [CrossRef]
- Tsallis, C.; Mendes, R.S.; Plastino, A.R. The role of constraints within generalized nonextensive statistics. Phys. A Stat. Mech. Appl. 1998, 261, 534–554. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Tsallis, C. Nonextensive Entropy: Interdisciplinary Applications; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Gibbs, J.W. Elementary Principles in Statistical Mechanics; Charles Scribner’s Sons: New York, NY, USA, 1902. [Google Scholar]
- Livadiotis, G. Non-Euclidean-normed statistical mechanics. Phys. A Stat. Mech. Appl. 2016, 445, 240–255. [Google Scholar] [CrossRef]
- Livadiotis, G. Modeling anisotropic Maxwell–Jüttner distributions: Derivation and properties. Ann. Geophys. 2016, 34, 1–14. [Google Scholar] [CrossRef]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Livadiotis, G. On the Simplification of Statistical Mechanics for Space Plasmas. Entropy 2017, 19, 285. https://doi.org/10.3390/e19060285
Livadiotis G. On the Simplification of Statistical Mechanics for Space Plasmas. Entropy. 2017; 19(6):285. https://doi.org/10.3390/e19060285
Chicago/Turabian StyleLivadiotis, George. 2017. "On the Simplification of Statistical Mechanics for Space Plasmas" Entropy 19, no. 6: 285. https://doi.org/10.3390/e19060285
APA StyleLivadiotis, G. (2017). On the Simplification of Statistical Mechanics for Space Plasmas. Entropy, 19(6), 285. https://doi.org/10.3390/e19060285



