1. Introduction
This article presents the results of the computation of the entropy generation rates occurring through the dissipation of ordered regions in the nonlinear time series solutions of the fluctuating spectral velocity wave vector equations for several helium boundary layer environments. These equations are cast in a Lorenz format and solved with the three-dimensional helium boundary layer profiles as input parameters. The computational procedures employed for these calculations have been presented previously in Isaacson [
1,
2]. This article follows closely the format of [
2], indicating the major mathematical equations used in the computational procedures. The purpose of this approach is to provide the reader the opportunity to follow the equations as they are presented, rather than requiring a continuous reference to previous literature.
The computational procedure used for the studies reported in [
1,
2] consists of two fundamental thermodynamic components. The first component, classified as the thermodynamic reservoir, is made up of the three-dimensional steady laminar boundary layer velocity profiles in the
x–y and the
z–y planes of the flow. This thermodynamic reservoir provides the steady state velocity gradients in the
x–y and the
z–y planes that serve as input control parameters for the second thermodynamic component, the time-dependent subsystem producing the nonlinear flow instabilities within the boundary layer. The second thermodynamic system, the time dependent subsystem, includes the set of equations describing the development of the spectral wave components and the set of coupled, nonlinear equations describing the development of the spectral velocity wave components with time. The set of equations describing the nonlinear time development of the spectral velocity wave components are cast into a Lorenz-type format that is sensitive to the initial conditions applied to the integration of the equations. The steady state boundary layer velocity gradients serve as control parameters for these equations and are determined by the particular value of the kinematic viscosity for the system. While the control parameters are obtained from the steady state boundary layer solutions, which are controlled by the kinematic viscosity, the initial conditions for the integration of the Lorenz-type equations are dependent upon the turbulence levels imposed on the system from the free stream. Walsh and Hernon [
3] have presented experimental measurements of the unsteady fluctuation levels in laminar boundary layers when subjected to free stream turbulence. These measurements indicate that the free stream turbulence level must be taken into account when computing the entropy generation rates in three-dimensional boundary layers. We have accounted for the free stream turbulence level by choosing the initial conditions applied to the time integration of the modified Lorenz equations for the nonlinear solutions for the spectral velocity wave components.
Isaacson [
1] presents computational results for the entropy generation rates through the dissipation of ordered regions in an air boundary layer with crosswind velocities at a temperature of 1068.0 K and a pressure of 0.912 × 10
5 N/m
2 at a normalize vertical location of
η = 3.00 (see Equation (5) for the definition of
η). The kinematic viscosity for air at these conditions is
ν = 1.51634 × 10
−4 m
2/s. Isaacson [
2] presents similar results for the laminar boundary-layer layer, also with a crosswind velocity, at a normalized vertical location of
η = 1.40, with the same value of kinematic viscosity.
The results presented in [
1,
2] also indicate that instabilities are produced for this value of kinematic viscosity at these two vertical locations for several stations along the stream wise laminar boundary layer development. Thus, the generation of these instabilities has the general configuration of the formation of turbulent spots within the three-dimensional boundary layer flow environment. Boiko et al. [
4] report the experimentally observed development of two turbulent spots measured within the boundary layer, thus validating the predicted general configuration of the instabilities as the development of turbulent spots.
It has been noted in [
1,
2] that instabilities are predicted for a narrow range of kinematic viscosities, namely, for
ν = 1.5 × 10
−4 m
2/s to
ν = 1.6 × 10
−4 m
2/s. The value of the kinematic viscosity applied to the solution of the steady three-dimensional boundary layer equations for the velocity gradient control parameters in the primary thermodynamic reservoir determines the values for these particular control parameters. It is thus of fundamental engineering interest that helium, with a very low density, has kinematic viscosities in this range over a considerable variety of temperatures and pressures. The values for the kinematic viscosities of helium for a selection of temperatures and pressures are given in
Table 1. We have applied our computational procedure to engineering flow systems that use helium in a three-dimensional flow configuration for this set of values of kinematic viscosity.
A significant component in Generation IV Nuclear Energy Systems is dependent on the further development of the Helium Brayton Cycle with Interstage Heating and Cooling [
5]. It is therefore prudent to explore areas of entropy production in helium flow systems with the objective of improving the overall thermal efficiencies of these systems.
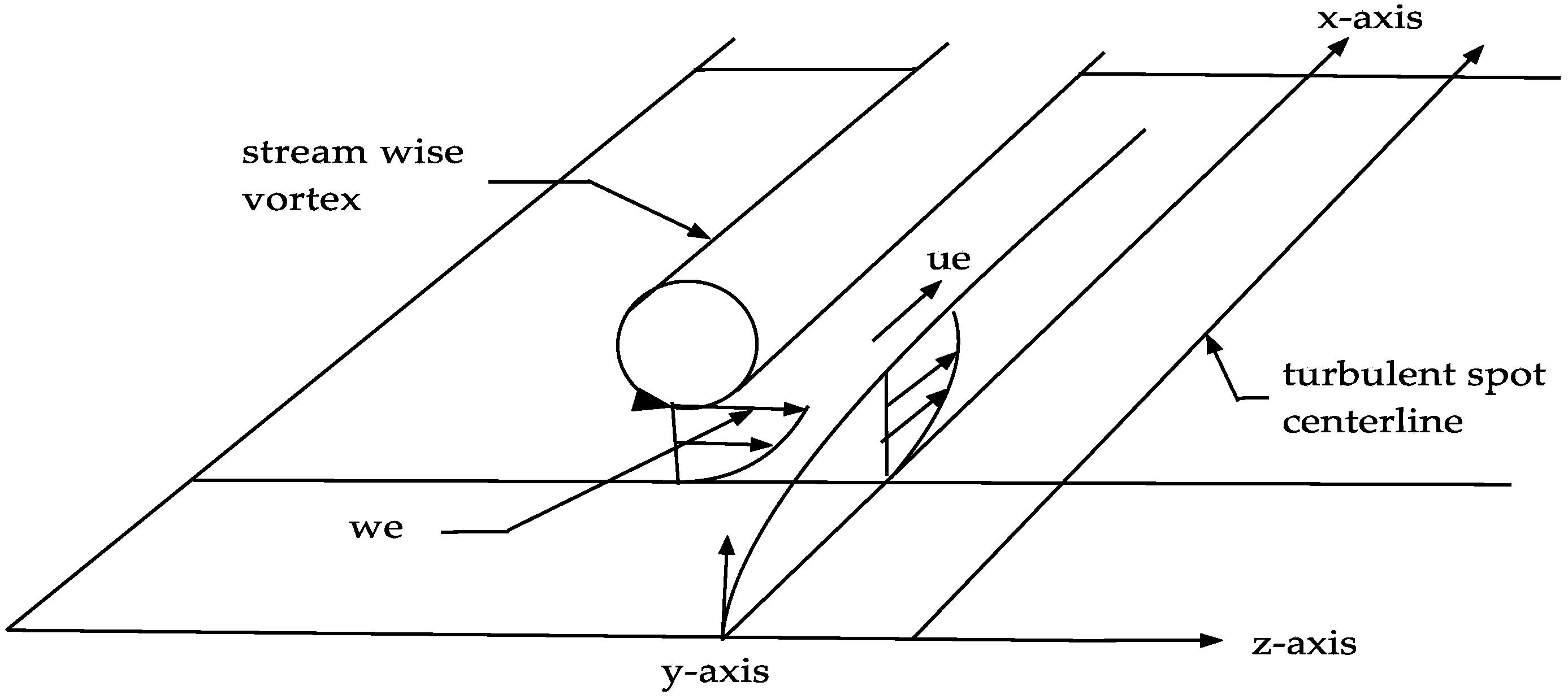
The flow configuration modeled in this study is that of the initial formation of a turbulent spot within the laminar flow as shown in
Figure 1. This configuration is discussed in detail in Schmid and Henningson [
6] and Belotserkovskii and Khlopkov [
7]. The flow consists essentially of two counter rotating stream wise vortices which meet at a point in the downstream direction, thus forming the shape of an arrow, with the tip pointing in the downstream direction. Between the two vortices, a stream wise laminar boundary layer is formed along the flow surface. We model only the left hand side configuration, consisting of a counter-clockwise rotating vortex interacting with the stream wise laminar boundary layer flow.
This article includes the following sections: in
Section 2, the thermodynamic and transport processes of the working substance required for the computational procedures are discussed. In this study, the working substance is the flow of a helium mixture at five sets of specified temperature and pressure. In
Section 3, the mathematical and computational bases for the evaluation of the steady three-dimensional boundary layer environment are reviewed. In
Section 4, the fluctuation equations of Townsend [
8] and Hellberg and Orszag [
9] are transformed into the spectral plane and written in the Lorenz format.
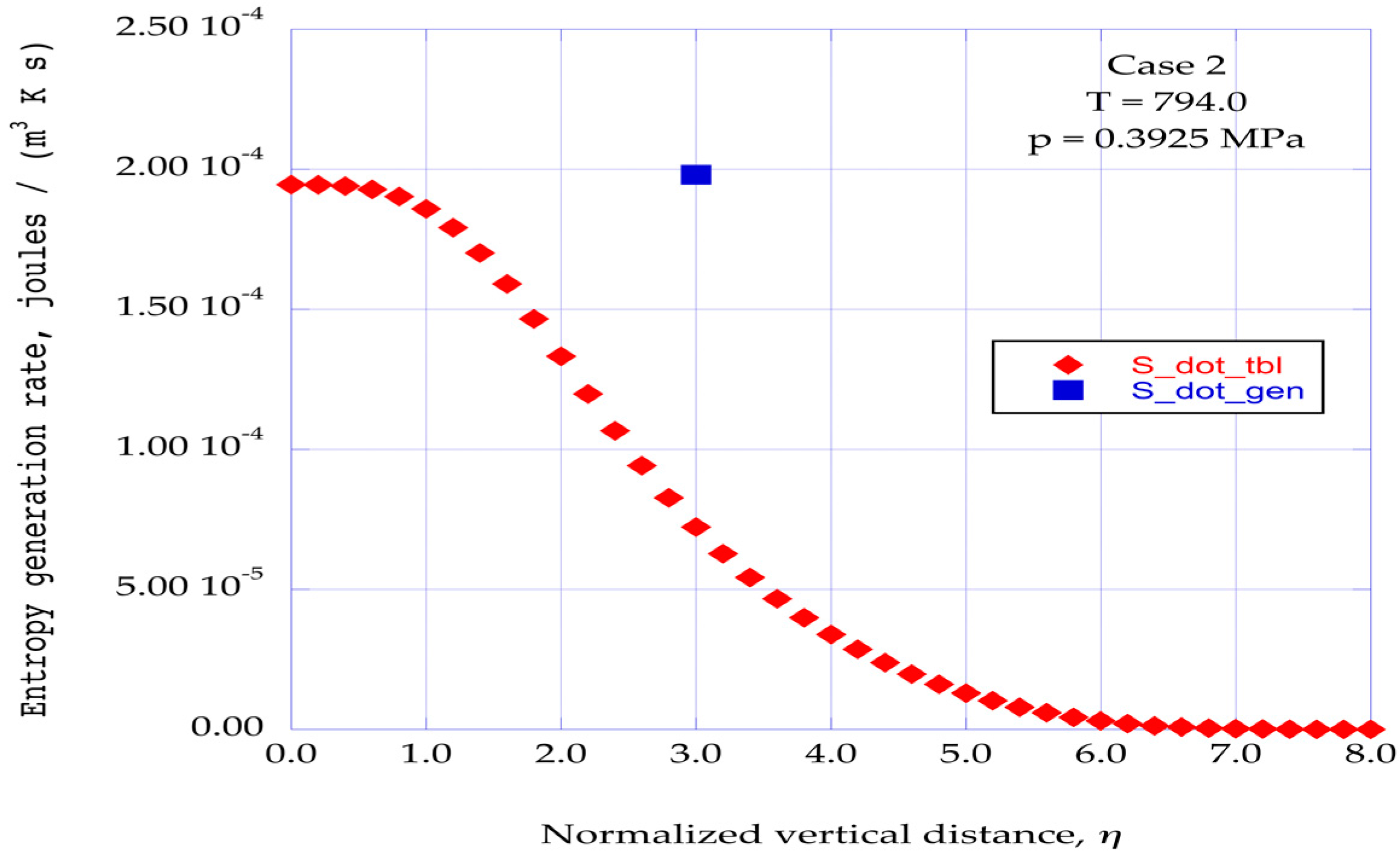
Section 5 presents computational results for the time-dependent spectral velocity components for a temperature of 794.0 K and a pressure of 0.3925 MPa.
Section 6 discusses the extraction of empirical entropies, empirical entropic indices, and intermittency exponents from the nonlinear time series solutions of the modified Lorenz equations.
Section 7 includes a comparison of the entropy generation rate for each of the five sets of temperature and pressure for the normalized vertical location of
η = 3.00 and the stream wise distance of
x = 0.120 with the entropy generated across a corresponding turbulent boundary layer. The article closes with a discussion of the results and final conclusions.
3. Steady-Flow Laminar Boundary-Layer Environment
This section presents a summary of the mathematical and computational methods used for the determination of the
x–y plane and the
z–y plane steady-state laminar boundary-layer velocity gradients. These boundary layer mean velocity gradients are time independent but vary with the stream wise distance
x. The boundary-layer mean velocity gradients serve as control parameters for the solution of the time-dependent fluctuating spectral velocity equations, yielding the initiation of instabilities within the boundary layer for each stream wise station, as summarized in
Section 4 of the article.
Singer [
10] has reported the results of the direct numerical simulation of the development of a young turbulent spot in an incompressible constant-pressure boundary layer in a flow stream with strong free stream turbulence. These studies indicate the development of a counter-clockwise stream wise vortex flow that produces a viscous laminar boundary layer in the
z–y plane of the flow environment as shown in
Figure 1. Ersoy and Walker [
11] discuss the development of this
z–y plane boundary layer produced by the interaction of the vortex tangential velocity with the flow surface. The stream wise flow along the flow surface in the central region of the turbulent spot produces a laminar boundary layer flow along the surface in the
x–y plane of the flow configuration, also shown in
Figure 1.
Cebeci and Bradshaw [
12] and Cebeci and Cousteix [
13] provide computer source code listings that we have used to compute the laminar boundary layer velocity profiles for both the
x–y plane and the
z–y plane. Hansen [
14] has shown that these orthogonal profiles are similar in nature and thus allow the simultaneous use of these profiles in our three-dimensional flow computations.
The steady three-dimensional boundary layer solutions are obtained for a sequence of stations along the
x-axis. These solutions provide the profiles of the respective steady state boundary layer velocity gradients. These steady boundary layer velocity gradients serve as control parameters for the solutions of both the spectral wave component equations and the fluctuating spectral velocity wave component equations.
Figure 2 shows a flow chart of the sequence of computational procedures from the solution of the steady boundary layer equations to the final computation of the entropy generation rates [
1]. Each of the computational procedures shown
Figure 2 is discussed in following sections.
There are three fundamental objectives in presenting the classical transformation of the boundary layer equations to the form employed for integration. First, the Falkner–Skan transformation method provides three, first-order, differential equations which are solved with the Keller–Cebeci Box method yielding the steady boundary-layer velocity profiles, either for a laminar boundary layer or a turbulent boundary layer. Second, these first-order equations are extended to the evaluation of the mean boundary-layer velocity gradients [
15] that serve as the control parameters for the time-dependent Lorenz-type equations for the computations of the instabilities produced by the interactions of the
z–y velocity gradients with the
x–y boundary layer gradients. The third objective is to obtain velocity gradient values for the laminar case of entropy generation rates from Equation (40) and turbulent velocity gradients for the prediction of the entropy generation rates in turbulent boundary layers from Equation (45).
The boundary-layer configuration considered in this article consists of a laminar boundary layer in the
x–y plane produced by the stream wise velocity along the horizontal surface and a laminar boundary layer in the
z–y plane produced by the vortex tangential edge velocity in the
z-direction. The momentum equation for the thin-shear boundary layer approximation may be written [
12] as:
The boundary conditions for Equation (1) are:
The Reynolds shear stress for the computation of turbulent boundary layers is modeled with the “eddy viscosity”,
εm, having the dimensions of (viscosity)/(density), by:
The computer program we have chosen to implement for the solution of the boundary layer equation (Equation (1)) is based on the Keller–Cebeci Box method presented by Cebeci and Bradshaw [
12] and Cebeci and Cousteix [
13]. One of the basic aspects of this method is to transform Equation (1) into a system of first-order ordinary differential equations. The Falkner–Skan transformation, in the form:
is introduced into the transformation process. The dimensionless stream function,
f(
x,η), is defined by
These definitions yield the results for the mean boundary layer velocities
u and
v as
Differentiation with respect to
η is indicated by the prime in these expressions.
From Bernoulli’s equation, the pressure gradient term is given by
. To simplify the resulting equations, the parameter
m is defined as:
Applying these transformations, the momentum equation for the boundary layer (Equation (1)) becomes:
with boundary conditions:
The computer solution procedures for this third-order differential equation, as developed by Cebeci and Bradshaw [
12], replace the third-order differential equation, Equation (9), with three first-order differential equations in the following fashion:
The corresponding boundary conditions for these equations are:
Note that in Equation (13),
v is not the
y-component velocity.
Cebeci and Bradshaw [
12] present computer program listings for the numerical solutions for both laminar and turbulent boundary layers over flat plate surfaces. The program listings used in the study reported here are those presented in [
12].
Hansen [
14] has indicated that orthogonal laminar boundary layer profiles in a three-dimensional coordinate system possess the characteristic of similarity. We therefore use the boundary layer computations for both the profiles in the
x–y plane and in the
z–y plane. The steady state boundary layer equations and the corresponding velocity gradients serve as the thermodynamic steady state reservoir that provides the control parameters for the time-dependent development of the spectral fluctuations within the boundary layer environment [
16].
6. Entropy Generation Rates through the Ordered Regions
From the concepts of non-equilibrium thermodynamics, de Groot and Mazur [
29].we write the equation for the entropy generation rate in an internal relaxation process as:
Here, s is the entropy per unit mass, μ is the mechanical potential for the transport of the ordered regions in an external context and J(x) is the flux of kinetic energy through the ordered regions available for dissipation into thermal internal energy.
The dissipation of the ordered regions into background thermal energy may be considered as a two-stage process from the transition of the ordered regions into equilibrium thermodynamic states and a relaxation process of the downstream velocity in the initial state to the final equilibrium state of the velocity over the internal distance
x. At the final equilibrium state, the dissipated ordered regions vanish into thermal equilibrium with the reservoir. The local boundary layer steady state velocity is written as
u = ue f′, where
f′ is the derivative of the Falkner–Skan stream function
f with respect to the normalized distance
η. The expression for the entropy generation rate (in joules/(m
3·K·s)) through the non-equilibrium ordered regions is then written as [
1]:
In this expression,
ρ is the density of the working substance, in this case the helium mixture at the given pressure and temperature for each case listed in
Table 1. The dissipation rate for each of the fluctuating spectral velocity components is included in Equation (40).
The kinetic energy in each spectral mode available for final dissipation into equilibrium internal energy is computed for each of the spectral peaks. The empirical entropy for each of the regions indicated by the spectral peaks is found from the singular value decomposition process applied to the given time series data segment. The connecting parameter, the empirical entropic index, is then extracted from the resulting value of the empirical entropy.
Glansdorff and Prigogine [
30] find that for the general evolution criterion for non-equilibrium processes,
dSempj/
dt < 0. When the Tsallis entropic index is negative, Mariz [
31] found that the empirical entropy change is also negative,
dSempj/
dt < 0. The results presented in
Figure 8 indicate that significant non-equilibrium regions exist within the specified time frame of the particular nonlinear time series solution. These regions may therefore be classified as ordered, non-equilibrium regions. Therefore, the significant negative nature for the extracted empirical entropic indices at the third station at
x = 0.120 is in agreement with both the Prigogine criterion and the Mariz results for the Tsallis entropic index. The ad hoc introduction of an empirical entropy index thus provides a representation of the nonlinear, non-equilibrium ordered regions in a significant way.
Given the absolute value of the empirical entropic index,
qj, the intermittency exponent, ζ
j for the mode,
j, is extracted from Equation (38) [
22] by the use of Brent’s method [
18].
For a comparison of these values for the entropy generation rates, the entropy generation rates within a turbulent boundary layer are computed for each given stream wise location. Moore and Moore [
32] give the entropy generation rate near the wall in a turbulent boundary layer as:
Introducing the skin friction coefficient as:
and applying the Falkner–Skan transformation (Equation (5)) to the velocity gradient, we may write:
The often-quoted expression for the skin friction coefficient for a turbulent boundary layer on a flat plate may be written as [
33]:
Substituting this expression for the skin friction coefficient into Equation (43) yields:
This expression is used to compute the entropy generation rates across a hypothetical turbulent boundary layer as a function of the normalized vertical distance
η along the horizontal surface of the turbulent spot. The computation of the turbulent boundary layer begins at the initial station
x = 0.02 with transition enforced at this location. Hence, the turbulent boundary layer for our calculations at the stream wise location
x = 0.120 is much smaller than for a naturally occurring transition further along the
x-direction. The distributions of the entropy generation rates across a flat plate turbulent boundary layer are also shown in
Figure 9,
Figure 10,
Figure 11,
Figure 12 and
Figure 13.
The contrast in the fundamental meaning of entropy generation rates between the two sets of data shown in these figure should be clarified. The entropy generation rates computed for the turbulent boundary layer use a well-established empirical relation for the turbulent skin friction coefficient (Equation (44)) and an empirical eddy viscosity expression for the computation of the mean turbulent velocity profiles across the boundary layer. These types of results are useful to the designer of thermal power equipment for the estimation of the loss in stagnation pressure due to turbulent irreversible boundary-layer processes within the system.
On the other hand, the computation of the entropy generation rates for the ordered regions (Equation (40)) proceeds from the identification of time-dependent instabilities within the laminar boundary layer due to nonlinear interactions with a vortex tangential velocity, through to the evaluation of the dissipation of energy within non-equilibrium ordered regions.
White [
33] has discussed the development of turbulent spots in the stream wise transition of the flow from the initial laminar state to the fully turbulent state. Belotserkovskii and Khlopkov [
7] discuss the application of Monte Carlo computational methods to predict the spread of these turbulent spots across the channel into fully turbulent flow. These methods should be applicable for the extension of the results addressed in this article to the fully developed turbulent flow region.
7. Discussion
A computational procedure made up of a steady state thermodynamic reservoir of three-dimensional boundary layer velocity gradients and an embedded time-dependent thermodynamic subsystem of coupled, nonlinear, modified Lorenz equations in the spectral plane has been applied to several helium boundary layer flows. The helium flow configuration considered is that of a turbulent spot, consisting of a counterclockwise vortex structure interacting with a stream wise laminar boundary layer profile. Computational results for entropy generation rates are presented for several different sets of temperature and pressure applicable to the flow of helium in the Helium Brayton Cycle with Interstage Heating and Cooling. This power cycle is a part of the development of Generation IV Nuclear Energy Systems.
The counter clockwise rotating stream wise vortex structure creates a viscous boundary layer along the
z–y plane of the flow configuration. This viscous boundary layer is orthogonal to the laminar boundary layer in the
x–y plane in the stream wise direction. It is shown that this nonlinear interaction creates instabilities within the three-dimensional flow configuration. These instabilities are produced over several stations in the stream wise direction of the flow. The computations indicate that the initial instabilities grow in strength in the stream wise direction, reach a maximum, and then decrease over the remaining stations. This stream wise structure of the region of instabilities is in close agreement with the results reported by Singer [
10], obtained through the spatially developing direct numerical simulation of a young turbulent spot.
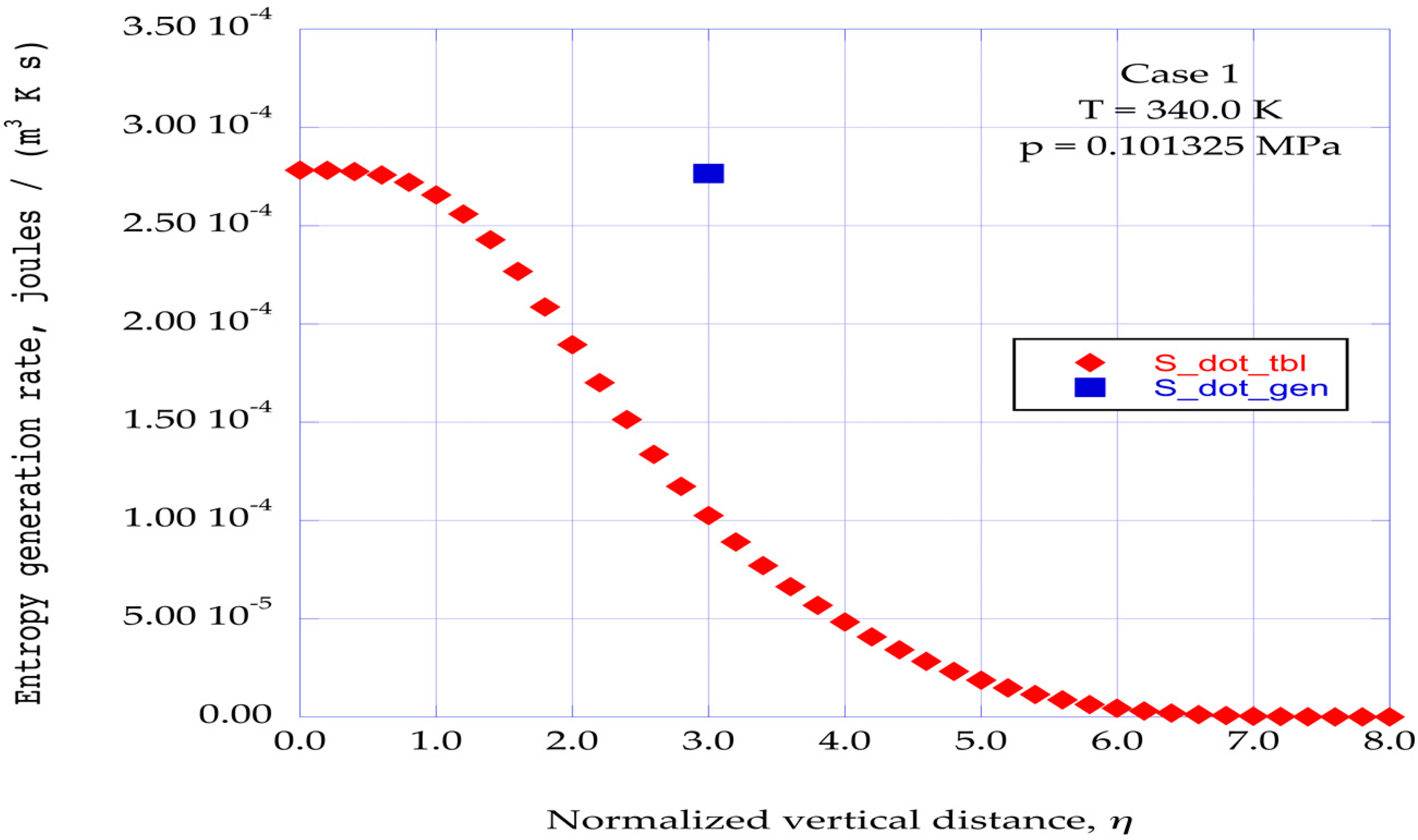
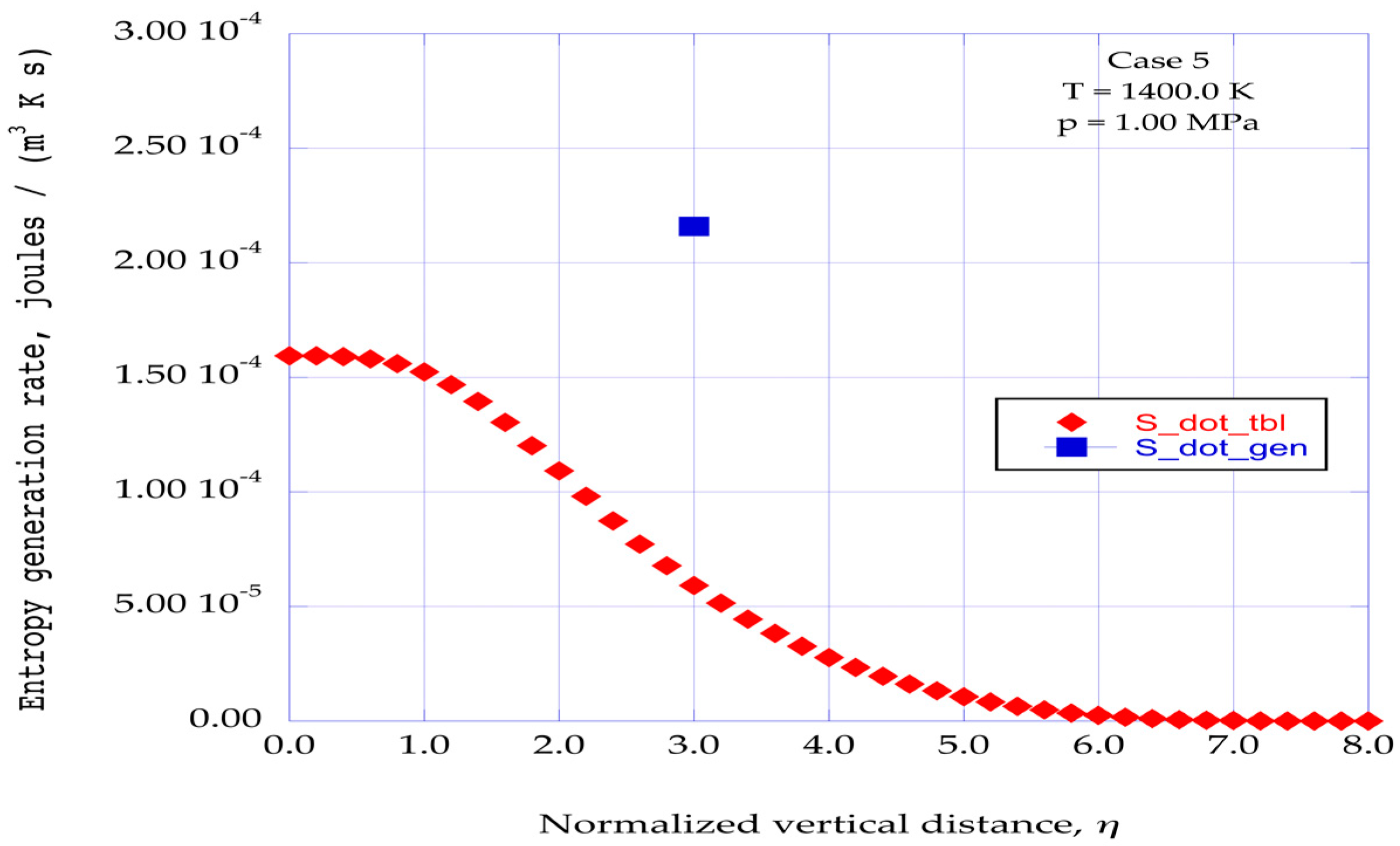
The computational results reported here for the entropy generation rates for several helium boundary layer flows are obtained at the stream wise location where the intensity of the predicted instabilities is most intense, namely, x = 0.120, in the range of instability locations from x = 0.06 to x = 0.18, for the normalized vertical station of η = 3.00.
Fluctuating spectral velocity components are found within the three spectral velocity component time-series solutions for the modified Lorenz equations. Statistical processing of the solutions indicates the presence of ordered regions embedded within the nonlinear time-series solutions. The dissipation of these ordered regions into equilibrium thermodynamic states yields the entropy generation rates for the helium turbulent spot environment. Significant entropy generation rates are predicted for the specified helium flow environments.
The sensitivity to initial conditions of the Lorenz format spectral velocity equations may provide a means of connecting the incorporation of these time dependent spectral equations in the computational procedure with the concept of receptivity of the boundary layer flow to outside disturbances.
To gain a perspective on the magnitude of the predicted rates of entropy generation through the transition of ordered regions, a comparison is made with the rates of entropy generation in a flat plate turbulent boundary layer for the same given flow conditions. The distribution of the entropy generation rates across a turbulent boundary layer at the distance of x = 0.120 is computed for a turbulent boundary layer initiated at x = 0.02 from the leading edge of the horizontal surface. The entropy generation rates through the ordered regions at the normalized vertical distance of η = 3.0 are then compared with the turbulent boundary layer distributions for each of the given helium flow conditions.
White [
33] and Schlichting [
34] have discussed the development of turbulent spots in the stream wise transition of the flow from the initial laminar state to the fully turbulent state. Belotserkovskii and Khlopkov [
7] discuss the application of Monte Carlo simulation methods to predict the spread of turbulent spots across the channel into fully turbulent flow. The dynamic growth of the turbulent spots has been included in these simulation methods. These simulation methods appear to provide computational methods for the inclusion of the local entropy generation rates within the turbulent spots and thus evaluate the overall entropy generation rates for the fully develop turbulent flow. These methods should thus be applicable for the extension of the results presented in this article to the computational fluid dynamics of fully developed turbulent flow.