A Novel Distance Metric: Generalized Relative Entropy
Abstract
:1. Background
2. Related Work
3. Generalized Relative Entropy
3.1. Structure of Generalized Relative Entropy
3.2. Properties of Generalized Relative Entropy
4. Experiment
4.1. Model Predicting Nucleosome Positoning
4.2. Evaluations of the Equality of Predition
4.3. Results and Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Biaynicki-Birula, I.; Mycielski, J. Uncertainty relations for information entropy in wave mechanics. Commun. Math. Phys. 1975, 44, 129–132. [Google Scholar] [CrossRef]
- Uhlmann, A. Relative entropy and the Wigner-Yanase-Dyson-Lieb concavity in an interpolation theory. Commun. Math. Phys. 1977, 54, 21–32. [Google Scholar] [CrossRef]
- Shore, J.; Johnson, R. Axiomatic derivation of the principle of maximum entropy and the principle of minimum cross-entropy. IEEE Trans. Inf. Theory 1980, 26, 26–37. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Hyvärinen, A. New Approximations of Differential Entropy for Independent Component Analysis and Projection Pursuit. 1998. Available online: https://papers.nips.cc/paper/1408-new-approximations-of-differential-entropy-for-independent-component-analysis-and-projection-pursuit.pdf (accessed on 12 June 2017).
- Petersen, I.R.; James, M.R.; Dupuis, P. Minimax optimal control of stochastic uncertain systems with relative entropy constraints. IEEE Trans. Autom. Control 2000, 45, 398–412. [Google Scholar] [CrossRef]
- Kwak, N.; Choi, C.-H. Input feature selection by mutual information based on Parzen window. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1667–1671. [Google Scholar] [CrossRef]
- Pluim, J.P.W.; Maintz, J.B.A.; Viergever, M.A. Mutual-information-based registration of medical images: A survey. IEEE Trans. Med. Imaging 2003, 22, 986–1004. [Google Scholar] [CrossRef] [PubMed]
- Arif, M.; Ohtaki, Y.; Nagatomi, R.; Inooka, H. Estimation of the Effect of Cadence on Gait Stability in Young and Elderly People using Approximate Entropy Technique. Meas. Sci. Rev. 2004, 4, 29–40. [Google Scholar]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Krishnaveni, V.; Jayaraman, S.; Ramadoss, K. Application of Mutual Information based Least dependent Component Analysis (MILCA) for Removal of Ocular Artifacts from Electroencephalogram. Int. J. Biomed. Sci. 2006, 1, 63–74. [Google Scholar]
- Wolf, M.M.; Verstraete, F.; Hastings, M.B.; Cirac, J.I. Area laws in quantum systems: Mutual information and correlations. Phys. Rev. Lett. 2008, 100, 070502. [Google Scholar] [CrossRef] [PubMed]
- Baldwin, R.A. Use of Maximum Entropy Modeling in Wildlife Research. Entropy 2009, 11, 854–866. [Google Scholar] [CrossRef]
- Verdu, S. Mismatched Estimation and Relative Entropy. IEEE Trans. Inf. Theory 2010, 56, 3712–3720. [Google Scholar] [CrossRef]
- Batina, L.; Gierlichs, B.; Prouff, E.; Rivain, M.; Standaert, F.X.; Veyrat-Charvillon, N. Mutual Information Analysis: A Comprehensive Study. J. Cryptol. 2011, 24, 269–291. [Google Scholar] [CrossRef]
- Audenaert, K.M.R. On the asymmetry of the relative entropy. J. Math. Phys. 2013, 54, 073506. [Google Scholar] [CrossRef]
- Gong, M.; Zhao, S.; Jiao, L.; Tian, D.; Wang, S. A Novel Coarse-to-Fine Scheme for Automatic Image Registration Based on SIFT and Mutual Information. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4328–4338. [Google Scholar] [CrossRef]
- Giagkiozis, I.; Purshouse, R.C.; Fleming, P.J. Generalized decomposition and cross entropy methods for many-objective optimization. Inf. Sci. 2014, 282, 363–387. [Google Scholar] [CrossRef]
- Tang, M.; Mao, X. Information Entropy-Based Metrics for Measuring Emergences in Artificial Societies. Entropy 2014, 16, 4583–4602. [Google Scholar] [CrossRef]
- De SÁ, C.R.; Soares, C.; Knobbe, A. Entropy-based discretization methods for ranking data. Inf. Sci. 2015, 329, 921–936. [Google Scholar] [CrossRef]
- Li, Z.; Gu, J.; Zhuang, H.; Kang, L.; Zhao, X.; Guo, Q. Adaptive molecular docking method based on information entropy genetic algorithm. Appl. Soft Comput. 2015, 26, 299–302. [Google Scholar] [CrossRef]
- Ma, C.W.; Wei, H.L.; Wang, S.S.; Ma, Y.G.; Wada, R.; Zhang, Y.L. Isobaric yield ratio difference and Shannon information entropy. Phys. Lett. B 2015, 742, 19–22. [Google Scholar] [CrossRef]
- König, R.; Renner, R.; Schaffner, C. The operational meaning of min- and max-entropy. IEEE Trans. Inf. Theory 2015, 55, 4337–4347. [Google Scholar] [CrossRef]
- Müller, M.P.; Pastena, M. A Generalization of Majorization that Characterizes Shannon Entropy. IEEE Trans. Inf. Theory 2016, 62, 1711–1720. [Google Scholar] [CrossRef]
- Zhang, X.; Mei, C.; Chen, D.; Li, J. Feature selection in mixed data: A method using a novel fuzzy rough set-based information entropy. Pattern Recognit. 2016, 56, 1–15. [Google Scholar] [CrossRef]
- Guariglia, E. Entropy and Fractal Antennas. Entropy 2016, 18, 84. [Google Scholar] [CrossRef]
- Ebrahimzadeh, A. Logical entropy of quantum dynamical systems. Open Phys. 2016, 14, 1–5. [Google Scholar] [CrossRef]
- Lopez-Garcia, P.; Onieva, E.; Osaba, E.; Masegosa, A.D.; Perallos, A. A Hybrid Method for Short-Term Traffic Congestion Forecasting Using Genetic Algorithms and Cross Entropy. IEEE Trans. Intell. Transp. Syst. 2016, 17, 557–569. [Google Scholar] [CrossRef]
- Sutter, D.; Tomamichel, M.; Harrow, A.W. Strengthened Monotonicity of Relative Entropy via Pinched Petz Recovery Map. IEEE Trans. Inf. Theory 2016, 62, 2907–2913. [Google Scholar] [CrossRef]
- Opper, M. An estimator for the relative entropy rate of path measures for stochastic differential equations. J. Comput. Phys. 2017, 330, 127–133. [Google Scholar] [CrossRef]
- Tang, L.; Lv, H.; Yu, L. An EEMD-based multi-scale fuzzy entropy approach for complexity analysis in clean energy markets. Appl. Soft Comput. 2017, 56, 124–133. [Google Scholar] [CrossRef]
- Guo, S.-H.; Deng, E.-Z.; Xu, L.-Q.; Ding, H.; Lin, H.; Chen, W.; Chou, K.-C. iNuc-PseKNC: A sequence-based predictor for predicting nucleosome positioning in genomes with pseudo k-tuple nucleotide composition. Bioinformatics 2014, 30, 1522–1529. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Feng, P.; Ding, H.; Lin, H.; Chou, K.-C. Using deformation energy to analyze nucleosome positioning in genomes. Genomics 2016, 107, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Awazu, A. Prediction of nucleosome positioning by the incorporation of frequencies and distributions of three different nucleotide segment lengths into a general pseudo k-tuple nucleotide composition. Bioinformatics 2017, 33, 42–48. [Google Scholar] [CrossRef] [PubMed]
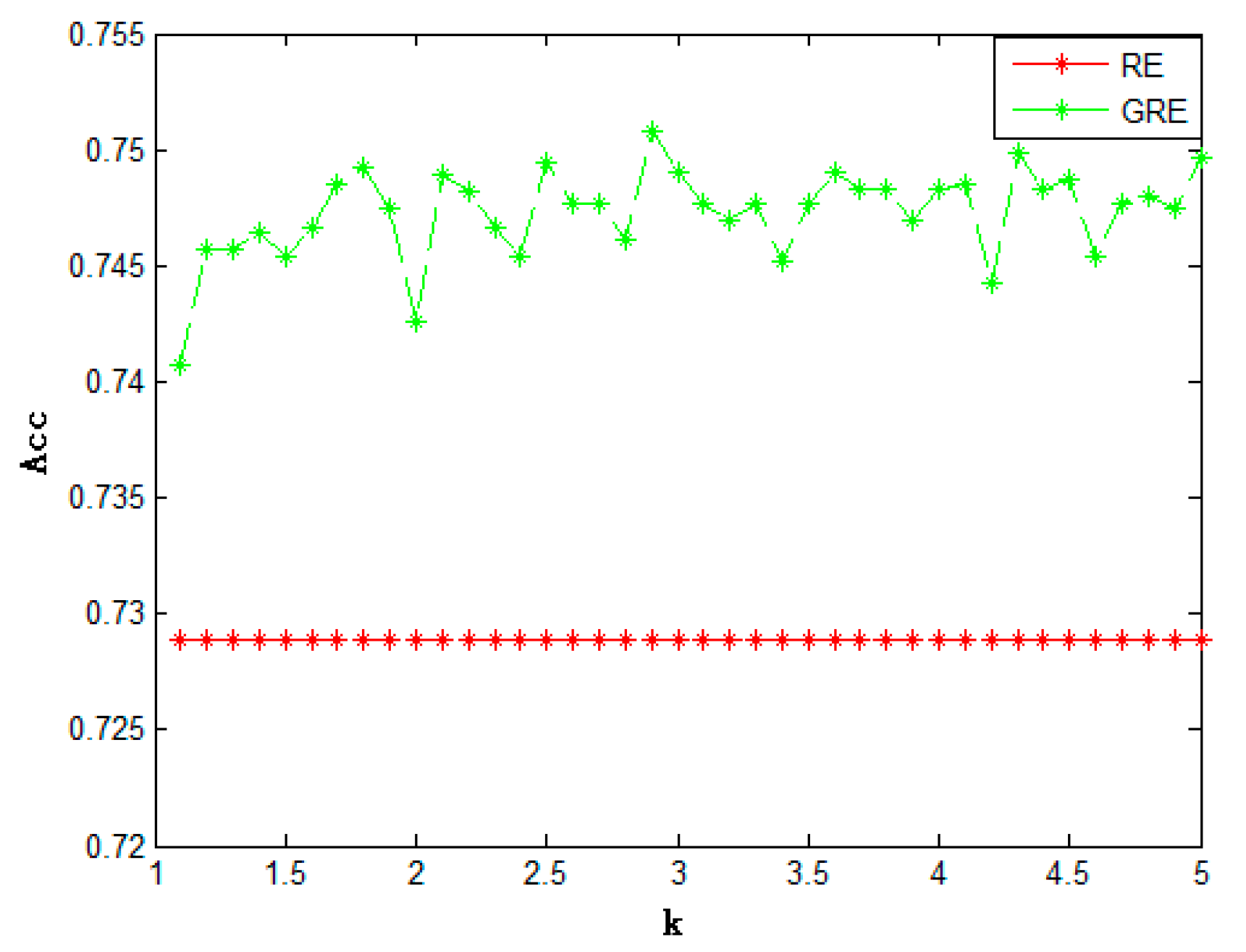
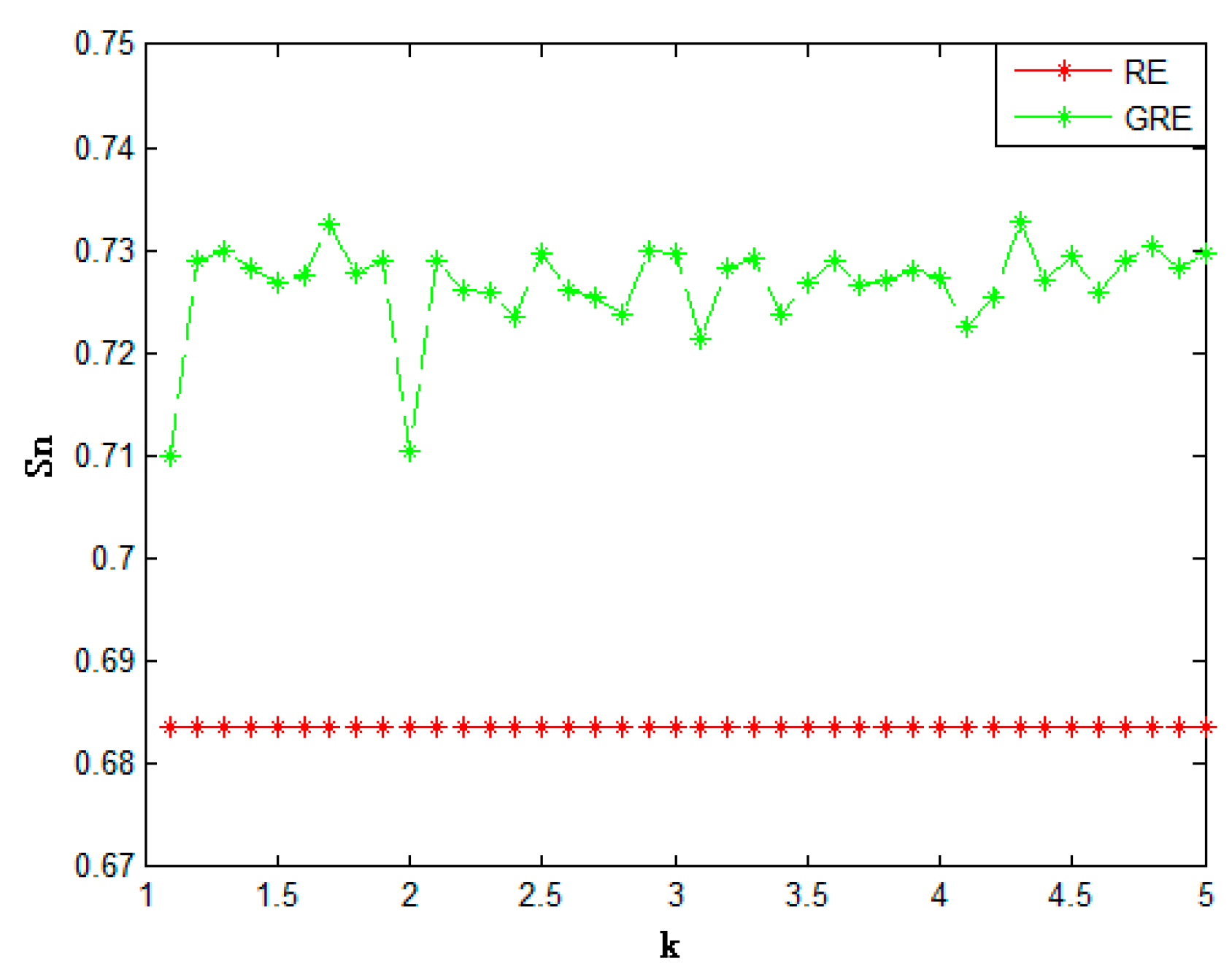
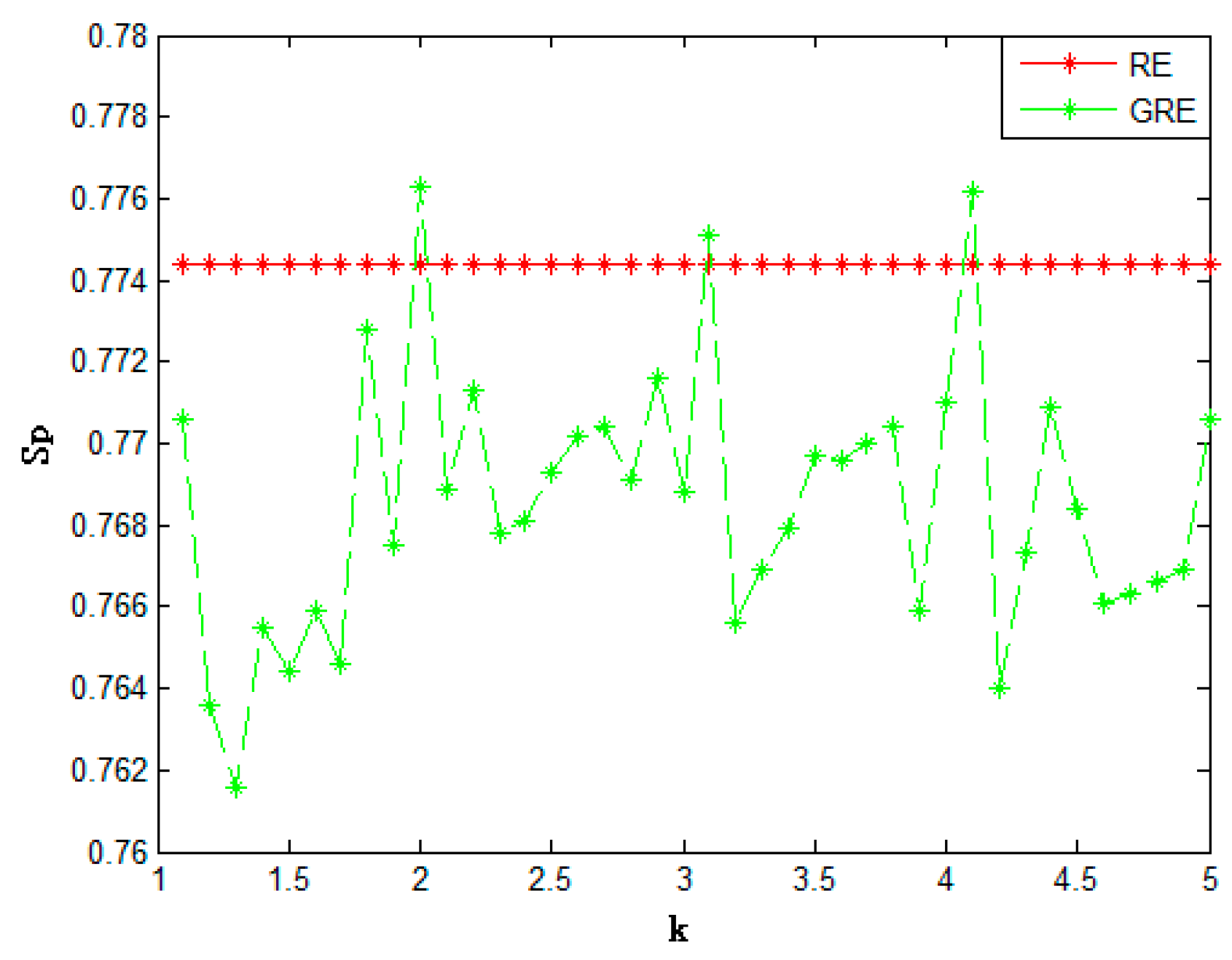
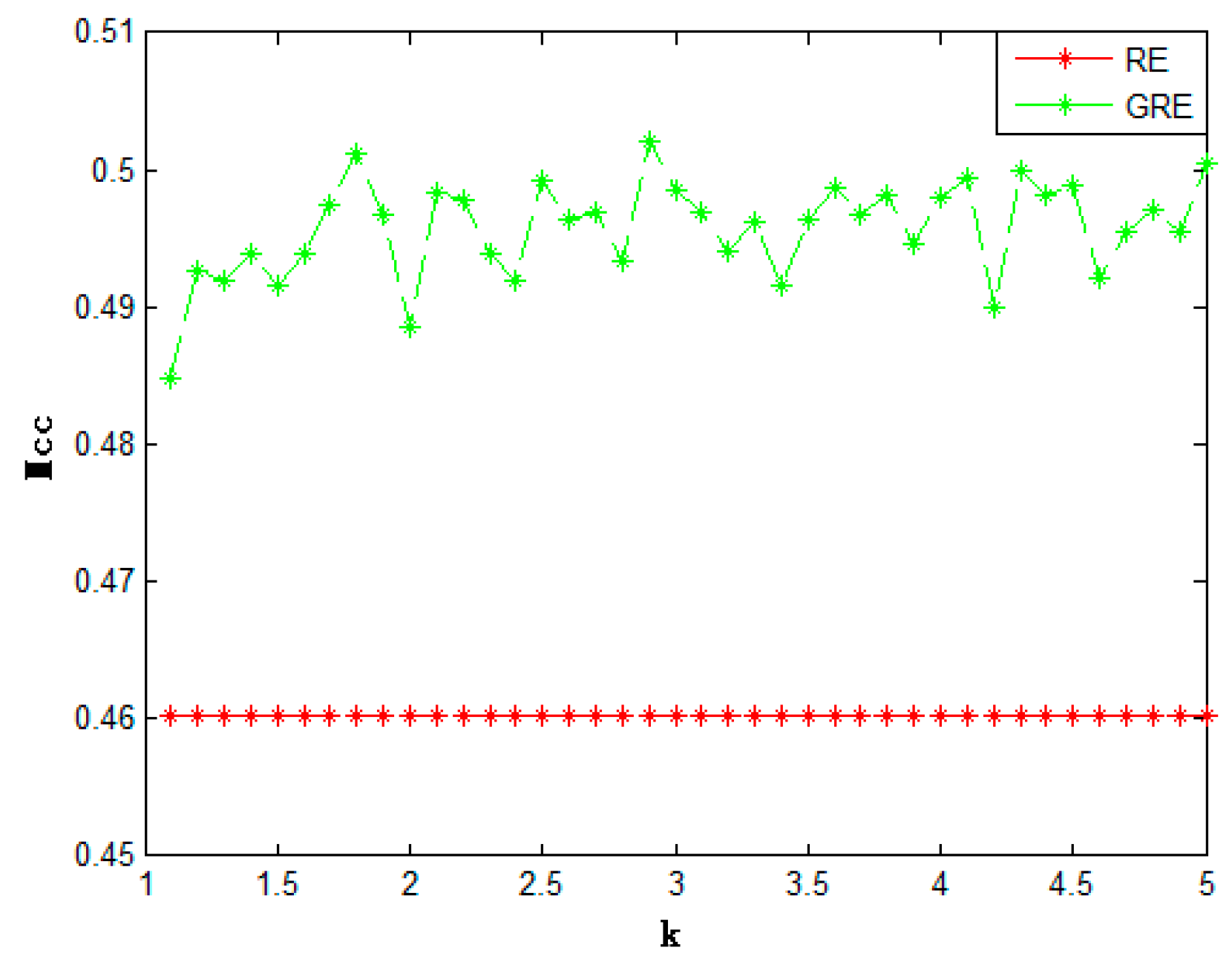
| Method | Acc | Sn | Sp | Mcc | |
|---|---|---|---|---|---|
| Relative entropy | 0.7289 | 0.6837 | 0.7744 | 0.4603 | |
| Generalized relative entropy | (k = 2) | 0.7426 | 0.7105 | 0.7763 | 0.4885 |
| (k = 3.1) | 0.7477 | 0.7215 | 0.7751 | 0.4970 | |
| (k = 4.1) | 0.7485 | 0.7225 | 0.7762 | 0.4994 | |
| Method | Acc | Sn | Sp | Mcc |
|---|---|---|---|---|
| Relative entropy | 0.9843 | 0.9875 | 0.9809 | 0.9684 |
| Generalized relative entropy (k = 2) | 0.9901 | 0.9937 | 0.9860 | 0.9801 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Lu, M.; Liu, G.; Pan, Z. A Novel Distance Metric: Generalized Relative Entropy. Entropy 2017, 19, 269. https://doi.org/10.3390/e19060269
Liu S, Lu M, Liu G, Pan Z. A Novel Distance Metric: Generalized Relative Entropy. Entropy. 2017; 19(6):269. https://doi.org/10.3390/e19060269
Chicago/Turabian StyleLiu, Shuai, Mengye Lu, Gaocheng Liu, and Zheng Pan. 2017. "A Novel Distance Metric: Generalized Relative Entropy" Entropy 19, no. 6: 269. https://doi.org/10.3390/e19060269
APA StyleLiu, S., Lu, M., Liu, G., & Pan, Z. (2017). A Novel Distance Metric: Generalized Relative Entropy. Entropy, 19(6), 269. https://doi.org/10.3390/e19060269




