Information Geometry of Non-Equilibrium Processes in a Bistable System with a Cubic Damping
Abstract
:1. Introduction
2. Models
- Forward Process (FP): : at , a unimodal PDF with a peak at , which evolves into a bimodal PDF with peaks at as ;
- Backward Process (BP): : at , a bimodal PDF with peaks at , which evolves into a unimodal PDF with a peak at as .
3. Time-Evolution of PDFs
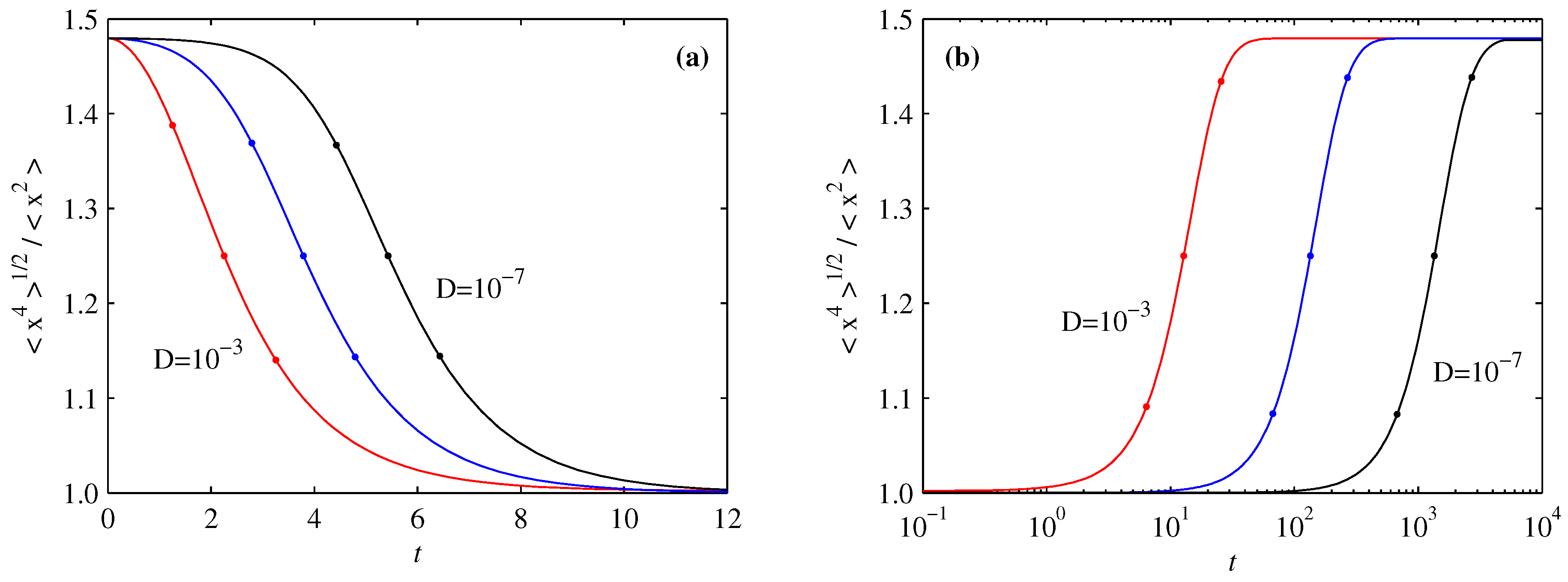
3.1. Overall Comparison of FP and BP
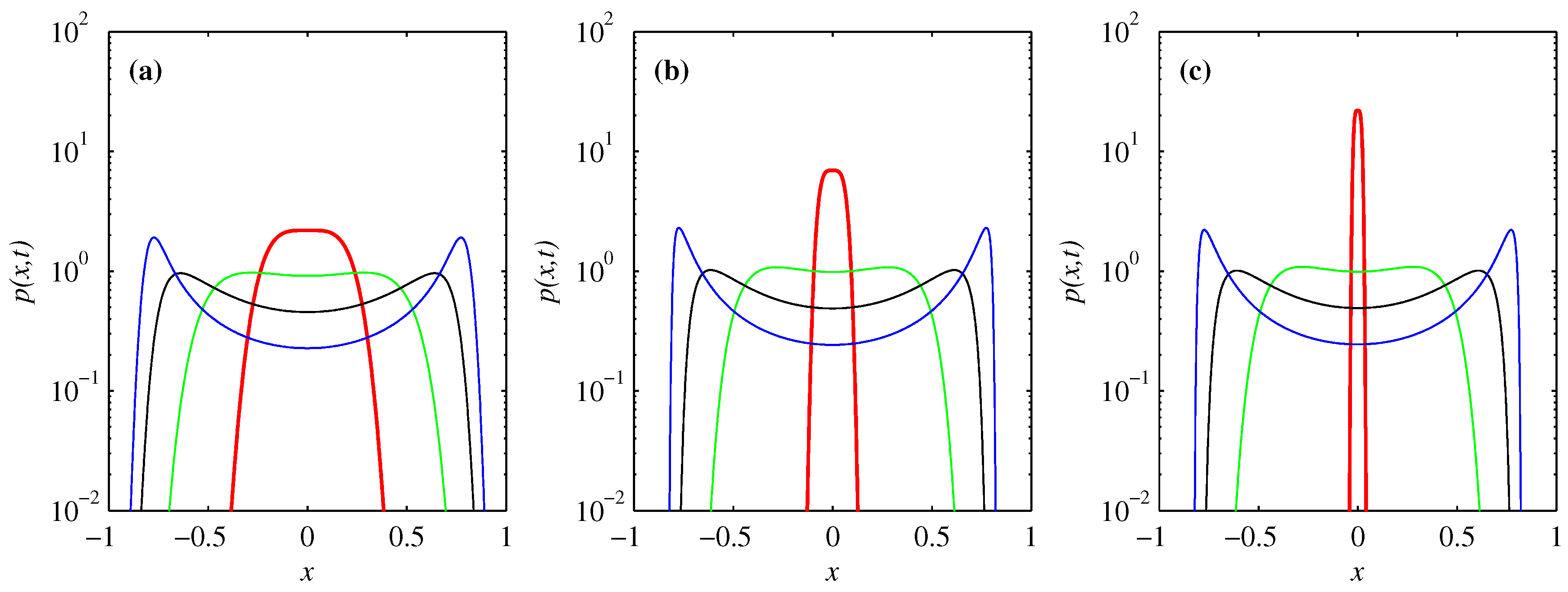
3.2. PDF of Forward Process
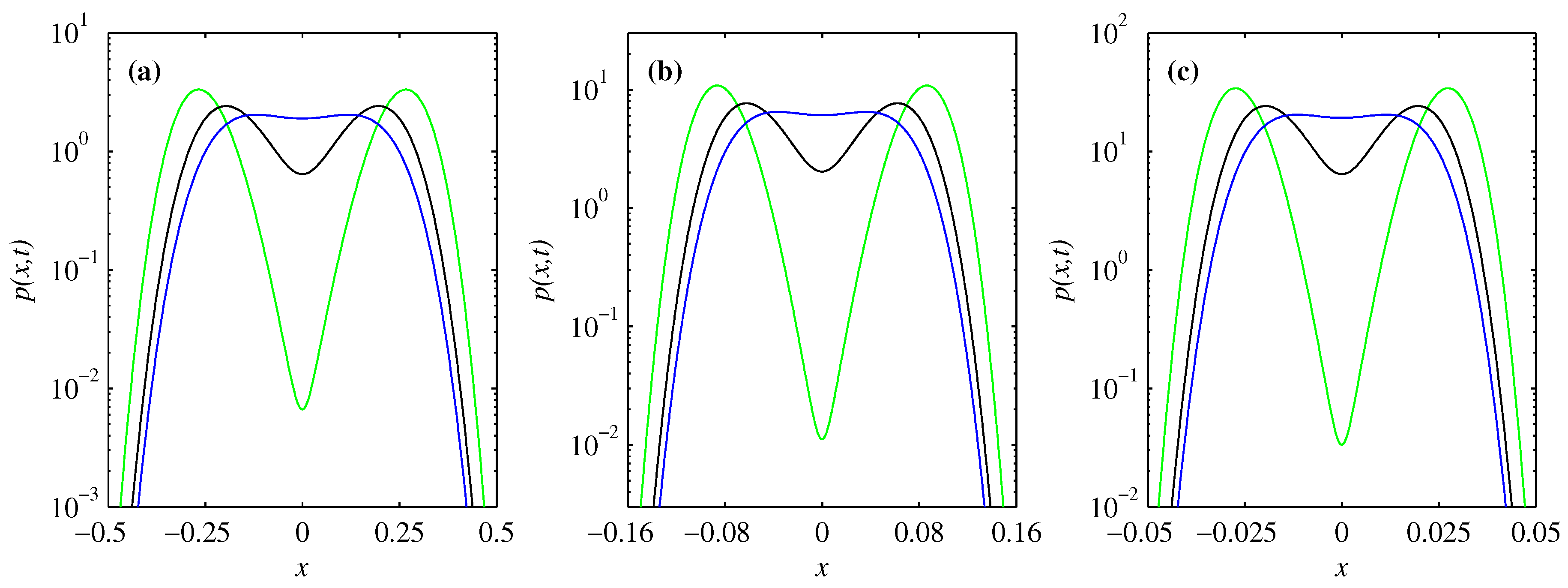
3.3. PDF of Backward Process
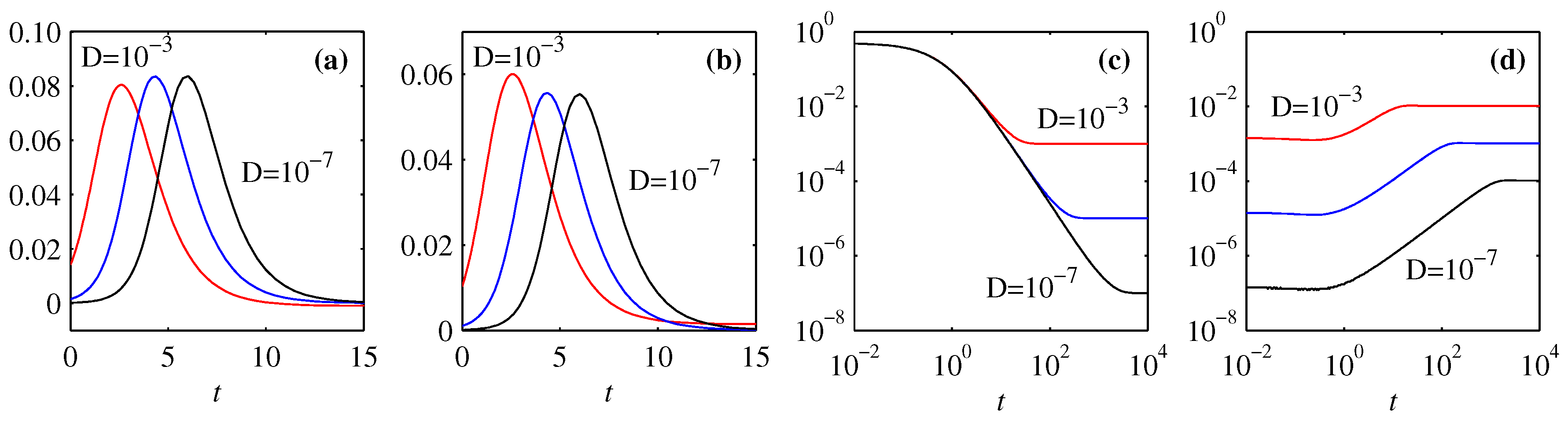
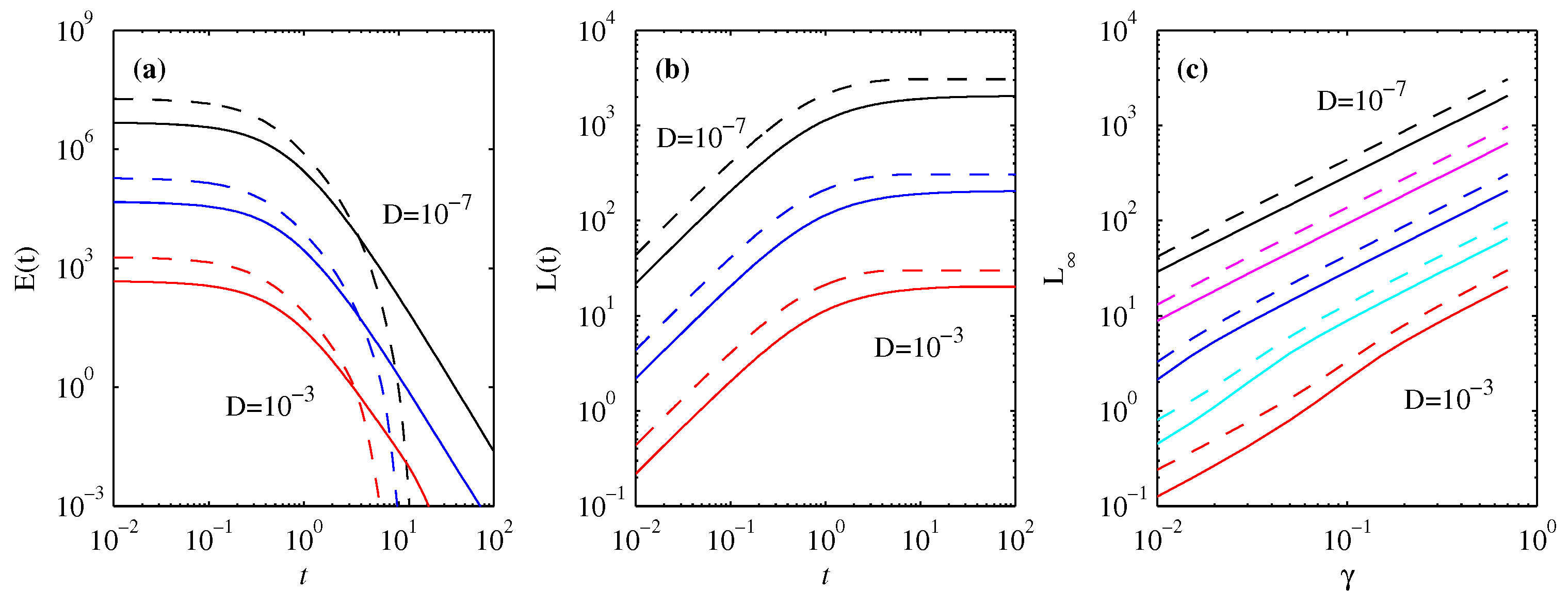
3.4. Energy Diagnostics
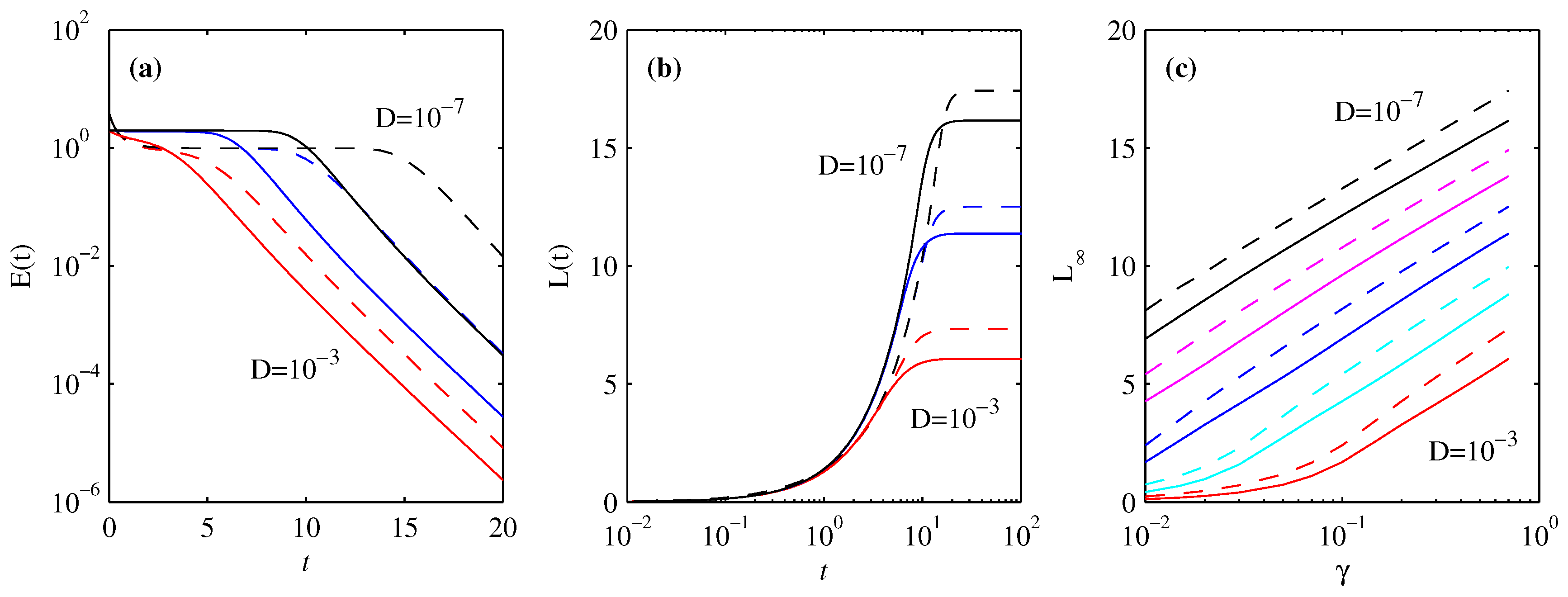
4. Information Length
4.1. Forward Process
4.2. Backward Process
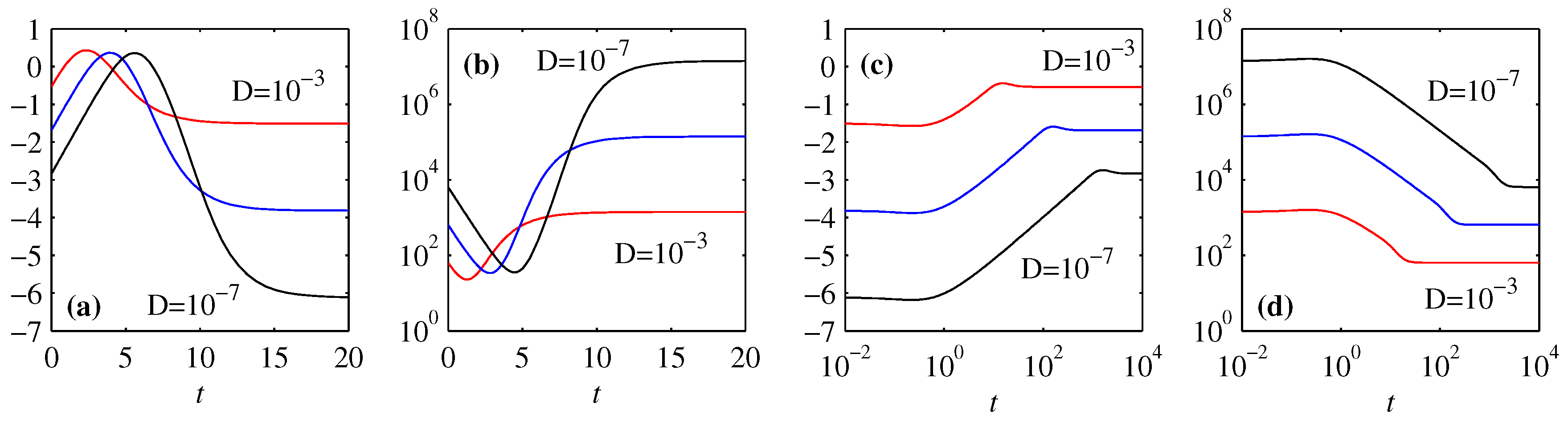
5. Differential Entropy and Fisher Information
6. Conclusions
Author Contributions
Conflicts of Interest
Appendix A. Relation between 𝓛 and Relative Entropy
Appendix B. Derivation of Equation (28)
Appendix C. Properties of the Sum of Two Gaussian PDFs
References
- Kibble, T.W.B. Some implications of a cosmological phase transition. Phys. Rep. 1980, 67, 183–199. [Google Scholar] [CrossRef]
- Nagashima, Y.; Nambu, Y. Elementary Particle Physics: Quantum Field Theory and Particles; Wiley-VCH: Weinheim, Germany, 2010. [Google Scholar]
- Mazenko, G. Theory of unstable growth. Phys. A 1994, 204, 437–449. [Google Scholar] [CrossRef]
- Longo, G.; Montévil, M. From physics to biology by extending criticality and symmetry breakings. Prog. Biophys. Mol. Biol. 2011, 106, 340–347. [Google Scholar] [CrossRef] [PubMed]
- Bossomaier, T.; Barnett, R.; Harré, M. Information and phase transitions in socio-economic systems. Complex Adapt. Syst. Model. 2013, 1, 9. [Google Scholar] [CrossRef]
- Haken, H. Information and Self-Organization: A Macroscopic Approach to Complex Systems; Springer: Berlin, Germany, 2006. [Google Scholar]
- Kim, E.; Diamond, P.H. Zonal flows and transient dynamics of the L-H transition. Phys. Rev. Lett. 2003, 90, 185006. [Google Scholar] [CrossRef] [PubMed]
- Kim, E. Consistent theory of turbulent transport in two-dimensional magnetohydrodynamics. Phys. Rev. Lett. 2006, 96, 084504. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, K.; Young, W.R. Zonostrophic instability. J. Atmos. Sci. 2012, 69, 1633–1656. [Google Scholar] [CrossRef]
- Sayanagi, K.M.; Showman, A.P.; Dowling, T.E. The emergence of multiple robust zonal jets from freely evolving, three-dimensional stratified geostrophic turbulence with applications to Jupiter. J. Atmos. Sci. 2008, 65, 12. [Google Scholar] [CrossRef]
- Kim, E.; Liu, H.; Anderson, J. Probability distribution function for self-organization of shear flows. Phys. Plasmas 2009, 16, 052304. [Google Scholar] [CrossRef]
- Newton, A.P.L.; Kim, E.; Liu, H.L. On the self-organizing process of large scale shear flows. Phys. Plasmas 2013, 20, 092306. [Google Scholar] [CrossRef]
- Tsuchiya, M.; Giuliani, A.; Hashimoto, M.; Erenpreisa, J.; Yoshikawa, K. Emergent self-organized criticality in gene expression dynamics: Temporal development of global phase transition revealed in a cancer cell line. PLoS ONE 2015, 10, e0128565. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Bak, P. Mean field theory of self-organized critical phenomena. J. Stat. Phys. 1988, 51, 797–802. [Google Scholar] [CrossRef]
- Jensen, H.J. Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Pruessner, G. Self-Organised Criticality; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Fauve, S.; Heslot, F. Stochastic resonance in a bistable system. Phys. Lett. A 1983, 97, 5–7. [Google Scholar] [CrossRef]
- Angeli, D.; Ferrell, J.E.; Sontag, E.D. Detection of multistability, bifurcations, and hysteresis in a large class of biological positive-feedback systems. Proc. Natl. Acad. Sci. USA 2004, 101, 1822–1827. [Google Scholar] [CrossRef] [PubMed]
- Holcman, D.; Tsodyks, M. The emergence of up and down states in cortical networks. PLoS Comp. Biol. 2006, 2, e23. [Google Scholar] [CrossRef] [PubMed]
- Mejias, J.F.; Kappen, H.J.; Torres, J.J. Irregular dynamics in up and down cortical states. PLoS ONE 2010, 5, e13651. [Google Scholar] [CrossRef] [PubMed]
- Hidalgo, J.; Seoane, L.F.; Cort́es, J.M.; Munoz, M.A. Stochastic amplification of fluctuations in cortical up-states. PLoS ONE 2012, 7, e40710. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, S. Tuning noise in gene expression. Mol. Syst. Biol. 2015, 11, 805. [Google Scholar] [CrossRef] [PubMed]
- Di Santo, S.; Burioni, R.; Vezzani, A.; Muñoz, M.A. Self-organized bistability associated with first-order phase transitions. Phys. Rev. Lett. 2016, 116, 240601. [Google Scholar] [CrossRef] [PubMed]
- Nicholson, S.B.; Kim, E. Investigation of the statistical distance to reach stationary distributions. Phys. Lett. A 2015, 379, 83–88. [Google Scholar] [CrossRef]
- Nicholson, S.B.; Kim, E. Entropy structures in sound: Analysis of classical music using the information length. Entropy 2016, 18, 258. [Google Scholar] [CrossRef]
- Heseltine, J.; Kim, E. Novel mapping in non-equilibrium stochastic processes. J. Phys. A 2016, 49, 175002. [Google Scholar] [CrossRef]
- Kim, E.; Lee, U.; Heseltine, J.; Hollerbach, R. Geometric structure and geodesic in a solvable model of nonequilibrium process. Phys. Rev. E 2016, 93, 062127. [Google Scholar] [CrossRef] [PubMed]
- Kim, E.; Hollerbach, R. Signature of nonlinear damping in geometric structure of a nonequilibrium process. Phys. Rev. E 2017, 95, 022137. [Google Scholar] [CrossRef] [PubMed]
- Gibbs, A.L.; Su, F.E. On choosing and bounding probability metrics. Int. Stat. Rev. 2002, 70, 419–435. [Google Scholar] [CrossRef]
- Wootters, W.K. Statistical distance and Hilbert space. Phys. Rev. D 1981, 23, 357–362. [Google Scholar] [CrossRef]
- Ruppeiner, G. Thermodynamics: A Riemannian geometric model. Phys. Rev. A 1979, 20, 1608–1613. [Google Scholar] [CrossRef]
- Schlögl, F. Thermodynamic metric and stochastic measures. Z. Phys. B Cond. Matt. 1985, 59, 449–454. [Google Scholar] [CrossRef]
- Feng, E.H.; Crooks, G.E. Far-from-equilibrium measurements of thermodynamic length. Phys. Rev. E 2009, 79, 012104. [Google Scholar] [CrossRef] [PubMed]
- Braunstein, S.L.; Caves, C.M. Statistical distance and the geometry of quantum states. Phys. Rev. Lett. 1994, 72, 3439–3443. [Google Scholar] [CrossRef] [PubMed]
- Strobel, H.; Muessel, W.; Linnemann, D.; Zibold, T.; Hume, D.B.; Pezzé, L.; Smerzi, A.; Oberthaler, M.K. Fisher information and entanglement of non-Gaussian spin states. Science 2014, 345, 424–427. [Google Scholar] [CrossRef] [PubMed]
- Nulton, J.; Salamon, P.; Andresen, B.; Anmin, Q. Quasistatic processes as step equilibrations. J. Chem. Phys. 1985, 83, 334–338. [Google Scholar] [CrossRef]
- Crooks, G.E. Measuring thermodynamic length. Phys. Rev. Lett. 2007, 99, 100602. [Google Scholar] [CrossRef] [PubMed]
- Sivak, D.A.; Crooks, G.E. Thermodynamic metrics and optimal paths. Phys. Rev. Lett. 2012, 8, 190602. [Google Scholar] [CrossRef] [PubMed]
- Salamon, P.; Nulton, J.D.; Siragusa, G.; Limon, A.; Bedeaus, D.; Kjelstrup, S. A simple example of control to minimize entropy production. J. Non-Equilib. Thermodyn. 2002, 27, 45–55. [Google Scholar] [CrossRef]
- Kim, E.; Hollerbach, R. Geometric structure and information change in phase transitions. Phys. Rev. E 2017, 95, 062107. [Google Scholar] [CrossRef]
- Bhattacharjee, J.K.; Meakin, P.; Scalapino, D.J. Nonequilibrium dynamics of N-component Ginzburg–Landau fields in zero and one dimension. Phys. Rev. A 1984, 30, 1026. [Google Scholar] [CrossRef]
- Kim, E.; Hollerbach, R. Time-dependent probability density function in cubic stochastic processes. Phys. Rev. E 2016, 94, 052118. [Google Scholar] [CrossRef] [PubMed]
- Klebaner, F. Introduction to Stochastic Calculus with Applications; Imperial College Press: London, UK, 2012. [Google Scholar]
- Risken, H. The Fokker–Planck Equation: Methods of Solution and Applications; Springer: Berlin, Germany, 1996. [Google Scholar]
- Suzuki, M. Scaling theory of transient phenomena near the instability point. J. Stat. Phys. 1977, 16, 11–32. [Google Scholar] [CrossRef]
- Caroli, B.; Caroli, C.; Roulet, B. Diffusion in a bistable potential: A systematic WKB treatment. J. Stat. Phys. 1979, 21, 415–437. [Google Scholar] [CrossRef]
- Suzuki, M. Theory of instability, nonlinear Brownian motion and formation of macroscopic order. Phys. Lett. A 1978, 67, 339–341. [Google Scholar] [CrossRef]
- Kubo, R.; Matsuo, K.; Kitahara, K. Fluctuation and relaxation of macrovariables. J. Stat. Phys. 1973, 9, 51–96. [Google Scholar] [CrossRef]
- Michalowicz, J.V.; Nichols, J.M.; Bucholtz, F. Calculation of differential entropy for a mixed Gaussian distribution. Entropy 2008, 10, 200–206. [Google Scholar] [CrossRef]
- Ferguson, M.L.; Le Coq, D.; Jules, M.; Aymerich, S.; Radulescue, O.; Declerck, N.; Royer, C.A. Reconciling molecular regulatory mechanisms with noise patterns of bacterial metabolic promoters in induced and repressed states. Proc. Natl. Acad. Sci. USA 2012, 109, 155–160. [Google Scholar] [CrossRef] [PubMed]
- Schuetz, R.; Zamboni, N.; Zampieri, M.; Heinemann, M.; Sauer, U. Multidimensional optimality of microbial metabolism. Science 2012, 336, 601–604. [Google Scholar] [CrossRef] [PubMed]
| Case | |||||
|---|---|---|---|---|---|
| FP | |||||
| BP | 0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hollerbach, R.; Kim, E.-j. Information Geometry of Non-Equilibrium Processes in a Bistable System with a Cubic Damping. Entropy 2017, 19, 268. https://doi.org/10.3390/e19060268
Hollerbach R, Kim E-j. Information Geometry of Non-Equilibrium Processes in a Bistable System with a Cubic Damping. Entropy. 2017; 19(6):268. https://doi.org/10.3390/e19060268
Chicago/Turabian StyleHollerbach, Rainer, and Eun-jin Kim. 2017. "Information Geometry of Non-Equilibrium Processes in a Bistable System with a Cubic Damping" Entropy 19, no. 6: 268. https://doi.org/10.3390/e19060268
APA StyleHollerbach, R., & Kim, E.-j. (2017). Information Geometry of Non-Equilibrium Processes in a Bistable System with a Cubic Damping. Entropy, 19(6), 268. https://doi.org/10.3390/e19060268







