Spurious Results of Fluctuation Analysis Techniques in Magnitude and Sign Correlations

Abstract

Fluctuation Analysis (FA) and specially Detrended Fluctuation Analysis (DFA) are techniques commonly used to quantify correlations and scaling properties of complex time series such as the observable outputs of great variety of dynamical systems, from Economics to Physiology. Often, such correlated time series are analyzed using the magnitude and sign decomposition, i.e., by using FA or DFA to study separately the sign and the magnitude series obtained from the original signal. This approach allows for distinguishing between systems with the same linear correlations but different dynamical properties. However, here we present analytical and numerical evidence showing that FA and DFA can lead to spurious results when applied to sign and magnitude series obtained from power-law correlated time series of fractional Gaussian noise (fGn) type. Specifically, we show that: (i) the autocorrelation functions of the sign and magnitude series obtained from fGns are always power-laws; However, (ii) when the sign series presents power-law anticorrelations, FA and DFA wrongly interpret the sign series as purely uncorrelated; Similarly, (iii) when analyzing power-law correlated magnitude (or volatility) series, FA and DFA fail to retrieve the real scaling properties, and identify the magnitude series as purely uncorrelated noise; Finally, (iv) using the relationship between FA and DFA and the autocorrelation function of the time series, we explain analytically the reason for the FA and DFA spurious results, which turns out to be an intrinsic property of both techniques when applied to sign and magnitude series.

1. Introduction

Since the observation of the Hurst effect [1] in the Nile river, a huge number of dynamical systems whose observable outputs are time series with complex long-range power-law correlations and scaling properties have been identified. The diversity of such time series include meteorological data, physiological signals such as heart rate, brain activity, gait or postural system, biological signals as DNA sequences, stock market activity, seismic signals and many others. In order to properly analyze this great variety of (possibly non-stationary) signals, several techniques were proposed. In this work, we consider two of them: Fluctuation Analysis (FA) [2] and Detrended Fluctuation Analysis (DFA) [3]. Both are based on similar grounds, and try to characterize the scaling properties of the fluctuations of a signal. In particular, DFA has probably become the standard method of choice when analyzing complex time series and it has been used in hundreds of scientific articles.

Often, given a non-stationary strongly correlated time series $\left\{Y_i\right\},i=1,2,\dots ,N$ i.e., of fractional Brownian motion type, its increment time series $\left\{x_i\right\}$ given by $x_i=Y_{i+1}-Y_i$ is more informative and can be easier to analyze than the original series itself. On the one hand, the dynamical properties of the increments can shed light on the underlying dynamics of the system. On the other hand, the increment series is very likely (quasi)stationary, i.e., of fractional Gaussian noise type. However, for nonlinear systems, it is worth going beyond the study of linear correlations since they do not account for all the dynamical properties of the systems. For example, increment time series with identical linear correlations may well correspond to systems with different nonlinear and multifractal behavior [4,5]. To overcome this problem and break the possible degeneration, the magnitude and sign decomposition method was proposed [4], consisting of studying separately the correlation properties of the magnitude and sign of the increment time series, typically using DFA or FA. The correlations in the magnitude series (termed volatility series in Economics contexts) are usually related to nonlinear correlations and multifractal properties [4,5,6,7]. Intuitively, the magnitude series carries the information on how big are the changes in the original signal. In contrast, the correlations in the sign series are uniquely determined by the linear correlations [4,6] and, from an intuitive point of view, the sign series provide the information of the direction of the changes of the original signal. The applications of the magnitude and sign decomposition method include heart rate analysis [8,9], fluid dynamics [10], geological [11,12], geophysical [13,14], and economical time series [15].

In this work, we use fractional Gaussian noises with different correlation strengths as a model for typical increment time series, apply to them the magnitude and sign decomposition method and study their correlations by using both FA and DFA. We obtain that, below a certain degree of the strength of the correlations (different for sign and magnitude series), FA and DFA interpret that the magnitude and sign series are purely uncorrelated. However, by studying analytically and numerically the corresponding autocorrelation functions, we show that, in all cases, the magnitude and sign series are power-law correlated, and therefore that FA and DFA provide spurious results. Finally, we explain the origin of these spurious results by obtaining analytically the FA and DFA scaling properties when applied to sign and magnitude series.

The paper is organized as follows: in Section 2, we introduce FA and DFA, and the analytical relationship between both techniques and the autocorrelation function is presented in Section 3. The magnitude and sign decomposition method is described in Section 4, and the results of FA and DFA when analyzing magnitude and sign series obtained from fractional Gaussian noises are presented in Section 5. In Section 6, we obtain the exact autocorrelation functions of the magnitude and sign series analyzed in Section 5 and show that the FA and DFA scaling results are spurious, and the reason for these results is analyzed in Section 7. Finally, we present our conclusions.

2. Fluctuation Analysis and Detrended Fluctuation Analysis

Let us consider a stationary time series $\left\{x_i\right\}$ ($i=1,2,...,N)$. The autocorrelation function $C\left(r\right)$ of $\left\{x_i\right\}$ can be calculated as

$$C\left(r\right)=\frac{\langle x_i{x}_{i+r}\rangle -{\langle x_i\rangle }^2}{{\sigma }^2},$$

(1)

where $\langle \dots \rangle$ denotes average over the whole time series, and ${\sigma }^2$ is the variance of the time series. Without loss of generality, in the following, we assume that $〈x_i〉=0$. When the time series $\left\{x_i\right\}$ is long-range power-law correlated, such as, for example, in fractional Gaussian noises (fGn), then its autocorrelation function, $C\left(r\right),$ behaves asymptotically as a power law of the lag r [16]:

$$C\left(r\right)\simeq \frac{H(2H-1)}{r^{2-2H}}\sim \frac{\mathrm{sign}(1-\gamma )}{r^{\gamma }},$$

(2)

where H is the well-known Hurst exponent with values in the range $H\in (0,1)$, and then the autocorrelation exponent $\gamma$ given by $\gamma =2-2H$, must be in the range $\gamma \in (0,2)$. For $\gamma <1$ ($H>0.5$), the correlations are positive, while for $\gamma >1$$(H<0.5),$ the time series is anticorrelated. Note that, for the special case $\gamma =1$ ($H=0.5$), the autocorrelation function vanishes, and the time series is uncorrelated (white noise behavior).

However, in many cases, the autocorrelation function is not convenient to determine the exponent $\gamma$, since $C\left(r\right)$ is noisy and very sensitive to the time series size N [16,17], and it is only properly estimated for large N, very often not available in real experiments. This is the reason motivating the use of indirect methods to quantify correlations and scaling, being paradigmatic examples Fluctuation Analysis and Detrended Fluctuation Analysis.

Fluctuation Analysis (FA) [2,18] is a technique aimed at calculating the scaling properties of the fluctuations of a given stationary signal. It works as follows: the time series is interpreted as the steps of a walk in a diffusion process, and then consider the “accumulated walk” $Y_j$ of the signal as

$$Y_j=\sum _{i=1}^j{x}_i.$$

(3)

The FA method tries to determine the averaged diffused distance in ℓ steps as the Mean Square Distance $F_{FA}\left(\ell \right)$ obtained as:

$$F_{FA}\left(\ell \right)=\sqrt{\langle {(Y_{i+\ell }-Y_i)}^2\rangle }.$$

(4)

Scaling is present when

$$F_{FA}\left(\ell \right)\sim {\ell }^{\alpha }.$$

(5)

Typically, $\alpha$ is estimated as the slope of a linear fitting of $\log \left(F_{FA}\left(\ell \right)\right)$ vs. $\log \left(\ell \right)$. The exponent $\alpha$ quantifies the strength of the correlations present in the time series. The exponents $\gamma$ and $\alpha$ are related via [19,20,21]

$$\gamma =2-2\alpha .$$

(6)

Then, for stationary correlated signals, $\alpha \in (0,1)$ and it coincides with the Hurst exponent H (Equation (2)). $\alpha =0.5$ indicates absence of correlations (white noise), $\alpha >0.5$ indicates positive power-law correlations which are stronger as $\alpha$ increases, and $\alpha <0.5$ indicates anticorrelations, stronger as $\alpha$ decreases.

Detrended Fluctuation Analysis was created [3] to solve some drawbacks of FA, especially the ones related to the presence of non-stationarities in the time series. The behavior of DFA when applied to signals with different characteristics (trends, nonlinear filters, etc.) has been intensively studied [22,23] and, since then, DFA has become one of the standard methods used to analyze complex time series in many scientific fields [15,24,25]. DFA works as follows: (i) calculate the “accumulated walk” $Y_j$ (3) of the analyzed time series $x_i$ of length N; (ii) divide the walk $Y_j$ into boxes of equal length ℓ (the scale of observation); (iii) In each box of length ℓ, calculate a linear fit of $Y_j$ to determine the linear trend within that box. The Y coordinate of the fit line in each box is denoted by $Y_{\ell ,j}$; (iv) the walk $Y_j$ is detrended by subtracting the local trend $Y_{\ell ,j}$ in each box of length ℓ; and (v) for a given box size ℓ, the root mean-square (r.m.s.) fluctuation for the detrended walk is calculated:

$$F_{DFA}\left(\ell \right)=\sqrt{\langle {(Y_j-Y_{\ell ,j})}^2\rangle };$$

(7)

and (vi) the above computation is repeated for a broad range of scales (box sizes ℓ) in order to provide a relationship between $F_{DFA}\left(\ell \right)$ and the scale ℓ. As in the case of FA, scaling is present when

$$F_{DFA}\left(\ell \right)\sim {\ell }^{\alpha }.$$

(8)

This equation is identical to Equation (5), and the exponent $\alpha$ is also the same and with the same interpretation as the one in Equation (5) when the analyzed signal is stationary and power-law correlated ($0<\alpha <1$), i.e., of fractional Gaussian noise type. However, DFA can be also applied to non-stationary long-range correlated signals of fractional Brownian motion type, and in this case, $1<\alpha <2$. For example, for the standard Brownian motion, $\alpha =3/2$.

In this work, we restrict ourselves to the case of stationary long-range correlated signals ($0<\alpha <1$), where both FA and DFA can be applied.

3. The Relationship of the Autocorrelation Function with FA and DFA

When the analyzed time series $\left\{x_i\right\}$ is stationary, then it is possible to obtain analytical equations relating the autocorrelation function $C\left(r\right)$ and the FA and DFA fluctuation functions $F_{FA}\left(\ell \right)$ and $F_{DFA}\left(\ell \right)$. In the case of FA, the calculation is simpler. Let us consider that $\left\{x_i\right\}$ has zero mean and variance ${\sigma }^2$. Starting from Equation (4), note first that

$$\langle {(Y_{i+\ell }-Y_i)}^2\rangle =\langle {(x_{i+1}+x_{i+2}+\dots +x_{i+\ell })}^2\rangle .$$

(9)

After expanding the square in the R.H.S. of Equation (9), we obtain

$$\langle {\left(\dots \right)}^2\rangle =〈\sum _{j=1}^{\ell }{x}_{i+j}^2+2\sum _{j=1}^{\ell -1}\sum _{k=j+1}^{\ell }{x}_{i+j}{x}_{i+k}〉,$$

and then, noting that the series is stationary with 0 mean and variance ${\sigma }^2$, we can evaluate the averages to get

$$F_{FA}^2\left(\ell \right)={\sigma }^2\left(\ell +2\sum _{r=1}^{\ell -1}(\ell -r)C\left(r\right)\right),$$

(10)

in agreement with [26].

For the case of DFA, the relationship between $F_{DFA}\left(\ell \right)$ and $C\left(r\right)$ is more complicated with an elaborated derivation recently obtained by Höll and Kantz [27]. The final result is

$$F_{DFA}^2\left(\ell \right)={\sigma }^2\left(W\left(\ell \right)+\sum _{r=1}^{\ell -1}L(\ell ,r)C\left(r\right)\right),$$

(11)

with

$$W\left(\ell \right)=\frac{{\ell }^2-4}{15\ell },$$

(12)

and

$$L(\ell ,r)=\frac{1}{15({\ell }^4-{\ell }^2)}\left[(3r^5+(-20{\ell }^2+5)r^3+30({\ell }^3-\ell )r^2+(-15{\ell }^4+35{\ell }^2-8)r+2{\ell }^5-10{\ell }^3+8\ell \right].$$

(13)

We note that, although expressed in a different manner as in Equation (11), the relation between $F_{DFA}^2\left(\ell \right)$ and $C\left(r\right)$ was also obtained by Talkner and Weber [28].

We end this section with two important remarks on Equations (10) and (11). First, the variance ${\sigma }^2$ of the time series $x_i$ appears as a multiplicative constant in both equations, and then from now on, we can consider without loss of generality that ${\sigma }^2=1$. Secondly, we want to stress that Equations (10) and (11) are exact results, and therefore independent of the particular behavior of the autocorrelation function $C\left(r\right)$ of $\left\{x_i\right\}$. Then, provided that $\left\{x_i\right\}$ is stationary, no matter whether the correlations are short- or long-ranged, positive or negative, power-law (with scaling) or exponentially decaying, etc., both equations hold.

4. Magnitude and Sign Decomposition. Volatility

As we mentioned above, the observable output of many complex systems, from heart rate to seismic signals, consists of time series with scaling properties. In many cases, such time series are non-stationary (of fractional Brownian motion type) and are originated as a consequence of the coupling of different underlying mechanisms. In order to shed light on the possible mechanisms responsible for the observed dynamics, the magnitude and sign decomposition method [4,6] is used. The method works as follows: given a non-stationary time series $\left\{Y_i\right\}$ ($i=1,\dots ,N+1$), first we obtain its increments time series $\left\{x_i\right\}$ as

$$x_i=Y_{i+1}-Y_i,i=1,2,\dots ,N.$$

(14)

Typically, the increment time series is stationary and approximately Gaussian, i.e., of fractional Gaussian noise type. Then, the increment time series is decomposed into the sign $\left\{s_i\right\}$ and the magnitude $\left\{m_i\right\}$ time series defined as:

$$\begin{array}{ccc}\hfill s_i& =& \mathrm{sign}\left(x_i\right),\hfill \\ \hfill m_i& =& |x_i|,i=1,2,\dots ,N.\hfill \end{array}$$

(15)

The sign series carries the information about the direction of the increments (positive or negative) and the magnitude time series, the information about the size of the increments, i.e., whether the increment is big or small. The utility of the magnitude and sign decomposition method is then the possibility of studying independently both types of information [4,5,6,7,8,10]. In addition, the correlations of the sign series is associated with the linear correlations of the original signal [4,6], and the sign series contains also important information related to the recurrence intervals of the original signal [29]. In addition, the correlations in the magnitude series are usually associated with nonlinear correlations and multifractal properties [4,5,6,7].

In the particular case of financial time series, which are strongly correlated and non-stationary, a convenient way to make stationary the time series consists of a logarithmic transformation. For example, let us consider a stock prize time series $\left\{P_i\right\}$, ($i=1,\dots ,N+1$), where the index i defines a time unit (minute, hour, day, etc.). For these series, instead of the increments of $\left\{P_i\right\}$, the returns time series $\left\{r_i\right\}$ is defined as [15]

$$r_i=\log \left(\frac{P_{i+1}}{P_i}\right)i=1,\dots ,N.$$

(16)

Typically, the return time series $\left\{r_i\right\}$ is correlated and approximately Gaussian with zero mean, and therefore of fractional Gaussian noise type. Then, in a similar way to Equation (15), one could analyze separately the sign and the magnitude series obtained from $\left\{r_i\right\}$. In economics, the magnitude of the returns time series $\left\{r_i\right\}$ is known as volatility [7,15] time series $\left\{v_i\right\}$, i.e.,

$$v_i=\left|r_i\right|,i=1,\dots ,N.$$

(17)

Then, in general, both the increment $\left\{x_i\right\}$ and the return $\left\{r_i\right\}$ time series are stationary and can be modeled to a first approximation by fractional Gaussian noises. Therefore, the correlation properties of their corresponding sign and magnitude (or volatility) [7] time series can be studied by decomposing fGns as in Equation (15). In the next section, we study the scaling properties of the sign and magnitude of fGns by applying FA and DFA.

5. Magnitude and Sign Study Using FA and DFA

Gaussian linear noises of fGn type can be generated using the Fourier Filtering Method (FFM) [30,31]. FFM works as follows: (i) generate a Gaussian white noise in the time domain $\left\{g_i\right\}$; (ii) Fourier-transform $\left\{g_i\right\}$ to obtain a white noise $\left\{G_f\right\}$ in the frequency domain; (iii) multiply $\left\{G_f\right\}$ by a power-law of the type $f^{-\beta /2}$; and (iv) Fourier-transform the result back to time domain to obtain $\left\{x_i\right\}$. Then, the power spectrum $S\left(f\right)$ of the final time series $\left\{x_i\right\}$ behaves by constructions as:

$$S\left(f\right)\sim \frac{1}{f^{\beta }},$$

(18)

with $\beta \in (-1,1)$ for stationary time series. Since $S\left(f\right)$ behaves as a power-law, then according to the Wiener–Khinchim theorem, $C\left(r\right)$ behaves also as a power law (see Equation (2)), with the exponents $\beta$ and $\gamma$ related via $\gamma =1-\beta$. Then, using Equation (6), the three exponents $\alpha$, $\beta$ and $\gamma$ are related as [21]

$$\alpha =1-\frac{\gamma }{2}=\frac{\beta +1}{2}.$$

(19)

Due to the relation (19), we use for convenience the FA and DFA exponent $\alpha$ as the input parameter of FFM, which we term ${\alpha }_{\mathrm{in}}$ from now on. Then, we choose a large time series size N to avoid as much as possible finite-size effects. For any ${\alpha }_{\mathrm{in}}$ value, using FFM, we generate a large number of correlated time series $\left\{x_i\right\}$, each one with an exponent $\alpha ={\alpha }_{\mathrm{in}}$ by construction. 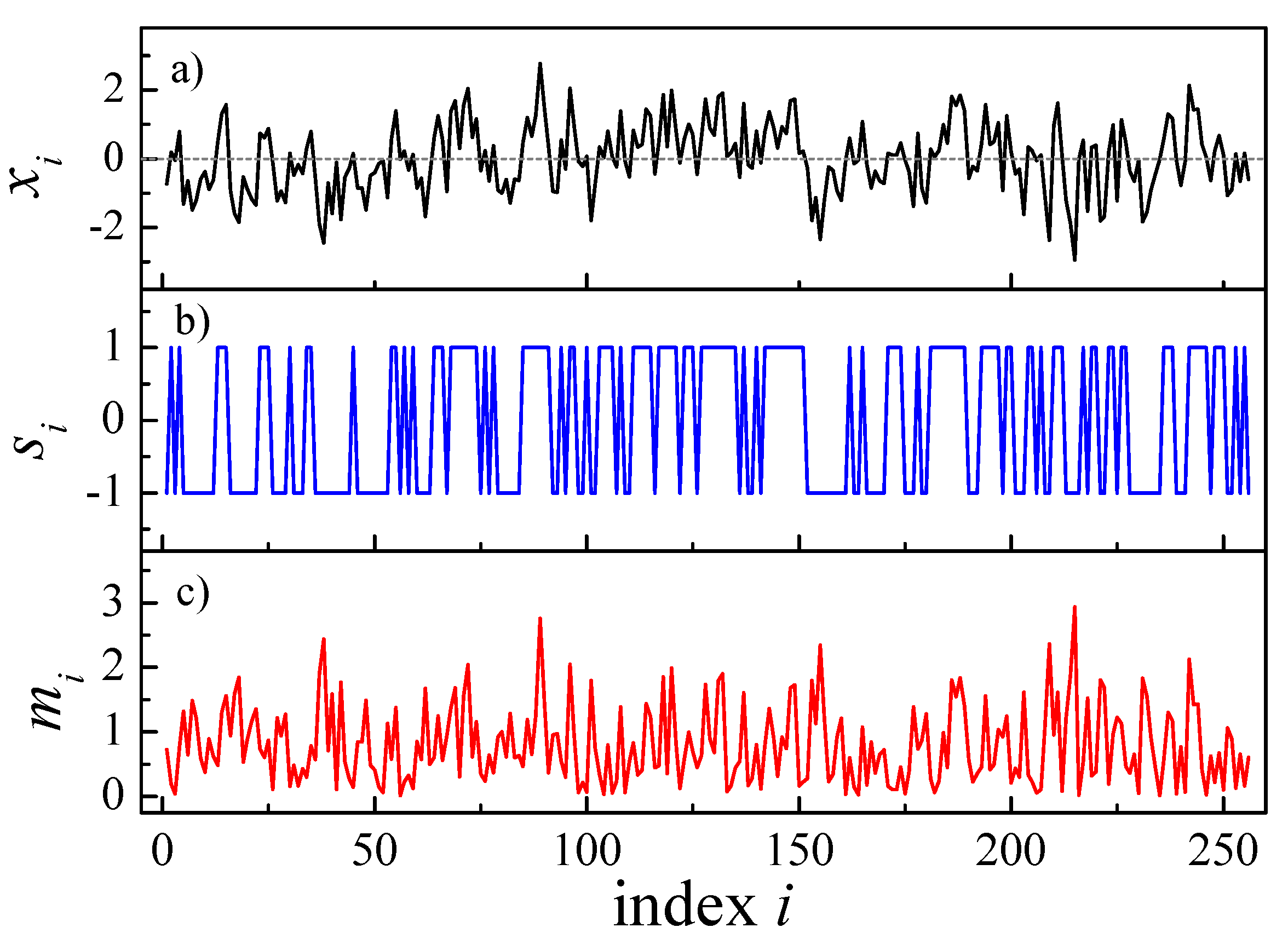Then, we decompose any individual series into its sign series $\left\{s_i\right\}$ and its magnitude series $\left\{m_i\right\}$ (see Figure 1 for an example with small N) according to (15) and apply FA and DFA to $\left\{s_i\right\}$ and $\left\{m_i\right\}$ to obtain the sign ${\alpha }_s$ and magnitude ${\alpha }_m$ scaling exponents. Then, we average the sets of individual ${\alpha }_s$ and ${\alpha }_m$ values to obtain ${\alpha }_s\left({\alpha }_{\mathrm{in}}\right)$ and ${\alpha }_m\left({\alpha }_{\mathrm{in}}\right)$. 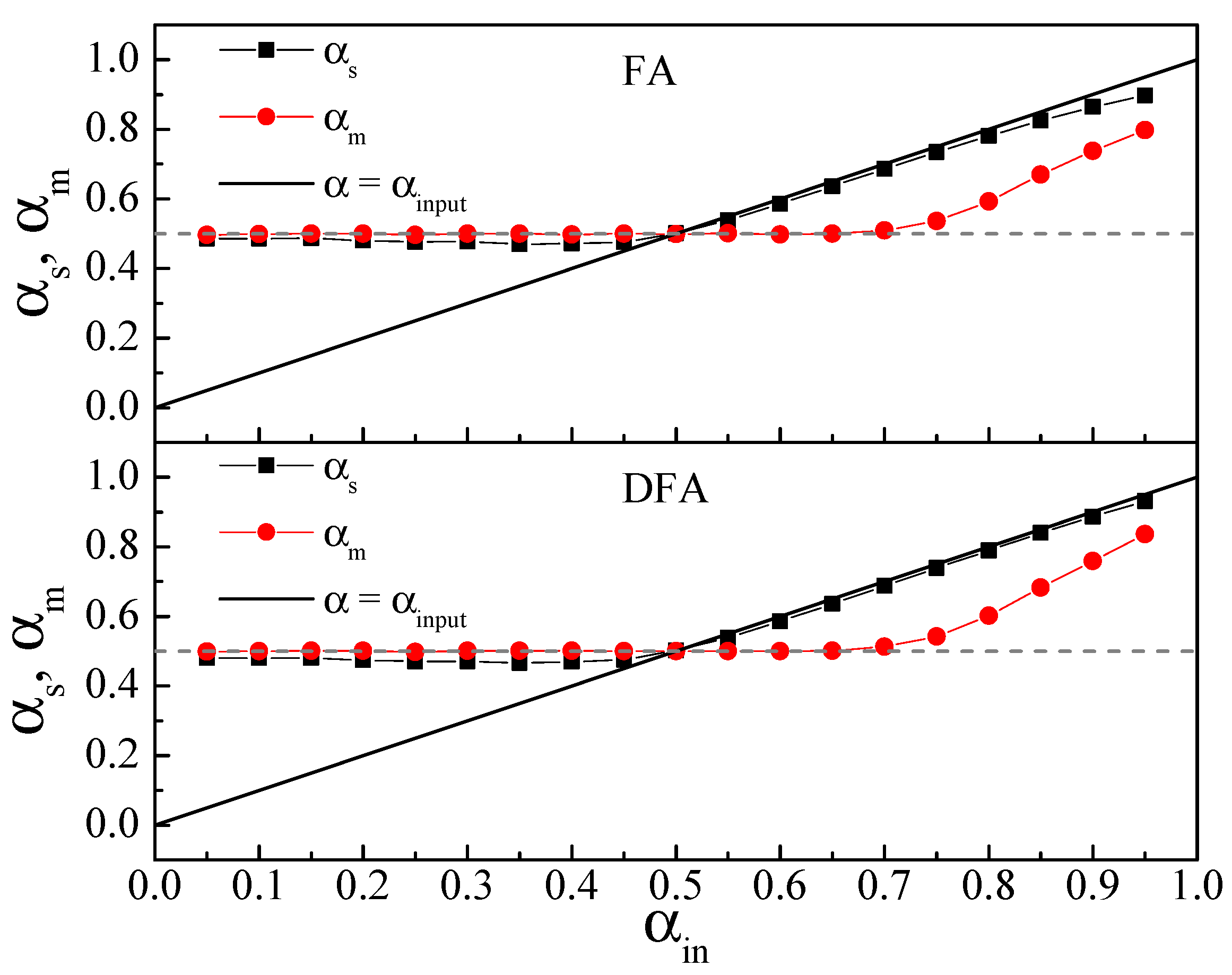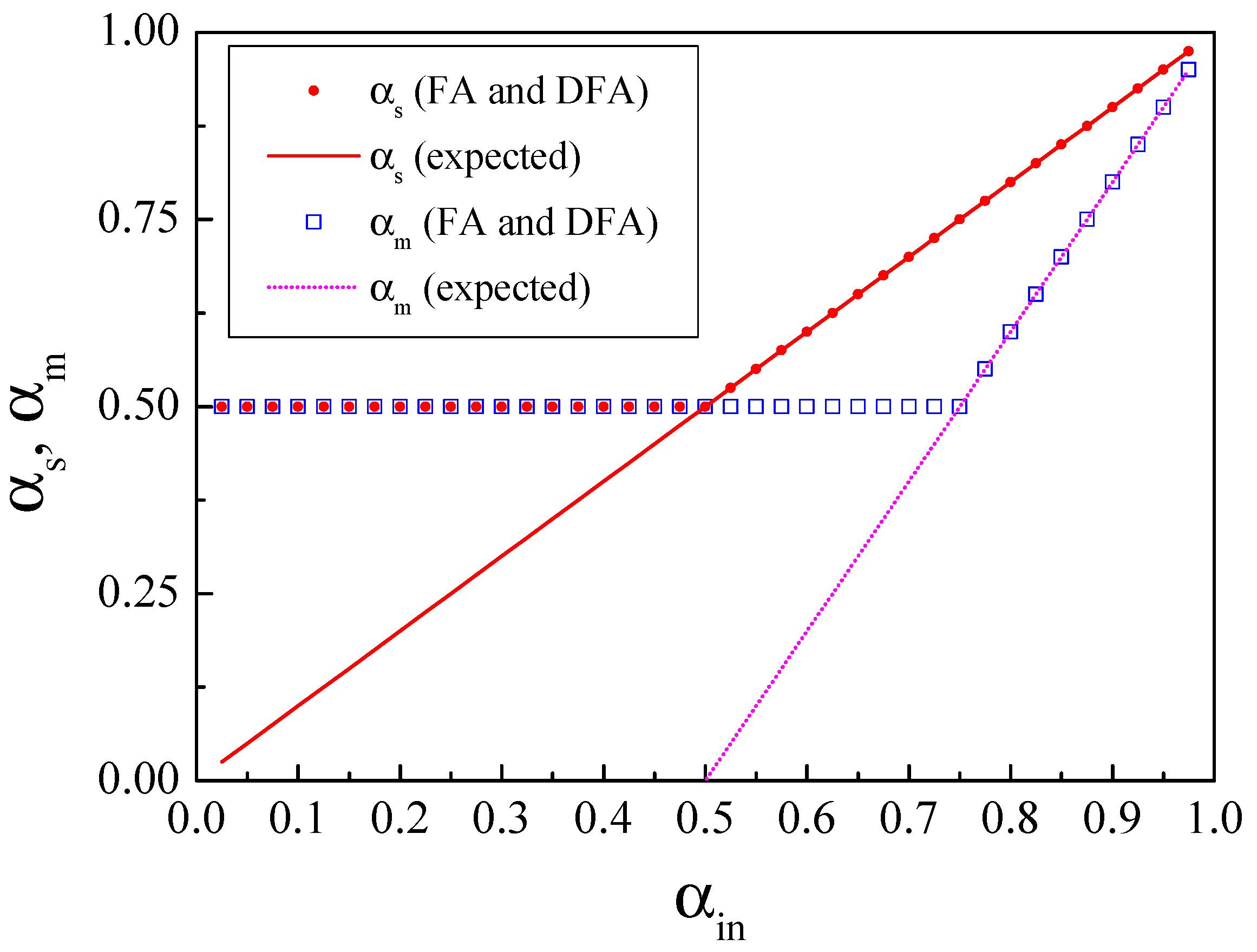The behavior of ${\alpha }_s$ and ${\alpha }_m$ as a function of ${\alpha }_{\mathrm{in}}$ is shown in Figure 2. We note that both FA and DFA provide very similar scaling exponents ${\alpha }_s$ and ${\alpha }_m$. For the sign series, ${\alpha }_s\simeq 0.5$ for ${\alpha }_{\mathrm{in}}<0.5$, and ${\alpha }_s\simeq {\alpha }_{\mathrm{in}}$ when ${\alpha }_{\mathrm{in}}>0.5$. In the magnitude series case, we observe that ${\alpha }_m\simeq 0.5$ for ${\alpha }_{\mathrm{in}}<0.75$, and ${\alpha }_m\simeq 2{\alpha }_{\mathrm{in}}-1$ when ${\alpha }_{\mathrm{in}}>0.75$. In both cases, the approximate equality ’≃’ tends to the strict equality as the series size N increases. In the particular case of DFA, these results are in agreement with previous works [5,7]. The most noticeable difference between FA and DFA is that, for a given large series size N, the former presents larger deviations from the asymptotic behaviors (20) and (21) than the latter when ${\alpha }_{\mathrm{in}}\to 1$ (Figure 2). Note that the limiting value ${\alpha }_{\mathrm{in}}=1$ corresponds to a non-stationary time series where FA is not applicable, and therefore a slower convergence of FA to the asymptotic results for ${\alpha }_{\mathrm{in}}$ close to 1 is expected.

In the asymptotic limit $N\to \infty$, the ${\alpha }_s$ and ${\alpha }_m$ results provided by both FA and DFA can be summarized as follows:

$${\alpha }_s=\left\{\begin{array}{ccc}0.5& \mathrm{for}& {\alpha }_{\mathrm{in}}\le 0.5,\\ {\alpha }_{\mathrm{in}}& \mathrm{for}& {\alpha }_{\mathrm{in}}>0.5,\end{array}\right.$$

(20)

$${\alpha }_m=\left\{\begin{array}{ccc}0.5& \mathrm{for}& {\alpha }_{\mathrm{in}}\le 0.75,\\ 2{\alpha }_{\mathrm{in}}-1& \mathrm{for}& {\alpha }_{\mathrm{in}}>0.75.\end{array}\right.$$

(21)

The common interpretation of these results is the following: (i) the sign series of fractional Gaussian noises with ${\alpha }_{\mathrm{in}}\le 0.5$ is uncorrelated (white noise behavior) because in that case ${\alpha }_s$ = 0.5. However, when ${\alpha }_{\mathrm{in}}>0.5$, the scaling properties of the time series and of its sign series are the same since for that range ${\alpha }_s={\alpha }_{\mathrm{in}}$. Note that this interpretation precludes the existence of anticorrelations in the sign series, for which ${\alpha }_s<0.5$ are expected; and (ii) the magnitude series of fractional Gaussian noises with ${\alpha }_{\mathrm{in}}\le 0.75$ is uncorrelated (white noise behavior) since ${\alpha }_m=0.5$. In contrast, for ${\alpha }_{\mathrm{in}}$ > 0.75, the magnitude scaling exponent depends linearly on ${\alpha }_{\mathrm{in}}$ as ${\alpha }_m=2{\alpha }_{\mathrm{in}}-1$. According to this, the magnitude time series should behave randomly and thus without correlations for $0<{\alpha }_{\mathrm{in}}<0.75$.

However, in the next sections, we show that the above interpretation is misleading: on the one hand, the sign series presents power-law anticorrelations for ${\alpha }_{\mathrm{in}}\le 0.5$. On the other hand, the magnitude series is power-law correlated for ${\alpha }_{\mathrm{in}}\le 0.75$. The problem is that both FA and DFA do not work properly in the sign and magnitude series, and therefore the scaling provided by both methods is spurious for ${\alpha }_{\mathrm{in}}\le 0.5$ in the sign case and for ${\alpha }_{\mathrm{in}}\le 0.75$ in the magnitude case.

6. Exact Autocorrelation Function of Magnitude and Sign Series

The correlations in the sign and magnitude series obtained from correlated and stationary time series of fractional Gaussian noise type can be derived analytically. Let x and y be two stochastic Gaussian variables, and let us assume that the linear correlation between both variables is C, i.e.,

$$C=\frac{\langle xy\rangle -\langle x\rangle \langle y\rangle }{{\sigma }_x{\sigma }_y},$$

(22)

where $\sigma$ denotes the standard deviation. Without loss of generality, from now on, we consider that $\langle x\rangle =\langle y\rangle =0$ and ${\sigma }_x={\sigma }_y=1$, i.e., x and y are of $N(0,1)$ type. Note that Equation (22) is equivalent to affirm that the joint probability density of x and y, $p(x,y)$, is the bivariate Gaussian distribution. If x and y are $N(0,1)$ variables, then $p(x,y)={(2\pi \sqrt{1-C^2})}^{-1}\exp \left[-(x^2+y^2-2Cxy)/\left(2(1-C^2)\right)\right]$. Now, let us consider the pairs of stochastic variables $\mathrm{sign}\left(x\right)$ and $\mathrm{sign}\left(y\right)$, and $\left|x\right|$ and $\left|y\right|$. Then, the correlation $C_s$ of the pair $\mathrm{sign}\left(x\right)$ and $\mathrm{sign}\left(y\right)$, and the correlation $C_m$ of the pair $\left|x\right|$ and $\left|y\right|$ are given by

$$\begin{array}{ccc}\hfill C_s& \equiv & \frac{\langle \mathrm{sign}\left(x\right)\mathrm{sign}\left(y\right)\rangle -\langle \mathrm{sign}\left(x\right)\rangle \langle \mathrm{sign}\left(y\right)\rangle }{{\sigma }_{\mathrm{sign}\left(x\right)}{\sigma }_{\mathrm{sign}\left(y\right)}}=\langle \mathrm{sign}\left(x\right)\mathrm{sign}\left(y\right)\rangle ,\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill C_m& \equiv & \frac{\langle \left|x\right|\left|y\right|\rangle -\langle \left|x\right|\rangle \langle \left|y\right|\rangle }{{\sigma }_{\left|x\right|}{\sigma }_{\left|y\right|}}=\frac{\langle \left|x\right|\left|y\right|\rangle -\frac{2}{\pi }}{1-\frac{2}{\pi }},\hfill \end{array}$$

(24)

where we have used that, as x and y are $N(0,1)$ variables, then $\langle \mathrm{sign}\left(x\right)\rangle$=$\langle \mathrm{sign}\left(y\right)\rangle$$=0$ and ${\sigma }_{\mathrm{sign}\left(x\right)}$=${\sigma }_{\mathrm{sign}\left(y\right)}$$=1$. In addition, $\langle \left|x\right|\rangle$=$\langle \left|y\right|\rangle$ = $\sqrt{2/\pi }$, and ${\sigma }_{\left|x\right|}$=${\sigma }_{\left|y\right|}$=$\sqrt{1-(2/\pi )}$.

Interestingly, both $C_s$ and $C_m$ are determined exactly by C. For $C_s$, Apostolov et al. have shown [32] that

$$C_s=\frac{2}{\pi }\arcsin C.$$

(25)

In the $C_m$ case, we have obtained recently [9] that

$$C_m=\frac{2C\arcsin C-2(1-\sqrt{1-C^2})}{\pi -2}.$$

(26)

In the time series language, Equations (25) and (26) can be easily written in terms of autocorrelation functions. Note that for a stationary and correlated Gaussian time series $\left\{x_i\right\}$, just replacing x by $x_i$ and y by $x_{i+r}$ in Equation (22), we obtain the autocorrelation function $C\left(r\right)$ (Equation (1)). Similarly, replacing $\mathrm{sign}\left(x\right)$ and $\mathrm{sign}\left(y\right)$ by $\mathrm{sign}\left(x_i\right)$ and $\mathrm{sign}\left(x_{i+r}\right)$, we obtain the autocorrelation function of the sign series $C_s\left(r\right)$. Finally, just replacing $\left|x\right|$ and $\left|y\right|$ by $|x_i|$ and $|x_{i+r}|$ in Equation (23), we obtain the autocorrelation function of the magnitude series, $C_m\left(r\right)$. Then, from (25) and (26), we can write directly

$$\begin{array}{cc}\hfill & C_s\left(r\right)=\frac{2}{\pi }\arcsin C\left(r\right),\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & C_m\left(r\right)=\frac{2C\left(r\right)\arcsin C\left(r\right)-2(1-\sqrt{1-C^2\left(r\right)})}{\pi -2}.\hfill \end{array}$$

(28)

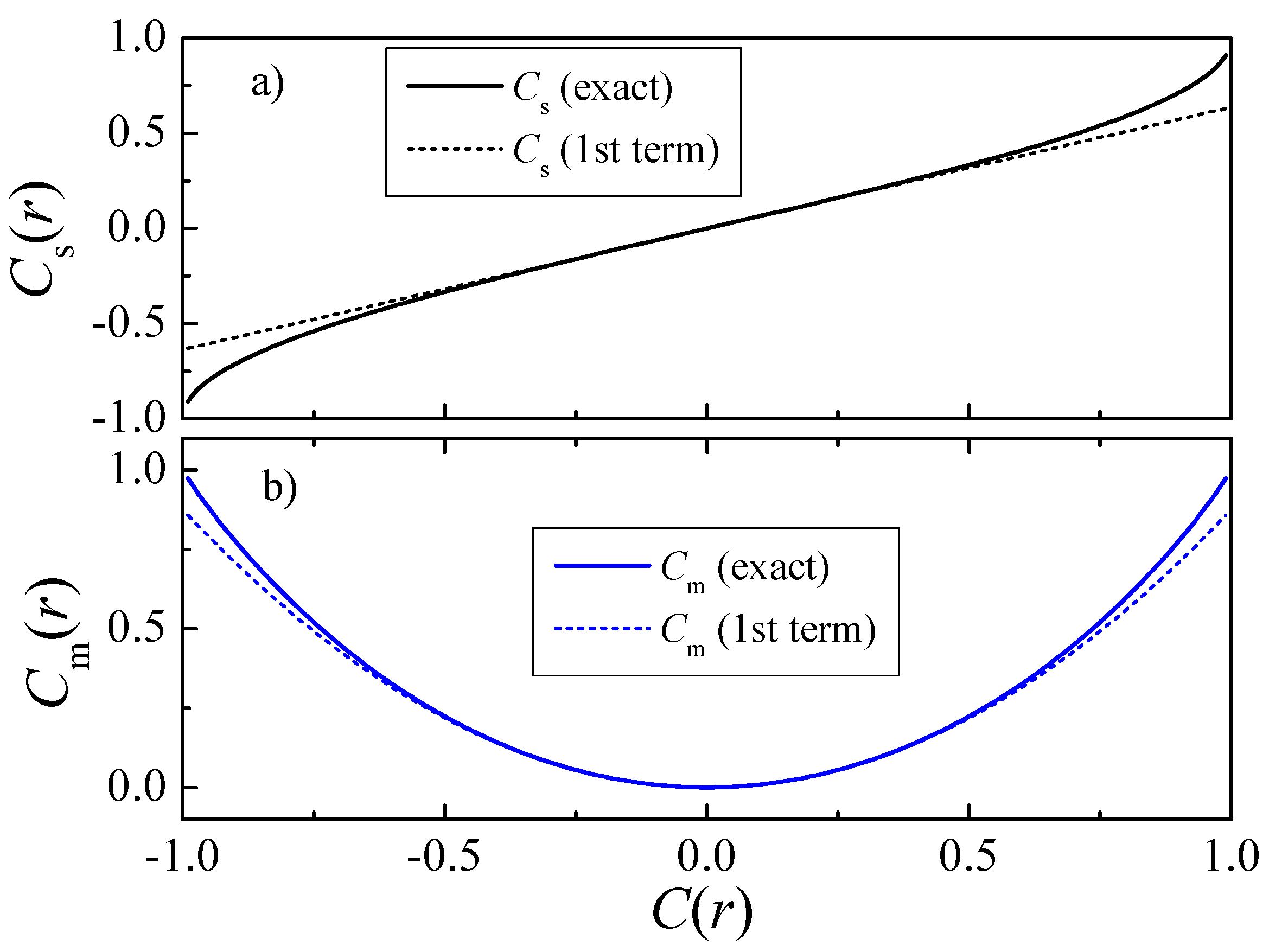
As $-1<C\left(r\right)<1$, we can plot $C_s\left(r\right)$ and $C_m\left(r\right)$ for any $C\left(r\right)\in (-1,1)$, and both curves are shown in Figure 3. The sign autocorrelation $C_s\left(r\right)$ is an odd function of $C\left(r\right)$, and then negative values of $C\left(r\right)$ produce negative values of $C_s\left(r\right)$. In other words, when the time series is (anti)correlated, the sign series is also (anti)correlated. In contrast, $C_m\left(r\right)$ is an even function of $C\left(r\right)$, and then no matter the sign of $C\left(r\right)$, the correlations in the magnitude series, $C_m\left(r\right)$, are always positive. In addition, note that both (27) and (28) are exact, independently of the behavior of $C\left(r\right)$ (positive or negative, power-law or exponentially decaying, etc.).

Very typically, $C\left(r\right)$ is a decaying function of the lag r and then small for large enough r. Therefore, in these conditions, we can expand Equations (27) and (28) in a Taylor series of $C\left(r\right)$ and, considering only the first term in the expansions, we get

$$\begin{array}{c}\hfill C_s\left(r\right)\simeq \frac{2}{\pi }C\left(r\right),\end{array}$$

(29)

$$\begin{array}{c}\hfill C_m\left(r\right)\simeq \frac{C^2\left(r\right)}{\pi -2}.\end{array}$$

(30)

These two approximations are also shown in Figure 3 (dashed lines), and are fairly precise for $C\left(r\right)\in (-0.4,0.4)$. According to Equations (29) and (30), the correlations in the sign series behave as a linear function of $C\left(r\right)$, while the correlations in the magnitude series are quadratic with $C\left(r\right)$.

These last results have profound implications, especially when the analyzed time series are stationary Gaussian power-law correlated (fGns), as the cases studied in Section 5. Indeed, in that case, $C\left(r\right)$ behaves as a decaying power-law of r (Equation (2)) and for large enough r, using Equations (29) and (30), we obtain finally:

$$\begin{array}{c}\hfill C_s\left(r\right)\simeq \frac{2}{\pi }\frac{{\alpha }_{\mathrm{in}}(2{\alpha }_{\mathrm{in}}-1)}{r^{2-2{\alpha }_{\mathrm{in}}}}\propto \frac{\mathrm{sign}(1-\gamma )}{r^{\gamma }},\end{array}$$

(31)

$$\begin{array}{c}\hfill C_m\left(r\right)\simeq \frac{1}{\pi -2}\frac{{\alpha }_{\mathrm{in}}^2{(2{\alpha }_{\mathrm{in}}-1)}^2}{r^{2(2-2{\alpha }_{\mathrm{in}})}}\propto \frac{1}{r^{2\gamma }},\end{array}$$

(32)

where, for convenience, we have used the FA and DFA exponents ${\alpha }_{\mathrm{in}}$ characterizing the original time series instead of H since they are equivalent in this case. Note that Equations (31) and (32) are valid for $\gamma \in (0,2)$ and then for ${\alpha }_{\mathrm{in}}\in (0,1)$. The consequences of these two equations are important: given a power-law correlated time series characterized by an exponent $\gamma \in (0,2)$ (or by ${\alpha }_{\mathrm{in}}=1-\gamma /2\in (0,1)$), the corresponding sign and magnitude series are also power-law correlated. In the sign series, its autocorrelation function exponent is identical to that of the original series, $\gamma$ (Equation (31)). In the magnitude series, the exponent characterizing $C_m\left(r\right)$ is given by twice the exponent $\gamma$ of the original series (Equation (32)). The only case in which there is absence of correlations in the three time series corresponds to ${\alpha }_{\mathrm{in}}=0.5$ or $\gamma =1$, where the three autocorrelation functions, $C\left(r\right)$, $C_s\left(r\right)$ and $C_m\left(r\right)$, vanish.

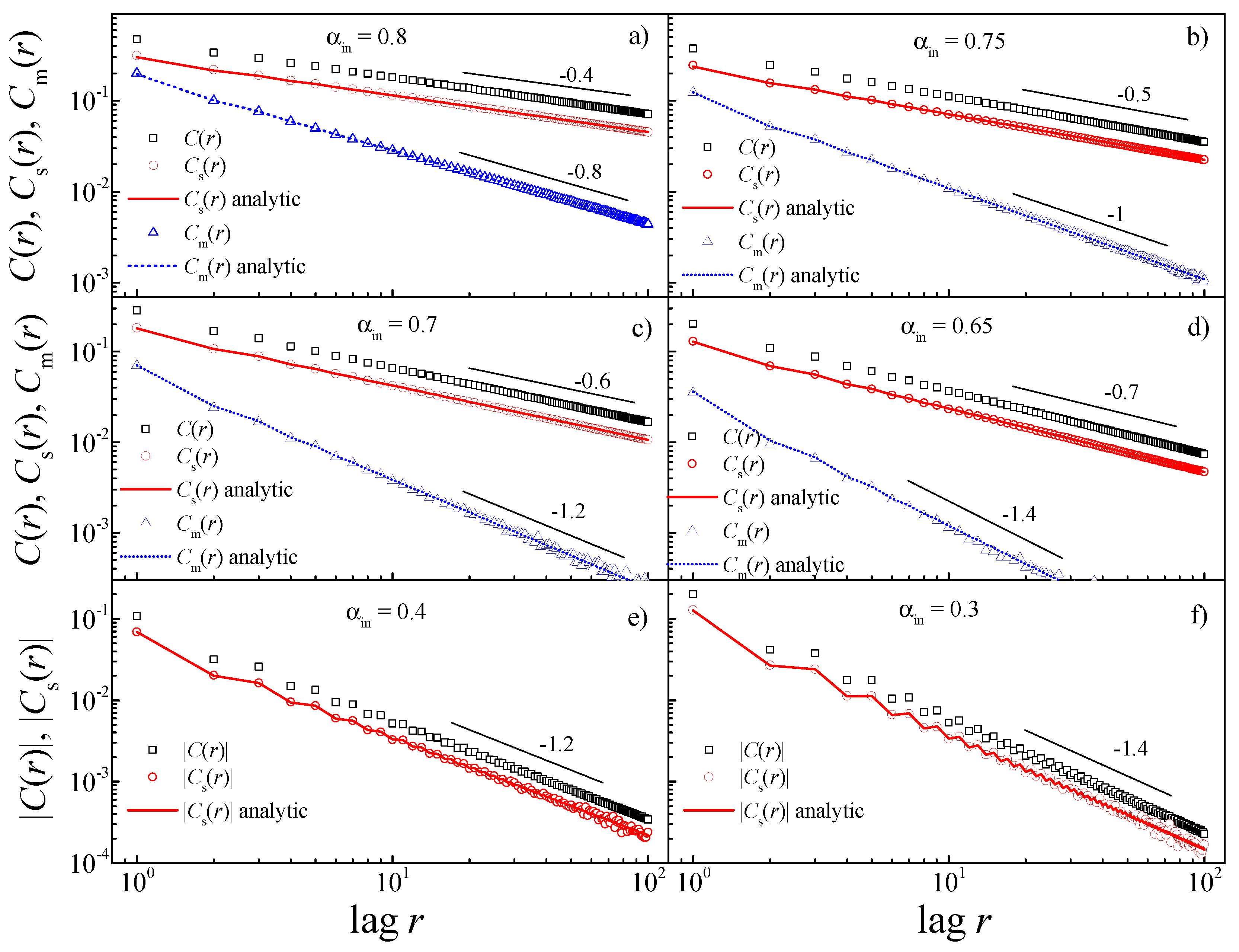
To show the validity of these results, in Figure 4, we show the autocorrelation functions $C\left(r\right)$, $C_s\left(r\right)$ and $C_m\left(r\right)$ obtained numerically for power-law correlated synthetic $N(0,1)$ fractional Gaussian noises generated using FFM with different ${\alpha }_{\mathrm{in}}$ values. We observe that Equations (31) and (32) provide correct results: on the one hand, the sign autocorrelation function $C_s\left(r\right)$ behaves as a power law with the same exponent as the original time series. Indeed, both $C\left(r\right)$ and $C_s\left(r\right)$ behave as parallel power-laws and then differ essentially in a multiplicative constant, in agreement with Equation (29). This last equation has been used to plot the solid lines representing $C_s\left(r\right)$ in Figure 4. On the other hand, the magnitude autocorrelation function $C_m\left(r\right)$ behaves as a power-law with an exponent twice the exponent $\gamma$ of the original series, and the results for $C_m\left(r\right)$ are also in perfect agreement with Equation (30), which has been used to plot the dotted lines for $C_m\left(r\right)$ in Figure 4. One last remark concerning the results on Figure 4: for ${\alpha }_{\mathrm{in}}<0.5$, both the original and the sign series are power-law anticorrelated, i.e., $C\left(r\right),C_s\left(r\right)<0$, and, for this reason, we use the absolute values $\left|C\right(r\left)\right|$ and $|C_s\left(r\right)|$ in panels (e) and (f) to produce a log-log plot.

6.1. Spurious Results and Misinterpretations of FA and DFA on Sign and Magnitude Series

According to our analytical (Equations (29)–(32)) and numerical results (Figure 4), the sign and magnitude series from power-law correlated fractional Gaussian noises are also power-law correlated. However, when FA and DFA are applied to these series, then the results shown in Figure 2 and summarized in Equations (20) and (21) spuriously indicate a different behavior.

For the sign series, since both $C\left(r\right)$ and $C_s\left(r\right)$ are power-laws with the same exponent $\gamma$, then one should expect that ${\alpha }_s={\alpha }_{\mathrm{in}}$ in the whole range ${\alpha }_{\mathrm{in}}\in (0,1)$. FA and DFA provide the correct result ${\alpha }_s={\alpha }_{\mathrm{in}}$ only in the case ${\alpha }_{\mathrm{in}}\in (0.5,1)$. However, both FA and DFA predict ${\alpha }_s=0.5$ (white noise behavior) when ${\alpha }_{\mathrm{in}}\in (0,0.5)$ or, in other words, the two techniques consider that the sign series is completely uncorrelated in this case, which is clearly not the case (see Figure 4e,f).

For the magnitude series, $C_m\left(r\right)$ behaves as a power-law with an exponent $2\gamma$, twice the exponent $\gamma$ of $C\left(r\right)$ (in Figure 4a–d). Then, according to Equation (6), one has ${\alpha }_{\mathrm{in}}=1-\gamma /2$ for the original series and ${\alpha }_m=1-\gamma$ for the magnitude series. Combining both expressions, we get that the relation between ${\alpha }_{\mathrm{in}}$ and ${\alpha }_m$ should be ${\alpha }_m=2{\alpha }_{\mathrm{in}}-1$, and this relation holds for ${\alpha }_{\mathrm{in}}\in (0,1)$. Both FA and DFA predict (correctly) ${\alpha }_m=2{\alpha }_{\mathrm{in}}-1$ only in the case ${\alpha }_{\mathrm{in}}\in (0.75,1)$. However, the two techniques wrongly estimate that ${\alpha }_m=0.5$ when ${\alpha }_{\mathrm{in}}\in (0,0.75)$ (Figure 2 and Equation (21)). In other words, FA and DFA consider that, for ${\alpha }_{\mathrm{in}}\le 0.75$, the magnitude series in completely uncorrelated (white noise behavior), which is clearly false (see Figure 4b–d).

Then, according to the autocorrelation function behavior, the results for ${\alpha }_s$ and ${\alpha }_m$ can be summarized as

$$\left.\begin{array}{c}{\alpha }_s={\alpha }_{\mathrm{in}}\hfill \\ {\alpha }_m=2{\alpha }_{\mathrm{in}}-1\hfill \end{array}\right\}\mathrm{for}{\alpha }_{\mathrm{in}}\in (0,1).$$

(33)

The discrepancies between the values of ${\alpha }_s$ and ${\alpha }_m$ predicted using FA and DFA (Equations (20) and (21) and Figure 2 ) and the correct expected values for ${\alpha }_s$ and ${\alpha }_m$ given by Equation (33) are shown in Figure 5. Indeed, both expected values are linear functions of ${\alpha }_{\mathrm{in}}$, and lack of the abrupt corners exhibited by the FA and DFA results.

Before concluding this section, we add a final remark on the behavior of ${\alpha }_m$: the correct result ${\alpha }_m=2{\alpha }_{\mathrm{in}}-1$ indicates that, for ${\alpha }_{\mathrm{in}}<0.75$, then ${\alpha }_m<0.5$. Traditionally, values of the FA and DFA scaling exponent $\alpha$ smaller than 0.5 are interpreted as an indicator of anticorrelations. However, this is not the case: we have proved above (Equations (28) and (30)) that, in general, the correlations in the magnitude series are always positive (see also Figure 3 and Figure 4) even in the case ${\alpha }_m<0.5$.

In the next section, we derive an analytical explanation for the spurious scaling results of FA and DFA on sign and magnitude series.

7. Analytical FA and DFA Scaling on Sign and Magnitude Series

Let us consider a fractional Gaussian noise with $\sigma =1$, and with an autocorrelation function given in terms of ${\alpha }_{\mathrm{in}}$ by

$$C\left(r\right)\simeq \frac{{\alpha }_{\mathrm{in}}(2{\alpha }_{\mathrm{in}}-1)}{r^{2-2{\alpha }_{\mathrm{in}}}}.$$

(34)

For this signal, by construction both FA and DFA give a scaling of the type:

$$F_{FA}\left(\ell \right)\sim F_{DFA}\left(\ell \right)\sim {\ell }^{{\alpha }_{\mathrm{in}}}.$$

(35)

We analyze first the FA and DFA scaling properties of the sign series. We recall Equation (10) establishing the relationship between $F_{FA}^2\left(\ell \right)$ and $C\left(r\right)$. Since the sign series is also stationary, from Equation (10), we can also write

$$F_{s,FA}^2\left(\ell \right)=\ell +2\sum _{r=1}^{\ell -1}(\ell -r)C_s\left(r\right),$$

(36)

where $F_{s,FA}\left(\ell \right)$ is the FA fluctuation function for the sign series. As $C\left(r\right)$ decays as a power-law, for large enough ℓ, we can use the approximation (29) to write Equation (36) in terms of $C\left(r\right)$:

$$F_{s,FA}^2\left(\ell \right)=\ell +\frac{4}{\pi }\sum _{r=1}^{\ell -1}(\ell -r)C\left(r\right).$$

(37)

Note that the sum in Equation (37) also appears in Equation (10) and then, combining both equations, we finally obtain

$$F_{s,FA}\left(\ell \right)=\sqrt{\left(1-\frac{2}{\pi }\right)\ell +\left(\frac{2}{\pi }\right)F_{FA}^2\left(\ell \right)}.$$

(38)

This equation establishes the relationship between the FA fluctuation functions of the original series, $F_{FA}\left(\ell \right)$, and of the sign series, $F_{s,FA}\left(\ell \right)$, and explains perfectly the (spurious) ${\alpha }_s$ value provided by FA. Indeed, for an fGn, Equation (35) holds and then $F_{FA}\left(\ell \right)\sim {\ell }^{{\alpha }_{\mathrm{in}}}$. Thus, obviously for ${\alpha }_{\mathrm{in}}>0.5$, the second term in the sum inside the square root dominates for large ℓ and then $F_{s,FA}\left(\ell \right)\sim {\ell }^{{\alpha }_{\mathrm{in}}}$, i.e., ${\alpha }_s={\alpha }_{\mathrm{in}}$. In contrast, for ${\alpha }_{\mathrm{in}}<0.5$, the first term dominates for large ℓ and then $F_{s,FA}\left(\ell \right)\sim {\ell }^{1/2}$, i.e., ${\alpha }_s=1/2$. In other words, we recover exactly the numerical results in Equation (20).

Similar calculations can be carried out for DFA: in this case, starting from Equation (11) and using Equation (29), we get:

$$F_{s,DFA}^2\left(\ell \right)=W\left(\ell \right)+\frac{2}{\pi }\sum _{r=1}^{\ell -1}L(\ell ,r)C\left(r\right),$$

(39)

where $F_{s,DFA}\left(\ell \right)$ is the DFA fluctuation function for the sign series. Again, the sum in Equation (39) also appears in Equation (11) and, combining both equations and using the definition of $W\left(\ell \right)$ in Equation (12), we obtain

$$F_{s,DFA}\left(\ell \right)=\sqrt{\left(1-\frac{2}{\pi }\right)\frac{{\ell }^2-4}{15\ell }+\left(\frac{2}{\pi }\right)F_{DFA}^2\left(\ell \right)}.$$

(40)

This equation relates the DFA fluctuation function of the sign series, $F_{s,DFA}\left(\ell \right)$, to the DFA fluctuation function of the original series, $F_{DFA}\left(\ell \right)$. Similarly to the FA case, $F_{s,DFA}\left(\ell \right)$ presents two terms inside the square root, which can explain the ${\alpha }_s$ value provided by DFA. Indeed, when the original series is a fGn, then Equation (35) holds and $F_{DFA}\left(\ell \right)\sim {\ell }^{{\alpha }_{\mathrm{in}}}$. Thus, for ${\alpha }_{\mathrm{in}}>0.5$, the second term inside the square root dominates for large ℓ, and, therefore, $F_{s,DFA}\left(\ell \right)\sim {\ell }^{{\alpha }_{\mathrm{in}}}$, i.e., ${\alpha }_s={\alpha }_{\mathrm{in}}$. In contrast, for ${\alpha }_{\mathrm{in}}<0.5$, for large ℓ, the first term dominates and is proportional to ℓ, thus implying $F_{s,DFA}\left(\ell \right)\sim {\ell }^{1/2}$, i.e., ${\alpha }_s=1/2$. In other words, we also recover the numerical results in Equation (20), which are spurious for ${\alpha }_{\mathrm{in}}<0.5$.

In conclusion, the reason behind the spurious FA and DFA result ${\alpha }_s=1/2$ for ${\alpha }_{\mathrm{in}}<1/2$ is the presence of a first term proportional to ℓ inside the square root of Equations (38) and (40), which dominates for large ℓ when ${\alpha }_{\mathrm{in}}<1/2$. Note that this ℓ term should be absent in order to obtain the correct result ${\alpha }_s={\alpha }_{\mathrm{in}}$ for ${\alpha }_{\mathrm{in}}\in (0,1)$, but it is an intrinsic property of the FA and DFA techniques.

Next, we study the FA and DFA scaling properties of the magnitude series. Concerning FA, since the original series is an fGn, then the magnitude series is stationary and, from Equation (10), we can write

$$F_{m,FA}^2\left(\ell \right)={\sigma }_m^2\left(\ell +2\sum _{r=1}^{\ell -1}(\ell -r)C_m\left(r\right)\right),$$

(41)

with ${\sigma }_m^2$ the variance of the magnitude series. Noting that we are considering fGns with ${\sigma }^2=1$, then ${\sigma }_m^2=1-2/\pi$. For large ℓ, we can use the approximation in Equation (30) to obtain

$$F_{m,FA}^2\left(\ell \right)=\left(1-\frac{2}{\pi }\right)\ell +\frac{2}{\pi }\sum _{r=1}^{\ell -1}(\ell -r)C^2\left(r\right).$$

(42)

Contrary to the sign case, in this last equation the sum is not the same as the one in Equation (10) because we have the square of $C\left(r\right)$. Then, to evaluate Equation (42), we proceed as follows: first, we note that $C\left(r\right)$ is given by Equation (34) and insert it in Equation (42). Then, in order to evaluate the sum, we substitute it by a definite integral that we solve and simplify by keeping only the highest powers of ℓ with constant and non-constant exponents. In this way, after regrouping terms, we get finally:

$$F_{m,FA}^2\left(\ell \right)=\left[1-\frac{2}{\pi }\left(1+{\alpha }^2\frac{{(2{\alpha }_{\mathrm{in}}-1)}^2}{4{\alpha }_{\mathrm{in}}-3}\right)\right]\ell +\left[\frac{{\alpha }_{\mathrm{in}}^2(2{\alpha }_{\mathrm{in}}-1)}{\pi (4{\alpha }_{\mathrm{in}}-3)}\right]{\ell }^{4{\alpha }_{\mathrm{in}}-2}.$$

(43)

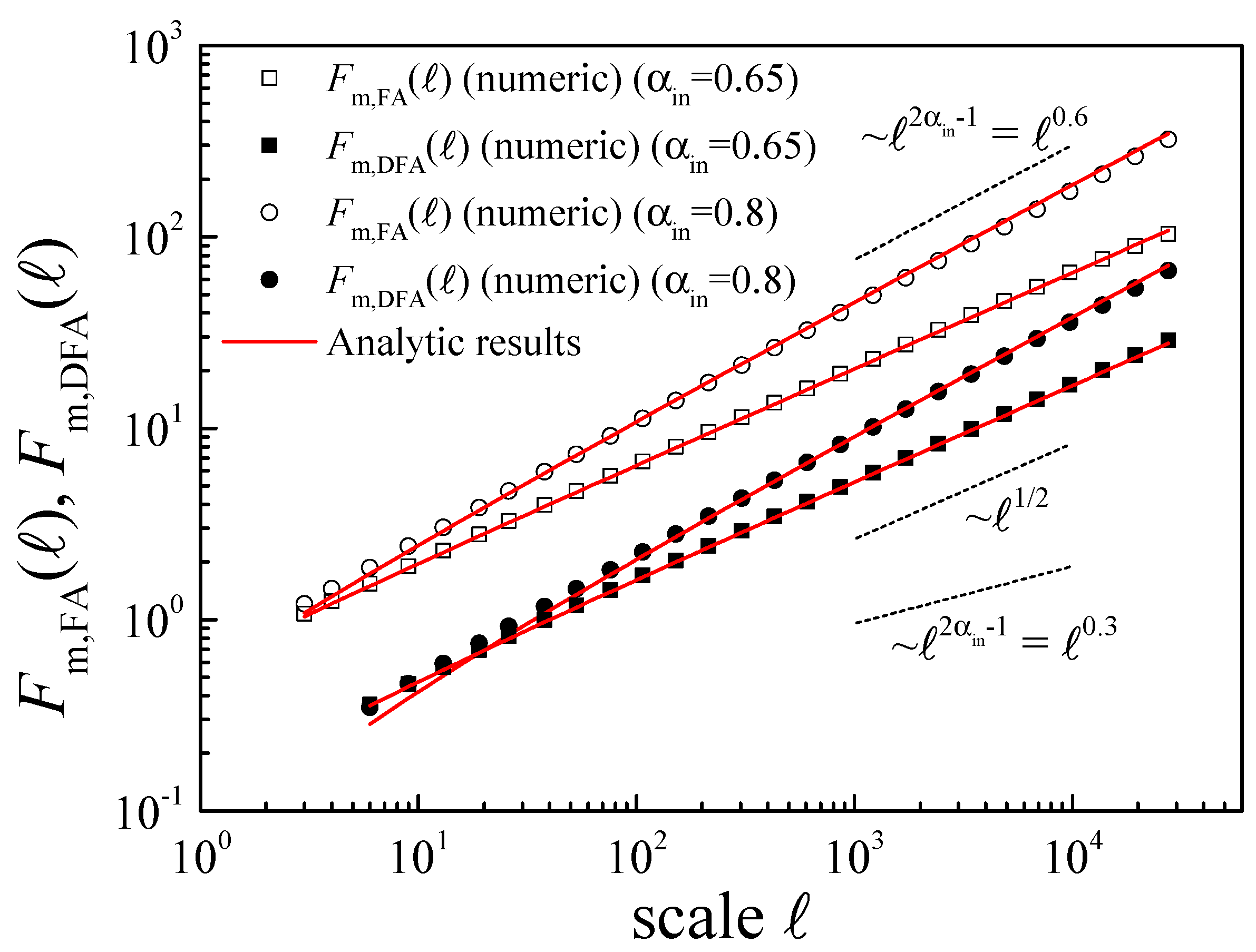
The validity of this analytic result is shown in Figure 6, where we plot $F_{m,FA}\left(\ell \right)$ obtained numerically in magnitude time series from fGns generated using FFM for two values of ${\alpha }_{\mathrm{in}}$ (open symbols), and also the corresponding analytical values using Equation (43), shown in solid lines. Equation (43) explains the ${\alpha }_m$ results obtained using FA (21): for $4{\alpha }_{\mathrm{in}}-2>1$, i.e., ${\alpha }_{\mathrm{in}}>3/4$, the second term in the sum dominates asymptotically and then $F_{m,FA}\left(\ell \right)\sim {\ell }^{2{\alpha }_{\mathrm{in}}-1}$ leading to ${\alpha }_m=2{\alpha }_{\mathrm{in}}-1$ (see the case ${\alpha }_{\mathrm{in}}=0.8$ in Figure 6). In contrast, for $4{\alpha }_{\mathrm{in}}-2<1$, i.e., ${\alpha }_{\mathrm{in}}<3/4$, the first term in the sum is the dominant one and $F_{m,FA}\left(\ell \right)\sim {\ell }^{1/2}$ from where ${\alpha }_m=1/2$, as the case ${\alpha }_{\mathrm{in}}=0.65$ in Figure 6.

A similar, though more elaborated calculation can be carried out for the scaling of the magnitude series using DFA. In this case, starting from Equation (11), we write for the magnitude series

$$F_{m,DFA}^2\left(\ell \right)={\sigma }_m^2\left(W\left(\ell \right)+\sum _{r=1}^{\ell -1}L(\ell ,r)C_m\left(r\right)\right),$$

(44)

where, as before, ${\sigma }_m^2=1-2/\pi$. Using Equation (30), we get:

$$F_{m,DFA}^2\left(\ell \right)=\left(1-\frac{2}{\pi }\right)W\left(\ell \right)+\frac{1}{\pi }\sum _{r=1}^{\ell -1}L(\ell ,r)C^2\left(r\right).$$

(45)

To evaluate this equation, we insert the expression of $C\left(r\right)$ (Equation (34)), use the definitions of $W\left(\ell \right)$ (Equation (12)) and $L(\ell ,r)$ (Equation (13)), substitute the sum by a definite integral and calculate it, and simplify the results by keeping the highest powers of ℓ to get the (asymptotically correct) result:

$$F_{m,DFA}^2\left(\ell \right)=\left[\frac{1}{15}-\frac{2}{15\pi }\left(1+\frac{{\alpha }_{\mathrm{in}}^2{(2{\alpha }_{\mathrm{in}}-1)}^2}{4{\alpha }_{\mathrm{in}}-3}\right)\right]\ell +\left[\frac{{\alpha }_{\mathrm{in}}(1-{\alpha }_{\mathrm{in}})(2{\alpha }_{\mathrm{in}}-1)}{\pi (2{\alpha }_{\mathrm{in}}+1)(4{\alpha }_{\mathrm{in}}-1)(4{\alpha }_{\mathrm{in}}-3)}\right]{\ell }^{4{\alpha }_{\mathrm{in}}-2}.$$

(46)

The validity of this last equation is also shown in Figure 6, where we plot for two different ${\alpha }_{\mathrm{in}}$ values the numerical $F_{m,FA}\left(\ell \right)$ functions provided by DFA (solid symbols) and the corresponding analytic $F_{m,DFA}\left(\ell \right)$ functions from Equation (46) (solid lines). Similarly to the FA case, Equation (46) allows for understanding the spurious ${\alpha }_m$ results (21) obtained using DFA. As before, for $4{\alpha }_{\mathrm{in}}-2>1$, i.e., for ${\alpha }_{\mathrm{in}}>3/4$ (see the case ${\alpha }_{\mathrm{in}}=0.8$ in Figure 6), the second term in the sum dominates for large ℓ and then $F_{m,DFA}\left(\ell \right)\sim {\ell }^{2{\alpha }_{\mathrm{in}}-1}$, or ${\alpha }_m=2{\alpha }_{\mathrm{in}}-1$. For $4{\alpha }_{\mathrm{in}}-2<1$, i.e., ${\alpha }_{\mathrm{in}}<3/4$ (see the case ${\alpha }_{\mathrm{in}}=0.65$ in Figure 6), the first term in the sum is the dominant one and $F_{m,DFA}\left(\ell \right)\sim {\ell }^{1/2}$ from where ${\alpha }_m=1/2$.

We conclude that the spurious FA and DFA result ${\alpha }_m=1/2$ for ${\alpha }_{\mathrm{in}}<3/4$ is due to the existence of a first term proportional to ℓ in Equations (43) and (46), which dominates asymptotically when ${\alpha }_{\mathrm{in}}<3/4$. The correct result ${\alpha }_m=2{\alpha }_{\mathrm{in}}-1$ for ${\alpha }_{\mathrm{in}}\in (0,1)$ could only be obtained by FA and DFA without such ℓ-term in Equations (43) and (46), which, regrettably, is an intrinsic property of both techniques.

8. Conclusions

We have shown that the magnitude and sign series obtained from power-law correlated stationary time series, such as fractional Gaussian noises, are also power-law correlated for any scaling of the original series. Indeed, we have obtained analytical expressions for both power-law autocorrelation functions confirmed by numerical results. However, when the magnitude and sign series are analyzed using Fluctuation Analysis and Detrended Fluctuation Analysis, also known as the magnitude and sign decomposition method, depending on the scaling of the original time series, both techniques can provide spurious scaling results and lead to wrongly interpreting the magnitude and sign series as completely uncorrelated (white noises). By using the relationships between the autocorrelation functions and the fluctuation functions of FA and DFA, we find analytically and confirm numerically the reason for these spurious results, which turns out to be an intrinsic property of both methods.