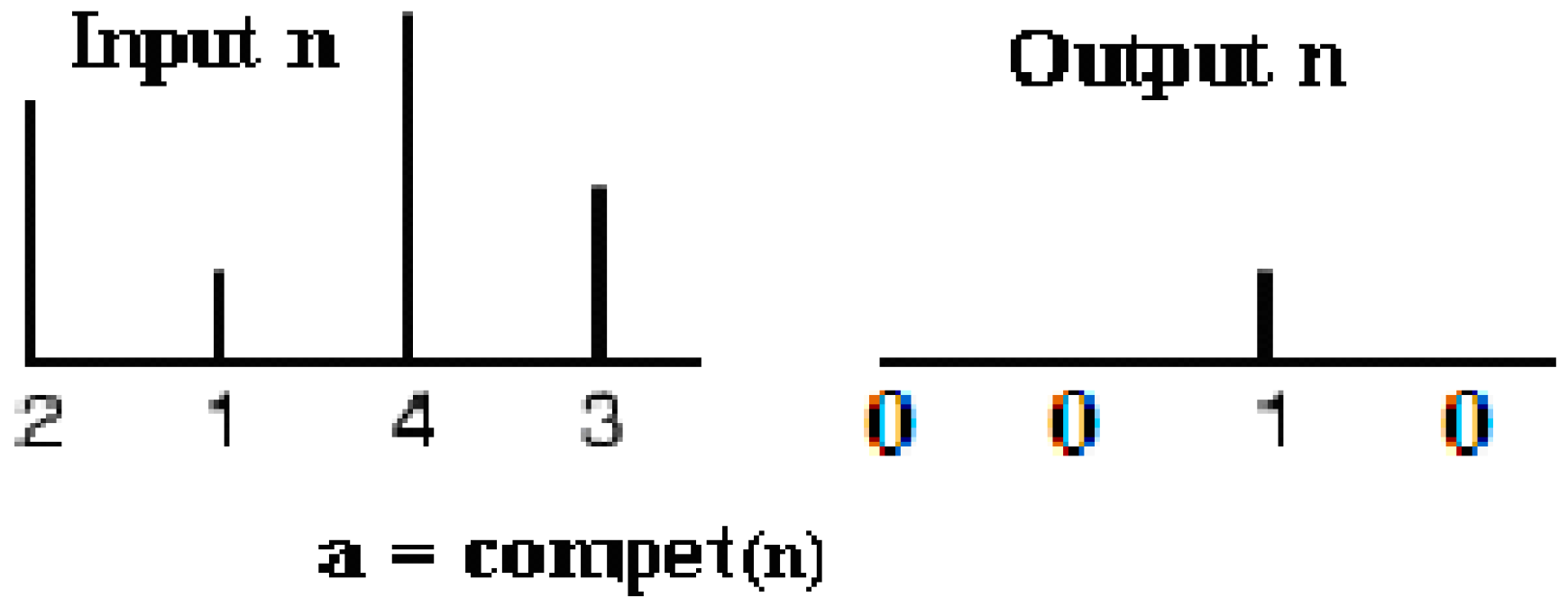1. Introduction
Handwritten signatures have a very widely known tradition of use in commonly encountered recognition tasks such as financial transactions and document authentication. Moreover, signatures are easily used and well accepted by the public, and signatures are straightforward to produce with fairly cheap devices. Signature recognition is divided into verification and identification. In the verification, we detect whether or not a claimed signature is genuine and belongs to the claiming signer (accept or reject), in contrast to identification, in which an imposter signature is recognized and referred to the correct signer.
The advantages of signature recognition make it more preferable over other biometrics. Nevertheless, signature recognition also has some weaknesses: It has a puzzling pattern recognition problem due to the large variations between different signatures made by the same person. These variations may be caused by instabilities, emotions, environmental changes, etc., and are person-dependent. Moreover, signatures can be forged more easily than other biometrics [
1]. User recognition by his or her signature can be divided into static (offline), where the signature written on paper is digitized, and dynamic, where users write their signature in a digitizing tablet, tablet-personal computer, personal digital assistant (PDA) stylus [
2] or similar; the information acquired depends on the input device. Taking into consideration the highest security ranks that can be attained by dynamic systems, most of the efforts of the international scientific community are concentrated on this type [
3,
4]. Static systems are limited to use in legal-related cases [
5]. However, most academic and research tasks start from analyzing the signature recognition with an off-line procedure. Forensic document examiners, e.g., Robertson [
6], Russell, et al. [
7], Hilton [
8], and Huber and Headrick [
9], have cited in their textbooks the method of automatic writer verification and identification based on offline handwriting. A correspondence can be drawn between this writer identification process and offline signature verification and identification because the individuality analysis of words is similar to signature verification. The approaches that have been seen in the literature to extract significant information from signatures can be broadly split into the following [
10]:
Feature-based approaches, in which a holistic vector, consisting of global features such as signature duration, standard deviation, etc., is derived from the acquired signature trajectories.
Function-based approaches, in which time sequences describing local properties, such as position trajectory, pressure, and azimuth, are used. A system for verifying handwritten signatures where various static and dynamic signature features are extracted and used as a pattern to train several network topologies is presented [
11]. A signature verification system based on a Hidden Markov Model approach for verifying the hand signature data is presented in [
12]. Instrumented data gloves furnished with sensors for detecting finger bend, hand position, and orientation for detecting hand signatures are used in handwritten verification [
13]. A method for automatic handwritten signature verification that depends on global features that summarize different aspects of signature shape and dynamics of signature production is studied in [
14]. A signature recognition algorithm, relying on a pixel-to-pixel relationship between signature images based on extensive statistical examination, standard deviation, variance, and theory of cross-correlation, is investigated in [
15]. Online reference data acquired through a digitizing tablet is used with three different classification schemes to recognize handwritten signatures, as discussed in [
16]. The influence of an incremental level of skill in the forgeries against signature verification systems is clarified in [
17]. Principles for an improved writer enrollment based on an entropy measure for genuine signatures is presented in [
18]. Dynamic signature verification systems, using a set of 49 normalized features that tolerate inconsistencies in genuine signatures while retaining the power to discriminate against forgeries, are studied in [
19]. A statistical quantization mechanism to suppress the intra-class variation in signature features and statistical quantization mechanism, thus distinguishing the difference between genuine signature and its forgery, is emphasized in [
20]. This method is not well-established in the field of signature recognition and needs to be analyzed based on several databases. Other signature verification systems based on extracting local information time functions of various dynamic properties of the signatures are used for comparison. The use of a discrete wavelet transform (DWT) in extracting features from handwritten signatures that achieved higher verification rates than that of a time domain verification system is reported in [
21,
22,
23]. The limitation of 1D DWT is that it generates discrete wavelet sub-signals from the approximation first level sub-signal. Therefore, the DWT representation could lose the high-frequency components.
According to the classification stage, different proposals can be found in the literature to measure the similarity between the claimed identity model and the input features. In the Signature Verification Competition 2004 (SVC04), dynamic time warping (DTW) [
24] and hidden Markov model (HMM)-based schemes [
25] were shown to be the most popular; the system based on DTW was the first. A similar result can be seen in [
26], where a vector quantization (VQ) pattern recognition algorithm is also tested. Recent proposals show some improvements, by combining systems (VQ-DTW) in [
26], by fusing local and global information [
12], or by combining different system outputs [
25]. In [
26] was seen that DTW had performed well in the problem of measuring similarity when the signatures to be compared have different lengths. On the other hand, if the signatures have the same length, i.e., the same number of points, the similarity of which can be computed in a more straightforward way, as a simple distance measurement between vectors can be applied. This distance calculation is based on the use of the Euclidean one. However, due to the high dimensionality of feature vectors, the authors proposed the use of fractional distances to alleviate the concentration phenomena [
26]. A system for handwriting signature verification using a two-level verification method, by extracting wavelet features and through neural network recognition, is presented [
27]. Dynamic handwritten signature verification by the wavelet transform with verification using the backpropagation neural network (BPNN) is studied [
28]. DTW, VQ, HMM, and BPNN are widely employed in different tasks. These methods are not spatial signature recognition methods. And many modifications and combinations of VQ, DWT, DTW or other methods have been suggested in the literature. That could have success in some places, but we still need original signature methods designed to meet the needs with less limitation related to complexity, time consumption, and accuracy.
For the offline signature verification and identification tasks, many approaches based on neural networks [
29], Hidden Markov Models, and regional correlation [
30], have been discussed in the literature [
31,
32]. The paper by Lee and Pan gave a summary of feature selection [
33], broadly classifying them into global, statistical and topological features. Global features, as well as statistical features, were extracted and verified using statistical distance distribution, where a simple approach for offline signature verification was adopted [
34].
In the literature, many methods have been used widely in recognition tasks, such as DTW, VQ, or HMM. Speaking, they have been used in recognition applications such as speaker identification, speech recognition, face recognition, and signature recognition. They could have good results in some places, but we are sure that the mentioned methods are not designed particularly for signature recognition. Therefore, we need to develop a particular way that possesses a structure inspired from the signature recognition task basis.
In this paper, we have proposed a new method for an off-line signature recognition system based on the use of wavelet AFE. Two proposals by DWT and WP are used for feature extraction. For classification, PNN is suggested. In the proposed system, the entropy wavelet feature vectors are fed to PNN classifier to be recognized. The essential motivations of such choice are as follows:
- (1)
For the wavelet, the crucial feature of a signature is the signature morphology, as well as the lines concentration [
35]. Bearing in mind this fact, the use of wavelet transform entropy would benefit immensely in features tracking, because of the possibility of signal analysis over several passbands of frequency.
- (2)
For PNN, the feature vector is relatively not long, and that would not affect the PNN algorithm computational complexity. On the other hand, the possibility of working in an embedded training mode makes the system works online. This is easier for implementation, as well as giving PNN the ability to provide the confidence in its decision that follows directly from the Bayes’ theorem [
36,
37]. Although this process doesn’t affect the system’s performance, it will offer a speedy process as well as perform in a very timely manner.
In this paper, we divide the content into seven parts. The first part is an introduction of detailed information about the topic background and a literature survey. Parts 2 and 3 cover an elaboration on the presented feature extraction method. In the fourth part, we explained the mathematical intuition of the PNN. The results and discussion were managed in
Section 5. Finally, conclusions are presented in
Section 6.
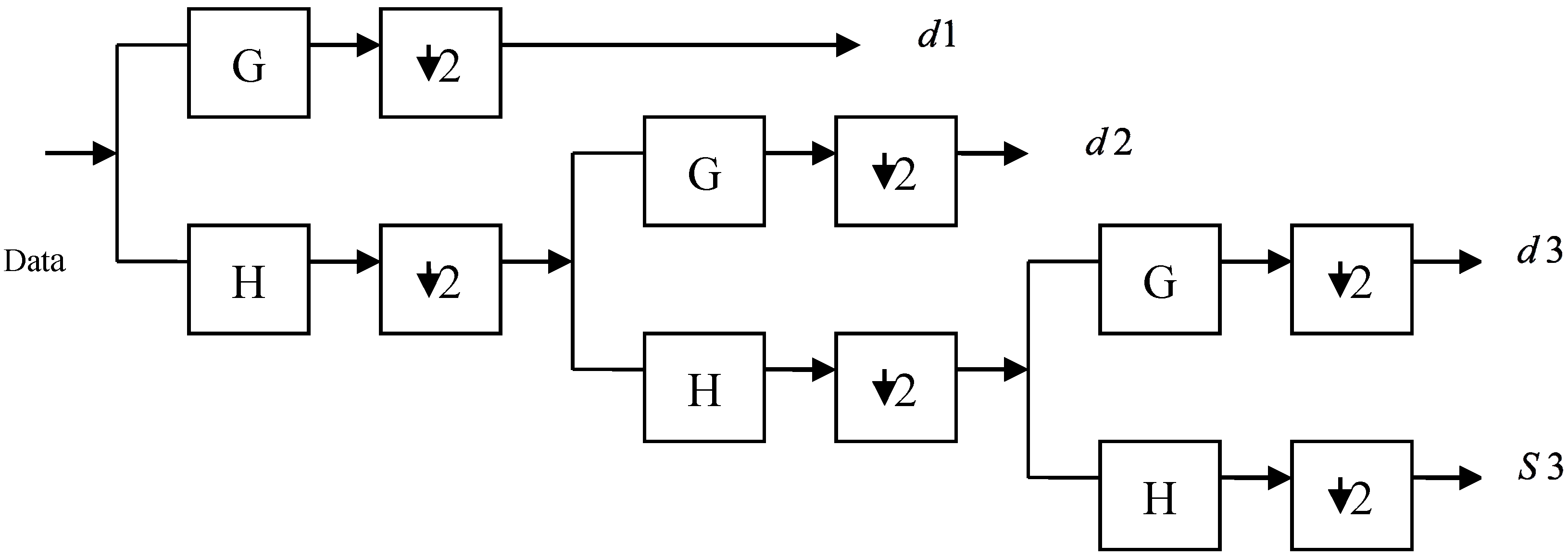
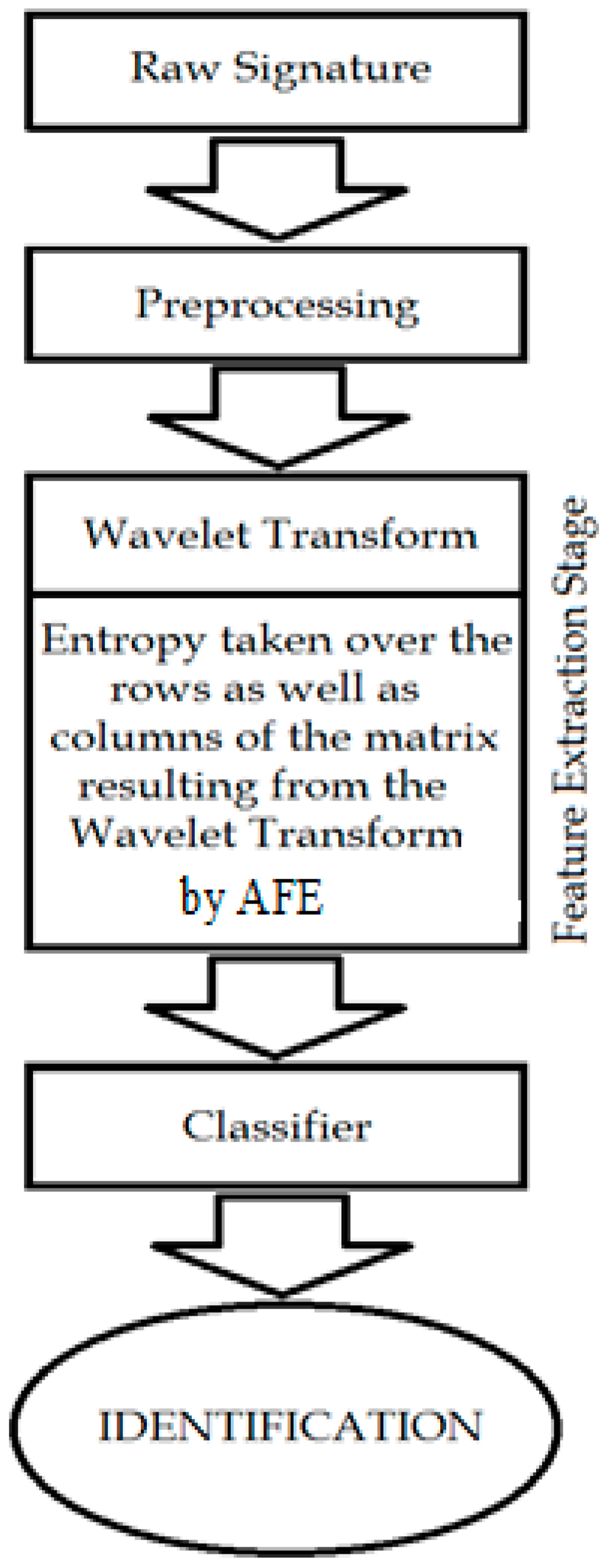
2. Wavelet Transform Entropy for Feature Extraction
For a given orthogonal wavelet function, a library of wavelet packet bases is generated. Each of these bases offers a particular way of coding the data, preserving global energy and reconstructing exact features. The wavelet transform is used to extract additional features to guarantee a higher recognition rate. In this study, either WPT or DWT are applied at the stage of feature extraction [
38], but the extracted data are not proper for the classifier due to their great length. Thus, we have to seek for a better representation of the signature features. Previous studies showed that the use of entropy of WP, as features in recognition tasks, is efficient. A method was proposed in [
39] to calculate the entropy value of the wavelet norm in digital modulation recognition. In the biomedical field, Ref. [
40] presented a combination of genetic algorithm and wavelet packet transform used in the pathological evaluation was introduced [
40], and the energy features were determined from a group of wavelet packet coefficients. A wavelet packet entropy adaptive network-based fuzzy inference system was developed to classify twenty 512 × 512 texture images obtained from the Brodatz image album [
41]. Reference [
42] proposed a features extraction method for speaker recognition based on a combination of three entropy types (i.e., sure, logarithmic energy, and norm) was proposed. The proposed scheme by Sengur [
43] is composed of a wavelet domain feature extractor and an ANFIS classifier, where both entropy and energy features were are used in the wavelet domain. An effective rotation and scale invariant holistic handwritten word recognition system is proposed in [
44] is introduced, such that the packet wavelet transform entropy was utilized to extract the feature vector of a Farsi word image. As seen above, the entropy of the particular sub-band signal may be employed as features for image recognition tasks. In this paper, the entropy obtained from the wavelet transform will be employed over the extracted data from either WPT or DWT, thus creating feature vectors with the appropriate length for the signature classification process. We should take into account the fact that signature recognition differs from speech/speaker recognition, as the length of the training set is rather short, and it is hard in this situation to estimate an accurate statistical model.
4. Classification
Along with the introduction of the original probabilistic neural network by Specht [
48], several extensions, enhancements, and generalizations have been proposed. These attempts are intended to improve either the classification accuracy of PNNs or the learning capability; on the other hand, they optimize network size, which depresses the memory requirements and the resulting complexity of the model, as well as attaining lower operational times [
49]. For the classification of the signature’s feature vectors, we use the PNN as a classifier (seen in
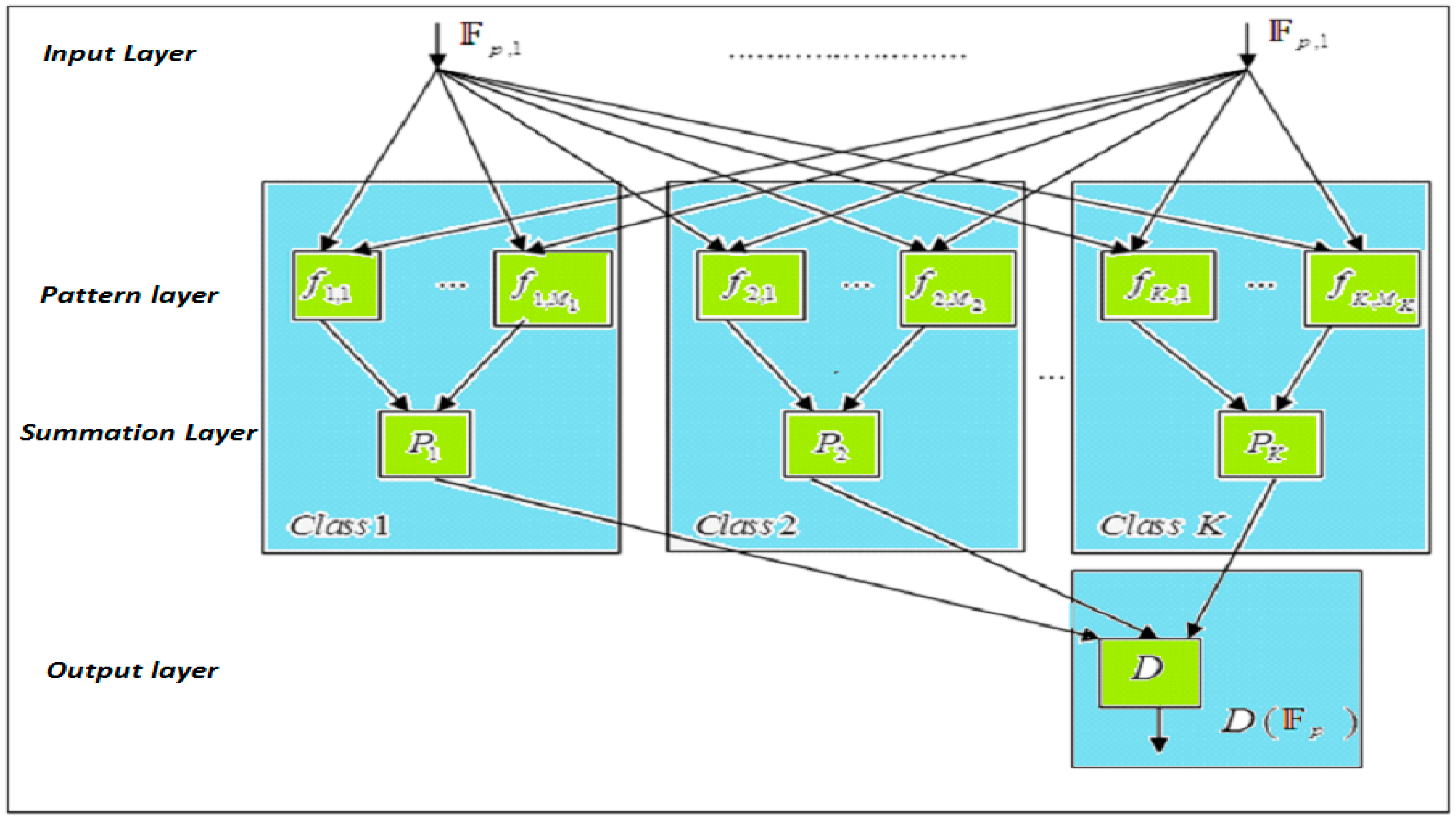
Figure 4). The primary stimulus of such choice is the potential of working in an embedded training mode, which lets the system operate online and makes implementation easier, as well as PNN; moreover, it can provide a credible decision that follows directly from Bayes’ theorem. In addition to the harmless impact, this procedure has on the system performance; it will speed up the process, as well as operate in a real-time manner.
Figure 5 demonstrates the basic configuration of a PNN for classification in K classes. As illustrated in the figure, the first layer of the PNN, indicated as an input layer receives the input vectors to be classified. The nodes in the second layer, namely the pattern layer, are aggregated in K groups according to the class they belong to. All nodes in the pattern layer, also referred to as pattern units or kernels, are connected to all inputs of the input layer. Even though there are various possible probability density function estimators, here, we assume that every pattern unit can be realized as having an activation function, namely the Gaussian basis function:
where
i = 1,…,
K,
j = 1,…,
Mi and
Mi is the number of pattern units in a given class
ki.
σ is the standard deviation, it is also referred to as the smoothing or spread factor. It regulates the receptive field of the kernel. The input vector
x and the centers
of the kernel have a dimensionality
d. exp stands for the exponential function, and the transpose of the vector is indicated by the superscript
T [
46].
Obviously, the total number of the pattern layer nodes is represented as a sum of the pattern units for all classes:
Next, the weighted outputs of the pattern units from the pattern layer that belong to the group
ki are connected to the third layer that is chosen as summation layer corresponding to that specific class
ki. The weights are resolved with the assistance of the decision cost process and the a priori class distribution. The positive weight coefficients
used for weighing the member functions of class
ki need to fulfill the following requirement:
PNN for the classification task is proposed in [
50,
51]. Even though there exist many improved versions of the original PNN, that can be either more economical or show an appreciably better performance, for simplicity of exposition, we embrace the original PNN for classification process. The used algorithm is denoted by
PNN (we used Matlab function “newpnn” to create a PNN) and relies on the following construction:
where
is the input writers feature vectors (pattern) resulting from the feature extraction method discussed previously, and it is used for net training:
where,
is the training vectors’ number.
is the target class vector
The
SP parameter is known as the spread of radial basis functions. The value of one is used for the
SP, since that is a typical distance among the input vectors. If the
SP value approaches zero, the network will perform as the nearby neighbor classifier. The larger the
SP becomes, the more the designed network will account for several nearby design vectors. A two-layer network is created. The first layer acquires radial basis transfer function (RB) neurons (as appears in
Figure 6):
With the use of Euclidean distance (ED) the weighted inputs are calculated;
and its net input with net product functions, which calculate a layer’s net input by combining its weighted inputs and biases. The pattern layer has competitive transfer function (see
Figure 7) neurons, and it utilizes dot product weight function to calculate its weighted input. Its weight function applies weights to an input to get weighted inputs. The proposed net calculates its net input functions (called NETSUM), which calculate a layer’s net input by combining its weighted inputs and biases. Only the first layer has biases. PNN sets the first layer weights to
and the first layer biases are all set to 0.8326/
SP resulting in radial basis functions that cross 0.5 at weighted inputs of +/−
SP. The pattern layer weights are set to
P [
47].
Now, we test the network on new feature vector (testing signatures) with our network to be classified. This process will be called simulation.
5. Results and Discussion
In this work, we deal with two databases. Database A is the GPDS960 offline signature database [
45], which contains data from 960 individuals: there are 24 genuine signatures per writer, and for each genuine signature there are 30 skilled forgeries made by 10 forgers from 10 different genuine specimens. The contained signatures are in “bmp” format, in greyscale and 300 dpi resolution. Database B is also an offline database that contains data from 20 individuals, with 15 signatures per writer. This database was constructed by giving each writer a 5 min session to complete a form that asks for 15 signatures. The signatures were later digitized using a handheld scanner, namely the LG LSM-100 mouse scanner with a 300 dpi resolution. The signatures in database A are in black and white “PNG” format and a 300 dpi resolution. The signatures images were turned into the binary format using fixed thresholding [
45]. Moreover, the signatures in database B are processed by cropping the background margins that have no data, followed by the conversion into a black and white “PNG” format. The signature images were turned into the binary format by thresholding using Otsu’s method and eliminating any possible noise originating from the background. It is worthwhile mentioning that signatures, in both databases, were unified to a fixed size of (80 × 250) matrix, to prepare them for the feature extraction process. The conducted experiments will tackle two main recognition tasks: the identification task (for academic purposes) and the verification task. The verification task is more popular in practice. For the all conducted experiments, database A is considered, 900 writers called class (24 signatures per class), where 10 or 15 signatures for the training of each writer and 14 or nine signatures for testing of each writer were used. For verification, 15 signatures for the training of each writer and nine signatures for testing of each writer were used. This was selected after trying different numbers of training signatures. The choice was taken to the tradeoff between degreasing the dimensionality of the input matrix and the performance. For example, ten signatures for the training of each writer choice decreased the dimensionality of the input matrix but stepped down the identification rate of about 7%. At each time, 50 classes (750 signatures) were trained.
Table 1 shows the typical signature identification results of the proposed system using DWENN concerning the different wavelet functions and the different entropies (Shannon, Log energy, and Threshold). The comparison of the scores with five sub wavelet functions for each wavelet family is also shown. From these tabulated results, we conclude that the system performance of DWENN, by threshold entropy (in our experiments, we have set Threshold over the rows is 250, and Threshold over the columns is 15, this was selected empirically for the best performance), and db10 wavelet function, with recognition rate reaching 89.99%, was the best. The second database, B, had a slightly worse rate, 87%. Besides, the performance concerning the proposed system by means of WPENN was studied. Similar to the previous experiment, the comparison of the identification scores with five subwavelet functions (i.e., Daubechies (Db), Coiflet (Coif), Symlet (Sym), and Biorthanol (Bior)) for each wavelet family is shown in
Table 2.
From these results, we conclude that the system performance of WPENN, by Threshold (in our experiments, we have set Threshold over the rows is 175, and Threshold over the columns is 10) entropy and coif5 wavelet function, with a recognition rate that reaches 92.06%, is the best. Concerning second database B, it had the slightly better rate that reached 92.20%. The conclusions from those results tabulated in
Table 1 and
Table 2 are as follows:
The performance of identification rates WPENN is slightly better than that achieved with DWENN. That why it will be chosen for the final system.
Threshold entropy results outperformed other used entropies.
Concerning the wavelet function, the best results are achieved with coif5. Wavelet functions should be selected empirically, for a given database, method or other circumstances.
Table 3 shows the signature identification results of the proposed system using WPENN by threshold entropy about the different wavelet functions for the fraud-testing database. Looking at
Table 3, we investigate the system’s capability to detect the fraud-testing signatures. Since the results of identification rate of fraudulent signatures are worse to those of genuine signatures, we conclude that the proposed system is capable of detecting the fraudulent ones. It means the fraudulent ones were very bad as testing signals when genuine ones were trained.
To test our method with regards to the number of training/testing signatures, an experiment based on 15/9, 10/14 and first 5/random 5 was conducted. The results are tabulated in
Table 4. Based on the results shown in the table we can conclude that the 15/9 training/testing system is the best choice.
For verification, we construct, at each time for each signer, a training matrix from 10 signatures (five genuine and five fraudulent ones). Then we test the remaining signatures (genuine and fraudulent) to see which are rejected or accepted. If the genuine testing signature is recognized as genuine, it is signified as a true positive (TP) result, but if it is recognized as a fraud, it is signified as a false negative (FN) result. On the other hand, if the fraudulent testing signature is recognized as a fraud it is signified as a true negative (TN) result, but if it is recognized as genuine, it is signified as a false negative (FP) result. This means, the system has Jbeen tested for its accuracy and effectiveness on the 900 classes, which contains both their genuine and skilled fraudulent signature sample counterparts’ (24 genuine signatures and 30 fraudulent signatures per class). At each time, five genuine signatures and five fraudulent signatures of a particular class were trained.
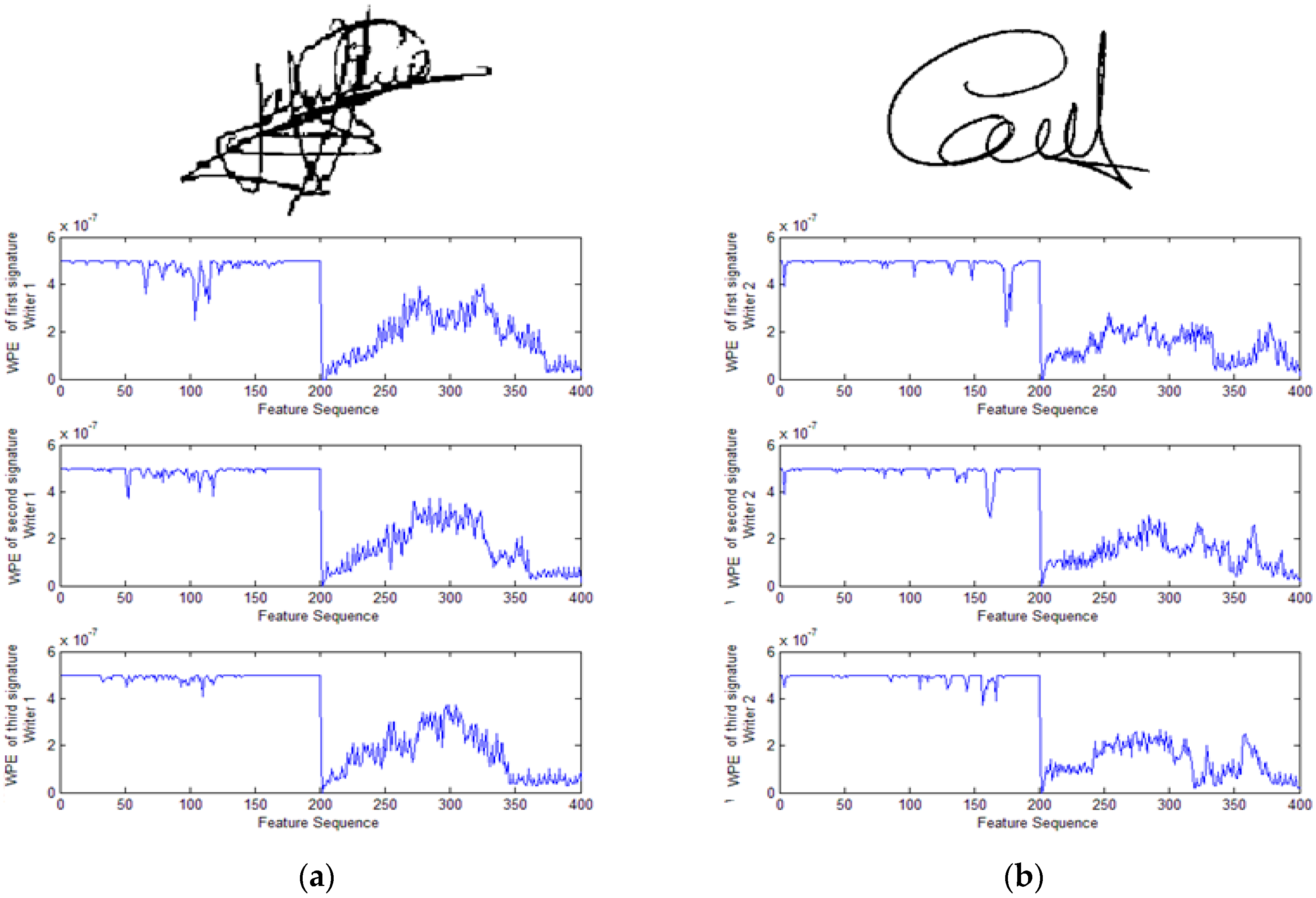
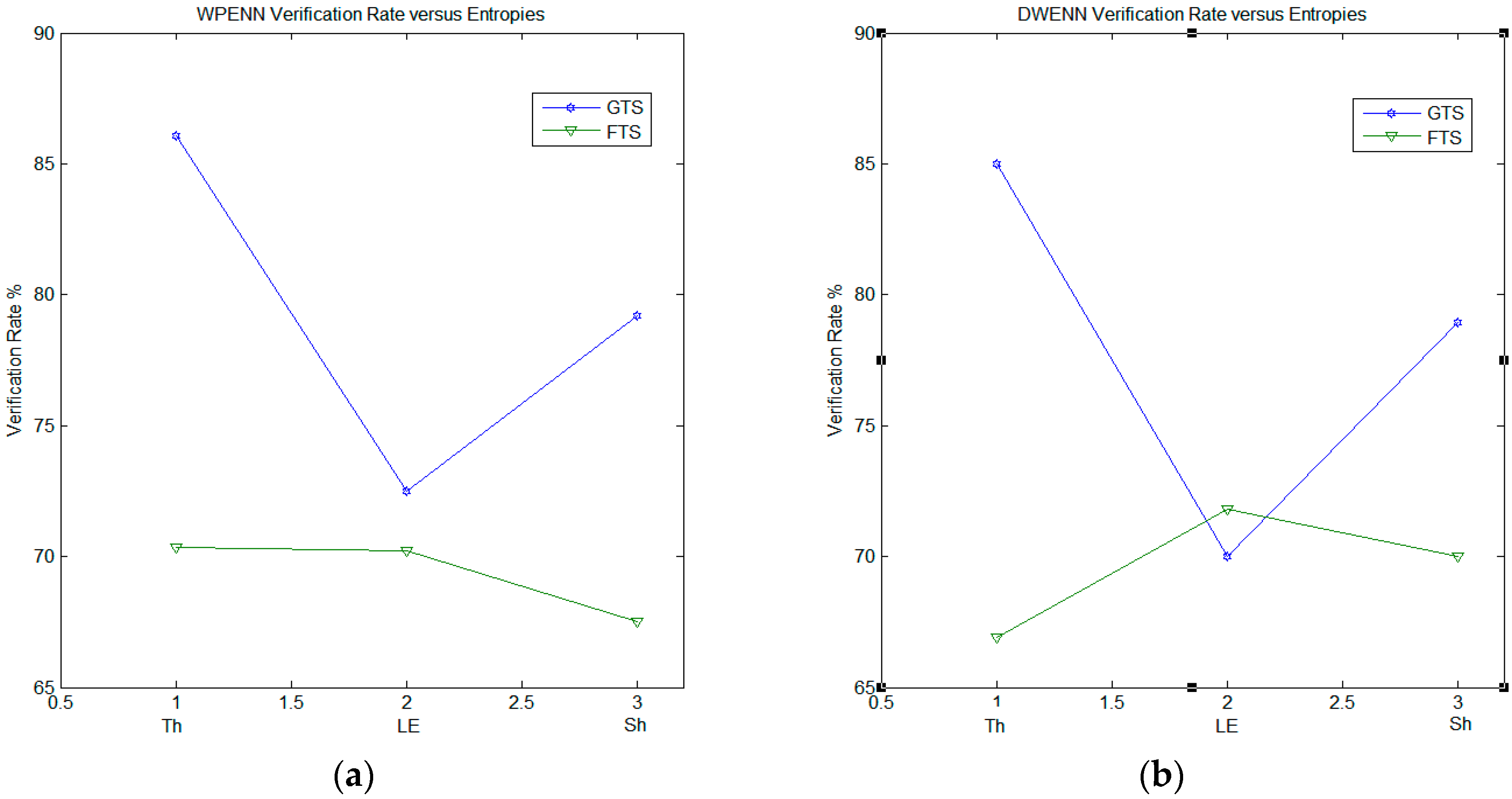
Figure 8 illustrates the verification rate results obtained with regard to the genuine testing signatures (GTS) and the fraudulent testing signatures (FTS) and for three types of entropy (threshold, log energy and Shannon). WPENN (
Figure 8a) and DWENN (
Figure 8b) were involved in the experiment. We can notice that the result of WPENN at threshold entropy is the best.
For comparison purposes, a support vector machine (SVM) [
52] classifier is utilized instead of PNN.
Table 5 contains the verification rate results with regards to GTS and FTS for WPENN, DWENN, WP with SVM (WPESVM) and DWT with SVM (DWESVM). The experiments were conducted over different wavelet functions selected for the best recognition rate. The best recognition rate was achieved for WPENN, at 87.14% for GTS and 74.22% for FTS. In general, Bior2.2 wavelet (its results are bold in the table) function had the highest average calculated for all the methods. SVM had very good results for FTS, particularly in DWESVM.
Table 6 contains the verification rate results with regards to GTS and FTS for WPENN, DWENN, WPESVM and SVM (DWESVM), with a radial basis SVM, with margin parameter C and a Gaussian kernel with parameter G. C and G were optimized through a grid-search with 1 < C < 10
4 and 1 < G < 10
3.
The experiments were conducted over different wavelet transform levels (2, 3, 4 and 5). The best recognition rate achieved for WPENN reached 87.14% for GTS and 74.22% for FTS at level 5 (its results are in bold). In general, level 5 had the highest average calculated for all the methods. We can see that SVM is competitive for PNN particularly for FTS.
In the case of systems that are tested under dissimilar, either unpredicted or predicted conditions (it is to extract objective conclusions), it is very difficult to judge quality. Bearing in mind these restrictions, several systems that are known in the literature methods were used for comparison. Taking into consideration these limitations the same database (GPDS960), some testing samples and some training samples were used.
Table 7 shows the performance of several system proposal results.
The Gaussian Mixture Model (GMM) applied on the sums of the direct signatures matrix rows (without using any extra transformation of the raw data) denoted by RGMM, the GMM applied on the sums of the direct signatures matrix rows and columns denoted by row column GMM (RCGMM), and the GMM applied on the Fast Fourier Transform (FFT) of the vector of the sums of the direct signatures matrix rows and columns denoted by FFTGMM were utilized for comparison. Besides, for these above-mentioned methods, the PNN was investigated, providing that the same feature vectors were considered: the PNN with sums of the direct signatures matrix rows (RPNN), the PNN with sums of the direct signatures matrix rows and columns (RCPNN), the PNN [
51] with the sums of the direct signatures matrix rows (RPNN), and the PNN with FFT of the vector of the sums of the direct signatures rows and columns (FFTPNN) [
57]. The results are tabulated in
Table 7. In this table, the best performance achieved was for our proposed method. We claim that our proposal results would also progress if combined with other systems or by adding original or derived features. In
Table 7, the confidence interval was introduced for each method. The confidence interval states that 95% of the determined recognition rates for different signers are contained in this interval. A wider confidence interval is a bad database sign or not a good feature extraction method. In conclusion, all intervals calculated for presented methods in
Table 7 are sensible. Concerning the second database B, it had a slightly better rate, reaching 92.87%.
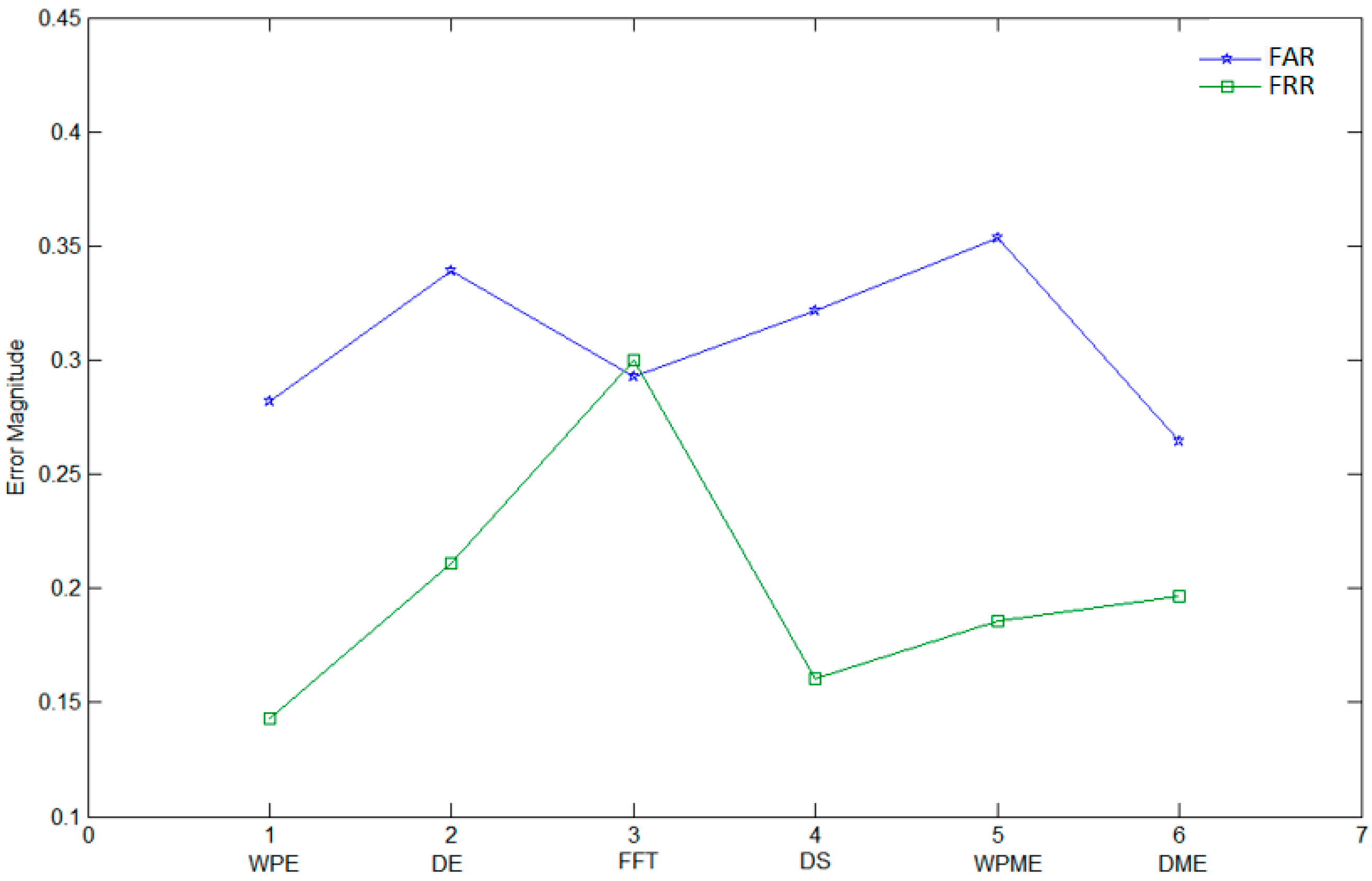
Figure 9 illustrates the comparison results between several feature extraction methods based on False reject rate (FRR) = FN/(TP + FN) and False accept rate (FAR) = FP/(FP + TN). Some genuine signatures are correctly classified as positive (TP), while others are classified as negative (FN); likewise, some fraud signatures are correctly classified as negative (TN), while some are classified as positive (FP). In our experiments, six feature extraction methods were involved in the experimental investigation by testing the first 900 signers from GPDS960 offline signature database. These methods are: the proposed WPE method; DWT with threshold entropy (DE); FFT applied on the rows and columns [
47]; Shannon entropy applied directly on the rows and columns (DS); mix of Threshold, Log energy and Shannon applied on WP (WPME) and mix of Threshold, Log energy and Shannon applied on DWT (DME) [
18,
56]; mix of Threshold, Log energy and Shannon applied on WP (WPME); and a mix of Threshold, Log energy and Shannon applied on DWT (DME). For FRR, the best results were achieved by WPE and DS; WPE was better. For FAR, the best results were achieved by WPE, FFT and DME; DME was the best. The averages of the FAR and FRR results were calculated for the six methods, and the ones for WPE was the best.
In order to assess the performance of the suggested system, we utilize FAR, FRR, and Equal Error Rate (EER). The first 40 signers of GPDS960 offline signature database were utilized for the verification task [
58]. Two other state-of-the-art methods were used for comparison [
59]. EER is determined as the value where FAR and FRR are equal. The EER is the best and most popular single explanation of the error rate of a verification algorithm, and the lower the EER, the lower the error rate of the algorithm. The method with the lowest ERR is considered as the most precise method. Therefore, the results presented in
Table 8 show that our technique proved to be the most efficient method for the accurate signature feature verification of offline handwritten signatures.
One of the most common systems of cross-validation is the leave-one-out cross-validation (LOOCV) system, where the model is continually refit, leaving out a single signature, which is then used to derive recognition for the left-out sample. LOOCV is a case of cross-validation in which the learning procedure is implemented once for each signature, utilizing all other signatures as a training matrix and having the given signature as a single-instance test set [
60]. We applied LOOCV for (40 signers) × (24 signatures) verification so that 960-1 signatures (50% genuine and 50% fraud) was used for training, and one signature was used for testing; we repeatedly changed the testing signature. The final result was calculated as a total result of the 960 testing cases achieved as an 83.37% verification rate.