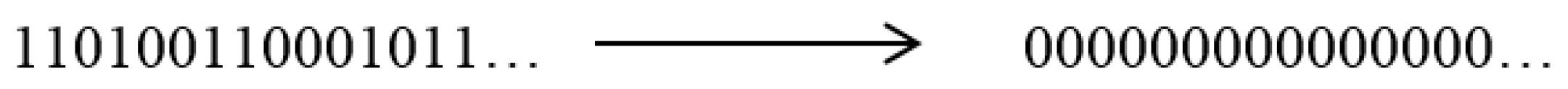Maxwell’s Demon—A Historical Review

Abstract

For more than 140 years Maxwell’s demon has intrigued, enlightened, mystified, frustrated, and challenged physicists in unique and interesting ways. Maxwell’s original conception was brilliant and insightful, but over the years numerous different versions of Maxwell’s demon have been presented. Most versions have been answered with reasonable physical arguments, with each of these answers (apparently) keeping the second law of thermodynamics intact. Though the laws of physics did not change in this process of questioning and answering, we have learned a lot along the way about statistical mechanics and thermodynamics. This paper will review a selected history and discuss some of the interesting historical characters who have participated.

1. Introduction

Many challenges to the second law of thermodynamics involve a device widely known as a Maxwell’s demon. It has been more than 140 years since Maxwell presented the first form of this hypothetical, eponymous device, but since then many other forms have been proposed. This brief historical review cannot possibly discuss all such forms. Instead, this paper will discuss a few landmark results that helped to identify key principles and to lay the foundations for work done up to approximately the year 2000 in Section 2, Section 3 and Section 4. Section 5, Section 6, Section 7 and Section 8 will briefly describe some of the progress made since the beginning of this century. The references given here contain more results that the interested reader can follow to gain a deeper understanding. Other papers in this symposium are devoted to current research.

2. Early History

The main purpose of this review is to discuss the history, and of course that begins with Maxwell, himself. However, it is appropriate to begin a few years after Maxwell and then get back to him in due course. There is a global statement about the second law of thermodynamics that many people working in this field have seen. It was presented as an opening and a challenge to the symposium:

The law that entropy always increases—the second law of thermodynamics—holds, I think, the supreme position among the laws of Nature. If someone points out to you that your pet theory of the universe is in disagreement with Maxwell’s equations—then so much the worse for Maxwell’s equations. If it is found to be contradicted by observation, well, these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of thermodynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation [1].

—Arthur Eddington

This symposium includes some interesting challenges to the Second Law, with and without Maxwell’s demon, but Eddington reminds us that this work is not easy and that the price of failure can be high. If you want to convince me that you have built a Maxwell’s demon, then give me a computer that I can plug into my bathtub. Once you do that, we can all agree that we have a successful demon. The computer in the bathtub includes many relevant parameters, such as heat, entropy, and information.

Now it is appropriate to return to the roots of the problem. This was presented in his 1871 book Theory of Heat and is as follows:

One of the best established facts in thermodynamics is that it is impossible in a system enclosed in an envelope which permits neither change of volume nor passage of heat, and in which both the temperature and the pressure are everywhere the same, to produce any inequality of temperature or of pressure without the expenditure of work. This is the second law of thermodynamics, and it is undoubtedly true as long as we can deal with bodies only in mass, and have no power of perceiving or handling the separate molecules of which they are made up. But if we conceive a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are still as essentially finite as our own, would be able to do what is at present impossible to us. For we have seen that the molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower ones to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics.

[2]

Figure 1 shows a common graphic used to illustrate Maxwell’s description.

Notice that Maxwell did not use the term “demon” in this passage. That designation was given several years later by William Thomson who, coincidentally, was himself named later as Lord Kelvin. To be precise, Thomson called it “Maxwell’s intelligent demon” [3]. As it stood in the late 19th century, there was no satisfactory explanation of why this version of Maxwell’s demon could not work. Any device that could make such measurements and manipulations on individual molecules was certainly beyond the ability of experimentalists of the day.

3. Different Demons

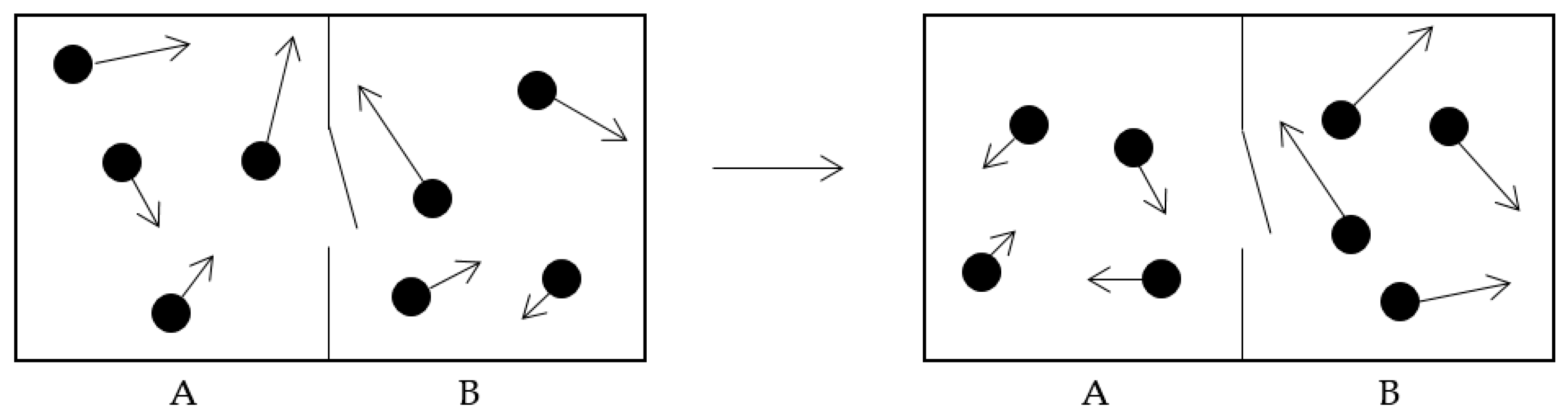
Maxwell’s device described above is an example of what is called a “temperature demon”, because it creates a temperature difference that can be used to run a heat engine. The same intelligent creature might pay no attention to the relative speeds and simply open the trap door selectively to allow molecules to flow one way and not the other, again taking advantage of their random motion in a gas. This would violate the Second Law in a statistical sense by reducing the entropy of the ensemble. In a practical thermodynamic sense the violation of the Second Law follows because the resulting pressure difference could also be used to do work, with zero work input. Thus, this version is called a “pressure demon”.

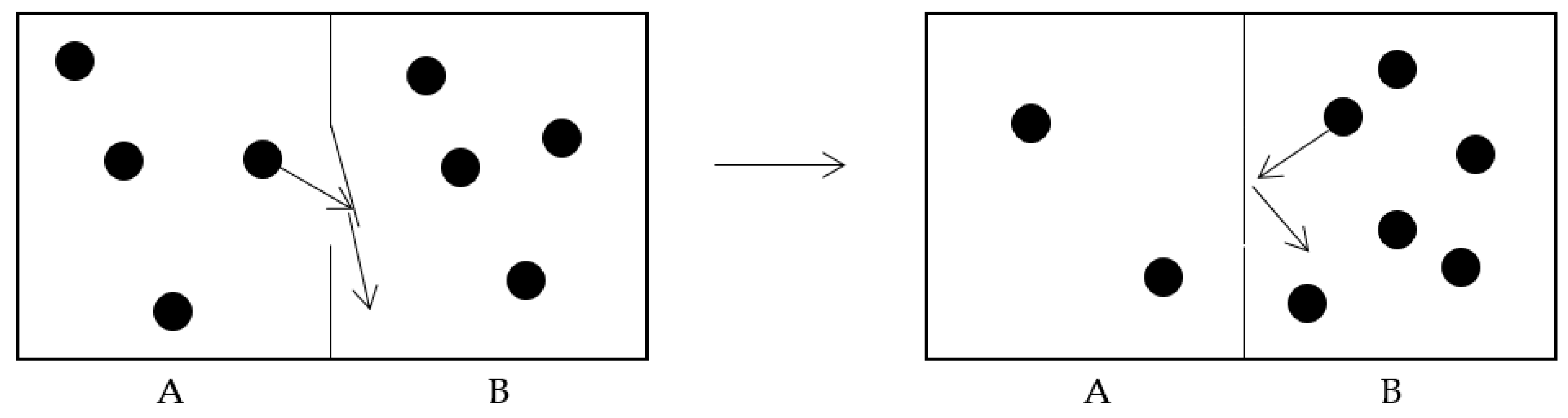
Moving forward to 1912, Marian von Smoluchowski [4] envisioned an automated pressure demon, as shown in Figure 2. A spring-loaded trapdoor acts as a one-way valve to allow for an increase in density on one side while preventing flow in the reverse direction. Like the temperature difference considered above, the resulting pressure difference could be used to do work. The net result would be a cyclic process, with some work output and zero work input, in violation of the Second Law.

An advantage here is that no intelligent being is needed to sort the molecules, nor is any futuristic, science-fiction-based equipment needed to measure and process information on individual molecules. However, this device seems not to work because the door must become thermalized and spring open without being struck by a gas molecule. This allows a backflow of molecules, which becomes increasingly probable as soon as any pressure difference arises. The process will not be cyclic unless the thermal energy is removed from the door, which presumably increases the entropy of a heat bath and saves the Second Law.

The automated pressure demon has been studied extensively in recent years by computer modeling. Such computational study allows for quantitative analysis of the energy and entropy balance. One interesting study was done by Skordos and Zurek [5], who modeled the Smoluchowki system using up to 500 molecules and a trap door that could slide on frictionless rails to prevent energy loss. They first showed that if the system is allowed to evolve naturally, the result is an equal distribution of particles between the two chambers. This was verified by adding a second hole away from the trap door and looking for particle flow through the hole. The net flow turned out to be zero, verifying that the system is in equilibrium when the particle densities are equal. Finally, Skordos and Zurek showed that if some thermal energy is removed from the door systematically, then the device does achieve the goal of establishing a density difference. Thus, they showed that such a device could act as a one-way valve for molecules, provided the door was de-thermalized by removing its thermal energy systematically. De-thermalizing the door does in fact reduce its random motion and prevents undesired opening and backflow of molecules.

The Skordos/Zurek system was extended by Rex and Larsen to include a computational accounting of statistical entropy changes in the process [6]. In this study, we began by designing a similar numerical simulation and obtaining results equivalent to those of Skordos and Zurek. We then computed the entropy decrease created by this “demon” using the refrigerated door system. According to the Second Law, this entropy decrease should be compensated at a minimum by the entropy increase associated with dumping the trap door’s thermal energy into a heat reservoir. Upon performing this simulation and comparing the two entropy changes, we were at first astounded to find that we were able to obtain a net entropy decrease. Naturally, at this point we checked our programming and varied different parameters, in an attempt to discover an error. This demon could not really defeat the Second Law, could it?

What was happening was actually quite subtle and turned out to be an important lesson. Using the models described by Maxwell and Smoluchowski, we began the simulations with an initial configuration in which the two densities were equal, with the goal of using the refrigerated trap door to make the densities unequal. With that initial configuration, our simulation was quite robust in producing the net entropy decrease. However, that was not the case when we tried other initial configurations. If there is an initial density difference, the system’s net entropy can increase significantly in the sorting process. We found that there is a functional dependence of net entropy change upon initial density difference, with the largest initial density differences resulting in the largest net entropy increase.

In retrospect this result should not have been surprising. Consider Maxwell’s original conception of the demon, shown in Figure 1: Assume (analogous to our assumption described above) that there are initially identical distributions of molecules and molecular speeds in the two halves of the box. Then one could simply open the trap door for a time, allowing molecular flow, but making no effort to observe or sort the molecules, before closing the door and examining the two halves of the box. What will be the result, in terms of particle flow and entropy change? Notice that the initial configuration was one of maximum entropy. Therefore, any particle flow at all will either leave the net entropy unchanged or decreased. Such a “non-demon” device seems to have lowered the entropy of the universe, in violation of the Second Law.

Of course, the Second Law is not violated by the non-demon. In any real experiment, the initial configuration would be a random one. Statistically speaking, it is quite likely that the multiplicity Ω of the initial configuration would be slightly less than the maximum. The non-demon experiment might increase or decrease that multiplicity. On average, one expects that the multiplicity (and, hence, the statistical entropy) would not change at all, provided that there are no other losses.

In an attempt to examine this proposition using our simulation, we computed the entropy change for each of a series of initial configurations, including a range of initial density differences. We then computed a weighted average of the net entropy change for all the simulations, with the weighting taking into account the relative probability of the assumed random initial state. In other words, we created an ergodic ensemble of initial states. The result of the ergodic ensemble was a net entropy change of zero, within the margin of error of our computational model. Our numerical simulation showed that one could only decrease entropy by starting with a specially-prepared state of relatively high entropy, and that if one instead begins with an ergodic ensemble of such states, there will be at minimum zero net entropy change for all states.

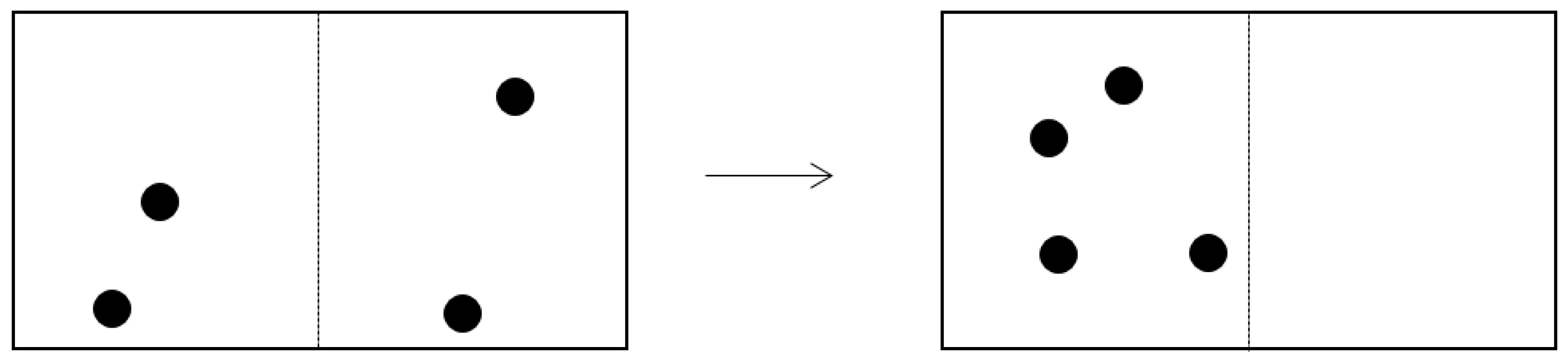
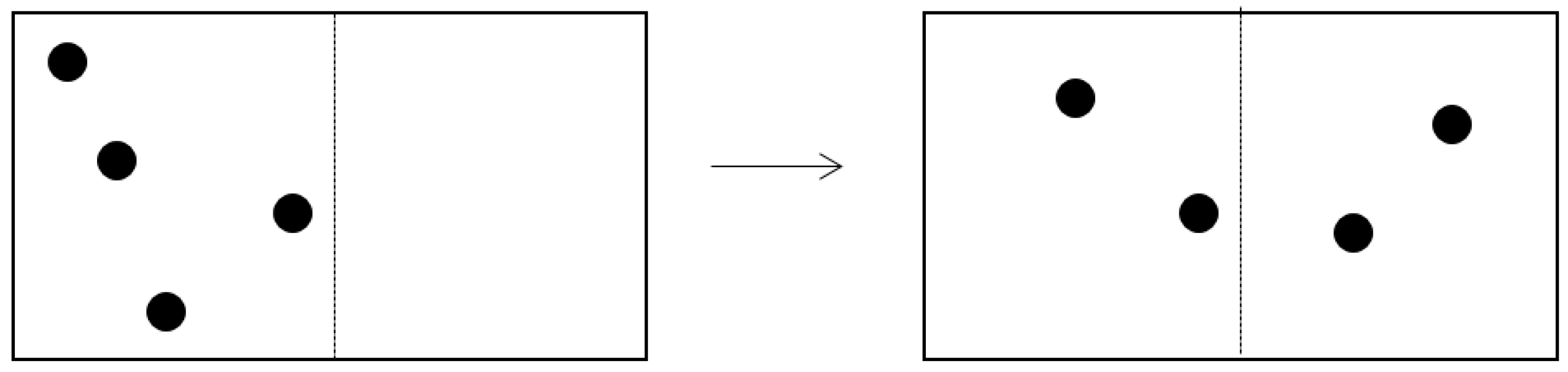
A simpler version of this principle is illustrated by the following. Suppose you have a gas of four molecules. If you start with two molecules in each half (Figure 3), this is the maximum entropy state because it has the maximum multiplicity Ω. Observed later, there cannot be larger multiplicity, but there may be less, as shown in Figure 3.

The statistical entropy of the final state is lower and, thermodynamically speaking, there is a significant pressure difference, which could be used to do work. This does not mean you have created a demon or reduced entropy. This is because any fair accounting has to start with an ergodic ensemble of states, including this one (Figure 4) that offsets the first.

It is straightforward to show that an ergodic ensemble of initial and final configurations leads to exactly zero net entropy change for the four-molecule gas.

An objection might be raised, saying that a particularly clever device (or demon) could prepare an initial state with maximum multiplicity, which could subsequently be expected to decrease, either with the trap door device or the non-demon. However, such an initial preparation raises the issues of measurement and information, which will be addressed later in this paper (Section 4). Additionally, note that there is a negligible chance for any such fluctuation from equilibrium in a macroscopic system.

Returning to the history, in 1929 Leo Szilard made an important observation [7] that led to a good deal of subsequent progress. Incidentally, in addition to his work as a theoretical physicist, Szilard was an important historical figure. To mention just one thing, in 1939 he wrote a letter that Einstein signed, which was then sent to President Roosevelt. This letter encouraged the government to look into the dangers and possibilities of a fission weapon and began a chain of events the resulted in the production of atomic bombs in 1945.

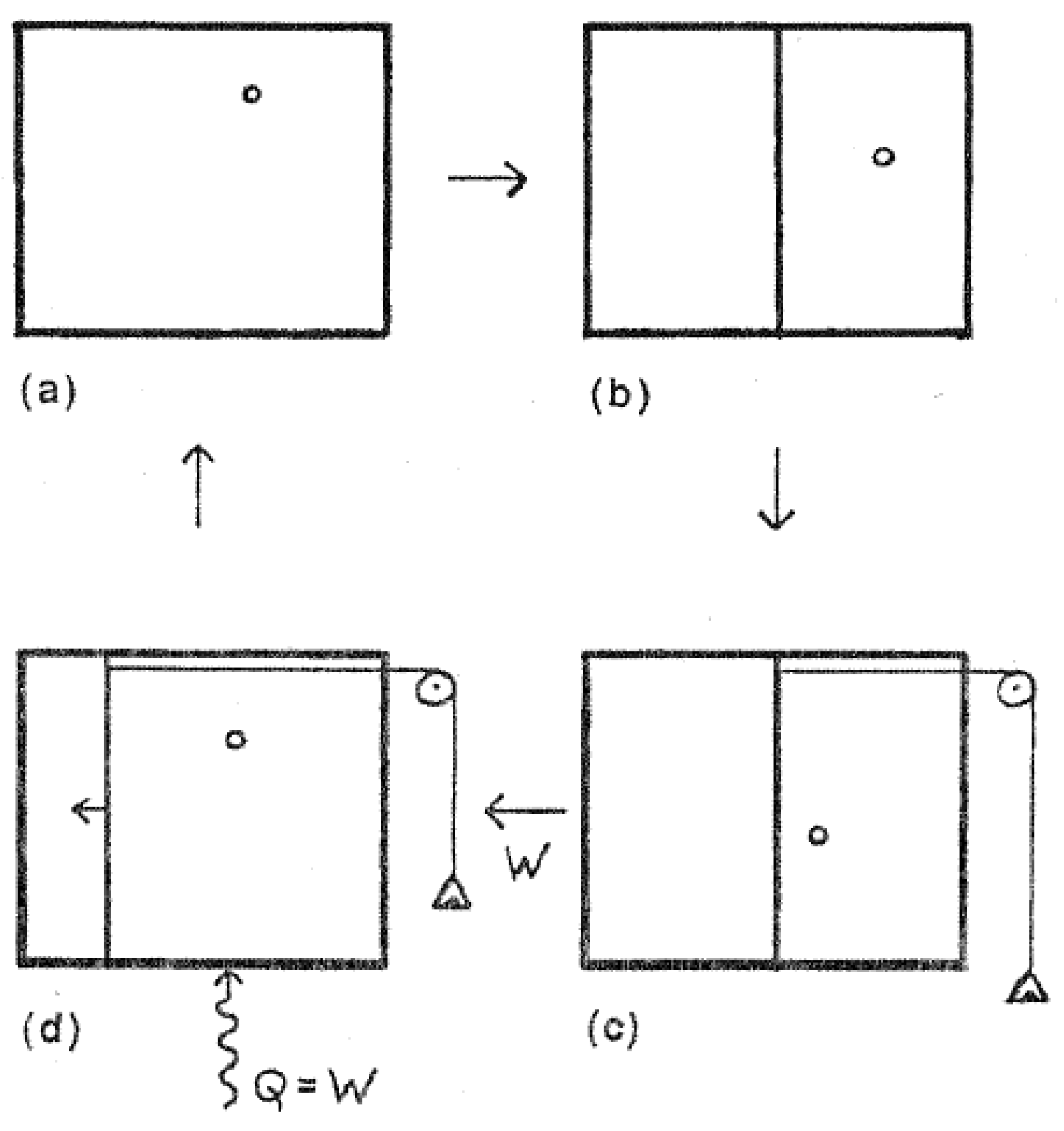
The device Szilard invented in 1929 is called a one-molecule engine and is illustrated in Figure 5. A good account of Szilard’s one-molecule engine is given in [8].

The Szilard engine is delightfully simple. In the initial configuration (a), a one-molecule gas is enclosed in a chamber. It is assumed that the gas is in thermal equilibrium with the container walls, which are insulated from the outside world. In (b) a partition is placed in the chamber, separating the chamber into two parts. This forces the molecule to be on one side or the other. In Figure 5 the molecule happens to be on the right side of the partition. In (c) the partition, which is free to slide horizontally without friction, is attached to a frictionless pulley and hanging weight. The weight is small enough so that when the molecule strikes the partition and rebounds, the collision drives the partition to the left. This raises the weight and in doing so does work W against gravity. In the process energy is transferred from the gas to the weight, so in order to complete a cyclic process it is necessary for the gas to absorb heat Q = W from a reservoir (d), thus restoring the gas to its initial state. The net result over one cycle or many cycles is that 100% of the heat absorbed has been converted to work, in violation of the Kelvin-Planck form of the Second Law.

This is a beautiful conception in that it is perfectly automated. Like Smoluchowski’s demon, it may seem to require no smart microscopic creature to make a measurement. However, the description in the preceding paragraph ignores the subtle fact that some measurement is necessary. In step (c) it is necessary to know the location of the molecule relative to the partition, so that the weight-pulley system can be placed properly. In order for the device to work as described, the weight and pulley have to be positioned with knowledge of the molecule’s location, on the left or right of the partition. If the pulley and weight are placed on the incorrect side, the molecule colliding with the partition pushes the weight downward. The experiment is then uncontrolled, and there is no guarantee of net positive work in an ensemble of experiments.

Why is measurement such an important part of the picture for this and some other demons? This will be elucidated in Section 4. However, Szilard deserves a good deal of credit for advancing the discussion. To quote from the summary in [8]:

While he did not fully solve the puzzle, the tremendous import of Szilard’s 1929 paper is clear: He identified the three central issues related to information-gathering Maxwell’s demons as we understand them today—measurement, information, and entropy—and he established the underpinnings of information theory and its connections with physics.

[8]

4. Measurement, Information, and Erasure

The possibility that there might be some cost in making measurements vital to a demon’s operation brings us to 1951 and the work of Leon Brillouin [9,10]. He focused on the process of measurement. By that time quantum mechanics was well established, and because we are dealing with molecular motion, it is proper to ask whether the observer or the act of measurement has any effect on the outcome. Brillouin examined what would happen if scattered photons are used to determine the positions and speeds of molecules in a Maxwell’s demon device. He noted that doing so generates entropy in the system, via thermal energy transferred from the photons. Brillouin showed that this entropy is sufficient to offset the entropy reduction accomplished by sorting of a traditional demon or the work done by a Szilard engine. This is because locating any particle to within a certain positional uncertainty requires scattering a photon with wavelength no longer than that uncertainty. Locating a particle more precisely requires a photon with shorter wavelength and, thus, higher energy E = hc/λ.

More precisely, Brillouin showed that the minimum entropy added in measurement is k ln 2 per particle, where k is Boltzmann’s constant. In the Szilard engine, this would be exactly equivalent to the difference in statistical entropy between knowing and not knowing on which half of the partition the molecule is located. Brillouin noticed this connection and defined negentropy, or negative entropy, associated with having information. For a time this connection between entropy and information seemed to save the day for the Second Law by showing how a Maxwell’s demon could not succeed in its entropy-reducing mission.

Incidentally, the connection between information and entropy had been addressed independently by Claude Shannon and Warren Weaver [11]. They introduced a concept called information entropy to study the carrying capacity of communication channels. The connection between Shannon’s entropy and thermodynamic/statistical entropy was made by Jaynes [12].

Brillouin’s analysis was interesting, but one might argue that it relies too heavily on the process used to gather information. This leads us to the seminal work of Rolf Landauer, who in 1961 [13] suggested that we ignore the information-gathering process and focus instead on what happens when information is discarded. The logic of this argument is two-fold. First, as with any demon-involved process that is designed to reduce net entropy, it is necessary to consider a cyclic process. In other words, the physical state at the end of the process must be exactly the same as at the beginning, in order to give a fair accounting of all entropy changes. Then the entropy increase that results from memory erasure appears in the environment. This leads to the second part of the argument, in the form of a phrase attributed to Landauer: “Information is physical.” (For example, it appears in the title of one widely quoted article [14]). That is, information is not some ethereal quality, but rather it corresponds to a particular physical state that carries information because it is distinguishable from other possible states.

In [13] Landauer defined “logical irreversibility” in reference to memory erasure, analogous to a physically irreversible process such as heat flowing from a warmer body to a cooler one. For example, erasing a segment of memory might look like the process shown in Figure 6. The initial state is mapped irreversibly into a standard reference, and the initial memory cannot be recovered without repeating the process that created it. The result is a loss in the number of degrees of freedom for the system, which is “dissipation” in a computational sense.

Landauer stressed that erasure was the key, because computational processes, such as reading and writing that essentially move bits around, but do not involve erasure can, in fact, be done with arbitrarily little dissipation, approaching reversibility.

Landauer’s work was extended by his colleague Charles Bennett [15,16]. Bennett first imagined that a reversible computer might be built by making each step logically reversible. After obtaining the program’s output, the computing steps can be retraced to restore the initial state. Bennett then considered a Maxwell’s demon having a memory that was initially in a standard reference state prior to measurement. Making the measurement expands the phase space of the memory, which is compressed again in the erasure process, as in Figure 6. The erasure generates entropy, which offsets the entropy reduction effected by the demon. Quantitatively, the entropy generation is k ln 2 per bit of memory, which is simply the Boltzmann entropy of a two-state bit. The generation of entropy by memory erasure is generally referred to as Landauer’s principle.

The Landauer-Bennett analysis is quite general in that it can be applied to any information-gathering demon, such as Szilard’s engine or Maxwell’s original conception. For example, Szilard’s demon retains information about the molecule’s location, which was needed for proper placement of the weight-pulley system. Because information is physical, a physical process is needed to erase the memory. For Maxwell’s original demon, the same is true. There is at least one bit of information about each gas molecule to be sorted, and that information does not disappear after sorting. Of course, information erasure does not apply to automated demons, such as Smoluchowski’s demon.

The analysis just described might still sound rather mysterious. Consider, however, that it is analogous to the well-known laboratory method of adiabatic demagnetization, which is used to cool materials by using the statistical-thermal properties of paramagnetic salts. The process is analogous (though in reverse) because the paramagnetic spins can be binary, just like the computer memory. Eliminating the external magnetic field increases the salt’s entropy, resulting in a flow of thermal energy from the sample, and a compensating generation of entropy in a thermal bath.

This analysis—applying Landauer’s principle to defeat the demon—has come under some criticism, specifically from John Norton, who has argued that the Landauer-Bennett analysis invokes the Second Law in order to prove it [17,18]. Instead Norton has proposed to exorcise the demon without resorting to the Landauer-Bennett approach and, indeed, without any reference to information. On the other hand, Jeffrey Bub has used an analysis of the thermodynamics of computation to claim that Landauer’s analysis is correct and that Norton’s is not [19]. A similar approach to Norton’s was described by D’Abramo [20], who considered a modified Szilard engine that does not depend on information and concluded that thermal fluctuations make it impossible for such an engine to work.

5. Molecular Ratchets

Theoretical discussions of the late twentieth century, including the work of Landauer, Bennett, and Norton described above, focused attention on some of the key elements of the Maxwell’s demon phenomenon, particularly on the relationship between entropy and information. Around the end of the century, some researchers began to turn attention on building a real device that could replicate some features of a Maxwell’s demon. Such a device would need to be small, at least at first, so that any motion away from equilibrium would be easily detectable and so that results might be replicable. This is analogous to building Maxwell’s original demon using a gas that contains only a small number of particles.

In his Lectures on Physics series, Richard Feynman introduced a now familiar device [21] that served to inspire some of this work. Feynman’s idea was to have a ratchet and pawl machine on one end of a long axle. The other end of the axle has propeller vanes that can be turned using the random molecular motion of a gas. The ratchet and pawl allows the axle to be turned in only one direction. As the axle turns, a weight is lifted by a string that is wrapped around the middle of the axle. It is the lifting of the weight that ultimately does work, reminiscent of the Szilard demon. The intended effect of this device is to convert the random thermal motion of a gas to work, which would be in violation of the Second Law. Feynman showed in careful detail why this could not happen. Similar to the Smoluchowski demon, continued motion of the mechanism results in heating, which would cause random thermal motion of increasing amplitude. This eventually lifts the pawl off the wheel, and it does so with increasing amplitude as more work is done. The weight would then fall backwards, resulting in zero net work in keeping with the Second Law. Although Feynman’s analysis has been shown to be flawed [22], that flaw dies not invalidate the conceptual ratchet model, as long as conduction through the device is negligible.

Although Feynman’s ratchet and pawl cannot defeat the Second Law, it suggests that there is hope in using some kind of device that moves preferentially in one direction. Many years ago Brillouin [23] suggested that a circuit containing a diode and a resistor might electronically simulate Feynman’s device, because the diode serves as a one-way valve for current flow, within the proper applied voltage limits. Applying voltage to the circuit heats the resistor, causing current fluctuations that can be rectified by the diode. The net effect is to use heat to produce work, in violation of the Second Law. However, it is impossible to run such a device in a cyclic operation, because the operation requires a temperature difference between the diode and resistor, which could not be maintained without intervention. Brillouin cited this result as an example of the principle of detailed balancing [23].

Early in this century, a number of research efforts in this area focused on reactions involving complex organic molecules. At first glance, consideration of the thermochemistry of reactions suggests that this is no way to make a Maxwell’s demon, because chemical reactions generally proceed toward equilibrium in a way that minimizes free energy. On the other hand, we know that living systems constitute an extreme case of non-equilibrium. Living systems are small islands of relative improbability in a large sea of entropy. Therefore, under the right conditions, some organic systems can clearly move in a preferred direction away from equilibrium.

A good example of such a device is the one created by David Leigh [24]. For this purpose the Leigh group developed a complex motor protein called rotaxane. They showed that having information about the location of a particular macrocycle in rotaxane allowed them to use directed light energy to drive the system into a preferred, non-equilibrium state. This device effectively uses the Brownian motion within the system to create a lower-entropy state, reminiscent of Maxwell’s original conception. Later it was shown that a rotaxane can be driven away from equilibrium in a similar way through chemical means [25]. However, it should be noted that these devices (and similar molecular ratchets that have been created in the laboratory) do not threaten the Second Law because of the required energy input.

6. Photonic Maxwell’s Demon

A novel version of Maxwell’s demon does not require anything as complex as a large organic molecule but instead uses two beams of light [26]. Consider again Maxwell’s original conception, with two volumes of gas originally in equilibrium that are then sorted to produce an imbalance of temperature or pressure. The photonic version of the demon uses two light beams, which are initially identical. Sorting is accomplished using a device called a feed-forward operation that directs brighter and dimmer pulses in different directions. The two pulses are subsequently directed to photodiodes that use the energy imbalance to charge a capacitor.

There is no claim here that the Second Law has been violated. As it was put succinctly in [26]:

As the measurement devices are randomized in this process, the experiment cannot violate the second law of thermodynamics.

However, there is still the possibility of using the photonic demon as a practical generator of energy, if the information about the photon beams can be correlated to the capacitor output. Such information would then allow for the directed output to create useful work, in an analogy with the Szilard demon. Whether or not such a practical device is ever realized, the result of this work is further extension of the ideas expressed by Landauer and Bennett on the role of information for Maxwell’s demon. For example, in a recent study Shu et al. examined the power output of an optical Maxwell’s demon as a function of the photon correlation and obtained results consistent with the Landauer/Bennett analysis [27]. This is still a very new field that has exciting prospects for the future.

7. Information and Quantum Computing

Due to the connection between Maxwell’s demon and information, it is natural to consider connections to the relatively new field of quantum computing, which is distinguished by containing information in quantum states (and their superpositions) rather than discrete bits as in classical computing. This novel way of encoding information might have implications for how information is connected to entropy and the Second Law.

A good summary of these connections was given by Vlatko Vedral [28,29]. It turns out that Landauer’s principle (described above) places a limit on the entanglement that is possible between to separately manipulated quantum subsystems. Error-correcting codes are analogous to Maxwell’s demon, in that they prevent an increase in entropy that is associated with propagation of error. In terms of error correction, Vedral showed that information is required for such correction, and further that the completion of a cyclic operation requires that the information be discarded, with a corresponding generation of entropy as per Landauer’s principle.

8. Other Recent Work

What can be left to do? There are several other variations of Maxwell’s demon that have been tried in recent years.

After experiments using large molecules, photons, and entangled quantum states (all described above), it makes sense to make a system using the simplest possible particle, the electron. This was done recently by Koski and others [30]. This elegant experiment involved measurement of one electron as a single bit of information, and in doing so provided direct evidence supporting Landauer’s principle.

The Koski experiment is modeled after the Szilard engine described earlier but is entirely made up of solid-state electronics. Instead of Szilard’s two chambers separated by a partition, there are two metallic islands connected by a tunnel junction. The entire apparatus is kept at low temperature (about 0.1 K) to limit thermal noise. In Szilard’s device, there is hypothetically only a single gas molecule. In Koski’s electronic system, there are naturally many free electrons on the metal islands, but a single excess electron can be detected by an electrometer. (Note that this corresponds to the detection step in the Szilard engine.) After detection, an applied voltage is used to control the electron’s tunneling, and work kT ln 2 is induced by thermal activation. This amount of work corresponds to the theoretical value for a single bit of information. As with the Szilard engine, the conversion of heat to work kT ln 2 cannot be viewed as a violation of the Second Law, because the information bit remains at the end of the process and most be erased, as per the Landauer principle.

Mark Raizen and colleagues have built a device that uses the technique of laser cooling to accomplish something very close to Maxwell’s original conception, by laser cooling a gas of rubidium atoms [31]. In this device gas atoms are effectively sorted using a pair of lasers. One laser excites the gas atoms into an energy state in which they are affected by a second laser, which effectively pushes the atoms to one side of the container. Thus, this device simulates the Smoluchowski type of demon. Analysis shows that this sorting does not imperial the Second Law. As Raizen explains:

“…whereas the original photon was part of an orderly train of photons (the laser beam), the scattered photons go off in random directions. The photons thus become more disordered, and we showed that the corresponding increase in the entropy of the light exactly balanced the entropy reduction of the atoms because they get confined by the one-way gate. Therefore, single-photon cooling works as a Maxwell demon in the very sense envisioned by Leo Szilard in 1929.”

[31]

Sagawa and Ueda have addressed the Maxwell’s demon issue in the framework of a much larger work on the thermodynamics of feedback control [32]. After establishing a general theory of feedback control, Sagawa and Ueda consider as an example a Szilard engine with measurement errors. Measurement of the Szilard gas particle is assumed to be done with a particular error rate. Then work is extracted from the engine and the barrier removed, as in Szilard’s conception. The work extracted is found as a function of the measurement error rate assumed above and is found to be consistent with the Second Law. As a second example, Sagawa and Ueda analyzed a feedback-controlled Brownian ratchet and found it also to be in agreement with the Second Law.

Landauer’s principle and the physics of information are the basis for further analysis done by Mandal and Jarzynski [33]. They describe a fully automated device that uses thermal energy from a reservoir to perform mechanical work. Doing so, however, requires that information be stored in a memory register, with one bit of information corresponding to work kT ln 2. As in the Szilard engine, this work is assumed to consist of raising a weight in a gravitational field. The demon can then reverse the process, or if you prefer complete a cyclic process, by lowering the weight in a step that simultaneously erases the stored memory. The idea of using an information reservoir to address the Maxwell’s demon problem has been studied further by Barato and Seifert, who developed a generalized theory of stochastic thermodynamics, first for a single information reservoir [34] and then for multiple reservoirs [35].

An excellent up-to-date review was done recently by Parrondo, Horowitz, and Sagawa [36]. This comprehensive review touches on most of the topics that are typically related to Maxwell’s demon, including the Szilard engine, measurement, information, and Landauer’s principle. It contains 93 references, mostly to recent work, and anyone interested in following the recent work is urged to peruse those references. I will cite here two important examples that speak directly to Landauer’s principle. First, Toyabe et al. have used non-equilibrium feedback manipulation of a Brownian particle to perform a Szilard-type conversion of information to energy [37]. Second, Bérut et al. demonstrated the Landauer principle experimentally using a single colloidal particle in a double-well potential [38]. Examples of earlier results that are important but do not address quantitative information are those of Eggers [39] and Cao et al. [40].

Parrondo et al. provide a cautious but optimistic summary:

We believe that we are still several steps away from a complete understanding of the physical nature of information. First, it is necessary to unify the existing theoretical frameworks, and investigate a comprehensive theory for general processes. Second, we need to verify if other phenomena, such as copolymerization and proofreading, can be analyzed within this unified framework. And third, we must return to Maxwell’s original concern about the second law and try to address the basic problems of statistical mechanics, such as the emergence of the macroscopic world and the subjectivity of entropy, in the light of a general theory of information.

[36]

It is striking that Landauer’s phrase “Information is physical” is still so relevant in research more than a half-century after he conceived it.

9. Conclusions and a Parable

There are many more historical highlights than can be contained in this kind of review. Leff and Rex [8] list over 500 articles and books, and that includes only relevant scholarship that was published before 2003. Parrondo et al. [36] list 93 references, most of which are to work done in the last decade. Maxwell’s demon seems to be alive and well, nearly 150 years after its initial conception by Maxwell. As per Eddington’s injunction, we should continue to scrutinize carefully any challenges to the Second Law.

I will end with an anecdote that turns into a parable. The anecdote explains how I got started in this Maxwell’s demon business more than 30 years ago. I was a relatively new professor teaching a modern physics class (second-year physics majors) about classical statistics. I had heard of Maxwell’s demon—that is, Maxwell’s original one—and I thought it would be good to describe the demon to my class and cite it as an example of why the Second Law cannot be violated. I planned to take the last 15 min or so before class to think it over and come up with a good explanation of why Maxwell’s demon would not work. Thirty years later I am still thinking about it. The lesson in the parable may be that no 15-minute preparation is sufficient, or it may be that a 15-minute preparation can turn into 30 years and leave much more to study, with new ideas and examples all the time. It is still interesting, but tricky, for all the reasons I have elucidated here.