Stochastic Stirling Engine Operating in Contact with Active Baths
Abstract
:1. Introduction
2. Stirling Cycle between Equilibrium States: A Quick Review
2.1. Modeling the Motion of a Colloidal Particle
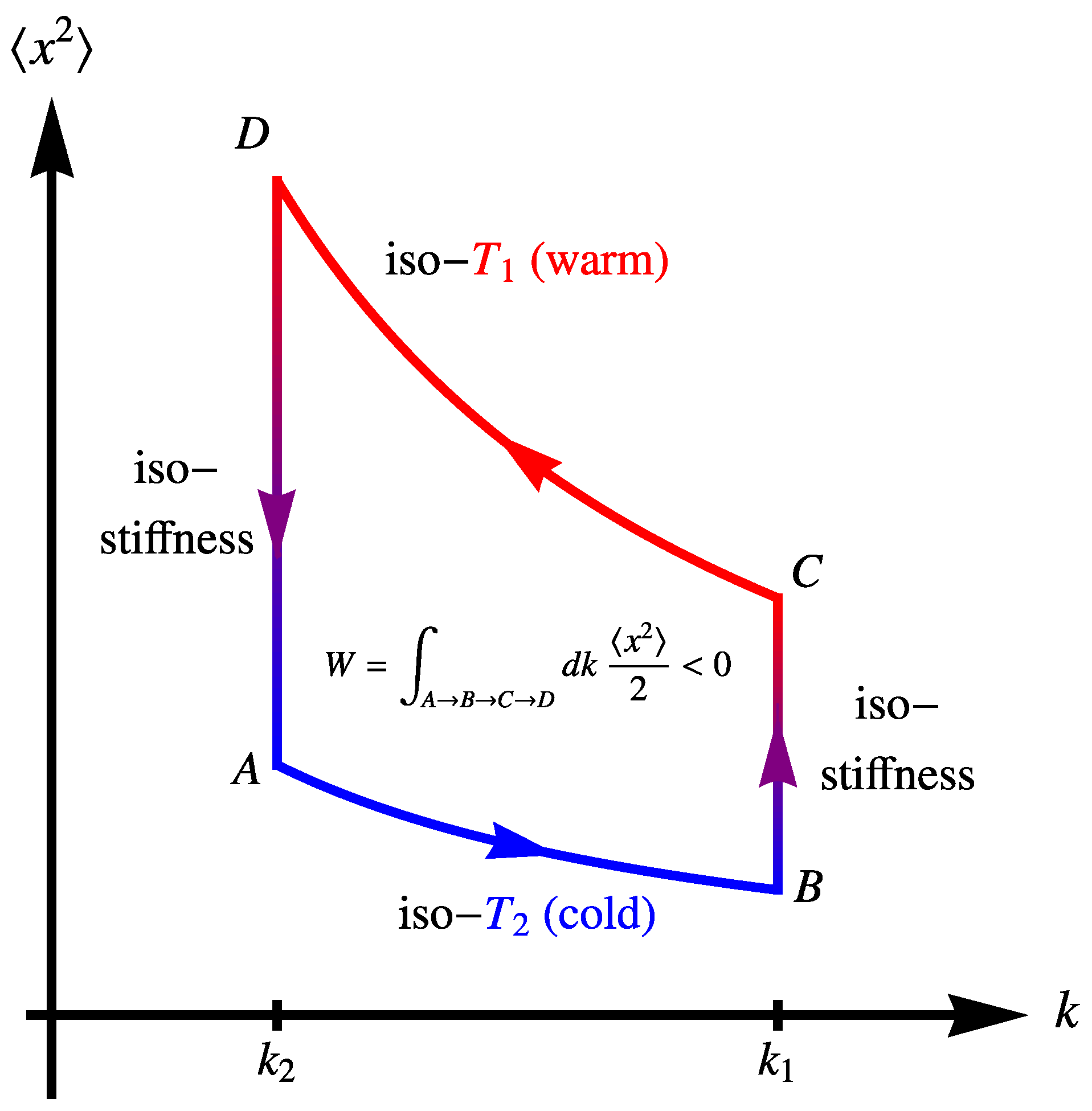
2.2. Energetics of the Stirling Cycle
3. Engine Operating between Nonequilibrium Baths
3.1. Modified Langevin Equation
3.2. The Energetics Is Not Altered If We Use Iso-Tact Steps
4. Energetics Using the Diffusion Constant as an Active Temperature
4.1. A Bath with White but Non-Gaussian Statistics
4.2. A Bath with a Persistent Noise
4.3. A Bath Described by a More General Langevin Equation
5. Discussion: Back to Experiments
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Active Particle Dynamics
Appendix B. Is Kurtosis Related to Efficiency?
References
- Sekimoto, K. Stochastic Energetics; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. 2012, 75, 126001. [Google Scholar] [CrossRef] [PubMed]
- Schmiedl, T.; Seifert, U. Efficiency at maximum power: An analytically solvable model for stochastic heat engines. Eur. Lett. 2008, 81, 20003. [Google Scholar] [CrossRef]
- Blickle, V.; Bechinger, C. Realization of a micrometre-sized stochastic heat engine. Nat. Phys. 2011, 8, 143–146. [Google Scholar] [CrossRef]
- Horowitz, J.M.; Parrondo, J.M.R. Thermodynamics: A Stirling effort. Nat. Phys. 2012, 8, 108–109. [Google Scholar] [CrossRef]
- Martínez, I.A.; Roldán, E.; Dinis, L.; Petrov, D.; Rica, R.A. Adiabatic Processes Realized with a Trapped Brownian Particle. Phys. Rev. Lett. 2015, 114, 120601. [Google Scholar] [CrossRef] [PubMed]
- Martinez, I.A.; Roldan, E.; Dinis, L.; Petrov, D.; Parrondo, J.M.R.; Rica, R.A. Brownian Carnot engine. Nat. Phys. 2016, 12, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Krishnamurthy, S.; Ghosh, S.; Chatterji, D.; Ganapathy, R.; Sood, A.K. A micrometre-sized heat engine operating between bacterial reservoirs. Nat. Phys. 2016, 12, 1134–1138. [Google Scholar] [CrossRef]
- Wu, X.L.; Libchaber, A. Particle Diffusion in a Quasi-Two-Dimensional Bacterial Bath. Phys. Rev. Lett. 2000, 84, 3017–3020. [Google Scholar] [CrossRef] [PubMed]
- Kanazawa, K.; Sagawa, T.; Hayakawa, H. Stochastic Energetics for Non-Gaussian Processes. Phys. Rev. Lett. 2012, 108, 210601. [Google Scholar] [CrossRef] [PubMed]
- Kanazawa, K.; Sagawa, T.; Hayakawa, H. Heat conduction induced by non-Gaussian athermal fluctuations. Phys. Rev. E 2013, 87, 052124. [Google Scholar] [CrossRef] [PubMed]
- Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 1966, 29, 255. [Google Scholar] [CrossRef]
- Feynman, R.P.; Vernon, F.L. The theory of a general quantum system interacting with a linear dissipative system. Ann. Phys. 1963, 24, 118–173. [Google Scholar] [CrossRef]
- Solon, A.; Cates, M.; Tailleur, J. Active brownian particles and run-and-tumble particles: A comparative study. Eur. Phys. J. Spec. Top. 2015, 224, 1231–1262. [Google Scholar] [CrossRef]
- Szamel, G. Self-propelled particle in an external potential: Existence of an effective temperature. Phys. Rev. E 2014, 90, 012111. [Google Scholar] [CrossRef] [PubMed]
- Van Kampen, N. Stochastic Processes in Physics and Chemistry; Elsevier: Amsterdam, The Netherlands, 1992; Volume 1. [Google Scholar]
- Pawula, R. Generalizations and extensions of the Fokker–Planck–Kolmogorov equations. IEEE Trans. Inf. Theory 1967, 13, 33–41. [Google Scholar] [CrossRef]
- Popescu, D.M.; Lipan, O. A Kramers-Moyal Approach to the Analysis of Third-Order Noise with Applications in Option Valuation. PLoS ONE 2015, 10, e0116752. [Google Scholar] [CrossRef] [PubMed]
- Fodor, E.H.; Hayakawa, J.T.; van Wijland, F. What is the role of non Gaussian noise in assemblies of self-propelled active particles? in preparation.
- Fodor, É.; Nardini, C.; Cates, M.E.; Tailleur, J.; Visco, P.; van Wijland, F. How far from equilibrium is active matter? Phys. Rev. Lett. 2016, 117, 038103. [Google Scholar] [CrossRef] [PubMed]
- Berthier, L.; Kurchan, J. Non-equilibrium glass transitions in driven and active matter. Nat. Phys. 2013, 9, 310–314. [Google Scholar] [CrossRef]
- Nikola, N.; Solon, A.P.; Kafri, Y.; Kardar, M.; Tailleur, J.; Voituriez, R. Active Particles with Soft and Curved Walls: Equation of State, Ratchets, and Instabilities. Phys. Rev. Lett. 2016, 117, 098001. [Google Scholar] [CrossRef] [PubMed]
- Tailleur, J.; Cates, M.E. Sedimentation, trapping, and rectification of dilute bacteria. Eur. Lett. 2009, 86, 60002. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakine, R.; Solon, A.; Gingrich, T.; Van Wijland, F. Stochastic Stirling Engine Operating in Contact with Active Baths. Entropy 2017, 19, 193. https://doi.org/10.3390/e19050193
Zakine R, Solon A, Gingrich T, Van Wijland F. Stochastic Stirling Engine Operating in Contact with Active Baths. Entropy. 2017; 19(5):193. https://doi.org/10.3390/e19050193
Chicago/Turabian StyleZakine, Ruben, Alexandre Solon, Todd Gingrich, and Frédéric Van Wijland. 2017. "Stochastic Stirling Engine Operating in Contact with Active Baths" Entropy 19, no. 5: 193. https://doi.org/10.3390/e19050193
APA StyleZakine, R., Solon, A., Gingrich, T., & Van Wijland, F. (2017). Stochastic Stirling Engine Operating in Contact with Active Baths. Entropy, 19(5), 193. https://doi.org/10.3390/e19050193





