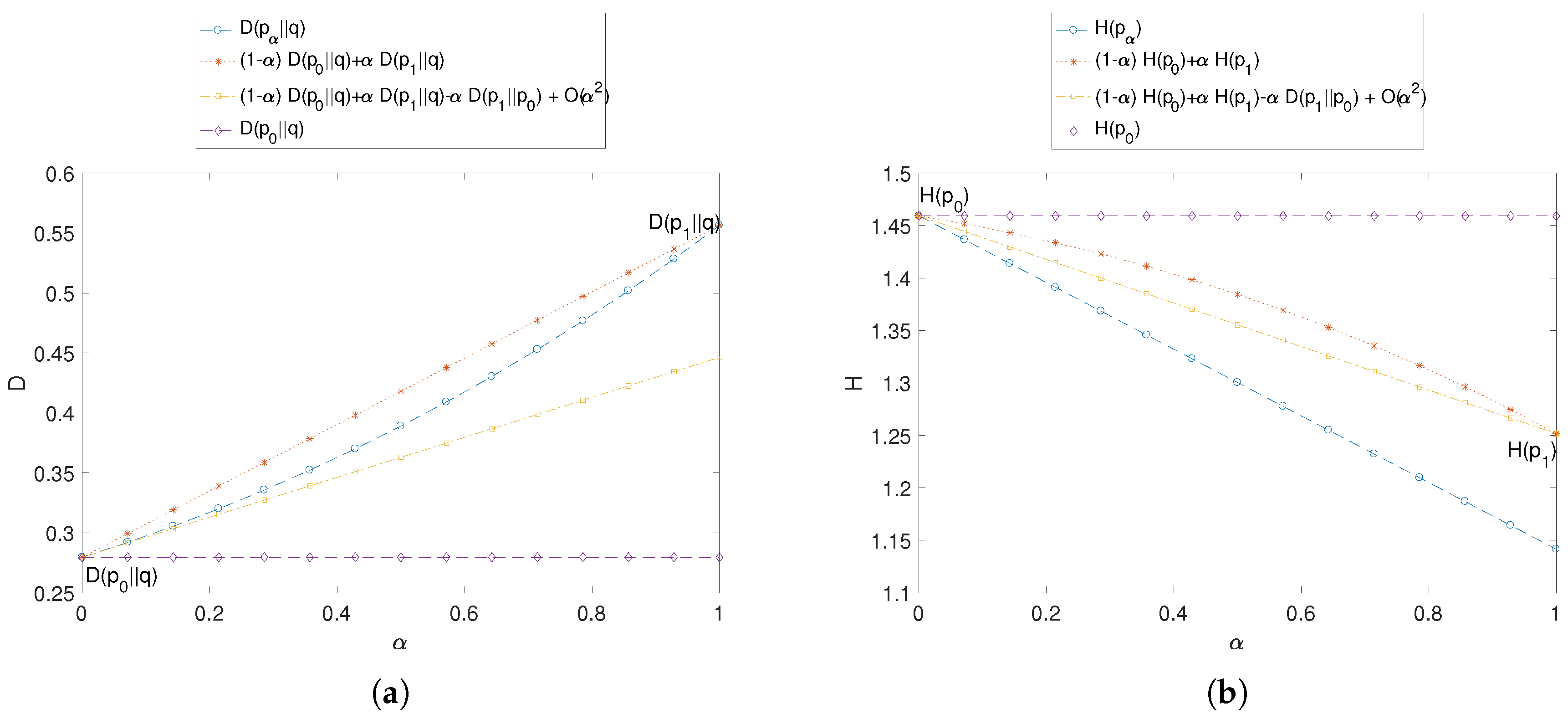On the Anonymity Risk of Time-Varying User Profiles

Abstract

Websites and applications use personalisation services to profile their users, collect their patterns and activities and eventually use this data to provide tailored suggestions. User preferences and social interactions are therefore aggregated and analysed. Every time a user publishes a new post or creates a link with another entity, either another user, or some online resource, new information is added to the user profile. Exposing private data does not only reveal information about single users’ preferences, increasing their privacy risk, but can expose more about their network that single actors intended. This mechanism is self-evident in social networks where users receive suggestions based on their friends’ activities. We propose an information-theoretic approach to measure the differential update of the anonymity risk of time-varying user profiles. This expresses how privacy is affected when new content is posted and how much third-party services get to know about the users when a new activity is shared. We use actual Facebook data to show how our model can be applied to a real-world scenario.

1. Introduction

Personalisation and advertising services collect user’s activities to provide tailored suggestions. This data contributes to form over time what is considered the user online footprint. With the term online footprint, we include every possible trace left by individuals when using communication services. It follows that the same notion of digital footprint spans all layers of the Internet protocol suite conceptual model (TCP/IP), depending on the type of data taken into consideration. It is also important to note that the digital footprint of an individual is formed by their interaction with their social relationships, not only by their singular actions on a medium or platform.

We can therefore consider users’ online footprints as linked data, where each event generated by a single user includes information regarding other users but also regarding other events and entities. This way of considering online footprints is very similar to the very structure of the Web, where web pages link to other pages when they reference a certain individual or object. This social and interconnected aspect of digital footprints is particularly evident for services like Facebook [1], where users are suggested new pages and social connections based on their friends’ network of relationships and expressed preferences or likes.

Users’ profiles also change over time, reflecting how real-world individuals change their tastes and preferences in comparison to, for example, a reference population. Every time new information is shared, the user is disclosing more about themselves or their social interactions, eventually changing their privacy risk.

More importantly, users tend to share their data and access to their identity accounts, such as Google [2] or Facebook [1], when interacting with third-party applications. These applications use federated log in mechanisms through the user’s identity account. To use the application, users grant it a certain level of access to their private data through their profile. This data includes details about their real offline identity, their whereabouts and in some situations even the company they work for. Once it has gained access, the application can now store user data and assume control over how it is further shared. The user will never be notified again about who is accessing their data, nor if these are transferred to third parties.

This aspect of privacy protection is particularly relevant since the right to privacy is commonly interpreted as the user’s right to prevent information disclosure. When a user shares some content online, they are actively choosing to disclose some of their profile. At the same time, though, they might give away more that they intended, since no information is shared from app and service about how the profile is analysed or how the user’s data is further shared.

Online services ask the user to access certain information, yet no concrete information is passed on about how the data will be used or stored. Furthermore, these services are often designed as mobile applications where all the devices installing the app communicate with a centralised server and constantly exchange users’ information, eventually allowing for unknown third parties, or potential attackers, to fetch and store this data. In addition, this information is often shared with insecure communication through the HTTP protocol, making it possible for a malicious entity to intercept these communications and steal user data.

In this model, the management of privacy and trust of the platform to which users handle their data is highly centralised. The user entrusts the service with all their data, often as part of a service agreement. Generally, a few services control the market and therefore can inevitably know more about the users. This is the case of popular email or messaging services, but also social networks, relationship apps and so on. These entities can easily know who is talking to whom and sometimes also the topic of their conversations.

Contribution

We analyse user online footprints as a series of events belonging to a certain individual. Each event is a document containing different pieces of information. An event corresponds to an action generated by the user or one of their devices. When a user visits a website or creates a post on a blog, an event is created. We can think of an event as a hypermedia document, i.e., an object possibly containing graphics, audio, video, plain text, and hyperlinks. We call the hyperlinks selectors, and we use them to build the connections between the user’s different identities or events. Each identity can be a profile or account that the user has created onto a service or platform, or just a collection of events, revealing something about the user. With account, we mean an application account or a social network account, such as their LinkedIn or Facebook unique IDs.

When the user decides to share some new content, or subscribes to a service by sharing part of their profile data, novel information is released. This information is either made public or shared to a group of people, like for a new social network post, or it is rather shared to a third party app.

We are interested to measure the differential update of the anonymity risk of user profiles due to a marginal release of novel information, based on an information-theoretic measure of anonymity risk, precisely, the Kullback–Leibler divergence between a user profile and the average population’s profile.

We particularly considered real data shared by Facebook users as part of the Facebook-Tracking-Exposed project [3]. For the purpose of this study, we considered categorised Facebook posts. We imagined that an attacker is interested in capturing users’ preferences by looking at their posts and imagined a scenario where the information shared through a new event (i.e., sharing new content) increases or decreases the user’s privacy risk, in other words, how much an attacker knows about them, once they have captured the new information.

In this work, we build upon a recent information-theoretic model for measuring the privacy risk incurred in the disclosure of a user’s interests though online activity. Among other refinements, we incorporate an aspect of substantial practical importance in the aforementioned model, namely, the aspect of time-varying user profiles.

More precisely, we propose a series of refinements of a recent information-theoretic model characterising a user profile by means of a histogram of categories of interest, and measuring the corresponding privacy risk as the Kullback–Leibler divergence with respect to the histogram accounting for the interests of the overall population. Loosely speaking, this risk may be interpreted as an anonymity risk, in the sense that the interests of a specific user may diverge from those of the general population. Our main contributions are as follows:

• We preface our main analysis with an argument to tackle populations in which the distribution of profiles of interest is multimodal, that is, user profiles concentrate around distinguishable clusters of archetypical interests. We suggest that the said information-theoretic model be applied after segmentation of the overall population according to demographic factors, effectively extending the feasibility of the original, unimodal proposal.
• However, the most important refinement and undoubtedly the main focus of this paper consists in the extension of the aforementioned model to time-varying user profiles. Despite the practical significance of the aspect of time in the analysis of privacy risks derived from disclosed online activity, it is nevertheless an aspect all too often neglected, which we strive to remedy with this preliminary proposal. Here, the time variation addresses not only changes over time in the interests of a user, construed as a dynamic profile, but also novel activity of a possibly static profile, in practice known only in part.
• The changes in anonymity risk are formulated as a gradient of the Kullback–Leibler divergence of a user profile reflecting newly observed activity, with respect to a past history, and are inspired in the abstract formulation of Bregman projections onto convex sets, whose application to the field of privacy is, to the best of our knowledge, entirely novel.
• For a given activity and history, we investigate the profile updates leading to the best and worst overall anonymity risk, and connect the best case to the fairly recent information-theoretic framework of optimised query forgery and tag suppression for privacy protection.
• We contemplate certain special cases of interest. On the one hand, we provide a corollary of our analysis for the special case in which the anonymity risk is measured as the Shannon entropy of the user profile. On the other hand, we particularise our model in the extreme case in which the new observation consists of a single sample of categorised online activity.
• Last but not least, we verify and illustrate our model with a series of examples and experiments with both synthetic and real online activity.

2. State-of-the-Art

Online services and applications constantly share user-generated data in the form of information regarding locations, browsing habits, communication records, health information, financial information, and general preferences regarding user’s online and offline activities. This information is often shared with third-party services, in order to provide tailored product experience or to receive other services. A common example of this are third-party analytics services used by websites and mobile applications to understand user behaviour within their product. This level of access to generated data is often directly granted from the user of such services. On a wide number of occasions, though, private information is captured by online services without the direct user consent or even knowledge.

For example, to personalise their services or offer tailored advertising, web applications could use tracking services that identify a user through different networks [4,5]. These tracking services usually combine information from different profiles that users create—for example, their Gmail address or their Facebook or LinkedIn accounts. In addition, specific characteristics of the user’s device can be used to identify them through different sessions and websites, as described by the Panopticlick project [6].

Tags or interest-based profiling is another approach for web applications to collect and analyse users’ behaviour that has been studied extensively in the literature. Category-based filtering techniques are very popular for web search applications. In recommendation systems employing tags or in any system allowing resource annotation, users decide to disclose personal data in order to receive, in exchange, a certain benefit [7]. This earned value can be quantified in terms of the customised experience of a certain product. In the realm of geographical filtering, for example, tags are used to monitor user interests connected to places, and suggest events and places of interest [8].

When users generate more activity across a platform, their profile changes over time. Privacy-enhancing technologies (PETs) have been proposed following the idea of perturbing the information implicitly or explicitly disclosed by the user. They therefore represent a possible alternative to hinder attackers in their efforts to profile their activity precisely, when using a personalised service. The submission of bogus user data, together with genuine data, is an illustrative example of a data-perturbative mechanism. In the context of information retrieval, query forgery [9,10] prevents privacy attackers from profiling users accurately based on the content of queries, without having to trust the service provider or the network operator, but obviously at the cost of traffic overhead. In this kind of mechanism, the perturbation itself typically takes place on the user side. This means that users do not need to trust any external entity such as the recommender, the Internet Service Provider (ISP) or their neighbouring peers. Naturally, this does not signify that data perturbation cannot be used in combination with other third-party based approaches or mechanisms relying on user collaboration.

The problem of measuring user privacy in systems that profile users is complex. After modelling user profiles as histograms of relative frequencies of online activity along predefined categories of interest, References [9,11] propose the use of Shannon entropy and Kullback–Leibler divergence for a quantifiable measure of user privacy, in part justified by Jaynes’ rationale on maximum entropy methods [12].

Certainly, the distortion of user profiles for privacy protection may be done not only by means of the insertion of false activity, but also by suppression. An example of this latter kind of data perturbation is the elimination of tags as a privacy-enhancing strategy [13,14]. This strategy allows users to preserve their privacy to a certain degree, but it comes at the cost of some degradation in the usability of the service. Precisely, the privacy-utility trade-off posed by the suppression of tags was investigated mathematically in [13], measuring privacy as the Shannon entropy of the perturbed profile, and utility as the percentage of tags users are willing to eliminate. Closely related to this are also other studies regarding the impact of suppressive PETs [15,16,17], where the impact of tag suppression is assessed experimentally in the context of various applications and real-world scenarios.

This is particularly relevant when online services provide the users with the perception that sharing less data impacts their optimal service experience. Different classes of applications are being developed based on the concept of serendipitous discoveries. The idea of serendipity wants the user to accidentally discover people, places and/or interests around them. To present the user with a tailored and seamless experience, serendipity applications need to learn the user’s preferences and interests, as well as specific personal information, like their physical location, their work place or their social circles. This is usually accomplished by connecting several of the user’s identities with other social networks [18]. A typical example is asking the user to register onto an application through their Facebook, Twitter, or Google+ account. This technique usually consists of a variant of the OAuth2.0 protocol used to confirm a person’s identity and to control which data they will share with the application requesting log in.

Another important aspect to consider is that the average online user joins different social networks with the objective to enjoy distinct services and features. On each service or application, an identity gets created containing personal details, preferences, generated content, and a network of relationships. The set of attributes used to describe these identities is often unique to the user. In addition, applications or services sometimes require the disclosure of different personal information, such as email or full name, to create a profile. Users possessing different identities on different services, often use those to verify another identity on a particular application, i.e., a user will employ their Facebook and LinkedIn profile to verify their account on the third service [19]. A piece of information required by one service could, in fact, add credibility to the information the user has provided for a second application, by demonstrating that certain personal details overlap, and by adding other information—for example, a set of shared social relationships.

Users’ online footprints could therefore be reconstructed by combining the publicly available information provided to different services [20,21]. A possible attacker could start by identifying a common pseudonym, i.e., a username that users often use across different social networks, and then goes on measuring how many possible profiles it can find across different services. Therefore, a user’s activity on one site can implicitly reveal their identity on another site, also investigating how locations attached to posts could be used uniquely to identify a profile among a certain number of similar candidates.

The analysis of publicly available attributes in public profiles shows a correlation between the amount of information revealed in social network profiles, specific occupations or job titles, and use of pseudonyms. It is possible to identify certain patterns regarding how and when users reveal precise information [22]. Finally, aggregating this information can lead an attacker to obtain direct contact information by cross-linking the obtained features with other publicly available sources, such as online phone directories. A famous method for information correlation was presented by Alessandro Acquisti and Ralph Gross [23]. Leveraging on the correlation between individuals’ social security numbers and their birth data, they were able to infer people’s social security numbers by using only publicly available information.

Social connections can be inferred also by user behaviours. Messaging services, applications able to access messages, or phone metadata are able to predict conversations patterns, and, eventually, users’ relationships. An example is the study of telephone metadata to infer whether a user is or is not in a relationship based on their mutual call frequencies [24]. A user’s social graph and community network structures can therefore also be derived by studying communications patterns. This technique is often used by friends’ recommendation systems [25], often clustering people based on their interactions, therefore creating implicit groups.

3. An Information-Theoretic Model for Measuring Anonymity Risk

In this section, we build upon a recent information-theoretic model for measuring the privacy risk incurred in the disclosure of a user’s interests though online activity. Among other refinements, we incorporate an aspect of substantial practical importance in the aforementioned model, namely, the aspect of time-varying user profiles.

Consider a user profile p, together with an average population profile q, both represented as histograms of relative frequencies of online activity along predefined categories of interest $i=1,\cdots ,m$. In the absence of a specific statistical model on the frequency distribution of user profiles, as argued extensively in [9,11,26] on the basis of Jaynes’ rationale for maximum entropy methods, we assume that anonymity risk may be adequately measured as the Kullback–Leibler (KL) divergence $\mathrm{D}(p||q)$ between the user profile p and the population’s q. The idea is that user profiles become less common as they diverge from the average of the population. Precisely, we define anonymity risk as

$$\mathcal{R}\stackrel{\mathrm{def}}{=}\mathrm{D}(p||q)\stackrel{\mathrm{def}}{=}\sum _{i=1}^m{p}_{i}log\frac{p_i}{q_i}.$$

Usually, the basis of logarithm is 2 and the units of the divergence are bits.

Intuitively, the empirical histogram of relative frequencies (or type) t of n independent, identically distributed drawings should approach the true distribution $\overline{t}$ as n increases. Those drawings may be loosely interpreted as sequences of online queries according to some underlying user interests represented by $\overline{t}$. More technically, the extension of Jaynes’ approximation to KL divergences for a sequence of independent events shows that the probability $p_T\left(t\right)$ of the empirical distribution t is related to the KL divergence $\mathrm{D}(t||\overline{t})$ with respect to the true distribution $\overline{t}$ by means of the limit

$$-\frac{1}{n}log{p}_T\left(t\right)\underset{n\to \infty }{\to }\mathrm{D}(t||\overline{t}).$$

According to this model, the user profile p plays the role of the empirical distribution t, and the population’s profile q, the role of the true distribution $\overline{t}$. In a way, we construe a user profile as an empirical instantiation of the population’s profile. Concordantly, the divergence $\mathrm{D}(p||q)$ between the user profile p and the population’s q is a measure of how rare p should be, which we regard in turn as a measure of anonymity risk. The argument that the rarity of a profile may also be understood as a measure of how sensitive a user profile may be considered offers a measure of privacy risk. Admittedly, this model is limited to applications where the underlying assumptions may be deemed adequate, particularly when no specific, possibly multimodal distribution of the user profiles is available.

Another helpful interpretation of this measure stems from rewriting the user profile as a distribution $p_{I|J}$ of a random variable I indexing online activity into predefined categories $i=1,\cdots ,m$, conditioned on the user identity J, defined on the user indexes $j=1,\cdots ,n$. Observing that the population profile is the expectation across all user profiles,

$$q_I={\mathrm{E}}_J{p}_{I|J}(·|J),(\mathrm{more}\mathrm{explicitly},q_I(i)=\frac{1}{n}\sum _{j=1}^n{p}_{I|J}(i|j)\mathrm{for}\mathrm{all}i),$$

we immediately conclude that the expected risk is

$${\mathrm{E}}_J\mathcal{R}\left(J\right)={\mathrm{E}}_J\mathrm{D}\left(p_{I|J}(·|J)||q_I\right)=\mathrm{I}(I;J),$$

namely, the mutual information between the online activity I and the user identity J.

3.1. Multimodality of the KL Divergence Model and Conditioning on Demography

Perhaps one of the major limitations of the direct application of the KL divergence model for characterising the anonymity of a profile is made clear when the distribution of profiles is concentrated around several predominant modes, contradicting the implicit unimodal assumption revolving around the population’s profile q. Intuitively, one may expect several clusters in which profiles are concentrated, corresponding to various demographic groups, characterised by sex, age, cultural background, etc.

In order to work around this apparent limitation, we may simply partition the data into a number of meaningful demographic groups, indexed by k, and calculate the average population profile $q_{I|K}(·|k)$ for each group k. Then, redefine the demographically contextualised anonymity risk as the KL divergence between the profile $p_{I|J}(·|j)$ of user j, in group $k\left(j\right)$, and the corresponding reference $q_{I|K}(·|k\left(j\right))$, that is,

$${\mathcal{R}}_{\mathrm{context}}\left(j\right)\stackrel{\mathrm{def}}{=}\mathrm{D}\left(p_{I|J}(·|j)||q_{I|K}(·|k\left(j\right))\right).$$

Obviously, the model will be suitable as long as the profile distribution is unimodal within each demographic context, in the absence of a more specific model. Note that the measure of anonymity risk of the disclosed interests is now conditioned on demographic data potentially observable by a privacy attacker.

3.2. Gradient of the KL Divergence and Information Projection

Before addressing the problem of the differential update per se, we quickly review an interesting result on the gradient of the KL divergence, and its application to convex projections with said divergence. Directly from the definition of the KL divergence between distributions p and q for a general logarithmic basis, compute the gradient on the first argument

$${\nabla }_p\mathrm{D}(p||q)={\left(log\frac{p_i}{q_i}+loge\right)}_i.$$

Swift algebraic manipulation shows that

$$\mathrm{D}(p||q)=\mathrm{D}(p||p^{*})+\mathrm{D}(p^{*}||q)+{\nabla }_{p^{*}}\mathrm{D}{(p^{*}||q)}^{\mathrm{T}}(p-p^{*}),$$

(1)

for any additional distribution $p^{*}$, where the constant term $loge$ in the gradient becomes superfluous, on account of the fact that ${\sum }_i{p}_i-p_i^{*}=0$. Observe that part of the above expression may be readily interpreted as the Taylor expansion of $\mathrm{D}(p||q)$ about $p^{*}$,

$$\mathrm{D}(p||q)=\mathrm{D}(p^{*}||q)+{\nabla }_{p^{*}}\mathrm{D}{(p^{*}||q)}^{\mathrm{T}}(p-p^{*})+O(||p-p^{*}{||}^2),$$

(2)

with error precisely $\mathrm{D}(p||p^{*})$.

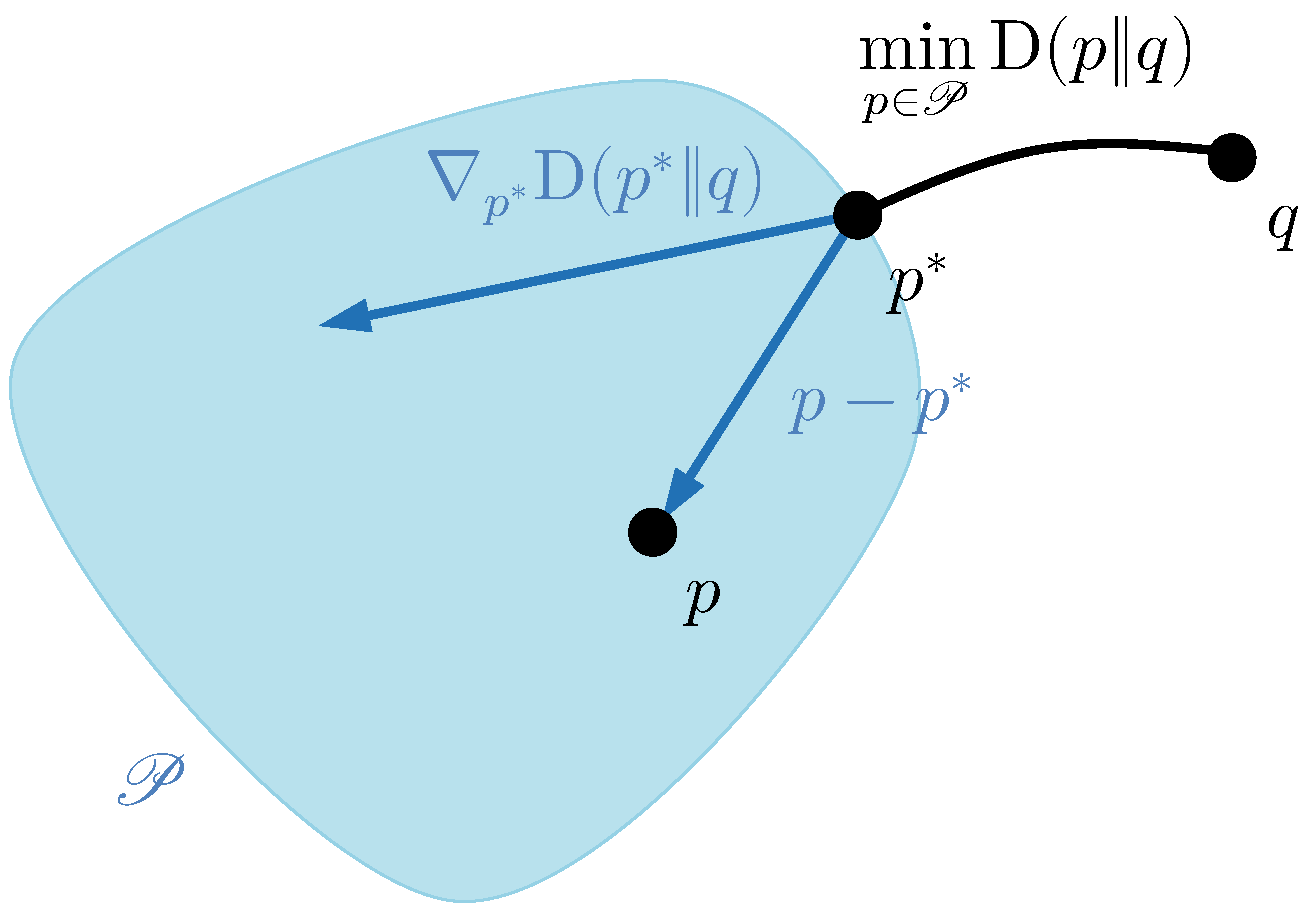
In the context of convex projections, suppose that we wish to find the closest point $p^{*}$ inside a convex set $\mathcal{P}$ to a reference point q, in KL divergence, succinctly,

$$p^{*}=\underset{p\in \mathcal{P}}{arg\; min}\mathrm{D}(p||q).$$

This problem is represented in Figure 1. The solution $p^{*}$ is called the information projection of q onto $\mathcal{P}$. Because for such $p^{*}$ the projection of the gradient of the objective onto the vector difference $p-p^{*}$ for any $p\in \mathcal{P}$ must be nonnegative, i.e.,

$${\nabla }_{p^{*}}\mathrm{D}{(p^{*}||q)}^{\mathrm{T}}(p-p^{*})⩾0,$$

we may conclude from the previous equality involving the gradient that

$$\mathrm{D}(p||q)⩾\mathrm{D}(p||p^{*})+\mathrm{D}(p^{*}||q).$$

This last inequality is, in fact, a known generalisation of the Pythagorean theorem for projections onto convex sets, generally involving obtuse triangles. (The expression relating the gradient with a set of divergences shown here may be readily generalised to prove an analogue of the Pythagorean theorem for Bregman projections. Recall that Bregman divergences encompass both squared Euclidean distances and KL divergences as a special case. An alternative proof of the Pythagorean theorem for KL divergences, which inspired a small part of the analysis in this manuscript, can be found in [27] (Theorem 11.6.1)).

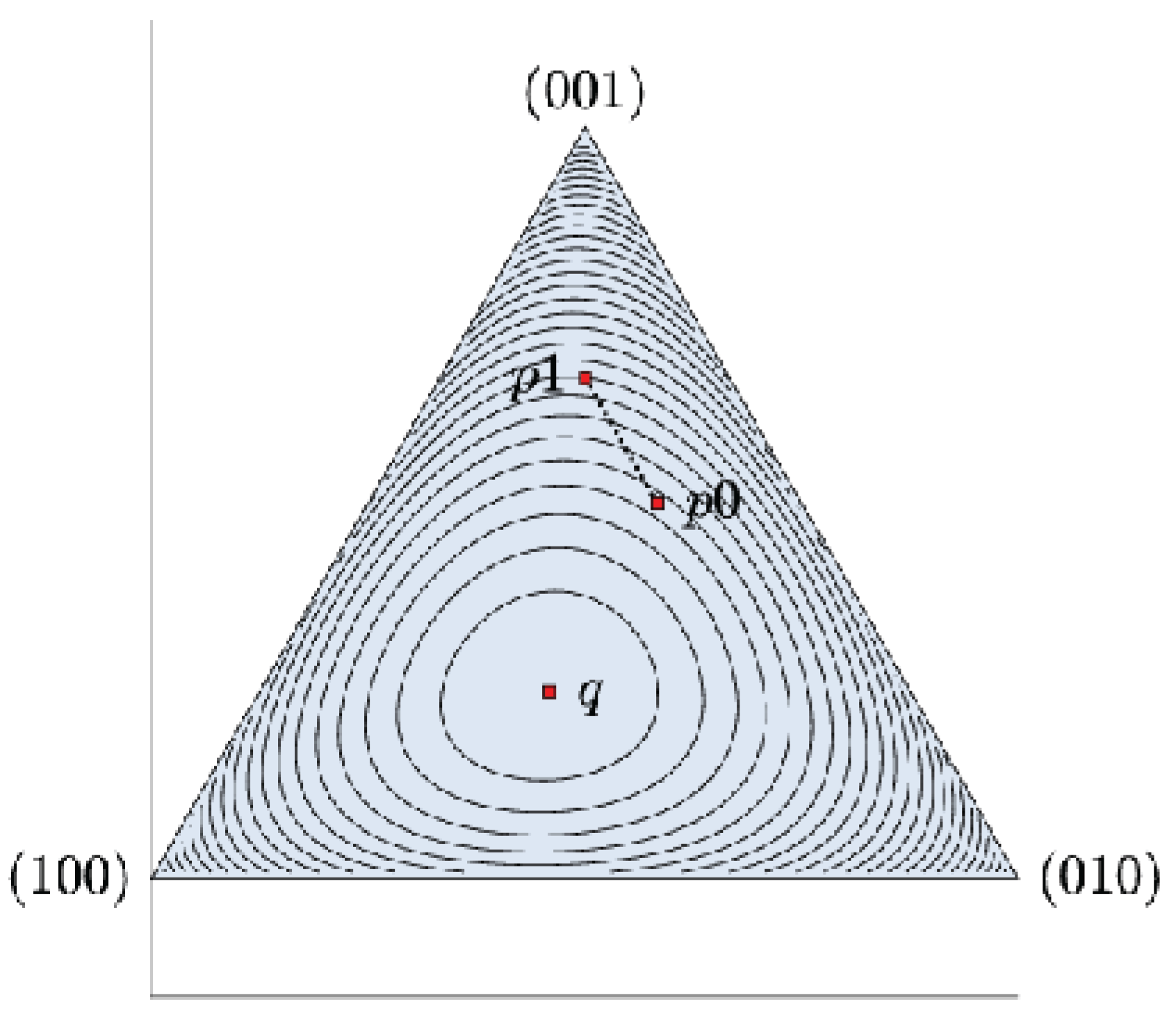
3.3. Differential Update of the Anonymity Risk Due to Revealing New Information

Under this simple model, we consider the following problem. Suppose that the distribution $p_0$ represents a history of online activity of a given user up to this time, with associated anonymity risk $\mathrm{D}(p_0||q)$. Consider now a series of new queries, with interests matching a profile $p_1$ and associated risk $\mathrm{D}(p_1||q)$ (Figure 2). If those new queries were observed, the overall user profile would be updated to

$$p_{\alpha }=(1-\alpha )p_0+\alpha p_1,$$

where the activity parameter $\alpha \in (0,1)$ is the fraction of new queries with respect to the total amount of queries released. We investigate the updated anonymity risk (Figure 3)

$$\mathrm{D}((1-\alpha )p_0+\alpha p_1||q),$$

in terms of the risks associated with the past and current activity, for a marginal activity increment $\alpha$. To this end, we analyse the first argument of the KL divergence, in the form of a convex combination, through a series of quick preliminary lemmas. (The mathematical proofs and results developed here may be generalised in their entirety from KL divergences to Bregman divergences, and they are loosely inspired by a fundamental Pythagorean inequality for Bregman projections on convex sets.)

On the one hand, since the KL divergence is a convex function, we may bound the updated risk as

$$\mathrm{D}\left((1-\alpha )p_0+\alpha p_1||q\right)⩽(1-\alpha )\mathrm{D}(p_0||q)+\alpha \mathrm{D}(p_1||q).$$

(3)

On the other hand, we may resort to our previous gradient analysis in Section 3.2, specifically to Equations (1) and (2), to write the first-order Taylor approximation

$$\mathrm{D}\left((1-\alpha )p_0+\alpha p_1||q\right)=(1-\alpha )\mathrm{D}(p_0||q)+\alpha \mathrm{D}(p_1||q)-\alpha \mathrm{D}(p_1||p_0)+O\left({\alpha }^2\right).$$

(4)

This last expression is consistent with the convexity bound (3), and, quite intuitively, the term $-\alpha \mathrm{D}(p_1||p_0)$ in the Taylor approximation refining the convex bound vanishes for negligible activity $\alpha$ or new activity profile $p_1$ similar to the history $p_0$ revealed thus far. We may alternatively write the updated risk as an increment with respect to that based on the user’s online history, as

$$\mathrm{D}\left((1-\alpha )p_0+\alpha p_1||q\right)-\mathrm{D}(p_0||q)=\alpha \left(\mathrm{D}(p_1||q)-\mathrm{D}(p_0||q)-\mathrm{D}(p_1||p_0)\right)+O\left({\alpha }^2\right),$$

which we observe to be approximately proportional to the relative activity parameter $\alpha$, and to an expression that only depends on the divergences between the profiles involved.

3.4. Special Cases of Delta Update and Uniform Reference

In the special case when the new activity contains a single query, the new profile $p_1$ is a Kronecker delta ${\delta }^i$ at some category i. In this case,

$$\mathrm{D}(p_1||q)=\mathrm{D}({\delta }^i||q)=-log{q}_i,\mathrm{and}$$

$$\mathrm{D}\left((1-\alpha )p_0+\alpha p_1||q\right)=(1-\alpha )\mathrm{D}(p_0||q)+\alpha log\frac{p_{0i}}{q_i}+O\left({\alpha }^2\right).$$

A second corollary follows from taking the reference profile q as the uniform distribution $u=\frac{1}{m}$, and replacing KL divergences in Equations (3) and (4) with Shannon entropies according to

$$\mathrm{D}(p||u)=logm-\mathrm{H}\left(p\right).$$

(5)

Precisely,

$$\mathrm{H}\left((1-\alpha )p_0+\alpha p_1\right)⩾(1-\alpha )\mathrm{H}\left(p_0\right)+\alpha \mathrm{H}\left(p_1\right),$$

(6)

consistently with the concavity of the entropy, and

$$\mathrm{H}\left((1-\alpha )p_0+\alpha p_1\right)=(1-\alpha )\mathrm{H}\left(p_0\right)+\alpha \mathrm{H}\left(p_1\right)+\alpha \mathrm{D}(p_1||p_0)+O\left({\alpha }^2\right).$$

(7)

Even more specifically, in the case of a delta update $p_1={\delta }^i$ and uniform reference profile,

$$\mathrm{H}\left((1-\alpha )p_0+\alpha p_1\right)=(1-\alpha )\mathrm{H}\left(p_0\right)-\alpha log{p}_{0i}+O\left({\alpha }^2\right).$$

3.5. Best and Worst Update

For a given activity $\alpha$ and history $p_0$, we investigate the profile updates $p_1$ leading to the best and worst overall anonymity risk $\mathrm{D}\left((1-\alpha )p_0+\alpha p_1||q\right)$. The problem of finding the best profile, yielding the smallest risk, is formally identical to that of optimal query forgery extensively analysed in [9]. Note that this problem may also be interpreted as the information projection of the population profile q onto the convex set of possible forged profiles

$$\mathcal{P}=\left\{(1-\alpha )p_0+\alpha p_1\right\},$$

with fixed $\alpha$ and $p_0$, a scaled, translated probability simplex. In this case, the generalized Pythagorean theorem shown earlier guarantees

$$\mathrm{D}\left((1-\alpha )p_0+\alpha p_1||q\right)⩾\mathrm{D}\left((1-\alpha )p_0+\alpha p_1^{*}||(1-\alpha )p_0+\alpha p_1\right)+\mathrm{D}\left((1-\alpha )p_0+\alpha p_1^{*}||q\right).$$

We may now turn to the case of the worst profile update $p_1$, leading to the highest anonymity risk. Consider two distributions p and q on the discrete support alphabet $i=1,\cdots ,m$, representing predefined categories of interest in our context. Recall that p is said to be absolutely continuous with respect to q, denoted $p\ll q$, whenever $q_i=0$ implies $p_i=0$ for each i. Otherwise, if for some i, we had $p_i>0$ but $q_i=0$, then $\mathrm{D}(p||q)=\infty$. In the context at hand, we may assume that the population profile incorporates all categories of interest, so that $q_i>0$, which ensures absolute continuity, i.e., $p\ll q$. Therefore, we would like to solve

$$\underset{p_1\ll q}{max}\mathrm{D}\left((1-\alpha )p_0+\alpha p_1||q\right).$$

We shall distinguish two special cases, and leave the general maximisation problem for future investigation. Let us tackle first the simpler case $\alpha =1$, and call $p_1=p$. Recall that the cross-entropy between two distributions p and q is defined as

$$\mathrm{H}(p||q)=-\sum _{i=1}^m{p}_{i}log{q}_i,$$

and is related to the (Shannon) entropy and the KL divergence via

$$\mathrm{H}(p||q)=\mathrm{H}\left(p\right)+\mathrm{D}(p||q).$$

Clearly,

$$\underset{p\ll q}{max}\mathrm{H}(p||q)=-log{q}_{\min },$$

attained for $p={\delta }^i$ corresponding to the category i minimising q. It turns out that this is also the solution to the maximisation problem in the divergence because

$$\mathrm{D}(p||q)=\mathrm{H}(p||q)-\mathrm{H}\left(p\right),$$

and $\mathrm{H}\left({\delta }^i\right)=0$, which means that $p={\delta }^i$ simultaneously maximises the cross-entropy and minimises the entropy.

The second special case we aim to solve is that of a uniform reference $q=u$, discussed in Section 3.4. The corresponding problem is

$$\underset{p_1}{min}\mathrm{H}\left((1-\alpha )p_0+\alpha p_1\right).$$

We claim that the worst profile update $p_1$ is again a Kronecker delta, but this time at the category i maximising $p_0$. Indeed, assume without loss of generality that $p_0$ is sorted in decreasing order, observe that $(1-\alpha )p_0+\alpha {\delta }^1$ majorises any other convex combination $(1-\alpha )p_0+\alpha p_1$, and recall that the entropy is Schur-concave.

As for the general case, the associated cross-entropy problem is fairly simple. We have

$$\underset{p_1\ll q}{max}\mathrm{H}\left((1-\alpha )p_0+\alpha p_1||q\right)=(1-\alpha )\mathrm{H}(p_0||q)-\alpha log{q}_{\min },$$

(8)

for $p={\delta }^i$ at the category minimising q. Unfortunately, the terms in the difference

$$\mathrm{D}\left((1-\alpha )p_0+\alpha p_1||q\right)=\mathrm{H}\left((1-\alpha )p_0+\alpha p_1||q\right)-\mathrm{H}\left((1-\alpha )p_0+\alpha p_1\right)$$

are respectively maximised and minimised for deltas at different categories, in general, namely that minimising q, and that maximising $p_0$. We may however provide an upper bound on the anonymity risk based on these considerations; by virtue of the convexity of the divergence and the previous result on its maximisation,

$$\mathrm{D}\left((1-\alpha )p_0+\alpha p_1||q\right)⩽(1-\alpha )\mathrm{D}(p_0||q)-\alpha log{q}_{\min }.$$

(9)

4. Experimental Results

In the previous section, we formulated the theoretical problem of the differential update of the anonymity risk of time-varying user profiles due to a marginal release of novel information, based on an information-theoretic measure of anonymity risk, specifically, the Kullback–Leibler (KL) divergence between a user profile and the average population’s profile. In this section, we verify the theoretical conclusions drawn in the referred section with a series of numerical examples and experimental scenarios.

More precisely, we analyse the updated anonymity risk in terms of the profile’s history and the current activity, for a given marginal increment $\alpha$. Furthermore, we present how, with a fixed an activity parameter $\alpha$ and given a certain initial profile, it is possible to identify the best and worst profile update leading to a new privacy risk. All of this is shown for the general case of anonymity risk measured as the KL divergence between a user profile and the overall profile of a population, and for the special case in which the population’s profile is assumed uniform, in which divergences become Shannon entropies.

The examples simply resort to synthetic values of the reference profiles. As for the experimental scenario, we employ Facebook data. We consider a user sharing some new information through a series of posts on their timeline. We are interested in verifying the theoretical analysis carried out in this work. All divergences and entropies are in bits.

4.1. Synthetic Examples

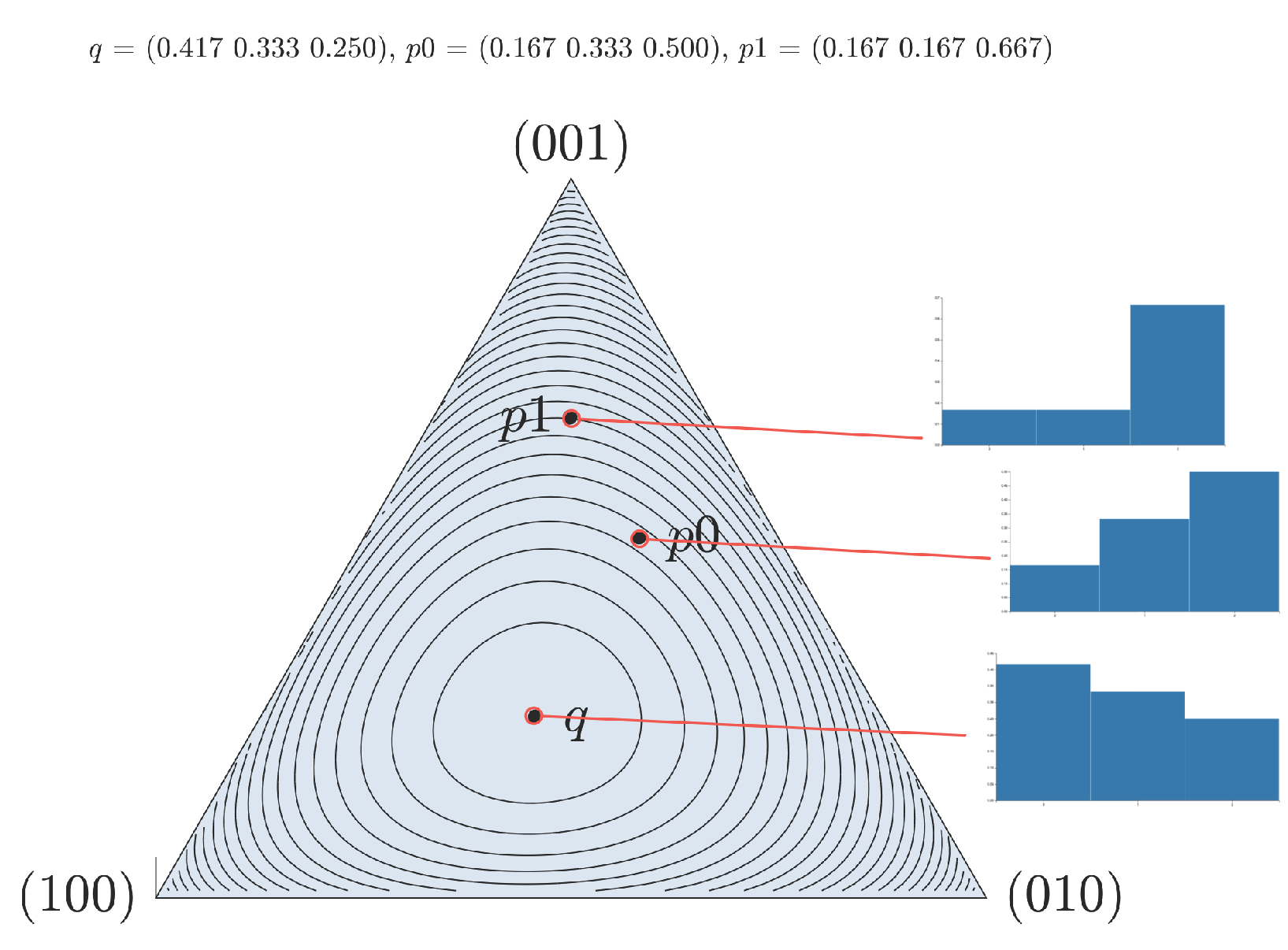
In our first proposed example, we choose an initial profile $p_0=(1/6,1/3,1/2)$, representing a user’s past online history, an updated profile $p_1=(1/6,1/6,2/3)$ containing more recent activity, and a population distribution $q=(5/12,1/3,1/4)$ of reference, across three hypothetical categories of interest. For different values of the recent activity parameter $\alpha$, Figure 4a plots the anonymity risk $\mathrm{D}(p_{\alpha }||q)$ of our synthetic example of updated user profile $p_{\alpha }=(1-\alpha )p_0+\alpha p_1$, with respect to the population’s profile q, the user’s history $p_0$, and the recent activity $p_1$. Specifically, we verify the convexity bound (3) and the first-order Taylor approximation (4) in our theoretical analysis. In addition, we plot Figure 4b the special case of uniform population profile, in which the anonymity risk becomes $\mathrm{H}\left(p_{\alpha }\right)$. We should hasten to point out that the dually additive relationship (5) between KL divergence and entropy translates to vertically reflected versions of analogous plots, verifying the entropic properties (6) and (7).

In our second example, we consider two categories of interest, so that profiles actually represent a binary preference. In this simple setting, profiles are completely determined by a single scalar p, corresponding to the relative frequency of one of the two categories, $1-p$ being the other frequency. We fix the activity parameter $\alpha =1/20$, set the historical profile to $p_0=2/3$, the reference profile to $q=3/5$, and verify the analysis on the worst anonymity risk update of Section 3.5 plotting $D(p_{\alpha }||q)$ against profile updates $p_1$ ranging from 0 to 1, where, as usual, $p_{\alpha }=(1-\alpha )p_0+\alpha p_1$. We illustrate this both for the privacy risk based on the KL divergence, in Figure 5a, and for the special case of Shannon entropy, in Figure 5b.

In the entropy case, our analysis, summarised in the minimisation problem (8), concluded that the worst update is a delta in the most frequent category. In this simple example with two categories, since $p_0>1/2$, the worst update corresponds to $p_1=1$, giving the lowest entropy. The reference line in the plot corresponds to $\mathrm{H}\left(p_0\right)\approx 0.918\mathrm{bit}$. For the more general measure of risk as a divergence, since $q=3/5$, we have $q_{\min }=2/5$, and the bound (9) becomes

$$\mathrm{D}(p_{\alpha }||q)⩽(1-\alpha )\mathrm{D}(p_0||q)-\alpha {log}_2{q}_{\min }\approx 0.0791,$$

fairly loose for the particular values of this example. The reference line in the plot indicates $\mathrm{D}(p_0||q)\approx 0.0137$.

These two examples confirm that new activity certainly has an impact on the overall anonymity risk, in accordance with the quantitative analysis in Section 3.5. This can of course be regarded from the perspective of introducing dummy queries in order to alter the apparent profile of interests, for example, in line with the problem of optimized query forgering investigated in [9].

4.2. Experiment Based on Facebook Data

We continue our verification of the theory presented, this time with experiments based on Facebook data, that is, a realistic scenario for which a population of users is sharing posts on Facebook. For the purpose of this study, we have used data extracted from the Facebook-Tracking-Exposed project [3], where users contribute their data to gain more insights on Facebook personalisation algorithm.

The extracted dataset contained 59,188 posts of 4975 timelines, categorised over 10 categories of interest. We selected two users out of this dataset and considered the total of posts collected for each of them, i.e., their entire timelines. The population distribution for the users in the dataset is expressed by the following Probability Mass Function (PMF):

$$q=(0.0401,0.0870,0.1485,0.1691,0.1025,0.2081,0.0435,0.0525,0.0558,0.0924).$$

Note that q is computed by taking into account not only the selected users, but the entire population of users across the dataset.

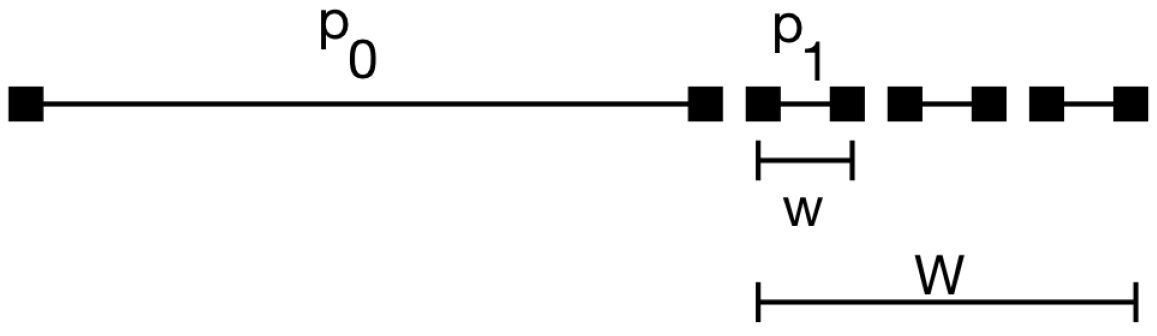
For each user, we considered a historical profile comprised of the entirety of their posts minus a window of 15 posts. Over this window, we consider a smaller sliding window for computing $p_1$, of five posts, hence we set the activity parameter $\alpha =w/L$, where $L=len\left(timeline\right)$ is the total number of posts in the timeline, and w represents the sliding window of five posts (Figure 6). For User A ${\alpha }_A=0.0182$, while for User B ${\alpha }_B=0.0820$. This choice captures the idea that we want to simulate how the profile changes when the user shares n new posts.

For User A, we consider a series 376 shared posts, and, for User B, we consider a total of 61 posts. We can express the two users’ profiles with the following PMFs:

$$p{\left(A\right)}_0=(0.0146,0.0036,0.0810,0.2311,0.0397,0.1931,0.0156,0.0324,0.3705,0.0179),$$

$$p{\left(B\right)}_0=(0.0159,0.0090,0.0804,0.2280,0.0609,0.1991,0.0194,0.0749,0.2846,0.0274).$$

For the set value of activity parameter $\alpha$, Figure 7a,c plot the anonymity risk $\mathrm{D}(p_{\alpha }||q)$ between a user’s updated profile $p_{\alpha }=(1-\alpha )p_0+\alpha p_1$, with respect to the population distribution q. Recall that $p_0$ is a user’s profile in the Facebook dataset, built taking into consideration a long series of samples. This captures the idea that a user’s profile is computed out of their history over a long series of actions.

These experiments confirm the theoretical analysis and examples presented, verifying in a real-world setting the convexity bound (3) and the first-order Taylor approximation (4) described in our theoretical analysis. In addition, we can compute the bound (9) for the general measure of the privacy risk as the KL divergence, which becomes, for User A,

$$\mathrm{D}(p_{\alpha }||q)⩽(1-\alpha )\mathrm{D}(p_0||q)-\alpha {log}_2{q}_{\min }\approx 0.8870,$$

and for User B,

$$\mathrm{D}(p_{\alpha }||q)⩽0.7723.$$

Furthermore, we considered, in Figure 7b,d, the privacy risk increments between the user profiles and an updated profile given by a certain activity over time. Recall that these deltas are computed as

$$\Delta \mathcal{R}=\mathrm{D}(p_{\alpha }||q)-\mathrm{D}(p_0||q),$$

to show how a certain activity can theoretically result in an anonymity risk gain or loss.

Note that the theoretical analysis and results proposed in this article apply to dynamic profiles that change over time. This aspect is particularly interesting, since we are not simply considering profiles as a snapshot of the user’s activity, over a small interval, but we are also taking into account changes in interests and general behaviour that can impact the privacy risk.

As a result, we can reach another interesting observation, which consists of the fact that profiles might have different privacy risks in different moments of time. This confirms the intuitive assumption that individuals might change their tastes and interests compared to a reference population, therefore having an impact on their overall privacy risk. In this case, we reasonably assume that the profile of certain individuals might change more rapidly over time than that of the entire population.

5. Conclusions

We proposed a series of refinements of a recent information-theoretic model of a user profile expressed through a histogram of categories of interest. The corresponding privacy risk is measured as the Kullback–Leibler divergence with respect to the histogram accounting for the interests of the overall population. Loosely speaking, this risk may be interpreted as an anonymity risk, in the sense that the interests of a specific user may diverge from those of the general population, extrapolating Jaynes’ rationale on maximum-entropy methods.

We investigate the profile updates leading to the best and worst overall anonymity risk for a given activity and history. Thus, we connect the best case to the fairly recent information-theoretic framework of optimised query forgery and tag suppression for privacy protection.

Furthermore, the analysis of our model is applied to an experimental scenario, using Facebook timeline data. Our main objective was measuring how privacy is affected when new content is posted. Often, a user of some online service is unable to verify how much a possible privacy attacker can find out about them. We used real Facebook data to show how our model can be applied to a real world scenario. This aspect is particularly important for content filtering in Facebook. In fact, as users are profiled on Facebook, the very same activity is used to filter the information they are able to access, based on their interests. There is no transparency on Facebook’s side about how this filtering and profiling happens. We hope that studies like this might encourage users to seek more transparency in the filtering techniques used by online services in general.

With regard to future work, we would like to express the relationships between users as well as the people they communicate with, taking them all into consideration when calculating users’ privacy risk.