The Solution of Modified Fractional Bergman’s Minimal Blood Glucose-Insulin Model
Abstract
:1. Introduction
2. The Caputo–Fabrizio Fractional Order Derivative
3. Bergman’s Minimal Model Fractional Module
4. Existence of the Coupled Solutions
Uniqueness of the Solutions
5. Application of Caputo–Fabrizio Derivative to Bergman’s Minimal Model
Solution of Fractional Module by Sumudu Transform
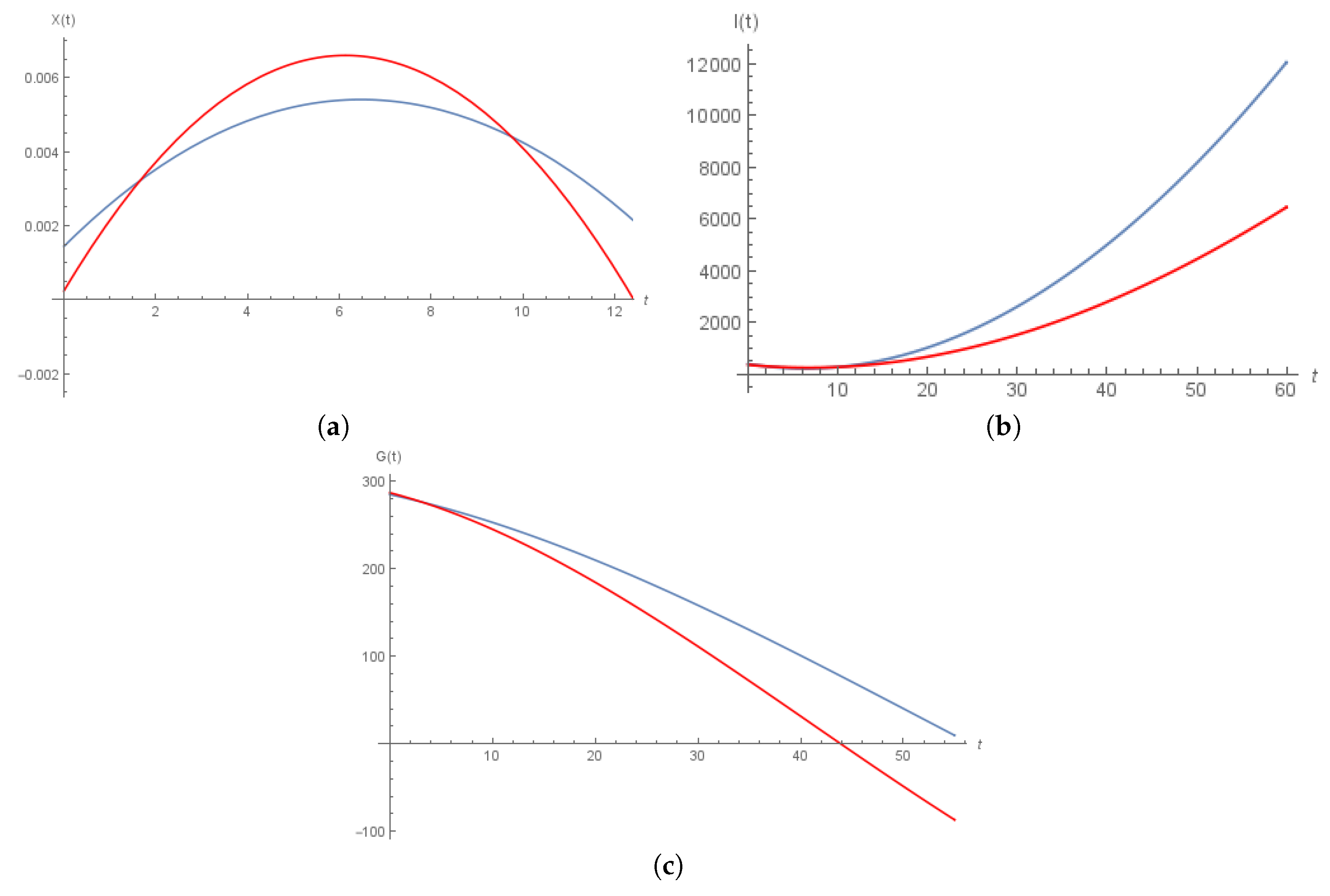
6. Numerical Solution
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Eckstein, E.C.; Belgacem, F.B.M. Model of platelet transport in flowing blood with drift and diffusion terms, extended platelet transport equation. Biophys. J. 1991, 60, 53–69. [Google Scholar] [CrossRef]
- Mountrakis, L.; Lorenz, E.; Hoekstra, A.G. Where do the platelets go? A simulation study of fully resolved blood flow through aneurysm vessels. Interface Focus 2013, 3, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Bourouiba, L.; Dehandschoewercker, E.; Bush, J.W.M. Violent expiratory events: On coughing and sneezing. J. Fluid Mech. 2014, 745, 537–563. [Google Scholar] [CrossRef]
- Caumo, A.; Cobelli, C.; Omenetto, M. Overestimation of minimal model glucose effectiveness in presence of insulin response is due to under modeling. Am. J. Physiol. 1999, 278, 481–488. [Google Scholar]
- Bergman, R.N.; Ider, Y.Z.; Bowden, C.R.; Cobelli, C. Quantitative estimation of insulin sensitivity. Am. J. Physiol. 1979, 236, 667–677. [Google Scholar]
- Bowden, C.R.; Bergman, R.N.; Toffolo, G.; Cobelli, C. Minimal modeling, partition analysis, and identification of glucose disposal in animals and man. IEEE Trans. Biomed. Eng. 1980, 18, 129–135. [Google Scholar]
- Gaetano, A.D.; Arino, O. Mathematical modeling of the intravenous glucose tolerance test. J. Math. Biol. 2000, 40, 136–168. [Google Scholar] [CrossRef] [PubMed]
- Gatewood, L.C.; Ackerman, E.; Rosevear, J.W.; Molnar, G.D.; Burns, T.W. Tests of a mathematical model of the blood-glucose regulatory system. Comput. Biomed. Res. 1968, 2, 1–14. [Google Scholar] [CrossRef]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent, part II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Chaurasia, V.B.L.; Dubey, R.S. Analytical solution for the differential equation containing generalized fractional derivative operators and Mittag-Leffler-type function. ISRN Appl. Math. 2011, 2011, 682381. [Google Scholar] [CrossRef]
- Chaurasia, V.B.L.; Dubey, R.S. Analytical solution for the generalized time-fractional telegraph equation. Fract. Differ. Calc. 2013, 3, 21–29. [Google Scholar] [CrossRef]
- Atangana, A.; Alabaraoye, E. Solving a system of fractional partial differential equations arising in the model of HIV infection of CD4+ cells and attractor one-dimensional Keller-Segel equations. Adv. Differ. Equ. 2013, 2013, 94. [Google Scholar] [CrossRef]
- Chaurasia, V.B.L.; Dubey, R.S.; Belgacem, F.B.M. Fractional radial diffusion equation analytical solution via hankel and Sumudu transforms. Math. Eng. Sci. Aerosp. 2012, 3, 1–10. [Google Scholar]
- Dubey, R.S.; Goswami, P.; Belgacem, F.B.M. Generalized time-fractional telegraph equation analytical solution by Sumudu and Fourier transforms. J. Fract. Calc. Appl. 2014, 5, 52–58. [Google Scholar]
- Belgacem, F.B.M. Diffusion and drift models for population dispersal from stochastic and continuum views. Int. J. Appl. Math. 2001, 5, 85–106. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new Definition of Fractional Derivative without Singular Kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Losada, J.; Nieto, J.J. Properties of a New Fractional Derivative without Singular Kernel. Fract. Differ. Appl. 2015, 1, 87–92. [Google Scholar]
- Atangana, A.; Alkahtani, B.S.T. Extension of the RLC electrical circuit to fractional derivative without singular kernel. Adv. Mech. Eng. 2015, 7, 1–6. [Google Scholar]
- Dubey, R.S.; Alkahtani, B.S.T.; Atangana, A. Analytical solution of space-time fractional Fokker–Plank equation by homotopy perturbation Sumudu transform method. Math. Probl. Eng. 2015, 2015, 780929. [Google Scholar] [CrossRef]
| Parameter | Unit | Description |
|---|---|---|
| G(t) | (mg/dL) | Blood glucose concentration |
| X(t) | (1/min) | The effect of active insulin |
| I(t) | (mU/L) | Blood insulin concentration |
| (mg/dL) | Basal blood glucose concentration | |
| (mU/L) | Basal blood insulin concentration | |
| (1/min) | Insulin-independent glucose clearance rate | |
| (1/min) | Active insulin clearance rate (upt. decrease) | |
| (L/(min2·mU)) | Increase in uptake ability caused by insulin | |
| (1/min) | Decay rate of blood insulin | |
| (mg/dL) | The target glucose level | |
| (mUdL/L·mg·min) | Pancreatic release rate after glucose bolus |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alkahtani, B.S.; Algahtani, O.J.; Dubey, R.S.; Goswami, P. The Solution of Modified Fractional Bergman’s Minimal Blood Glucose-Insulin Model. Entropy 2017, 19, 114. https://doi.org/10.3390/e19050114
Alkahtani BS, Algahtani OJ, Dubey RS, Goswami P. The Solution of Modified Fractional Bergman’s Minimal Blood Glucose-Insulin Model. Entropy. 2017; 19(5):114. https://doi.org/10.3390/e19050114
Chicago/Turabian StyleAlkahtani, Badr S., Obaid J. Algahtani, Ravi S. Dubey, and Pranay Goswami. 2017. "The Solution of Modified Fractional Bergman’s Minimal Blood Glucose-Insulin Model" Entropy 19, no. 5: 114. https://doi.org/10.3390/e19050114
APA StyleAlkahtani, B. S., Algahtani, O. J., Dubey, R. S., & Goswami, P. (2017). The Solution of Modified Fractional Bergman’s Minimal Blood Glucose-Insulin Model. Entropy, 19(5), 114. https://doi.org/10.3390/e19050114






