Citizen Science and Topology of Mind: Complexity, Computation and Criticality in Data-Driven Exploration of Open Complex Systems
Abstract
:1. Introduction
- Section 2: How can we formalize and treat the databases of varying quality from both machine and human observations, which range from subjective bias to objective fact? How can we set up scientific measures that should assure the compatibility with the principles of accuracy and reproducibility ?
- Section 3: How can we generalize the concept of complexity measures in application to the human–computer hybrid systems in citizen science?
- Section 4: What is the nature of computational complexities in actual data processing?
- Section 5: What is the general condition to yield guided self-organization for cost-effective citizen science?
2. Inter-Subjective Objectivity Model
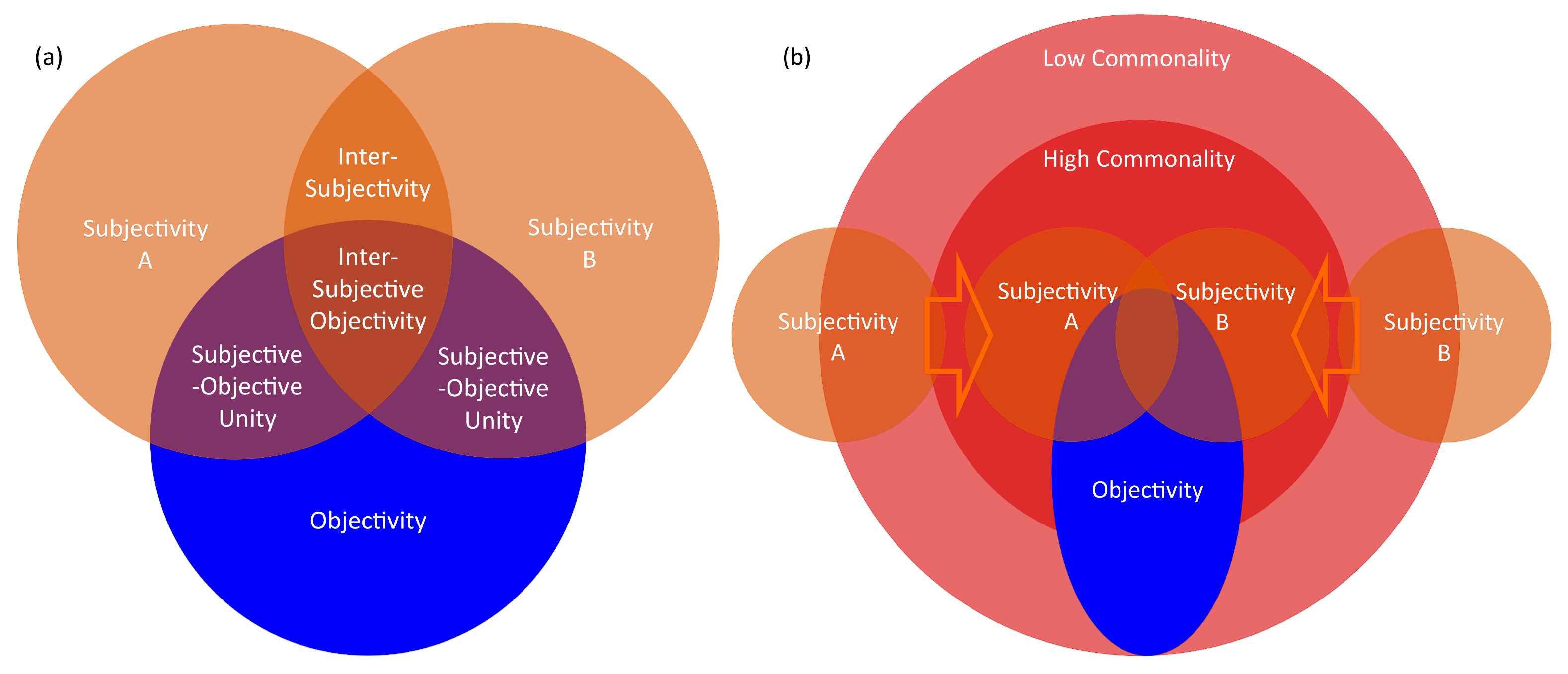
2.1. Formalization of Subjectivity, Inter-Subjectivity, Subjective–Objective Unity, and Objectivity
- Subjectivity is the quality of observation that is based on human perception without the substantial support of a machine.
- Inter-Subjectivity is the degree of commonality between the subjectivities of multiple subjects.
- Objectivity is the quality of observation that is based on a machine measurement whose consequence does not depend on the operator’s will.
- Subjective–Objective Unity is the degree of commonality between the subjectivity and objectivity.
- Inter-Subjective Objectivity is the quality of observation that satisfies the coincidence of both inter-subjectivity and subjective–objective unity.
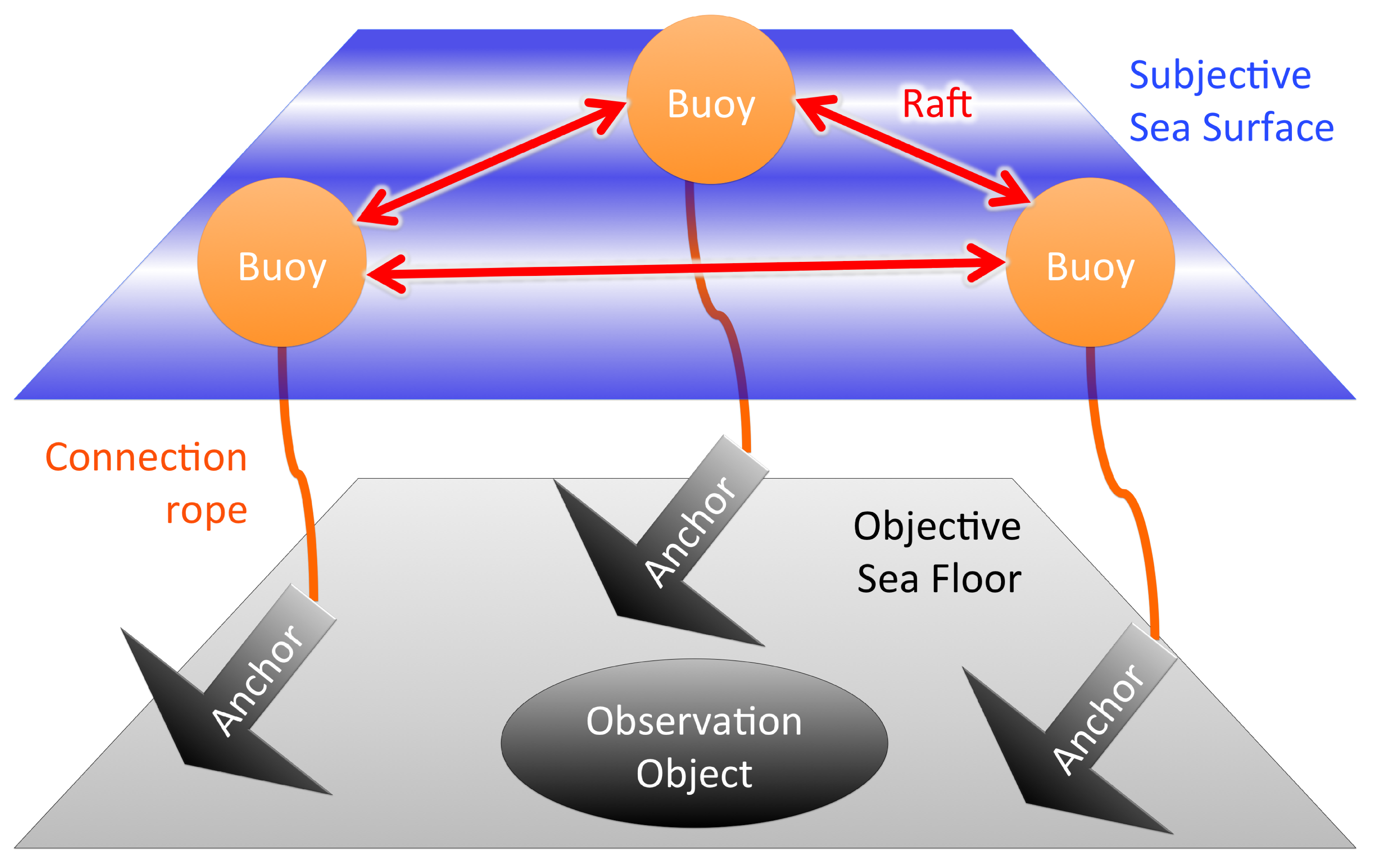
2.2. Representative Model: Buoy–Anchor–Raft Model
- Buoy refers to subjective data that fluctuates on the sea surface, representing subjectivity. Buoy can provide subjective estimates of an observation object lying on the objective sea floor, but the observation is biased by subjective fluctuations.
- Anchor refers to objective data that is fixed on the sea floor representing objectivity, without the influence from the subjective sea surface. Anchors can be connected to buoys, which provide the evaluation of subjective fluctuation with respect to objective machine measurements.
- Raft represents the relationship between buoys, and refers to inter-subjectivity of data without reference to anchors. A buoy can evaluate another buoy using relative difference of fluctuation on a subjective sea surface, and the overall commonality between buoys is represented as the raft. Nevertheless, it is based on an internal observation between buoys without an objective system of units, and is therefore susceptible to a global drift of collective standard.
- Buoy–Anchor connection rope defines the degree of subjective–objective unity. As a buoy’s movement is more controlled by its anchor, higher subjective–objective unity is assured.
- Raft–Anchor connection ropes define the degree of inter-subjective objectivity. In addition to the commonality between buoys represented as a raft, the effects of the global drift from subjective sea surface could be controlled with anchors within a plausible range of error with respect to the objective sea floor.
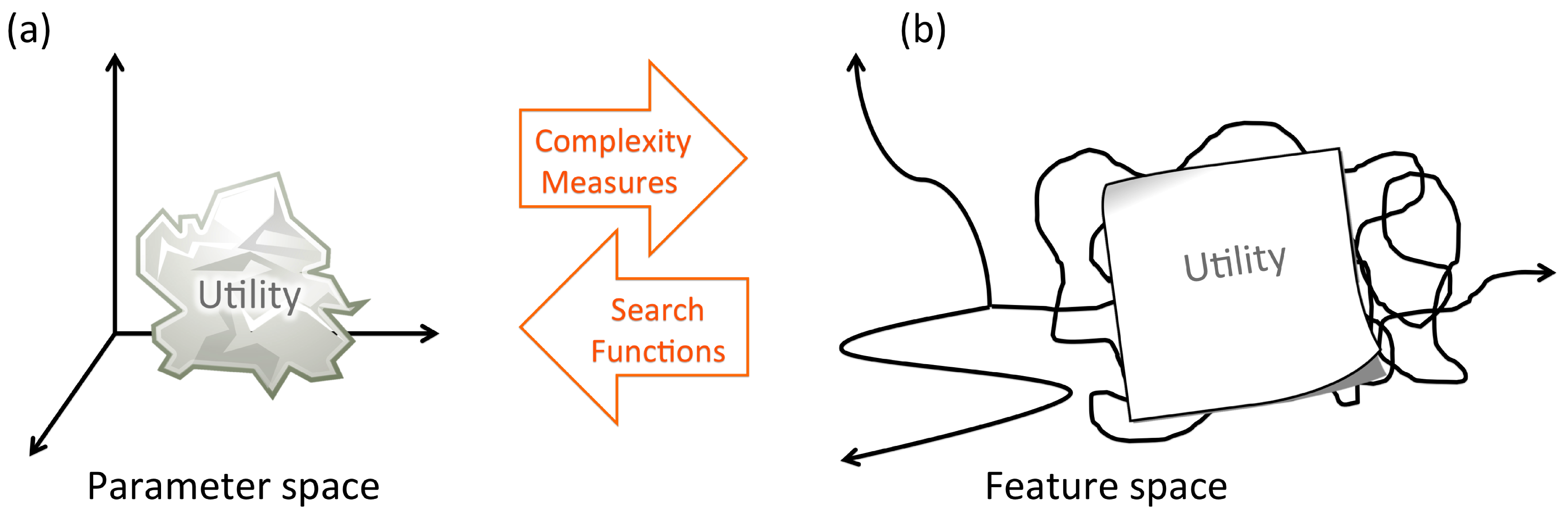
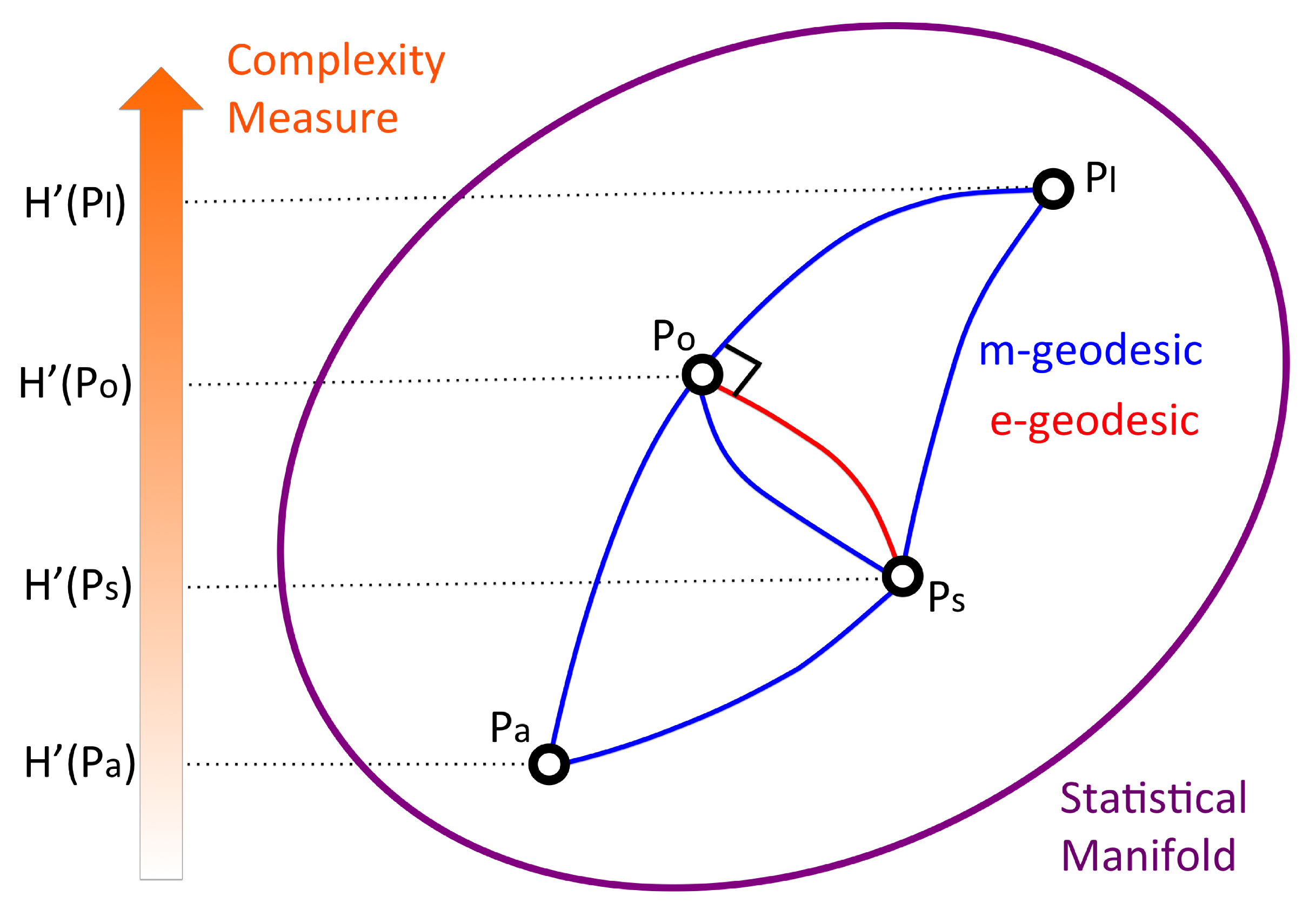
3. Complexity Measures
3.1. Complexity Measure and Search Function
3.2. Observation Commonality as Complexity
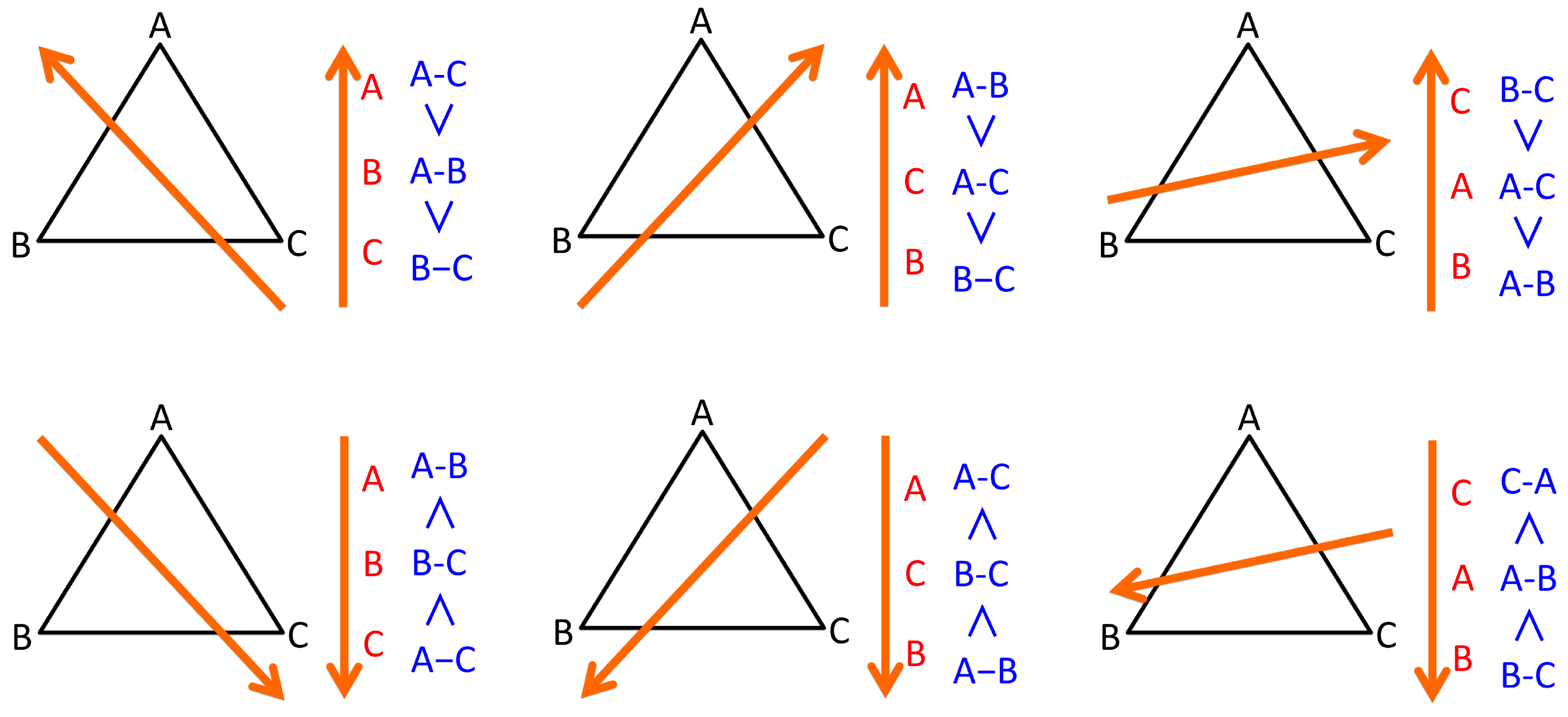
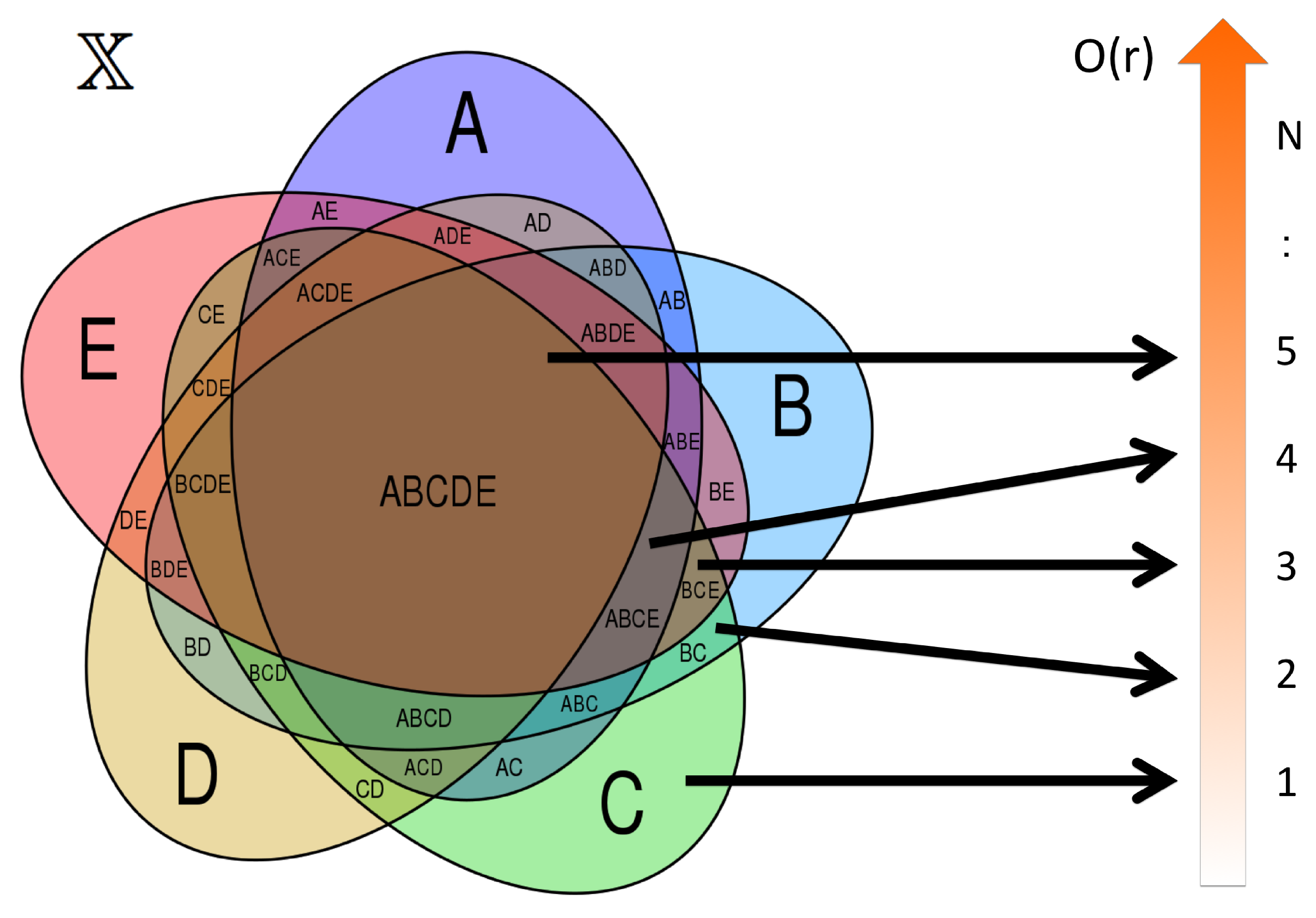
3.3. Topological Structure of Complexity 1: Total Order of Observations
- For each pair of edges , calculate the order relation or with respect to the given complexity measure as an edge attribute such as length.
- Score each edge by mapping to integer by adding if and by adding if , with respect to all other edges .
- The sorting with the score provides the total order of E.
- For each triplet of observation and associated edges , update score of each observation by mapping to integer with the following six rules:
- If , then , , .
- If , then , , .
- If , then , , .
- If , then , , .
- If , then , , .
- If , then , , .
- The sorting with the score provides the total order of V.
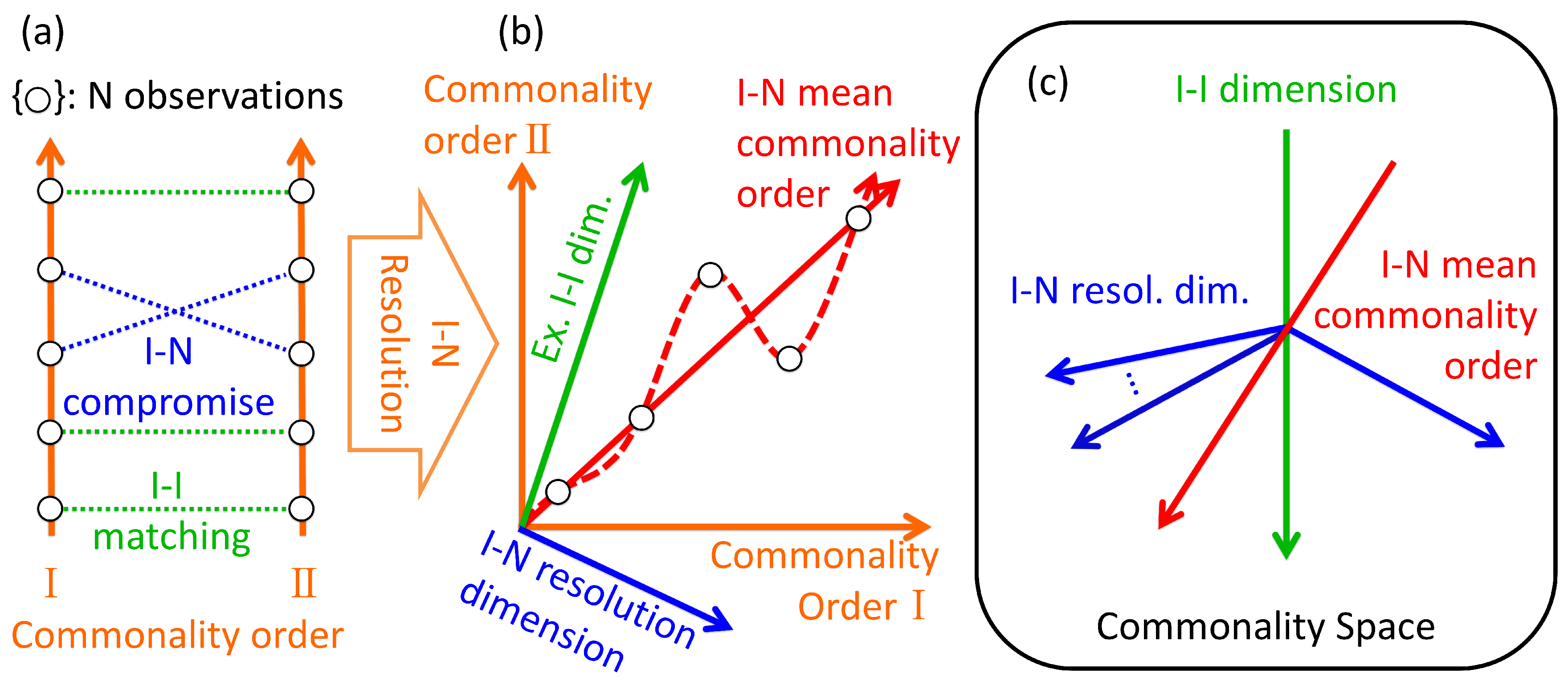
3.4. Topological Structure of Complexity 2: Permutation between Total Orders of Observations
- Two observers observing N objects: Commonality orders I and can correspond to either subjective (buoy) or objective (anchor) observation. The I–N resolution provides integrated commonality measure such as buoy–anchor connection and raft evaluation according to the nature of the observation. TDC provides connections between buoys and/or anchors.
- N observers observing two different objects: The commonality of N observers—whether it be subjective (buoy) or objective (anchor)—are ranked with respect to two different objects I and . The I–N resolution provides a mean ranking of N observers’ commonality upon these observations. TDC provides the reproducibility of commonality among N observers.
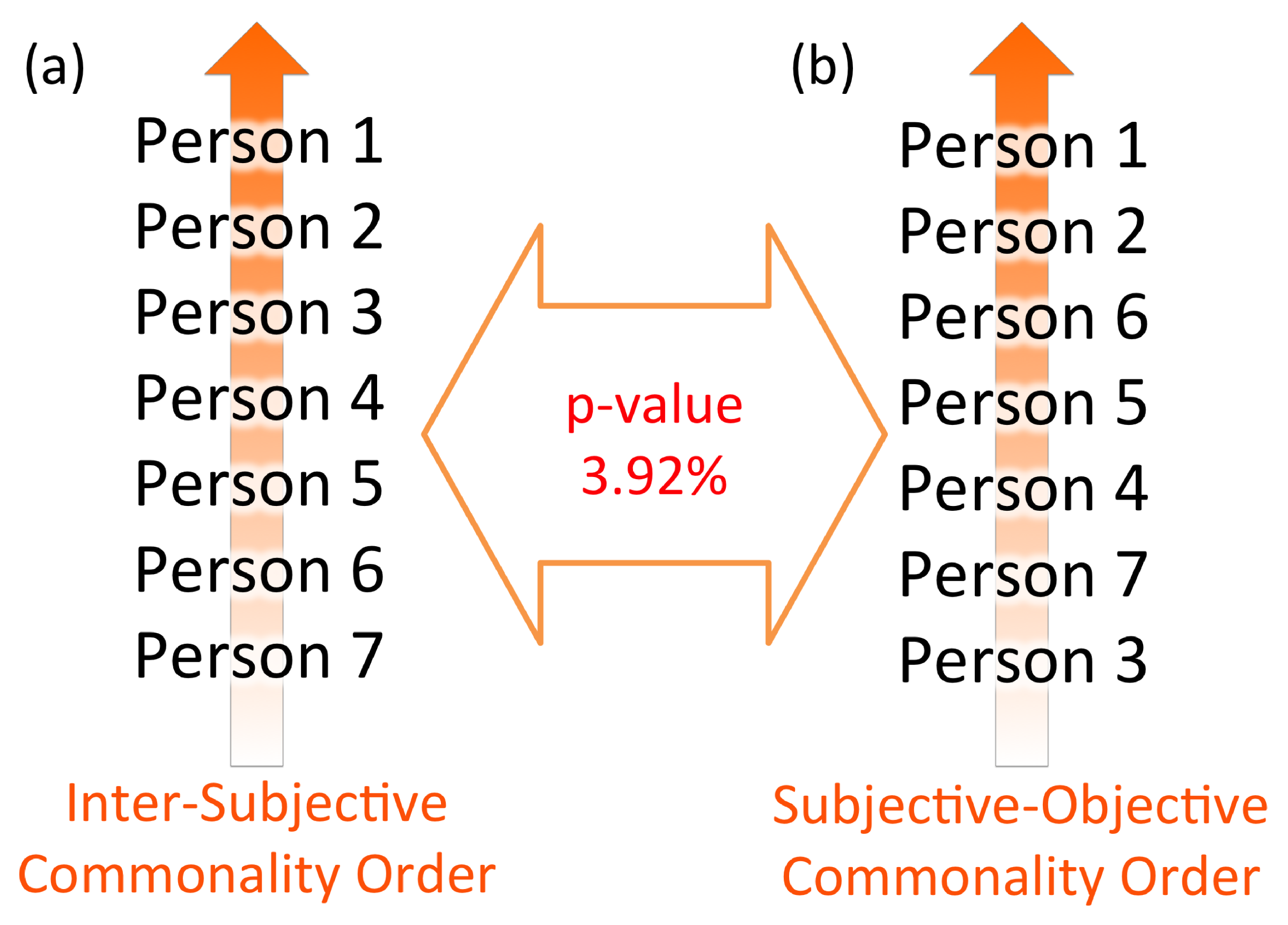
- Application of two different complexity measures to N observations: For example, the case of raft–anchor connection where N subjective observers (buoys) are ranked with inter-subjective commonality (raft evaluation) and weighted with two different anchors. The I–N resolution provides mean ranking of N observers’ inter-subjective objectivity, integrating multiple criteria of inter-subjective and objective evaluation. TDC represents statistical dependencies between two complexity measures in response to a given inter-subjective objective measurement. While significant matching between two commonality orders assures the reproducibility based on the coincidence of observation with these measures, non-significance can also be used to quantify complementarity of different evaluations [32].
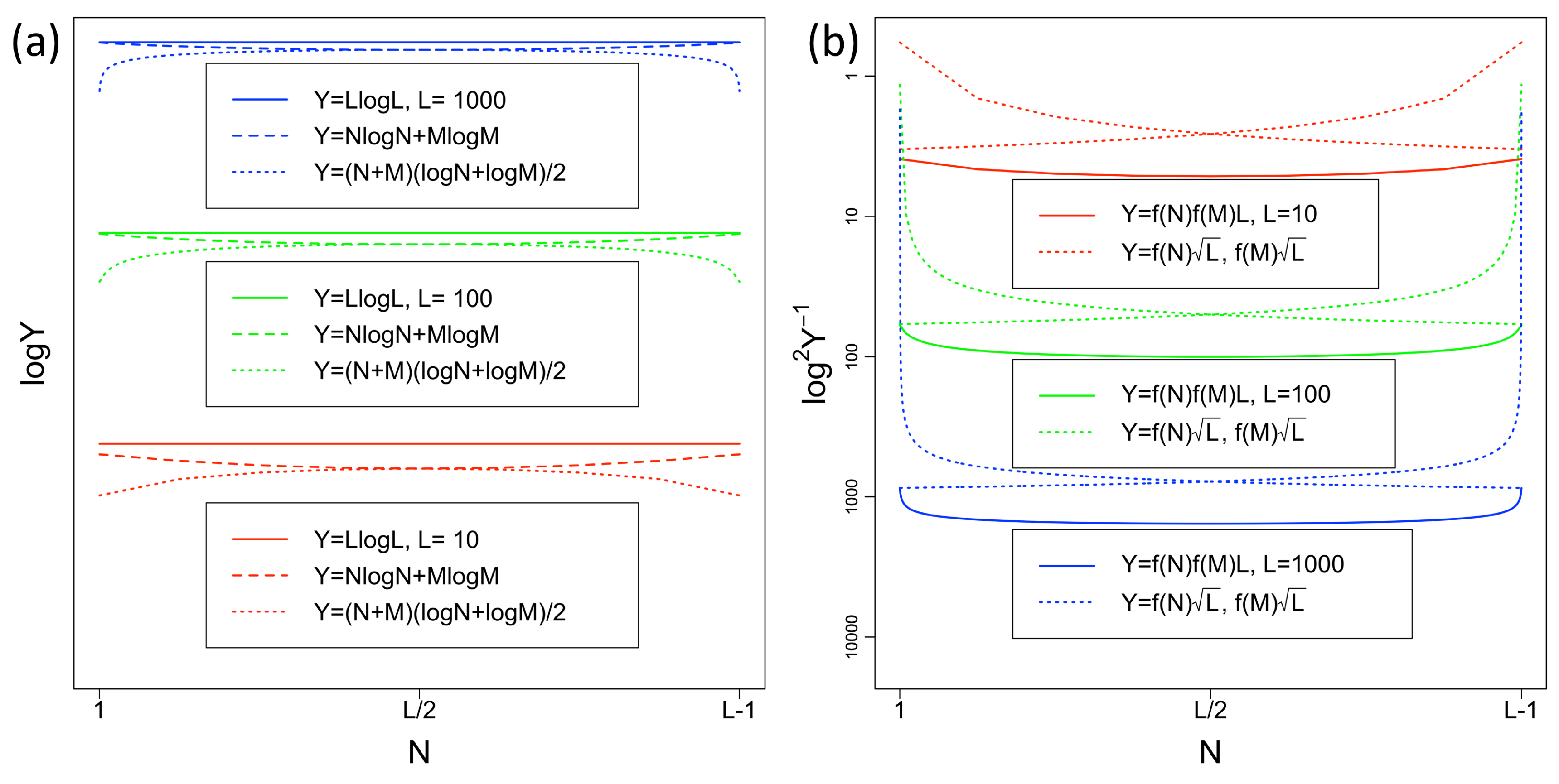
4. Computational Complexity
4.1. Topological Complexity of Commonality
4.2. Algorithmic Complexity
4.3. Big Data Integration
5. Conjectures on Guided Self-Organization
5.1. Criticality by Limitation
- Limitation by principle: Deterministic chaos inherent in a natural system does not allow for long-term prediction, because the tiniest observation error of the present state will develop in exponential order [35]. Short-term validity of meteorological prediction is a typical example.
- Limitation by computational complexity: As explored in Section 4.2, extensive feedback based on exhaustive computing is often impossible with respect to available computing resources. The resolution of feedback may include time delay or incomplete optimization. Spatial-temporal scale of the forecast also sets the constraint as a general trade-off between prediction accuracy and computational resources. The coarser the forecast granularity is, the more costly the calculation becomes, but the more likely it is to realize an accurate long-term prediction.
5.2. Criticality by Successful Learning
- When the actual prediction accuracy is high and human–machine interaction is high, this indicates the successful modelling of observing phenomenon with the use of computation.
- When actual prediction accuracy is high and human–machine interaction is low, it means the human has achieved a successful understanding of the phenomenon with less dependency on a machine.
- When actual prediction accuracy is low and human–machine interaction is high, it indicates the possibility that computational capacity is not sufficient to effectively treat the phenomenon. Otherwise, the observing phenomenon might be in dynamical transition that effective computational model needs to be changed.
- When actual prediction accuracy is low and human–machine interaction is low, more human effort needs to be engaged both on actual observation and the utilization of the machine interface.
5.3. Criticality by Guided Optimization
- : Discrepancy between actual distribution and optimum portfolio strategy that orthogonally decomposes and attempts to achieve a balance between short-term management objective and long-term sustainability.
- : Target risk of short-term management objective.
- : Buffering element of robustness trade-off between short-term management objective and long-term sustainability.
- : Potential risk of optimum portfolio w.r.t. long-term sustainability.
- : Potential risk of short-term management objective w.r.t. long-term sustainability.
- , : Potential risk of actual distribution w.r.t. long-term sustainability.
6. Results from Biodiversity Management
7. Discussion
Acknowledgments
Conflicts of Interest
Appendix A
References
- Schwab, K. The Fourth Industrial Revolution; Crown Business: New York, NY, USA, 2017. [Google Scholar]
- Nature’s Notebook. Available online: https://www.usanpn.org/natures_notebook (accessed on 21 April 2017).
- Funabashi, M.; Hanappe, P.; Isozaki, T.; Maes, A.M.; Sasaki, T.; Steels, L.; Yoshida, K. Foundation of CS-DC e-Laboratory: Open Systems Exploration for Ecosystems Leveraging. In First Complex Systems Digital Campus World E-Conference 2015, Springer Proceedings in Complexity; Springer International Publishing Switzerland: Cham, Switzerland, 2017; pp. 351–374. [Google Scholar]
- Funabashi, M. Open Systems Exploration: An Example with Ecosystems Management. In First Complex Systems Digital Campus World E-Conference 2015, Springer Proceedings in Complexity; Springer International Publishing Switzerland: Cham, Switzerland, 2017; pp. 223–243. [Google Scholar]
- Tokoro, M. Open Systems Science: A Challenge to Open Systems Problems. In First Complex Systems Digital Campus World E-Conference 2015, Springer Proceedings in Complexity; Springer International Publishing Switzerland: Cham, Switzerland, 2017; pp. 213–221. [Google Scholar]
- Bak, P. How Nature Works: The Science of Self-Organized Criticality; Copernicus: New York, NY, USA, 1996. [Google Scholar]
- Jensen, H.J. Self-Organized Criticality; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Takayasu, H.; Sato, A.; Takayasu, A. Stable Infinite Variance Fluctuations in Randomly Amplified Langevin Systems. Phys. Rev. Lett. 1997, 79, 966. [Google Scholar] [CrossRef]
- Scanlon, T.M.; Caylor, K.K.; Levin, S.A.; Rodriguez-Iturbe, I. Positive feedbacks promote power-law clustering of Kalahari vegetation. Nature 2007, 449, 209–212. [Google Scholar] [CrossRef] [PubMed]
- Gabaix, X. Power Laws in Economics: An Introduction. J. Econ. Perspect. 2016, 30, 185–206. [Google Scholar] [CrossRef]
- Alves, L.G.A.; Ribeiroa, H.V.; Lenzi, E.K.; Mendes, R.S. Empirical analysis on the connection between power-law distributions and allometries for urban indicators. Phys. A 2014, 409, 175–182. [Google Scholar] [CrossRef]
- Michelucci, P.; Dickinson, J.L. The power of crowds. Science 2016, 351, 32–33. [Google Scholar] [CrossRef] [PubMed]
- Hanappe, P.; Dunlop, R.; Maes, A.; Steels, L.; Duval, N. Agroecology: A Fertile Field for Human Computation. Hum. Comput. 2016, 1, 1–9. [Google Scholar] [CrossRef]
- Scott, S.L. A modern Bayesian look at the multi-armed bandit. Appl. Stoch. Models Bus. Ind. 2010, 26, 639–658. [Google Scholar] [CrossRef]
- Prokopenko, M. Guided Self-Organization: Inception; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Rekimoto, J.; Nagao, K. The World through the Computer: Computer Augmented Interaction with Real World Environments. In Proceedings of the 8th Annual ACM Symposium on User Interface and Software Technology (UIST’95), Pittsburgh, PA, USA, 15–17 November 1995; pp. 29–36. [Google Scholar]
- Funabashi, M. IT-Mediated Development of Sustainable Agriculture Systems: Toward a Data-Driven Citizen Science. J. Inf. Technol. Appl. Educ. 2013, 2, 179–182. [Google Scholar] [CrossRef]
- Aichi Biodiversity Targets. Available online: https://www.cbd.int/sp/targets/ (accessed on 21 April 2017).
- Funabashi, M. Synecological farming: Theoretical foundation on biodiversity responses of plant communities. Plant Biotechnol. 2016, 33, 213–234. [Google Scholar] [CrossRef]
- Goodchild, M.F. Citizens as sensors: the world of volunteered geography. GeoJoumal 2007, 69, 211–221. [Google Scholar] [CrossRef]
- ISC-PIF (Institut des Systèmes Complexes, Paris Île-de-France). French Roadmap for Complex Systems. ISC-PIF, 2009. Available online: http://cnsc.unistra.fr/uploads/media/FeuilleDeRouteNationaleSC09.pdf (accessed on 21 April 2017).
- Solomon, R.C. Subjectivity. In Oxford Companion to Philosophy; Honderich, T., Ed.; Oxford University Press: Oxford, UK, 2005; p. 900. [Google Scholar]
- Gillespie, A.; Cornish, F. Intersubjectivity: Towards a Dialogical Analysis. J. Theory Soc. Behav. 2009, 40, 19–46. [Google Scholar] [CrossRef]
- Galaxy Zoo. Available online: https://www.galaxyzoo.org/ (accessed on 21 April 2017).
- iNaturalist. Available online: http://www.inaturalist.org/ (accessed on 21 April 2017).
- Rowell, D.L. Soil Science: Methods & Applications; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Kitano, H. Artificial Intelligence to Win the Nobel Prize and Beyond: Creating the Engine for Scientific Discovery. AI Mag. 2016, 37, 39–50. [Google Scholar]
- Ioannidis, J.P. Why most published research findings are false. PLoS Med. 2005, 2, e124. [Google Scholar] [CrossRef] [PubMed]
- Linked Data. Available online: http://linkeddata.org (accessed on 21 April 2017).
- Akao, Y. QFD: Quality Function Deployment—Integrating Customer Requirements into Product Design; Productivity Press: New York, NY, USA, 2004. [Google Scholar]
- Hawker, G.A.; Mian, S.; Kendzerska, T.; French, M. Measures of adult pain: Visual Analog Scale for Pain (VAS Pain), Numeric Rating Scale for Pain (NRS Pain), McGill Pain Questionnaire (MPQ), Short-Form McGill Pain Questionnaire (SF-MPQ), Chronic Pain Grade Scale (CPGS), Short Form-36 Bodily Pain Scale (SF-36 BPS), and Measure of Intermittent and Constant Osteoarthritis Pain (ICOAP). Arthritis Care Res. 2011, 63, 240–252. [Google Scholar]
- Funabashi, M. Network Decomposition and Complexity Measures: An Information Geometrical Approach. Entropy 2014, 16, 4132–4167. [Google Scholar] [CrossRef]
- Walter, R. Fourier Analysis on Groups, Interscience Tracts in Pure and Applied Mathematics, No. 12; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Symmetrical 5-Set Venn Diagram. Available online: https://commons.wikimedia.org/wiki/File:Symmetrical_5-set_Venn_diagram.svg (accessed on 21 April 2017).
- Funanashi, M. Synthetic Modeling of Autonomous Learning with a Chaotic Neural Network International Journal of Bifurcation and Chaos. Int. J. Bifurc. Chaos 2015, 25, 1550054. [Google Scholar] [CrossRef]
- Doya, K.; Ishii, S.; Pouget, A.; Rao, R.P.N. Bayesian Brain: Probabilistic Approaches to Neural Coding; The MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Yoshimura, J.; Clark, C.W. Individual adaptations in stochastic environments. Evol. Ecol. 1991, 5, 173–192. [Google Scholar] [CrossRef]
- Harte, J. Maximum Entropy and Ecology: A Theory of Abundance, Distribution, and Energetics; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Amari, S.; Nagaoka, H. Method of Information Geometry; American Mathematical Society: Providence, RI, USA, 2007. [Google Scholar]
- Rao, C.R. Information and accuracy attainable in the estimation of statistical parameters. Bull. Calcutta Math. Soc. 1945, 37, 81–91. [Google Scholar]
- Murota, K. Matrices and Matroids for Systems Analysis; Springer: Berlin, Germany, 2000. [Google Scholar]
- Roy, S.S.; Dasgupta, R.; Bagchi, A. A Review on Phylogenetic Analysis: A Journey through Modern Era. Comput. Mol. Biosci. 2014, 4, 39–45. [Google Scholar] [CrossRef]
- Brooks, R.A. Intelligence without representation. Artif. Intell. 1991, 47, 139–159. [Google Scholar] [CrossRef]
- Gibson, J.J. The Ecological Approach to Visual Perception; Houghton Mifflin: Boston, MA, USA, 1979. [Google Scholar]

| Economy | Judiciary | Biodiversity Record | Medical Treatment | |
|---|---|---|---|---|
| Buoy | Demand, satisfaction | Sense of justice, guilt | Visual identification of species | Pain, psychological state |
| Raft | Price, exchange rate | Law, court decision | Identification with voting | Diagnosis, prescription |
| Anchor | Goods abundance | Evidential matter | DNA sequences | Physiological markers |
| Section Number | 2.2 | 3.1 | 3.2 | 3.3 | 3.4 | 4 | 5 |
|---|---|---|---|---|---|---|---|
| Buoy | , | , | Data contained in vertices V | Com. order I and between N objects | Observations A, B, C, D, E | , , , , , | |
| Anchor | |||||||
| Raft | , | , | Edge attribute of E | Com. order I and b/w N observers, TDC, I-I and I-N res. dim. | , , | ||
| Buoy–Anchor | |||||||
| Raft–Anchor |
| Maximum Commonality Order | Number of Combination | Sorting Time () |
|---|---|---|
| 2 | ||
| 3 | ||
| ⋮ | ⋮ | ⋮ |
| or | = | |
| ⋮ | ⋮ | ⋮ |
| N |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Funabashi, M. Citizen Science and Topology of Mind: Complexity, Computation and Criticality in Data-Driven Exploration of Open Complex Systems. Entropy 2017, 19, 181. https://doi.org/10.3390/e19040181
Funabashi M. Citizen Science and Topology of Mind: Complexity, Computation and Criticality in Data-Driven Exploration of Open Complex Systems. Entropy. 2017; 19(4):181. https://doi.org/10.3390/e19040181
Chicago/Turabian StyleFunabashi, Masatoshi. 2017. "Citizen Science and Topology of Mind: Complexity, Computation and Criticality in Data-Driven Exploration of Open Complex Systems" Entropy 19, no. 4: 181. https://doi.org/10.3390/e19040181
APA StyleFunabashi, M. (2017). Citizen Science and Topology of Mind: Complexity, Computation and Criticality in Data-Driven Exploration of Open Complex Systems. Entropy, 19(4), 181. https://doi.org/10.3390/e19040181






