Abstract
Interpretational problems with quantum mechanics can be phrased precisely by only talking about empirically accessible information. This prompts a mathematical reformulation of quantum mechanics in terms of classical mechanics. We survey this programme in terms of algebraic quantum theory.
1. Introduction
The mathematical formalism of quantum mechanics is open to interpretation. For example, the possibility of deterministic hidden variables, the uncertainty principle, the measurement problem, and the reality of the wave function, are all up for debate. (The first and the last of course have rigorous restrictions: hidden variables by the Bell inequalities [1] and the Kochen–Specker theorem [2], discussed below, and reality of the wave function by the Pusey–Barrett–Rudolph theorem [3].) Classical mechanics shares none of those interpretational questions. This article surveys a mathematical reformulation of quantum mechanics in terms of classical mechanics, intended to bring the interpretational issues with the former to a head. This programme proposes to replace the usual notion of state space of a quantum-mechanical system by a new one, in a way that avoids the interpretational questions above and leaves classical systems unaffected:
- known obstructions to hidden variable interpretations merely say that states cannot be located with exact precision in the state space, and are circumvented via open regions of states;
- the uncertainty principle cannot be expressed and therefore poses no interpretational problem;
- the measurement problem is obviated because the new notion of state space incorporates all classical data resulting from possible measurements.
If we also take dynamics into account, the new notion of configuration space, called an active lattice:
- yields the same predictions as traditional quantum mechanics.
This programme branches into a number of related themes, spread over the literature; see the extensive bibliography. The aim of this article is to bring all these active developments together to give an overview. There are hardly any new results. Instead, the novelty lies in rephrasing foundations to give an accessible, coherent, and complete overview of the current state-of-the-art. To do so, we will have to be rather brief and refer to references for many technical details. Nevertheless, there is a novel contribution regarding topological structure of the new notion of configuration space. We will use an n-level physical system as a running example to illustrate new notions (though many results have exceptions for , and most interesting features occur in infinite dimension). The rest of this introduction summarizes the framework and discusses four salient features, before giving an overview of the rest of this article.
1.1. Algebraic Quantum Theory
The traditional formalism of quantum theory holds that the (pure) state space is a Hilbert space H, that (sharp) observables correspond to self-adjoint operators on that Hilbert space, and that (undisturbed) evolution corresponds to unitary operators. Algebraic quantum theory instead takes the observables as primitive, and the state space is a derived notion. Self-adjoint operators combine with unitaries to give all bounded operators, and these form a so-called C*-algebra . However, superselection rules mandate that not all self-adjoint operators correspond to valid observables. Thus, one considers arbitrary C*-algebras, rather than only those of the form . Nevertheless, it turns out that any C*-algebra A embeds into for some Hilbert space H, and in that sense C*-algebra theory faithfully captures quantum theory. Finally, one could impose extra conditions on a C*-algebra, leading to so-called AW*-algebras, and W*-algebras, also known as von Neumann algebras. A good example to keep in mind is the algebra of n-by-n complex matrices, that models (the observables of) an n-level system, or direct sums .
To pass from pure to mixed states (density matrices), from sharp to unsharp observables (positive operator valued measurements), and from undisturbed evolution to including measurement (quantum channels), the traditional formalism prescribes completely positive maps. These find their natural home in the algebraic formulation. States of a C*-algebra A can then be recovered as unital (completely) positive maps . Observables with n outcomes are unital (completely) positive maps ; sharp observables correspond to homomorphisms. Evolution is described by a completely positive map ; undisturbed evolution corresponds to a homomorphism. Indeed, if , then states are precisely density matrices; observables are precisely positive operator valued measurements with n outcomes; completely positive maps are precisely those that map density matrices to density matrices; and homomorphisms are precisely the linear functions that map pure states to pure states.
For more information on algebraic quantum theory, see [4,5,6,7,8,9,10,11,12,13].
1.2. Gelfand Duality
The advantage of algebraic quantum theory is that it places quantum mechanics on the same footing as classical mechanics. The (pure) state space in classical mechanics can be any locally compact Hausdorff topological space X, (sharp) observables are continuous functions , and evolution is given by homeomorphisms . This leads to the C*-algebra of continuous complex-valued functions on X vanishing at infinity; for compact X, we write . A simple example is the algebra , where X is a discrete space with n points. Indeed, in that case there are n (pure) states; (sharp) observables are precisely vectors in ; and (deterministic) evolutions are just functions .
Again, we can pass from classical mechanics to the probabilistic setting of statistical mechanics by considering completely positive maps. States of can be recovered as unital (completely) positive maps as before; pure states correspond to homomorphisms. Observables with m outcomes are (completely) positive maps , and sharp observables correspond to homomorphisms. Stochastic evolution is described by a (completely) positive map ; deterministic evolution corresponds to a homomorphism. Indeed, for X, the discrete space with n points, states are precisely probability distributions on n points; observables with m outcomes are precisely m-tuples of probability distributions on n points summing to one; sharp observables are just functions ; and evolutions are simply stochastic m-by-n matrices.
Note that multiplication in is commutative, whereas was noncommutative. Gelfand duality says that any commutative C*-algebra C is of the form for some compact Hausdorff space X, called its spectrum and written as . That is, and . Moreover, this gives a dual equivalence of categories: if is a continuous function then is a homomorphism, and conversely, if is a homomorphism, then is a continuous function. Thus, C*-algebra theory is often regarded as noncommutative topology. In the case of a discrete space X with n points, this simply says that up to isomorphism is the only commutative C*-algebra of dimension n, and that functions are the only way to describe deterministic evolutions.
For more information, we refer to [14,15,16,17] in addition to references above.
1.3. Bohr’s Doctrine of Classical Concepts
To summarize, both classical systems and quantum systems are first-class citizens that can interact in the algebraic framework. Classical systems are commutative algebras C, and quantum systems are noncommutative ones A. An example interaction is measurement, given by maps . For n-level systems, a measurement with m outcomes is a map . Having no superfluous outcomes in of the measurement corresponds to the injectivity of these maps. So the information that all possible measurements can give us about a possibly noncommutative algebra A is its collection of commutative subalgebras C. In other words, all empirically accessible information in a quantum system is encoded in its family of classical subsystems. This observation is known as the doctrine of classical concepts and dates back to Bohr [18,19]. For an n-level system , elements of indeed correspond to all possible measurement setups: the ways of choosing an orthonormal basis of and a partition of an n-element set with m equivalence classes for outcomes.
The main aim of this paper is to survey what can be said about the quantum structure A based on its many classical faces , explaining the title.
1.4. The Kadison–Singer Problem
A case in point is the long-standing but recently solved Kadison–Singer problem [20,21]. In a noncommutative C*-algebra, not all observables are compatible, in the sense that they can be measured simultaneously (without uncertainty). What can at most be measured in an experiment are those observables in a single commutative subalgebra. The best an experimenter can do is repeat the experiment to determine the values of those observables, giving a pure state of that commutative subalgebra. Ideally, this tomography procedure should determine the state of the entire system. Indeed, there are various protocols for performing such tomography on n-level systems that have been experimentally verified [22].
The Kadison–Singer result says that this procedure indeed works in the discrete case. Let H be a Hilbert space of countable dimension. Then has a discrete maximal commutative subalgebra consisting of operators that are diagonal in a fixed basis. The precise result is that a pure state of extends uniquely to a pure state of . Thus, (the state of) a quantum system is characterized by what we can learn about it from experiments, giving a positive outlook on Bohr’s doctrine of classical concepts.
1.5. The Kochen–Specker Theorem
Nevertheless, Bohr’s doctrine of classical concepts should be interpreted carefully. It does not say that collections of states of each classical subsystem assemble to a state of the quantum system. That is ruled out by the Kochen–Specker theorem. In physical terms, local deterministic hidden variables are impossible; one cannot assign definite values to all observables of a quantum system in a noncontextual way, i.e., giving coherent states on classical subsystems. In mathematical terms, Gelfand duality does not extend to noncommutative algebras via ; this will be discussed in more detail in Section 2. More precisely, the zero map is the only function that restricts to homomorphisms for each when . That is, there is no way to assign measurement outcomes in to all possible positive operator valued measures on an n-level system with m outcomes in a consistent way. This extends to more general noncommutative A that do not contain a subalgebra . See [2,11,23].
1.6. Overview of This Article
Section 2 continues in more depth the discussion of the structure of quantum systems from the perspective just sketched. In particular, it covers exactly how much of A can be reconstructed from , and makes precise the link between the Kochen–Specker theorem and noncommutative Gelfand duality. Section 3 shows how to interpret a quantum system A as a classical system via by changing the rules of the ambient set theory, and discusses the surrounding interesting interpretational issues. Section 4 considers fine-graining. Increasing chains of classical subsystems give more and more information about the quantum system. We discuss from this information-theoretic point of view, called domain theory. Section 5 explains how to incorporate dynamics into , turning it into a so-called active lattice. It turns out that this extra information does make into a full invariant, from which one can reconstruct A. This raises interesting interpretational questions: its active lattice can be regarded as a configuration space that completely determines a quantum system. By encoding more than static hidden variables, it circumvents the obstructions of Section 2. To obtain an equivalence for quantum systems like Gelfand duality did for classical ones, it thus suffices to characterize the active lattices arising this way. This is examined in Section 6. Finally, Section 7 considers to what extent the successes of the doctrine of classical concepts in the previous sections are due to the use of algebraic quantum theory, and to what extent they generalize to other formulations.
2. Invariants
Bohr’s doctrine of classical concepts teaches that a quantum system can only be empirically understood through its classical subsystems. These classical subsystems should therefore contain all the physically relevant information about the quantum system.
Definition 1.
For a unital C*-algebra A, write for its family of commutative unital C*-subalgebras C (with the same unit as A). We may think of it either as partially ordered set by inclusion, or as a diagram that remembers that the points of the partially ordered set are C*-algebras C.
For example, the partially ordered set of a 2-level system has Hasse diagram
 with a point on the upper level for each unitary in .
with a point on the upper level for each unitary in .
 with a point on the upper level for each unitary in .
with a point on the upper level for each unitary in .The question is then: how does the mathematical formalism of the quantum theory of A translate into terms of ? For example, it turns out that the entropy of a state of A can be reconstructed from the entropies of its restriction to [24], see also [25]. Ideally, we would like to completely reconstruct A from . A priori, is merely an invariant of A. This section investigates how strong an invariant it is. The first step is to realize that, from , we can reconstruct A as a set, as well as operations between commuting elements. This can be made precise by the notion of a piecewise C*-algebra, which is basically a C*-algebra that forgot how to add or multiply noncommuting operators.
Definition 2.
A piecewise C*-algebra consists of a set A with
- a reflexive and symmetric binary (commeasurability) relation ;
- elements ;
- a (total) involution ;
- a (total) function ;
- a (total) function ;
- (partial) binary operations ;
such that every set of pairwise commeasurable elements is contained in a set of pairwise commeasurable elements that forms a commutative C*-algebra under the above operations.
Of course, any commutative C*-algebra is a piecewise C*-algebra. More generally, the normal elements (those commuting with their own adjoint) of any C*-algebra A form a piecewise C*-algebra. For an n-level system , the piecewise C*-algebra consists of all normal n-by-n matrices, together with their norms and adjoints, as well as the knowledge of how commuting elements add and multiply. Notice that makes perfect sense for any piecewise C*-algebra A. To make precise how we can reconstruct the piecewise structure of A from , we will use the language of category theory [26]. C*-algebras, with ∗-homomorphisms between them, form a category. We can also make piecewise C*-algebras into a category with the following arrows: (total) functions that preserve commeasurability and the algebraic operations, whenever defined.
The precise notion we need is that of a colimit. Suffice to say here, a colimit, when it exists, is a universal solution that compatibly pastes together a given diagram into a single object. Thinking of A as the whole and as its parts, we would like to know whether the whole is determined by the parts. The following theorem says that indeed contains enough information to reconstruct A as a piecewise C*-algebra.
Theorem 1
([27]). Every piecewise C*-algebra is the colimit of its commutative C*-subalgebras in the category of piecewise C*-algebras.
This means that the diagram determines the piecewise C*-algebra A: if and are isomorphic diagrams, then A and B are isomorphic piecewise C*-algebras. Moreover, the previous theorem gives a concrete way to reconstruct A from . For the n-level system , this means we can reconstruct from the normal n-by-n matrices, as well as sums and products of commuting ones. An important point to note here is that the reconstruction is happening in the setting of piecewise C*-algebras. We could not have taken the colimit in the category of commutative C*-algebras instead. Indeed, one way to reformulate the Kochen–Specker theorem in terms of colimits is the following. The following reformulation might not look much like the original, but it is nevertheless equivalent, and more suited to our purposes; see also ([2], p. 66).
Theorem 2
([2,28]). If , then the colimit of in the category of commutative C*-algebras is the degenerate, 0-dimensional, C*-algebra.
In fact, the colimit of degenerates for many more C*-algebras A than just , such as any C*-algebra of the form for some C*-algebra B, or any W*-algebra that has no direct summand or [29,30].
As mentioned in the introduction, Gelfand duality is a functor from the category of commutative C*-algebras to the category of compact Hausdorff topological spaces. That is, a systematic way to assign a space to a C*-algebra, that respects functions. Interpreted physically: any classical system is determined by a configuration space in a way that respects operations on the system. The previous theorem can be used to show that there is no such configuration space determining quantum systems—at least, if the notion of configuration space is to be a conservative extension of the classical notion. The latter can be made precise as a continuous functor from the category of compact Hausdorff spaces to some category with a degenerate space like the empty set, more precisely, a strict initial object 0.
Theorem 3
([29]). Suppose there exist a category conservatively extending that of compact Hausdorff spaces and a functor F completing the following square.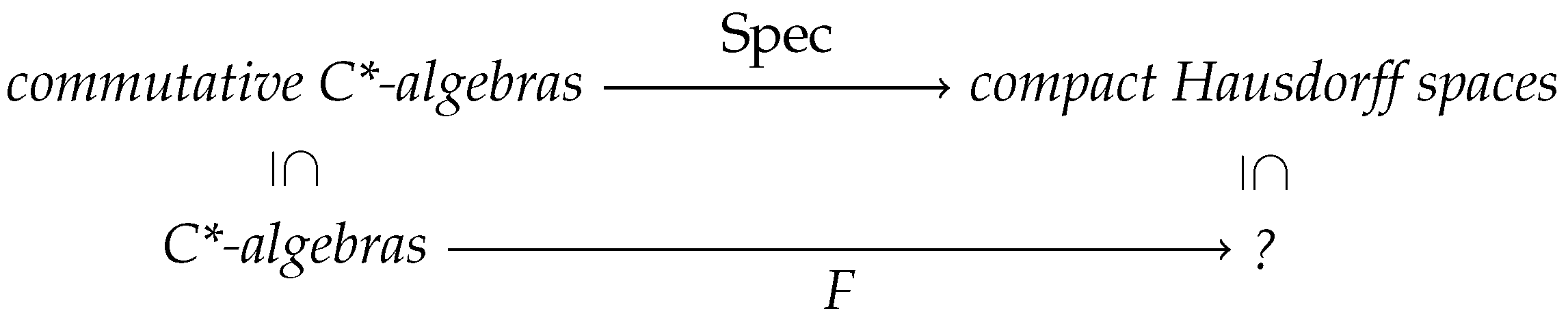
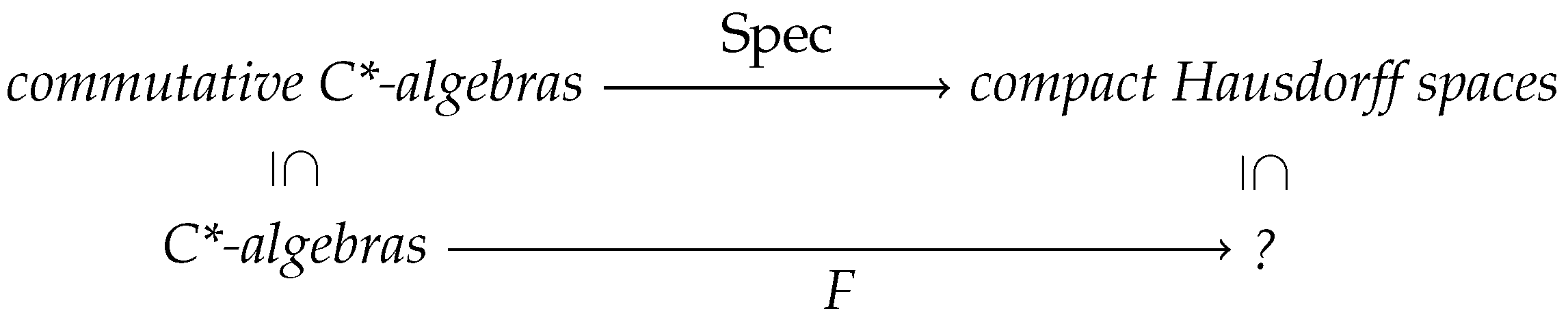
Then for . In particular, F cannot be a dual equivalence.
Asking the functor on the right to be continuous is appropriate to model the classical limit of quantum systems converging to a classical one, because then the state space of the product of two limiting classical systems should be computed as the classical limit of the joint quantum systems. In fact, the proof in [29] holds if the category on the bottom right has limits, and the functor on the right reflects them. However, one might still wonder if it is reasonable to ask the diagram to commute on the nose. Instead, we could ask it to commute up to a natural isomorphism. This is precisely the way out we will explore in Section 3 and Section 5.
This rules out many possible quantum configuration spaces that have been proposed for the bottom right role in the square; in particular many generalized notions of topological spaces, such as sets, topological spaces themselves, pointfree topological spaces, ringed spaces, quantales, toposes, categories of sheaves, and many more [28,29,31]. In particular, the state space of a C*-algebra, as discussed in the introduction, will not do for us, even though it is one of the most important tools associated with a C*-algebra [32]. That explains why we deliberately talk about “configuration spaces”. In the classical case, the two notions coincide. The previous theorem shows that serious notions of quantum configuration space must be less conservative. This points the way towards good candidates: Section 3 and Section 5 will cover two that do fit the bill.
The question of noncommutative extensions of Gelfand duality is also very interesting from a purely mathematical perspective. As mentioned in the introduction, C*-algebra theory can be regarded as noncommutative topology. Adding more structure than mere topology leads to noncommutative geometry, which is a rich field of study [33]. However, it takes place entirely on the algebraic side. Finding the right notion of quantum configuration space could reintroduce geometric intuition, which is usually very powerful [34,35]. For example, in certain cases, extensions of can be used to compute the K-theory of A, which is a way to study homotopies of the configuration space underlying A, that includes many local-to-global principles [36]. Similarly, closed ideals of a W*-algebra A, that are important because they correspond to open subsets in the classical case, are in bijection with certain piecewise ideals of [37].
So far, we have considered as a diagram of parts of the whole. We finish this section by considering it as a mere partially ordered set, where we forget that elements have the structure of commutative C*-algebras. That is, we only consider the shape of how the parts fit together. This information is already enough to determine the piecewise structure of A, but as a Jordan algebra. (In fact, considering as a mere partially ordered set gives precisely the same information as considering it as a diagram [38]. This justifies Definition 1.) The self-adjoint elements of a C*-algebra form a Jordan algebra under the product ; this even gives a so-called JB-algebra. In fact, any JB-algebra is a subalgebra of the direct sum of one of this form and an exceptional one, such as quaternionic matrices [39]. For example, the n-level system gives the JB-algebra of hermitian n-by-n matrices multiplied via anticommutators. Piecewise Jordan algebras and their homomorphisms are defined analogously to Definition 2. The structure of quantum observables leads naturally to the axioms of Jordan algebras [8] (Modern mathematical physics tends to prefer C*-algebras, as their theory is slightly less complicated, and the connections to Jordan algebras are so tight anyway [39].) The following theorem justifies that point of view.
Theorem 4
([40]). Let A and B be C*-algebras. If and are isomorphic partially ordered sets, then A and B are isomorphic as piecewise Jordan algebras.
A little more can be said. Any isomorphism is implemented by an isomorphism of piecewise Jordan algebras, in the sense that . In fact, this g is unique, unless A is either or . For AW*-algebras more is true because of Gleason’s theorem, that we will meet in Section 5, we can actually reconstruct the full linear structure rather than just the piecewise linear structure. (An AW*-algebra is a C*-algebra A that has enough projections, in the sense that every is the closed linear span of its projections, and those projections work together well, in the sense that orthogonal families in the partially ordered set of projections have least upper bounds [7,41]. See also Section 5. They are more general than W*-algebras, and much of the theory of W*-algebra generalizes to AW*-algebras, such as the type decomposition. An n-level system forms a W*-algebra, and hence also an AW*-algebra.) Type AW*-algebras are those of the form for a commutative AW*-algebra C. AW*-algebras with a type direct summand correspond to the exceptional case in the Kochen–Specker Theorem 2. We will call them atypical, and algebras without a type direct summand typical, as we will meet this exception often. An n-level system is typical when .
Corollary 1
([42,43]). Let A and B be typical AW*-algebras. If and are isomorphic partially ordered sets, then A and B are isomorphic as Jordan algebras.
Whereas the C*-algebra product is associative but need not be commutative, the Jordan product is commutative but need not be associative; commutative C*-subalgebras correspond to associative Jordan subalgebras. Indeed, the previous theorem generalizes to Jordan algebras in those terms [44].
3. Toposes
In this section, we consider as a diagram. That is, we regard it as an operation that assigns to each classical subsystem of the quantum system A a classical system C. What kind of operation is this diagram ? We can think of it as a set that varies with the context . Moreover, this contextual set respects coarse-graining: if , then . That is, when the measurement context C grows to include more observables, the information contained in the set assigned to it grows along accordingly. For example, for an 2-level system , this comes down to a choice of set for each unitary , that all include a fixed set . Hence, these contextual sets are functors S from , now regarded as a partially ordered set, to the category of sets and functions. The totality of all such functors forms a category. In fact, contextual sets form a particularly nice category, namely a topos.
A topos is a category that shares a lot of the properties of the category of sets and functions. In particular, one can do mathematics inside a topos: we may think about objects of a topos as sets, that we may specify and manipulate using logical formulae. Of course, this internal perspective comes with some caveats. Most notably, if a proof is to hold in the internal language of any topos, it has to be constructive: we are not allowed to use the axiom of choice or proofs by contradiction, and have to be careful about real numbers. We cannot go into more detail here, but for more information on topos theory, see [45].
One particular object of interest in the topos of contextual sets over is our canonical contextual set . It turns out that, according to the logic of the topos of contextual sets, this object is a commutative C*-algebra.
Theorem 5
([19]). Let A be a C*-algebra. In the topos of contextual sets over , the canonical contextual set is a commutative C*-algebra.
This procedure is called Bohrification:
- Start with a quantum system A.
- Change the logical rules of set theory by moving to the topos of contextual sets over .
- The quantum system A turns into a classical one given by the canonical contextual set .
See also [46].
Thus, we may study the quantum system A as if it were a classical system. Of course, we lose the same information as in the previous section. For example, we can only hope to reconstruct the Jordan structure of A from the contextual set . Nevertheless, placing it in a topos of its peers opens up many possibilities. In particular, we may try to find a configuration space inside the topos. It turns out that Gelfand duality can be formulated so that its proof is constructive, and hence applies inside the topos. This involves talking about locales rather than topological spaces. We may think of a locale as a topological space that forgot it had points.
More precisely, a locale may be thought of as the partially ordered family of open sets of a topological space, but without a carrier set of points. Most of topology can be formulated to work for locales as well. Again, we cannot go into more detail here, but for more information on locales see [47].
Corollary 2
([48]). Let A be a C*-algebra. In the topos of contextual sets over , there is a compact Hausdorff locale X such that the canonical contextual set is of the form .
For example, if A is the 2-level system , then X is the contextual set S that assigns to the orthonormal basis of corresponding to u, and that assigns to 0 the zero vector in , where locally carries the structure of a 2-element discrete space, and carries the structure of a 1-element discrete space. We will call this locale X the spectral contextual set. In general, it is not just the contextual set . However, it does resemble that if we think about bundles instead of contextual sets [49,50]: a bundle is a map of locales into the locale of ideals of , and by restricting the intuitionistic logic of a topos further to so-called geometric logic, the bundle corresponding to the spectral contextual set does have fibre over C. Also, if we reverse the partial order on , the assignment plays the role of the canonical contextual set. So there are two approaches:
- Either one uses ; the canonical contextual set is a commutative C*-algebra, and the spectral contextual set X does not take a canonical form [19,51,52,53,54,55].
- Or one uses the opposite order; the spectral contextual set X is a locale of the canonical form , and the commutative C*-algebra does not take a canonical form [56,57,58,59].
For a comparison, see [60]. For this overview article, the choice of direction does not matter so much. In any case, X is an object inside the topos of contextual sets, and as such we may reason about it as a locale. In particular, we may wonder whether it is a topological space, that is, whether it does in fact have enough points. It turns out that the Kochen–Specker Theorem 2 can be reformulated as saying that not only does X not have enough points, in fact it has no points at all. In terms of bundles: the canonical bundle has no global sections. This illustrates the need for locales rather than topological spaces.
Proposition 1
([23]). Let A be a C*-algebra satisfying the Kochen–Specker Theorem 2. In the topos of contextual sets over , the spectral contextual set has no points.
Thus, Bohrification turns a quantum system A into a locale X inside the topos of contextual sets over . There is an equivalence between locales X inside such a topos over , and certain continuous functions from a locale to outside the topos [61]. This gives a way to cut out the whole topos detour, and assign to the quantum system A a configuration space that we will temporarily call for the rest of this section.
Proposition 2
([62]). For any C*-algebra A, the internal locale X is determined by a continuous function from some locale to .
In many cases, will in fact have enough points, i.e., will be a topological space [60,62]—despite Proposition 1. The construction circumvents the obstruction of Theorem 3 for several reasons. First, when the C*-algebra A is commutative, turns out to be a locale based on , rather than on A itself; therefore what we are currently denoting by does not match the Gelfand spectrum of A. Second, the construction is only partially functorial: if we regard as a locale, the construction only respects functions that reflect commutativity [27], and to get functorality we have to regard as a localed topos, that is, a topos with a locale in it [63].
We can only touch on it briefly here, but one of the main features of building the topos of contextual sets over and distilling the configuration space is that they encode a contextual logic. This logic is intuitionistic, and therefore very different from traditional quantum logic [52]. The latter concerns the set of yes–no questions on the quantum system A; more precisely, the set of sharp observables with two outcomes. These correspond to projections: satisfying . They are partially ordered by when , which should be read as saying that p implies q. Similarly, least upper bounds in are logical disjunctions [11]. In an n-level system , projections correspond to subspaces of , regarded logically as the set of (pure) states where the proposition is true; the order becomes inclusion of subspaces; and the disjunction of subspaces is their linear span. AW*-algebras A are determined to a great extent by their projections, and indeed the quantum logic carries precisely the same amount of information as [64]. For more information about this topos-theoretic approach to quantum logic, we refer to [19,49,51,52,53,54,56,57,58].
To connect contextual sets to probabilities and the Born rule, we have to translate states of A into some notion based on the spectral contextual set X, and observables of A into some notion based on the canonical contextual set . For the latter, one has to resort to approximations, as not every will be present in each ; this process is sometimes called daseinisation [57]. The former has a satisfying solution in terms of piecewise states: piecewise linear (completely) positive maps .
Theorem 6
([23,51,65]). There is a bijective correspondence between piecewise states on an AW*-algebra A, and states of the canonical contextual set inside the topos of contextual sets over .
(The cited references consider W*-algebras, but the proof holds for AW*-algebras because Corollary 5 does so, see Section 5. The same goes for the references in Corollary 3.) By Gleason’s theorem (see Section 5), we can say more for AW*-algebras. See also [25].
Corollary 3
([66,67]). There is a bijective correspondence between states of a typical AW*-algebra A, and states of the canonical contextual set inside the topos of contextual sets over .
In the n-level system for , this means that n-by-n density matrices correspond precisely to a choice of probability distribution over m points that is consistent over all unitaries and partitions of n points into m equivalence classes.
Combining daseinisation with the above results gives rise to a contextual Born rule, justifying the Bohrification procedure of Theorem 5 [50]. Summarizing, we can formulate the physics of the quantum system A completely in terms of and its topos of contextual sets, and work within there as if dealing with a classical system.
To end this section, let us mention some other related work. The “amount of nonclassicality” of the contextual logic discussed of A measures the computational power of the quantum system A [68]. For philosophical aspects of Bohrification and related constructions, see [69,70]. Similar contextual ideas have been used to model quantum numbers [71]. Transfering C*-algebras between different toposes has been used successfully before in so-called Boolean-valued analysis [72,73,74]. Finally, contextuality and the Kochen–Specker theorem can be formulated more generally than in algebraic quantum theory [75].
4. Domains
The partially ordered set of empirically accessible classical contexts C of a quantum system A embodies coarse-graining. As in the introduction, we think of each as consisting of compatible observables that we can measure together in a single experiment. Larger experiments, involving more observables, should give us more information, and this is reflected in the partial order: if , then D contains more observables, and hence provides more information. If A itself is noncommutative, the best we can do is approximate it with larger and larger commutative subalgebras C. This sort of informational approximation is studied in computer science under the name domain theory [76,77]. This section discusses the domain-theoretic properties of . Domain theory is mostly concerned with partial orders where every element can be approximated by finite ones, as those are the ones we can measure in practice, leading to the following definitions.
Definition 3.
A partially ordered set is directed complete when every ascending chain has a least upper bound . An element C approximates D, written , when implies for any chain and some i. An element C is finite when . A continuous domain is a directed complete partially ordered set, every element of which satisfies . An algebraic domain is a directed complete partially ordered set, every element of which is approximated by finite ones: .
Lemma 1
([65,78]). If A is a C*-algebra, then is a directed complete partially ordered set, in which is the norm-closure of .
We saw in Section 2 that captures precisely the structure of A as a (piecewise) Jordan algebra. Order-theoretic techniques give an alternative proof of Corollary 1. First, we can recognize the dimension of A from . Recall that a partially ordered set is Artinian when: every nonempty subset has a minimal element; every nonempty filtered subset has a least element; every descending sequence eventually becomes constant. The dual notion, satisfying an ascending chain condition, is called Noetherian.
Proposition 3
([79]). A C*-algebra A is finite-dimensional if and only if is Artinian, if and only if is Noetherian.
Indeed, in an n-level system , elements correspond to a choice of unitary and a partition of n points into m equivalence classes. Because when the partition for D is finer than that for C, the partially ordered set can only have strictly increasing chains of length at most n.
By the Artin–Wedderburn theorem, we know that any finite-dimensional C*-algebra A is a finite direct sum of matrix algebras . It is therefore specified up to isomorphism by the numbers , which we can extract from the partially ordered set . A partially ordered set is called directly indecomposable when implies that either or is a singleton set.
Proposition 4
([79,80]). If , then the C*-subalgebras correspond to directly indecomposable partially ordered subsets of , and furthermore is the length of a maximal chain in .
The previous proposition does not generalize to arbitrary C*-algebras, which need not have a decomposition as a direct sum of factors. One might expect that is a domain when A is approximately finite-dimensional, as this would match with the intuition of approximation using practically obtainable information. However, there also needs to be a large enough supply of projections for this to work; see also Section 3. It turns out that the correct notion is that of scattered C*-algebras [81], that is, C*-algebras A for which every positive map is a sum of pure ones. The n-level system is scattered.
Theorem 7
([38]). A C*-algebra A is scattered if and only if is a continuous domain if and only if is an algebraic domain.
Compare this to the situation using commutative W*-subalgebras of a W*-algebra A: is a continuous or algebraic domain only when A is finite-dimensional [78]. Connecting back to Theorem 6 and Corollary 3, let us notice that can also be regarded as a domain using the interval topology: smaller intervals approximate an ideal complex number better than larger ones. Moreover, (piecewise) states respect such approximations: the induced functions from to the interval domain on are Scott continuous [65,78].
There are several topologies with which one could adorn . As any partially ordered set, it carries the order topology. We have just mentioned the Scott topology on directed complete partially ordered sets. For the purposes of information approximation that we are interested in, there is the Lawson topology, which refines both the Scott topology and the order topology. If the domain is continuous, the topological space will be Hausdorff. The topological space will be compact for so-called FS-domains, which happens to be.
Corollary 4
([77]). For a scattered C*-algebra A, the Lawson topology makes compact Hausdorff. Hence to each scattered C*-algebra A we may assign a commutative C*-algebra .
The assignment is not functorial, does not leave commutative C*-algebras invariant, and of course only works for scattered C*-algebras A in the first place [38]. Hence there is no contradiction with Theorem 3.
One can also furnish with a topology inspired by the topology of A itself. We will use the topology induced by the following variation on the Hausdorff metric; similar variations are named after Banach–Mazur, Kadets [82], Gromov–Hausdorff, Effros–Maréchal [83], and Kadison–Kastler [84] . See also [85]. Define the distance between to be
Now if C and D are generated by projections p and q, and A is represented on a Hilbert space H, then
is the Hausdorff distance between and . It follows that the distance between C and D is . This topology on matches the case of the 2-level system , where is in bijection with the one-point compactification of the real projective plane [50].
5. Dynamics
So far, we have only considered kinematics of the quantum system A, by looking for configuration spaces based on . It is clear, however, that in itself is not enough to reconstruct all of A. For a counterexample, observe that any C*-algebra A has an opposite C*-algebra in which the multiplication is reversed. Clearly, and are isomorphic as partially ordered sets, but there exist C*-algebras A that are not isomorphic to as C*-algebras [86]. So we need to add more information to to be able to reconstruct A as a C*-algebra, which is the topic of this section. To do so, we bring dynamics into the picture. For motivation of why dynamics and configuration spaces should go together, see also [87].
We begin by viewing dynamics as a time-dependent group of evolutions. The traditional view is that the 1-parameter group consists of unitary evolutions of the Hilbert space. For an n-level system, these 1-parameter groups are continuous homomorphisms . In algebraic quantum theory, it becomes a 1-parameter group of isomorphisms of the C*-algebra.
The group inherits the pointwise norm topology from A, that has subbasis
for , , and finite, and makes conjugation continuous [88]. We can similarly consider 1-parameter groups of isomorphisms of partially ordered sets.
Similarly, becomes a topological group with subbasis
for , , and finite sets S of atoms of .
Definition 4.
Let A be a C*-algebra. A 1-parameter group on A is a continuous injection , that assigns to each an isomorphism of C*-algebras, satisfying and . A 1-parameter group on is a continuous injection , that assigns to each an isomorphism of partially ordered sets, satisfying .
The following theorem shows that both notions in fact coincide. A factor is an algebra with trivial center, that is, a single superselection sector: the n-level system is a factor, but is not, because its center is two-dimensional. More precisely, the following theorem shows that the only freedom between the two notions in the previous definition lies in permutations of the center, because for typical AW*-factors.
Theorem 8
([89,90]). Let A be a typical AW*-factor. Any 1-parameter group on is induced by a 1-parameter group on A, and vice versa.
So C*-dynamics of A can be completely justified in terms of . This also justifies our choice of the topology on induced by the Hausdorff metric. See also [91]. Equilibrium states are described in algebraic quantum theory by Kubo–Martin–Schwinger states, and these can be described in terms of as well, see [92].
We now switch gear. By Stone’s theorem, 1-parameter groups of unitaries in certain W*-algebras correspond to self-adjoint (possibly unbounded) observables h. Thus, we may forget about the explicit dependence on a time parameter and consider single self-adjoint elements of C*-algebras. In fact, we will mostly be interested in symmetries: self-adjoint unitary elements .
Symmetries are tightly linked to projections. Every projection p gives rise to a symmetry , and every symmetry s comes from a projection . As they are unitary, the symmetries of a C*-algebra A generate a subgroup of the unitary group. For a commutative C*-algebra , symmetries compose, so that consists of symmetries only. For an n-level system , it turns out that consists of those unitaries whose determinant is 1 or . This ‘orientation’ is what we will add to to make it into a full invariant of A. See also [93].
Having enough symmetries means having enough projections. Therefore, we now consider AW*-algebras rather than general C*-algebras. For commutative AW*-algebras , the Gelfand spectrum X is not just compact Hausdorff, but Stonean, or extremally disconnected, in the sense that the closure of an open set is still open. (For comparison, the Lawson topology in Corollary 4 is totally disconnected, in the sense that connected components are singleton sets, which is weaker than Stonean).
Gelfand duality restricts to commutative AW*-algebras and Stonean spaces. Another way to put this is to say that the projections of a commutative AW*-algebra A form a complete Boolean algebra, and vice versa, every complete Boolean algebra gives a commutative AW*-algebra. The appropriate homomorphisms between AW*-algebras are normal, meaning that they preserve least upper bounds of projections [94]. There are versions of Definition 2 for piecewise AW*-algebras, and piecewise complete Boolean algebras, too [94]. One could also define a piecewise Stonean space, but the following lemma suffices here.
Lemma 2
([94]). The category of piecewise complete Boolean algebras and the category of piecewise AW*-algebras are equivalent.
The orthocomplement makes sense for the projections of any C*-algebra A. We can now make precise what equivariance under symmetries achieves: it makes the difference between being able to recover Jordan structure and C*-algebra structure.
Proposition 5
([43,94]). Let A and B be typical AW*-algebras, and suppose that preserve least upper bounds and orthocomplements. Then f extends to a Jordan homomorphism . It extends to a homomorphism if additionally .
To arrive at a good configuration space for A, we can package all this information up. We saw that embedded in . Conversely, acts on : a symmetry s and a projection p give rise to a new projection . In this way, acts on itself, and we may forget about . Including this action leads to the notion of an active lattice . More precisely, an active lattice consists of a complete orthomodular lattice P, a group G generated by for within the unitary group of the piecewise AW*-algebra with projections P, and an action of G on P that becomes conjugation on . The active lattice of an n-level system has, for P, the lattice of subspaces of ; for G, the group ; the injection sends to the reflection in V; and acts on as . For morphisms of active lattices, we refer to [94], but let us point out that thanks to Lemma 2 they can be phrased in terms of projections alone, just like the above definition of the active lattice itself. See also [95]. We can now make precise that we can reconstruct an AW*-algebra A from its active lattice . Up to now, we have mostly considered reconstructions of the form “if some structures based on A and B are isomorphic, then so are A and B”. The following theorem gives a much stronger form of reconstruction. Recall that a functor F is fully faithful when it gives a bijection between morphisms and .
Theorem 9
([94]). The functor that assigns to an AW*-algebra A its active lattice is fully faithful.
It follows immediately that if A and B are AW*-algebras with isomorphic active lattices , then are isomorphic AW*-algebras. That is, its active lattice completely determines an AW*-algebra. We can therefore think of them as configuration spaces. As mentioned before, contains precisely the same information as , so we could phrase active lattices in terms of as well. This configuration space circumvents the obstruction of Theorem 3, because active lattices are not a conservative extension of the “passive lattices” coming from compact Hausdorff spaces. Another thing to note about the previous theorem is that it has no need to except atypical cases such as . Finally, let us point out that functoriality of is nontrivial [96].
To get a good notion of configuration space for general quantum systems, we would eventually like to pass from AW*-algebras to C*-algebras. One way to think about this step is as refining an underlying carrying set to a topological space, that is, moving from algebras of all (bounded) functions on the set X to algebras of continuous functions on the topological space X. One might hope that AW*-algebras or W*-algebras play the former role in a noncommutative generalization, and to some extent this works [97,98]. Unfortunately, the Kadison–Singer problem raises rigorous obstructions to the most obvious noncommutative generalization of such a “discretization” of C*-algebras to AW*-algebras [99].
Nevertheless, AW*-algebras are pleasant to work with. Their theory is entirely algebraic, whereas the theory of (commutative) W*-algebras involves a good deal of measure theory. For example, Gelfand spectra of commutative AW*-algebras are Stonean spaces, whereas Gelfand spectra of commutative W*-algebras are so-called hyperstonean spaces; they additionally have to satisfy a measure-theoretic condition that seems divorced from topology. A similar downside occurs with projections: the projection lattice of a commutative W*-algebra is not just a complete Boolean algebra, it additionally has to satisfy a measure-theoretic condition. In particular, projections of an enveloping AW*-algebra should correspond to certain ideals in a C*-algebra, without needing measure-theoretic intricacies.
Much of the theory of W*-algebra finds its natural home in AW*-algebras at any rate. As a case in point, consider Gleason’s theorem. It states that any probability measure on extends to a positive linear function when . Roughly speaking, any quantum probability measure is of the form for some density matrix . In the algebraic formulation, any probability measure extends to a state , for an n-level system [100]. One can replace A by an arbitrary W*-algebra, and one can even replace by an arbitrary operator algebra B [101,102]. Thanks to Proposition 5, Gleason’s theorem generalizes to many typical AW*-algebras A, such as those of so-called homogeneous type I, and those generated by two projections, which leads to the following corollary, that supports many results in Section 2 and Section 3.
Corollary 5
([43]). Any normal piecewise Jordan homomorphism between typical AW*-algebras is a Jordan homomorphism.
6. Characterization
Now that we have seen that most of the algebraic quantum theory of A can be phrased in terms of only, let us try to axiomatize itself. Given any partially ordered set, when is it of the form for some quantum system A? An answer to this question would, for example, make Theorem 9 into an equivalence of categories, bringing configuration spaces for quantum systems on a par with Gelfand duality for classical systems. An axiomatization would also open up the possibility of generalizations, that might go beyond algebraic quantum theory.
We start with the classical case, of commutative C*-algebras . By Gelfand duality, any corresponds to a quotient . In turn, the equivalence relation corresponds to a partition of X into equivalence classes. Partitions are partially ordered by refinement: if , then any equivalence class in the partition corresponding to D is contained in an equivalence class of the partition corresponding to C. Hence axiomatizing comes down to axiomatizing partition lattices, and this has been well-studied, both in the finite-dimensional case [103,104], and in the general case [105]. The list of axioms is too long to reproduce here, but let us remark that it is based on a definition of points of the partition lattice. In the case of a finite partition lattice, the points are simply the atoms, that is, the minimal nonzero elements. So for a classical system with n states, the elements of the partition lattice are the ways to partition a set of n points into m equivalence classes; the atoms put two of the n points in an equivalence class and all the others in their own equivalence class of one point each. The other axioms are geometric in nature.
Lemma 3
([64]). A partially ordered set is isomorphic to for a compact Hausdorff space X if and only if it is opposite to a partition lattice whose points are in bijection with X.
Thanks to (a variation of) Lemma 2, the same strategy applies to piecewise Boolean algebras B. Write for the partially ordered set of Boolean subalgebras of B. The downset of an element D of a partially ordered set consists of all elements . In fact, the idea that any quantum logic (piecewise Boolean algebra) should be seen as many classical sublogics (Boolean algebras) pasted together, is not new, and drives much of the research in that area [27,106,107,108,109].
Theorem 10
([110]). A partially ordered set is isomorphic to for a piecewise Boolean algebra B if and only if:
- it is an algebraic domain;
- any nonempty subset has a greatest lower bound;
- a set of atoms has an upper bound whenever each pair of its elements does;
- the downset of each compact element is isomorphic to the opposite of a finite partition lattice.
In the case of a classical system with n states, B is the powerset of n points, and the above conditions merely say that is a partition lattice.
Just like in Section 3, if we consider as a diagram rather than a mere partially ordered set, we can reconstruct B. Starting from just the partially ordered set , the same issues surface as in Section 2 and Section 5, about Jordan structure verses full algebra structure. In the current piecewise Boolean setting, it can be solved neatly by adding an orientation to [110]. This comes down to making a consistent choice of atom in the Boolean subalgebras with two atoms, corresponding to the atypical cases for AW*-algebras before.
Returning to C*-algebras, Lemma 3 reduces the question of characterizing for a C*-algebra A to finding relationships between and for . One prototypical case where we know such a relationship is for the n-level system . Namely, inspired by the previous section, there is an action of the unitary group on : if is some rotation, and is diagonal in some basis, then also the rotation is diagonal in the rotated basis and therefore is in again. In fact, any will be a rotation of an element of that is diagonal in the standard basis. Therefore, we can recognize as a semidirect product of and . Such semidirect products can be axiomatized; for details, we refer to [64]. This can be generalized to C*-algebras A that have a weakly terminal commutative C*-subalgebra D, in the sense that any allows an injection . This includes all finite-dimensional C*-algebras, as well as algebras of all bounded operators on a Hilbert space. For example, for the n-level system , the matrices that are diagonal in the standard basis form a terminal subalgebra .
However, the mere partially ordered set cannot detect this unitary action. For this we need injections rather than inclusions. Therefore, we now switch to a category of commutative C*-subalgebras, with injective ∗-homomorphisms between them. For , these morphisms consist of a rotation in followed by an inclusion with . The following theorem characterizes this category up to equivalence. This is the same as characterizing up to Morita equivalence, meaning that it determines the topos of contextual sets on discussed in Section 3 up to categorical equivalence, rather than determining itself up to equivalence. To phrase the following theorem, we introduce the monoid of continuous surjections on a compact Hausdorff space X. In the finite-dimensional case, this is just the symmetric group . Because of our switch from to , it plays the role of the unitary group we need.
Theorem 11
([64]). Suppose that a C*-algebra A has a weakly terminal commutative C*-subalgebra . A category is equivalent to if and only if it is equivalent to a semidirect product of and .
See also [111].
The unitary action can also be used to determine for small A such as . Combining Lemma 3 with Theorem 11, we see that k-dimensional C in are parametrized by a partition of n into k nonempty parts together with an element of . Two such parameters induce the same subalgebra when the unitary permutes equal-sized parts of the partition. This can be handled neatly in terms of Young tableaux and Grassmannians, see [50,51].
Using this concrete parametrization of for , to characterize it would suffice to characterize the unitary group . Surprisingly, this question is open, even in the finite-dimensional case. All that seems to be known is that, up to isomorphism, is the unique nondiscrete locally compact Hausdorff group all of whose proper closed subgroups are finite [112]. This characterization does not generalize to finite dimensions higher than one, although closed subgroups have received study in the infinite-dimensional case [113]. The unitary group is also, up to isomorphism, the unique irreducible subgroup of the trace of whose elements is bounded [114]. It is known that unitary groups of C*-algebras cannot be countably classified [115]. Finally, the characterization of for Hilbert spaces H could give rise to a description of the category of Hilbert spaces in terms of generators and relations [116].
7. Generalizations
As mentioned in the introduction, the idea to describe quantum structures in terms of their classical substructures applies very generally. This final section discusses to what extent algebraic quantum theory is special, by considering a generalization as an example of another framework.
Namely, we consider categorical quantum mechanics [117]. This approach formulates quantum theory in terms of the category of Hilbert spaces, and then abstracts away to more general categories with the same structures. Specifically, what is retained is the notion of a tensor product to be able to build compound systems, the notion of entanglement in the form of objects that form a duality under the tensor product, and the notion of reversibility in the sense that every map between Hilbert spaces has an adjoint in the reverse direction. It turns out that these primitives suffice to derive a lot of quantum-mechanical features, such as scalars, the Born rule, no-cloning, quantum teleportation, and complementarity. As a case in point, one can define so-called Frobenius algebras in any category with this structure, which is important because of the following proposition.
Theorem 12
([118,119]). Finite-dimensional C*-algebras correspond to Frobenius algebras in the category of Hilbert spaces.
The point is that these notions make sense in any category with a tensor product, entanglement, and reversibility. A different example of such a category is that of sets with relations between them. That is, objects are sets X, and arrows are relations . For the tensor product, we take the Cartesian product of sets, which makes every object dual to itself and thereby fulfulling the structure of entanglement, and time reversibility is given by taking the opposite relation . Two relations and compose to . We may regard this as a toy example of possibilistic quantum theory: rather than complex matrices, we now care about entries ranging over . A groupoid is a small category, every arrow of which is an isomorphism; they may be considered as a multi-object generalization of groups.
Theorem 13
([120]). Frobenius algebras in the category of sets and relations correspond to groupoids.
Algebraic quantum theory, as set out in the introduction, makes perfect sense in categories such as sets and relations as well [121]. However, in this generality, it is not true that all classical subsystems determine a quantum system at all. The previous theorem provides a counterexample. In commutative groupoids, there can only be arrows , for arrows between different objects cannot commute with their inverse, as and . Therefore, any arrow between different objects in a groupoid can never be recovered from any commutative subgroupoid.
Similarly, quantum logic, as discussed in Section 3, makes perfect sense in this general categorical setting [122]. Moreover, it matches neatly with algebraic quantum theory via taking projections [123]. However, it is no longer true that commutative subalgebras correspond to Boolean sublattices. Again, a counterexample can be found using Theorem 13 [124].
One could object that commutativity might be too narrow a notion of classicality. However, consider broadcastability instead: classical information can be broadcast, but quantum information cannot. More precisely, a Frobenius algebra A is broadcastable when there exists a completely positive map such that both partial traces are the identity . Again, this makes perfect sense in general categories. It turns out that the broadcastable objects in the category of sets and relations are the groupoids that are totally disconnected, in the sense that there are no arrows between different objects [117]. So even with this more liberal operational notion of classicality, classical subsystems do not determine a quantum system.
This breaks a well-known information-theoretic characterization of quantum theory, that is phrased in terms of C*-algebras [125,126]. Hence there is something about (algebraic) quantum theory beyond the categorical properties of having tensor products, entanglement, and reversibility, that underwrites Bohr’s doctrine of classical concepts. It relates to characterizing unitary groups, as discussed in Section 6. We close this overview by raising the interesting interpretational question of just what this defining property is.
Acknowledgments
Supported by EPSRC Fellowship EP/L002388/1.
Conflicts of Interest
The author declares no conflict of interest.
References
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Physics 1964, 1, 195–200. [Google Scholar]
- Kochen, S.; Specker, E. The problem of hidden variables in quantum mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Pusey, M.; Barrett, J.; Rudolph, T. On the reality of the quantum state. Nat. Phys. 2012, 8, 475–478. [Google Scholar]
- Busch, P.; Grabowski, M.; Lahti, P.J. Operational Quantum Physics; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Keyl, M. Fundamentals of quantum information theory. Phys. Rep. 2002, 369, 431–548. [Google Scholar] [CrossRef]
- Kadison, R.V.; Ringrose, J.R. Fundamentals of the Theory of Operator Algebras; Number 15–16 in Graduate Studies in Mathematics; Academic Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Berberian, S.K. Baer *-Rings; Springer: Berlin/Heidelberg, Germany, 1972. [Google Scholar]
- Emch, G.G. Mathematical and Conceptual Foundations of 20th-Century Physics, 1st ed.; North-Holland: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Davies, E.B. Quantum Theory of Open Systems; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Earman, J. Superselection rules for philosophers. Erkenn 2008, 69, 377–414. [Google Scholar] [CrossRef]
- Rédei, M. Quantum Logic in Algebraic Approach; Springer: Cham, The Netherlands, 1998. [Google Scholar]
- Haag, R. Local Quantum Physics; Texts and Monographs in Physics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Strocchi, F. An Introduction to the Mathematical Structure of Quantum Mechanics; World Scientific: Singapore, 2008. [Google Scholar]
- Emch, G.G. Algebraic Methods in Statistical Mechanics and Quantum Field Theory; Wiley: Hoboken, NJ, USA, 1972. [Google Scholar]
- Alberti, P.M.; Uhlmann, A. Existence and density theorems for stochastic maps on commutative C*-algebras. Math. Nachr. 1980, 97, 279–295. [Google Scholar] [CrossRef]
- Landsman, N.P. Mathematical Topics between Classical and Quantum Mechanics; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Weaver, N. Mathematical Quantization; Chapman & Hall: London, UK, 2001. [Google Scholar]
- Bohr, N. Chapter Discussion with Einstein on epistemological problems in atomic physics. In Albert Einstein: Philosopher-Scientist; Cambridge University Press: Cambridge, UK, 1949. [Google Scholar]
- Heunen, C.; Landsman, N.P.; Spitters, B. A topos for algebraic quantum theory. Commun. Math. Phys. 2009, 291, 63–110. [Google Scholar] [CrossRef]
- Kadison, R.V.; Singer, I.M. Extensions of pure states. Am. J. Math. 1959, 81, 383–400. [Google Scholar] [CrossRef]
- Marcus, A.; Spielman, D.A.; Srivastava, N. Interlacing families II: Mixed characteristic polynomials and the Kadison–Singer problem. Ann. Math. 2015, 182, 327–350. [Google Scholar] [CrossRef]
- Altepeter, J.B.; James, D.F.V.; Kwiat, P.G. Qubit quantum state tomography. In Quantum State Estimation; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Butterfield, J.; Isham, C.J. A topos perspective on the Kochen–Specker theorem: I. Quantum States as Generalized Valuations. Int. J. Theor. Phys. 1998, 37, 2669–2733. [Google Scholar]
- Constantin, C.M.; Döring, A. Contextual entropy and reconstruction of quantum states. arXiv, 2012; arXiv:1208.2046. [Google Scholar]
- Hamhalter, J.; Turilova, E. Orthogonal measures on state spaces and context structure of quantum theory. Int. J. Theor. Phys. 2016, 55, 3353–3365. [Google Scholar] [CrossRef]
- Mac Lane, S. Categories for the Working Mathematician, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1971. [Google Scholar]
- Berg, B.; Heunen, C. Noncommutativity as a colimit. Appl. Categorical Struct. 2012, 20, 393–414. [Google Scholar] [CrossRef]
- Reyes, M.L. Obstructing extensions of the functor Spec to noncommutative rings. Isr. J. Math. 2012, 192, 667–698. [Google Scholar] [CrossRef]
- Berg, B.; Heunen, C. Extending obstructions to noncommutative functorial spectra. Theory Appl. Categories 2014, 29, 457–474. [Google Scholar]
- Döring, A. Kochen–Specker theorem for von Neumann algebras. Int. J. Theor. Phys. 2005, 44, 139–160. [Google Scholar] [CrossRef]
- Reyes, M.L. Sheaves that fail to represent matrix rings. In Ring theory and Its Applications; American Mathematical Society: Providence, RI, USA, 2014; Volume 609, pp. 285–297. [Google Scholar]
- Alfsen, E.M.; Shultz, F.W. State Spaces of Operator Algebras: Basic Theory, Orientations, and C*-Products; Birkhäuser: Basel, Switzerland, 2001. [Google Scholar]
- Connes, A. Noncommutative Geometry; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Akemann, C.A. The general Stone–Weierstrass problem. J. Funct. Anal. 1969, 4, 277–294. [Google Scholar] [CrossRef]
- Giles, R.; Kummer, H. A non-commutative generalization of topology. Indiana Univ. Math. J. 1971, 21, 91–102. [Google Scholar] [CrossRef]
- De Silva, N. From topology to noncommutative geometry: K-theory. arXiv, 2014; arXiv:1408.1170. [Google Scholar]
- De Silva, N.; Soares Barbosa, R. Partial and total ideals of von Neumann algebras. arXiv, 2014; arXiv:1408.1172. [Google Scholar]
- Heunen, C.; Lindenhovius, A.J. Domains of commutative C*-subalgebras. In Proceedings of the 2015 30th Annual ACM/IEEE Symposium on Logic in Computer Science (LICS), Kyoto, Japan, 6–10 July 2015; pp. 450–461. [Google Scholar]
- Hanche-Olsen, H.; Størmer, E. Jordan Operator Algebras; Pitman Advanced Publishing Program: Boston, MA, USA, 1984. [Google Scholar]
- Hamhalter, J. Isomorphisms of ordered structures of abelian C*-subalgebras of C*-algebras. J. Math. Anal. Appl. 2011, 383, 391–399. [Google Scholar] [CrossRef]
- Kaplansky, I. Projections in Banach algebras. Ann. Math. 1951, 53, 235–249. [Google Scholar] [CrossRef]
- Döring, A.; Harding, J. Abelian subalgebras and the Jordan structure of von Neumann algebras. arXiv, 2015; arXiv:1009.4945. [Google Scholar]
- Hamhalter, J. Dye’s theorem and Gleason’s theorem for AW*-algebras. J. Math. Anal. Appl. 2015, 422, 1103–1115. [Google Scholar] [CrossRef]
- Hamhalter, J.; Turilova, E. Structure of associative subalgebras of Jordan operator algebras. Q. J. Math. 2013, 64, 397–408. [Google Scholar] [CrossRef]
- Johnstone, P.T. Sketches of an Elephant: A Topos Theory Compendium; Clarendon Press: Oxford, UK, 2002. [Google Scholar]
- Landsman, N.P. Bohrification: From Classical Concepts to Commutative Operator Algebras; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Johnstone, P.T. Stone Spaces; Number 3 in Cambridge Studies in Advanced Mathematics; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Banaschewski, B.; Mulvey, C.J. A globalisation of the Gelfand duality theorem. Ann. Pure Appl. Log. 2006, 137, 62–103. [Google Scholar] [CrossRef]
- Spitters, B.; Vickers, S.; Wolters, S. Gelfand spectra in Grothendieck toposes using geometric mathematics. Electron. Proc. Theor. Comput. Sci. 2014, 158, 77–107. [Google Scholar] [CrossRef]
- Fauser, B.; Raynaud, G.; Vickers, S. The Born rule as structure of spectral bundles. Electron. Proc. Theor. Comput. Sci. 2012, 95, 81–90. [Google Scholar] [CrossRef]
- Heunen, C.; Landsman, N.P.; Spitters, B. Bohrification. In Deep Beauty: Understanding the Quantum World through Mathematical Innovation; Halvorson, H., Ed.; Cambridge University Press: Cambridge, UK, 2011; pp. 217–313. [Google Scholar]
- Caspers, M.; Heunen, C.; Landsman, N.P.; Spitters, B. Intuitionistic quantum logic of an n-level system. Found. Phys. 2009, 39, 731–759. [Google Scholar] [CrossRef]
- Heunen, C.; Landsman, N.P.; Spitters, B. Bohrification of operator algebras and quantum logic. Synthese 2012, 186, 719–752. [Google Scholar] [CrossRef]
- Wolters, S. Topos models for physics and topos theory. J. Math. Phys. 2013, 55, 082110. [Google Scholar] [CrossRef]
- Nuiten, J. Bohrification of local nets. Electron. Proc. Theor. Comput. Sci. 2011, 95, 211–218. [Google Scholar] [CrossRef]
- Döring, A.; Isham, C.J. Topos Methods in the Foundations of Physics. In Deep Beauty: Understanding the Quantum World through Mathematical Innovation; Halvorson, H., Ed.; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Döring, A.; Isham, C.J. New Structure for Physics; Chapter What is a thing? Topos theory in the founcations of physics. In Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2011; Volume 813, pp. 753–940. [Google Scholar]
- Döring, A.; Isham, C.J. A topos founcation for theories of physics. J. Math. Phys. 2008, 49, 053515. [Google Scholar] [CrossRef]
- Flori, C. A First Course in Topos Quantum Theory; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 868. [Google Scholar]
- Wolters, S. A comparison of two topos-theoretic approaches to quantum theory. Commun. Math. Phys. 2013, 317, 3–53. [Google Scholar]
- Joyal, A.; Tierney, M. An Extension of the Galois Theory of Grothendieck (Memoirs of the American Mathematical Society); Proquest Info & Learning: Ann Arbor, MI, USA, 1984; Volume 51. [Google Scholar]
- Heunen, C.; Landsman, N.P.; Spitters, B.; Wolters, S. The Gelfand spectrum of a noncommutative C*-algebra: A topos-theoretic approach. J. Aust. Math. Soc. 2011, 90, 39–52. [Google Scholar] [CrossRef]
- Berg, B.; Heunen, C. Erratum to: Noncommutativity as a colimit. Appl. Categorical Struct. 2013, 21, 103–104. [Google Scholar] [CrossRef]
- Heunen, C. Characterizations of categories of commutative C*-subalgebras. Commun. Math. Phys. 2014, 331, 215–238. [Google Scholar] [CrossRef]
- Spitters, B. The space of measurement outcomes as a spectral invariant for non-commutative algebras. Found. Phys. 2012, 42, 896–908. [Google Scholar] [CrossRef]
- De Groote, H.F. Observables IV: The presheaf perspective. arXiv, 2007; arXiv:0708.0677. [Google Scholar]
- Döring, A. Quantum states and measures on the spectral presheaf. Adv. Sci. Lett. 2009, 2, 291–301. [Google Scholar] [CrossRef]
- Loveridge, L.; Dridi, R.; Raussendorf, R. Topos logic in measurement-based quantum computation. Proc. R. Soc. A 2015, 471, 20140716. [Google Scholar] [CrossRef]
- Heunen, C.; Landsman, N.P.; Spitters, B. The principle of general tovariance. Int. Fall Workshop Geom. Phys. 2008, 1023, 93–102. [Google Scholar]
- Epperson, M.; Zafiris, E. Foundations of Relational Realism: A Topological Approach to Quantum Mechanics and the Philosophy of Nature; Lexington: Lanham, MD, USA, 2013. [Google Scholar]
- Adelman, M.; Corbett, J.V. A sheaf model for intuitionistic quantum mechanics. Appl. Categorical Struct. 1995, 3, 79–104. [Google Scholar] [CrossRef]
- Takeuti, G. C*-algebras and Boolean-valued analysis. Jpn. J. Math. 1983, 9, 207–245. [Google Scholar]
- Ozawa, M. A transfer principle from von Neumann algebras to AW*-algebras. J. Lond. Math. Soc. 1985, 32, 141–148. [Google Scholar] [CrossRef]
- Ozawa, M. A classification of type I AW*-algebras and Boolean-valued analysis. J. Math. Soc. Jpn. 1984, 36, 589–608. [Google Scholar] [CrossRef]
- Abramsky, S.; Brandenburger, A. The sheaf-theoretic structure of non-locality and contextuality. New J. Phys. 2011, 13, 113036. [Google Scholar] [CrossRef]
- Abramsky, S.; Jung, A. Domain Theory. In Handbook of Logic in Computer Science; Oxford University Press: Oxford, UK, 1994; Volume 3. [Google Scholar]
- Gierz, G.; Hofmann, K.H.; Keimel, K.; Lawson, J.D.; Mislove, M.W.; Scott, D.S. Continuous Lattices and Domains; Number 93 in Encyclopedia of Mathematics and its Applications; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Döring, A.; Barbosa, R.S. Unsharp values, domains and topoi. In Quantum Field Theory and Gravity: Conceptual and Mathematical Advances in the Search for a Unified Framework; Springer: Berlin/Heidelberg, Germany, 2011; pp. 65–96. [Google Scholar]
- Lindenhovius, A.J. Classifying finite-dimensional C*-algebras by posets of their commutative C*-subalgebras. Int. J. Theor. Phys. 2015, 54, 4615–4635. [Google Scholar] [CrossRef]
- Lindenhovius, A.J. . Ph.D. Thesis, Radboud University, Nijmegen, The Netherlands, 5 July 2016. [Google Scholar]
- Jensen, H.E. Scattered C*-algebras. Math. Scand. 1977, 41, 308–314. [Google Scholar] [CrossRef]
- Kalton, N.J.; Ostrovskii, M.I. Distances between Banach spaces. Forum Math. 1999, 11, 17–48. [Google Scholar]
- Haagerup, U.; Winsløw, C. The Effros–Maréchal topology in the space of von Neumann algebras. Am. J. Math. 1998, 120, 567–617. [Google Scholar] [CrossRef][Green Version]
- Kadison, R.V.; Kastler, D. Perturbations of von Neumann algebras I: Stability of type. Am. J. Math. 1972, 94, 38–54. [Google Scholar] [CrossRef]
- Chetcuti, E.; Hamhalter, J.; Weber, H. The order topology for a von Neumann algebra. Stud. Math. 2015, 230, 95–120. [Google Scholar] [CrossRef]
- Connes, A. A factor not anti-isomorphic to itself. Ann. Math. 1975, 101, 536–554. [Google Scholar] [CrossRef]
- Spekkens, R.W. The paradigm of kinematics and dynamics must yield to causal structure. Foundational Questions Institute essay contest winner. arXiv, 2013; arXiv:1209.0023. [Google Scholar]
- Moffat, J. Groups of Automorphisms of Operator Algebras. Ph.D. Thesis, University of Newcastle upon Tyne, Newcastle, UK, 1974. [Google Scholar]
- Hamhalter, J.; Turilova, E. Automorphisms of ordered structures of abelian parts of operator algebras and their role in quantum theory. Int. J. Theor. Phys. 2014, 53, 3333–3345. [Google Scholar] [CrossRef]
- Döring, A. Flows on generalised Gelfand spectra of nonabelian unital C*-algebras and time evolution of quantum systems. arXiv, 2012; arXiv:1212.4882. [Google Scholar]
- Heunen, C.; Lindenhovius, A.J. Domains of commutative C*-subalgebras. arXiv, 2015; arXiv:1504.02730. [Google Scholar]
- Geloun, J.B.; Flori, C. Topos analogues of the KMS state. arXiv, 2012; arXiv:1207.0227. [Google Scholar]
- Alfsen, E.M.; Shultz, F.W. Orientation in operator algebras. Proc. Natl. Acad. Sci. USA 1998, 95, 6596–6601. [Google Scholar] [CrossRef] [PubMed]
- Heunen, C.; Reyes, M.L. Active lattices determine AW*-algebras. J. Math. Anal. Appl. 2014, 416, 289–313. [Google Scholar] [CrossRef]
- Chevalier, G. Automorphisms of an orthomodular poset of projections. Int. J. Theor. Phys. 2005, 44, 985–998. [Google Scholar] [CrossRef]
- Heunen, C.; Reyes, M.L. Diagonalizing matrices over AW*-algebras. J. Funct. Anal. 2013, 264, 1873–1898. [Google Scholar] [CrossRef]
- Kornell, A. Quantum Collections. arXiv, 2012; arXiv:1202.2994. [Google Scholar]
- Kornell, A. V*-algebras. arXiv, 2015; arXiv:1502.01516. [Google Scholar]
- Heunen, C.; Reyes, M.L. On discretization of C*-algebras. J. Oper. Theory 2017, 77, 19–37. [Google Scholar] [CrossRef]
- Mackey, G.W. The Mathematical Foundations of Quantum Mechanics; W. A. Benjamin: New York, NY, USA, 1963. [Google Scholar]
- Bunce, L.J.; Wright, J.D.M. The Mackey–Gleason problem. Bull. Am. Math. Soc. 1992, 26, 288–293. [Google Scholar]
- Hamhalter, J. Quantum Measure Theory; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Birkhoff, G. Lattice Theory; American Mathematical Society: Providence, RI, USA, 1948. [Google Scholar]
- Stonesifer, J.R.; Bogart, K.P. Characterizations of partition lattices. Algebra Univers. 1984, 19, 92–98. [Google Scholar]
- Firby, P.A. Lattices and compactifications I. Proc. Lond. Math. Soc. 1973, 27, 22–50. [Google Scholar] [CrossRef]
- Gudder, S.P. Partial algebraic structures associated with orthomodular posets. Pac. J. Math. 1972, 41, 717–730. [Google Scholar] [CrossRef]
- Finch, P.D. On the structure of quantum logic. J. Symb. Log. 1969, 34, 415–425. [Google Scholar] [CrossRef]
- Hughes, R.I.G. Omnibus review. J. Symb. Log. 1985, 50, 558–566. [Google Scholar] [CrossRef]
- Scheibe, E. The Logical Analysis of Quantum Mechanics; Pergamon Press: Oxford, UK, 1973. [Google Scholar]
- Heunen, C. Piecewise Boolean algebras and their domains. Lect. Notes Comput. Sci. 2014, 8573, 208–219. [Google Scholar]
- Flori, C.; Fritz, T. Compositories and gleaves. Theory Appl. Categories 2016, 31, 928–988. [Google Scholar]
- Morris, S.A. A characterization of the topological group of real numbers. Bull. Aust. Math. Soc. 1986, 34, 473–475. [Google Scholar] [CrossRef]
- Kadison, R.V. Infinite unitary groups. Trans. Am. Math. Soc. 1952, 72, 386–399. [Google Scholar] [CrossRef]
- Marcus, M.; Newman, M. Some results on unitary matrix groups. Linear Algebra Its Appl. 1970, 3, 173–178. [Google Scholar] [CrossRef]
- Kerr, D.; Lupini, M.; Phillips, N.C. Borel complexity and automorphisms of C*-algebras. J. Funct. Anal. 2015, 268, 3767–3789. [Google Scholar] [CrossRef]
- Heunen, C. On the functor ℓ2. In Computation, Logic, Games, and Quantum Foundations; Springer: Berlin/Heidelberg, Germany, 2013; pp. 107–121. [Google Scholar]
- Heunen, C.; Vicary, J. Categories for Quantum Theory: An Introduction; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Vicary, J. Categorical formulation of finite-dimensional quantum algebras. Commun. Math. Phys. 2011, 304, 765–796. [Google Scholar] [CrossRef]
- Abramsky, S.; Heunen, C. H*-algebras and nonunital Frobenius algebras: First steps in infinite-dimensional categorical quantum mechanics. Clifford Lect. AMS Proc. Symp. Appl. Math. 2012, 71, 1–24. [Google Scholar]
- Heunen, C.; Contreras, I.; Cattaneo, A.S. Relative Frobenius algebras are groupoids. J. Pure Appl. Algebra 2013, 217, 114–124. [Google Scholar] [CrossRef]
- Coecke, B.; Heunen, C.; Kissinger, A. Categories of quantum and classical channels. Quantum Inf. Process. 2016, 15, 5179–5209. [Google Scholar] [CrossRef]
- Heunen, C.; Jacobs, B. Quantum logic in dagger kernel categories. Order 2010, 27, 177–212. [Google Scholar] [CrossRef]
- Heunen, C. Complementarity in categorical quantum mechanics. Found. Phys. 2012, 42, 856–873. [Google Scholar] [CrossRef]
- Coecke, B.; Heunen, C.; Kissinger, A. Chapter Compositional Quantum Logic. In Computation, Logic, Games, and Quantum Foundations; Springer: Berlin/Heidelberg, Germany, 2013; pp. 21–36. [Google Scholar]
- Clifton, R.; Bub, J.; Halvorson, H. Characterizing quantum theory in terms of information-theoretic constraints. Found. Phys. 2003, 33, 1561–1591. [Google Scholar] [CrossRef]
- Heunen, C.; Kissinger, A. Can quantum theory be characterized by information-theoretic constraints? arXiv, 2016; arXiv:1604.05948. [Google Scholar]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).