Effect of a Magnetic Quadrupole Field on Entropy Generation in Thermomagnetic Convection of Paramagnetic Fluid with and without a Gravitational Field
Abstract
:1. Introduction
2. Mathematical Model
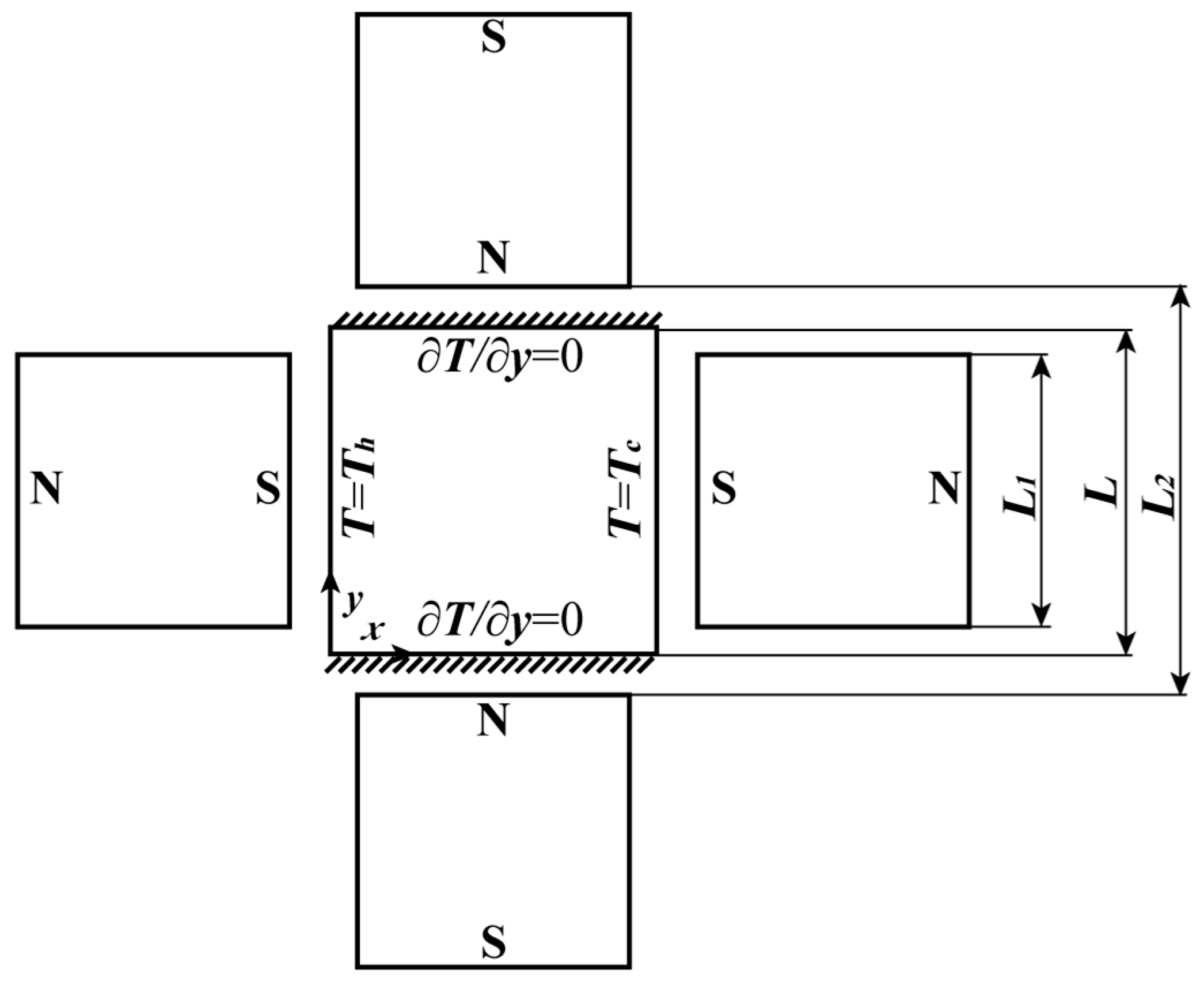
2.1. Physical Description
2.2. Governing Equations
- Continuity equation:
- Momentum equation:
- Energy equation:
- Continuity equation:
- Momentum equation:
- Energy equation:
2.3. Magnetic Field Calculation
2.4. Boundary Conditions
- U = V = 0 for all walls;
- Left and right vertical wall: , 0 for X = 0, 1; and
- Top and bottom horizontal adiabatic walls: for Y = 0 and 1.
2.5. Entropy Generation Calculation
2.6. Nusselt Number Calculation
3. Numerical Procedures and Code Verification
4. Results and Discussion
4.1. Numerical Results without a Gravitational Field
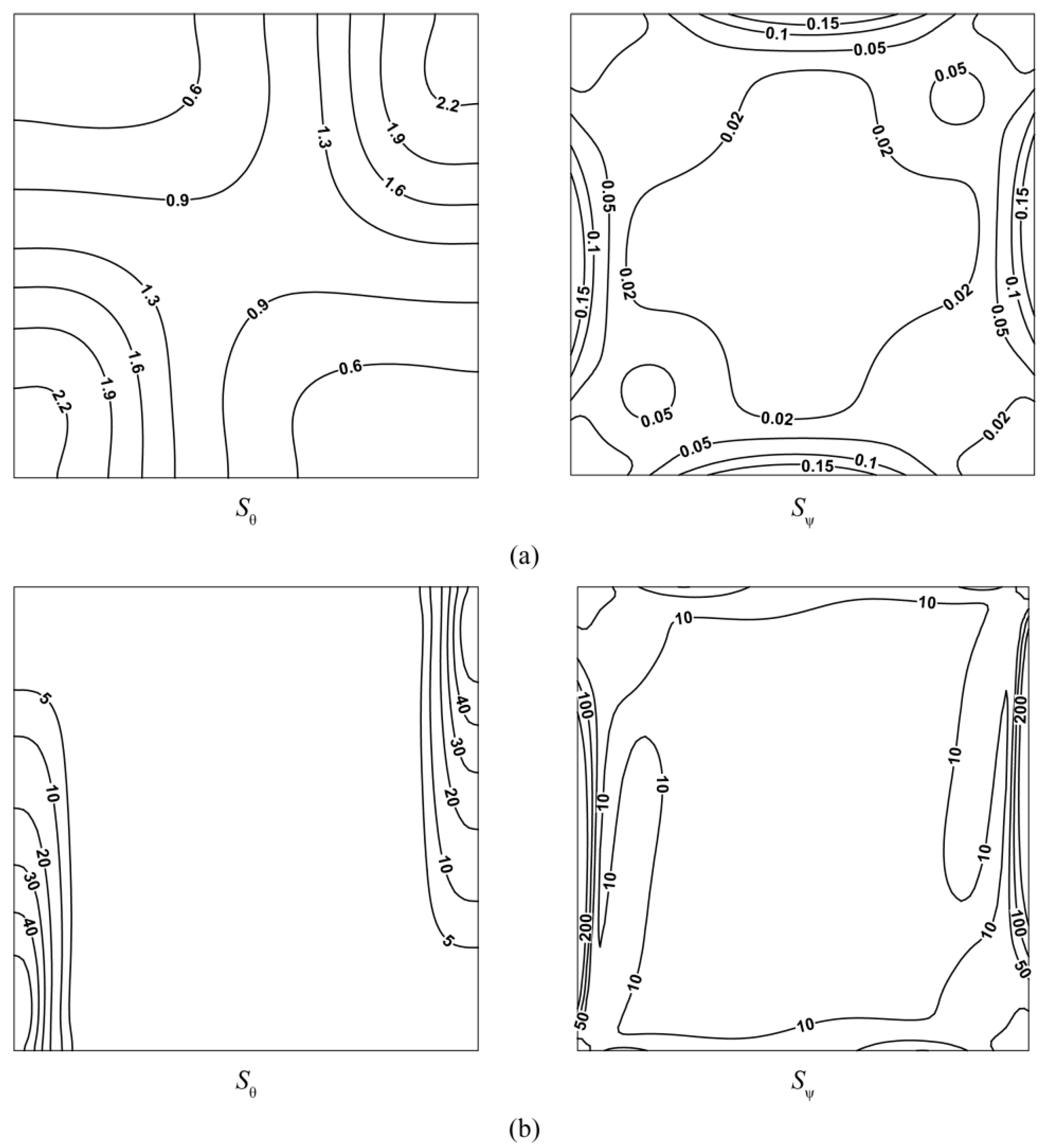
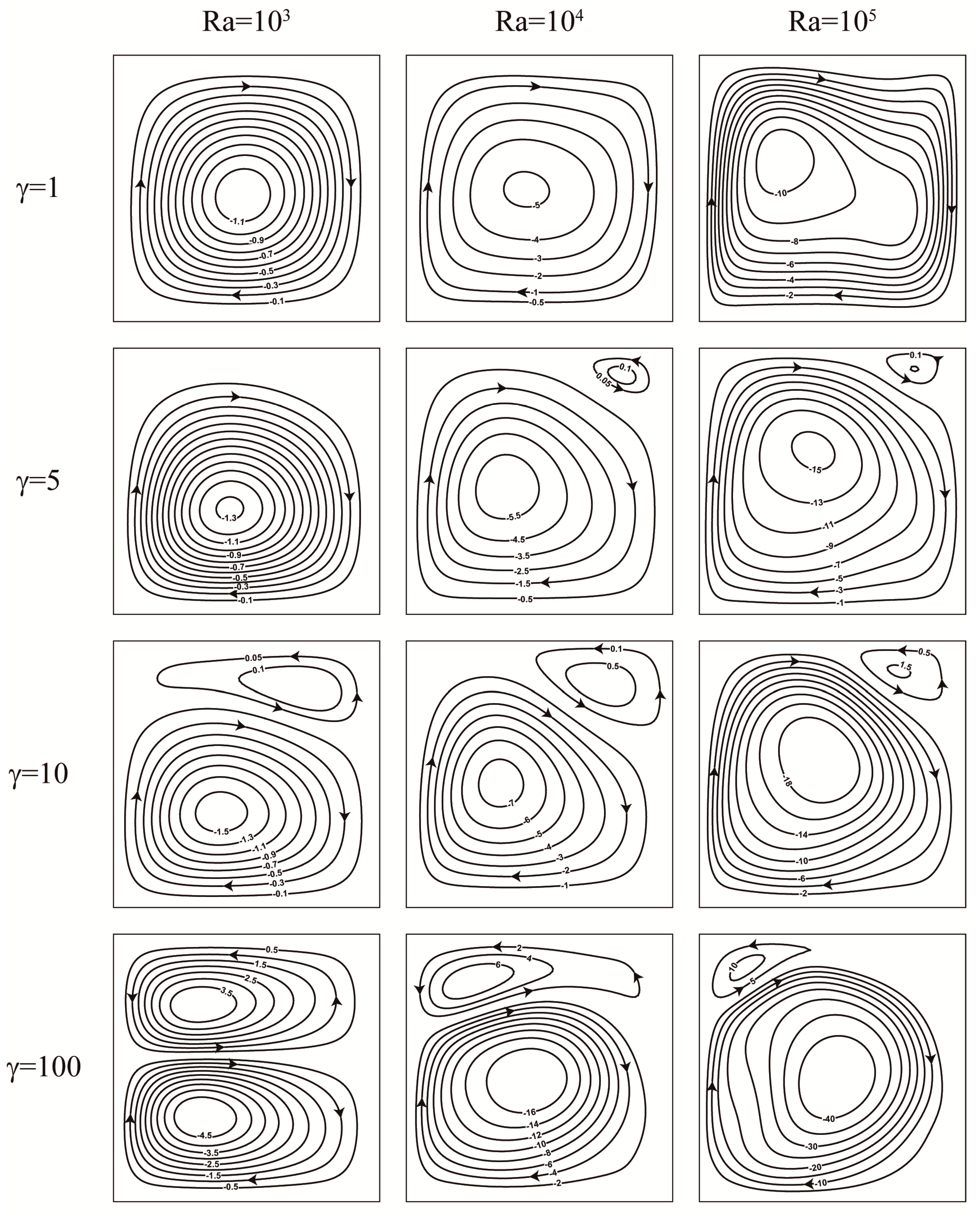
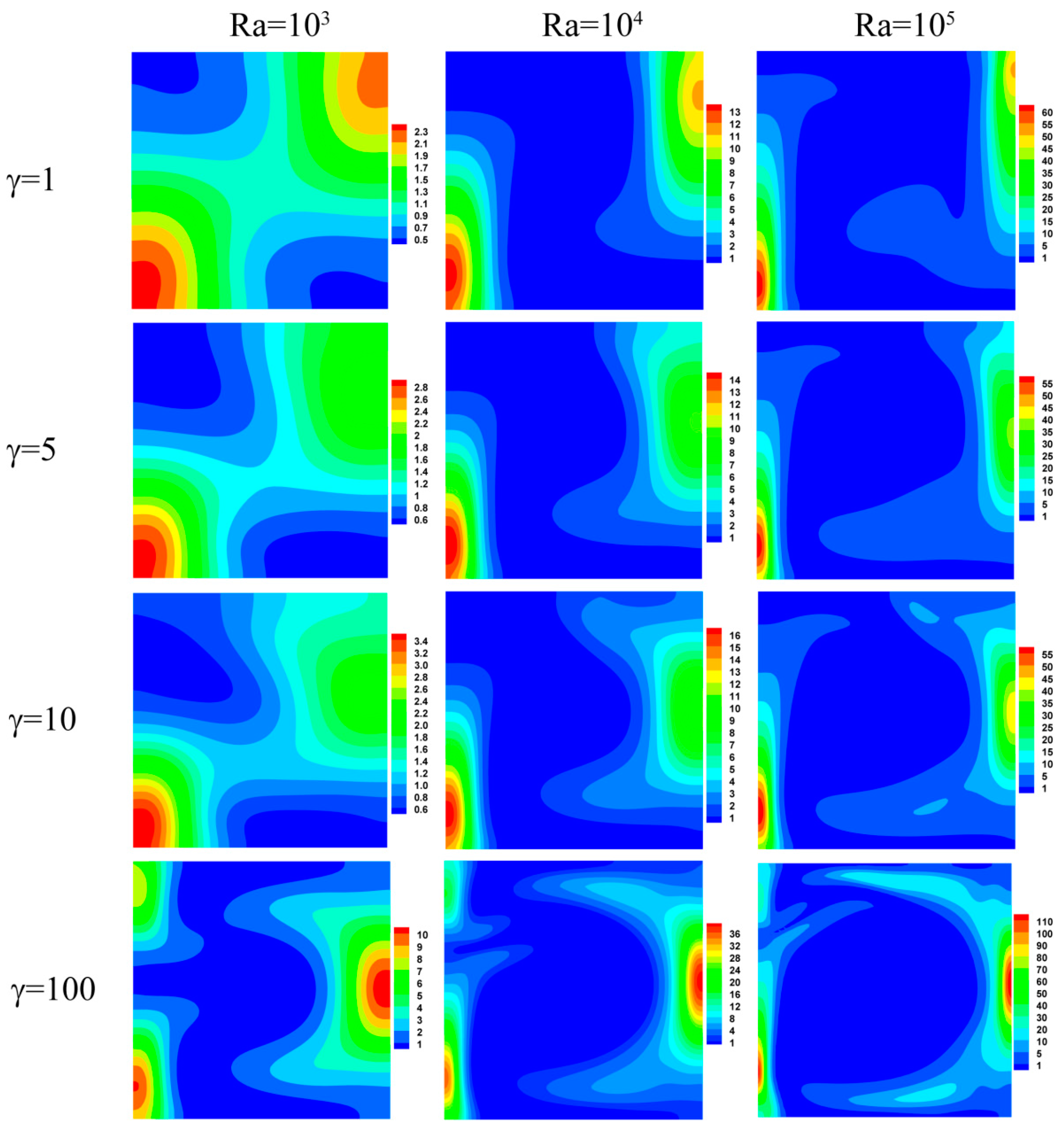
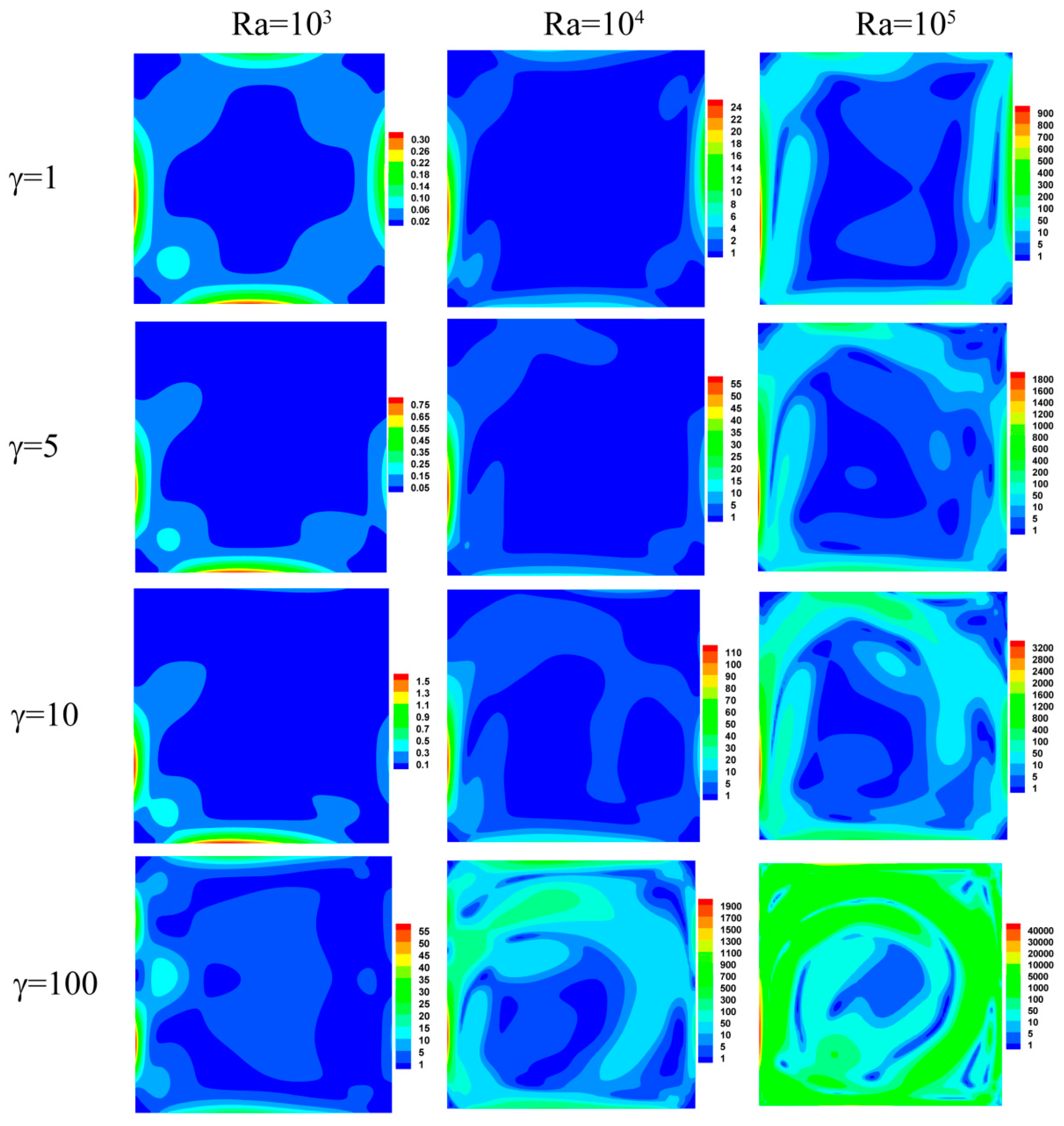
4.1.1. Streamlines, Isotherms, and Entropy Generation Characteristics
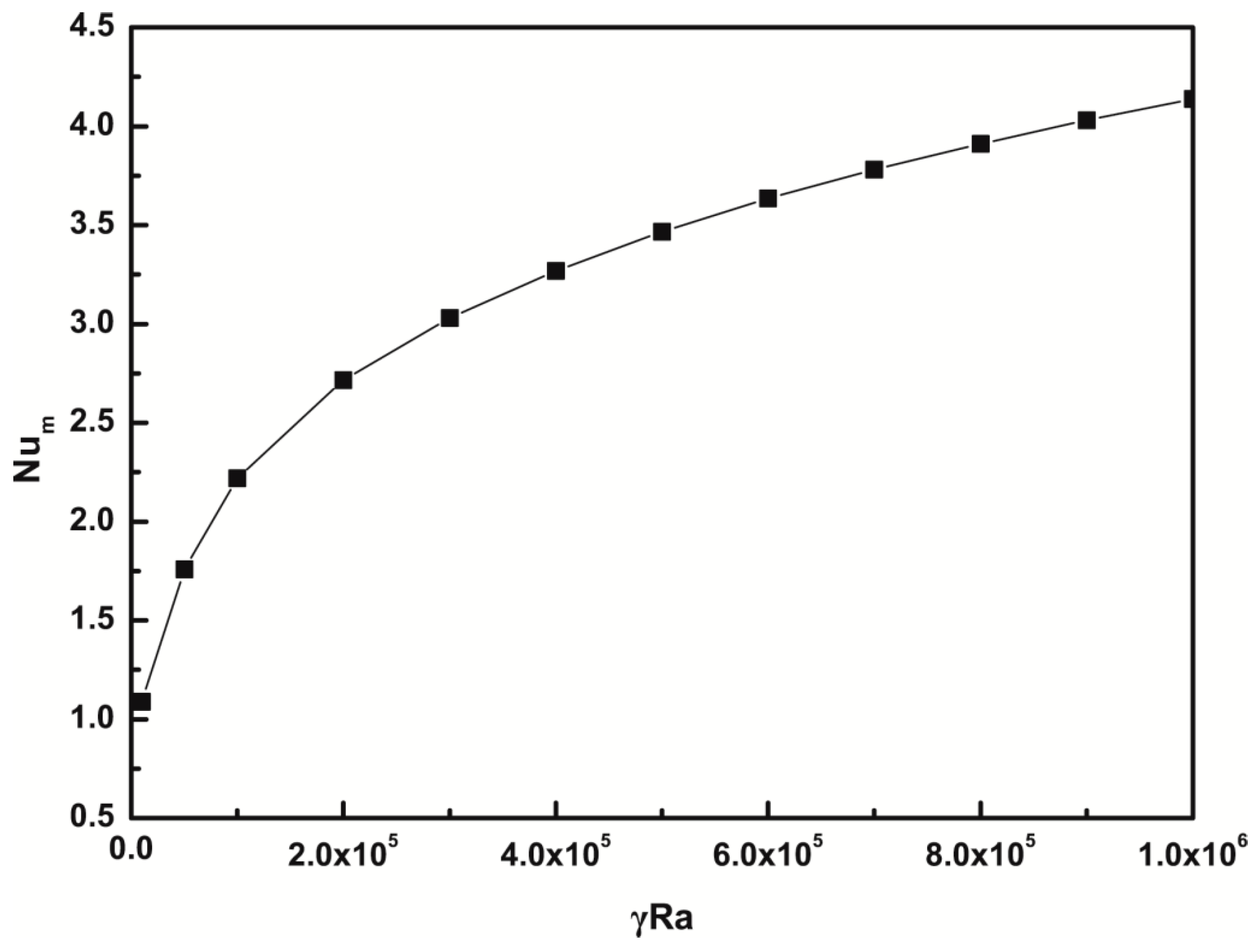
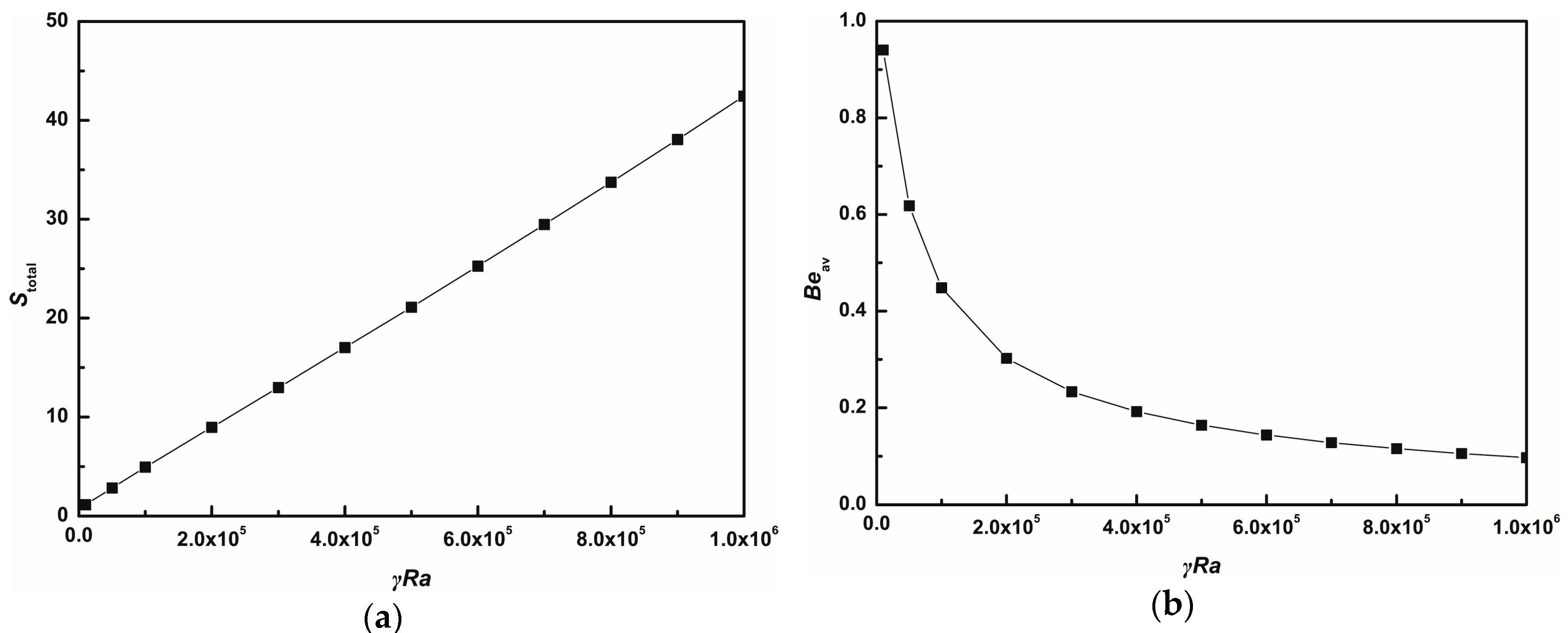
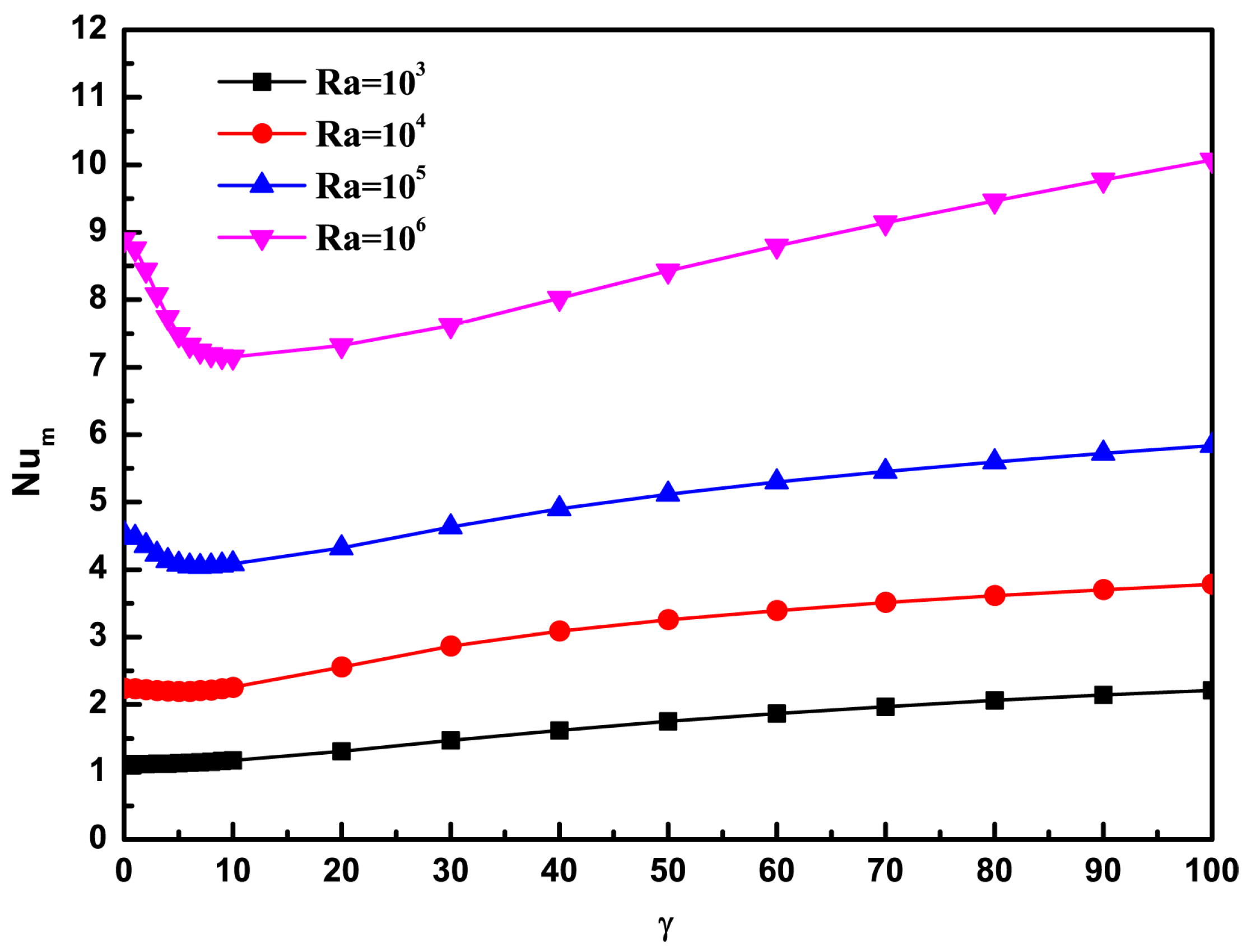
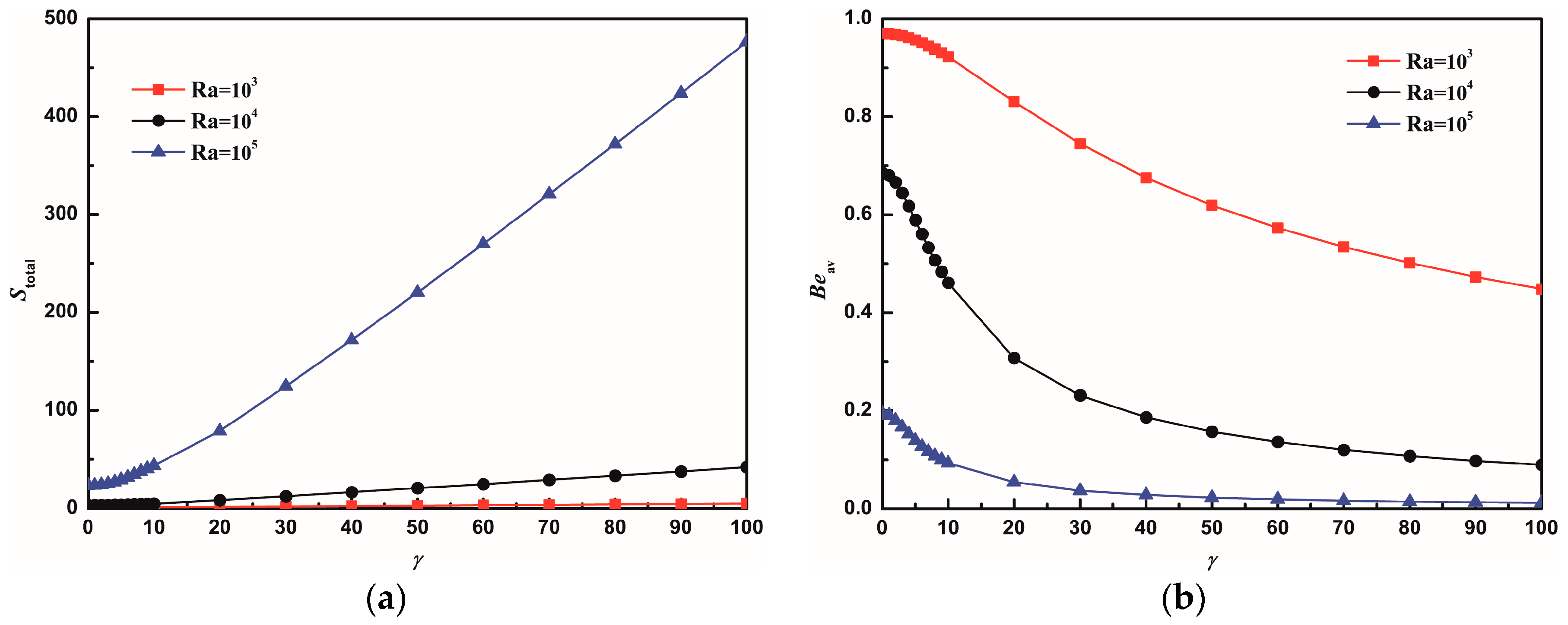
4.1.2. Average Nusselt Number, Total Entropy Generation, and Average Bejan Number
4.2. Numerical Results with a Gravitational Filed
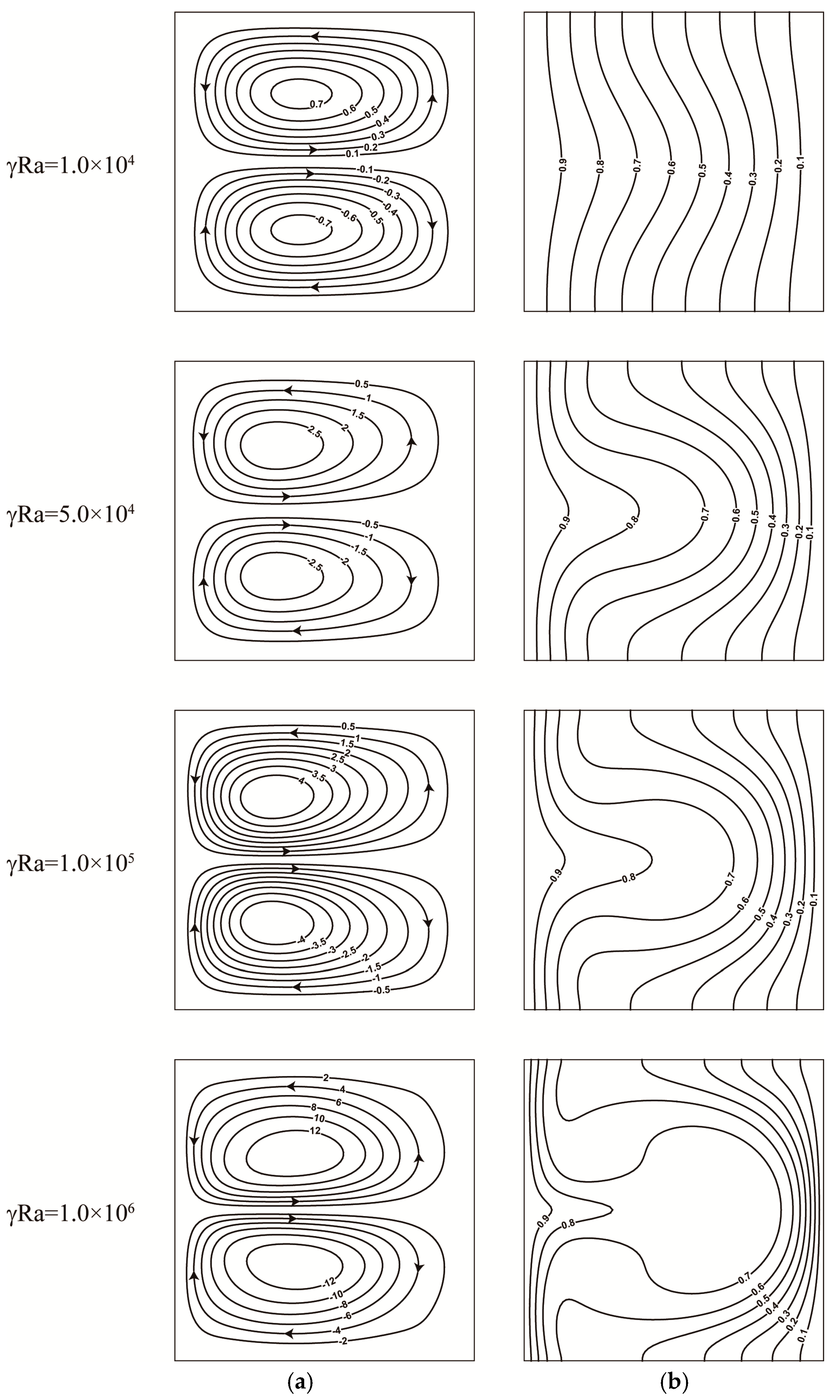
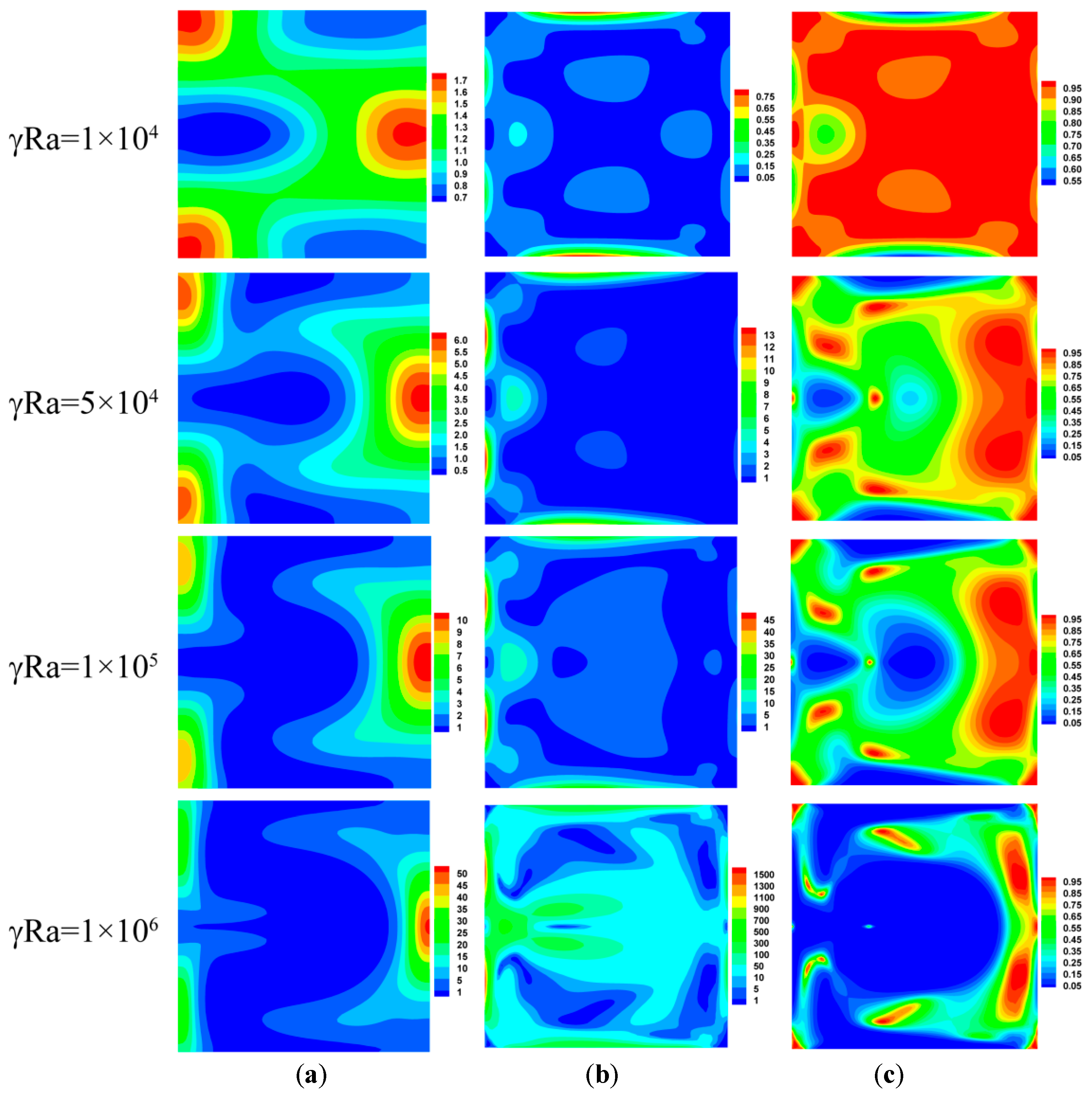
4.2.1. Streamlines, Isotherms, and Entropy Generation Characteristics
4.2.2. Average Nusselt Number, Total Entropy Generation, and Average Bejan Number
5. Conclusions
- In the absence of gravity, the flow field with two cellular structures is symmetric about the horizontal centerline. As the Nusslet number increases, the total entropy generation (Stotal) increases linearly as well with increasing γRa. When γRa < 1 × 105, entropy generation due to heat transfer is relatively dominant. However, when γRa > 1 × 105, the leading contributor to the irreversibility comes from fluid friction because the flow is enhanced by convection.
- In the presence of gravity, with an increase in the magnetic force number, a clockwise vortex reinforces and splitting phenomenon occurs, which results in two vortices with opposite circulating directions and strength. Fluid friction irreversibility begins to surpass heat transfer irreversibility for increasing Rayleigh numbers and magnetic field numbers. Entropy generation spreads throughout the domain at high Rayleigh numbers, but is restricted to the vicinity of the boundaries at small Rayleigh numbers. The total entropy generation is insensitive to the variation of the magnetic field number for low Rayleigh numbers; while the magnitude of the total entropy generation changes significantly for high Rayleigh numbers. Higher magnetic field numbers lead to lower Bejan numbers.
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| b | Magnetic flux density (T) |
| b0 | Reference magnetic flux density, b0 = Br (T) |
| B | Dimensionless magnetic flux |
| Be | Bejan number |
| Br | Magnetic flux density of permanent magnets (T) |
| E | Electric field (V·m−1) |
| fm | Magnetic force |
| g | Gravitational acceleration (m·s−2) |
| H | Magnetic field intensity |
| J | Electric current(A·m−2) |
| k | Thermal conductivity (W·m−1·k−1) |
| L | Length of the enclosure (m) |
| Num | Average Nusselt number |
| p | Pressure (Pa) |
| P | Dimensionless pressure |
| p0 | Pressure at reference temperature (Pa) |
| p′ | Pressure difference due to the perturbed state (Pa) |
| Pr | Prandtl number |
| Q | Electric charge density (C·m−3) |
| Ra | Rayleigh number |
| S | Entropy generation |
| T | Temperature (K) |
| T0 | (K) |
| u,v | Velocity components (m·s−1) |
| U,V | Dimensionless velocity components |
| U | Velocity vector |
| x, y | Cartesian coordinates |
| X, Y | Dimensionless Cartesian coordinates |
| Greek symbols | |
| Thermal diffusivity (m·s−1) | |
| Thermal expansion coefficient (K−1) | |
| λ | Thermal conductivity(W·m−1·K−1) |
| Dimensionless magnetic strength parameter | |
| θ | Dimensionless temperature |
| Magnetic permeability of vacuum (H·m−1) | |
| Magnetic permeability (H·m−1) | |
| Dynamic viscosity (kg·m−1·s−1) | |
| Kinematic viscosity (m2·s−1) | |
| Density (kg·m−3) | |
| Electrical conductivity (Ω−1·m−1) | |
| Irreversibility distribution ratio | |
| Mass magnetic susceptibility (m3·kg−1) | |
| Volume magnetic susceptibility | |
| Scalar magnetic potential | |
| Subscripts | |
| 0 | Reference value |
| av | Spatial average |
| c | Cold |
| h | Hot |
| total | Summation over the domain |
| θ | Heat transfer |
| ψ | Fluid friction |
References
- Wakayama, N.I.; Wakayama, M. Magnetic acceleration of inhaled and exhaled flows in breathing. Jpn. J. Appl. Phys. 2000, 39, 262–264. [Google Scholar] [CrossRef]
- Szabo, P.; Beković, M.; Früh, W. Using infrared thermography to investigate thermomagnetic convection under spatial non-uniform magnetic field. Int. J. Therm. Sci. 2017, 116, 118–128. [Google Scholar] [CrossRef]
- Braithwaite, D.; Beaugnon, E.; Tournier, R. Magnetically controlled convection in a paramagnetic fluid. Nature 1991, 354, 134–136. [Google Scholar] [CrossRef]
- Atia, A.; Ghernaout, B.; Bouabdallah, S.; Bessaïh, R. Three-dimensional oscillatory mixed convection in a Czochralski silicon melt under the axial magnetic field. Appl. Therm. Eng. 2016, 105, 704–715. [Google Scholar] [CrossRef]
- Bondareva, N.S.; Sheremet, M.A.; Pop, I. Magnetic field effect on the unsteady natural convection in a right-angle trapezoidal cavity filled with a nanofluid: Buongiorno’s mathematical model. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1924–1946. [Google Scholar] [CrossRef]
- Cho, C.C. Influence of magnetic field on natural convection and entropy generation in Cu–water nanofluid-filled cavity with wavy surfaces. Int. J. Heat Mass Transf. 2016, 101, 637–647. [Google Scholar] [CrossRef]
- Akamatsu, M.; Higano, M.; Takahashi, Y.; Ozoe, H. Numerical prediction on heat transfer phenomenon in paramagnetic and diamagnetic fluids under a vertical magnetic field gradient. IEEE Trans. Appl. Supercond. 2004, 14, 1674–1681. [Google Scholar] [CrossRef]
- Bednarz, T.P.; Lei, C.; Patterson, J.C.; Ozoe, H. Effects of a transverse, horizontal magnetic field on natural convection of a paramagnetic fluid in a cube. Int. J. Therm. Sci. 2009, 48, 26–33. [Google Scholar] [CrossRef]
- Naffouti, A.; Ben-Beya, B.; Lili, T. Three-dimensional Rayleigh–Bénard magneto-convection: Effect of the direction of the magnetic field on heat transfer and flow patterns. C. R. Mec. 2014, 342, 714–725. [Google Scholar] [CrossRef]
- Nakamura, H.; Takayama, T.; Uetake, H.; Hirota, N.; Kitazawa, A.K. Magnetically controlled convection in a diamagnetic fluid. Phys. Rev. Lett. 2005, 94, 144501. [Google Scholar] [CrossRef] [PubMed]
- Tipole, P.; Karthikeyan, A.; Bhojwani, V.; Patil, A.; Oak, N.; Ponatil, A.; Nagori, P. Applying a magnetic field on liquid line of vapour compression system is a novel technique to increase a performance of the system. Appl. Energy 2016, 182, 376–382. [Google Scholar] [CrossRef]
- Mani, K.; Selladurai, V. Energy savings with the effect of magnetic field using R290/600a mixture as substitute for CFC12 and HFC 134a. Therm. Sci. 2008, 12, 111–120. [Google Scholar] [CrossRef]
- Qi, J.; Wakayama, N.I.; Yabe, A. Magnetic control of thermal convection in electrically non-conducting or low-conducting paramagnetic fluids. Int. J. Heat Mass Transf. 2001, 44, 3043–3052. [Google Scholar] [CrossRef]
- Shigemitsu, R.; Tagawa, T.; Ozoe, H. Numerical computation for natural convection of air in a cubic enclosure under combination of magnetizing and gravitational forces. Numer. Heat Transf. Part A 2003, 43, 449–463. [Google Scholar] [CrossRef]
- Akamatsu, M.; Higano, M.; Takahashi, Y.; Ozoe, H. Numerical computation on the control of aerial flow by the magnetizing force in gravitational and nongravitational fields. Numer. Heat Transf. Part A 2003, 43, 9–19. [Google Scholar] [CrossRef]
- Kaneda, M.; Tagawa, T.; Ozoe, H. Convection induced by a cusp-shaped magnetic field for air in a cube heated from above and cooled from below. J. Heat Trans. 2002, 124, 17–25. [Google Scholar] [CrossRef]
- Yang, L.; Ren, J.; Song, Y.; Guo, Z. Free convection of a gas induced by a magnetic quadrupole field. J. Magn. Magn. Mater. 2003, 261, 377–384. [Google Scholar] [CrossRef]
- Yang, L.; Ren, J.; Song, Y.; Min, J.; Guo, Z. Convection heat transfer enhancement of air in a rectangular duct by application of a magnetic quadrupole field. Int. J. Eng. Sci. 2004, 42, 491–507. [Google Scholar] [CrossRef]
- Jiang, C.; Shi, E.; Hu, Z.; Zhu, X.; Xie, N. Numerical simulation of thermomagnetic convection of air in a porous square enclosure under a magnetic quadrupole field using LTNE models. Int. J. Heat Mass Transf. 2015, 91, 98–109. [Google Scholar] [CrossRef]
- Bednarz, T.P.; Tagawa, T.; Kaneda, M.; Ozoe, H.; Szmyd, J.S. Magnetic and gravitational convection of air with a coil inclined around the X axis. Numer. Heat Transf. Part A 2004, 46, 99–113. [Google Scholar] [CrossRef]
- Bednarz, T.; Fornalik, E.; Ozoe, H.; Szmyd, J.S.; Patterson, J.C.; Lei, C. Influence of a horizontal magnetic field on the natural convection of paramagnetic fluid in a cube heated and cooled from two vertical side walls. Int. J. Therm. Sci. 2008, 47, 668–679. [Google Scholar] [CrossRef]
- Kenjereš, S.; Pyrda, L.; Wrobel, W.; Fornalik-Wajs, E.; Szmyd, J.S. Oscillatory states in thermal convection of a paramagnetic fluid in a cubical enclosure subjected to a magnetic field gradient. Phys. Rev. E 2012, 85, 046312. [Google Scholar] [CrossRef] [PubMed]
- Kenjeres, S.; Wrobel, W.; Pyrda, L.; Fornalic-Wajs, E.; Szmyd, J.S. Transients and turbulence pockets in thermal convection of paramagnetic fluid subjected to strong magnetic field gradients. J. Phys. Conf. Ser. 2011, 318, 072028. [Google Scholar] [CrossRef]
- Purusothaman, A.; Oztop, H.F.; Nithyadevi, N.; Abu-Hamdeh, N.H. 3D natural convection in a cubical cavity with a thermally active heater under the presence of an external magnetic field. Comput. Fluids 2016, 128, 30–40. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; CRC Press: New York, NY, USA, 1996. [Google Scholar]
- Selimefendigil, F.; Öztop, H.; Abu-Hamde, N. Natural Convection and Entropy Generation in Nanofluid Filled Entrapped Trapezoidal Cavities under the Influence of Magnetic Field. Entropy 2016, 18, 43. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D. Entropy generation of nanofluid in presence of magnetic field using lattice Boltzmann method. Physica A 2015, 417, 273–286. [Google Scholar] [CrossRef]
- Chamkha, A.; Ismael, M.; Kasaeipoor, A.; Armaghani, T. Entropy generation and natural convection of CuO-Water nanofluid in C-shaped cavity under magnetic field. Entropy 2016, 18. [Google Scholar] [CrossRef]
- Kolsi, L.; Abidi, A.; Borjini, M.N.; Aissia, H.B. The effect of an external magnetic field on the entropy generation in three-dimensional natural convection. Therm. Sci. 2010, 14, 341–352. [Google Scholar] [CrossRef]
- Sathiyamoorthy, M.; Chamkha, A. Effect of magnetic field on natural convection flow in a liquid gallium filled square cavity for linearly heated side wall(s). Int. J. Therm. Sci. 2010, 49, 1856–1865. [Google Scholar] [CrossRef]
- El Jery, A.; Hidouri, N.; Magherbi, M.; Brahim, A.B. Effect of an external oriented magnetic field on entropy generation in natural convection. Entropy 2010, 12, 1391–1417. [Google Scholar] [CrossRef]
- Bouabid, M.; Hidouri, N.; Magherbi, M.; Brahim, A.B. Analysis of the magnetic field effect on entropy generation at thermosolutal convection in a square cavity. Entropy 2011, 13, 1034–1054. [Google Scholar] [CrossRef]
- Mahmud, S.; Fraser, R.A. Magnetohydrodynamic free convection and entropy generation in a square porous cavity. Int. J. Heat Mass Transf. 2004, 47, 3245–3256. [Google Scholar] [CrossRef]
- Jiang, C.; Feng, W.; Zhong, H.; Zeng, J.; Zhu, Q. Effects of a magnetic quadrupole field on thermomagnetic convection of air in a porous square enclosure. J. Magn. Magn. Mater. 2014, 357, 53–60. [Google Scholar] [CrossRef]
- Woods, L.C. The Thermodynamics of Fluid Systems; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Sheremet, M.A.; Öztop, H.F.; Pop, I.; Abu-Hamde, N. Analysis of entropy generation in natural convection of nanofluid inside a square cavity having hot solid block: Tiwari and Das’ model. Entropy 2016, 18. [Google Scholar] [CrossRef]
- Ilis, G.G.; Mobedi, M.; Sunden, B. Effect of aspect ratio on entropy generation in a rectangular cavity with differentially heated vertical walls. Int. Commun. Heat Mass Transf. 2008, 35, 696–703. [Google Scholar] [CrossRef]

| Grid Dimension | Num |
|---|---|
| 30 × 30 | 3.8762 |
| 40 × 40 | 3.5539 |
| 50 × 50 | 3.4814 |
| 60 × 60 | 3.4647 |
| 70 × 70 | 3.4642 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, E.; Sun, X.; He, Y.; Jiang, C. Effect of a Magnetic Quadrupole Field on Entropy Generation in Thermomagnetic Convection of Paramagnetic Fluid with and without a Gravitational Field. Entropy 2017, 19, 96. https://doi.org/10.3390/e19030096
Shi E, Sun X, He Y, Jiang C. Effect of a Magnetic Quadrupole Field on Entropy Generation in Thermomagnetic Convection of Paramagnetic Fluid with and without a Gravitational Field. Entropy. 2017; 19(3):96. https://doi.org/10.3390/e19030096
Chicago/Turabian StyleShi, Er, Xiaoqin Sun, Yecong He, and Changwei Jiang. 2017. "Effect of a Magnetic Quadrupole Field on Entropy Generation in Thermomagnetic Convection of Paramagnetic Fluid with and without a Gravitational Field" Entropy 19, no. 3: 96. https://doi.org/10.3390/e19030096
APA StyleShi, E., Sun, X., He, Y., & Jiang, C. (2017). Effect of a Magnetic Quadrupole Field on Entropy Generation in Thermomagnetic Convection of Paramagnetic Fluid with and without a Gravitational Field. Entropy, 19(3), 96. https://doi.org/10.3390/e19030096





