Fractional Jensen–Shannon Analysis of the Scientific Output of Researchers in Fractional Calculus
Abstract
:1. Introduction
2. The Dataset
3. Mathematical Background
3.1. The Canberra Distance
3.2. The Classical and Fractional Jensen–Shannon Divergence
3.3. Multidimensional Scaling
3.4. Hierarchichal Clustering
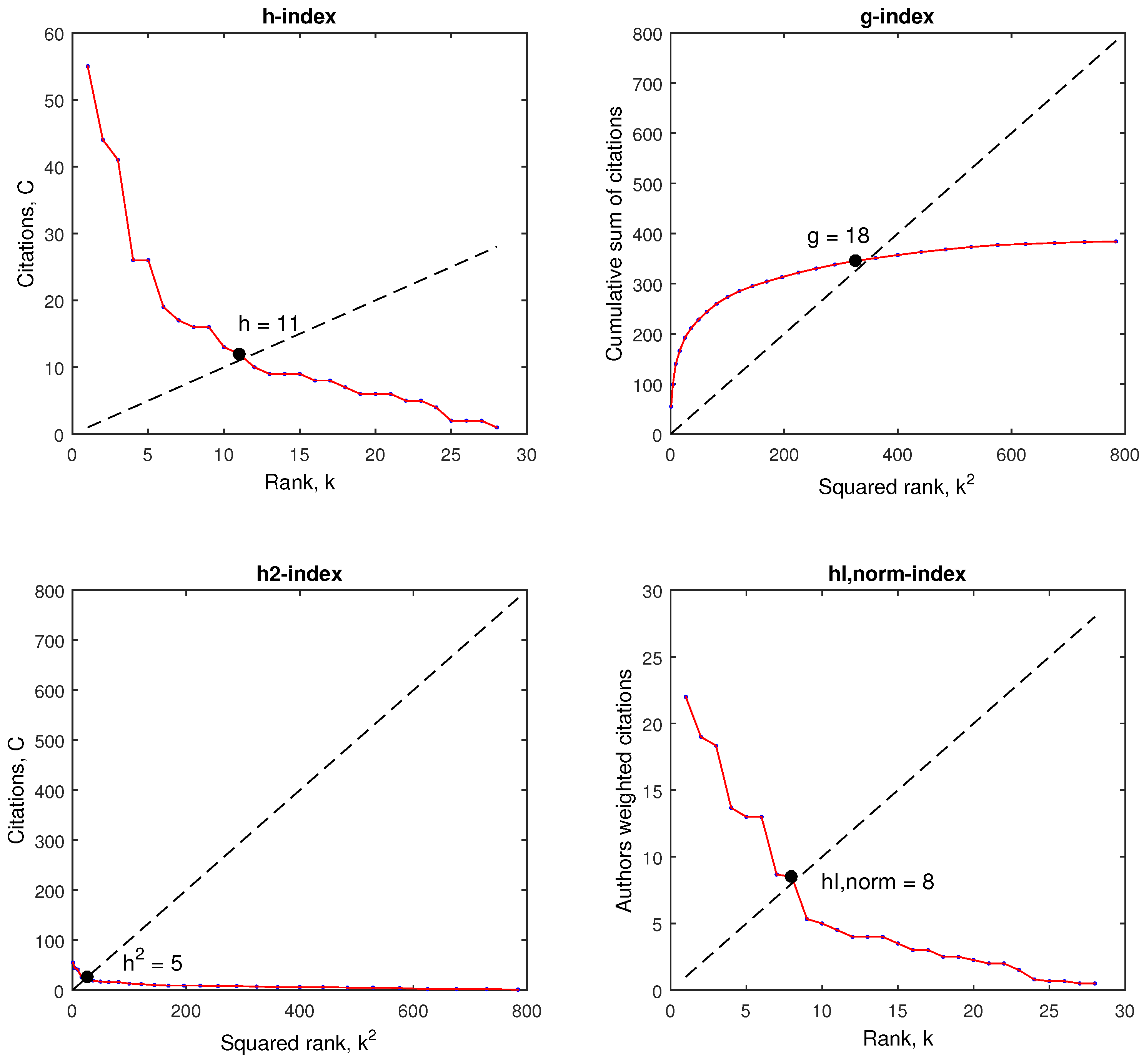
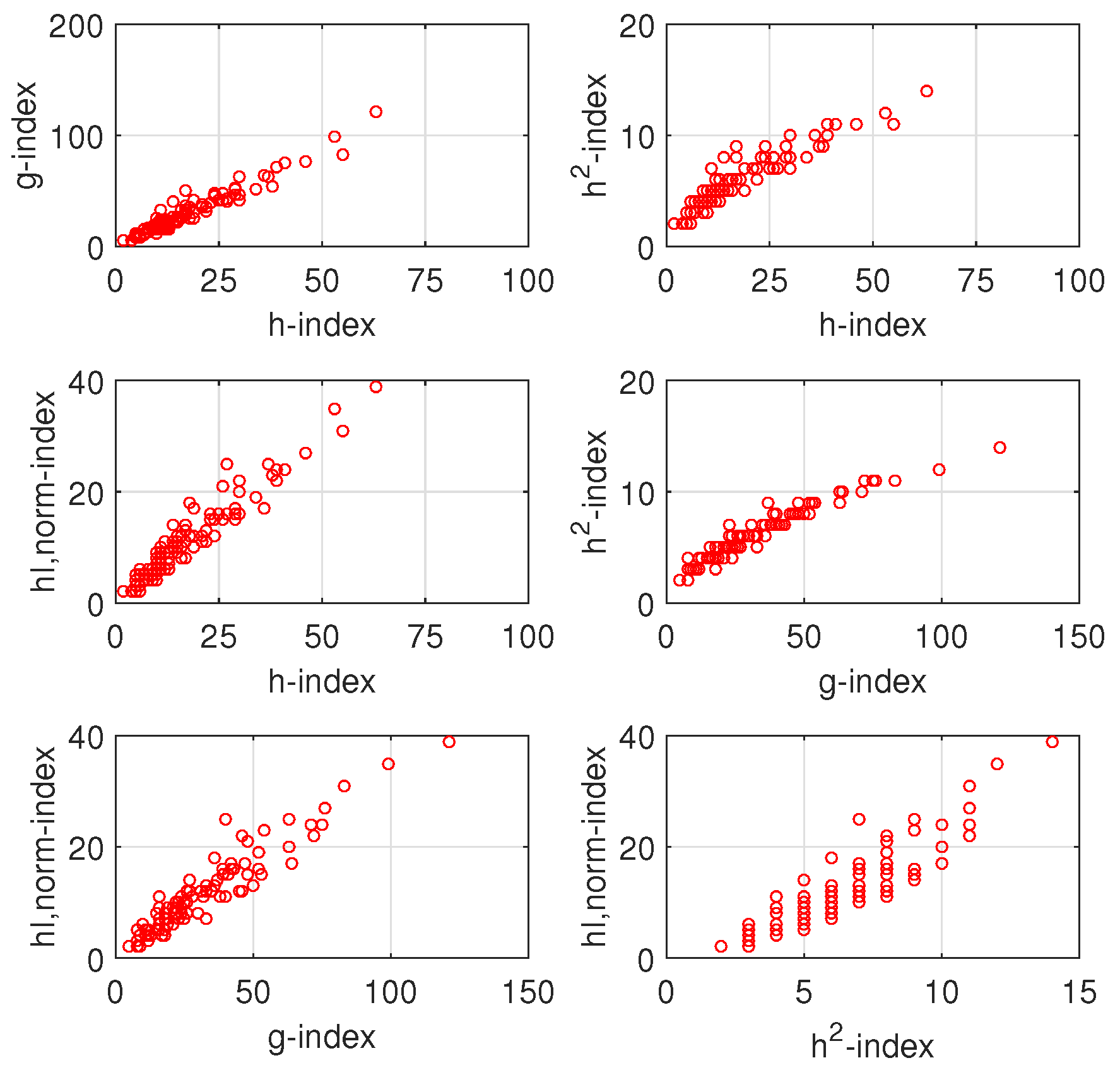
4. Data Analysis and Results
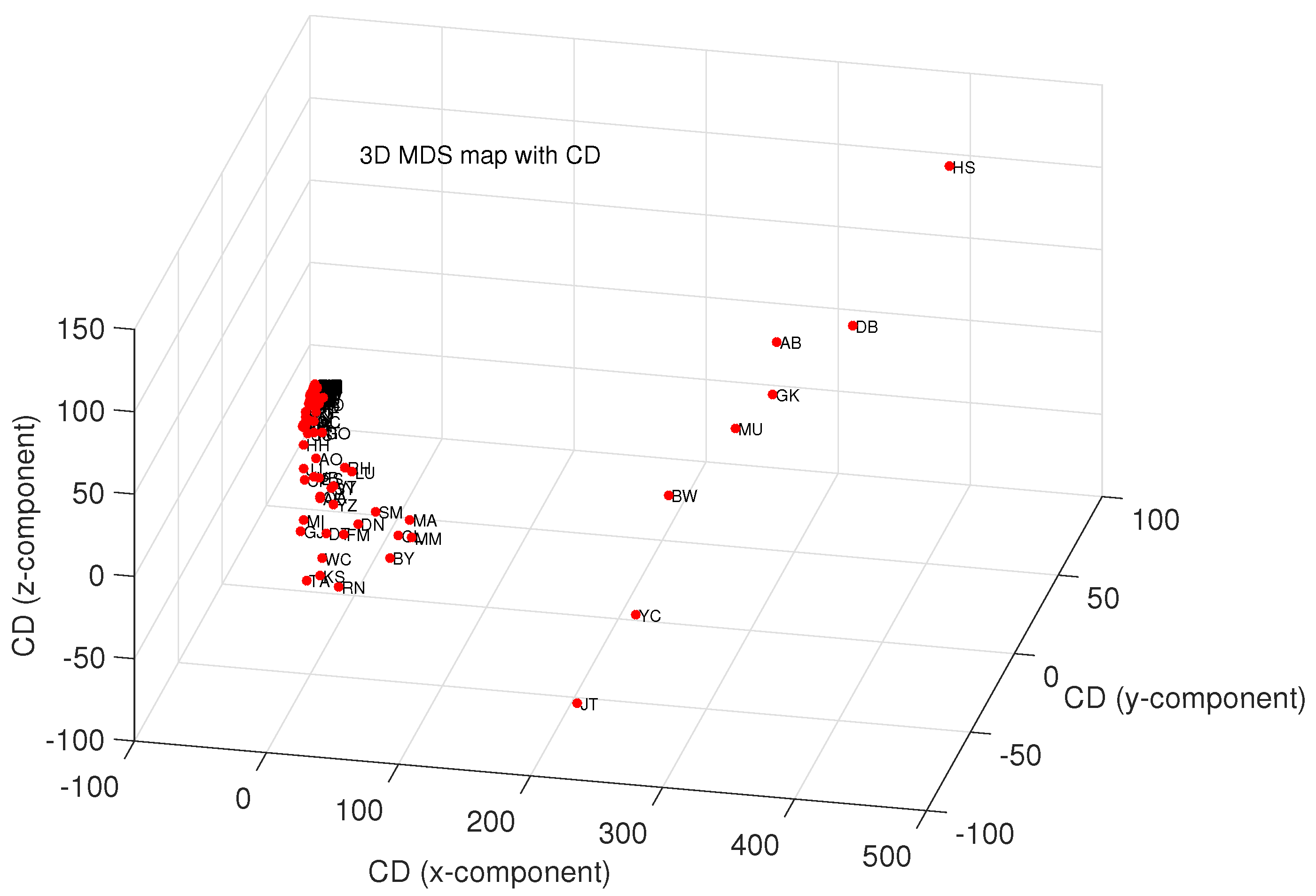
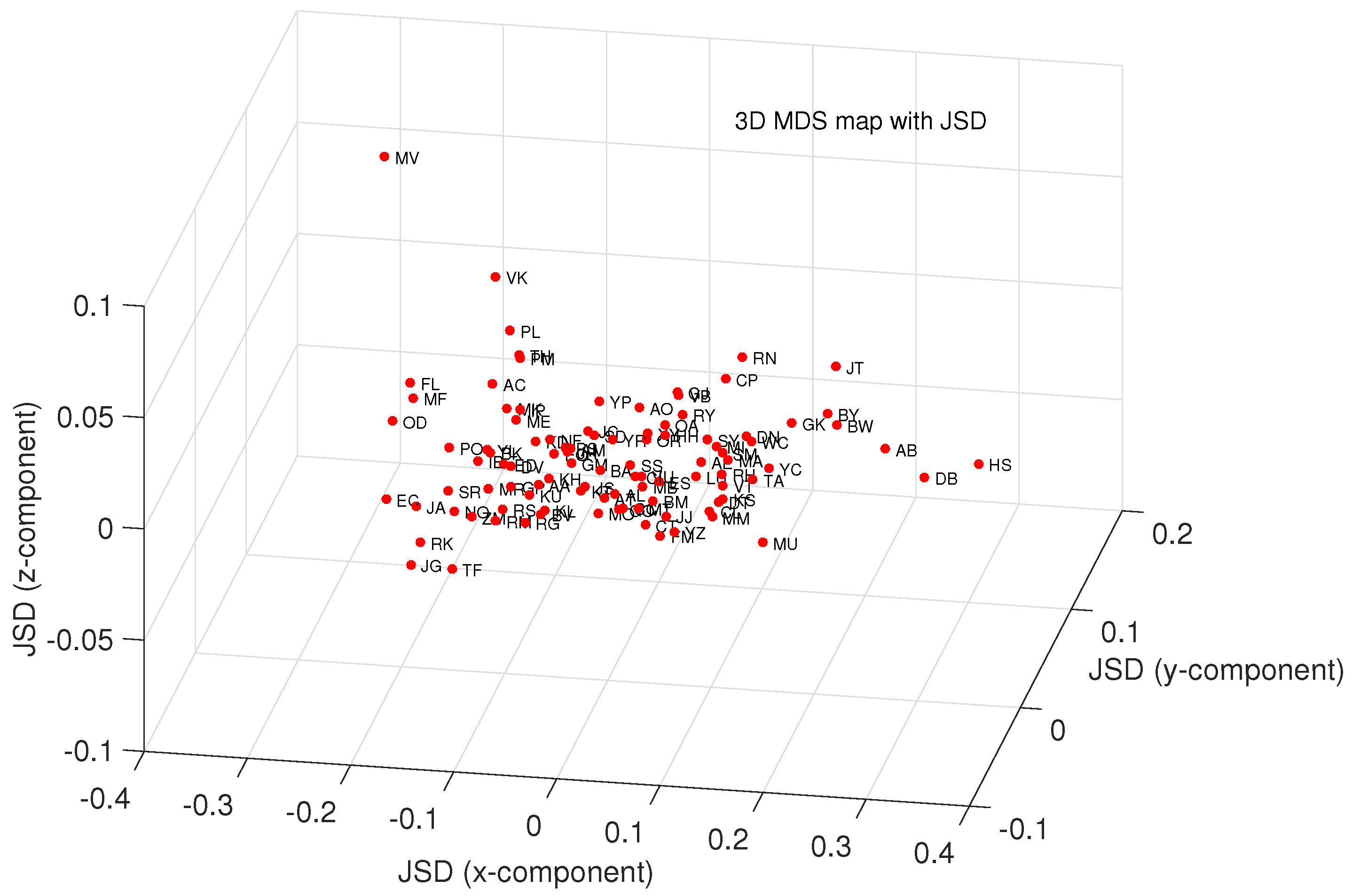
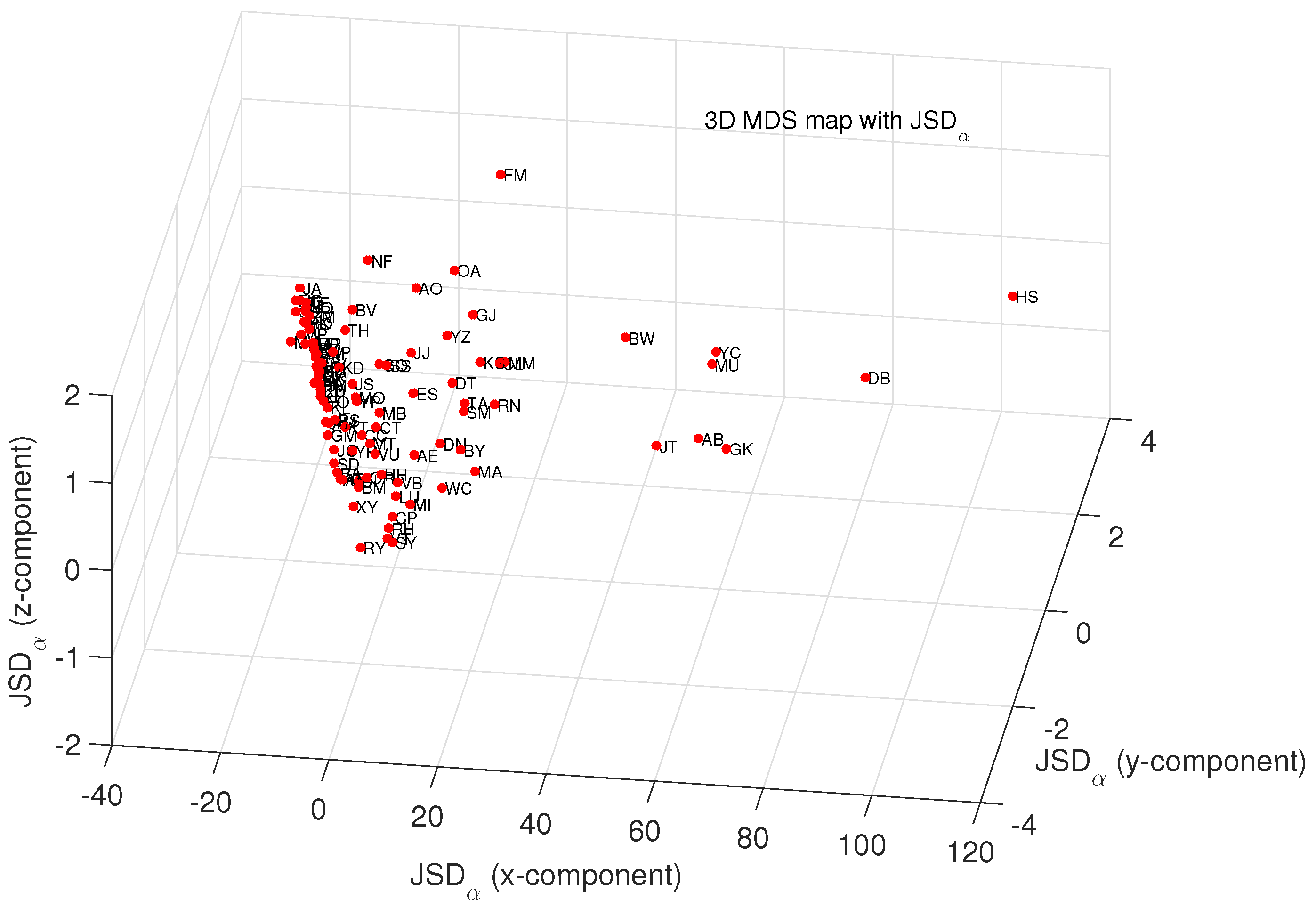
4.1. Comparing and Visualizing Scientific Output by Means of MDS
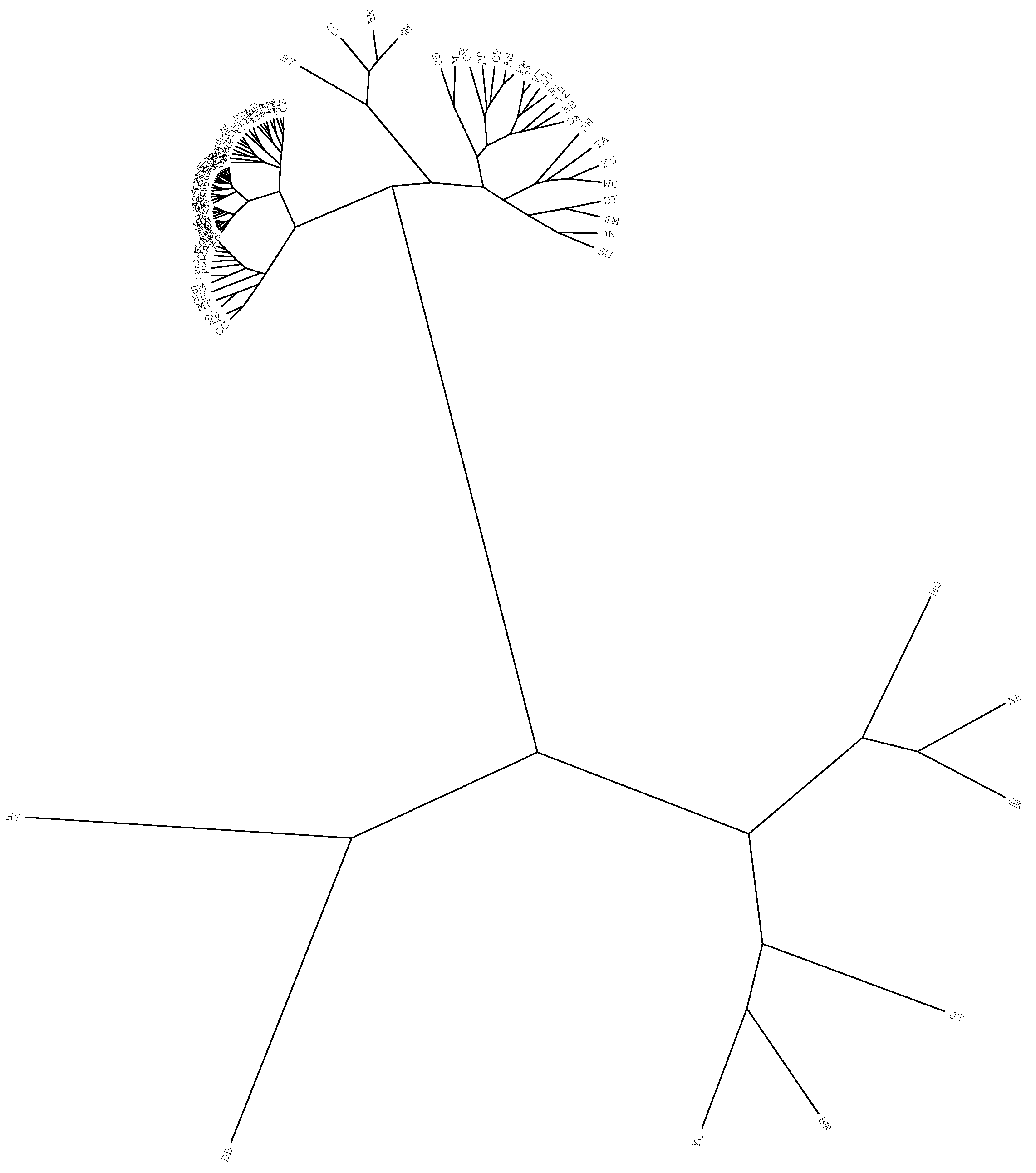
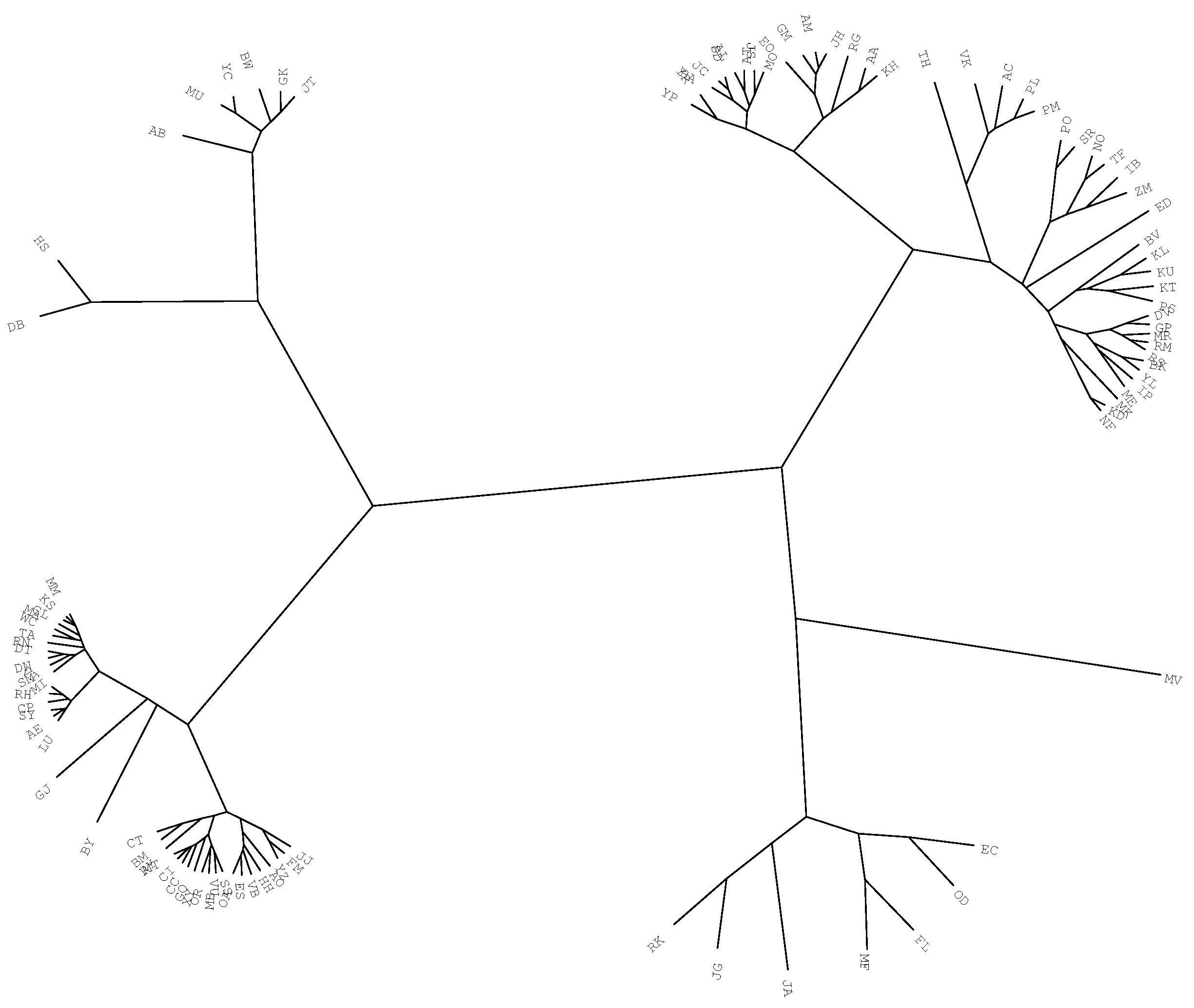
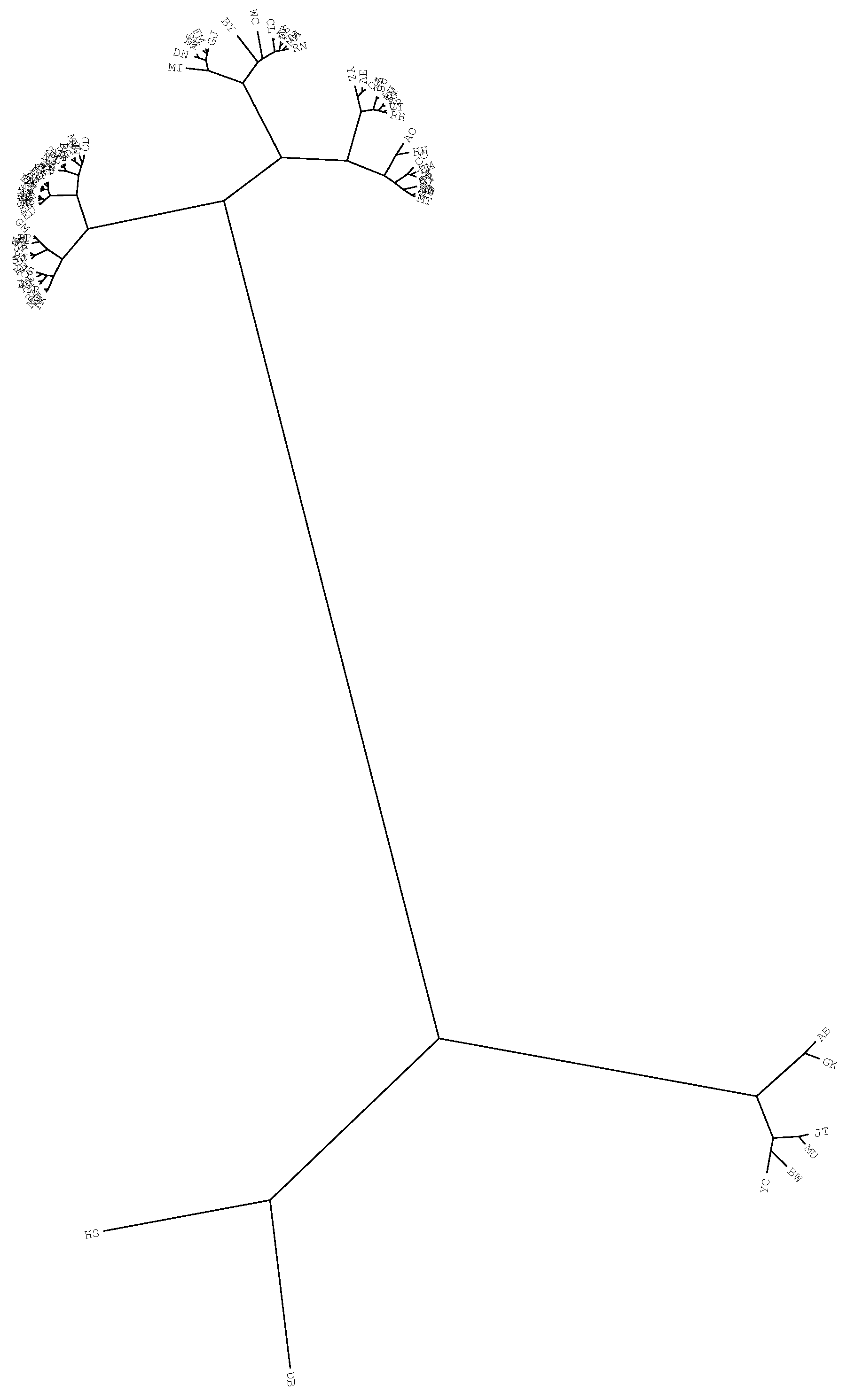
4.2. Comparing and Visualizing Scientific Output by Means of HC
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bornmann, L.; Daniel, H.D. Selecting scientific excellence through committee peer review—A citation analysis of publications previously published to approval or rejection of post-doctoral research fellowship applicants. Scientometrics 2006, 68, 427–440. [Google Scholar] [CrossRef]
- Hirsch, J.E. An index to quantify an individual’s scientific research output. Proc. Natl. Acad. Sci. USA 2005, 102, 16569–16572. [Google Scholar] [CrossRef] [PubMed]
- Bornmann, L.; Daniel, H.D. What do we know about the h index? J. Am. Soc. Inf. Sci. Technol. 2007, 58, 1381–1385. [Google Scholar] [CrossRef]
- Egghe, L. How to improve the h-index. Scientist 2006, 20, 15–16. [Google Scholar]
- Van Raan, A.F. Comparison of the Hirsch-index with standard bibliometric indicators and with peer judgment for 147 chemistry research groups. Scientometrics 2006, 67, 491–502. [Google Scholar] [CrossRef]
- Cronin, B.; Meho, L. Using the h-index to rank influential information scientists. J. Am. Soc. Inf. Sci. Technol. 2006, 57, 1275–1278. [Google Scholar] [CrossRef]
- Glänzel, W. On the opportunities and limitations of the H-index. Sci. Focus 2006, 1, 10–11. [Google Scholar]
- Ruscio, J. Taking Advantage of Citation Measures of Scholarly Impact: Hip Hip h Index! Perspect. Psychol. Sci. 2016, 11, 905–908. [Google Scholar] [CrossRef] [PubMed]
- Kelly, C.D.; Jennions, M.D. The h index and career assessment by numbers. Trends Ecol. Evol. 2006, 21, 167–170. [Google Scholar] [CrossRef] [PubMed]
- Díaz, I.; Cortey, M.; Olvera, À.; Segalés, J. Use of h-index and other bibliometric indicators to evaluate research productivity outcome on swine diseases. PLoS ONE 2016, 11, e0149690. [Google Scholar] [CrossRef] [PubMed]
- Asnafi, S.; Gunderson, T.; McDonald, R.J.; Kallmes, D.F. Association of h-index of Editorial Board Members and Impact Factor among Radiology Journals. Acad. Radiol. 2017, 24, 119–123. [Google Scholar] [CrossRef] [PubMed]
- Braun, T.; Glänzel, W.; Schubert, A. A Hirsch-type index for journals. Scientometrics 2006, 69, 169–173. [Google Scholar] [CrossRef]
- Lacasse, J.R.; Hodge, D.R. Ranking Disciplinary Journals with the Google Scholar H-index. J. Soc. Work Educ. 2017, 47, 579–596. [Google Scholar]
- Banks, M.G. An extension of the Hirsch index: Indexing scientific topics and compounds. Scientometrics 2006, 69, 161–168. [Google Scholar] [CrossRef]
- Yaminfirooz, M.; Gholinia, H. Multiple h-index: A new scientometric indicator. Electron. Libr. 2015, 33, 547–556. [Google Scholar] [CrossRef]
- Sidiropoulos, A.; Katsaros, D.; Manolopoulos, Y. Generalized Hirsch h-index for disclosing latent facts in citation networks. Scientometrics 2007, 72, 253–280. [Google Scholar] [CrossRef]
- Egghe, L. Dynamic h-index: The Hirsch index in function of time. J. Am. Soc. Inf. Sci. Technol. 2007, 58, 452–454. [Google Scholar] [CrossRef]
- Bornmann, L.; Daniel, H.D. What do citation counts measure? A review of studies on citing behavior. J. Doc. 2008, 64, 45–80. [Google Scholar] [CrossRef]
- Iglesias, J.E.; Pecharromán, C. Scaling the h-index for different scientific ISI fields. Scientometrics 2007, 73, 303–320. [Google Scholar] [CrossRef]
- Würtz, M.; Schmidt, M. The stratified H-index. Ann. Epidemiol. 2016, 26, 299–300. [Google Scholar] [CrossRef] [PubMed]
- Ausloos, M. Assessing the true role of coauthors in the h-index measure of an author scientific impact. Phys. A Stat. Mech. Its Appl. 2015, 422, 136–142. [Google Scholar] [CrossRef]
- Taber, D.F. Quantifying publication impact. Science 2005, 309, 2166. [Google Scholar] [CrossRef] [PubMed]
- Egghe, L. An improvement of the h-index: The g-index. ISSI Newslett. 2006, 2, 8–9. [Google Scholar]
- Jin, B. H-index: An evaluation indicator proposed by scientist. Sci. Focus 2006, 1, 8–9. [Google Scholar]
- Kosmulski, M. A new Hirsch-type index saves time and works equally well as the original h-index. ISSI Newslett. 2006, 2, 4–6. [Google Scholar]
- Zhang, C.T. The e-index, complementing the h-index for excess citations. PLoS ONE 2009, 4, e5429. [Google Scholar] [CrossRef] [PubMed]
- Harzing, A.W. The Publish or Perish Book; Tarma Software Research: Melbourne, Australia, 2010. [Google Scholar]
- Jin, B.; Liang, L.; Rousseau, R.; Egghe, L. The R-and AR-indices: Complementing the h-index. Chin. Sci. Bull. 2007, 52, 855–863. [Google Scholar] [CrossRef]
- Ruane, F.; Tol, R. Rational (successive) h-indices: An application to economics in the Republic of Ireland. Scientometrics 2008, 75, 395–405. [Google Scholar] [CrossRef]
- Guns, R.; Rousseau, R. Real and rational variants of the h-index and the g-index. J. Informetr. 2009, 3, 64–71. [Google Scholar] [CrossRef]
- Vinkler, P. The π-index: A new indicator for assessing scientific impact. J. Inf. Sci. 2009, 35, 602–612. [Google Scholar] [CrossRef]
- Dorogovtsev, S.N.; Mendes, J.F. Ranking scientists. Nat. Phys. 2015, 11, 882–883. [Google Scholar] [CrossRef]
- Kilbas, A.A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional Calculus; Springer: New York, NY, USA, 1997. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Models and Numerical Methods; World Scientific: Singapore, 2012; Volume 3. [Google Scholar]
- Ionescu, C.M. The Human Respiratory System: An Analysis of the Interplay between Anatomy, Structure, Breathing and Fractal Dynamics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Lopes, A.M.; Machado, J. Fractional order models of leaves. J. Vib. Control 2014, 20, 998–1008. [Google Scholar] [CrossRef]
- Machado, J.T.; Lopes, A.M. The persistence of memory. Nonlinear Dyn. 2015, 79, 63–82. [Google Scholar] [CrossRef]
- Machado, J.; Lopes, A.M. Analysis of natural and artificial phenomena using signal processing and fractional calculus. Fract. Calc. Appl. Anal. 2015, 18, 459–478. [Google Scholar] [CrossRef]
- Machado, J.; Lopes, A.; Duarte, F.; Ortigueira, M.; Rato, R. Rhapsody in fractional. Fract. Calc. Appl. Anal. 2014, 17, 1188–1214. [Google Scholar] [CrossRef]
- Machado, J.; Mata, M.E.; Lopes, A.M. Fractional state space analysis of economic systems. Entropy 2015, 17, 5402–5421. [Google Scholar] [CrossRef]
- Lance, G.N.; Williams, W.T. Computer programs for hierarchical polythetic classification (“similarity analyses”). Comput. J. 1966, 9, 60–64. [Google Scholar] [CrossRef]
- Lance, G.N.; Williams, W.T. Mixed-Data Classificatory Programs I—Agglomerative Systems. Aust. Comput. J. 1967, 1, 15–20. [Google Scholar]
- Machado, J.T. Fractional Order Generalized Information. Entropy 2014, 16, 2350–2361. [Google Scholar] [CrossRef]
- Valério, D.; Trujillo, J.J.; Rivero, M.; Machado, J.T.; Baleanu, D. Fractional calculus: A survey of useful formulas. Eur. Phys. J. Spec. Top. 2013, 222, 1827–1846. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Cox, T.F.; Cox, M.A. Multidimensional Scaling; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Hartigan, J.A. Clustering Algorithms; Wiley: Hoboken, NJ, USA, 1975. [Google Scholar]
- Aggarwal, C.C.; Hinneburg, A.; Keim, D.A. On the Surprising Behavior of Distance Metrics in High Dimensional Space; Springer: New York, NY, USA, 2001. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. The comparison of dendrograms by objective methods. Taxon 1962, 11, 33–40. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.T. Integer and fractional-order entropy analysis of earthquake data series. Nonlinear Dyn. 2016, 84, 79–90. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Lopes, A.M. Analysis and visualization of seismic data using mutual information. Entropy 2013, 15, 3892–3909. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.T. Analysis of temperature time-series: Embedding dynamics into the MDS method. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 851–871. [Google Scholar] [CrossRef]
| Country | Number | Country | Number | Country | Number |
|---|---|---|---|---|---|
| Algeria | 1 | Greece | 1 | Russia | 6 |
| Australia | 1 | Hungary | 1 | Serbia | 2 |
| Austria | 1 | India | 5 | Singapore | 1 |
| Belgium | 1 | Iran | 2 | Slovak Republic | 2 |
| Brazil | 1 | Italy | 8 | South Africa | 1 |
| Bulgaria | 2 | Japan | 1 | Spain | 7 |
| Canada | 3 | Jordan | 1 | Switzerland | 1 |
| Chile | 1 | Mexico | 1 | Turkey | 3 |
| China | 4 | Netherlands | 1 | UA Emirates | 3 |
| Egypt | 2 | Poland | 4 | UK | 1 |
| France | 6 | Portugal | 6 | USA | 13 |
| Germany | 5 | Romania | 1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Machado, J.A.T.; Mendes Lopes, A. Fractional Jensen–Shannon Analysis of the Scientific Output of Researchers in Fractional Calculus. Entropy 2017, 19, 127. https://doi.org/10.3390/e19030127
Machado JAT, Mendes Lopes A. Fractional Jensen–Shannon Analysis of the Scientific Output of Researchers in Fractional Calculus. Entropy. 2017; 19(3):127. https://doi.org/10.3390/e19030127
Chicago/Turabian StyleMachado, José A. Tenreiro, and António Mendes Lopes. 2017. "Fractional Jensen–Shannon Analysis of the Scientific Output of Researchers in Fractional Calculus" Entropy 19, no. 3: 127. https://doi.org/10.3390/e19030127
APA StyleMachado, J. A. T., & Mendes Lopes, A. (2017). Fractional Jensen–Shannon Analysis of the Scientific Output of Researchers in Fractional Calculus. Entropy, 19(3), 127. https://doi.org/10.3390/e19030127







