Witnessing Multipartite Entanglement by Detecting Asymmetry
Abstract
:1. Introduction
2. Measuring Asymmetry
2.1. Theoretically Consistent Measure of Asymmetry
- (i)
- It vanishes if and only if the state is incoherent. Since the quantum Fisher information is convex, for any incoherent state, one has . Also, we observe that and , which is a condition satisfied if and only if the state is incoherent.
- (ii)
- It cannot increase under free operations. Given , by Theorem II.1 of Ref. [5], any map admits a Stinespring dilation , where is a free unitary with respect to , and . In other words, any free map can be represented by the unitary, free evolution of the system of interest and an ancilla in an incoherent state (i.e., a free state). One then obtains . The first equality is due to the additivity of the quantum Fisher information for additive observables and uncorrelated states. The second one is due to the invariance of the quantum Fisher information under unitaries applied to both the state and the Hamiltonian, and to the fact that the unitary here is a free operation, . The inequality is due to the contractivity of the quantum Fisher information under partial trace.
2.2. Experimental Observability of the Asymmetry Bound
3. Detection of Multipartite Entanglement via Asymmetry
3.1. Asymmetry Witnesses Entanglement
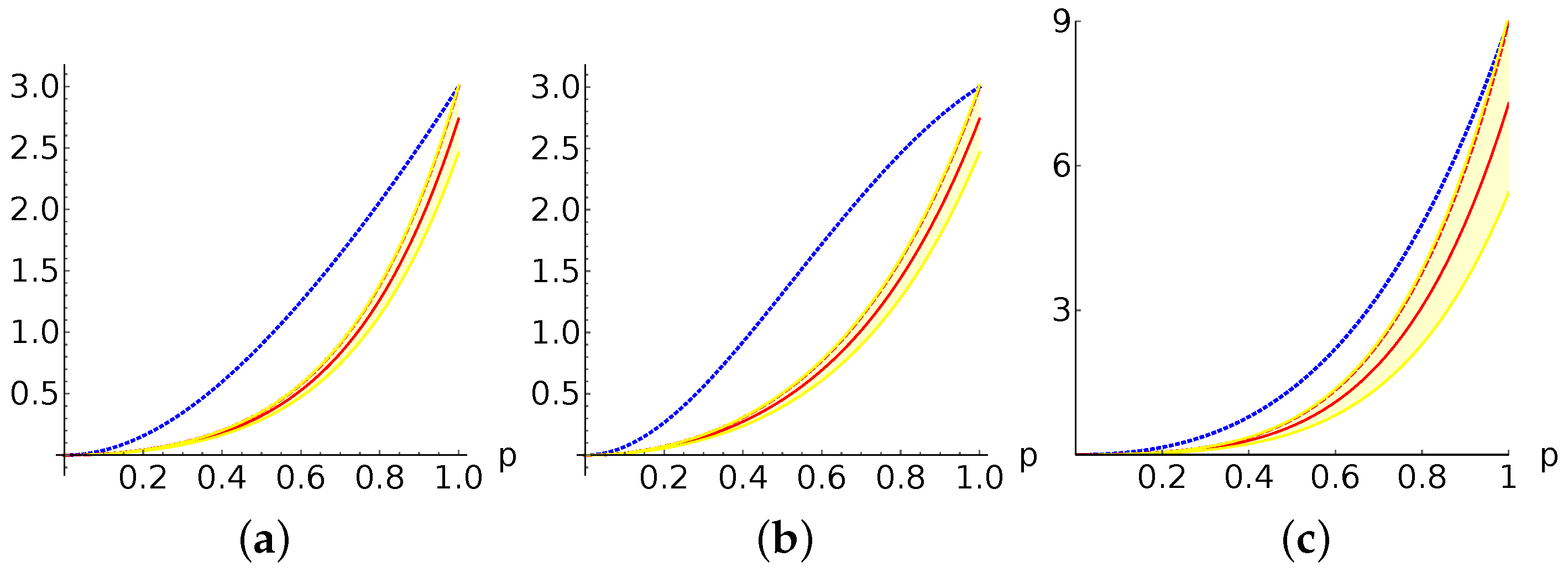
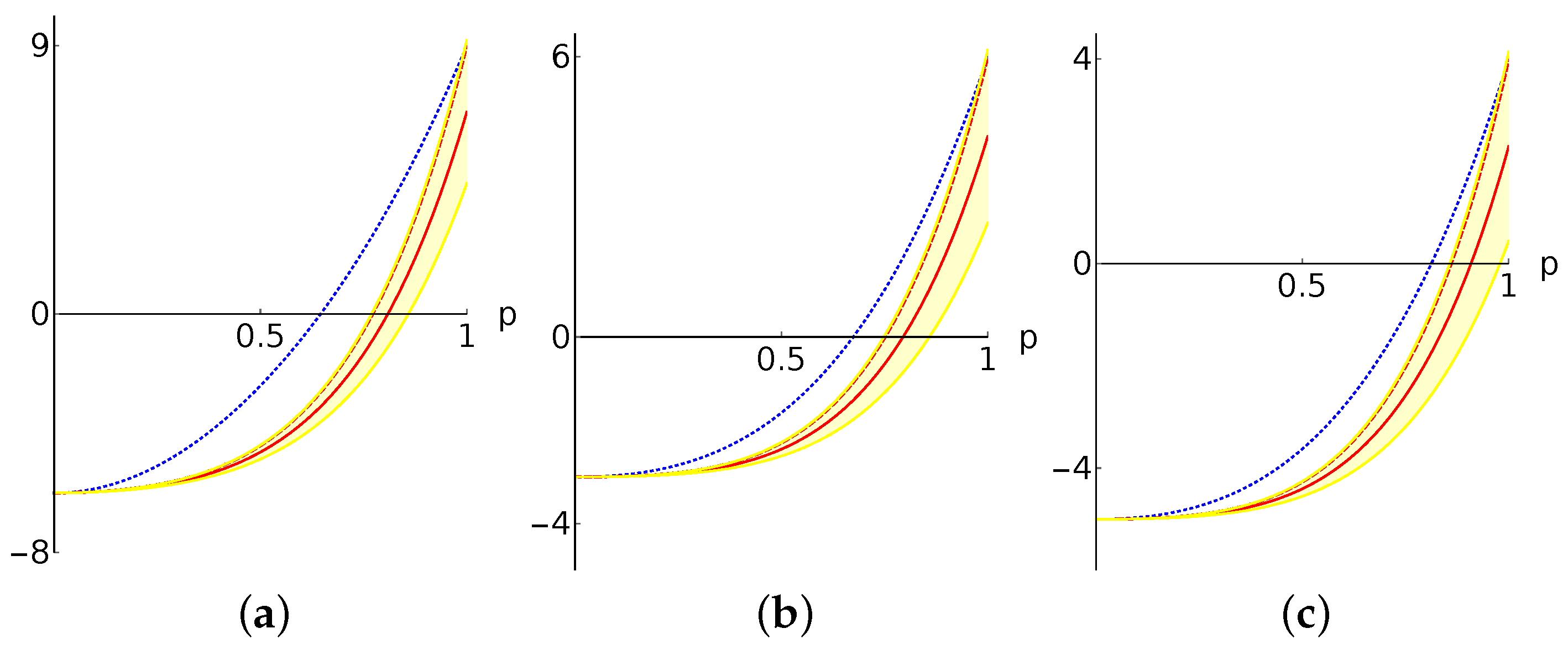
3.2. A Case Study
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Horodecki, M.; Oppenheim, J. (Quantumness in the context of) resource theories. Int. J. Mod. Phys. B 2013, 27, 1345019. [Google Scholar] [CrossRef]
- Bartlett, S.D.; Rudolph, T.; Spekkens, R.W. Reference frames, superselection rules, and quantum information. Rev. Mod. Phys. 2007, 79, 555–609. [Google Scholar] [CrossRef]
- Gour, G.; Spekkens, R.W. The resource theory of quantum reference frames: Manipulations and monotones. New J. Phys. 2008, 10, 033023. [Google Scholar] [CrossRef]
- Marvian, I. Symmetry, Asymmetry and Quantum Information. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2012. [Google Scholar]
- Ahmadi, M.; Jennings, D.; Rudolph, T. The WAY theorem and the quantum resource theory of asymmetry. New J. Phys. 2013, 15, 013057. [Google Scholar] [CrossRef]
- Girolami, D.; Tufarelli, T.; Adesso, G. Characterizing Nonclassical Correlations via Local Quantum Uncertainty. Phys. Rev. Lett. 2013, 110, 240402. [Google Scholar] [CrossRef] [PubMed]
- Marvian, I.; Spekkens, R.W. Extending Noether’s theorem by quantifying the asymmetry of quantum states. Nat. Commun. 2014, 5, 3821. [Google Scholar] [CrossRef] [PubMed]
- Girolami, D. Observable Measure of Quantum Coherence in Finite Dimensional Systems. Phys. Rev. Lett. 2014, 113, 170401. [Google Scholar] [CrossRef] [PubMed]
- Girolami, D.; Souza, A.M.; Giovannetti, V.; Tufarelli, T.; Filgueiras, J.G.; Sarthour, R.S.; Soares-Pinto, D.O.; Oliveira, I.S.; Adesso, G. Quantum discord determines the interferometric power of quantum states. Phys. Rev. Lett. 2014, 112, 210401. [Google Scholar] [CrossRef]
- Luo, S. Wigner-Yanase Skew Information and Uncertainty Relations. Phys. Rev. Lett. 2003, 91, 180403. [Google Scholar] [CrossRef] [PubMed]
- Aberg, J. Catalytic Coherence. Phys. Rev. Lett. 2014, 113, 150402. [Google Scholar] [CrossRef] [PubMed]
- Luo, S. Quantum versus classical uncertainty. Theor. Math. Phys. 2005, 143, 681–688. [Google Scholar] [CrossRef]
- Luo, S.; Fu, S.; Oh, C.H. Quantifying correlations via the Wigner-Yanase skew information. Phys. Rev. A 2012, 85, 032117. [Google Scholar] [CrossRef]
- Herbut, F. A quantum measure of coherence and incompatibility. J. Phys. A 2005, 38, 2959–2974. [Google Scholar] [CrossRef]
- Baumgratz, T.; Cramer, M.; Plenio, M.B. Quantifying Coherence. Phys. Rev. Lett. 2014, 113, 140401. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Xiao, X.; Ge, L.; Sun, C.P. Quantum coherence in multipartite systems. Phys. Rev. A 2015, 92, 022112. [Google Scholar] [CrossRef]
- Du, S.; Bai, Z.; Guo, Y. Conditions for coherence transformations under incoherent operations. Phys. Rev. A 2015, 91, 052120. [Google Scholar] [CrossRef]
- Streltsov, A.; Singh, U.; Dhar, H.S.; Bera, M.N.; Adesso, G. Measuring Quantum Coherence with Entanglement. Phys. Rev. Lett. 2015, 115, 020403. [Google Scholar] [CrossRef] [PubMed]
- Xi, Z.; Li, Y.; Fan, H. Quantum coherence and correlations in quantum system. Sci. Rep. 2015, 5, 10922. [Google Scholar] [CrossRef] [PubMed]
- Li, C.-M.; Lambert, N.; Chen, Y.-N.; Chen, G.-Y.; Nori, F. Witnessing Quantum Coherence: From solid-state to biological systems. Sci. Rep. 2012, 2, 885. [Google Scholar] [CrossRef] [PubMed]
- Monras, A.; Checinska, A.; Ekert, A.K. Witnessing quantum coherence in the presence of noise. New J. Phys. 2014, 16, 063041. [Google Scholar] [CrossRef]
- Pollock, F.A.; Checinska, A.; Pascazio, S.; Modi, K. Using a biased qubit to probe complex systems. Phys. Rev. A 2016, 94, 032112. [Google Scholar] [CrossRef]
- Altafini, C. Tensor of coherences parametrization of multiqubit density operators for entanglement characterization. Phys. Rev. A 2004, 69, 012311. [Google Scholar] [CrossRef]
- Bromley, T.R.; Cianciaruso, M.; Adesso, G. Frozen quantum coherence. Phys. Rev. Lett. 2015, 114, 210401. [Google Scholar] [CrossRef] [PubMed]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum Entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Jozsa, R.; Linden, N. On the role of entanglement in quantum-computational speed-up. Proc. R. Soc. A 2003, 459. [Google Scholar] [CrossRef]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in Quantum Metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Shimizu, A.; Morimae, T. Detection of Macroscopic Entanglement by Correlation of Local Observables. Phys. Rev. Lett. 2005, 95, 090401. [Google Scholar] [CrossRef] [PubMed]
- Huber, M.; Mintert, F.; Gabriel, A.; Hiesmayer, B.C. Detection of High-Dimensional Genuine Multipartite Entanglement of Mixed States. Phys. Rev. Lett. 2010, 104, 210501. [Google Scholar] [CrossRef] [PubMed]
- Gühne, O.; Tóth, G. Entanglement detection. Phys. Rep. 2009, 474, 1–75. [Google Scholar] [CrossRef]
- Helstrom, C.W. Quantum Detection and Estimation Theory; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Tóth, G.; Apellaniz, I. Quantum metrology from a quantum information science perspective. J. Phys. A Math. Theor. 2014, 47, 424006. [Google Scholar] [CrossRef]
- Zhang, C.; Yadin, B.; Hou, Z.; Cao, H.; Liu, B.; Huang, Y.; Maity, R.; Vedral, V.; Li, C.; Guo, G.; et al. Determining the speed of multipartite quantum systems by few local measurements. arXiv, 2016; arXiv:1611.02004. [Google Scholar]
- Paz, J.P.; Roncaglia, A. Quantum gate arrays can be programmed to evaluate the expectation value of any operator. Phys. Rev. A 2003, 68, 052316. [Google Scholar] [CrossRef]
- Brun, T.A. Measuring polynomial functions of states. Quant. Inf. Comp. 2004, 4, 401–408. [Google Scholar]
- D’Ariano, G.M.; Perinotti, P. Efficient Universal Programmable Quantum Measurements. Phys. Rev. Lett. 2005, 94, 090401. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.K.; Moura Alves, C.; Oi, D.K.L.; Horodecki, M.; Horodecki, P.; Kwek, L.C. Direct Estimations of Linear and Nonlinear Functionals of a Quantum State. Phys. Rev. Lett. 2002, 88, 217901. [Google Scholar] [CrossRef] [PubMed]
- Filip, R. Overlap and entanglement-witness measurements. Phys. Rev. A 2002, 65, 062320. [Google Scholar] [CrossRef]
- Jeong, H.; Noh, C.; Bae, S.; Angelakis, D.G.; Ralph, T.C. Detecting the degree of macroscopic quantumness using an overlap measurement. J. Opt. Soc. Am. B 2014, 31, 3057–3066. [Google Scholar] [CrossRef]
- Nakazato, H.; Tanaka, T.; Yuasa, K.; Florio, G.; Pascazio, S. Measurement scheme for purity based on two two-body gates. Phys. Rev. A 2012, 85, 042316. [Google Scholar] [CrossRef]
- Mintert, F.; Buchleitner, A. Observable Entanglement Measure for Mixed Quantum States. Phys. Rev. Lett. 2007, 98, 140505. [Google Scholar] [CrossRef] [PubMed]
- Walborn, S.P.; Souto Ribeiro, P.H.; Davidovich, L.; Mintert, F.; Buchleitner, A. Experimental determination of entanglement with a single measurement. Nature 2006, 440, 1022–1024. [Google Scholar] [CrossRef] [PubMed]
- Oszmaniec, M.; Kuś, M. Universal framework for entanglement detection. Phys. Rev. A 2013, 88, 052328. [Google Scholar] [CrossRef]
- Jin, J.; Zhang, F.; Yu, C.; Song, H. Direct scheme for measuring the geometric quantum discord. J. Phys. A Math. Theor. 2012, 45, 115308. [Google Scholar] [CrossRef]
- Yu, S. Quantum Fisher Information as the Convex Roof of Variance. arXiv, 2013; arXiv:1302.5311. [Google Scholar]
- Tóth, G.; Petz, D. Extremal properties of the variance and the quantum Fisher information. Phys. Rev. A 2013, 87, 032324. [Google Scholar] [CrossRef]
- Petz, D. Monotone metrics on matrix spaces. Linear Algebra Its Appl. 1996, 244, 81–96. [Google Scholar] [CrossRef]
- Gibilisco, P.; Imparato, D.; Isola, T. Inequalities for quantum Fisher information. Proc. Am. Math. Soc. 2008, 137, 317–327. [Google Scholar] [CrossRef] [Green Version]
- Paiva Pires, D.; Céleri, L.C.; Soares-Pinto, D.O. Geometric lower bound for a quantum coherence measure. Phys. Rev. A 2015, 91, 042330. [Google Scholar] [CrossRef]
- Wang, X.; Schirmer, S.G. Contractivity of the Hilbert-Schmidt distance under open-system dynamics. Phys. Rev. A 2009, 79, 052326. [Google Scholar] [CrossRef]
- Tufarelli, T.; Girolami, D.; Vasile, R.; Bose, S.; Adesso, G. Quantum resources for hybrid communication via qubit-oscillator states. Phys. Rev. A 2012, 86, 052326. [Google Scholar] [CrossRef]
- Piani, M. Problem with geometric discord. Phys. Rev. A 2012, 86, 034101. [Google Scholar] [CrossRef]
- Girolami, D.; Vasile, R.; Adesso, G. Theoretical insights on measuring quantum correlations. Int. J. Mod. Phys. B 2013, 27, 1345020. [Google Scholar] [CrossRef]
- Pezzé, L.; Smerzi, A. Ultrasensitive Two-Mode Interferometry with Single-Mode Number Squeezing. Phys. Rev. Lett. 2013, 110, 163604. [Google Scholar] [CrossRef] [PubMed]
- Tóth, G. Multipartite entanglement and high-precision metrology. Phys. Rev. A 2012, 85, 022322. [Google Scholar] [CrossRef]
- Hyllus, P.; Laskowski, W.; Krischek, R.; Schwemmer, C.; Wieczorek, W.; Weinfurter, H.; Pezzé, L.; Smerzi, A. Fisher information and multiparticle entanglement. Phys. Rev. A 2012, 85, 022321. [Google Scholar] [CrossRef]
- Hong, Y.; Luo, S.; Song, H. Detecting k-nonseparability via quantum Fisher information. Phys. Rev. A 2015, 91, 042313. [Google Scholar] [CrossRef]
- Li, N.; Luo, S. Entanglement detection via quantum Fisher information. Phys. Rev. A 2013, 88, 014301. [Google Scholar] [CrossRef]
- Luo, S. Wigner-Yanase skew information vs. quantum Fisher information. Proc. Am. Math. Soc. 2003, 132, 885–890. [Google Scholar] [CrossRef]
- Gühne, O.; Seevinck, M. Separability criteria for genuine multiparticle entanglement. New J. Phys. 2010, 12, 053002. [Google Scholar] [CrossRef]
- Apellaniz, I.; Lücke, B.; Peise, J.; Klempt, C.; Tóth, G. Detecting metrologically useful entanglement in the vicinity of Dicke states. New J. Phys. 2015, 17, 083027. [Google Scholar] [CrossRef]
- Daley, A.J.; Pichler, H.; Schachenmayer, J.; Zoller, P. Measuring Entanglement Growth in Quench Dynamics of Bosons in an Optical Lattice. Phys. Rev. Lett. 2012, 109, 020505. [Google Scholar] [CrossRef] [PubMed]
- Marvian, I.; Spekkens, R.W. How to quantify coherence: Distinguishing speakable and unspeakable notions. Phys. Rev. A 2016, 94, 052324. [Google Scholar] [CrossRef]
- Leggett, A. Macroscopic Quantum Systems and the Quantum Theory of Measurement. Prog. Theor. Phys. Supp. 1980, 69, 80–100. [Google Scholar] [CrossRef]
- Fröwis, F.; Dür, W. Measures of macroscopicity for quantum spin systems. New J. Phys. 2012, 14, 093039. [Google Scholar] [CrossRef]
- Yadin, B.; Vedral, V. A general framework for quantum macroscopicity in terms of coherence. Phys. Rev. A 2016, 93, 022122. [Google Scholar] [CrossRef]
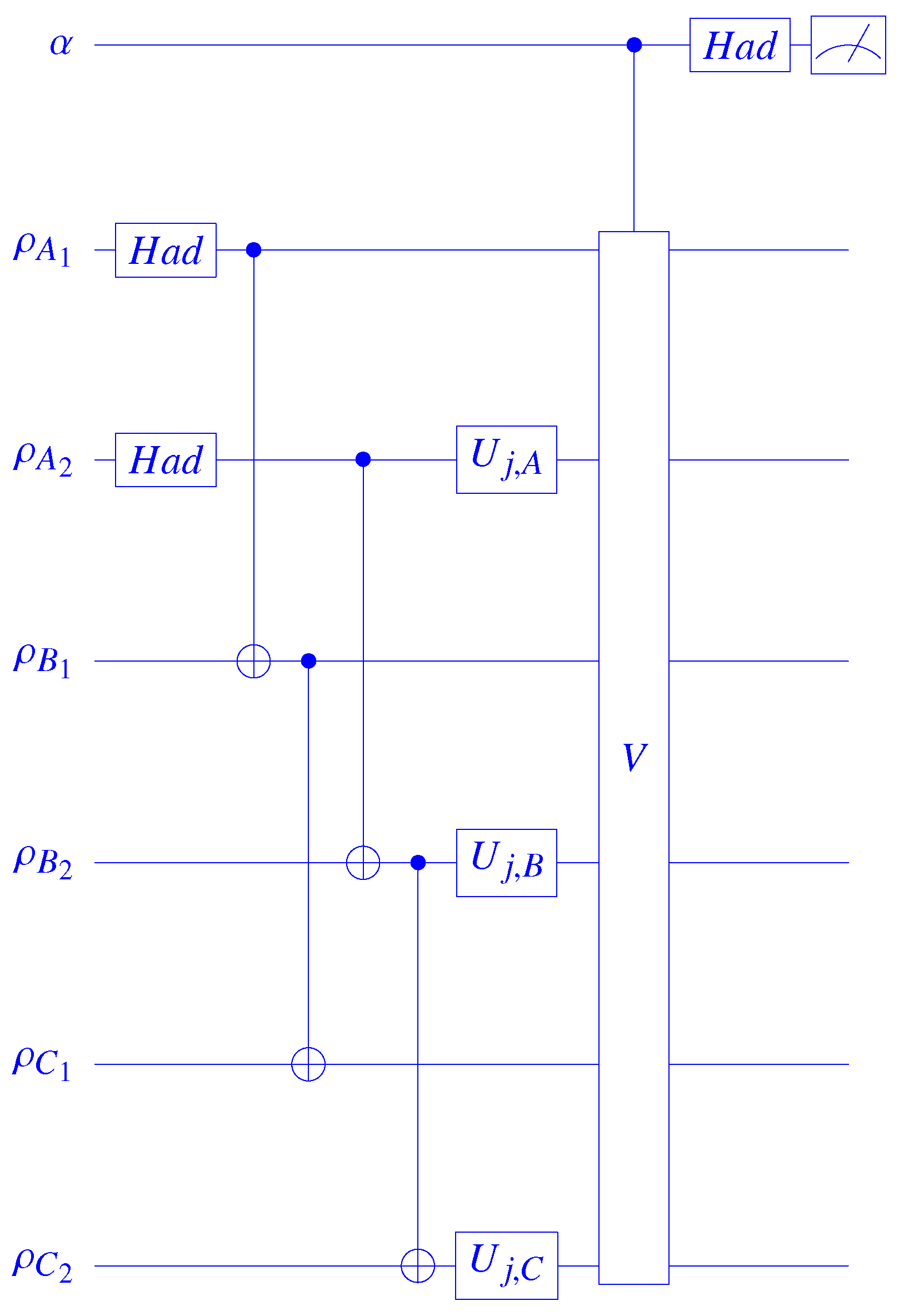
| / | / | |||
| / | / | |||
| / | ||||
| / | ||||
| / | / | ||
| / | / | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Girolami, D.; Yadin, B. Witnessing Multipartite Entanglement by Detecting Asymmetry. Entropy 2017, 19, 124. https://doi.org/10.3390/e19030124
Girolami D, Yadin B. Witnessing Multipartite Entanglement by Detecting Asymmetry. Entropy. 2017; 19(3):124. https://doi.org/10.3390/e19030124
Chicago/Turabian StyleGirolami, Davide, and Benjamin Yadin. 2017. "Witnessing Multipartite Entanglement by Detecting Asymmetry" Entropy 19, no. 3: 124. https://doi.org/10.3390/e19030124
APA StyleGirolami, D., & Yadin, B. (2017). Witnessing Multipartite Entanglement by Detecting Asymmetry. Entropy, 19(3), 124. https://doi.org/10.3390/e19030124





