Friction, Free Axes of Rotation and Entropy
Abstract
:1. Introduction
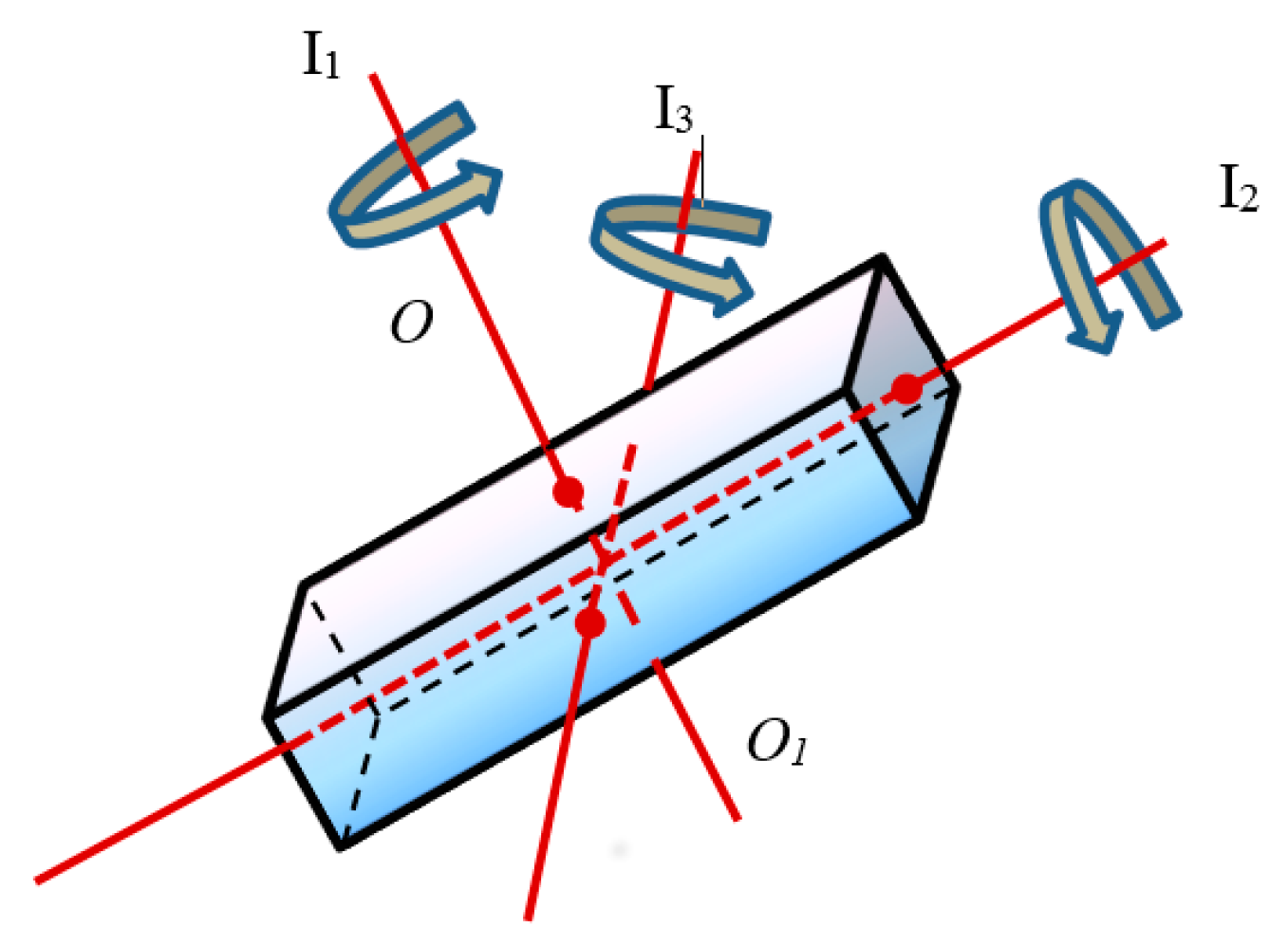
2. Friction-Induced Orientation of a Rotator
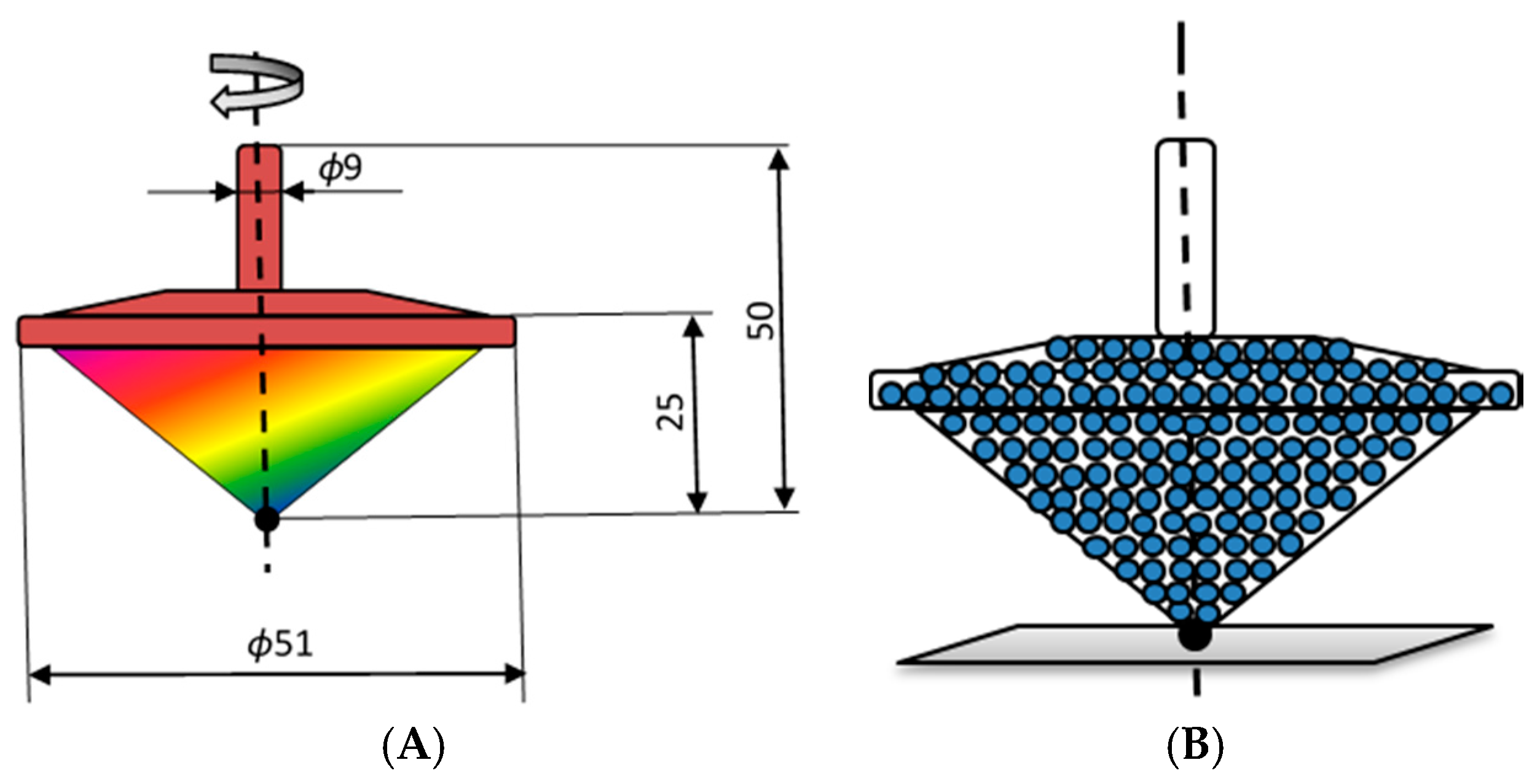
2.1. Friction-Induced Orientation of Hollow (Light) and Filled (Heavy) Tops of the Same Shape
2.2. Friction-Induced Orientation of Tops Filled by Agate and Steel Balls
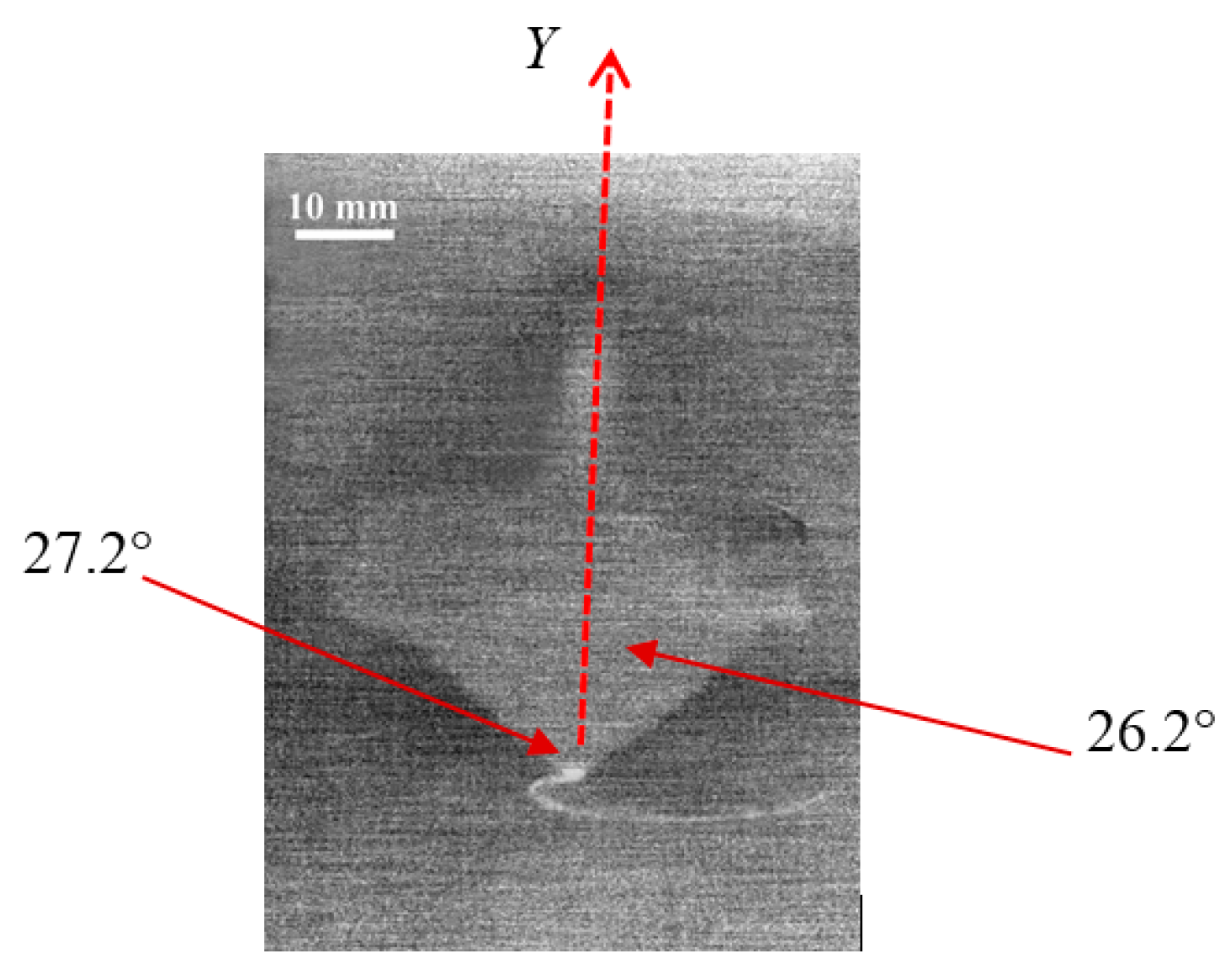
2.3. Friction-Induced Orientation and Re-Orientation of Coin-Like Tops
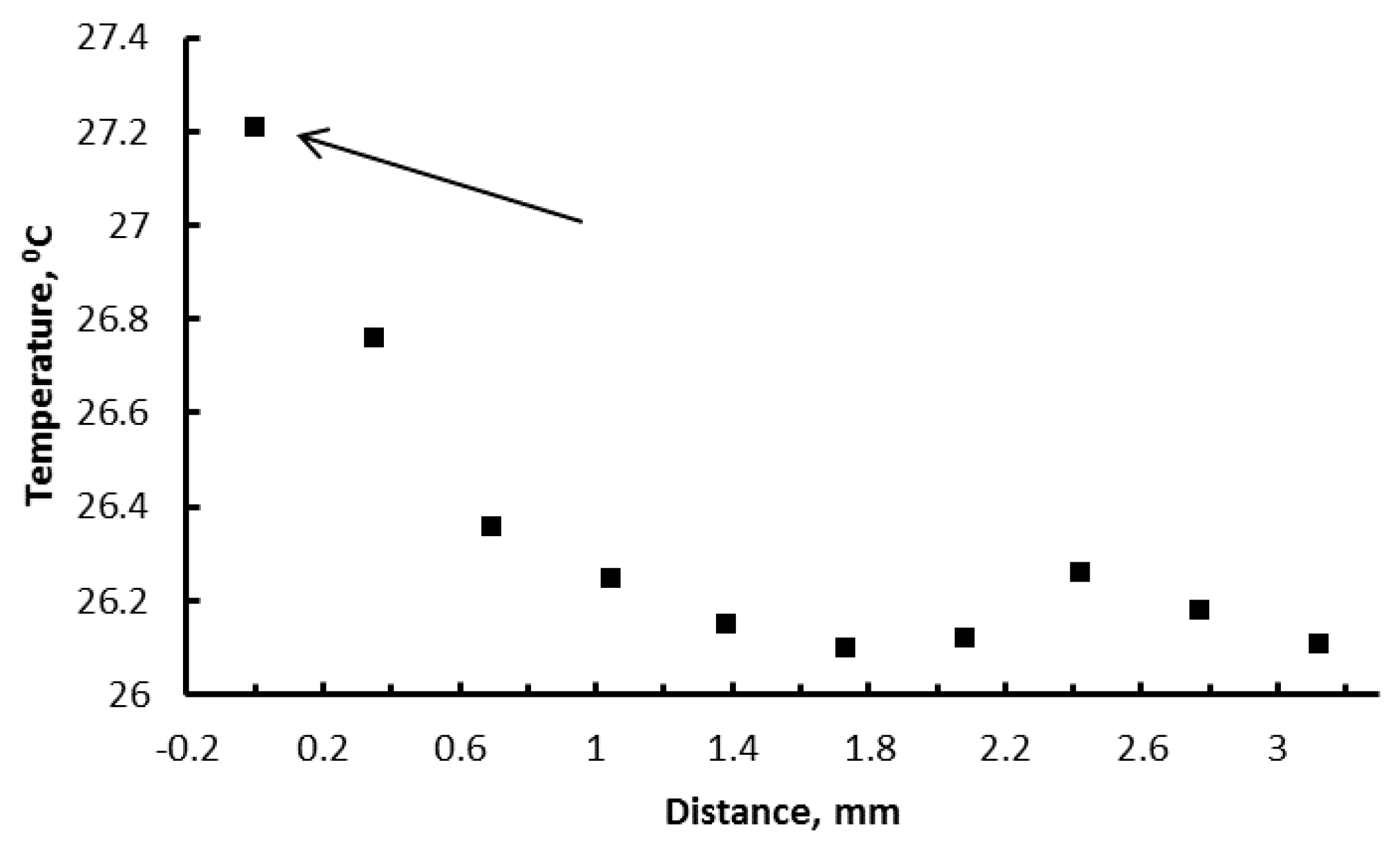
3. Estimation of the Entropy Generation Due to the Friction-Inspired Orientation of a Rotator
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gyarmati, I. Non-Equilibrium Thermodynamics (Field Theory and Variational Principles); Springer: Berlin, Germany, 1970. [Google Scholar]
- Bizarro, J.P.S. Entropy production in irreversible processes with friction. Phys. Rev. E 2008, 78, 021137. [Google Scholar] [CrossRef] [PubMed]
- Klamecki, B.E. Wear—An entropy production model. Wear 1980, 58, 325–330. [Google Scholar] [CrossRef]
- Singh, P.R.; Anoop, R.B.; Sundararajan, T.; Das, S.K. Entropy generation due to flow and heat transfer in nanofluid. Int. J. Heat Mass Transf. 2010, 53, 4757–4767. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Bhushan, B. Thermodynamics of surface degradation, self-organization and self-healing for biomimetic surfaces. Philos. Trans. R. Soc. A 2009, 367, 1607–1627. [Google Scholar] [CrossRef] [PubMed]
- Nosonovsky, M. Self-organization at the frictional interface for green tribology. Philos. Trans. R. Soc. A 2010, 368, 4755–4774. [Google Scholar] [CrossRef] [PubMed]
- Nosonovsky, M. Entropy in tribology: In the search for applications. Entropy 2010, 12, 1345–1390. [Google Scholar] [CrossRef]
- Fleurquin, P.; Fort, H.; Kornbluth, M.; Sandler, R.; Segall, M.; Zypman, F. Negentropy generation and fractality in the dry friction of polished surfaces. Entropy 2010, 12, 480–489. [Google Scholar] [CrossRef]
- Nosonovsky, M.; Bhushan, B. Surface self-organization: From wear to self-healing in biological and technical surfaces. Appl. Surf. Sci. 2010, 256, 3982–3987. [Google Scholar] [CrossRef]
- Khokhlov, A.R.; Semenov, A.N. Liquid-crystalline ordering in the solution of partially flexible macromolecules. Physica A 1982, 112, 605–614. [Google Scholar] [CrossRef]
- Van der Kooij, F.M.; Lekkerkerker, H.N.W. Liquid-crystalline phase behavior of a colloidal rod-plate mixture. Phys. Rev. Lett. 2000, 84, 781. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, D. Order through entropy. Nat. Mater. 2015, 14, 9–12. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, H. Classical Mechanics, 3rd ed.; Addison-Wesley Publishing: Reading, PA, USA, 2001. [Google Scholar]
- Strelkov, S.P. Mechanics; Mir Publishers: Moscow, Russia, 1978. [Google Scholar]
- Cohen, R.J. The tippe top revisited. Am. J. Phys. 1977, 45, 12–17. [Google Scholar] [CrossRef]
- Bou-Rabee, N.M.; Marsden, J.T.; Romero, L.A. Tippe top inversion as a dissipation-induced instability. SIAM J. Appl. Dyn. Syst. 2004, 3, 352–377. [Google Scholar] [CrossRef]
- Levi Civita, T.; Amaldi, U. Lezioni Di Meccanica Razionale; Liguori: Bologna, Italy, 1923. (In Italian) [Google Scholar]
- Stewart, R.E.; List, R. Gyrational motion of disks during free-fall. Phys. Fluids 1983, 26, 920–927. [Google Scholar] [CrossRef]
- Thomson, W. Floating magnets illustrating vortex-systems. Nature 1878, 18, 13–14. [Google Scholar] [CrossRef]
- Kelvin, W.T. Mathematical and Physical Papers; Cambridge University Press: Cambridge, UK, 1910; pp. 135–140. [Google Scholar]
- Kurakin, L.G.; Yudovich, V.I. The stability of stationary rotation of a regular vortex polygon. Chaos Interdiscip. J. Nonlinear Sci. 2002, 12, 574–595. [Google Scholar] [CrossRef] [PubMed]
- Tsytovich, V.N.; Sato, N.; Morfill, G.E. Note on the charging and spinning of dust particles in complex plasmas in a strong magnetic field. New J. Phys. 2003, 5, 43. [Google Scholar] [CrossRef]
- Llopis, I.; Pagonabarraga, I. Hydrodynamic regimes of active rotators at fluid interfaces. Eur. Phys. J. E 2008, 26, 103–113. [Google Scholar] [CrossRef] [PubMed]
- Fedorets, A.A.; Dombrovsky, L.A.; Smirnov, A.M. The use of infrared self-emission measurements to retrieve surface temperature of levitating water droplets. Infrared Phys. Technol. 2015, 69, 238–243. [Google Scholar] [CrossRef]
- Fedorets, A.A.; Dombrovsky, L.A. Generation of levitating droplet clusters above the locally heated water surface: A thermal analysis of modified installation. Int. J. Heat Mass Transf. 2017, 104, 1268–1274. [Google Scholar] [CrossRef]
- Lazaridis, T.; Karplus, M. Orientational correlations and entropy in liquid water. J. Chem. Phys. 1996, 105, 4294–4316. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Kittel, C. Elementary Statistical Physics; John Wiley & Sons: New York, NY, USA, 1960. [Google Scholar]
- Bormashenko, E. Entropy of relativistic mono-atomic gas and temperature relativistic transformation in thermodynamics. Entropy 2007, 9, 113–117. [Google Scholar] [CrossRef]
- Bormashenko, E.; Shkorbatov, A.; Gendelman, O. The Carnot engine based on the small thermodynamic system: Its efficiency and the ergodic hypothesis. Am. J. Phys. 2007, 75, 911–915. [Google Scholar] [CrossRef]
- Page, M.I.; Jencks, W.P. Entropic contributions to rate accelerations in enzymic and intramolecular reactions and the chelate effect. Proc. Natl. Acad. Sci. USA 1971, 68, 1678–1683. [Google Scholar] [CrossRef] [PubMed]
- Kenneth, P.; Murphy, R.P.; Xie, D.; Thompson, K.S.; Amzel, L.M.; Freire, E. Entropy in biological binding processes: Estimation of translational entropy loss. Proteins Struct. Funct. Bioinform. 1994, 18, 63–67. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Pergamon Press: Oxford, UK, 1987. [Google Scholar]
- Reichhardt, C.; Reichhardt, C.J.O. Nonequilibrium phases for driven particle systems with effective orientational degrees of freedom. Phys. Rev. E. 2009, 79, 061403. [Google Scholar] [CrossRef] [PubMed]
- Hasnain, J.; Jungblut, S.; Dellago, C. Dynamic phases of colloidal monolayers sliding on commensurate substrates. Soft Matter 2013, 9, 5867–5873. [Google Scholar] [CrossRef]
- Gendelman, O.; Pollack, Y.G.; Procaccia, I.; Sengupta, S.; Zylberg, J. What determines the static force chains in stressed granular media? Phys. Rev. Lett. 2016, 116, 078001. [Google Scholar] [CrossRef] [PubMed]
- Lyakhovsky, V.; Ben-Zion, Y. Damage–breakage rheology model and solid-granular transition near brittle instability. J. Mech. Phys. Solids 2014, 64, 184–197. [Google Scholar] [CrossRef]
- Kottas, G.S.; Clarke, L.I.; Horinek, D.; Michl, J. Artificial molecular rotors. Chem. Rev. 2005, 105, 1281–1376. [Google Scholar] [CrossRef] [PubMed]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazachkov, A.; Multanen, V.; Danchuk, V.; Frenkel, M.; Bormashenko, E. Friction, Free Axes of Rotation and Entropy. Entropy 2017, 19, 123. https://doi.org/10.3390/e19030123
Kazachkov A, Multanen V, Danchuk V, Frenkel M, Bormashenko E. Friction, Free Axes of Rotation and Entropy. Entropy. 2017; 19(3):123. https://doi.org/10.3390/e19030123
Chicago/Turabian StyleKazachkov, Alexander, Victor Multanen, Viktor Danchuk, Mark Frenkel, and Edward Bormashenko. 2017. "Friction, Free Axes of Rotation and Entropy" Entropy 19, no. 3: 123. https://doi.org/10.3390/e19030123
APA StyleKazachkov, A., Multanen, V., Danchuk, V., Frenkel, M., & Bormashenko, E. (2017). Friction, Free Axes of Rotation and Entropy. Entropy, 19(3), 123. https://doi.org/10.3390/e19030123







