Scaling Relations of Lognormal Type Growth Process with an Extremal Principle of Entropy
Abstract
:1. Introduction
2. The Method of Minimal Slope of Shannon Entropy
2.1. Shannon Entropy Property and Some Useful Relations
2.2. Sensitivity Analysis
3. Examples and Assessment
3.1. Method
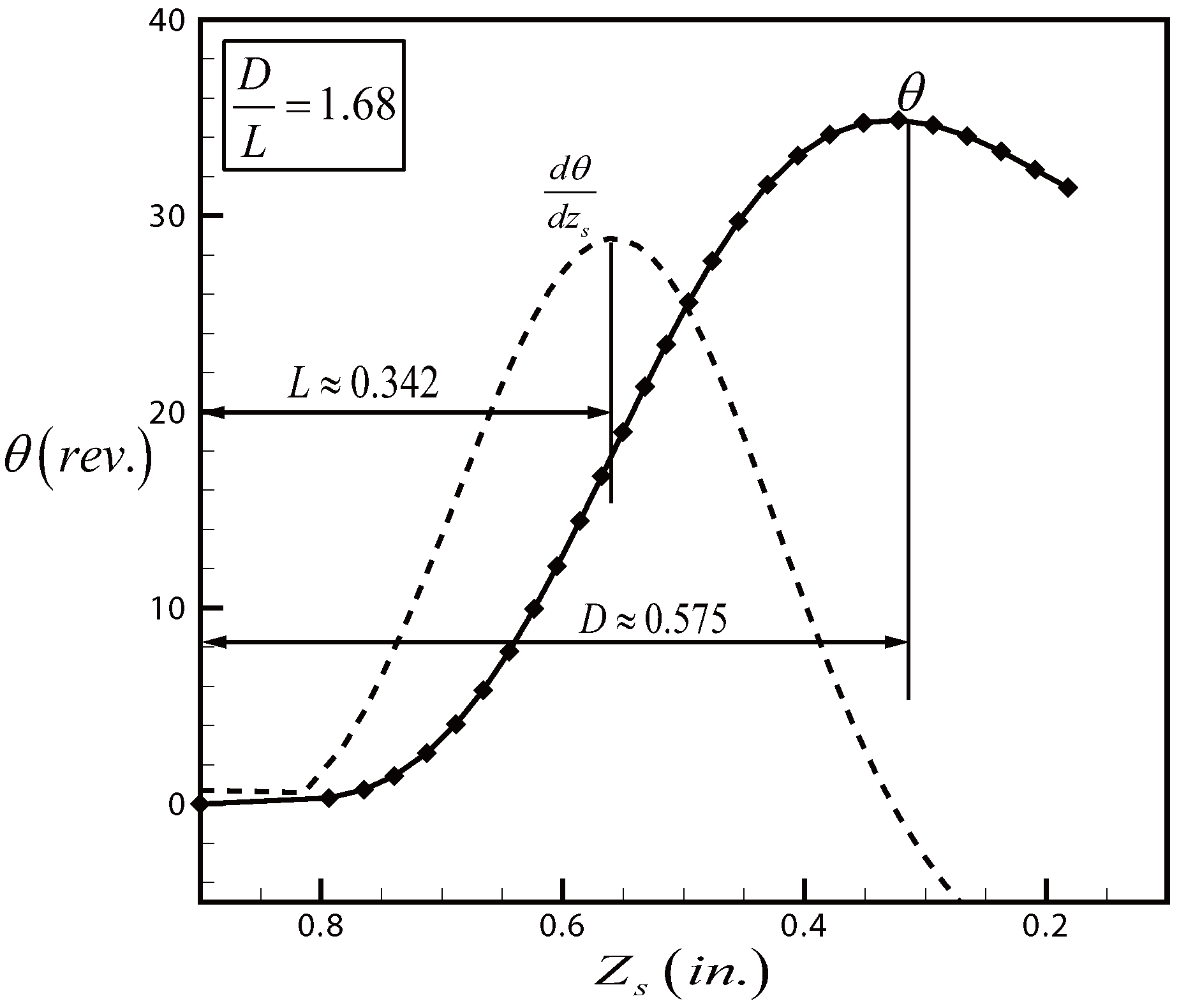
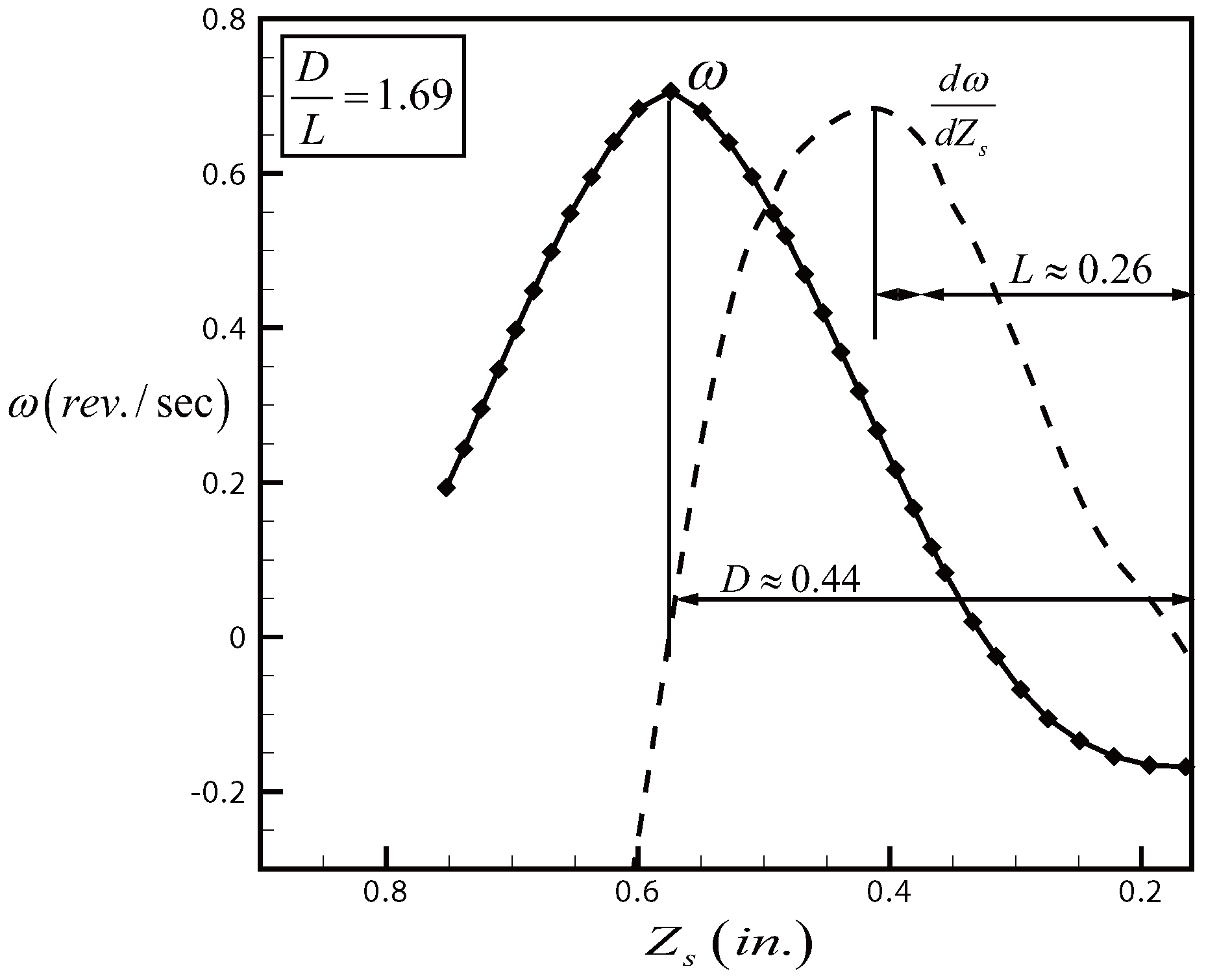
3.2. Bathtub Vortex
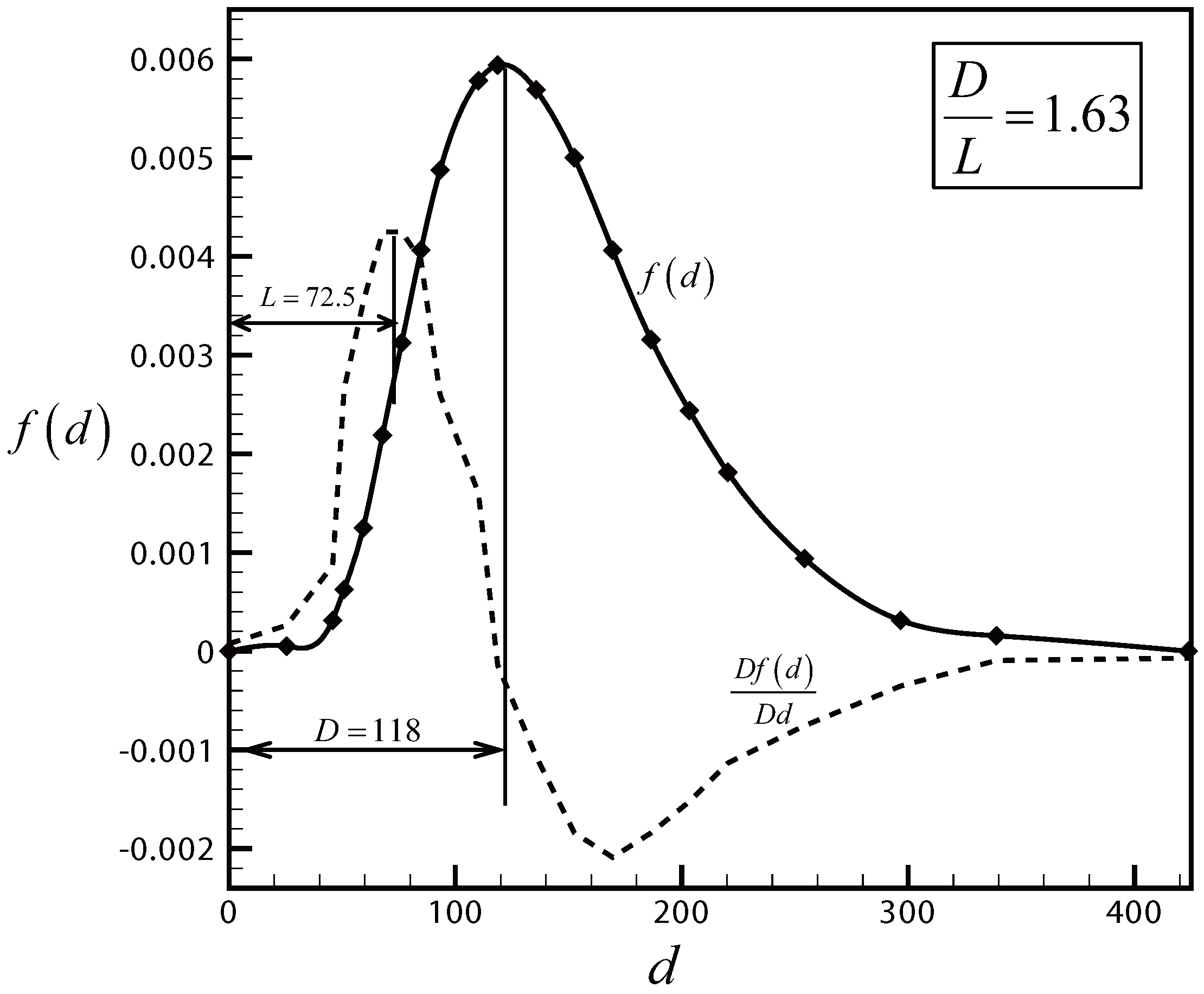
3.3. Further Data from Droplet Size Distribution for Droplet Splashing
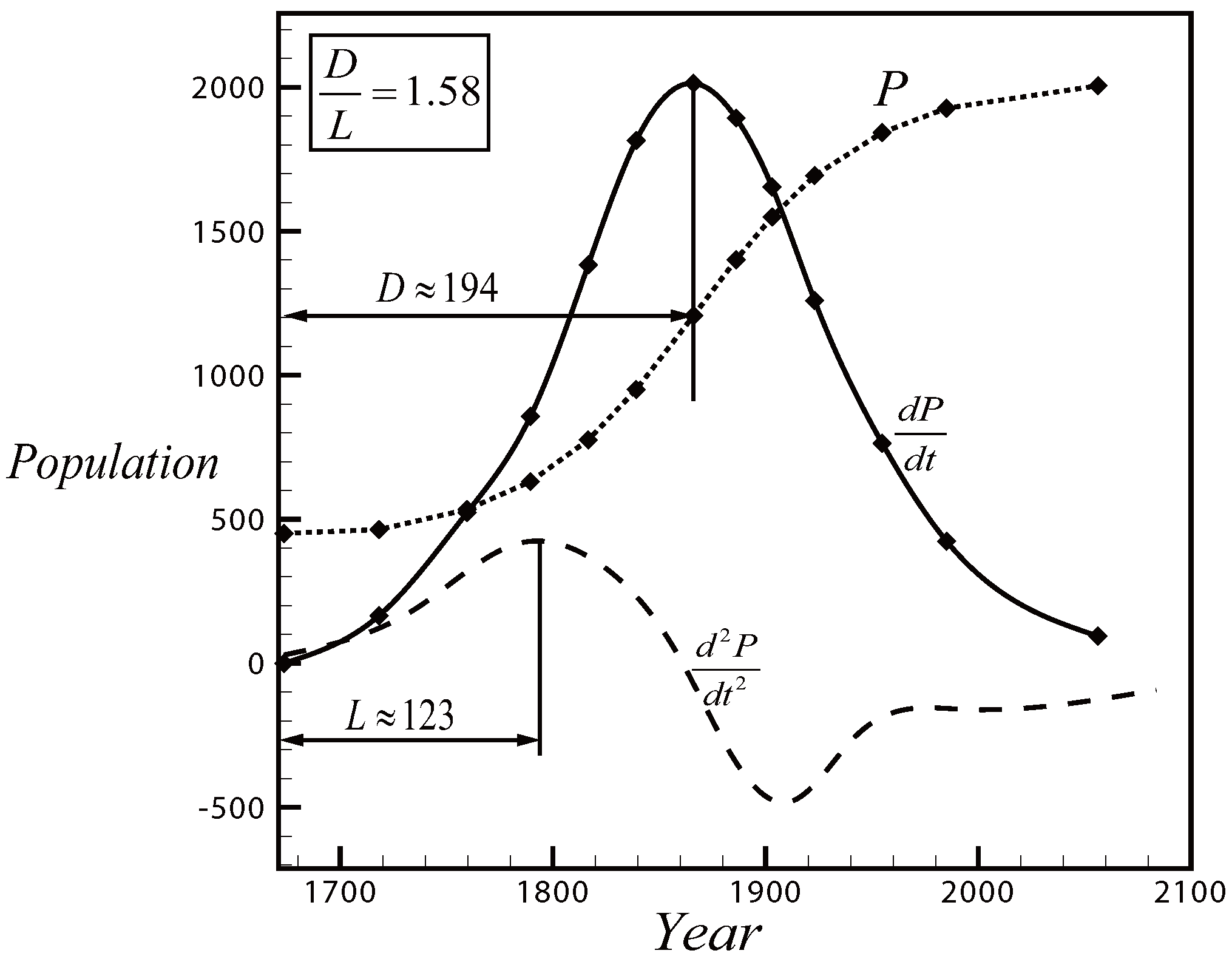
3.4. Population Growth
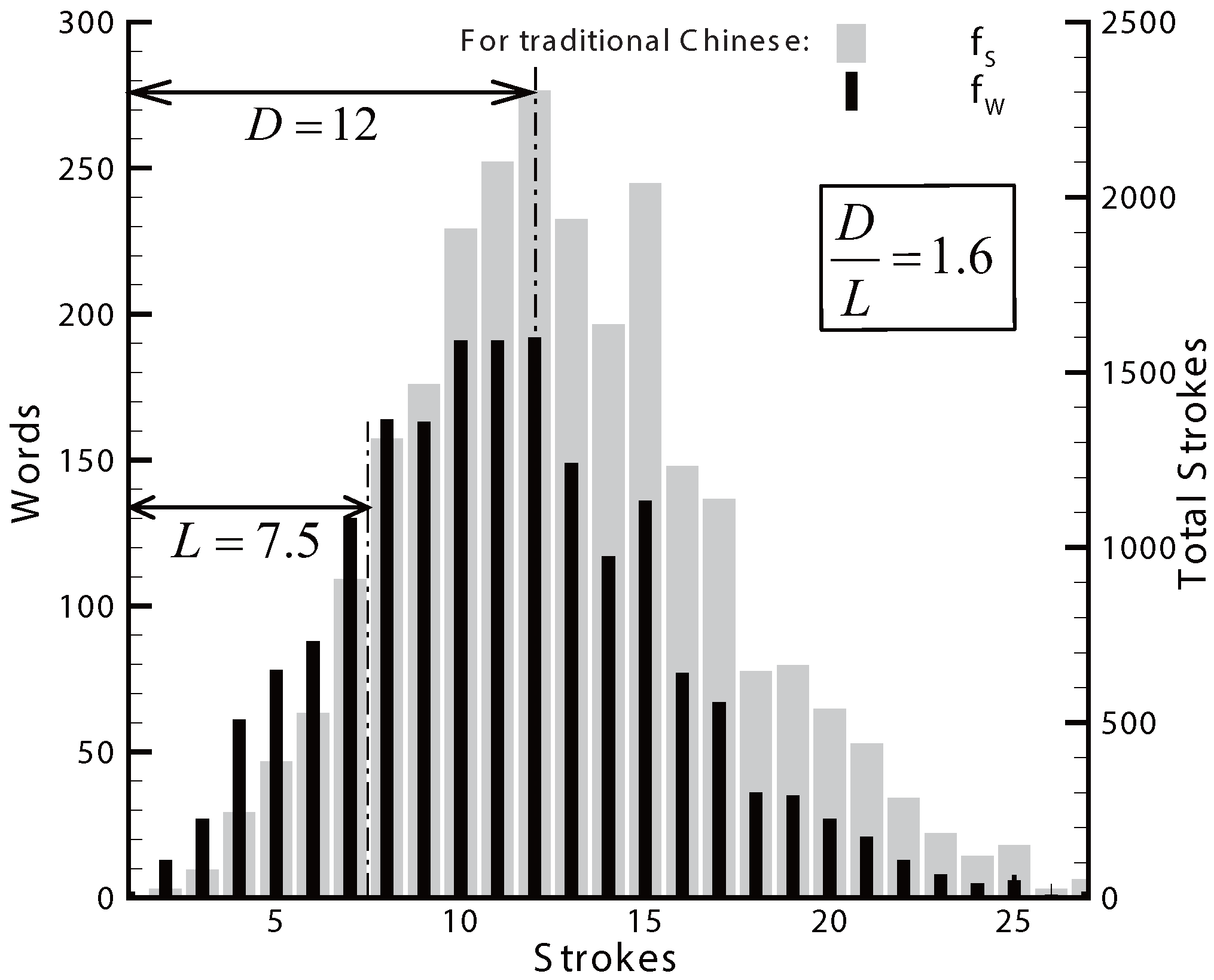
3.5. Stroke Distribution in Language
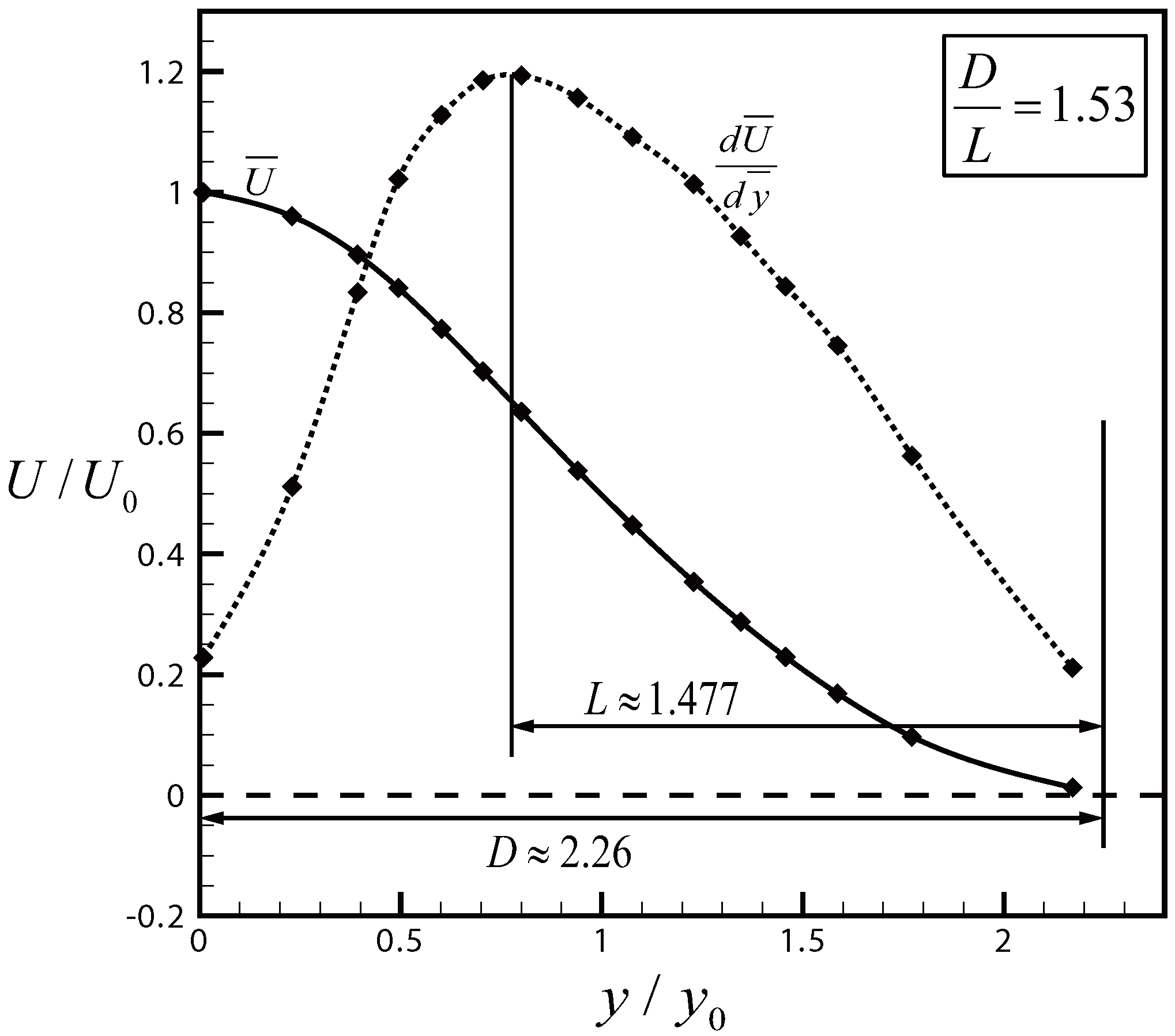
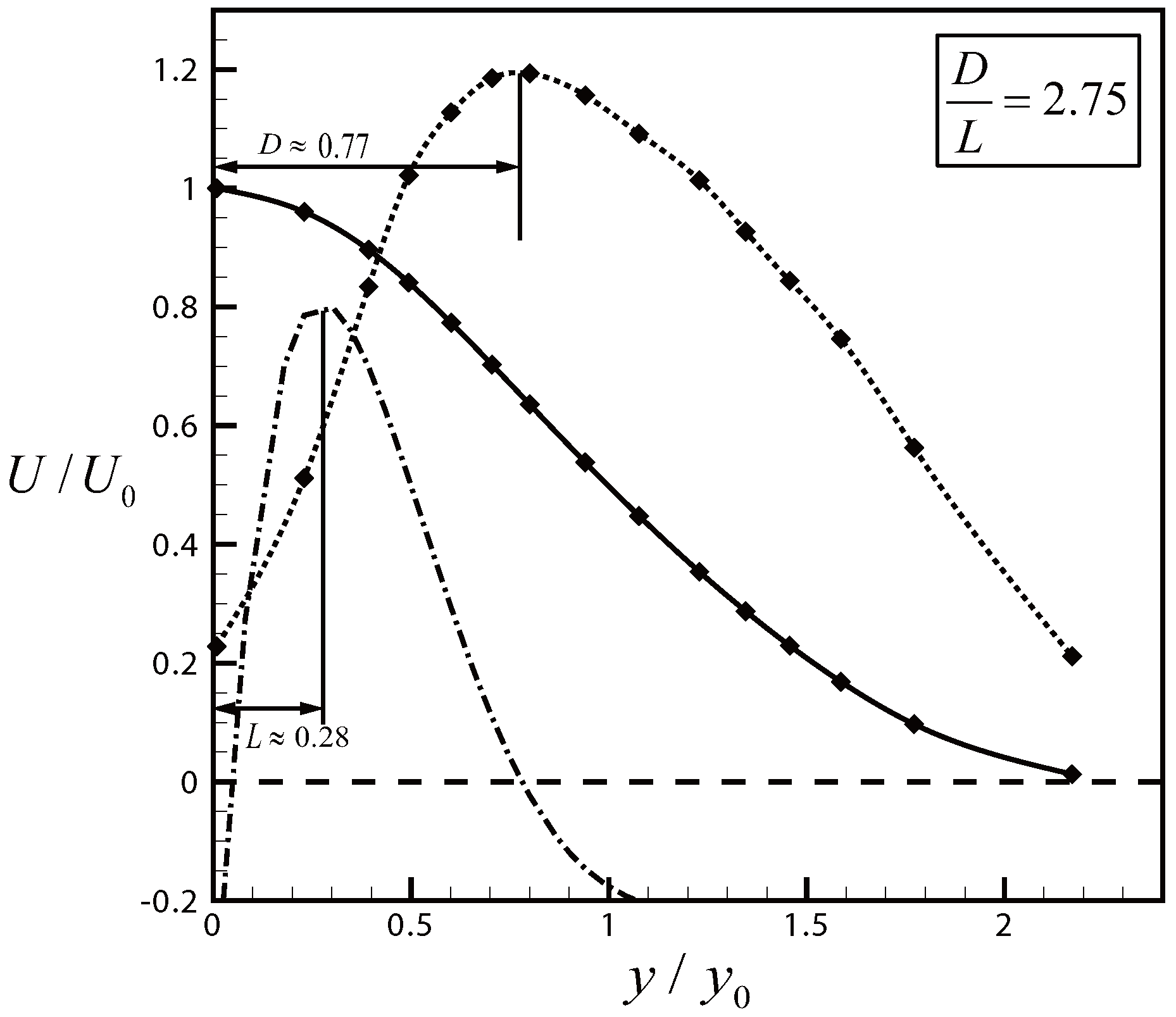
3.6. Possible Significance for Turbulent Flow
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Barry, B. Patterns of Human Growth, 2nd ed.; Cambridge Studies in Biological and Evolutionary Anthropology; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Sutton, J. Gibrat’s Legacy. J. Econ. Lit. 1997, 35, 40–59. [Google Scholar]
- Daley, D.J.; Gani, J. Epidemic Modeling: An Introduction; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Davidson, P.A. Turbulence—An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Stow, C.D.; Stainer, R.D. The physical products of a splashing water drop. J. Meteorol. Soc. Jpn. 1977, 55, 518–532. [Google Scholar]
- Hohler, S. A law of growth: the logistic curve and population control since world wall II. In Proceedings of the International Conference Technological and Aesthetic (Trans) formation of Society, Darmstadt, Germany, 12–14 October 2005.
- Gaddum, J.H. Log normal distributions. Nature 1945, 156, 463–466. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.; Abbt, M. Log-normal distributions across the sciences: Keys and clues. BioScience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Wu, Z.N. Prediction of the size distribution of secondary ejected droplets by crown splashing of droplets impinging on a solid wall. Probab. Eng. Mech. 2003, 18, 241–249. [Google Scholar] [CrossRef]
- Ziegler, H. An Introduction to Thermomechanics; North Holland Publishing: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Ziegler, H.; Wehrli, C. On a principle of maximal rate of entropy production. J. NonEquilib. Thermodyn. 1987, 12, 229–243. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. The restrictions of the maximum entropy production principle. Physica A 2014, 410, 17–21. [Google Scholar] [CrossRef]
- Ozawa, H.; Ohmura, A.; Lorenz, R.D.; Pujol, T. The second law of thermodynamics and the global climate system: A review of the maximum entropy production principle. Rev. Geophys. 2003, 41, 1018–1042. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Martyushev, L.M. The maximum entropy production principle: Two basic questions. Philos. Trans. R. Soc. B 2010, 365, 1333–1334. [Google Scholar] [CrossRef] [PubMed]
- Martyushev, L.M. Entropy and Entropy Production: Old Misconceptions and New Breakthroughs. Entropy 2013, 15, 1152–1170. [Google Scholar] [CrossRef]
- Ross, J.; Corlan, A.D.; Muler, S.C. Proposed Principle of Maximum Local Entropy Production. J. Phys. Chem. B 2012, 116, 7858–7865. [Google Scholar] [CrossRef] [PubMed]
- Moreira, A.L.N.; Moita, A.S.; Panao, M.R. Advances and challenges in explaining fuel sprayimpingement: How much of single droplet impact research is useful? Prog. Energy Combust. Sci. 2010, 36, 554–580. [Google Scholar] [CrossRef]
- Samenfink, W.; Elsaper, A.; Dullenkopf, K.; Wittig, S. Droplet interaction withshear-driven liquid films: Analysis of deposition and secondary droplet characteristics. Int. J. Heat Fluid Flow 1999, 20, 462–469. [Google Scholar] [CrossRef]
- Schmehl, R.; Rosskamp, H.; Willmann, M.; Wittig, S. CFD analysis of spray propagation and evaporation including wall film formation and spray/film interactions. Int. J. Heat Fluid Flow 1999, 20, 520–529. [Google Scholar] [CrossRef]
- Wang, W.B.; Wang, C.F.; Wu, Z.N.; Hu, R.F. Modelling the spreading rate of controlled communicable epidemics through an entropy-based thermodynamic model. Sci. China Phys. Mech. 2013, 56, 2143–2150. [Google Scholar] [CrossRef]
- Dumouchel, C. A new formulation of the Maximum Entropy formalism to model liquid spray drop-size distribution. Part. Part. Syst. Charact. 2006, 23, 469–479. [Google Scholar] [CrossRef]
- Lucia, U. Stationary open systems: A brief review on contemporary theories on irreversibility. Physica A 2013, 392, 1051–1062. [Google Scholar] [CrossRef]
- Luchko, Y. Entropy production rate of a one-dimensional alpha-fractional diffusion process. Axioms 2016, 5, 6. [Google Scholar] [CrossRef]
- Sibulkin, M. A note on the bathtub vortex. J. Fluid Mech. 1962, 14, 21–24. [Google Scholar] [CrossRef]
- Trefethen, L.M.; Bilger, R.W.; Fink, R.T.; Luxton, R.E.; Tanner, R.T. The bathtub vortex in the Southern Hemisphere. Nature 1965, 207, 1084–1085. [Google Scholar] [CrossRef]
- Chen, Y.C.; Huang, S.L.; Li, Z.Y.; Chang, C.C.; Chu, C.C. A bathtub vortex under the influence of a protruding cylinder in a rotating tank. J. Fluid Mech. 2013, 733, 134–157. [Google Scholar] [CrossRef]
- Raymond, P.; Author, T. The Biology of Population Growth; Alfred A. Knopf: New York, NY, USA, 1925. [Google Scholar]
- Statistics of strokes for the most used chinese characters. J. Lang. Innov. 1958, 3. (In Chinese) [CrossRef]
- Rodi, W. A review of experimental data of uniform density free turbulent boundary layers. In Studies in Convection I; Launder, B.E., Ed.; Academic Press: London, UK, 1975. [Google Scholar]
- Trinh, K.T. On the Karman constant. arxiv 2014. [Google Scholar]
- Landahl, M.T.; Mollo-Christensen, E. Turbulence and Random Processes in Fluid Mechanics; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Frisch, U. Turbulence: The Legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Polettini, M. Fact-Checking Ziegler’s Maximum Entropy Production Principle beyond the Linear Regime and towards Steady States. Entropy 2013, 15, 2570–2584. [Google Scholar] [CrossRef]

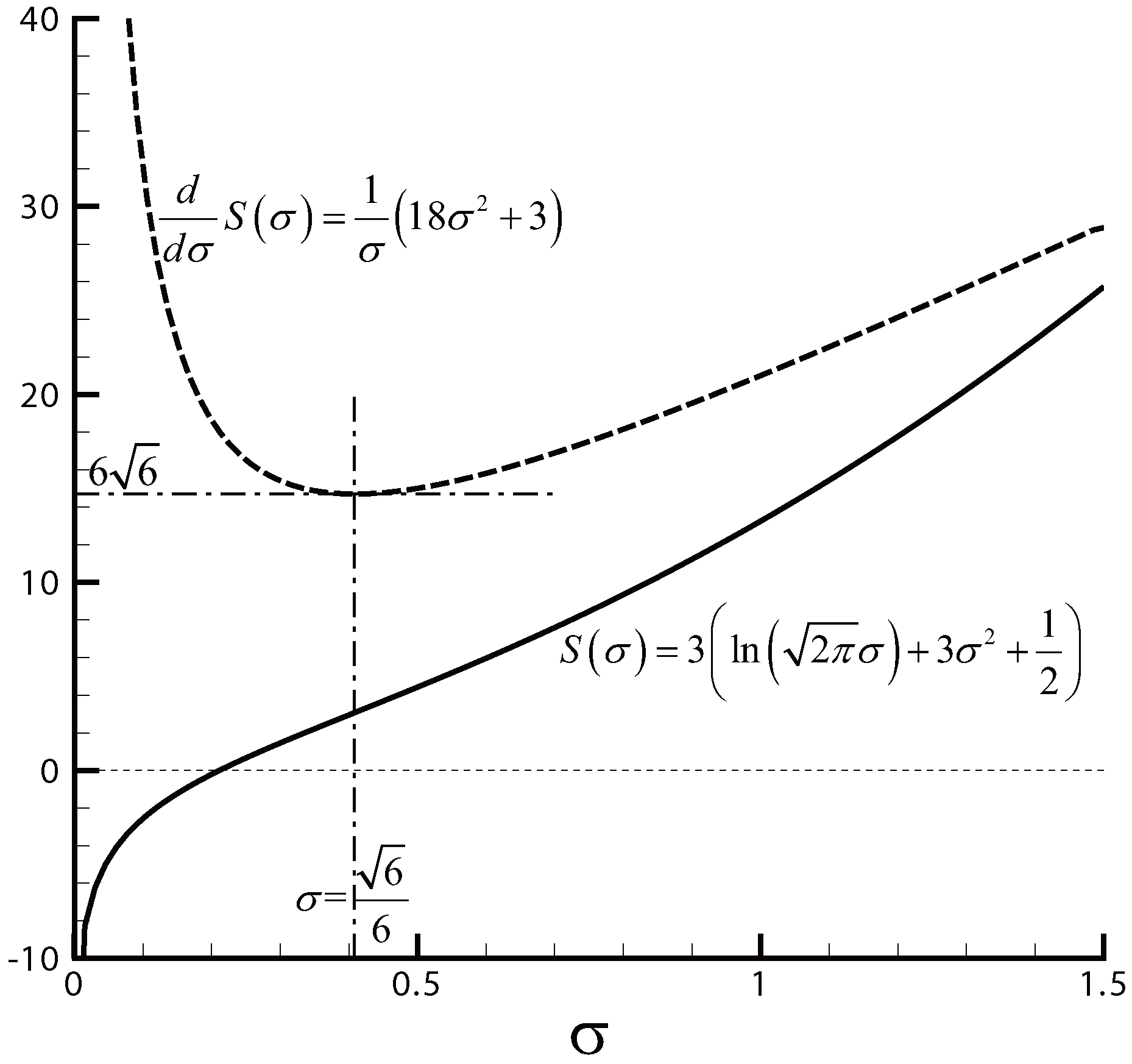

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.-N.; Li, J.; Bai, C.-Y. Scaling Relations of Lognormal Type Growth Process with an Extremal Principle of Entropy. Entropy 2017, 19, 56. https://doi.org/10.3390/e19020056
Wu Z-N, Li J, Bai C-Y. Scaling Relations of Lognormal Type Growth Process with an Extremal Principle of Entropy. Entropy. 2017; 19(2):56. https://doi.org/10.3390/e19020056
Chicago/Turabian StyleWu, Zi-Niu, Juan Li, and Chen-Yuan Bai. 2017. "Scaling Relations of Lognormal Type Growth Process with an Extremal Principle of Entropy" Entropy 19, no. 2: 56. https://doi.org/10.3390/e19020056
APA StyleWu, Z.-N., Li, J., & Bai, C.-Y. (2017). Scaling Relations of Lognormal Type Growth Process with an Extremal Principle of Entropy. Entropy, 19(2), 56. https://doi.org/10.3390/e19020056



