Abstract
We investigate herein the spin interaction during collisions between Kerr-(anti-)de Sitter black holes. The spin interaction potential depends on the relative rotation directions of the black holes, and this potential can be released as gravitational radiation upon collision. The energy of the radiation depends on the cosmological constant and corresponds to the spin interaction potential in the limit that one of the black holes has negligibly small mass and angular momentum. We then determine the approximate overall behaviors of the upper bounds on the radiation using thermodynamics. The results indicate that the spin interaction can consistently contribute to the radiation. In addition, the radiation depends on the stability of the black hole produced by the collision.
1. Introduction
As recently observed by the Laser Interferometer Gravitational–Wave Observatory, gravitational waves are generated by binary black hole mergers [1,2,3]. GW150914, which was the first detected gravitational wave [1], was particularly caused by black holes with masses more than 10-times that of the Sun. A third gravitational wave, GW170104, was recently detected. This wave was also created by a binary black hole system, in which the black holes had masses greater than 10-times that of the Sun [3]. The energy of the gravitational radiation was approximately three-times that of the Sun; hence, black hole collisions are an important source of gravitational radiation detectable in our universe. Another important observation is related to the value of the cosmological constant. Our universe is currently in a state of accelerated expansion; thus, the cosmological constant should be positive. According to several astrophysical observations [4,5,6], the value of the cosmological constant is definitely small. According to the theory of gravity proposed by Einstein, with a positive cosmological constant, the black hole solution is a de Sitter (dS) black hole. Therefore, dS black holes provide an appropriate description of the phenomena occurring in our universe. On the contrary, the curvature is negative in anti-de Sitter (AdS) spacetime. The AdS spacetime itself is different from that present in our universe, but plays an important role in gauge/gravity duality, which is called anti-de Sitter/conformal field theory (AdS/CFT) duality [7,8]. The theory of gravity in D-dimensional AdS spacetime corresponds to -dimensional CFT on the AdS boundary due to the AdS/CFT duality. Dual CFT can be described in terms of a finite temperature originating from an AdS black hole [9,10,11] because thermal properties, such as temperature, can appear at the boundary of AdS spacetime. An interesting correspondence with AdS spacetime can be found in condensed matter theory (CMT). This AdS/CMT correspondence, as well as the holographic superconductor given by the correspondence can be treated using charged AdS black holes [12,13,14].
The energy of a black hole can be extracted from a particle through the Penrose process [15,16]. In this process, the black hole only loses reducible energy, such as rotational and electric energy, but another type of energy, called irreducible mass, always increases even during the Penrose process [17,18]. This irreducible energy is distributed on the surface of the horizon [19] and is proportional to the square root of the area of the horizon. Like the square of the irreducible mass, the area of the horizon increases upon the addition of external particles or fields. In this regard, the area is similar to the entropy of the thermal system. Therefore, the Bekenstein–Hawking entropy of the black hole can be defined in terms of the area of the horizon [20,21]. In addition, the black hole can radiate energy via the quantum effect through which the Hawking temperature of the black hole can be made similar to that of a black body [22,23]. Hence, the black hole can be treated as a thermal system with temperature and entropy, and the laws of thermodynamics can also be defined in terms of its thermal properties.
The gravitational radiation released by a collision between black holes has an upper limit given by the laws of thermodynamics [24], but this upper limit is large in a collision between identical black holes. More precise results can be obtained by assuming that the black hole collision is a high-energy collision [25,26,27]. The collision between black holes and the waveform of the gravitational radiation can be identified using numerical relativity in the theory of gravity proposed by Einstein [28,29,30,31]. The waveform generated by a collision between black holes can currently be investigated under various initial conditions [32,33,34,35,36,37]. In addition, the gravitational radiation depends on the relative rotations of the black holes because of their spin interaction, which has an effect even if the rotation planes of the black holes are parallel. The interaction potential is negative for an anti-parallel arrangement of the rotation planes, but positive for a parallel one. Therefore, black holes in anti-parallel arrangements attract, and those in parallel arrangements repel [38,39,40,41]. The spin interaction can be modeled using a spinning particle moving in spacetime [42,43]. The spin interaction increases along with the mass and angular momentum of the black hole system. Hence, this interaction can be large enough to affect the stability of a binary black hole [44,45].
Black hole stability can be studied using various methods. The Kerr black holes present in the asymptotically flat case are stable against perturbations of massless fields [46,47], but the energy of these black holes can be extracted by external fields. A massive scalar field can extract energy from a Kerr black hole, causing the black hole to become unstable. Hence, Kerr black holes are unstable against massive scalar field perturbations [48,49,50,51,52]. In addition, for a Kerr black hole in a cavity, an external field can continuously take energy from the black hole. Consequently, the black hole can become unstable because of this process. This phenomenon is called superradiance [53]. Physically, a Kerr black hole in a cavity is similar to a Kerr-AdS black hole because the AdS boundary reflects the external field. Therefore, AdS black holes are unstable against superradiance [54,55,56,57]. For a positive cosmological constant, Kerr-dS black holes are also unstable against superradiance [58]. Non-perturbative instabilities can be tested using various black holes. One of these instabilities is fragmentation instability, which was first studied using Myers–Perry (MP) black holes [59]. Fragmentation instability suggests that rapidly-rotating black holes can be broken into multiple black holes because of centrifugal force. For MP black holes, the power of the gravitational force changes in higher dimensions. Thus, MP black holes are thermodynamically unstable during a rapid rotation, and their instability can be predicted. Furthermore, fragmentation instability can act as an indicator of the existence of other instabilities [60,61,62,63,64,65,66]. Fragmentation instability is also exhibited by Gauss–Bonnet and AdS black holes [67,68,69].
In this work, we investigated the effects of the cosmological constant on spin interaction and gravitational radiation by investigating the collisions between Kerr-(A)dS black holes. We used the generalized cosmological constant to determine the extent to which the spin interaction contributes to the gravitational radiation and how the released radiation is related to the instability of the final black hole. In addition, our results are consistent with previous investigations to the radiation of Kerr black holes [24,41] and the instability of AdS black holes [67]. The radiation and the interaction of black holes are generally too difficult and complex to formulate in terms of exact equations. We will obtain the upper bound of the radiation energy thermally allowed under the collision between black holes to avoid the complexity. Interestingly, when one of the black holes was assumed to be very small and slowly rotating, the upper bound of the radiation corresponds to the spin interaction obtained from the Mathisson–Papapetrou–Dixon (MPD) equations for the black hole and spinning particle system. Furthermore, this tendency given by the potential still maintains for the upper bounds of the radiation thermally allowed under the collision of two massive black holes. Thus, we can approximately expect that the interaction between the black holes works by a similar manner to that of the black hole and spinning particle system. We can then consistently and numerically generalize our analytical approach to massive cases using thermodynamics. The upper bounds of the radiation thermally allowed were obtained for the massive cases. We expanded our results to identify the overall behaviors of the upper bounds on the radiation with respect to the total angular momentum and mass of the black holes. In this analysis, the upper bounds on the radiation were importantly affected by the instability of the final black hole resulting from the collision.
An arbitrary cosmological constant was employed in this study. Hence, the initial settings were similar in each case. However, the positive case was different from the others because of the cosmological horizon of the spacetime. Hence, dS-Kerr black holes were used as generalizations of AdS-Kerr black holes, which was reasonable when the mass or cosmological constant was small. This point will be discussed in detail later.
The paper is organized as follows: Section 2 introduces the Kerr-(A)dS black holes and their thermodynamics; Section 3 presents the calculations of the energy of the gravitational radiation generated by a collision between the Kerr-(A)dS black holes and demonstrates that the energy exactly corresponds to the spin interaction potential of a system containing a black hole and a spinning particle; Section 4 provides the upper bounds of the radiation with respect to the total mass and angular momentum of the black holes; and in Section 5, we briefly summarize our results.
2. Kerr-(A)dS Black Hole
Kerr-(A)dS black holes are the solutions to the theory of gravity proposed by Einstein with a cosmological constant in a four-dimensional spacetime. The sign of the cosmological constant determines that of the spacetime curvature. We will discuss both the positive and negative cases. A black hole is a rotating solution given in terms of mass and spin parameters m and a,
where coefficient is defined as a positive value; hence, the bounds are Bogomol’nyi-Prasad- Sommerfield (BPS)-like for the AdS cases [70]. The mass and the angular momentum are presented as follows, respectively [71,72]:
The thermal properties of a black hole are defined at its horizons, and the definitions of these properties are consistent with all values of the cosmological constant. This study mainly focuses on the properties of the outer horizon . The Hawking temperature and the Bekenstein–Hawking entropy are given as:
The angular velocity is at the outer horizon, but includes the rotation of the coordinates, as shown by in Equation (1), where the rotation still exists [72,73]. The referential angular velocity at can be determined to remove this effect. Hence, the angular velocity of the black hole is [72]:
which is consistent with an arbitrary cosmological constant. The first law of thermodynamics at the outer horizon is:
In dS spacetime, the cosmological horizon is outside the outer horizon. Compared with the AdS and flat cases, the observable region is confined in the dS case. The first law of thermodynamics is defined the same way at the cosmological horizon as it is at the outer horizon, hence:
where the temperature , entropy and angular velocity on the cosmological horizon are:
The absolute values in the temperature expression are necessary to make the temperature positive definite because the surface gravity of the cosmological horizon is negative.
3. Spin Interaction and Gravitational Radiation
We will show herein that the energy of the spin interaction between two Kerr-(A)dS black holes contributes to the gravitational radiation released upon their collision. We will present the thermodynamic calculations of the energy of the radiation released when one of the black holes has a tiny mass and a small angular momentum, enabling it to be considered as a spinning particle and higher-multipole moments to be ignored. In this case, the energy of the radiation exactly corresponds to the spin interaction potential from the Mathisson-Papapetrou-Dixon (MPD) equation for a spinning particle near a black hole. In this analysis, the effects of the cosmological constant, such as the AdS boundary and cosmological horizon, were assumed to be governed by the more massive of the two black holes.
3.1. Gravitational Radiation Released by a Collision between Two Kerr-(A)dS Black Holes
This section addresses the energy resulting from the gravitational radiation released because of a collision between two Kerr-(A)dS black holes. One of the black holes is assumed to be small; hence, the radiation energy will match the spin interaction potential in a system consisting of a spinning particle and a black hole. We determine the energy of this radiation by assuming that the first and second Kerr-(A)dS black holes with masses and stay far away from each other and are separated in the direction of their rotating axes such that their rotating planes are parallel [41]. Slowly moving because of gravitational attraction, the two black holes then undergo a head-on collision and merge into one final black hole, which has mass [24]. The difference between the total masses in the initial and final states can be defined as the gravitational radiation, ,
where only the radiation swept the first time is included, and the radiation energy will equal the spin interaction energy. Hence, the reflections at the AdS boundary will not be considered. The radiation may be released in arbitrary directions rather than a specific direction; hence, most of the angular momentum can remain in the final state. In addition, the angular momentum is assumed to be conserved as:
where and are the angular momenta of the first and second initial black holes, respectively; and is the angular momentum of the final one. Two rotation planes of the black holes are parallel or anti-parallel to the direction of the approach. The Bekenstein–Hawking entropy of the final black hole should be greater than the sum of those of the first and second initial black holes, and , respectively, because the head-on collision between the initial black holes occurs due to gravitational attraction. Hence,
The radiation energy depends on the initial conditions of the black holes. Using the given initial conditions of the black holes, which are and for the first one and and for the second one, the upper bound on the radiation and the lower bound on the mass parameter of the final black hole with the spin parameter can specifically be obtained. The first black hole is fixed, and the second black hole is assumed to have mass and angular momentum smaller than those of the first one to describe the radiation in terms of the parameters of the second black hole. Therefore, and . The maximum value of the radiation in Equation (8) can then be calculated using the equality of Equation (10) by imposing Equation (9). By combining the partial derivatives of Equations (8)–(10), the change of the maximum radiation can be expressed in terms of the partial derivative with respect to the angular momentum of the second black hole, thereby making the following leading term:
With the integrated Equation (11) with respect to , the maximum value of the radiation can be obtained by applying the negative sign to compare it with the spin interaction potential and rewritten in terms of the cosmological constant using in Equation (1). Then, approximately:
which will be shown to be coincident to the spin interaction potential between the black holes. In the small-mass limit, the expected upper limit of the radiation does not include the mass of the second black hole, but includes the energy of the spin interaction between the black holes. The overall sign of the potential for both black holes depends only on the rotation direction. The potential in a parallel arrangement is positive; hence, the black holes repel each other. In contrast, an anti-parallel arrangement produces a negative potential; thus, the two black holes will be attracted by the spin interaction. At this point in the analysis, the potential is an effective value, but will exactly correspond to the potential obtained from the MPD equation for a spinning particle near the black hole. This correspondence will be explored in the section that follows.
One might question the feasibility of the initial state in the case of a dS-Kerr black hole. The second black hole cannot remain far away from the first one because of the cosmological constant, even in the small-mass limit. However, the procedure from Equations (8)–(12) is still reliable in the small-mass limit, assuming that the small second black hole is added to the pole of the first black hole. The potential will then be acceptable in the case of a dS-Kerr black hole and will be consistent with the results of the section that follows.
3.2. Spin Interaction Potential from the MPD Equation
The second black hole is small compared with the first one and, thus, can be treated as a spinning particle. This section demonstrates that the spin interaction potential in Equation (12) exactly corresponds to that of a spinning particle near a Kerr-(A)dS black hole. The motions of the spinning particle are governed by the MPD equation [74,75,76] with linear momentum and velocity such that:
where and s are the spin tensor and the proper time, respectively, in the spacetime of the Riemann curvature tensor . The trajectory of the spinning particle can be properly described by applying the supplementary condition [77] as:
The mass and the spin magnitude S of the spinning particle can be expressed in terms of the spin tensor and the linear momentum, respectively:
The spinning particle is now presumed to be the second black hole in Section 3.1. Thus, the spin monopole of the particle is only considered in the MPD equations. The momentum of the particle is proportional to the velocity.
The direction of the head-on collision is pole-to-pole. Therefore, the spinning particle also slowly comes toward the north pole of the first black hole in the initial conditions, and its spinning plane is parallel to that of the black hole. The normalized velocity and spin vectors are presented as follows assuming that the particle is non-relativistic:
where the components of the metric are those of a Kerr-AdS black hole. The kinetic energy of the spinning particle is not a conserved quantity because the energy now includes the spin interaction potential. Furthermore, the potential can change as the particle moves because the spin interaction potential depends on the spin of the particle. The conserved quantities in the Killing vector are [76]:
where the particle energy corresponds to the Killing vector . Then,
where the spin interaction potential can be directly obtained. The first term in the energy expression in Equation (19) refers to the kinetic energy corresponding to the linear momentum, while the second term represents the spin interaction potential. The radiation will be contributed by the spin interaction potential at the outer horizon; thus, the potential should be obtained at the outer horizon of the first black hole. Then,
in which the second term is caused by the spacetime rotation. This term can be removed when considering the referential angular velocity [72]. In the particle energy, the effect of this velocity appears as an additional energy proportional to the angular momentum [78]. The normalized spin interaction potential is given as follows:
which is exactly that yielded by Equation (12) with . Therefore, the spin interaction potential in the aforementioned limit is released as gravitational radiation. In addition, the parallel arrangement corresponds to the repulsion of the black holes, and the anti-parallel arrangement corresponds to the attraction. Therefore, the energy of the radiation is expected to be greater in the anti-parallel arrangement than in the parallel one. We confirm this behavior by presenting the results of the thermodynamic approach in Section 3.1 without applying a limit to the second black hole.
4. Upper Bound on the Radiation under the Collision
The results from Section 3.1 are expanded herein to illustrate the approximate dependences of the radiation on the mass and the angular momentum using a thermodynamic analysis with numerical approaches. The effects of the cosmological constant become greater than before if the mass and the angular momentum are large. Therefore, these effects cannot be ignored under the collisions. The analysis in this section is only applicable when the black hole mass or the cosmological constant is small. In this section, the upper bounds on the radiation are given with respect to the mass and the angular momentum under the dimensionless coordinates scaled by , in which is , 0 and for the AdS, flat and dS cases in Equation (22), respectively. Then,
where the tildes were omitted for simplicity. In the coordinates, the dependence on the cosmological constant can be removed by scaling. The upper bounds on the radiation can be obtained approximately by applying a thermodynamic approach without including the effect of the cosmological constant, such as the effect of the (A)dS boundary. However, the radiation trends can be determined approximately using this approach. In addition, the interesting behaviors between the gravitational radiation and the black hole stability can be investigated by applying this method.
The general procedure and the initial condition are similar to those in Equations (8)–(10). For a given cosmological constant , two black holes, and stay far from each other; thus, their interactions can be ignored in the initial state. Merged from the collision of the black holes, the final black hole, , will then have a larger entropy than the sum of the initial black holes because of the second law of thermodynamics after a sufficiently large time flowed. From Equation (10),
in which a possible mass range of the final black hole can be determined because of the inequality. Saturated to the inequality, the mass of the final black hole is the minimum mass. The black hole collision includes a non-equilibrium process. We have assumed the initial state that two black holes have a distance in a small cosmological constant, such that their interactions are negligible, to restrict the effect of the non-equilibrium process. After the black hole collision, we should then observe the black hole passing a sufficiently large time. The entropy can be expected to increase even if the middle of the collision is non-equilibrium because the initial and final states are approximately stable. Furthermore, the process from the initial to the final state is an irreversible process; hence, the entropy can increase. We impose the conservation of the angular momentum in Equation (9) to obtain the spin parameter of the final black hole . We can then find the minimum mass of the final black hole satisfying Equation (23). However, finding an analytical formula is quite difficult because the entropy of the rotating black hole depends on the spin parameter and the cosmological constant. The upper bound of the radiation is obtained from Equation (8) using the numerical method.
where mass is the minimum mass obtained from the initial condition. For example, as regards the collision of the non-rotating black holes, , the increase of the entropy is simply written as follows:
from which the minimum mass of the final black hole is at . The energy of the radiation is maximized at the minimum mass; hence, in terms of and ,
However, for , the minimum mass of the final mass should be obtained by a numerical method because of the non-trivial dependency on the spin parameters of the masses of the black holes. We ignore the entropy and the angular momentum of the radiation because the actual radiation is very small compared with the total mass of the system. Furthermore, in considering the entropy and the angular momentum of the radiation, this does not change its overall behaviors. The general behavior of the radiation remains nearly the same regardless of the cosmological constant, as is evident in Figure 1. As shown by Equation (11), the derivative of the bound on the radiation with respect to the angular momentum of the second black hole is negative.
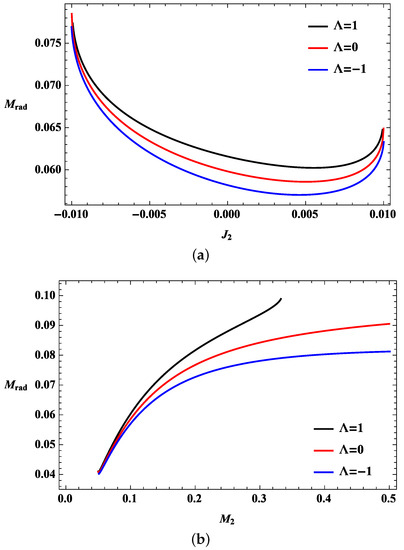
Figure 1.
Bounds on the radiation for the collisions of two KdS black holes. (a) Bounds on the radiation with respect to the angular momentum of the second black hole for different values of the cosmological constant. The black holes are , and ; (b) Bounds on the radiation with respect to the mass of the second black hole for different values of the cosmological constant. The black holes are , and .
Therefore, the bounds on the radiation are greater if the black hole arrangement is anti-parallel rather than parallel for any value of the cosmological constant in Figure 1a. The radiation in the anti-parallel arrangement includes the contribution from the negative spin interaction potential between the black holes. Consequently, the minimum radiation energy appears in the parallel arrangement, which has a positive potential. The radiation is greater when the cosmological constant is positive instead of negative (Figure 1a). The bounds on the radiation increase along with the mass of the second black hole (Figure 1b).
The minimum black hole masses for a fixed angular momentum are given by the extremal conditions because the angular momentum conservation causes the final black hole conditions to be saturated in the extremal conditions. Thus, the final state in the case of the masses smaller than the minimum mass of is not black holes. The radiation bounds correspond to the maximum of . Consequently, the bounds start at finite masses in Figure 1b, which become saturated to reach the extremal conditions. The radiation bounds are then proportional to the mass of the second black hole, but the dS and AdS cases have upper radiation limits because of the effects of the cosmological constant. The radiation in the dS case is limited by the cosmological horizon, while that in the AdS case is limited by the entropy preference.
The overall behaviors are similar to those for the Kerr black holes when the cosmological constant is positive. The parameter range, in which a Kerr-dS black hole can exist, is very limited because of the extremal conditions and the cosmological horizon causing the radiation to exhibit a narrow angular momentum range (Figure 2a).
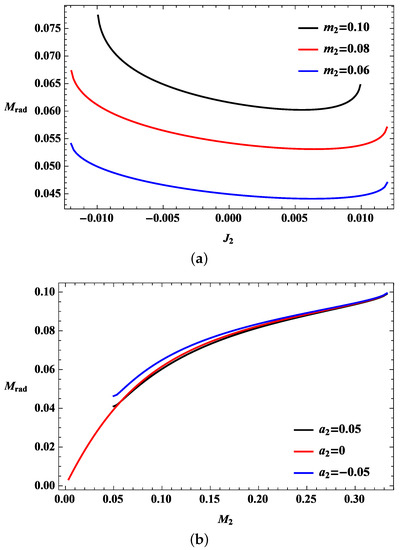
Figure 2.
Bounds on the radiation for the collisions of two KdS black holes. (a) Bounds on the radiation with respect to the angular momentum of the second black hole having different masses . The black holes are and in the positive cosmological constant; (b) Bounds on the radiation with respect to the mass of the second black hole having different spin parameters . The black holes are and in the positive cosmological constant.
Figure 2a,b shows that the radiation bounds normally increase according to the mass of the second black hole, and more radiation can be released by near-extremal black holes. A Kerr-dS black hole with a spin parameter of zero can have an outer horizon with a small mass; hence, radiation can be observed when the second black hole is small. In addition, the minimum masses of the second black hole enable the radiation to be released for the given spin parameters because of the extremal conditions in Figure 2b. The minimum mass is then started at the finite value. The second black hole in the case of does not contribute to the angular momentum; hence, it starts at the point.
The bounds for the Kerr-AdS black hole collisions are different from those of the flat or dS black holes because the cosmological constant is negative. With respect to the angular momentum of the second black hole, the radiation is greater in an anti-parallel arrangement than in a parallel one (Figure 3a). The radiation for the second small black hole increases along with the mass of the second black hole (Figure 3b). However, the radiation can decrease as the mass of the second black hole increases when the mass of the second black hole is large (Figure 4a). The radiation diminishes to zero as the mass of the second black hole continues to increase (Figure 4b). Approximately zero radiation can be predicted using an analytical method. To demonstrate this behavior, suppose that two large Schwarzschild-AdS black holes with the same mass collide. In this situation, the outer horizon of the initial black hole is , and that of the final black hole is . The difference between the masses is within the limit of :
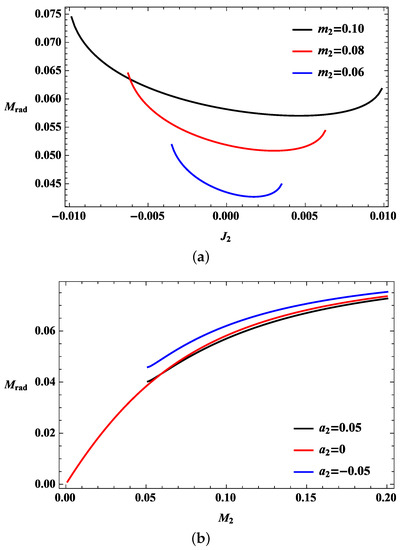
Figure 3.
Bounds on the radiation for the collisions of two Kerr-AdS black holes. (a) Bounds on the radiation with respect to the angular momentum of the second black hole having different masses . The black holes are and with the negative cosmological constant; (b) Bounds on the radiation with respect to the mass of the second black hole having different spin parameters . The black holes are and with the negative cosmological constant.
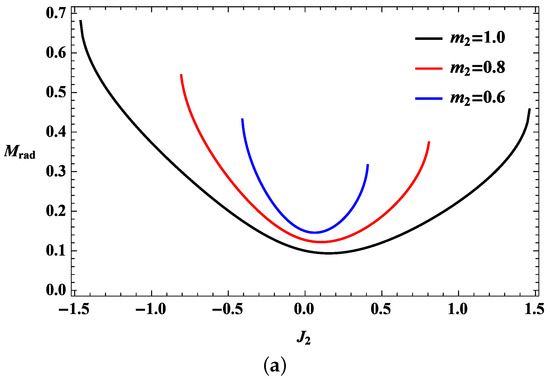
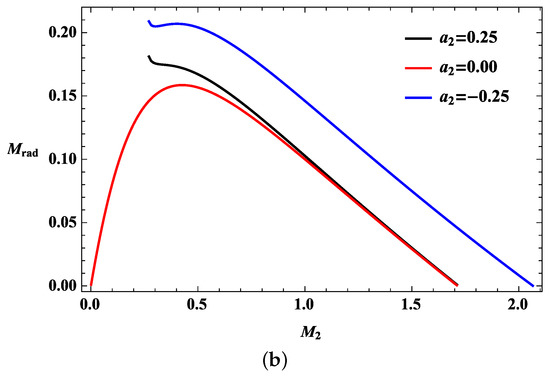
Figure 4.
Bounds on the radiation for the collisions of two Kerr-AdS black holes. (a) Bounds on the radiation with respect to the angular momentum of the second black hole. The black holes are and with the negative cosmological constant; (b) Bounds on the radiation with respect to the mass of the second black hole. The black holes are and with the negative cosmological constant.
Therefore, no radiation is released if the masses of the colliding black holes are sufficiently large. This result was obtained without considering the AdS effect on the initial conditions. Although a more detailed analysis may be required, zero radiation may originate from the instability of the Kerr-AdS black holes, which can increase according to the angular momentum. The fragmentation instability based on thermodynamics particularly yields results similar to those of a reversed collision process [67,79,80]. This characteristic implies that no more energy can be released as radiation because too much energy is needed to synthesize the unstable final state; hence, the initial state is thermodynamically preferable to the final state [81]. The instability of the black hole may affect the radiation released from the Kerr-AdS black hole collisions. However, as noted, the AdS effect from the spacetime boundary becomes important when the black holes are massive. Therefore, the preference for the initial state requires a more detailed analysis.
5. Summary
This study investigated the spin interaction and its relation to radiation in Kerr-(A)dS black hole collisions. Using a thermodynamic approach, we obtained the energy of the gravitational radiation emitted because of a collision between two black holes by assuming one to have very small mass and angular momentum. The energy of the radiation emitted in this limit exactly corresponds to the spin interaction potential between the black hole and a spinning particle. Therefore, the spin interaction energy can be released by the collision. Depending on the cosmological constant, the spin interaction causes the attraction if the black holes are in an anti-parallel arrangement and repulsion if they are in a parallel one. We simply expanded the thermodynamic approach to arbitrary masses and angular momenta to discover the overall characteristics of the radiation and obtain the upper bounds on the radiation instead of deriving the exact expressions. In most cases, the radiation is greater in the anti-parallel arrangement than in the parallel one and may be proportional to the masses of the initial black holes because of the spin interaction. The collisions between the Kerr-dS black holes were similar to those between the Kerr black holes, and a higher-energy radiation was expected for a given mass in these cases than in the flat cases. However, the radiation released because of a collision between the Kerr-AdS black holes was closely related to the instability of the black hole in the final state. An increased instability can decrease the energy of the radiation emitted from the collision because more energy is needed to synthesize an unstable final state than a stable one.
Acknowledgments
Bogeun Gwak was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (NRF-2015R1C1A1A02037523) and the faculty research fund of Sejong University in 2016. Daeho Ro was supported by the Korea Ministry of Education, Science and Technology, Gyeongsangbuk-Do and Pohang City.
Conflicts of Interest
The authors declare no conflict of interest.
References
- LIGO Scientific Collaboration; Virgo Collaboration; Abbott, B. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- LIGO Scientific Collaboration; Virgo Collaboration; Abbott, B. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef] [PubMed]
- LIGO Scientific Collaboration; Virgo Collaboration; Abbott, B. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef] [PubMed]
- Supernova Cosmology Project Collaboration; Perlmutter, S.; Gabi, S.; Goldhaber, G.; Groom, D.E.; Hook, I.M.; Kim, A.G.; Kim, M.Y.; Lee, J.C.; Pennypacker, C.R.; et al. Measurements of the cosmological parameters Omega and Lambda from the first 7 supernovae at z>=0.35. Astrophys. J. 1997, 483, 565. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological imprint of an energy component with general equation of state. Phys. Rev. Lett. 1998, 80, 1582–1585. [Google Scholar] [CrossRef]
- Supernova Search Team Collaboration; Garnavich, P.M.; Jha, S.; Challis, P.; Clocchiatti, A.; Diercks, A.; Filippenko, A.V.; Gilliland, R.L.; Hogan, C.J.; Kirshner, R.P.; et al. Supernova limits on the cosmic equation of state. Astrophys. J. 1998, 509, 74–79. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space, thermal phase transition, and confinement in gauge theories. Adv. Theor. Math. Phys. 1998, 2, 505–532. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 1999, 38, 1113–1133. [Google Scholar] [CrossRef]
- Gubser, S.S.; Klebanov, I.R.; Polyakov, A.M. Gauge theory correlators from noncritical string theory. Phys. Lett. 1998, B428, 105–114. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Aharony, O.; Gubser, S.S.; Maldacena, J.M.; Ooguri, H.; Oz, Y. Large N field theories, string theory and gravity. Phys. Rep. 2000, 323, 183–386. [Google Scholar] [CrossRef]
- Chaturvedi, P.; Sengupta, G. Rotating BTZ Black Holes and One Dimensional Holographic Superconductors. Phys. Rev. 2014, D90, 046002. [Google Scholar] [CrossRef]
- Haehl, F.M.; Loganayagam, R.; Rangamani, M. Effective actions for anomalous hydrodynamics. JHEP 2014, 3, 34. [Google Scholar] [CrossRef]
- Chang, H.-C.; Fujita, M.; Kaminski, M. From Maxwell-Chern-Simons theory in AdS3 towards hydrodynamics in 1 + 1 dimensions. JHEP 2014, 10, 118. [Google Scholar] [CrossRef]
- Bardeen, J.M. Kerr Metric Black Holes. Nature 1970, 226, 64–65. [Google Scholar] [CrossRef] [PubMed]
- Penrose, R.; Floyd, R.M. Extraction of rotational energy from a black hole. Nature 1971, 229, 177–179. [Google Scholar] [CrossRef]
- Christodoulou, D. Reversible and irreversible transforations in black hole physics. Phys. Rev. Lett. 1970, 25, 1596–1597. [Google Scholar] [CrossRef]
- Christodoulou, D.; Ruffini, R. Reversible transformations of a charged black hole. Phys. Rev. 1971, D4, 3552–3555. [Google Scholar] [CrossRef]
- Smarr, L. Mass formula for Kerr black holes. Phys. Rev. Lett. 1973, 30, 71–73. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. 1973, D7, 2333–2346. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Generalized second law of thermodynamics in black hole physics. Phys. Rev. 1974, D9, 3292–3300. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Hawking, S.W. Black Holes and Thermodynamics. Phys. Rev. 1976, D13, 191–197. [Google Scholar] [CrossRef]
- Hawking, S.W. Gravitational radiation from colliding black holes. Phys. Rev. Lett. 1971, 26, 1344–1346. [Google Scholar] [CrossRef]
- Eardley, D.M.; Giddings, S.B. Classical black hole production in high-energy collisions. Phys. Rev. 2002, D66, 044011. [Google Scholar] [CrossRef]
- Sperhake, U.; Cardoso, V.; Pretorius, F.; Berti, E.; Gonzalez, J.A. The High-energy collision of two black holes. Phys. Rev. Lett. 2008, 101, 161101. [Google Scholar] [CrossRef] [PubMed]
- Coelho, F.S.; Herdeiro, C.; Sampaio, M.O.P. Radiation from a D-dimensional collision of shock waves: A remarkably simple fit formula. Phys. Rev. Lett. 2012, 108, 181102. [Google Scholar] [CrossRef] [PubMed]
- Smarr, L.; Cadez, A.; DeWitt, B.S.; Eppley, K. Collision of Two Black Holes: Theoretical Framework. Phys. Rev. 1976, D14, 2443–2452. [Google Scholar] [CrossRef]
- Smarr, L. Gravitational Radiation from Distant Encounters and from Headon Collisions of Black Holes: The Zero Frequency Limit. Phys. Rev. 1977, D15, 2069–2077. [Google Scholar]
- Smarr, L.; York, J.W., Jr. Kinematical conditions in the construction of space-time. Phys. Rev. 1978, D17, 2529–2551. [Google Scholar]
- Witek, H.; Zilhao, M.; Gualtieri, L.; Cardoso, V.; Herdeiro, C.; Nerozzi, A.; Sperhake, U. Numerical relativity for D dimensional space-times: head-on collisions of black holes and gravitational wave extraction. Phys. Rev. 2010, D82, 104014. [Google Scholar] [CrossRef]
- Bantilan, H.; Romatschke, P. Simulation of Black Hole Collisions in Asymptotically Anti-de Sitter Spacetimes. Phys. Rev. Lett. 2015, 114, 081601. [Google Scholar] [CrossRef] [PubMed]
- Bednarek, W.; Banasinski, P. Non-thermal radiation from collisions of compact objects with intermediate scale jets in active galaxies. Astrophys. J. 2015, 807, 168. [Google Scholar] [CrossRef]
- Hirotani, K.; Pu, H.-Y. Energetic Gamma Radiation from Rapidly Rotating Black Holes. Astrophys. J. 2016, 818, 50. [Google Scholar] [CrossRef]
- Sperhake, U.; Berti, E.; Cardoso, V.; Pretorius, F. Gravity-dominated unequal-mass black hole collisions. Phys. Rev. 2016, D93, 044012. [Google Scholar] [CrossRef]
- Barkett, K.; Scheel, M.A.; Haas, R.; Ott, C.D.; Bernuzzi, S.; Brown, D.A.; Szilágyi, B.; Kaplan, J.D.; Lippuner, J.; Muhlberger, C.D.; et al. Gravitational waveforms for neutron star binaries from binary black hole simulations. Phys. Rev. 2016, D93, 044064. [Google Scholar] [CrossRef]
- Hinderer, T.; Taracchini, A.; Foucart, F.; Buonanno, A.; Steinhoff, J.; Duez, M.; Kidder, L.E.; Pfeiffer, H.P.; Scheel, M.A.; Szilagyi, B.; et al. Effects of neutron-star dynamic tides on gravitational waveforms within the effective-one-body approach. Phys. Rev. Lett. 2016, 116, 181101. [Google Scholar] [CrossRef] [PubMed]
- Schiff, L.I. Motion of a Gyroscope According to Einstein’s Theory of Gravitation. Proc. Nat. Acad. Sci. USA 1960, 46, 871. [Google Scholar] [CrossRef] [PubMed]
- Wilkins, D. General equation for the precession of a gyroscope. Ann. Phys. 1970, 61, 277–293. [Google Scholar] [CrossRef]
- Mashhoon, B. Particles with spin in a gravitational field. J. Math. Phys. 1971, 12, 1075–1077. [Google Scholar] [CrossRef]
- Wald, R.M. Gravitational spin interaction. Phys. Rev. 1972, D6, 406–413. [Google Scholar] [CrossRef]
- Plyatsko, R.; Fenyk, M. Highly relativistic spin-gravity coupling for fermions. Phys. Rev. 2015, D91, 064033. [Google Scholar] [CrossRef]
- d’Ambrosi, G.; Kumar, S.S.; van de Vis, J.; van Holten, J.W. Spinning bodies in curved spacetime. Phys. Rev. 2016, D93, 044051. [Google Scholar] [CrossRef]
- Majar, J.; Mikoczi, B. Second order spin effects in the spin precession of compact binaries. Phys. Rev. 2012, D86, 064028. [Google Scholar] [CrossRef]
- Zilhão, M.; Cardoso, V.; Herdeiro, C.; Lehner, L.; Sperhake, U. Collisions of oppositely charged black holes. Phys. Rev. 2014, D89, 044008. [Google Scholar] [CrossRef]
- Teukolsky, S.A. Rotating black holes—Separable wave equations for gravitational and electromagnetic perturbations. Phys. Rev. Lett. 1972, 29, 1114–1118. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A. Perturbations of a Rotating Black Hole. II. Dynamical Stability of the Kerr Metric. Astrophys. J. 1973, 185, 649–674. [Google Scholar] [CrossRef]
- Damour, T.; Deruelle, N.; Ruffini, R. On Quantum Resonances in Stationary Geometries. Lett. Nuovo Cimento 1976, 15, 257–262. [Google Scholar] [CrossRef]
- Zouros, T.J.M.; Eardley, D.M. Instabilities of Massive Scalar Perturbations of a Rotating Black Hole. Ann. Phys. 1979, 118, 139–155. [Google Scholar] [CrossRef]
- Detweiler, S.L. Klein-Gordon Equation and Rotating Black Holes. Phys. Rev. 1980, D22, 2323–2326. [Google Scholar] [CrossRef]
- Dolan, S.R. Instability of the massive Klein-Gordon field on the Kerr spacetime. Phys. Rev. 2007, D76, 084001. [Google Scholar] [CrossRef]
- Hod, S. Quasi-Bound States of Massive Scalar Fields in the Kerr Black-Hole Spacetime: Beyond the Hydrogenic Approximation. Phys. Lett. 2015, B749, 167–171. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A. Floating Orbits, Superradiant Scattering and the Black-hole Bomb. Nature 1972, 238, 211–212. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.J.C. Small Kerr-anti-de Sitter black holes are unstable. Phys. Rev. 2004, D70, 084011. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.J.C.; Yoshida, S. Classical instability of Kerr-AdS black holes and the issue of final state. Phys. Rev. 2006, D74, 044008. [Google Scholar] [CrossRef]
- Cardoso, V.; Dias, O.J.C.; Lemos, J.P.S.; Yoshida, S. The Black hole bomb and superradiant instabilities. Phys. Rev. 2004, D70, 044039. [Google Scholar] [CrossRef]
- Kunduri, H.K.; Lucietti, J.; Reall, H.S. Gravitational perturbations of higher dimensional rotating black holes: Tensor perturbations. Phys. Rev. 2006, D74, 084021. [Google Scholar] [CrossRef]
- Zhang, C.-Y.; Zhang, S.-J.; Wang, B. Superradiant instability of Kerr-de Sitter black holes in scalar-tensor theory. JHEP 2014, 8, 11. [Google Scholar] [CrossRef]
- Emparan, R.; Myers, R.C. Instability of ultra-spinning black holes. JHEP 2003, 9, 025. [Google Scholar] [CrossRef]
- Shibata, M.; Yoshino, H. Nonaxisymmetric instability of rapidly rotating black hole in five dimensions. Phys. Rev. 2010, D81, 021501. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Figueras, P.; Monteiro, R.; Santos, J.E.; Emparan, R. Instability and new phases of higher-dimensional rotating black holes. Phys. Rev. 2009, D80, 111701. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Figueras, P.; Monteiro, R.; Reall, H.S.; Santos, J.E. An instability of higher-dimensional rotating black holes. JHEP 2010, 5, 76. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Figueras, P.; Monteiro, R.; Santos, J.E. Ultraspinning instability of rotating black holes. Phys. Rev. 2010, D82, 104025. [Google Scholar] [CrossRef]
- Durkee, M.; Reall, H.S. Perturbations of higher-dimensional spacetimes. Class. Quantum Gravity 2011, 28, 035011. [Google Scholar] [CrossRef]
- Murata, K. Instability of higher dimensional extreme black holes. Class. Quantum Gravity 2013, 30, 075002. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Hartnett, G.S.; Santos, J.E. Quasinormal modes of asymptotically flat rotating black holes. Class. Quantum Gravity 2014, 31, 245011. [Google Scholar] [CrossRef]
- Gwak, B.; Lee, B.-H. Instability of rotating anti-de Sitter black holes. Phys. Rev. 2015, D91, 064020. [Google Scholar] [CrossRef]
- Ahn, W.-K.; Gwak, B.; Lee, B.-H.; Lee, W. Instability of Black Holes with a Gauss-Bonnet Term. Eur. Phys. J. 2015, C75, 372. [Google Scholar] [CrossRef]
- Gwak, B.; Lee, B.-H.; Ro, D. Instability of Charged Anti-de Sitter Black Holes. Phys. Lett. 2016, B761, 437–443. [Google Scholar] [CrossRef]
- Chrusciel, P.T.; Maerten, D.; Tod, P. Rigid upper bounds for the angular momentum and centre of mass of non-singular asymptotically anti-de Sitter space-times. JHEP 2006, 11, 084. [Google Scholar] [CrossRef]
- Dolan, B.P.; Kastor, D.; Kubiznak, D.; Mann, R.B.; Traschen, J. Thermodynamic Volumes and Isoperimetric Inequalities for de Sitter Black Holes. Phys. Rev. 2013, D87, 104017. [Google Scholar] [CrossRef]
- Caldarelli, M.M.; Cognola, G.; Klemm, D. Thermodynamics of Kerr-Newman-AdS black holes and conformal field theories. Class. Quantum Gravity 2000, 17, 399–420. [Google Scholar] [CrossRef]
- Akcay, S.; Matzner, R.A. Kerr-de Sitter Universe. Class. Quantum Gravity 2011, 28, 085012. [Google Scholar] [CrossRef]
- Mathisson, M. Neue mechanik materieller systemes. Acta Phys. Pol. 1937, 6, 163–2900. [Google Scholar]
- Papapetrou, A. Spinning test particles in general relativity. 1. Proc. R. Soc. Lond. 1951, A209, 248–258. [Google Scholar] [CrossRef]
- Dixon, W.G. Dynamics of extended bodies in general relativity. I. Momentum and angular momentum. Proc. R. Soc. Lond. 1970, A314, 499–527. [Google Scholar] [CrossRef]
- Beiglböck, W. The center-of-mass in Einsteins theory of gravitation. Commun. Math. Phys. 1967, 5, 106–130. [Google Scholar] [CrossRef]
- Gwak, B.; Lee, B.-H. Cosmic Censorship of Rotating Anti-de Sitter Black Hole. JCAP 2016, 1602, 15. [Google Scholar] [CrossRef]
- Gwak, B.; Ro, D. Dilaton field released under collision of dilatonic black holes with Gauss-Bonnet term. Eur. Phys. J. 2017, C77, 554. [Google Scholar] [CrossRef]
- Gwak, B. Collision of Two Rotating Hayward Black Holes. Eur. Phys. J. 2017, C77, 482. [Google Scholar] [CrossRef]
- Gwak, B.; Lee, B.-H. The Upper Bound of Radiation Energy in the Myers-Perry Black Hole Collision. JHEP 2016, 7, 79. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).