Abstract
This paper presents a theoretical investigation of the second law performance of double diffusive forced convection in microreactors with the inclusion of nanofluid and radiation effects. The investigated microreactors consist of a single microchannel, fully filled by a porous medium. The transport of heat and mass are analysed by including the thick walls and a first order, catalytic chemical reaction on the internal surfaces of the microchannel. Two sets of thermal boundary conditions are considered on the external surfaces of the microchannel; (1) constant temperature and (2) constant heat flux boundary condition on the lower wall and convective boundary condition on the upper wall. The local thermal non-equilibrium approach is taken to thermally analyse the porous section of the system. The mass dispersion equation is coupled with the transport of heat in the nanofluid flow through consideration of Soret effect. The problem is analytically solved and illustrations of the temperature fields, Nusselt number, total entropy generation rate and performance evaluation criterion (PEC) are provided. It is shown that the radiation effect tends to modify the thermal behaviour within the porous section of the system. The radiation parameter also reduces the overall temperature of the system. It is further demonstrated that, expectedly, the nanoparticles reduce the temperature of the system and increase the Nusselt number. The total entropy generation rate and consequently PEC shows a strong relation with radiation parameter and volumetric concentration of nanoparticles.
1. Introduction
The Second Law of Thermodynamics is amongst the most important laws of nature and plays an essential role in evaluating the available values of thermal and chemical energies. This law provides quantitative information about the level of irreversibility of the system and the amount of useful work destructed through a given process. The Second Law of Thermodynamics is currently widely used in various real world applications such as solar collectors [,], power plants [,] and desalination system [,]. However, its applications to biomedical and micro-thermal systems are still in the early stages and need more investigation.
Transport in microreactors has recently attracted the attention of different research communities [,]. Microreactors have been developed based on the advancements of micro manufacturing technology, and offer a number of advantages in comparison with the conventional macro-reactors []. The large surface to volume ratio in microreactors allows for enhanced transport and mixing characteristics in chemical processes []. Moreover, the porous medium commonly used in microreactors is a powerful tool for obtaining better temperature distribution and control within the system [,]. However, compared with the conventional reactors, microreactors have been less explored from the viewpoint of the second law of thermodynamics. This could be due to the peculiar features of microstructure devices that complicate the analysis. For example, the small dimensions of microreactors warrants inclusion of the solid walls of microchannels within the thermophysical calculations of the system [,]. Further, due to the internal heat generation within the microreactor, the local thermal non-equilibrium (LTNE) approach should be applied to the thermal analyses of porous microreactors [,]. Owing to these complexities, thermodynamic analysis of microreactors is amongst the state-of-the-art research categories in the broad field of thermo-chemical systems.
So far, a number of investigations have been devoted to the second law analyses of forced convection heat transfer in microchannels, which are indispensable parts of microreactors []. Pioneering investigations in this area have been conducted by Ting et al. [,]. These authors considered entropy generation during forced convection of heat within a porous microchannel. The LTNE model was used for the heat transfer analysis of nanofluid flow through the microchannel but the finite thickness of the walls was not included in the simulations. The temperature and entropy generation distributions were illustrated throughout the channel. Further, comprehensive analyses were conducted on the effects of different parameters upon the second law behaviour of the system. Later, Torabi and Zhang [] performed a second law analysis of forced convection in a porous channel with internal heat generation and magnetic effects. The Local Thermal Equilibrium (LTE) model for thermal analysis of the porous section of the microchannel was used in this investigation. The solid walls were incorporated in the simulations of Torabi and Zhang [] for the first time. It was demonstrated that thickness of the walls has strong influence on the thermal and entropic behaviours of the microchannel. Most recently, Hunt et al. [] have examined energetic and entropic performances of porous microreactors with thick walls through using the LTNE model. A partially filled microchannel was considered in the simulations and endothermicity/exothermicity of the microreactor was incorporated within the governing equations. It was shown that by choosing a specific value for the thicknesses of the walls, it is possible to minimise the entropy generation rate within the microchannel []. In another recent study, Elliott et al. [] extended the investigation of Hunt et al. [] to fully filled porous microchannels. Wang et al. [] have considered a microchannel with thick walls in premixed micro-combustor. The numerical results of the wall temperature were compared with the experimental data []. Also, entropy generation rates for different reactions have been reported in the investigation of Wang et al. [].
Mass transfer analysis is essential in any study of chemical reactors including that of microreactors. Further, the frequent use of catalysts and the importance of diffusive mass transfer in microreactors, highlight the necessity of considering all mechanisms of mass diffusion. Hence, in transport studies of microreactors, the thermal diffusion of mass or Soret effect should be taken into account. Yet, to the best of the authors’ knowledge so far, there exists only one investigation on the double diffusive forced convection in microreactors. Recently, Torabi et al. [] have investigated the entropic characteristics of porous microchannels with thick walls, when a first order chemical reaction occurs at the porous-solid wall interfaces. An LTE model was used to model the heat transport through the porous section of the microchannel and internal radiation heat transfer was also considered in the analysis. It was illustrated that the radiative heat transfer decreases the temperature of the microreactor and also reduces the entropy generation of the system. Although not directly related to this investigation, Sahu [] opted in favour of double diffusive effects on pressure-driven miscible flow in a two-dimensional horizontal channel. Here, two fluids and different viscosities were considered, and their effects on the instability mode and flow patterns of the system were investigated. Sahu [] solved the transient governing equations and illustrated the effects of diffusivity ratio on the concentration field. Later, the study of double diffusive convection in a planar channel [] was extended to an axisymmetric pipe by Bhagat et al. [].
The present study advances the previous investigation of Torabi et al. [] by two important modifications: (1) nanofluid flow has been considered through the microchannel and (2) LTNE model of thermal transport has been applied to the porous section of the system. As internal heat generation is an intrinsic feature of many microreactors, the use of LTNE model instead of LTE approach provides more accurate predictions of the temperature field [,]. Further, using a non-equilibrium model influences the entropy generation and species concentration field of the system [,]. This paper has been divided into five sections. After this section, which is devoted to the literature review, Section 2 provides a detailed illustration of the mathematical model and underlying assumptions. In Section 3, the dimensionless parameters and governing equations are given. Section 4 analytically solves the momentum, energy and dispersion differential equations. Section 5 provides a comprehensive discussion regarding the energetic and entropic behaviours of the microreactor versus various parameters such as nanoparticle volumetric concentration, radiation heat loss and Soret number. Finally, Section 6 concludes the manuscript with some remarks and future plans.
2. Theoretical methods
2.1. Problem Configuration and Assumptions
Figure 1 shows the schematics of the problem under investigation. A microreactor, which consists of a single porous microchannel is considered. Each microchannel can include internally heat generating/consuming processes within the porous section. Two scenarios for the external boundary conditions of the microchannels are considered. In case one, constant temperature boundary conditions have been assumed (Figure 1a) and for case two heat flux boundary condition is imposed on the lower wall and convection heat transfer is imposed on the upper wall (Figure 1b). The solid sections of the upper and lower walls of the microchannel have been included in the calculations and different thermal conductivities have been assigned to them. Further, these walls feature constant and uniform, but dissimilar, internal heat generations. The internal heat generation within the solid walls could be, for instance, the result of the absorption of microwave in the solid walls [,]. A first order chemical reaction has been considered at the solid-porous interfaces, which are applied on the dispersion equation. By considering the effects of thermal diffusion of species, the dispersion equation has been coupled to the energy equation.
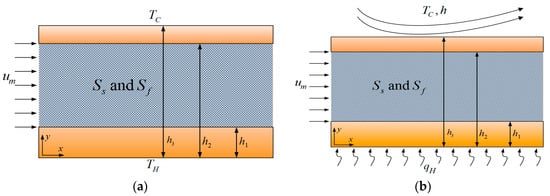
Figure 1.
Schematic configuration of the model microreactors, (a) Case one and (b) Case two.
The current investigation is based on the volume averaging theory of porous media [] and therefore pore scale phenomena [,] are not investigated. To provide a clear representation of thermophysical conditions within the microreactor under investigation, it has been assumed that the following conditions hold:
- The porous medium is homogenous and isotropic, fluid saturated and includes uniform and steady internal heat generation representing heat of reaction and/or absorption of electromagnetic waves.
- The fluid flow is laminar, steady and incompressible, with uniform heat generation.
- A local thermal non-equilibrium condition has been considered within the porous section of the microreactor.
- Fully developed conditions hold within the microreactor.
- It has been assumed that natural convection heat transfer is negligible compared with forced convection. This assumption has been fully justified in the previous investigations of similar configurations, e.g., [,].
- The investigated microreactor accommodates volumetrically uniform internal heat generations []. Hence, sharp reaction zones [] are excluded and consequently axial conduction effects are ignored in this investigation.
- It is assumed that the temperature of the solid phase of the porous medium is high enough to include the effect of radiation on the temperature distribution [].
2.2. Governing Equations
Since the Darcy–Brinkman model for transport in porous media has been considered in this study, the momentum equation reads []
where is the effective viscosity of the nanofluid. The four energy equations needed to express the transport of thermal energy in different components of the system are as follows [,].
These differential equations, respectively, correspond to the conservation of energy at the bottom wall, the fluid and solid phases within the porous region and the top wall. It is emphasised that the assumption of fully developed flow has been included in the derivation of Equations (2b) and (2c). The dispersion equation, which is coupled with the temperature of the nanofluid via the thermodiffusion coefficient can be written as []:
In Equation (2c), the radiation parameter takes the form of []
By using Rosseland approximation [], the last term of the left hand side of the energy equation for the nanofluid phase of the porous section of the channel is transformed to:
The two sets of thermal boundary conditions under consideration are as follows:
- Case one:
- Case two:
Due to the outer boundary conditions, the advection process in the axial direction can be neglected in this analysis. The validity of this assumption has been shown in a number of recent investigations of the systems with similar configurations to that of Figure 1 [,,,,,], and hence is not further discussed here. In particular, this assumption is very realisable in the limit of low thermal Peclet number, which is frequently reached in microreactors []. Moreover, the investigated configuration finds applications in micro-reformers [] in which the heat transfer perpendicular to the flow direction is much stronger than that parallel to the flow direction. Thus, the validity of neglecting the advection term, i.e., , is further confirmed. It follows that the system of energy Equation (2) can be reduced to the following set of equations.
In both cases, the following interface conditions are required for the closure of the system [,]
Unlike the viscous or dispersion effects, the radiation heat loss indirectly participates in the entropy generation of the porous systems []. This approach has been applied by a number of scholars to investigate the effects of radiation on the entropy generation of thermal systems []. Hence, the local entropy generation rate across the entire microchannel can be formulated as follows [,,].
3. Dimensionless Parameters and Non-Dimensionalised Equations
To facilitate analytical progress, the following dimensionless parameters are introduced.
where .
Non-dimensionalising the momentum equation yields the following dimensionless equation.
Applying the dimensionless parameters to the governing energy Equations (8a)–(8d) results in the following dimensionless equations.
where and . The constant parameters and can be any temperature-independent models for the ratio of viscosity and thermal conductivity of the nanofluid to those of base fluid, respectively. Here, the following empirical models were chosen [,].
and
Equation (14) relates thermal conductivity and viscosity of the base fluid to that of the nanofluid. These models are representative of copper-water nanofluids and were developed by Maxwell and Brinkman, respectively [,]. The values of and have been considered for thermal conductivity of copper particles and water, respectively []. Moreover, as the energy equations have been non-dimensionalised by parameters illustrated in Equation (11), the dimensionless energy equations provided in Equation (13) can be used for any porous medium. Hence, there is no need to provide the thermal properties of the porous material.
It should be noted that to analyse the flow and heat transfer in a nanofluid system, two different methods can be used. The first approach assumes a single homogenous phase for the nanofluid [,,], in which thermophysical properties of the nanofluid can be calculated using Equation (14). The second approach assumes a two-component nonhomogeneous equilibrium model of the nanofluid [,]. The latter is comparatively more accurate, yet it is computationally more expensive and generally not amenable to analytical procedures. Thus, due to the analytical nature of the current study, the homogeneous model of nanofluid is used here.
The dimensionless dispersion equation can be written as follows:
Further, the outer thermal boundary conditions (6) and (7) are converted to the following relations:
- Case one:
- Case two:
The thermal and hydrodynamic interface conditions for the two cases are given by [,,]
Algebraic manipulation of these equations and boundary conditions results in a set of fourth-order differential equations for the solid and nanofluid phases of the porous region. This reads
The dimensionless form of the Nusselt number using the parameters from Equation (11) is defined as follows:
where,
and,
Upon introduction of the dimensionless variables, introduced in Equation (11), the dimensionless local volumetric entropy generation rate, takes the form of
Finally, the dimensionless volumetric averaged entropy generation rate is given by
4. Solution of Momentum, Energy and Dispersion Equations
The thermophysical problem described above includes three main governing equations, namely momentum, energy and dispersion expressed by Equations (12), (13) and (15), respectively. Each of these equations can be solved analytically by a straightforward mathematical manipulation and integration. Regarding Equations (13b) and (13c), which are coupled together, an algebraic manipulation leads to Equations (19) and (20). By applying the boundary conditions, the particular solution for each specific case of the investigated microchannels can be found.
The solution of the normalised momentum Equation (12) reveals the following velocity profile for the fluid velocity in the porous region.
where .
The equations governing the transport of thermal energy in the system (Equations (13a) and (13d), and also Equations (19) and (20)) are solved analytically. This results in the following general solutions for the temperature distributions in the solid and nanofluid phases of the porous medium and those of the solid walls, respectively,
in which .
The solution for the normalised dispersion Equation (15) yields the concentration profile of the chemical species across the conduit,
Finding the particular solution requires incorporation of the boundary and interface conditions described by Equations (16)–(18). The associated algebraic manipulations for deriving the constant parameters in Equations (27a)–(27d) and (28) are quite substantial and therefore are not shown in here.
5. Results and Discussion
This section is divided into three parts. The first one is a discussion about the temperature profiles of the system under consideration. The second part puts forward a comprehensive discussion about the concentration profiles. This includes identification of the relative significance of different parameters in the mass transfer within the system. Finally a discussion about entropy generation including local and total entropy generation plots to compare the significances of different parameters upon entropy generation in the system. It is worth noting that in the rest of this paper parts a and b of each figure correspond, respectively, to cases 1 and 2 shown in Figure 1a,b. It should be also noted that in Figure 2 and Figure 3, the solid and dashed lines represent the solid and nanofluid components, respectively. Throughout all figures, the parameter values in the following table have been used unless stated otherwise.
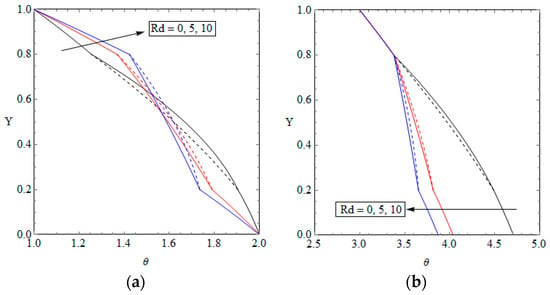
Figure 2.
Dimensionless temperature distribution for various values of radiation parameter, (a) Case one and (b) Case two.
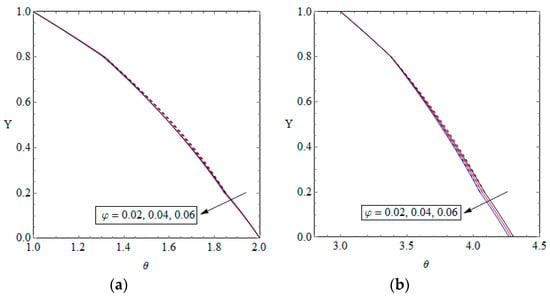
Figure 3.
Dimensionless temperature distribution for various values of nanoparticle volumetric concentration, (a) Case one and (b) Case two.
5.1. Validation
The temperature and Nusselt number solutions developed in Section 4 were compared with those developed by Elliott et al. [] for the case with ordinary fluid and no thermal radiation. This resulted in observing no difference between the two datasets and hence confirmed the validity of the mathematical model developed in Section 2, Section 3 and Section 4.
5.2. Temperature Distribution and Nusselt Number
Figure 2 shows the temperature distribution across the microchannel while different values have been assigned to radiation parameter. The radiation parameter is chosen to cover a wide range from porous microchannels without radiation effect, i.e., Rd = 0, to the porous microchannels with high radiation heat loss, i.e., Rd = 10. Figure 2 shows that, for both cases, radiation heat loss modifies the thermal behaviour of the porous section of the microchannel. Depending on the magnitude of the radiation parameter, the temperature of the nanofluid phase may be higher or lower than the temperature of the solid phase of the porous section. This is an important finding, which has been not shown in previous publications. It is further noted that as no temperature boundaries have been specified in case two, the radiation parameter has a strong effect on the temperature distributions of the system and noticeably decreases the temperature in lower parts of the microchannel.
Figure 3 shows the effects of volumetric concentration of nanoparticles on the temperature fields of the two investigated cases. In Figure 3a, it is seen that the nanoparticles volumetric concentration has a marginal impact on the temperature of the microchannel. Regarding Figure 3b, it is observed that the nanoparticles volumetric concentration tends to reduce the temperature of the lower parts of the microchannel, i.e., the lower solid wall and porous section of the microchannel. Also, the temperature of the upper solid wall of the microchannel slightly increases with an increase on the concentration of nanoparticles that may be due to the heat absorbed from the lower parts of the system. Figure 4 and Figure 5 are companions to Figure 2 and Figure 3 and provide graphs of Nusselt number versus radiation parameter and nanoparticles volumetric concentration for different values of porosity, respectively. As the temperature on the lower wall decreases with increasing the radiation parameter, it is expected that the Nusselt number versus radiation parameter follows a rising pattern for both cases. This is clearly seen in Figure 4. A similar trend is observed for Nusselt number versus nanoparticles volumetric concentration in Figure 5. An analogous behaviour has been recently reported in the studies of forced convection of nanofluid through porous channels [,]. Further, Figure 4 indicates that the Nusselt number almost linearly correlates with the values of the radiation parameter. In this figure, the growth of Nusselt number with respect to the radiation parameter for all of its values is almost equal.
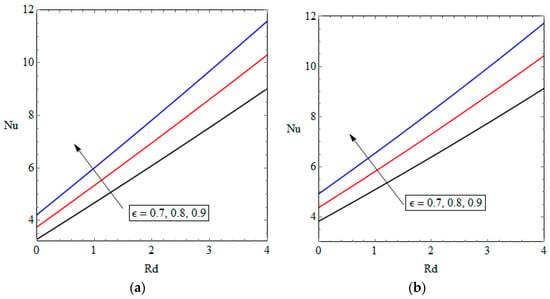
Figure 4.
Nusselt number versus radiation parameter for different values of porosity, (a) Case one and (b) Case two.
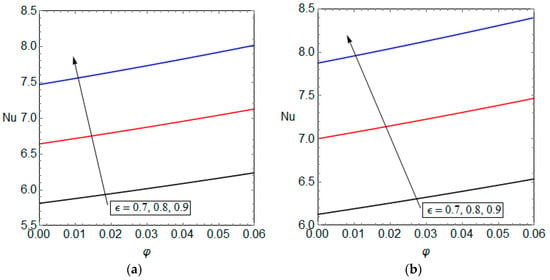
Figure 5.
Nusselt number versus nanoparticle volumetric concentration for different values for porosity, (a) Case one and (b) Case two.
5.3. Entropy Generation and Performance Evaluation Criterion
Figure 6, Figure 7 and Figure 8 are devoted to the variations of total entropy generation rate versus internal heat generations, nanoparticles volumetric concentration, radiation parameter and Soret number. Figure 6 illustrates the variation of dimensionless total entropy generation versus internal heat generations in porous solid and nanofluid phases of the microchannel, when internal heat generations vary in tandem. This figure shows that when the heat generation within the porous section changes from exothermic to endothermic, it is possible to find a specific value for the heat source, which minimises the total entropy generation. Interestingly, the effects of nanoparticles on the entropy generation in cases one and two are different from each other. While the overall entropy generation of the first system increases by introducing the nanofluid to the system, the entropy generation rate within the second system may marginally decrease or increase by adding nanoparticles to the base fluid. These can be seen from the illustrated data in Figure 6a,b. Figure 7 depicts the total entropy generation rate versus nanoparticles volumetric concentration for various values of Soret number. The effects of nanoparticles on the entropy generation rate on both cases are similar to those discussed in the previous figure. The nanoparticles increase the entropy generation for the first case, while it may increase or decrease the entropy generation rate depending on the value of Soret number.
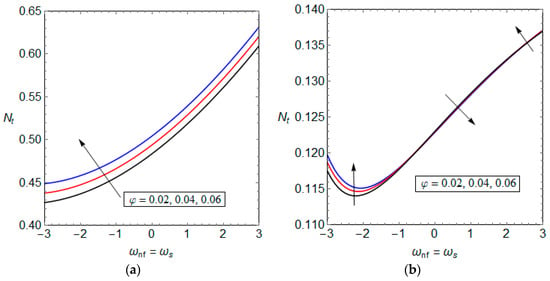
Figure 6.
Dimensionless entropy generation versus internal heat generation for different values of nanoparticle volumetric concentration, (a) Case one and (b) Case two.
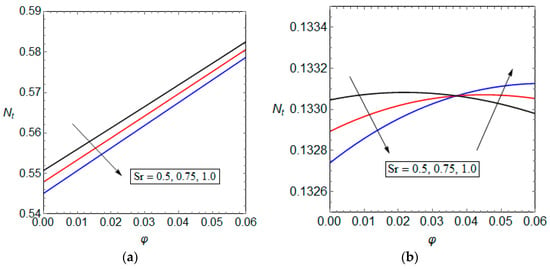
Figure 7.
Dimensionless entropy generation versus nanoparticle volumetric concentration for different values of Soret number, (a) Case one and (b) Case two.
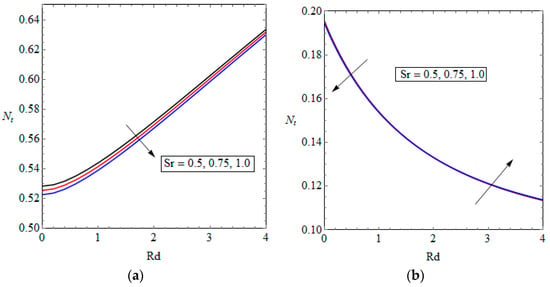
Figure 8.
Dimensionless entropy generation versus radiation parameter for different values of Soret number, (a) Case one and (b) Case two.
Although for both cases the effect of Soret number on the entropy generation rate seems marginal, case one shows more variation with respect to Soret number. For the used parametric values, the total entropy generation rate decreases with an increase of Soret number in case one. However, depending on the value of volumetric concentration of nanoparticles for the second case, the Soret number may slightly increase or decrease the total entropy generation rate. Figure 8 shows the total entropy generation rate versus radiation parameter for various values of Soret number. For case one, the internal radiation heat loss tends to decrease the total entropy generation rate. Yet, it decreases the total entropy generation for case two. Similar to the previous figure, the effect of Soret number on the total entropy generation rate for case one differs to its effect on case two. In the current problem, Soret number reduces the total entropy generation rate regardless of the value of radiation parameter in case one. However, in case two, the total entropy generation rate may slightly increase or decrease versus Soret number depending on the value of radiation parameter. Figure 9 is a companion to Figure 8, and provides similar information to those discussed in the context of Figure 8. The rising and falling of the total entropy generation trends versus Soret number can be also observed in this figure.
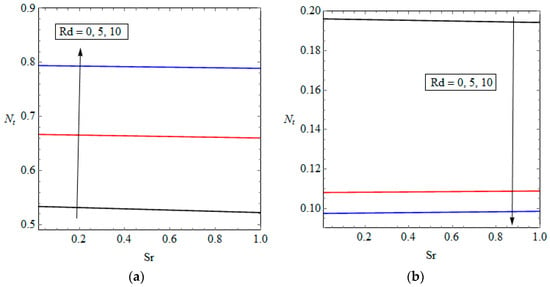
Figure 9.
Dimensionless entropy generation versus Soret number for different values of radiation parameter, (a) Case one and (b) Case two.
Performance evaluation criterion (PEC) is a means of measuring the performance of thermal systems that takes into account both first and second law characteristics []. This parameter is another tool to assess the thermodynamic performance of the system, while simultaneously incorporating the Nusselt number into the calculations. PEC is defined as:
Figure 10 and Figure 11 illustrate PEC versus volumetric concentration of nanoparticles and the radiation parameter for different values of porosity. Both figures show that the PEC increases with nanoparticles and radiation heat loss for both cases. This is a novel finding showing that the nanoparticles (Figure 7a) and radiation parameter (Figure 8a) increase the total entropy generation. This in turn reduces the exergy of the system and hence PEC rises versus both of these parameters. Figure 10 and Figure 11 also show that increasing the porosity of the microreactor leads to enhancements of PEC for both cases, although by comparing the values of PEC for both cases, it appears that the effect of porosity is more intense in the second case.
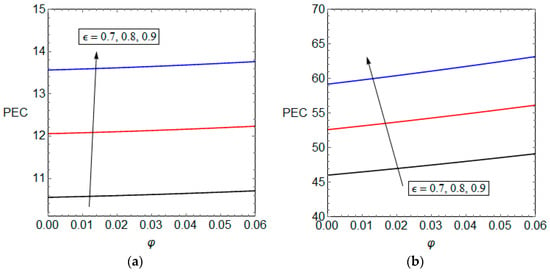
Figure 10.
PEC versus nanoparticle volumetric concentration for different values of porosity, (a) Case one and (b) Case two.
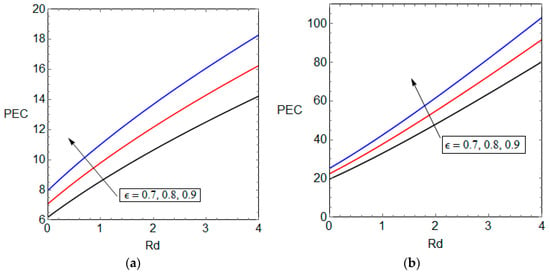
Figure 11.
PEC versus radiation parameter for different values of porosity, (a) Case one and (b) Case two.
6. Conclusions
A porous microreactor was analysed theoretically based on the first and second laws of thermodynamics. Nanoparticles were used to enhance the thermal conductivity of the base fluid and internal radiation heat losses were considered within the porous section of the microreactors. The thermochemical system which included a first order chemical reaction was considered on the solid-porous interfaces of the microchannel. An analytical methodology was employed to tackle the governing momentum, energy and dispersion equations. The results were incorporated into the entropy generation equation to calculate the second law performance of the system. Both nanoparticles volumetric concentration and radiation parameter seem to have marginal impact on the thermal performance of the first case. This was attributed to the outer temperatures of the microreactor being not fixed in the second case. The radiation parameter and volumetric concentration of nanoparticles appeared to have more influential impacts upon the thermal performance of the second case compared with the first case. It was shown that, for the second investigated case, the nanoparticles reduce the total entropy generation rate. However, in the second case, nanoparticles may decrease the entropy generation of the system. Finally, PEC for both cases was calculated and it was shown that PEC improves with the increases in the concentration of nanoparticles and radiation parameter.
Acknowledgments
Lilian Govone was funded through Erasmus programme. Graeme Hunt acknowledges the financial support of the University of Glasgow through EPSRC DTA (G. Hunt) funding award number EP/M506539/1. Nader Karimi acknowledges the partial support of EPSRC through grant number EP/N020472/1.
Author Contributions
Mohsen Torabi and Nader Karimi developed the mathematical model; Lilian Govone performed the simulations and Graeme Hunt contributed to the analysis; Mohsen Torabi and Nader Karimi wrote the paper. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| interfacial area per unit volume of porous media, | |
| Biot number | |
| Concentration of the chemical products per unit volume, | |
| Specific heat of the fluid phase of the porous medium, | |
| Diffusion coefficient, | |
| Darcy number | |
| Thermodiffusion coefficient, | |
| h1 | Height of the lower wall, |
| h2 | Height of the lower boundary of the upper wall, |
| h3 | Height of the upper boundary of the upper wall, |
| h | External heat convection coefficient, |
| hsf | Internal heat convection coefficient, |
| k | Solid to fluid effective thermal conductivity ratio |
| k1 | Reference thermal conductivity for lower solid material, |
| k2 | Reference thermal conductivity for upper solid material, |
| ke1 | Ratio of the fluid to lower solid material thermal conductivities |
| ke2 | Ratio of the fluid to upper solid material thermal conductivities |
| ke,nf | Effective thermal conductivity of the nanofluid phase of the porous medium, |
| kes | Effective thermal conductivity of the solid phase of the porous medium, |
| kf | Thermal conductivity of the base fluid, |
| knf | Thermal conductivity of the nanofluid, |
| kp | Thermal conductivity of the nanoparticles, |
| kR | Kinetic constant, |
| ks | Thermal conductivity of the solid phase of the porous medium, |
| Nc | dimensionless convection heat transfer (Case two) |
| Nu | Nusselt Number |
| Ns | Dimensionless local volumetric entropy generation rate |
| Nt | Dimensionless total entropy generation rate |
| p | Pressure, Pa |
| Dimensionless volumetric internal heat generation rate for the lower solid material | |
| Dimensionless volumetric internal heat generation rate for the upper solid material | |
| Dimensionless heat flux boundary condition (Case two) | |
| Volumetric internal heat generation rate for the lower solid material, | |
| Volumetric internal heat generation rate for the upper solid material, | |
| Heat flux boundary condition (Case two), | |
| Radiation heat flux, | |
| Rd | Dimensionless radiation parameter |
| Dimensionless volumetric internal heat generation rate for the solid phase of the porous medium | |
| Sr | Soret Number |
| Dimensionless volumetric internal heat generation rate for the nanofluid phase of the porous medium | |
| Temperature, | |
| Temperature of the lower solid material, | |
| Temperature of the upper solid material, | |
| Outer temperature of the upper solid material, | |
| Outer temperature of the lower solid material, | |
| Temperature of the fluid phase of the porous medium, | |
| Temperature of the solid phase of the porous medium, | |
| Um | Average dimensionless velocity |
| Velocity of the fluid in porous medium, | |
| Dimensionless velocity | |
| Y1 | Dimensionless height of the lower wall |
| Y2 | Dimensionless height of the upper wall lower boundary |
| Greek symbols | |
| Damköhler number | |
| Porosity | |
| Dimensionless temperature | |
| Dimensionless temperature of the lower solid material | |
| Dimensionless temperature of the upper solid material | |
| Dimensionless temperature of the fluid phase of the porous medium | |
| Dimensionless average temperature of the fluid phase of the porous medium | |
| Dimensionless temperature of the solid phase of the porous medium | |
| Dimensionless temperature at outer side of the lower wall | |
| Permeability, | |
| Rosseland mean absorption coefficient | |
| Dynamic viscosity of porous medium, | |
| Dynamic viscosity of the base fluid, | |
| Dynamic viscosity of the nanofluid, | |
| Dimensionless volumetric internal heat generation rate for the solid phase of the porous medium | |
| Dimensionless volumetric internal heat generation rate for the fluid phase of the porous medium | |
| density of the fluid phase, | |
| Stefan–Boltzmann constant, | |
| Dimensionless concentration | |
| Constant defined in entropy generation formulation | |
References
- Mahian, O.; Kianifar, A.; Sahin, A.Z.; Wongwises, S. Heat transfer, pressure drop, and entropy generation in a solar collector using SiO 2/water nanofluids: Effects of nanoparticle size and pH. J. Heat Transf. 2015, 137, 61011. [Google Scholar] [CrossRef]
- Hepbasli, A. Exergetic modeling and assessment of solar assisted domestic hot water tank integrated ground-source heat pump systems for residences. Energy Build. 2007, 39, 1211–1217. [Google Scholar] [CrossRef]
- Kuravi, S.; Trahan, J.; Goswami, D.Y.; Rahman, M.M.; Stefanakos, E.K. Thermal energy storage technologies and systems for concentrating solar power plants. Prog. Energy Combust. Sci. 2013, 39, 285–319. [Google Scholar] [CrossRef]
- Shamoushaki, M.; Ehyaei, M.A.; Ghanatir, F. Exergy, economic and environmental analysis and multi-objective optimization of a SOFC-GT power plant. Energy 2017, 134, 515–531. [Google Scholar] [CrossRef]
- Chen, Q.; Ja, M.K.; Li, Y.; Chua, K.J. On the second law analysis of a multi-stage spray-assisted low-temperature desalination system. Energy Convers. Manag. 2017, 148, 1306–1316. [Google Scholar] [CrossRef]
- Mistry, K.H.; Lienhard, J.H.; Zubair, S.M. Effect of entropy generation on the performance of humidification- dehumidification desalination cycles. Int. J. Therm. Sci. 2010, 49, 1837–1847. [Google Scholar] [CrossRef]
- Yao, X.; Zhang, Y.; Du, L.; Liu, J.; Yao, J. Review of the applications of microreactors. Renew. Sustain. Energy Rev. 2015, 47, 519–539. [Google Scholar] [CrossRef]
- Roberge, D.M.; Ducry, L.; Bieler, N.; Cretton, P.; Zimmermann, B. Microreactor technology: A revolution for the fine chemical and pharmaceutical industries? Chem. Eng. Technol. 2005, 28, 318–323. [Google Scholar] [CrossRef]
- Kolb, G.; Hessel, V. Micro-structured reactors for gas phase reactions. Chem. Eng. J. 2004, 98, 1–38. [Google Scholar] [CrossRef]
- Ju, Y.; Maruta, K. Microscale combustion: Technology development and fundamental research. Prog. Energy Combust. Sci. 2011, 37, 669–715. [Google Scholar] [CrossRef]
- Li, J.; Chou, S.K.; Li, Z.W.; Yang, W.M. Experimental investigation of porous media combustion in a planar micro-combustor. Fuel 2010, 89, 708–715. [Google Scholar] [CrossRef]
- Torabi, M.; Karimi, N.; Peterson, G.P.; Yee, S. Challenges and progress on the modeling of entropy generation in porous media: A review. Int. J. Heat Mass Transf. 2017, 114, 31–46. [Google Scholar] [CrossRef]
- Torabi, M.; Torabi, M.; Peterson, G.P. Entropy generation of double diffusive forced convection in porous channels with thick walls and Soret effect. Entropy 2017, 19, 171. [Google Scholar] [CrossRef]
- Hunt, G.; Karimi, N.; Torabi, M. Analytical investigation of heat transfer and classical entropy generation in microreactors—The influences of exothermicity and asymmetry. Appl. Therm. Eng. 2017, 119, 403–424. [Google Scholar] [CrossRef]
- Elliott, A.; Torabi, M.; Karimi, N. Thermodynamics analyses of porous microchannels with asymmetric thick walls and exothermicity: An entropic model of microreactors. J. Therm. Sci. Eng. Appl. 2017, 9, 41013. [Google Scholar] [CrossRef]
- Delsman, E.R.; de Croon, M.H.J.M.; Elzinga, G.D.; Cobden, P.D.; Kramer, G.J.; Schouten, J.C. The influence of differences between microchannels on microreactor performance. Chem. Eng. Technol. 2005, 28, 367–375. [Google Scholar] [CrossRef]
- Ting, T.W.; Hung, Y.M.; Guo, N. Entropy generation of viscous dissipative nanofluid convection in asymmetrically heated porous microchannels with solid-phase heat generation. Energy Convers. Manag. 2015, 105, 731–745. [Google Scholar] [CrossRef]
- Ting, T.W.; Hung, Y.M.; Guo, N. Entropy generation of viscous dissipative nanofluid flow in thermal non-equilibrium porous media embedded in microchannels. Int. J. Heat Mass Transf. 2015, 81, 862–877. [Google Scholar] [CrossRef]
- Torabi, M.; Zhang, K. Temperature distribution, local and total entropy generation analyses in MHD porous channels with thick walls. Energy 2015, 87, 540–554. [Google Scholar] [CrossRef]
- Wang, W.; Zuo, Z.; Liu, J.; Yang, W. Entropy generation analysis of fuel premixed CH4/H2/air flames using multistep kinetics. Int. J. Hydrog. Energy 2016, 41, 20744–20752. [Google Scholar] [CrossRef]
- Tang, A.; Xu, Y.; Pan, J.; Yang, W.; Jiang, D.; Lu, Q. Combustion characteristics and performance evaluation of premixed methane/air with hydrogen addition in a micro-planar combustor. Chem. Eng. Sci. 2015, 131, 235–242. [Google Scholar] [CrossRef]
- Sahu, K.C. Double diffusive effects on pressure-driven miscible channel flow: Influence of variable diffusivity. Int. J. Multiph. Flow 2013, 55, 24–31. [Google Scholar] [CrossRef]
- Bhagat, K.D.; Tripathi, M.K.; Sahu, K.C. Instability due to double-diffusive phenomenon in pressure-driven displacement flow of one fluid by another in an axisymmetric pipe. Eur. J. Mech. B Fluids 2016, 55, 63–70. [Google Scholar] [CrossRef]
- Karimi, N.; Agbo, D.; Talat Khan, A.; Younger, P.L. On the effects of exothermicity and endothermicity upon the temperature fields in a partially-filled porous channel. Int. J. Therm. Sci. 2015, 96, 128–148. [Google Scholar] [CrossRef]
- Yang, K.; Vafai, K. Analysis of temperature gradient bifurcation in porous media—An exact solution. Int. J. Heat Mass Transf. 2010, 53, 4316–4325. [Google Scholar] [CrossRef]
- Chen, W.H.; Cheng, T.C.; Hung, C.I. Modeling and simulation of microwave double absorption on methanol steam reforming for hydrogen production. Int. J. Hydrog. Energy 2011, 36, 333–344. [Google Scholar] [CrossRef]
- Chen, W.H.; Cheng, T.C.; Hung, C.I. Numerical predictions on thermal characteristic and performance of methanol steam reforming with microwave-assisted heating. Int. J. Hydrog. Energy 2011, 36, 8279–8791. [Google Scholar] [CrossRef]
- Civan, F. Porous Media Transport Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Torabi, M.; Peterson, G.P.; Torabi, M.; Karimi, N. A thermodynamic analysis of forced convection through porous media using pore scale modeling. Int. J. Heat Mass Transf. 2016, 99, 303–316. [Google Scholar] [CrossRef]
- Torabi, M.; Torabi, M.; Peterson, G.P. Heat transfer and entropy generation analyses of forced convection through porous media using pore scale modeling. J. Heat Transf. 2017, 139, 12601. [Google Scholar] [CrossRef]
- Chen, J.; Song, W.; Gao, X.; Xu, D. Hetero-/homogeneous combustion and flame stability of fuel-lean propane–air mixtures over platinum in catalytic micro-combustors. Appl. Therm. Eng. 2016, 100, 932–943. [Google Scholar] [CrossRef]
- Wang, P.; Vafai, K.; Liu, D.Y. Analysis of radiative effect under local thermal non-equilibrium conditions in porous media-application to a solar air receiver. Numer. Heat Transf. Part A 2014, 65, 931–948. [Google Scholar] [CrossRef]
- Torabi, M.; Dickson, C.; Karimi, N. Theoretical investigation of entropy generation and heat transfer by forced convection of copper–water nanofluid in a porous channel—Local thermal non-equilibrium and partial filling effects. Powder Technol. 2016, 301, 234–254. [Google Scholar] [CrossRef]
- Modest, M.F. Radiative Heat Transfer; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Elliott, A.; Torabi, M.; Karimi, N.; Cunningham, S. On the effects of internal heat sources upon forced convection in porous channels with asymmetric thick walls. Int. Commun. Heat Mass Transf. 2016, 73, 100–110. [Google Scholar] [CrossRef]
- Torabi, M.; Peterson, G.P. Effects of velocity slip and temperature jump on the heat transfer and entropy generation in micro porous channels under magnetic field. Int. J. Heat Mass Transf. 2016, 102, 585–595. [Google Scholar] [CrossRef]
- Ibáñez, G.; López, A.; Pantoja, J.; Moreira, J. Combined effects of uniform heat flux boundary conditions and hydrodynamic slip on entropy generation in a microchannel. Int. J. Heat Mass Transf. 2014, 73, 201–206. [Google Scholar] [CrossRef]
- Ibáñez, G. Entropy generation in MHD porous channel with hydrodynamic slip and convective boundary conditions. Int. J. Heat Mass Transf. 2015, 80, 274–280. [Google Scholar] [CrossRef]
- Ibáñez, G.; López, A.; Pantoja, J.; Moreira, J. Entropy generation analysis of a nanofluid flow in MHD porous microchannel with hydrodynamic slip and thermal radiation. Int. J. Heat Mass Transf. 2016, 100, 89–97. [Google Scholar] [CrossRef]
- Kaisare, N.S.; Vlachos, D.G. A review on microcombustion: Fundamentals, devices and applications. Prog. Energy Combust. Sci. 2012, 38, 321–359. [Google Scholar] [CrossRef]
- Ellahi, R.; Hassan, M.; Zeeshan, A. Shape effects of nanosize particles in Cu-H2O nanofluid on entropy generation. Int. J. Heat Mass Transf. 2015, 81, 449–456. [Google Scholar] [CrossRef]
- Torabi, M.; Karimi, N.; Zhang, K. Heat transfer and second law analyses of forced convection in a channel partially filled by porous media and featuring internal heat sources. Energy 2015, 93, 106–127. [Google Scholar] [CrossRef]
- Torabi, M.; Karimi, N.; Zhang, K.; Peterson, G.P. Generation of entropy and forced convection of heat in a conduit partially filled with porous media—Local thermal non-equilibrium and exothermicity effects. Appl. Therm. Eng. 2016, 106, 518–536. [Google Scholar] [CrossRef]
- Torabi, M.; Zhang, K.; Karimi, N.; Peterson, G.P. Entropy generation in thermal systems with solid structures—A concise review. Int. J. Heat Mass Transf. 2016, 97, 917–931. [Google Scholar] [CrossRef]
- Dickson, C.; Torabi, M.; Karimi, N. First and second law analyses of nanofluid forced convection in a partially-filled porous channel—The effects of local thermal non-equilibrium and internal heat sources. Appl. Therm. Eng. 2016, 103, 459–480. [Google Scholar] [CrossRef]
- Mehta, S.; Chauhan, K.P.; Kanagaraj, S. Modeling of thermal conductivity of nanofluids by modifying Maxwell’s equation using cell model approach. J. Nanopart. Res. 2011, 13, 2791–2798. [Google Scholar] [CrossRef]
- Mishra, P.C.; Mukherjee, S.; Nayak, S.K.; Panda, A. A brief review on viscosity of nanofluids. Int. Nano Lett. 2014, 4, 109–120. [Google Scholar] [CrossRef]
- Miroshnichenko, I.V.; Sheremet, M.A.; Oztop, H.F.; Al-Salem, K. MHD natural convection in a partially open trapezoidal cavity filled with a nanofluid. Int. J. Mech. Sci. 2016, 119, 294–302. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Oztop, H.F.; Pop, I.; Abu-Hamdeh, N. Analysis of entropy generation in natural convection of nanofluid inside a square cavity having hot solid block: Tiwari and das’ model. Entropy 2016, 18, 9. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Cimpean, D.S.; Pop, I. Free convection in a partially heated wavy porous cavity filled with a nanofluid under the effects of Brownian diffusion and thermophoresis. Appl. Therm. Eng. 2017, 113, 413–418. [Google Scholar] [CrossRef]
- Amani, M.; Amani, P.; Kasaeian, A.; Mahian, O.; Yan, W.M. Two-phase mixture model for nanofluid turbulent flow and heat transfer: Effect of heterogeneous distribution of nanoparticles. Chem. Eng. Sci. 2017, 167, 135–144. [Google Scholar] [CrossRef]
- Torabi, M.; Torabi, M.; Ghiaasiaan, S.M.; Peterson, G.P. The effect of Al2O3-water nanofluid on the heat transfer and entropy generation of laminar forced convection through isotropic porous media. Int. J. Heat Mass Transf. 2017, 111, 804–816. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).