Entropy Conditions Involved in the Nonlinear Coupled Constitutive Method for Solving Continuum and Rarefied Gas Flows
Abstract
:1. Introduction
2. Boltzmann Equations and Entropy Transport Equation
2.1. Boltzmann Equations and the Feature of Irreversibility
2.2. H Theorem and Entropy Balance Equation
3. Nonlinear Coupled Constitutive Method
3.1. Conservation Laws in the NCCM
3.2. Evolution Equations of the Nonconservation Variables in NCCM
3.3. Treatment of the Distribution Function in the Boltzmann Equation
- (1)
- The definition of the distribution function from nonequilibrium to equilibrium is weak in form and dynamic. In other words, the distribution function has no exact and specific expression in the process of nonequilibrium.
- (2)
- The distribution function should fulfil not only the conservations of mass, momentum, and energy, but also the H theorem and positive entropy generation.
3.4. Treatment of the Collision Term in the Boltzmann Equation
3.5. Nonlinear Coupled Constitutive Method
3.6. Comparisons among the Viscous Stress in the NCCM, the Grad Moment Method, and the Burnett Equation
- (1)
- The NCCM and the Burnett and Grad moment methods show nonlinear constitutive relations which is quite different from the NSF equation. However, the NCCM and the Burnett and Grad moment methods have the same linear relations as those of Newton’s laws near the equilibrium state. In other words, the NSF equation can be regarded as the low-order approximation of NCCM, Burnett, and Grad. Further discussion can be found in [4,22].
- (2)
- All three of these nonlinear relationships are consistent in the near-equilibrium region. Because both of the latter methods can solve the problem of near-equilibrium gas flows, the NCCM should be correct in the near-equilibrium region.
- (3)
- The NCCM has a different nonlinear trend than those of the Burnett equation and the Grad moment method in the far-from-equilibrium region. Note that both the Burnett equation and the Grad moment method cannot be used in far-from-equilibrium states. In contrast, the NCCM shows the opposite trends as those of the Grad moment and Burnett methods. This finding has been validated by the DSMC method, as shown in Figure 1. This feature indicates that the NCCM can be used to describe the gas flow in the far-from-equilibrium state.
4. Results
4.1. Verification and Validation
4.2. Cavity Flow
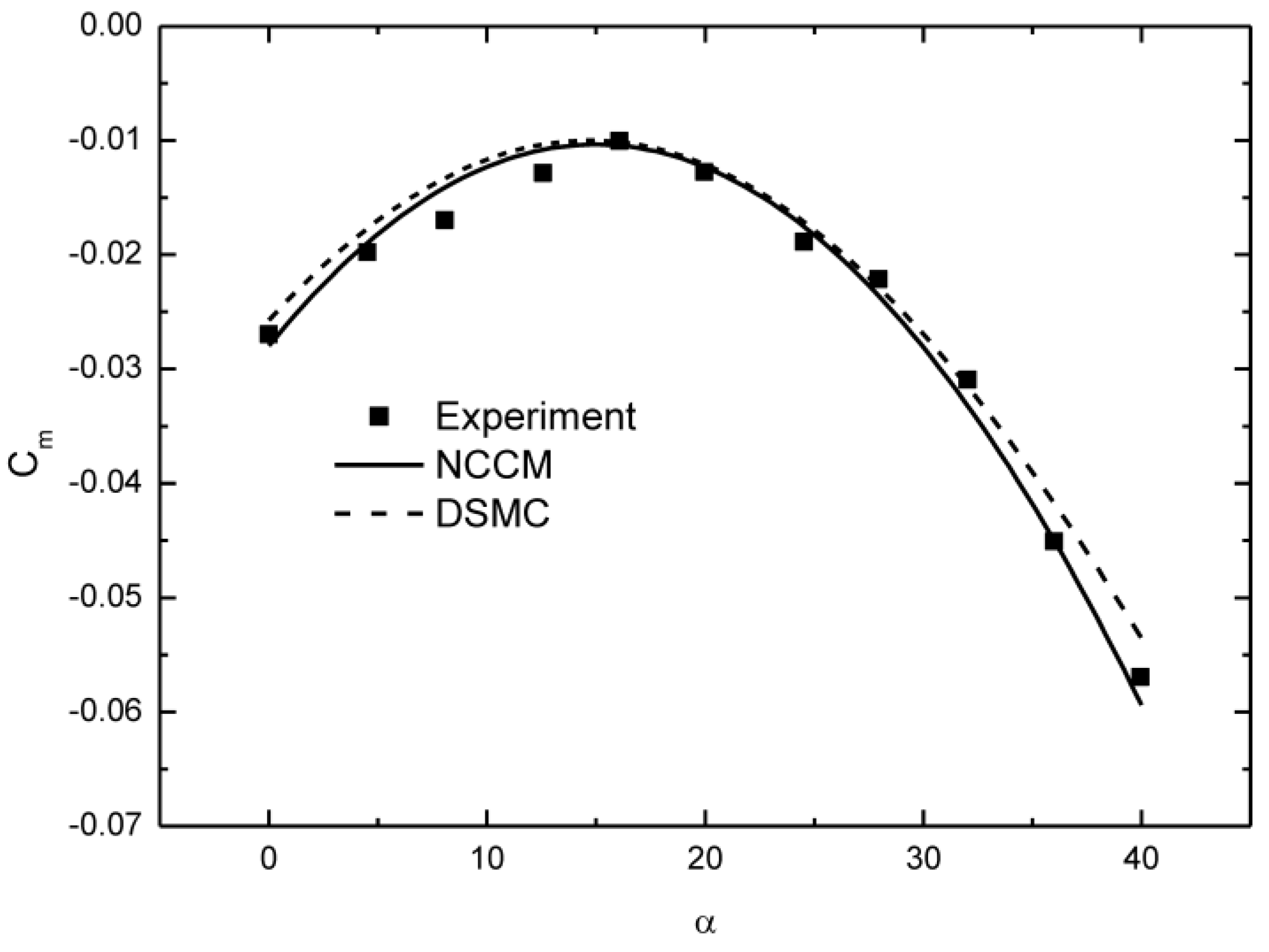
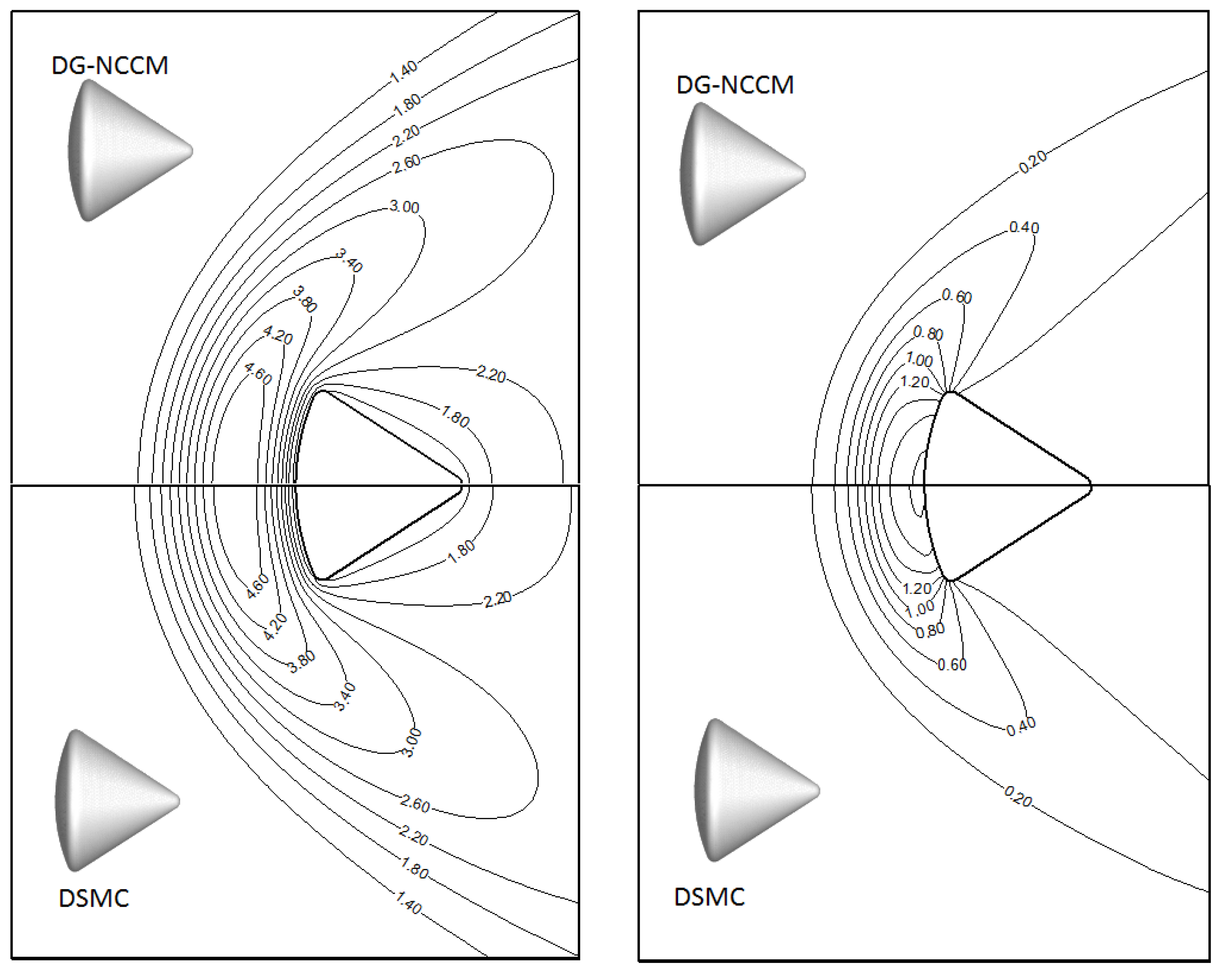
4.3. Hypersonic Gas Flow in a Low Kn Number
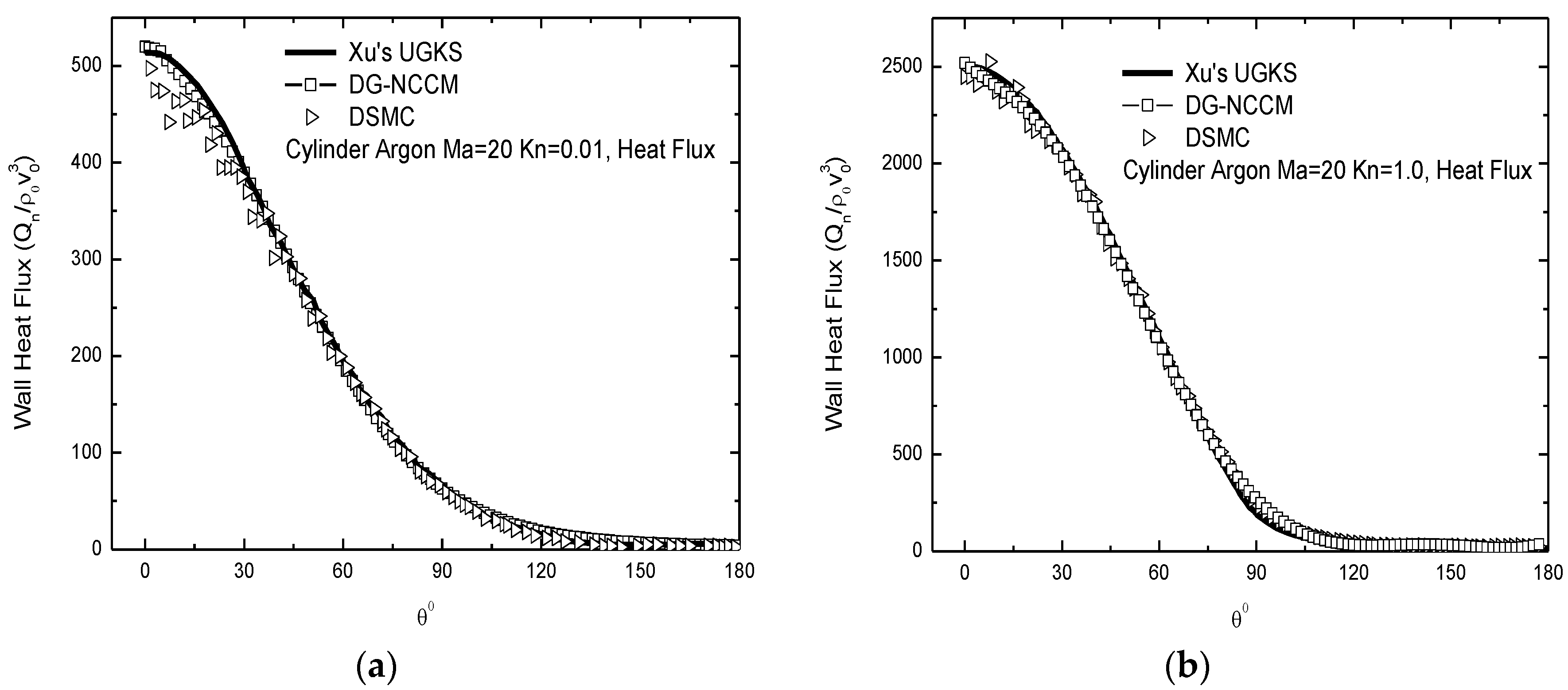
4.4. Hypersonic Gas Flow at a High Kn Number
5. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. The Derivation of the Nonlinear Parameter in the NCCM
Appendix B. Positive Entropy Production in Eu Moment Equations
References
- Shahabi, V.; Baier, T.; Roohi, E.; Hardt, S. Thermally induced gas flows in ratchet channels with diffuse and specular boundaries. Sci. Rep. 2017, 7, 41412. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Hu, L.; Meegoda, J.N.; Gao, S. Micro/nano-pore network analysis of gas flow in shale matrix. Sci. Rep. 2015, 5, 13501. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Yao, J.; Zhang, M.; Zhang, L.; Yang, Y.; Sun, H.; An, S.; Li, A. Study of gas flow characteristics in tight porous media with a microscale lattice Boltzmann model. Sci. Rep. 2016, 6, 32393. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H.; Tang, K. A Unified Framework for Modelling Continuum and Rarefied Gas Flows. Sci. Rep. 2017, 7, 13108. [Google Scholar] [CrossRef] [PubMed]
- Hadjiconstantinou, N.G. The limits of Navier-Stokes theory and kinetic extensions for describing small-scale gaseous hydrodynamics. Phys. Fluids 2006, 18, 111301. [Google Scholar] [CrossRef]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Claredon: Oxford, UK, 1994; pp. 115–123. [Google Scholar]
- Bird, G.A. The DSMC Method; Version 1.1.; Claredon: Oxford, UK, 2013; pp. 101–136. [Google Scholar]
- Fan, J.; Boyd, I.D.; Cai, C.P.; Hennighausen, K.; Candler, G.V. Computation of rarefied gas flows around a NACA 0012 airfoil. AIAA J. 2001, 39, 618–625. [Google Scholar] [CrossRef]
- Sun, Q.; Boyd, I.D. Flat-plate aerodynamics at very low Reynolds number. J. Fluid Mech. 2004, 502, 199–206. [Google Scholar] [CrossRef]
- Higuera, F.J.; Succi, S.; Benzi, R. Lattice gas dynamics with enhanced collisions. EPL (Europhys. Lett.) 1989, 9, 345. [Google Scholar] [CrossRef]
- Benzi, R.; Succi, S.; Vergassola, M. The lattice Boltzmann equation: Theory and applications. Phys. Rep. 1992, 222, 145–197. [Google Scholar] [CrossRef]
- Montessori, A.; Prestininzi, P.; la Rocca, M.; Succi, S. Lattice Boltzmann approach for complex nonequilibrium flows. Phys. Rev. E 2015, 92, 043308. [Google Scholar] [CrossRef] [PubMed]
- Nabovati, A.; Sellan, D.P.; Amon, C.H. On the lattice Boltzmann method for phonon transport. J. Comput. Phys. 2011, 230, 5864–5876. [Google Scholar] [CrossRef]
- He, X.; Chen, S.; Zhang, R. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh–Taylor instability. J. Comput. Phys. 1999, 152, 642–663. [Google Scholar] [CrossRef]
- Chen, H.; Kandasamy, S.; Orszag, S.; Shock, R.; Succi, S.; Yakhot, V. Extended Boltzmann kinetic equation for turbulent flows. Science 2003, 301, 633–636. [Google Scholar] [CrossRef] [PubMed]
- Burnett, D. The distribution of molecular velocities and the mean motion in a non-uniform gas. Proc. Lond. Math. Soc. 1936, 2, 382–435. [Google Scholar] [CrossRef]
- Comeaux, K.A.; Chapman, D.R.; MacCormack, R.W. An analysis of the Burnett equations based on the second law of thermodynamics. In Proceedings of the 33rd AIAA, Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12 January 1995. [Google Scholar]
- Grad, H. On the kinetic theory of rarefied gases. Commun. Pure Appl. Math. 1949, 2, 331–407. [Google Scholar] [CrossRef]
- Torrilhon, M.; Struchtrup, H. Boundary conditions for regularized 13-moment-equations for micro-channel-flows. J. Comput. Phys. 2008, 227, 1982–2011. [Google Scholar] [CrossRef]
- Torrilhon, M. Special issues on moment methods in kinetic gas theory. Contin. Mech. Thermodyn. 2009, 21, 341–343. [Google Scholar] [CrossRef]
- Eu, B.C. Kinetic Theory and Irreversible Thermodynamics; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Myong, R.S. A generalized hydrodynamic computational model for rarefied and microscale diatomic gas flows. J. Comput. Phys. 2004, 195, 655–676. [Google Scholar] [CrossRef]
- Myong, R.S. On the high Mach number shock structure singularity caused by overreach of Maxwellian molecules. Phys. Fluids 2014, 26, 056102. [Google Scholar] [CrossRef]
- Xiao, H.; Shang, Y.H.; Wu, D.; Shi, Y.Y. Nonlinear coupled constitutive relations and its validation for rarefied gas flows. Acta Aeronaut. Astronaut. Sin. 2015, 36, 2091–2104. [Google Scholar]
- Le, N.T.P.; Xiao, H.; Myong, R.S. A triangular discontinuous Galerkin method for non-Newtonian implicit constitutive models of rarefied and microscale gases. J. Comput. Phys. 2014, 273, 160–184. [Google Scholar] [CrossRef]
- Xiao, H.; Myong, R.S. Computational simulations of micro scale shock–vortex interaction using a mixed discontinuous Galerkin method. Comput. Fluids 2014, 105, 179–193. [Google Scholar] [CrossRef]
- Allegre, J.; Raffin, M.; Gottesdient, L. Slip Effect on Supersonic Flow Fields Around NACA 0012 Airfoils, Rarefied Gas Dynamics 15; Boffi, V., Cercigani, C., Eds.; Vieweg + Teubner Verlag: Braunschweig, Germany, 1986; pp. 548–557. [Google Scholar]
- Zhu, Y.; Zhong, C.; Xu, K. Implicit unified gas-kinetic scheme for steady state solutions in all flow regimes. J. Comput. Phys. 2016, 315, 16–38. [Google Scholar] [CrossRef]
- Chen, S.Z.; Guo, Z.L.; Xu, K. Simplification of the unified gas kinetic scheme. Phys. Rev. E 2016, 94, 023313. [Google Scholar] [CrossRef] [PubMed]

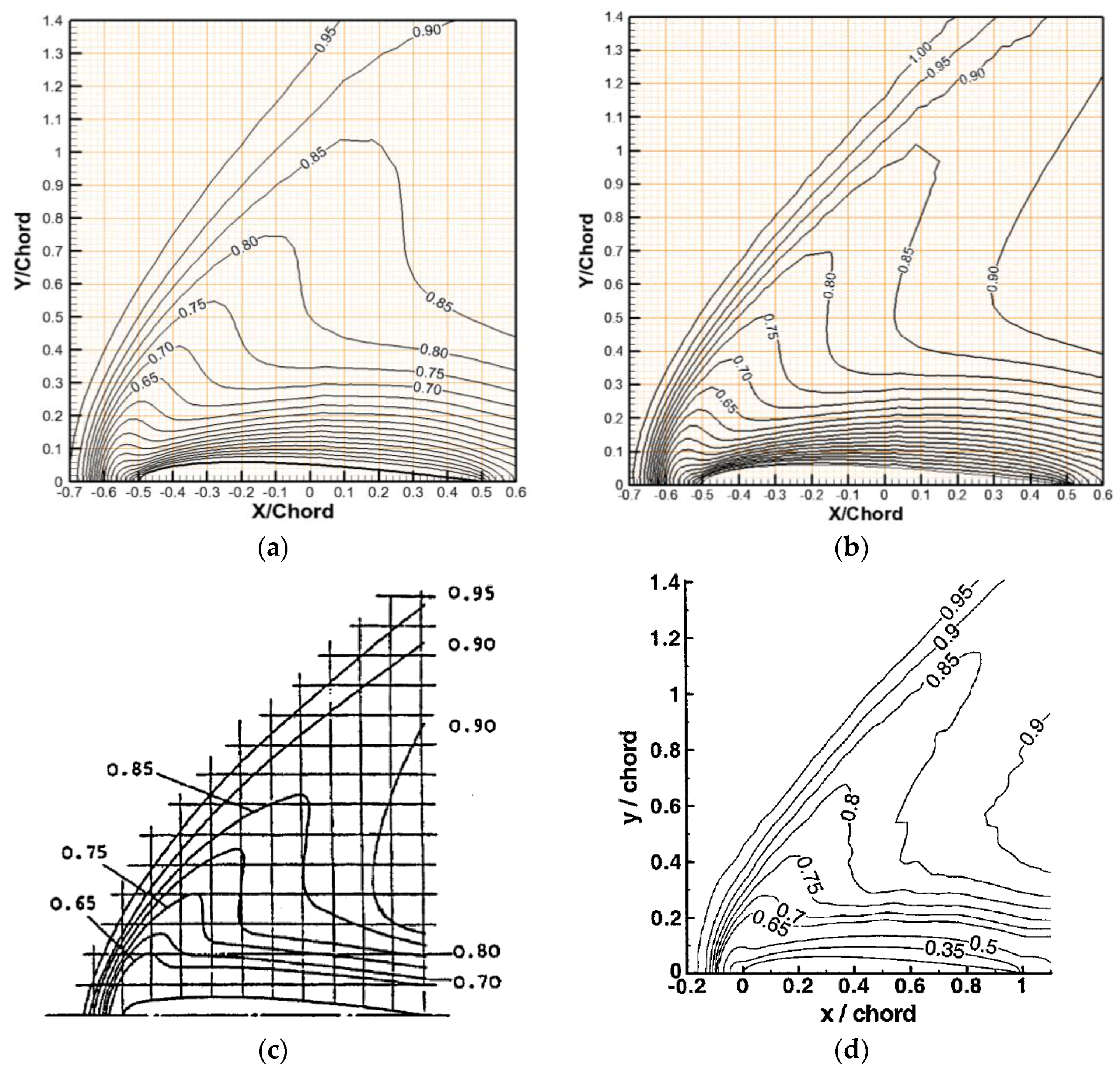
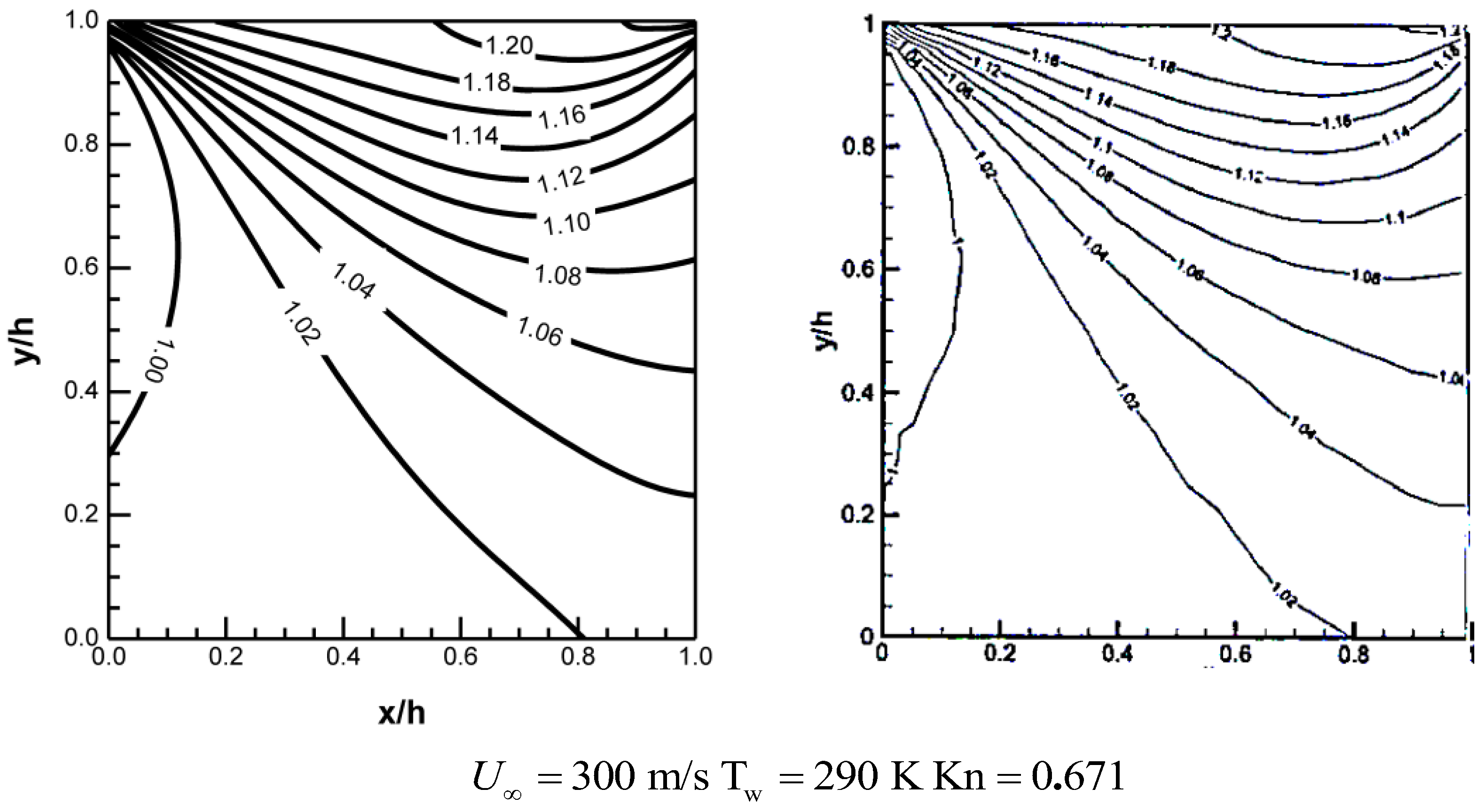
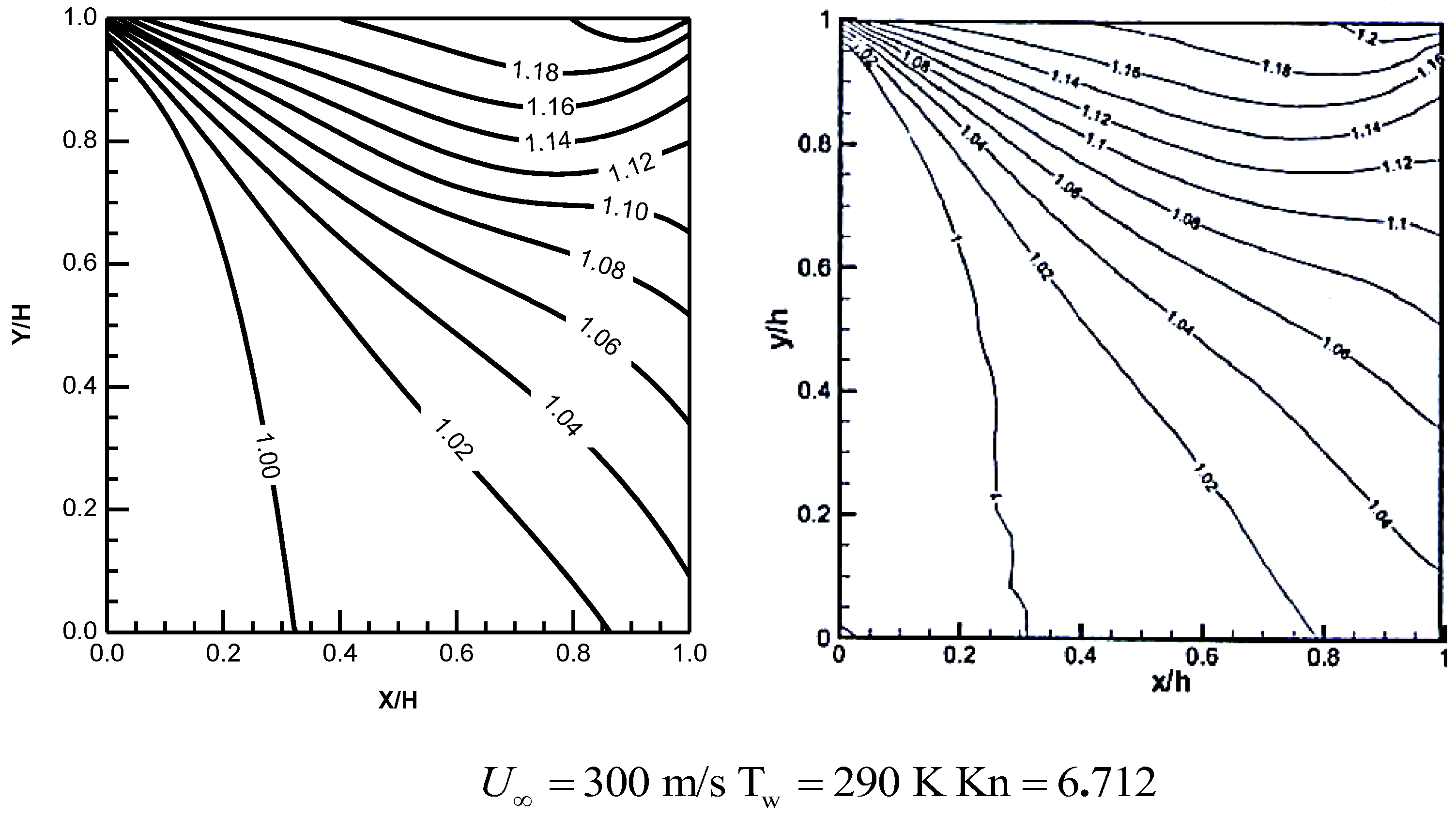
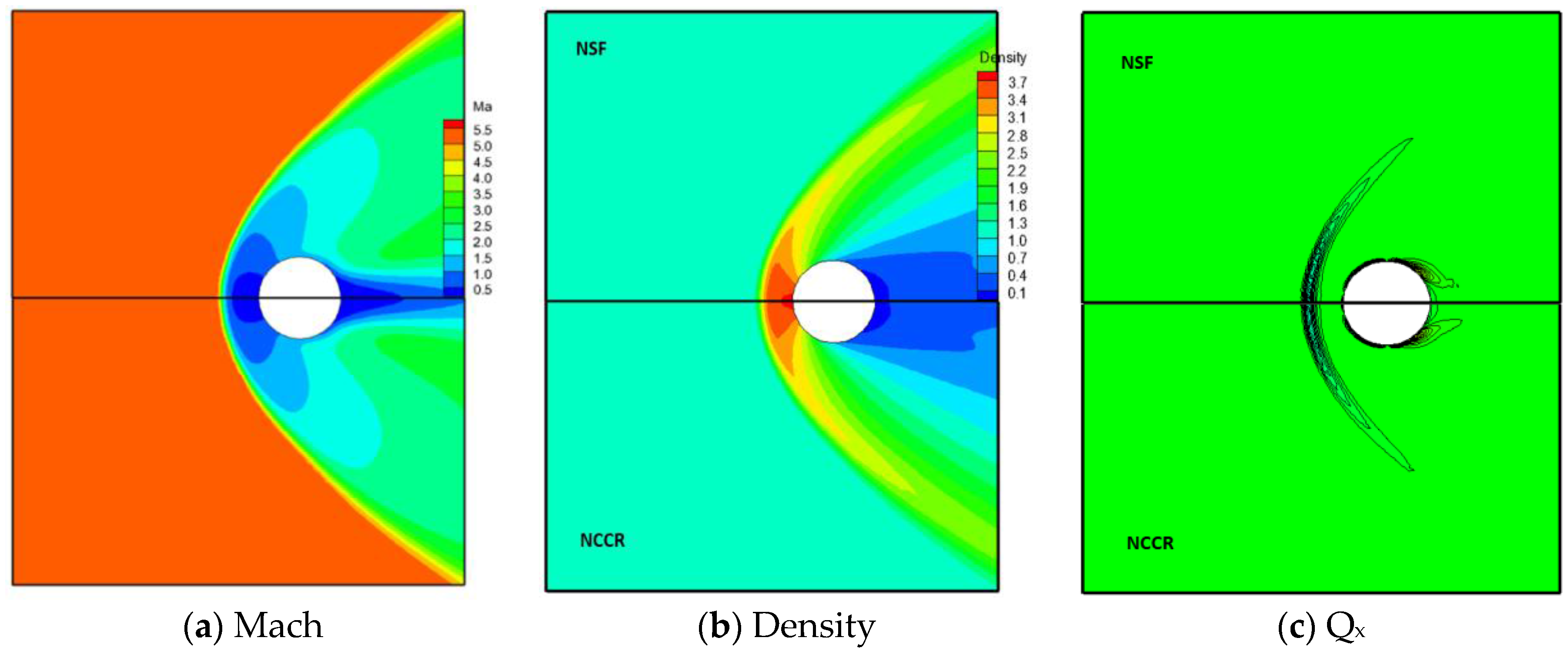
| Case | 20 × 20 | 40 × 40 | 80 × 80 | 100 × 100 |
|---|---|---|---|---|
| CD | 0.4101 | 0.3951 | 0.3901 | 0.3902 |
| CL | 9.0 × 10−3 | 1.23 × 10−4 | 1.02 × 10−6 | 1.11 × 10−6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, K.; Xiao, H. Entropy Conditions Involved in the Nonlinear Coupled Constitutive Method for Solving Continuum and Rarefied Gas Flows. Entropy 2017, 19, 683. https://doi.org/10.3390/e19120683
Tang K, Xiao H. Entropy Conditions Involved in the Nonlinear Coupled Constitutive Method for Solving Continuum and Rarefied Gas Flows. Entropy. 2017; 19(12):683. https://doi.org/10.3390/e19120683
Chicago/Turabian StyleTang, Ke, and Hong Xiao. 2017. "Entropy Conditions Involved in the Nonlinear Coupled Constitutive Method for Solving Continuum and Rarefied Gas Flows" Entropy 19, no. 12: 683. https://doi.org/10.3390/e19120683
APA StyleTang, K., & Xiao, H. (2017). Entropy Conditions Involved in the Nonlinear Coupled Constitutive Method for Solving Continuum and Rarefied Gas Flows. Entropy, 19(12), 683. https://doi.org/10.3390/e19120683





