Chaos in a Cancer Model via Fractional Derivatives with Exponential Decay and Mittag-Leffler Law

Abstract

In this paper, a three-dimensional cancer model was considered using the Caputo-Fabrizio-Caputo and the new fractional derivative with Mittag-Leffler kernel in Liouville-Caputo sense. Special solutions using an iterative scheme via Laplace transform, Sumudu-Picard integration method and Adams-Moulton rule were obtained. We studied the uniqueness and existence of the solutions. Novel chaotic attractors with total order less than three are obtained.

1. Introduction

Mathematical models for tumour growth have been extensively studied in the literature, and the main purpose of these studies is to understand the mechanism of the disease and to predict its future behavior. These models are governed by ordinary differential equations; however, the local differentiation has failed to portray real world problems due to the lack of non-locality effect into mathematical formulation; to solve them, mathematicians introduced the concept of differentiation with non-local operators. The concept of fractional calculus (FC) involved the concept of differentiation with non-local operators (fractional differentiation) is the natural generalization of the classical calculus. Fractional operators represent dissipative effects or damage; these considerations are important for modeling real world problems [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. Michele Caputo and Mauro Fabrizio in [16] presented a new definition of fractional operator based on the exponential decay law without singular kernel; its definition is based on the convolution of a first-order derivative and the exponential function. Losada and Nieto [17] analyzed the properties of this newly presented fractional derivative. Based on this new derivative, some interesting studies can be found in [18,19,20,21,22,23]. Recently, Atangana and Baleanu suggested two fractional operators in Liouville-Caputo and Riemann-Liouville sense based on the generalized Mittag-Leffler function; these fractional operators with non-singular and non-local kernel were introduced in order to better describe complex physical problems that follows at the same time the power and exponential decay law [24,25,26,27,28,29,30].

FC is applied in different directions of physics, control process, signal processing, mathematical biology and in many more. Particularly, mathematical biology is a rich source for mathematical ideas. Actually, several investigators begin to study the qualitative properties and numerical solutions of biological models considering fractional order derivatives. For instance, Area in [31] studied the fractional order ebola epidemic model. Singh in [32] explained a fractional biological population model. Based on a Caputo-Fabrizio fractional derivative, a new fractional model or giving up smoking dynamics was presented in [33]. Numerical solutions were obtained with the aid of an iterative technique, the existence and uniqueness of the solutions are obtained. González-Parra [34] studied the nonlinear fractional order influenza A (H1N1) model. Arshad in [35] considered a fractional HIV (human immunodeficiency virus) infection model with particular focus on the degree of T-cell depletion. Stability and equilibrium points were investigated. In these models, the fractional order equations are related to systems with memory that exists in the biological systems.

Another important area of application of the FC is the chaos theory. In the fractional case, the model of the system can be rearranged into three fractional equations, and each equation could contain the non integer fractional order. In these systems, the total order of the system is the sum of each particular order. In [36], the authors studied the chaotic behaviors in the fractional order Chen system. A synchronization scheme in fractional-order complex Lorenz systems is presented in [37]. Chaotic regions, periodic windows and routes to chaos were explored. The other fractional order chaotic systems were described in many other works [38,39,40,41]. In cancer models, the dynamics of the interactions of the tumour cells with other cells may exhibit chaos [42,43,44,45].

In this work, we consider a non-dimensionalized cancer system described in [46]. Starting from the integer-order cancer model defined as

$${\dot{x}}_1\left(t\right)=x_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right),$$

$${\dot{x}}_2\left(t\right)=C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right),$$

(1)

$${\dot{x}}_3\left(t\right)=E\frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right),$$

where {A, B, C, D, E, F, G, H} are system parameters.

This model considers three cell populations: $x_1\left(t\right)$ denotes the number of tumour cells at time t; $x_2\left(t\right)$ is the number of healthy host cells at time t, and $x_3\left(t\right)$ refers to the number of effector immune cells at time t in the single tumour-site compartment. The first equation gives the rate of change in the population of the tumour cells with time t. The second equation consider that healthy tissue cells grow logistically and involved to maximum carrying capacity. The model assumes that the cancer cells proliferate faster than the healthy cells. Finally, the third equation illustrates the stimulation of the immune system by the tumour cells with tumour specific antigens [46].

2. Fractional Operators

The Caputo-Fabrizio fractional derivative in Liouville-Caputo sense (CFC) is given by [16]

$${}_0^{CFC}{\mathcal{D}}_t^{\gamma }\left\{f\left(t\right)\right\}=\frac{M\left(\gamma \right)}{n-\gamma }{\int }_0^t{f}^n\left(\theta \right)exp\left[-\frac{\gamma }{n-\gamma }(t-\theta )\right]d\theta ,n-1<\gamma \le n,$$

(2)

where $M\left(\gamma \right)$ is a normalization function such that $M\left(0\right)=M\left(1\right)=1$. If $f\left(t\right)$ is a constant function, then, the Caputo-Fabrizio-Caputo derivative given by Equation (2) is zero. For this fractional derivative, the kernel in Equation (2) does not have singularity for $t=\theta$. This property is of particular interest because it can describe the full memory effect for a given system.

The Laplace transform of the CFC fractional derivative is given by

$$\mathcal{L}\left\{{}_0^{CFC}{\mathcal{D}}_t^{\gamma }f\left(t\right)\right\}\left(s\right)=\frac{sF\left(s\right)-f\left(0\right)}{s+\gamma (1-s)}.$$

(3)

The Sumudu transform (ST) of Equation (2) is defined as

$$ST\left\{{}_0^{CFC}{\mathcal{D}}_t^{\gamma }f\left(t\right)\right\}\left(s\right)=M\left(\gamma \right)\frac{ST\left[f\right(t\left)\right]-f\left(0\right)}{1+\gamma (s-1)}.$$

(4)

The fractional integral of order $\gamma$, $(0<\gamma <1)$ of the function $f\left(t\right)$ is defined below [17]

$${}_0^{CF}{I}_t^{\gamma }f\left(t\right)=\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}f\left(t\right)+\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\int }_0^{t}f\left(s\right)ds.t\ge 0,$$

(5)

where

$$M\left(\gamma \right)=\frac{2}{2-\gamma },0<\gamma <1.$$

(6)

The Atangana-Baleanu fractional derivative in Liouville-Caputo sense (ABC) is defined as follows [24]:

$${}_0^{ABC}{\mathcal{D}}_t^{\gamma }\left\{f\left(t\right)\right\}=\frac{B\left(\gamma \right)}{n-\gamma }{\int }_0^t{f}^n\left(\theta \right)E_{\gamma }\left[-\frac{\gamma }{n-\gamma }{(t-\theta )}^{\gamma }\right]d\theta ,n-1<\gamma \le n,$$

(7)

where $B\left(\gamma \right)=B\left(0\right)=B\left(1\right)=1$ is a normalization function and $E_{\gamma }$ is the Mittag-Leffler function.

The Laplace transform of Equation (7) is defined as follows:

$$\begin{array}{cc}\hfill \mathcal{L}\left\{{}_0^{ABC}{\mathcal{D}}_t^{\gamma }f\left(t\right)\right\}\left(s\right)& ={\displaystyle \frac{B\left(\gamma \right)}{1-\gamma }}\mathcal{L}\left[{\int }_a^t\dot{f}\left(\theta \right)E_{\gamma }\left[-\gamma {\displaystyle \frac{{(t-\theta )}^{\gamma }}{1-\gamma }}\right]d\theta \right]\left(s\right)\hfill \\ & ={\displaystyle \frac{B\left(\gamma \right)}{1-\gamma }}{\displaystyle \frac{s^{\gamma }\mathcal{L}\left[f\left(t\right)\right]\left(s\right)-s^{\gamma -1}f\left(0\right)}{s^{\gamma }+{\displaystyle \frac{\gamma }{1-\gamma }}}}.\hfill \end{array}$$

(8)

The Sumudu transform (ST) of Equation (7) is defined as

$$ST\left\{{}_0^{ABC}{\mathcal{D}}_t^{\gamma }f\left(t\right)\right\}\left(s\right)=\frac{B\left(\gamma \right)}{1-\gamma }\left(\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-\frac{1}{1-\gamma }{u}^{\gamma }\right)\right)\times [ST\left(f\left(t\right)\right)-f\left(0\right)].$$

(9)

The Atangana-Baleanu fractional integral of order $\gamma$ of a function $f\left(t\right)$ is defined as

$${}_0^{AB}{I}_t^{\gamma }f\left(t\right)=\frac{1-\gamma }{B\left(\gamma \right)}f\left(t\right)+\frac{\gamma }{B\left(\gamma \right)\mathsf{\Gamma }\left(\gamma \right)}{\int }_0^{t}f\left(s\right){(t-s)}^{\gamma -1}ds.$$

(10)

3. Cancer Model

In this section, we obtain alternative representations of the cancer model considering the Caputo-Fabrizio-Caputo and Atangana-Baleanu-Caputo fractional derivatives, special solution are obtained using Laplace transform method and Sumudu transform method.

3.1. Cancer Model with Exponential Decay Law

Considering Equation (2), the modified cancer model with exponential law kernel is given as

$$\begin{array}{c}{}_0^{CFC}{\mathcal{D}}_t^{\gamma }{x}_1\left(t\right)=x_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right),\\ {}_0^{CFC}{\mathcal{D}}_t^{\gamma }{x}_2\left(t\right)=C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right),\\ {}_0^{CFC}{\mathcal{D}}_t^{\gamma }{x}_3\left(t\right)=E{\displaystyle \frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right),\end{array}$$

(11)

where ${}_0^{CFC}{\mathcal{D}}_t^{\gamma }$, represents the fractional derivative of type Caputo-Fabrizio-Caputo, $0<\gamma \le 1$ is the fractional order. The model is subject to initial conditions

$$x_{1\left(0\right)}\left(t\right)=x_1\left(0\right);x_{2\left(0\right)}\left(t\right)=x_2\left(0\right);x_{3\left(0\right)}\left(t\right)=x_3\left(0\right).$$

(12)

By using the fixed-point theorem, we define the existence of the solution. First, transform Equation (11) into an integral equation as follows:

$$\begin{array}{c}{x}_1\left(t\right)-x_1\left(0\right){=}_0^{CF}{I}_t^{\gamma }[x_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right)],\\ x_2\left(t\right)-x_2\left(0\right){=}_0^{CF}{I}_t^{\gamma }[C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right)],\\ x_3\left(t\right)-x_3\left(0\right){=}_0^{CF}{I}_t^{\gamma }\left[E{\displaystyle \frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right)\right],\end{array}$$

(13)

considering the fractional integral of order $\gamma$ given by Equation (5), we get

$$\begin{array}{c}{x}_1\left(t\right)=x_1\left(0\right)+{\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}[x_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right)]\\ t+{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t[x_1\left(s\right)(1-x_1\left(s\right))-A{x}_1\left(s\right)x_2\left(s\right)-B{x}_1\left(s\right)x_3\left(s\right)]ds,\\ x_2\left(t\right)=x_2\left(0\right)+{\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}[C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right)]\\ +{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t[C{x}_2\left(s\right)(1-x_2\left(s\right))-D{x}_1\left(s\right)x_2\left(s\right)]ds,\\ x_3\left(t\right)=x_3\left(0\right)+{\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}[E{\displaystyle \frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right)]\\ +{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t[E{\displaystyle \frac{x_1\left(s\right)x_3\left(s\right)}{x_1\left(s\right)+F}}-G{x}_1\left(s\right)x_3\left(s\right)-H{x}_3\left(s\right)]ds.\end{array}$$

(14)

Now, we consider the following kernels

$$\begin{array}{c}\tau (t,x_1\left(t\right))=x_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right),\\ \upsilon (t,x_2\left(t\right))=C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right),\\ \varphi (t,x_3\left(t\right))=E{\displaystyle \frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right).\end{array}$$

(15)

Theorem 1.

We prove that the kernels τ, υ and φ satisfy the Lipschitz condition.

Proof of Theorem 1

We prove this condition for each kernel proposed. Let $x_1$ and $X_1$, for the kernel 1, $x_2$ and $X_2$, for the kernel 2, and $x_3$ and $X_3$, for the kernel 3, be two functions; then, we assess the following:

$$\begin{array}{c}\left|\right|\tau (t,x_1\left(t\right))-\tau (t,X_1\left(t\right))\left|\right|=\left|\right|(x_1\left(t\right)-X_1\left(t\right))[1-(x_1\left(t\right)-X_1\left(t\right))]\\ -A(x_1\left(t\right)-X_1\left(t\right))x_2\left(t\right)-B(x_1\left(t\right)-X_1\left(t\right))x_3\left(t\right)\left|\right|,\\ \left|\right|\upsilon (t,x_2\left(t\right))-\upsilon (t,X_2\left(t\right))\left|\right|=C\left|\right|(x_2\left(t\right)-X_2\left(t\right))[1-(x_2\left(t\right)-X_2\left(t\right))]\\ -D{x}_1\left(t\right)(x_2\left(t\right)-X_2\left(t\right))\left|\right|,\\ \left|\right|\varphi (t,x_3\left(t\right))-\varphi (t,X_3\left(t\right))\left|\right|=E\left|\right|{\displaystyle \frac{x_1\left(t\right)(x_3\left(t\right)-X_3\left(t\right))}{x_1\left(t\right)+F}}\\ -G{x}_1\left(t\right)(x_3\left(t\right)-X_3\left(t\right))-H(x_3\left(t\right)-X_3\left(t\right))\left|\right|.\end{array}$$

(16)

Using Cauchy’s inequality in Equation (16), we get

$$\begin{array}{c}\left|\right|\tau (t,x_1\left(t\right))-\tau (t,X_1\left(t\right))\left|\right|\le \left|\right|(x_1\left(t\right)-X_1\left(t\right))[1-(x_1\left(t\right)-X_1\left(t\right))]\\ -A(x_1\left(t\right)-X_1\left(t\right))x_2\left(t\right)-B(x_1\left(t\right)-X_1\left(t\right))x_3\left(t\right)\left|\right|,\\ \left|\right|\upsilon (t,x_2\left(t\right))-\upsilon (t,X_2\left(t\right))\left|\right|\le C\left|\right|(x_2\left(t\right)-X_2\left(t\right))[1-(x_2\left(t\right)-X_2\left(t\right))]\\ -D{x}_1\left(t\right)(x_2\left(t\right)-X_2\left(t\right))\left|\right|,\\ \left|\right|\varphi (t,x_3\left(t\right))-\varphi (t,X_3\left(t\right))\left|\right|\le E\left|\right|{\displaystyle \frac{x_1\left(t\right)(x_3\left(t\right)-X_3\left(t\right))}{x_1\left(t\right)+F}}\\ -G{x}_1\left(t\right)(x_3\left(t\right)-X_3\left(t\right))-H(x_3\left(t\right)-X_3\left(t\right))\left|\right|;\end{array}$$

(17)

considering the following recursive formula, we have

$$x_1\left(t\right)=\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\tau (t,x_{1(n-1)})+\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\int }_0^t\tau (s,x_{1(n-1)})ds,$$

$$x_2\left(t\right)=\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\upsilon (t,x_{2(n-1)})+\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\int }_0^t\upsilon (s,x_{2(n-1)})ds,$$

(18)

$$x_3\left(t\right)=\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\varphi (t,x_{3(n-1)})+\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\int }_0^t\varphi (s,x_{3(n-1)})ds.$$

Now, we present the difference between the successive terms, applying the norm and the triangular inequality, we get

$$\begin{array}{c}\left|\right|{\mathsf{{\rm Y}}}_n\left(t\right)\left|\right|=\left|\right|x_{1\left(n\right)}\left(t\right)-X_{1(n-1)}\left(t\right)\left|\right|\le \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\left|\right|\tau (t,x_{1(n-1)}\left(t\right))-\tau (t,X_{1(n-2)}\left(t\right))\left|\right|\\ +\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}\left|\right|{\int }_0^t\left[\tau (s,x_{1(n-1)}\left(s\right))-\tau (s,X_{1(n-2)}\left(s\right))\right]\left|\right|ds,\\ \left|\right|{\mathsf{\Phi }}_n\left(t\right)\left|\right|=\left|\right|x_{2\left(n\right)}\left(t\right)-X_{2(n-1)}\left(t\right)\left|\right|\le \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\left|\right|\upsilon (t,x_{2(n-1)}\left(t\right))-\upsilon (t,X_{2(n-2)}\left(t\right))\left|\right|\\ +\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}\left|\right|{\int }_0^t\left[\upsilon (s,x_{2(n-1)}\left(s\right))-\upsilon (s,X_{2(n-2)}\left(s\right))\right]\left|\right|ds,\\ \left|\right|{\mathsf{\Psi }}_n\left(t\right)\left|\right|=\left|\right|x_{3\left(n\right)}\left(t\right)-X_{3(n-1)}\left(t\right)\left|\right|\le \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\left|\right|\varphi (t,x_{3(n-1)}\left(t\right))-\varphi (t,X_{3(n-2)}\left(t\right))\left|\right|\\ +\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}\left|\right|{\int }_0^t\left[\varphi (s,x_{3(n-1)}\left(s\right))-\varphi (s,X_{3(n-2)}\left(s\right))\right]\left|\right|ds,\end{array}$$

(19)

where

$$x_{1\left(n\right)}\left(t\right)=\sum _{m=0}^{\infty }{\mathsf{{\rm Y}}}_m\left(t\right);x_{2\left(n\right)}\left(t\right)=\sum _{m=0}^{\infty }{\mathsf{\Phi }}_m\left(t\right);x_{3\left(n\right)}\left(t\right)=\sum _{m=0}^{\infty }{\mathsf{\Psi }}_m\left(t\right).$$

(20)

Since the kernels $\tau$, $\upsilon$ and $\varphi$ satisfy the Lipschitz condition, we have

$$\begin{array}{c}\left|\right|{\mathsf{{\rm Y}}}_n\left(t\right)\left|\right|=\left|\right|x_{1\left(n\right)}\left(t\right)-X_{1(n-1)}\left(t\right)\left|\right|\le {\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}{\Delta }_1\left|\right|x_{1(n-1)}\left(t\right)-X_{1(n-2)}\left(t\right)\left|\right|\\ +{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\Delta }_2{\int }_0^t\left|\right|x_{1(n-1)}\left(s\right)-X_{1(n-2)}\left(s\right)\left|\right|ds,\\ \left|\right|{\mathsf{\Phi }}_n\left(t\right)\left|\right|=\left|\right|x_{2\left(n\right)}\left(t\right)-X_{2(n-1)}\left(t\right)\left|\right|\le {\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}{\Delta }_3\left|\right|x_{2(n-1)}\left(t\right)-X_{2(n-2)}\left(t\right)\left|\right|\\ +{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\Delta }_4{\int }_0^t\left|\right|x_{2(n-1)}\left(s\right)-X_{2(n-2)}\left(s\right)\left|\right|ds,\\ \left|\right|{\mathsf{\Psi }}_n\left(t\right)\left|\right|=\left|\right|x_{3\left(n\right)}\left(t\right)-X_{3(n-1)}\left(t\right)\left|\right|\le {\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}{\Delta }_5\left|\right|x_{3(n-1)}\left(t\right)-X_{3(n-2)}\left(t\right)\left|\right|\\ +{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\Delta }_6{\int }_0^t\left|\right|x_{3(n-1)}\left(s\right)-X_{3(n-2)}\left(s\right)\left|\right|ds,\end{array}$$

(21)

and this completes the proof of Theorem 1. ☐

Theorem 2.

The system given by Equation (11) has a unique solution.

Proof of Theorem 2

Considering Equation (21) bounded, we have proven that the kernels $\tau$, $\upsilon$ and $\varphi$ satisfy the Lipschitz condition. Considering the results obtained in Equation (21) and using the recursive technique, we get the following relation:

$$\left|\right|{\mathsf{{\rm Y}}}_n\left(t\right)\left|\right|\le \left|\right|x_1\left(0\right)\left|\right|+\left\{{\left\{\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}{\Delta }_1\right\}}^n+{\left\{\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\Delta }_{2}t\right\}}^n\right\},$$

$$\left|\right|{\mathsf{\Phi }}_n\left(t\right)\left|\right|\le \left|\right|x_2\left(0\right)\left|\right|+\left\{{\left\{\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}{\Delta }_3\right\}}^n+{\left\{\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\Delta }_{4}t\right\}}^n\right\},$$

(22)

$$\left|\right|{\mathsf{\Psi }}_n\left(t\right)\left|\right|\le \left|\right|x_3\left(0\right)\left|\right|+\left\{{\left\{\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}{\Delta }_5\right\}}^n+{\left\{\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\Delta }_{6}t\right\}}^n\right\}.$$

Therefore, Equation (22) exists and is smooth. Nonetheless, to show that the above functions are a system of solutions of Equation (11), we assume

$$x_1\left(t\right)=x_{1\left(n\right)}\left(t\right)-{\mathsf{\Theta }}_{1\left(n\right)}\left(t\right);x_2\left(t\right)=x_{2\left(n\right)}\left(t\right)-{\mathsf{\Theta }}_{2\left(n\right)}\left(t\right);x_3\left(t\right)=x_{3\left(n\right)}\left(t\right)-{\mathsf{\Theta }}_{3\left(n\right)}\left(t\right),$$

(23)

where ${\mathsf{\Theta }}_{1\left(n\right)}$, ${\mathsf{\Theta }}_{2\left(n\right)}$ and ${\mathsf{\Theta }}_{3\left(n\right)}$ are reminder terms of series solution. Thus,

$$x_1\left(t\right)-X_{1\left(n\right)}\left(t\right)=\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\tau (t,x_1-{\mathsf{\Theta }}_{1\left(n\right)}\left(t\right))+\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\int }_0^t\tau (s,x_1-{\mathsf{\Theta }}_{1\left(n\right)}\left(s\right))ds,$$

$$x_2\left(t\right)-X_{2\left(n\right)}\left(t\right)=\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\upsilon (t,x_2-{\mathsf{\Theta }}_{2\left(n\right)}\left(t\right))+\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\int }_0^t\upsilon (s,x_2-{\mathsf{\Theta }}_{2\left(n\right)}\left(s\right))ds,$$

(24)

$$x_3\left(t\right)-X_{3\left(n\right)}\left(t\right)=\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\varphi (t,x_3-{\mathsf{\Theta }}_{3\left(n\right)}\left(t\right))+\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\int }_0^t\tau (s,x_3-{\mathsf{\Theta }}_{3\left(n\right)}\left(s\right))ds.$$

Applying the norm on both sides and using the Lipschitz condition, we get

$$\begin{array}{c}\left|\right|x_1\left(t\right)-{\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}\tau (t,x_1)-x_1\left(0\right)-{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t\tau (s,x_1\left(s\right))ds\left|\right|\\ \le \left|\right|{\mathsf{\Theta }}_{1\left(n\right)}\left(t\right))+\left\{{\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}{\Delta }_1+{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\Delta }_{2}t\right\}\left|\right|{\mathsf{\Theta }}_{1\left(n\right)}\left(t\right)\left|\right|,\\ \left|\right|x_2\left(t\right)-{\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}\upsilon (t,x_2)-x_2\left(0\right)-{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t\upsilon (s,x_2\left(s\right))ds\left|\right|\\ \le \left|\right|{\mathsf{\Theta }}_{2\left(n\right)}\left(t\right))+\left\{{\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}{\Delta }_3+{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\Delta }_{4}t\right\}\left|\right|{\mathsf{\Theta }}_{2\left(n\right)}\left(t\right)\left|\right|,\\ \left|\right|x_3\left(t\right)-{\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}\varphi (t,x_3)-x_3\left(0\right)-{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t\varphi (s,x_3\left(s\right))ds\left|\right|\\ \le \left|\right|{\mathsf{\Theta }}_{3\left(n\right)}\left(t\right))+\left\{{\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}{\Delta }_5+{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\Delta }_{6}t\right\}\left|\right|{\mathsf{\Theta }}_{3\left(n\right)}\left(t\right)\left|\right|.\end{array}$$

(25)

On taking the limit $n\to \infty$ of Equation (25), we get

$$x_1\left(t\right)=\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\tau (t,x_1\left(t\right))+x_1\left(0\right)+\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\int }_0^t\tau (s,x_1\left(s\right))ds,$$

$$x_2\left(t\right)=\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\upsilon (t,x_2\left(t\right))+x_2\left(0\right)+\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\int }_0^t\upsilon (s,x_2\left(s\right))ds,$$

(26)

$$x_3\left(t\right)=\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\varphi (t,x_3\left(t\right))+x_3\left(0\right)+\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\int }_0^t\tau (s,x_3\left(s\right))ds.$$

Equation (26) is the solution of Equation (11); therefore, we can say that a solution exists. ☐

Theorem 3.

We prove that the system given by Equation (11) has a unique solution.

Proof of Theorem 3

To prove this, we can get other solutions for Equation (11), say $x_1\left(t\right)$, $x_2\left(t\right)$ and $x_3\left(t\right)$; then,

$$\begin{array}{c}{x}_1\left(t\right)-X_1\left(t\right)={\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}\left[\tau (t,x_1\left(t\right))-\tau (t,X_1\left(t\right))\right]\\ +{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t\left[\tau (s,x_1\left(s\right))-\tau (s,X_1\left(s\right))\right]ds,\\ x_2\left(t\right)-X_2\left(t\right)=\frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}\left[\upsilon (t,x_2\left(t\right))-\upsilon (t,X_2\left(t\right))\right]\\ +{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t\left[\upsilon (s,x_2\left(s\right))-\upsilon (s,X_2\left(s\right))\right]ds,\\ x_3\left(t\right)-X_3\left(t\right)={\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}\left[\varphi (t,x_3\left(t\right))-\varphi (t,X_3\left(t\right))\right]\\ +{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t\left[\varphi (s,x_3\left(s\right))-\varphi (s,X_3\left(s\right))\right]ds.\end{array}$$

(27)

Applying the norm to both sides of Equation (27), we have

$$\begin{array}{c}\left|\right|x_1\left(t\right)-X_1\left(t\right)\left|\right|\le {\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}\left[\left|\right|\tau (t,x_1\left(t\right))-\tau (t,X_1\left(t\right))\left|\right|\right]\\ +{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t\left[\left|\right|\tau (s,x_1\left(s\right))-\tau (s,X_1\left(s\right))\left|\right|\right]ds,\\ \left|\right|x_2\left(t\right)-X_2\left(t\right)\left|\right|\le {\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}\left[\left|\right|\upsilon (t,x_2\left(t\right))-\upsilon (t,X_2\left(t\right))\left|\right|\right]\\ +{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t\left[\left|\right|\upsilon (s,x_2\left(s\right))-\upsilon (s,X_2\left(s\right))\left|\right|\right]ds,\\ \left|\right|x_3\left(t\right)-X_3\left(t\right)\left|\right|\le {\displaystyle \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}}\left[\left|\right|\varphi (t,x_3\left(t\right))-\varphi (t,X_3\left(t\right))\right]\\ +{\displaystyle \frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}}{\int }_0^t\left[\left|\right|\varphi (s,x_3\left(s\right))-\varphi (s,X_3\left(s\right))\left|\right|\right]ds.\end{array}$$

(28)

Considering the Lipschitz condition, having the fact in mind that the solution is bounded, we get

$$\left|\right|x_1\left(t\right)-X_1\left(t\right)\left|\right|\le \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}{\Delta }_1{W}_1+{\left\{\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\Delta }_2{W}_{2}t\right\}}^n,$$

$$\left|\right|x_2\left(t\right)-X_2\left(t\right)\left|\right|\le \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}{\Delta }_3{W}_3+{\left\{\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\Delta }_4{W}_{4}t\right\}}^n,$$

(29)

$$\left|\right|x_3\left(t\right)-X_3\left(t\right)\left|\right|\le \frac{2(1-\gamma )}{(2-\gamma )M\left(\gamma \right)}{\Delta }_5{W}_5+{\left\{\frac{2\gamma }{(2-\gamma )M\left(\gamma \right)}{\Delta }_6{W}_{6}t\right\}}^n.$$

This is true for any n; hence,

$$x_1\left(t\right)=X_1\left(t\right);x_2\left(t\right)=X_2\left(t\right);x_3\left(t\right)=X_3\left(t\right).$$

(30)

Hence, it shows the uniqueness of the solution of Equation (11). ☐

Now, we derive the approximate solution of the system given by Equation (11) using the Laplace transform operator given by Equation (3). Applying it on both sides of Equation (11), we obtain

$$\begin{array}{c}\frac{s\mathcal{L}\left[x_1\left(t\right)\right]-x_1\left(0\right)}{s+\gamma (1-s)}=\mathcal{L}[x_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right)]\left(s\right),\\ \frac{s\mathcal{L}\left[x_2\left(t\right)\right]-x_2\left(0\right)}{s+\gamma (1-s)}=\mathcal{L}[C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right)]\left(s\right),\\ \frac{s\mathcal{L}\left[x_3\left(t\right)\right]-x_3\left(0\right)}{s+\gamma (1-s)}=\mathcal{L}\left[E\frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right)\right]\left(s\right).\end{array}$$

(31)

By application of inverse Laplace transform on Equation (31), we get

$$x_1\left(t\right)=x_1\left(0\right)+{\mathcal{L}}^{-1}\left\{\frac{s+\gamma (1-s)}{s}\mathcal{L}[x_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right)]\left(s\right)\right\}\left(t\right),$$

$$x_2\left(t\right)=x_2\left(0\right)+{\mathcal{L}}^{-1}\left\{\frac{s+\gamma (1-s)}{s}\mathcal{L}[C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right)]\left(s\right)\right\}\left(t\right),$$

(32)

$$x_3\left(t\right)=x_3\left(0\right)+{\mathcal{L}}^{-1}\left\{\frac{s+\gamma (1-s)}{s}\mathcal{L}\left[E\frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right)\right]\left(s\right)\right\}\left(t\right).$$

The following recursive formula is then proposed

$$x_{1\left(n\right)}\left(t\right)={\mathcal{L}}^{-1}\{\frac{s+\gamma (1-s)}{s}\mathcal{L}[x_{1(n-1)}\left(t\right)(1-x_{1(n-1)}\left(t\right))-A{x}_{1(n-1)}\left(t\right)x_{2(n-1)}\left(t\right)$$

$$-B{x}_{1(n-1)}\left(t\right)x_{3(n-1)}\left(t\right)\left]\left(s\right)\right\}\left(t\right),$$

$$x_{2\left(n\right)}\left(t\right)={\mathcal{L}}^{-1}\left\{\frac{s+\gamma (1-s)}{s}\mathcal{L}[C{x}_{2(n-1)}\left(t\right)(1-x_{2(n-1)}\left(t\right))-D{x}_{1(n-1)}\left(t\right)x_{2(n-1)}\left(t\right)]\left(s\right)\right\}\left(t\right),$$

(33)

$$x_{3\left(n\right)}\left(t\right)={\mathcal{L}}^{-1}\left\{\frac{s+\gamma (1-s)}{s}\mathcal{L}\right[E\frac{x_{1(n-1)}\left(t\right)x_{3(n-1)}\left(t\right)}{x_{1(n-1)}\left(t\right)+F}-G{x}_{1(n-1)}\left(t\right)x_{3(n-1)}\left(t\right)$$

$$-H{x}_{3(n-1)}\left(t\right)\left]\left(s\right)\right\}\left(t\right),$$

where

$$x_{1\left(0\right)}\left(t\right)=x_1\left(0\right);x_{2\left(0\right)}\left(t\right)=x_2\left(0\right);x_{3\left(0\right)}\left(t\right)=x_3\left(0\right).$$

(34)

The approximate solution is assumed to be obtain as a limit when n tend to infinity

$$x_1\left(t\right)=\underset{n\to \infty }{lim}{x}_{1\left(n\right)}\left(t\right);x_2\left(t\right)=\underset{n\to \infty }{lim}{x}_{2\left(n\right)}\left(t\right);x_3\left(t\right)=\underset{n\to \infty }{lim}{x}_{3\left(n\right)}\left(t\right).$$

(35)

The prove of stability analysis of the iteration method given by Equation (35) is obtained similarly to the previous case.

Example 1.

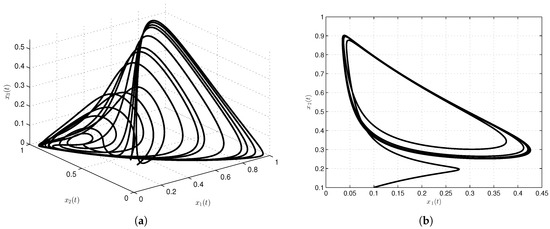
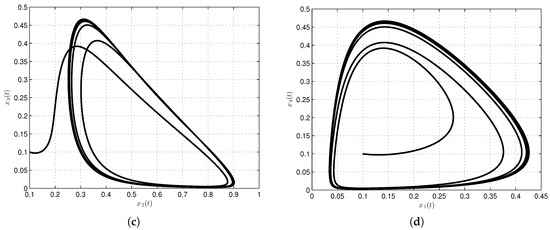
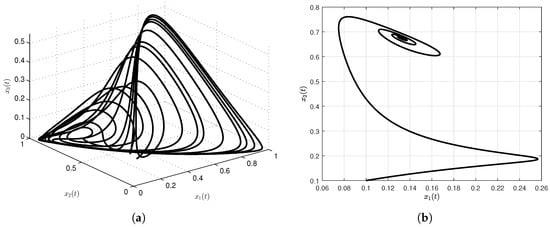
We present numerical simulations of the special solutions of our model using the Caputo-Fabrizio-Caputo fractional order derivative. For these simulations, we consider $A=1$, $B=2.5$, $C=0.6$, $D=1.5$, $E=4.5$, $F=1$, $G=0.2$, and $H=0.5$, with initial conditions, $x_1\left(0\right)=0.1$, $x_2\left(0\right)=0.1$ and $x_3\left(0\right)=0.1$. The simulation time is 500 s and the step size used in evaluating the approximate solutions was $h=0.005$. The numerical results given in Figure 1a and Figure 2d show numerical simulations of the special solutions of our model as a function of time.

Figure 1. Numerical simulation for cancer model via Caputo-Fabrizio-Caputo fractional operator. In (a), classical case; in (b–d), projected onto $x_1\left(t\right)-x_2\left(t\right)$, $x_2\left(t\right)-x_3\left(t\right)$ and $x_1\left(t\right)-x_3\left(t\right)$ planes, respectively; the commensurate order of the fractional cancer system is $\gamma =2.7$.

Figure 2. Numerical simulation for cancer model via Caputo-Fabrizio-Caputo fractional operator. In (a), classical case; in (b–d), projected onto $x_1\left(t\right)-x_2\left(t\right)$, $x_2\left(t\right)-x_3\left(t\right)$ and $x_1\left(t\right)-x_3\left(t\right)$ planes, respectively; the commensurate order of the fractional cancer system is $\gamma =2.4$.

3.2. Cancer Model with Mittag-Leffler Kernel

Considering Equation (7), the modified cancer model with Mittag-Leffler kernel is given as

$${}_0^{ABC}{\mathcal{D}}_t^{\gamma }{x}_1\left(t\right)=x_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right),$$

$${}_0^{ABC}{\mathcal{D}}_t^{\gamma }{x}_2\left(t\right)=C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right),$$

(36)

$${}_0^{ABC}{\mathcal{D}}_t^{\gamma }{x}_3\left(t\right)=E\frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right),$$

where ${}_0^{ABC}{\mathcal{D}}_t^{\gamma }$, represents the fractional derivative of type Atangana-Baleanu-Caputo, and $0<\gamma \le 1$ is the fractional order. The model is subject to initial conditions:

$$x_{1\left(0\right)}\left(t\right)=x_1\left(0\right);x_{2\left(0\right)}\left(t\right)=x_2\left(0\right);x_{3\left(0\right)}\left(t\right)=x_3\left(0\right).$$

(37)

We derive the approximate solution of the system given by Equation (36) using the Sumudu transform operator given by Equation (9). Applying it on both sides of Equation (36), we obtain

$$\begin{array}{c}{\displaystyle \frac{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)}{1-\gamma }}{E}_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)ST\left[x_1\left(t\right)\right]-x_1\left(0\right)\\ =ST[x_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right)],\\ {\displaystyle \frac{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)}{1-\gamma }}{E}_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)ST\left[x_2\left(t\right)\right]-x_2\left(0\right)\\ =ST[C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right)],\\ {\displaystyle \frac{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)}{1-\gamma }}{E}_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)ST\left[x_3\left(t\right)\right]-x_3\left(0\right)\\ =ST\left[E{\displaystyle \frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right)\right].\end{array}$$

(38)

Rearranging Equation (38), we obtain

$$\begin{array}{c}ST\left[x_1\left(t\right)\right]=x_1\left(0\right)+{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST[x_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right)],\\ ST\left[x_2\left(t\right)\right]=x_2\left(0\right)+{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST[C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right)],\\ ST\left[x_3\left(t\right)\right]=x_3\left(0\right)+{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST\left[E{\displaystyle \frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right)\right].\end{array}$$

(39)

Applying the inverse Sumudu transform on both sides of Equation (39), we obtain

$$\begin{array}{c}{x}_1\left(t\right)=x_1\left(0\right)+S{T}^{-1}\{{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST[x_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right)]\},\\ x_2\left(t\right)=x_2\left(0\right)+S{T}^{-1}\{{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST[C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right)]\},\\ x_3\left(t\right)=x_3\left(0\right)+S{T}^{-1}\{{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST\left[E{\displaystyle \frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right)\right]\}.\end{array}$$

(40)

Now, we obtain

$$\begin{array}{c}{x}_{1(n+1)}\left(t\right)=x_{1\left(n\right)}\left(0\right)+S{T}^{-1}\{{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST[x_{1\left(n\right)}\left(t\right)(1-x_{1\left(n\right)}\left(t\right))-A{x}_{1\left(n\right)}\left(t\right)x_{2\left(n\right)}\left(t\right)-B{x}_{1\left(n\right)}\left(t\right)x_{3\left(n\right)}\left(t\right)]\},\\ x_{2(n+1)}\left(t\right)=x_{1\left(n\right)}\left(0\right)+S{T}^{-1}\{{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST[C{x}_{2\left(n\right)}\left(t\right)(1-x_{2\left(n\right)}\left(t\right))-D{x}_{1\left(n\right)}\left(t\right)x_{2\left(n\right)}\left(t\right)]\},\\ x_{3(n+1)}\left(t\right)=x_{3\left(n\right)}\left(0\right)+S{T}^{-1}\{{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST\left[E{\displaystyle \frac{x_{1\left(n\right)}\left(t\right)x_{3\left(n\right)}\left(t\right)}{x_{1\left(n\right)}\left(t\right)+F}}-G{x}_{1\left(n\right)}\left(t\right)x_{3\left(n\right)}\left(t\right)-H{x}_{3\left(n\right)}\left(t\right)\right]\},\end{array}$$

(41)

and the solution of Equation (41) is provided by

$$x_1\left(t\right)=\underset{n\to \infty }{lim}{x}_{1\left(n\right)}\left(t\right);x_2\left(t\right)=\underset{n\to \infty }{lim}{x}_{2\left(n\right)}\left(t\right);x_3\left(t\right)=\underset{n\to \infty }{lim}{x}_{3\left(n\right)}\left(t\right).$$

(42)

Now, we provide the stability analysis of this method [47]. Let $(X,|·\left|\right)$ be a Banach space and H a self-map of X. Let $z_{n+1}=g(H,z_n)$ be particular recursive procedure. The following conditions must be satisfied for $z_{n+1}=H{z}_n$.

• The fixed point set of H has at least one element.
• $z_n$ converges to a point $P\in F\left(H\right)$.
• ${lim}_{n\to \infty }{x}_n\left(t\right)=P.$

Theorem 4.

Let $(X,|·\left|\right)$ be a Banach space and H a self-map of X satisfying

$$\left|\right|H_x-H_z\left|\right|\le \eta \left|\right|X-H_x\left|\right|+\eta \left|\right|x-z\left|\right|,$$

(43)

for all $x,z\in X$, where $0\le \eta$, $0\le \eta <1$. Suppose that H is Picard H-stable.

Let us take into account Equation (41), and we have

$$\frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-\frac{1}{1-\gamma }{u}^{\gamma }\right)},$$

(44)

where the above equation corresponds to the fractional Lagrange multiplier.

Theorem 5.

Let K be a self-map defined as

$$\begin{array}{c}K\left[x_{1(n+1)}\left(t\right)\right]=x_{1(n+1)}\left(t\right)=x_{1\left(n\right)}\left(t\right)+S{T}^{-1}\{{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST[x_{1\left(n\right)}\left(t\right)(1-x_{1\left(n\right)}\left(t\right))-A{x}_{1\left(n\right)}\left(t\right)x_{2\left(n\right)}\left(t\right)-B{x}_{1\left(n\right)}\left(t\right)x_{3\left(n\right)}\left(t\right)]\},\\ K\left[x_{2(n+1)}\left(t\right)\right]=x_{2(n+1)}\left(t\right)=x_{2\left(n\right)}\left(t\right)+S{T}^{-1}\{{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST[C{x}_{2\left(n\right)}\left(t\right)(1-x_{2\left(n\right)}\left(t\right))-D{x}_{1\left(n\right)}\left(t\right)x_{2\left(n\right)}\left(t\right)]\},\\ K\left[x_{3(n+1)}\left(t\right)\right]=x_{3(n+1)}\left(t\right)=x_{3\left(n\right)}\left(t\right)+S{T}^{-1}\{{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-{\displaystyle \frac{1}{1-\gamma }}{u}^{\gamma }\right)}}·\\ ST\left[E{\displaystyle \frac{x_{1\left(n\right)}\left(t\right)x_{3\left(n\right)}\left(t\right)}{x_{1\left(n\right)}\left(t\right)+F}}-G{x}_{1\left(n\right)}\left(t\right)x_{3\left(n\right)}\left(t\right)-H{x}_{3\left(n\right)}\left(t\right)\right]\}.\end{array}$$

(45)

Using the properties of the norm and considering the triangular inequality, we have

$$\left|\right|K\left[x_{1\left(n\right)}\left(t\right)\right]-K\left[X_{1\left(m\right)}\left(t\right)\right]\left|\right|\le \left|\right|x_{1\left(n\right)}\left(t\right)-X_{1\left(m\right)}\left(t\right)\left|\right|$$

$$+S{T}^{-1}\{\frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-\frac{1}{1-\gamma }{u}^{\gamma }\right)}·$$

$$ST[(x_{1\left(n\right)}\left(t\right)-X_{1\left(m\right)}\left(t\right))(1-(x_{1\left(n\right)}\left(t\right)-X_{1\left(m\right)}\left(t\right)))$$

$$+A[\left(x_{1\left(n\right)}\left(t\right)\right)\left(x_{2\left(n\right)}\left(t\right)\right)-\left(x_{1\left(m\right)}\left(t\right)\right)\left(x_{2\left(m\right)}\left(t\right)\right)]$$

$$+B[\left(x_{1\left(n\right)}\left(t\right)\right)\left(x_{3\left(n\right)}\left(t\right)\right)-\left(x_{1\left(m\right)}\left(t\right)\right)\left(x_{3\left(m\right)}\left(t\right)\right)]\left]\right\},$$

$$\left|\right|K\left[x_{2\left(n\right)}\left(t\right)\right]-K\left[X_{2\left(m\right)}\left(t\right)\right]\left|\right|\le \left|\right|x_{2\left(n\right)}\left(t\right)-X_{2\left(m\right)}\left(t\right)\left|\right|$$

$$+S{T}^{-1}\{\frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-\frac{1}{1-\gamma }{u}^{\gamma }\right)}·$$

(46)

$$ST[C(x_{2\left(n\right)}\left(t\right)-X_{2\left(m\right)}\left(t\right))(1-(x_{2\left(n\right)}\left(t\right)-X_{2\left(m\right)}\left(t\right)))$$

$$+D[\left(x_{1\left(n\right)}\left(t\right)\right)\left(x_{2\left(n\right)}\left(t\right)\right)-\left(x_{1\left(m\right)}\left(t\right)\right)\left(x_{2\left(m\right)}\left(t\right)\right)]\left]\right\},$$

$$\left|\right|K\left[x_{3\left(n\right)}\left(t\right)\right]-K\left[X_{3\left(m\right)}\left(t\right)\right]\left|\right|\le \left|\right|x_{3\left(n\right)}\left(t\right)-X_{3\left(m\right)}\left(t\right)\left|\right|$$

$$+S{T}^{-1}\{\frac{1-\gamma }{B\left(\gamma \right)\gamma \mathsf{\Gamma }(\gamma +1)E_{\gamma }\left(-\frac{1}{1-\gamma }{u}^{\gamma }\right)}·$$

$$ST[E\frac{\left(x_{1\left(n\right)}\left(t\right)x_{3\left(n\right)}\left(t\right)\right)-\left(x_{1\left(m\right)}\left(t\right)x_{3\left(m\right)}\left(t\right)\right))}{(x_{1\left(n\right)}\left(t\right)-x_{1\left(m\right)}\left(t\right))+F}$$

$$+G[\left(x_{1\left(n\right)}\left(t\right)x_{3\left(n\right)}\left(t\right)\right)-\left(x_{1\left(m\right)}\left(t\right)x_{3\left(m\right)}\left(t\right)\right)]+H[x_{3\left(n\right)}\left(t\right)-x_{3\left(m\right)}\left(t\right)]\left]\right\}.$$

K satisfies the conditions in Theorem 4 when

$$\eta (0,0,0),\eta =\left\{\begin{array}{c}\left|\right|x_{1\left(n\right)}\left(t\right)-X_{1\left(m\right)}\left(t\right)\left|\right|\times \left|\right|-(x_{1\left(n\right)}\left(t\right)+X_{1\left(m\right)}\left(t\right))\left|\right|+\left|\right|x_{1\left(n\right)}\left(t\right)-X_{1\left(m\right)}\left(t\right)\left|\right|\hfill \\ \times \left|\right|1-(x_{1\left(n\right)}\left(t\right)-X_{1\left(m\right)}\left(t\right))\left|\right|-A\left|\right|x_{1\left(n\right)}\left(t\right)x_{2\left(n\right)}\left(t\right)-X_{1\left(m\right)}\left(t\right)X_{2\left(m\right)}\left(t\right)\left|\right|\hfill \\ -B\left|\right|x_{1\left(n\right)}\left(t\right)x_{3\left(n\right)}\left(t\right)-X_{1\left(m\right)}\left(t\right)X_{3\left(m\right)}\left(t\right)\left|\right|\times \left|\right|x_{2\left(n\right)}\left(t\right)-X_{2\left(m\right)}\left(t\right)\left|\right|\times \hfill \\ \left|\right|-(x_{2\left(n\right)}\left(t\right)+X_{2\left(m\right)}\left(t\right))\left|\right|+C\left[\right||x_{2\left(n\right)}\left(t\right)-X_{2\left(m\right)}\left(t\right)\left|\right|]\hfill \\ \left[\right||1-(x_{2\left(n\right)}\left(t\right)-X_{2\left(m\right)}\left(t\right))\left|\right|]-D\left[\right||x_{1\left(n\right)}\left(t\right)x_{2\left(n\right)}\left(t\right)-X_{1\left(m\right)}\left(t\right)X_{2\left(m\right)}\left(t\right)\left|\right|]\times \hfill \\ \left|\right|x_{3\left(n\right)}\left(t\right)-X_{3\left(m\right)}\left(t\right)\left|\right|\times \left|\right|-(x_{3\left(n\right)}\left(t\right)+X_{3\left(m\right)}\left(t\right))\left|\right|+\hfill \\ E\left[\left|\right|\frac{x_{1\left(n\right)}\left(t\right)x_{3\left(n\right)}\left(t\right)-X_{1\left(m\right)}\left(t\right)X_{3\left(m\right)}\left(t\right)}{x_{1\left(n\right)}\left(t\right)-X_{1\left(m\right)}\left(t\right)+F}\left|\right|\right]\hfill \\ -G\left[\right||x_{1\left(n\right)}\left(t\right)x_{3\left(n\right)}\left(t\right)+X_{1\left(m\right)}\left(t\right)X_{3\left(n\right)}\left(t\right)\left|\right|]-H\left[\right||x_{3\left(n\right)}\left(t\right)-X_{3\left(n\right)}\left(t\right)\left|\right|],\hfill \end{array}\right.$$

and we conclude that K is Picard K-stable.

Theorem 6.

We show that the special solution of Equation (36) using the iteration method is unique.

Proof of Theorem 6.

Consider the following Hilbert space $H=L^2((a,b)\times (0,k))$

$$v:(a,b)\times [0,T]\to \mathbb{R},\int \int uvdudv<\infty .$$

(47)

We now consider the following operator

$$\eta (0,0),\eta =\left\{\begin{array}{c}{x}_1\left(t\right)(1-x_1\left(t\right))-A{x}_1\left(t\right)x_2\left(t\right)-B{x}_1\left(t\right)x_3\left(t\right),\hfill \\ C{x}_2\left(t\right)(1-x_2\left(t\right))-D{x}_1\left(t\right)x_2\left(t\right),\hfill \\ E\frac{x_1\left(t\right)x_3\left(t\right)}{x_1\left(t\right)+F}-G{x}_1\left(t\right)x_3\left(t\right)-H{x}_3\left(t\right).\hfill \end{array}\right.$$

We prove that the inner product of

$$(T(x_{11}\left(t\right)-x_{12}\left(t\right),x_{21}\left(t\right)-x_{22}\left(t\right),x_{31}\left(t\right)-x_{32}\left(t\right),({\omega }_1,{\omega }_2,{\omega }_3)),$$

(48)

where $(x_{11}\left(t\right)-x_{12}\left(t\right),x_{21}\left(t\right)-x_{22}\left(t\right),x_{31}\left(t\right)-x_{32}\left(t\right))$, are special solutions of the system.

Considering the norm and the inner function, we obtain

$$\begin{array}{c}((x_{11}\left(t\right)-x_{12}\left(t\right))(1-(x_{11}\left(t\right)-x_{12}\left(t\right)))-A(x_{11}\left(t\right)-x_{12}\left(t\right))(x_{21}\left(t\right)-x_{22}\left(t\right))-\\ -B(x_{11}\left(t\right)-x_{12}\left(t\right))(x_{21}\left(t\right)-x_{32}\left(t\right)),{\omega }_1)\le \\ \left|\right|x_{11}\left(t\right)-x_{12}\left(t\right)\left|\right|\left|\right|1-(x_{11}\left(t\right)-x_{12}\left(t\right))\left|\right|\left|\right|{\omega }_1\left|\right|+A\left|\right|x_{12}\left(t\right)-x_{11}\left(t\right)\left|\right|\left|\right|x_{22}\left(t\right)-x_{21}\left(t\right)\left|\right|\left|\right|{\omega }_1\left|\right|+\\ +B\left|\right|x_{12}\left(t\right)-x_{11}\left(t\right)\left|\right|\left|\right|x_{32}\left(t\right)-x_{31}\left(t\right)\left|\right|\left|\right|{\omega }_1\left|\right|,\\ \left(C(x_{21}\left(t\right)-x_{22}\left(t\right))(1-(x_{21}\left(t\right)-x_{22}\left(t\right)))-D(x_{11}\left(t\right)-x_{12}\left(t\right))(x_{21}\left(t\right)-x_{22}\left(t\right)),{\omega }_2\right)\le \\ C\left|\right|x_{21}\left(t\right)-x_{22}\left(t\right)\left|\right|\left|\right|1-(x_{21}\left(t\right)-x_{22}\left(t\right))\left|\right|\left|\right|{\omega }_2\left|\right|+D\left|\right|x_{12}\left(t\right)-x_{11}\left(t\right)\left|\right|\left|\right|x_{22}\left(t\right)-x_{21}\left(t\right)\left|\right|\left|\right|{\omega }_2\left|\right|,\\ (E\left[{\displaystyle \frac{(x_{11}\left(t\right)-x_{12}\left(t\right))(x_{31}\left(t\right)-x_{32}\left(t\right))}{(x_{11}\left(t\right)-x_{12}\left(t\right))+F}}\right]-G(x_{11}\left(t\right)-x_{12}\left(t\right))(x_{31}\left(t\right)-x_{32}\left(t\right))-\\ -H(x_{31}\left(t\right)-x_{32}\left(t\right)),{\omega }_3)\le E\left[{\displaystyle \frac{\left|\right|x_{31}\left(t\right)-x_{32}\left(t\right){\left|\right|}^2}{\left|\right|(x_{31}\left(t\right)-x_{32}\left(t\right))+F\left|\right|}}\right]\left|\right|{\omega }_3\left|\right|+\\ +G\left|\right|x_{12}\left(t\right)-x_{11}\left(t\right)\left|\right|\left|\right|x_{32}\left(t\right)-x_{31}\left(t\right)\left|\right|\left|\right|{\omega }_3\left|\right|+H\left|\right|x_{32}\left(t\right)-x_{31}\left(t\right)\left|\right|\left|\right|{\omega }_3\left|\right|.\end{array}$$

(49)

For large number m, n and k, both solutions converge to the exact solution. Using the topology concept, we can find three very small positive parameters (${\lambda }_m$, ${\lambda }_n$ and ${\lambda }_k$):

$$\begin{array}{c}\left|\right|x_1\left(t\right)-x_{11}\left(t\right)\left|\right|,\left|\right|x_1\left(t\right)-x_{12}\left(t\right)\left|\right|<{\displaystyle \frac{{\lambda }_m}{\varpi }},\\ \left|\right|x_2\left(t\right)-x_{21}\left(t\right)\left|\right|,\left|\right|x_2\left(t\right)-x_{22}\left(t\right)\left|\right|<{\displaystyle \frac{{\lambda }_n}{\xi }},\end{array}$$

(50)

and

$$\left|\right|x_3\left(t\right)-x_{31}\left(t\right)\left|\right|,\left|\right|x_2\left(t\right)-x_{32}\left(t\right)\left|\right|<\frac{{\lambda }_k}{\kappa },$$

where

$$\varpi =3\left(\right|\left|(x_{11}\left(t\right)-x_{22}\left(t\right))(1-(x_{11}\left(t\right)-x_{22}\left(t\right)))\right||+$$

$$+A\left|\right|(x_{11}\left(t\right)-x_{22}\left(t\right))(x_{21}\left(t\right)-x_{22}\left(t\right))\left|\right|+B\left|\right|(x_{11}\left(t\right)-x_{22}\left(t\right))(x_{31}\left(t\right)-x_{32}\left(t\right))\left|\right|\left)\right||{\omega }_1\left|\right|,$$

$$\xi =3\left(C\right||(x_{21}\left(t\right)-x_{22}\left(t\right))(1-(x_{21}\left(t\right)-x_{22}\left(t\right)))\left|\right|+D\left|\right|(x_{11}\left(t\right)-x_{21}\left(t\right))(x_{21}\left(t\right)-x_{22}\left(t\right))\left|\right|\left)\right||{\omega }_2\left|\right|$$

(51)

$$\varpi =3\left(E\right|\left|\frac{x_{31}\left(t\right)-x_{32}\left(t\right)}{(x_{31}\left(t\right)-x_{32}\left(t\right))+F}\right||+G\left|\right|(x_{11}\left(t\right)-x_{22}\left(t\right))(x_{31}\left(t\right)-x_{32}\left(t\right))\left|\right|+$$

$$+H\left|\right|x_{31}\left(t\right)-x_{32}\left(t\right)\left|\right|\left)\right||{\omega }_3\left|\right|,$$

where

$$\left(\right|\left|(x_{11}\left(t\right)-x_{22}\left(t\right))(1-(x_{11}\left(t\right)-x_{22}\left(t\right)))\right||+A|\left|(x_{11}\left(t\right)-x_{22}\left(t\right))(x_{21}\left(t\right)-x_{22}\left(t\right))\right||$$

$$+B\left|\right|(x_{11}\left(t\right)-x_{22}\left(t\right))(x_{31}\left(t\right)-x_{32}\left(t\right))\left|\right|)\ne 0,$$

$$\left(C\right|\left|(x_{21}\left(t\right)-x_{22}\left(t\right))(1-(x_{21}\left(t\right)-x_{22}\left(t\right)))\right||+D|\left|(x_{11}\left(t\right)-x_{21}\left(t\right))(x_{21}\left(t\right)-x_{22}\left(t\right))\right|\left|\right)\ne 0,$$

(52)

$$\left(E\right|\left|\frac{x_{31}\left(t\right)-x_{32}\left(t\right)}{(x_{31}\left(t\right)-x_{32}\left(t\right))+F}\right||+G\left|\right|(x_{11}\left(t\right)-x_{22}\left(t\right))(x_{31}\left(t\right)-x_{32}\left(t\right))\left|\right|$$

$$+H\left|\right|x_{31}\left(t\right)-x_{32}\left(t\right)\left|\right|)\ne 0,$$

where $\left|\right|{\omega }_1\left|\right|$, $\left|\right|{\omega }_2\left|\right|$, $\left|\right|{\omega }_3\left|\right|$$\ne 0$; $\left|\right|x_{12}\left(t\right)-x_{11}\left(t\right)\left|\right|=\left|\right|x_{22}\left(t\right)-x_{21}\left(t\right)\left|\right|=\left|\right|x_{31}\left(t\right)-x_{32}\left(t\right)\left|\right|=0$; $x_{11}\left(t\right)=x_{12}\left(t\right)$, $x_{21}\left(t\right)=x_{22}\left(t\right)$ and $x_{31}\left(t\right)=x_{32}\left(t\right)$.

This completes the proof of uniqueness. ☐

The Adams-Moulton rule for the Atangana-Baleanu fractional integral (10) [27] is given by

$${}_0^{AB}{\mathcal{I}}_t^{\gamma }\left[f\left(t_{n+1}\right)\right]=\frac{1-\gamma }{B\left(\gamma \right)}\left[\frac{f\left(t_{n+1}\right)-f\left(t_n\right)}{2}\right]+\frac{\gamma }{\mathsf{\Gamma }\left(\gamma \right)}\sum _{k=0}^{\infty }\left[\frac{f\left(t_{k+1}\right)-f\left(t_k\right)}{2}\right]b_k^{\gamma },$$

(53)

where

$$b_k^{\gamma }={(k+1)}^{1-\gamma }-{\left(k\right)}^{1-\gamma }.$$

(54)

For our system, we have

$$\begin{array}{c}{x}_{1(n+1)}\left(t\right)-x_{1\left(n\right)}\left(t\right)=x_{0\left(1\right)}^n\left(t\right)+\left\{{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)}}\right[\left({\displaystyle \frac{x_{1(n+1)}\left(t\right)-x_{1\left(n\right)}\left(t\right)}{2}}\right)\left(1-{\displaystyle \frac{x_{1(n+1)}\left(t\right)-x_{1\left(n\right)}\left(t\right)}{2}}\right)\\ -A\left({\displaystyle \frac{x_{1(n+1)}\left(t\right)-x_{1\left(n\right)}\left(t\right)}{2}}\right)\left({\displaystyle \frac{x_{2(n+1)}\left(t\right)-x_{2\left(n\right)}\left(t\right)}{2}}\right)\\ -B\left({\displaystyle \frac{x_{1(n+1)}\left(t\right)-x_{1\left(n\right)}\left(t\right)}{2}}\right)\left({\displaystyle \frac{x_{3(n+1)}\left(t\right)-x_{3\left(n\right)}\left(t\right)}{2}}\right)\left]\right\}\\ +{\displaystyle \frac{\gamma }{B\left(\gamma \right)}}\sum _{k=0}^{\infty }{b}_k^{\gamma }[\left({\displaystyle \frac{x_{1(k+1)}\left(t\right)-x_{1\left(k\right)}\left(t\right)}{2}}\right)\left(1-{\displaystyle \frac{x_{1(k+1)}\left(t\right)-x_{1\left(k\right)}\left(t\right)}{2}}\right)\\ -A\left({\displaystyle \frac{x_{1(k+1)}\left(t\right)-x_{1\left(k\right)}\left(t\right)}{2}}\right)\left({\displaystyle \frac{x_{2(k+1)}\left(t\right)-x_{2\left(k\right)}\left(t\right)}{2}}\right)\\ -B\left({\displaystyle \frac{x_{1(k+1)}\left(t\right)-x_{1\left(k\right)}\left(t\right)}{2}}\right)\left({\displaystyle \frac{x_{3(k+1)}\left(t\right)-x_{3\left(k\right)}\left(t\right)}{2}}\right)],\\ x_{2(n+1)}\left(t\right)-x_{2\left(n\right)}\left(t\right)=x_{0\left(2\right)}^n\left(t\right)+\left\{{\displaystyle \frac{1-\gamma }{B\left(\gamma \right)}}\right[C\left({\displaystyle \frac{x_{2(n+1)}\left(t\right)-x_{2\left(n\right)}\left(t\right)}{2}}\right)\left(1-{\displaystyle \frac{x_{2(n+1)}\left(t\right)-x_{2\left(n\right)}\left(t\right)}{2}}\right)\\ -D\left({\displaystyle \frac{x_{1(n+1)}\left(t\right)-x_{1\left(n\right)}\left(t\right)}{2}}\right)\left({\displaystyle \frac{x_{2(n+1)}\left(t\right)-x_{2\left(n\right)}\left(t\right)}{2}}\right)\left]\right\}\\ +{\displaystyle \frac{\gamma }{B\left(\gamma \right)}}\sum _{k=0}^{\infty }{b}_k^{\gamma }[C\left({\displaystyle \frac{x_{2(k+1)}\left(t\right)-x_{2\left(k\right)}\left(t\right)}{2}}\right)\left(1-{\displaystyle \frac{x_{2(k+1)}\left(t\right)-x_{2\left(k\right)}\left(t\right)}{2}}\right)\\ -D\left({\displaystyle \frac{x_{1(k+1)}\left(t\right)-x_{1\left(k\right)}\left(t\right)}{2}}\right)\left({\displaystyle \frac{x_{2(k+1)}\left(t\right)-x_{2\left(k\right)}\left(t\right)}{2}}\right)],\end{array}$$

(55)

and

$$x_{3(n+1)}\left(t\right)-x_{3\left(n\right)}\left(t\right)=x_{0\left(3\right)}^n\left(t\right)+\left\{\frac{1-\gamma }{B\left(\gamma \right)}\right\{E\left[\frac{\left(\frac{x_{1(n+1)}\left(t\right)-x_{1\left(n\right)}\left(t\right)}{2}\right)\left(\frac{x_{3(n+1)}\left(t\right)-x_{3\left(n\right)}\left(t\right)}{2}\right)}{\frac{x_{1(n+1)}\left(t\right)-x_{1\left(n\right)}\left(t\right)}{2}+F}\right]$$

$$-G\left(\frac{x_{1(n+1)}\left(t\right)-x_{1\left(n\right)}\left(t\right)}{2}\right)\left(\frac{x_{3(n+1)}\left(t\right)-x_{3\left(n\right)}\left(t\right)}{2}\right)$$

$$-H\left(\frac{x_{3(n+1)}\left(t\right)-x_{3\left(n\right)}\left(t\right)}{2}\right)\left\}\right\}$$

$$+\frac{\gamma }{B\left(\gamma \right)}\sum _{k=0}^{\infty }{b}_k^{\gamma }\{E\left[\frac{\left(\frac{x_{1(k+1)}\left(t\right)-x_{1\left(k\right)}\left(t\right)}{2}\right)\left(\frac{x_{3(k+1)}\left(t\right)-x_{3\left(k\right)}\left(t\right)}{2}\right)}{\frac{x_{1(k+1)}\left(t\right)-x_{1\left(k\right)}\left(t\right)}{2}+F}\right]$$

$$-G\left(\frac{x_{1(k+1)}\left(t\right)-x_{1\left(k\right)}\left(t\right)}{2}\right)\left(\frac{x_{3(k+1)}\left(t\right)-x_{3\left(k\right)}\left(t\right)}{2}\right)$$

$$-H\left(\frac{x_{3(k+1)}\left(t\right)-x_{3\left(k\right)}\left(t\right)}{2}\right)\}.$$

Example 2.

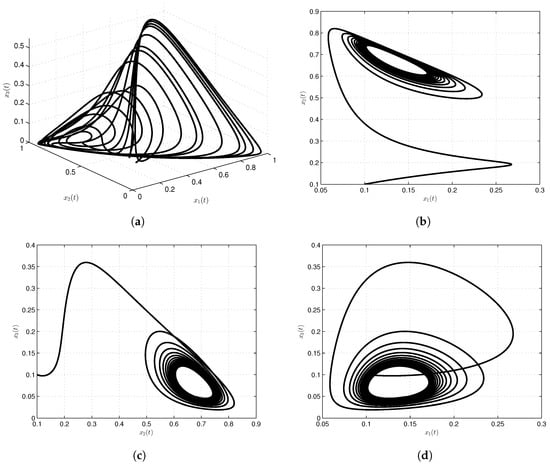
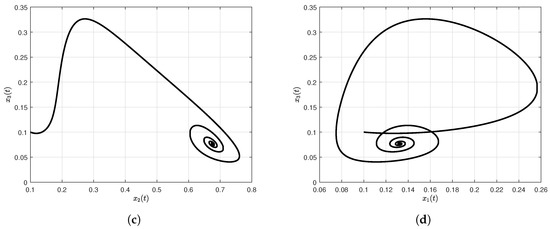
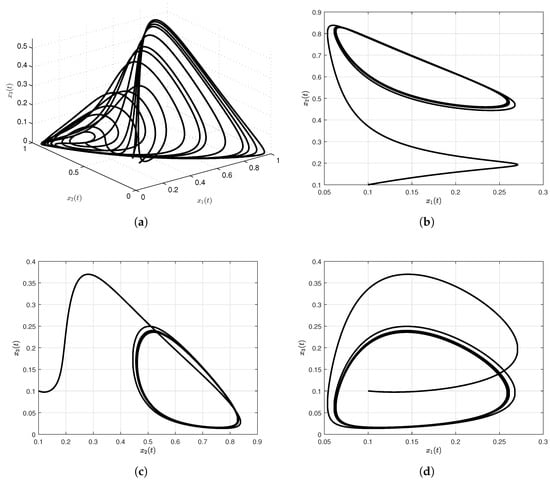
We present numerical simulations of the special solutions of our model using the Atangana-Baleanu-Caputo fractional order derivative. For these simulations, we consider, $A=1$, $B=2.5$, $C=0.6$, $D=1.5$, $E=4.5$, $F=1$, $G=0.2$, $H=0.5$, with initial conditions, $x_1\left(0\right)=0.1$, $x_2\left(0\right)=0.1$ and $x_3\left(0\right)=0.1$. The simulation time is 500 s and the step size used in evaluating the approximate solutions was $h=0.005$. The numerical results given in Figure 3a and Figure 4d show numerical simulations of the special solutions of our model as a function of time.

Figure 3. Numerical simulation for cancer model via Atangana-Baleanu-Caputo fractional operator. In (a), classical case; in (b–d), projected onto $x_1\left(t\right)-x_2\left(t\right)$, $x_2\left(t\right)-x_3\left(t\right)$ and $x_1\left(t\right)-x_3\left(t\right)$ planes, respectively; the commensurate order of the fractional cancer system is $\gamma =2.7$.

Figure 4. Numerical simulation for cancer model via Atangana-Baleanu-Caputo fractional operator. In (a), classical case; in (b–d), projected onto $x_1\left(t\right)-x_2\left(t\right)$, $x_2\left(t\right)-x_3\left(t\right)$ and $x_1\left(t\right)-x_3\left(t\right)$ planes, respectively; the commensurate order of the fractional cancer system is $\gamma =2.4$.

4. Conclusions

In this paper, we have analyzed a three-dimensional fractional order dynamical model for the evolution of cancer growth, which includes the interactions between healthy tissue cells, tumour cells, and activated immune system cells. This model was considered via the Caputo-Fabrizio-Caputo and Atangana-Baleanu-Caputo fractional order derivatives. The solution of the alternative models were obtained using an iterative scheme—for the Caputo-Fabrizio-Caputo fractional order derivative based in the Laplace transform and for the Atangana-Baleanu-Caputo fractional order derivative based in the Sumudu transform. Furthermore, the stability analysis of the iterative methods and the uniqueness of the special solutions were presented in detail.

Considering these fractional derivatives, the numerical simulations showed that the fractional commensurate order cancer system with total order less than three exhibits chaos. In our model, with the variation in the choice of the fractional order γ, a great variety of novel chaotic attractors can be formed. In this sense, we showed that the concept of fractional differentiation is a powerful mathematical tool to express the non-locality of a given dynamical system.

In the next papers, we shall study other cancer models—for instance, glioma growth, breast tumours—as well as metastasising tumours and comparing them against experimental data obtained from the literature.