Automated Detection of Paroxysmal Atrial Fibrillation Using an Information-Based Similarity Approach
Abstract
:1. Introduction
2. Materials and Methods
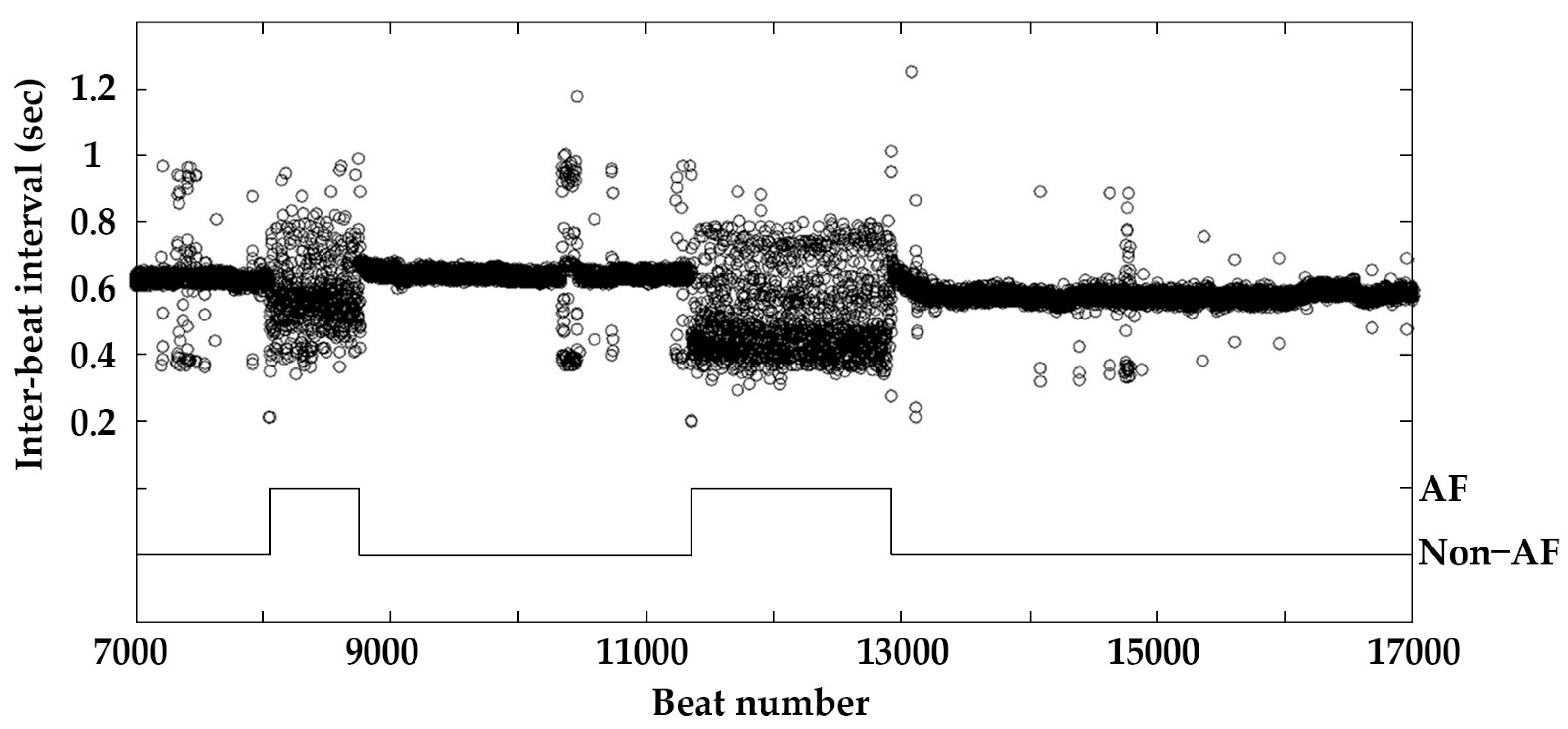
2.1. Data
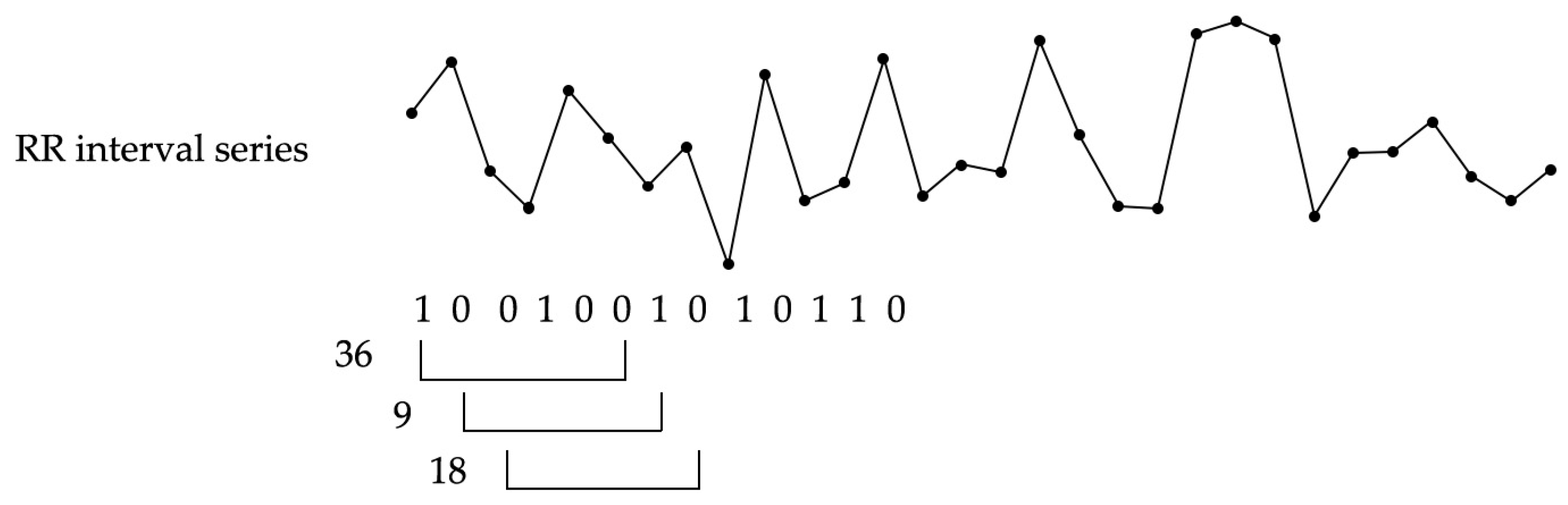
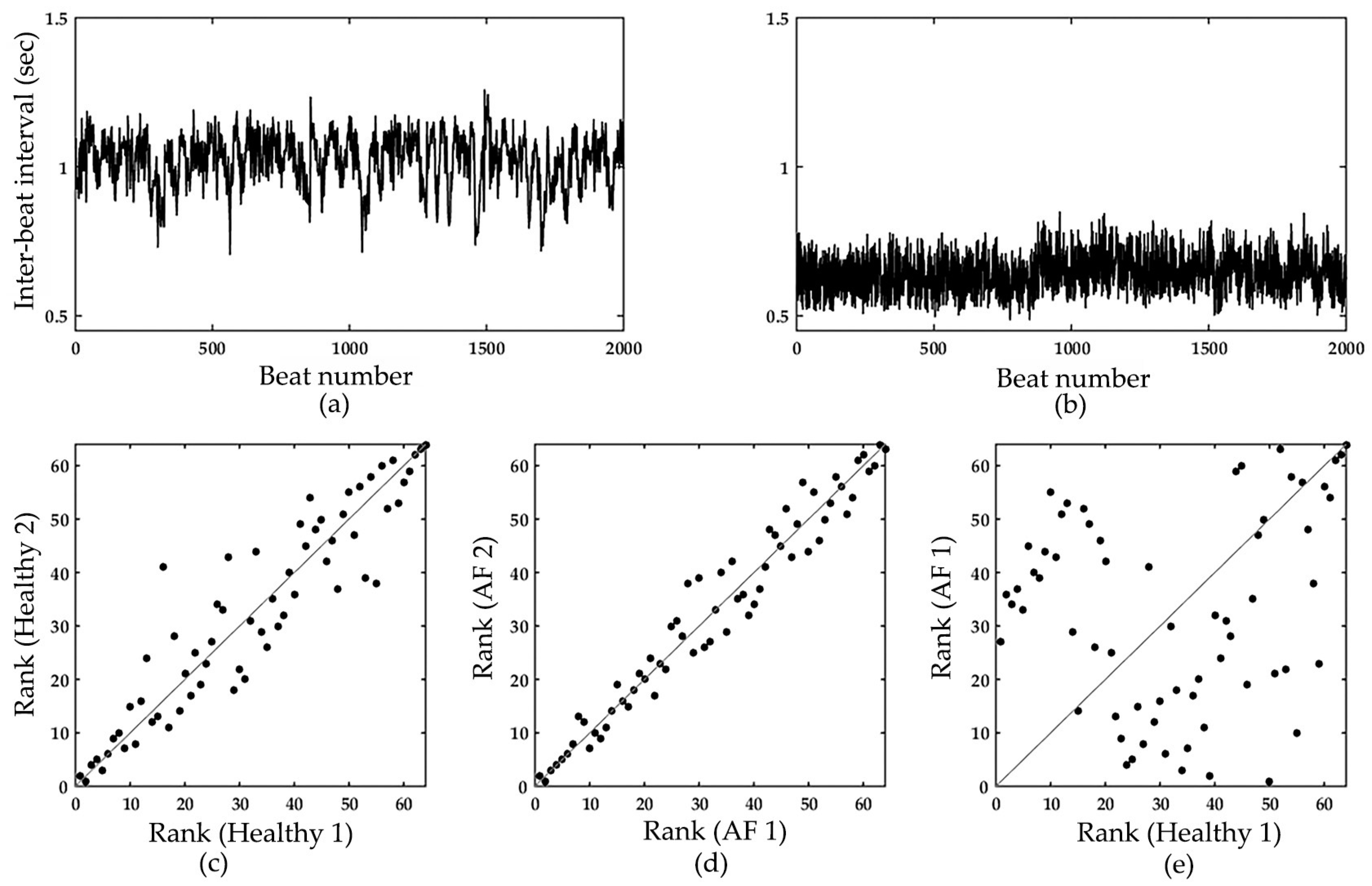
2.2. Information-Based Similarity Index
2.3. Ensemble Model of Automated AF Detector
2.3.1. Overall Algorithm of the Ensemble Model
- Retrieving sets of AF and NSR RR-interval series from PhysioNet ECG data;
- randomly setting aside a percentage of AF and NSR sets as training data and the rest as testing data. In AF training data, only AF segments were picked according to annotations provided on the PhysioNet database. This procedure was repeated five times such that five datasets (i.e., datasets 1–5) with different training and testing data could be generated;
- extracting RR-interval increment signatures (i.e., the rank-frequency of m-bit word) of the desired observation window length from training and testing data, respectively;
- building templates to represent AF and NSR signature patterns;
- designing an ensemble classifier, which is composed of various pairs of AF and NSR templates;
- comparing the information-based dissimilarity index between an unknown RR-interval time series and the templates; and
- tuning ensemble parameters to achieve our twin aims of high detection accuracy and low detection variance.
2.3.2. Weighted Dissimilarity Index
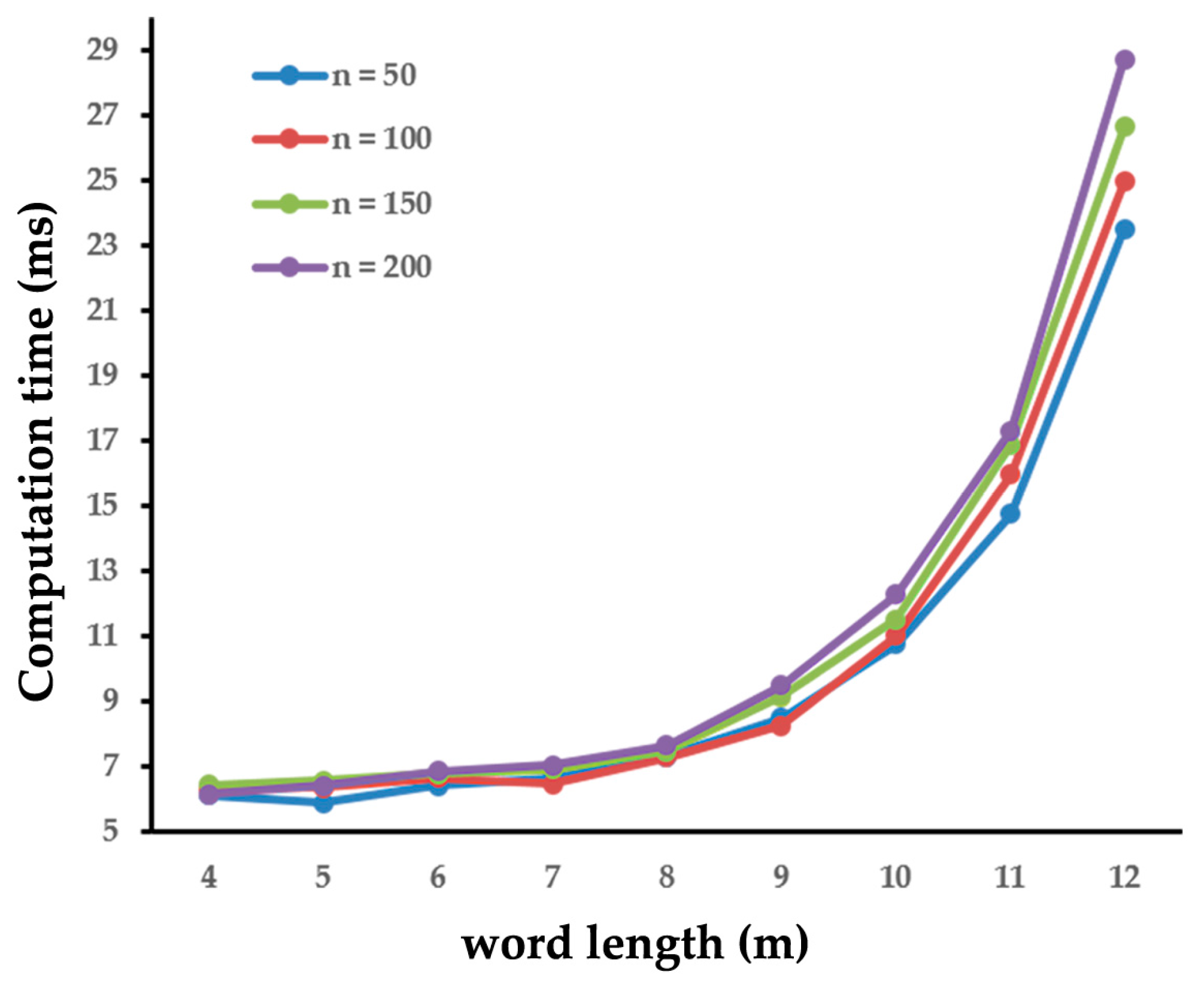
2.3.3. Parameter Tuning
3. Results
3.1. Overall Performance of the Ensemble Model
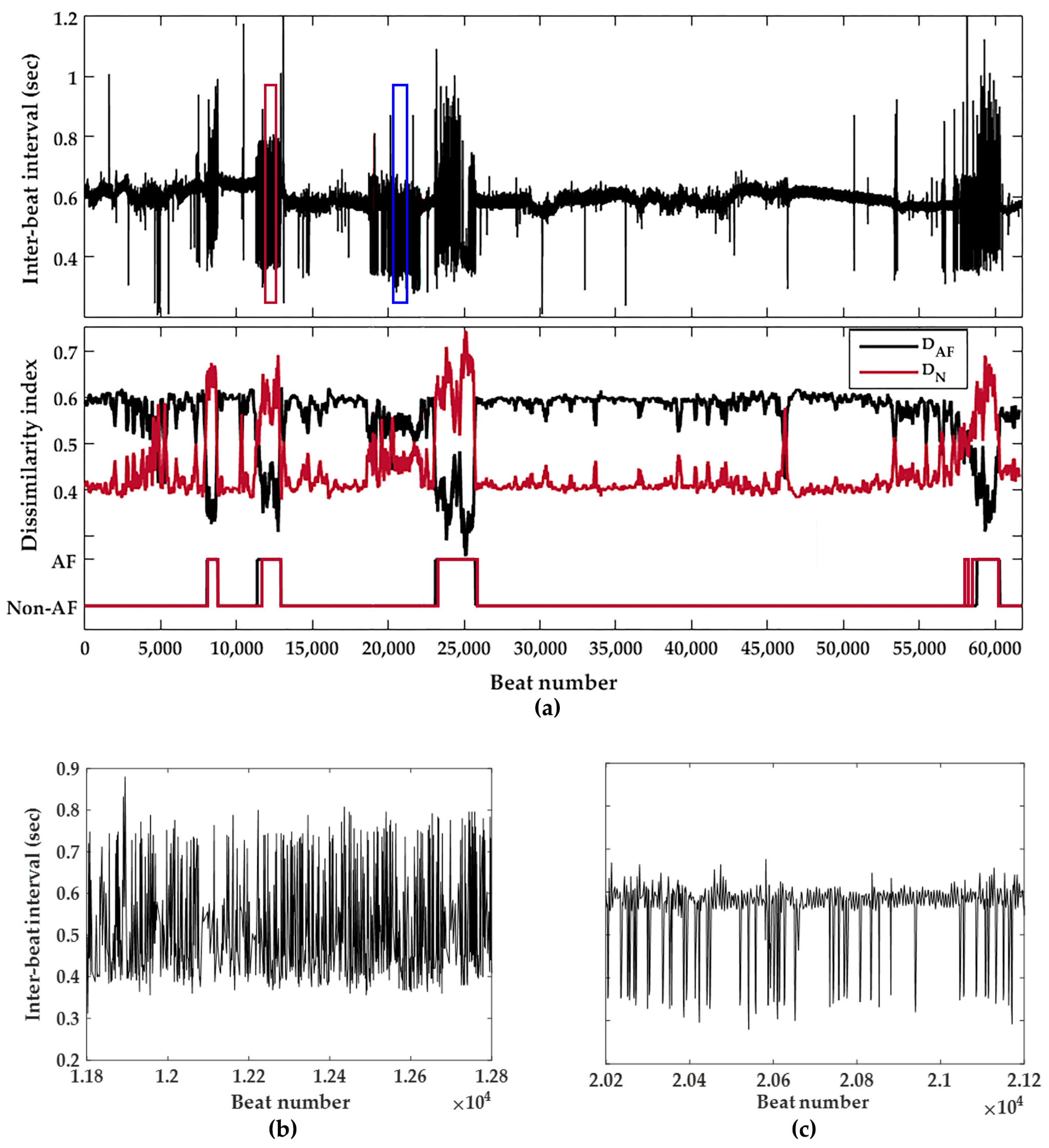
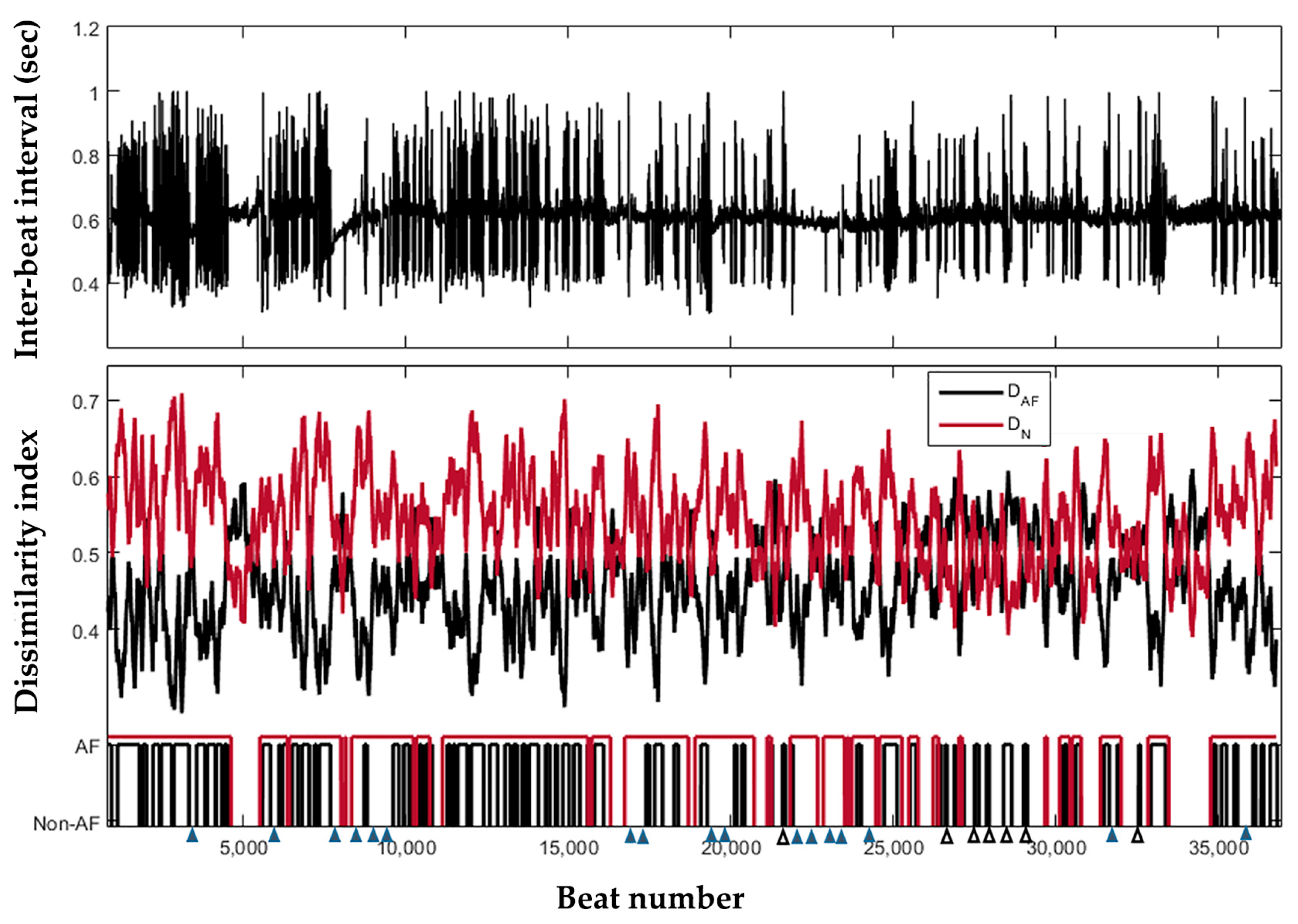
3.2. Continuous Behavior of the Detector
4. Discussion
4.1. Main Findings
4.2. Advantages of Ensemble Model
4.3. Comparison with Published Works
4.4. Study Limitations and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Iwasaki, Y.-K.; Nishida, K.; Kato, T.; Nattel, S. Atrial Fibrillation Pathophysiology. Circulation 2011, 124, 2264–2274. [Google Scholar] [CrossRef] [PubMed]
- Munger, T.M.; Wu, L.Q.; Shen, W.K. Atrial fibrillation. J. Biomed. Res. 2014, 28, 1–17. [Google Scholar] [PubMed]
- January, C.T.; Wann, L.S.; Alpert, J.S.; Calkins, H.; Cigarroa, J.E.; Cleveland, J.C., Jr.; Conti, J.B.; Ellinor, P.T.; Ezekowitz, M.D.; Field, M.E.; et al. 2014 AHA/ACC/HRS guideline for the management of patients with atrial fibrillation: A report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines and the Heart Rhythm Society. J. Am. Coll. Cardiol. 2014, 64. [Google Scholar] [CrossRef]
- Israel, C.W.; Grönefeld, G.; Ehrlich, J.R.; Li, Y.G.; Hohnloser, S.H. Long-term risk of recurrent atrial fibrillation as documented by an implantable monitoring device: Implications for optimal patient care. J. Am. Coll. Cardiol. 2004, 43, 47–52. [Google Scholar] [CrossRef] [PubMed]
- Page, R.L.; Wilkinson, W.E.; Clair, W.K.; McCarthy, E.A.; Pritchett, E.L. Asymptomatic arrhythmias in patients with symptomatic paroxysmal atrial fibrillation and paroxysmal supraventricular tachycardia. Circulation 1994, 89, 224–227. [Google Scholar] [CrossRef] [PubMed]
- Andresen, D.; Bruggemann, T. Heart rate variability preceding onset of atrial fibrillation. J. Cardiovasc. Electrophysiol. 1998, 9, S26–S29. [Google Scholar] [PubMed]
- Glass, L.; Tateno, K. A method for detection of atrial fibrillation using the RR intervals. Comput. Cardiol. 2000, 27, 391–394. [Google Scholar]
- Langley, P.; Bourke, J.P.; Murray, A. Frequency analysis of atrial fibrillation. Comput. Cardiol. 2000, 27, 65–68. [Google Scholar]
- Stridh, M.; Sornmo, L. Spatiotemporal QRST cancellation techniques for analysis of atrial fibrillation. IEEE Trans. Biomed. Eng. 2001, 48, 105–111. [Google Scholar] [CrossRef] [PubMed]
- Fischer, R.; Klein, G.; Widiger, B.; Hoy, L.; Zywietz, C. Discrimination between atrial flutter and atrial fibrillation by computing a flutter index. Comput. Cardiol. 2005, 32, 81–84. [Google Scholar]
- Moody, G.; Mark, R. A new method for detecting atrial fibrillation using R-R intervals. Comput. Cardiol. 1983, 10, 227–230. [Google Scholar]
- Tateno, K.; Glass, L. Automatic detection of atrial fibrillation using the coefficient of variation and density histograms of RR and deltaRR intervals. Med. Biol. Eng. Comput. 2001, 39, 664–671. [Google Scholar] [CrossRef] [PubMed]
- Kikillus, N.; Hammer, G.; Lentz, N.; Stockwald, F.; Bolz, A. Three different algorithms for identifying patients suffering from atrial fibrillation during atrial fibrillation free phases of the ECG. In Proceedings of the Computers in Cardiology, Durham, NC, USA, 30 September–3 October 2007; Volume 34, pp. 801–804. [Google Scholar]
- Babaeizadeh, S.; Gregg, R.E.; Helfenbein, E.D.; Lindauer, J.M.; Zhou, S.H. Improvements in atrial fibrillation detection for real-time monitoring. J. Electrocardiol. 2009, 42, 522–526. [Google Scholar] [CrossRef] [PubMed]
- Lian, J.; Wang, L.; Muessig, D. A simple method to detect atrial fibrillation using RR intervals. Am. J. Cardiol. 2011, 107, 1494–1497. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Ye, S.; Chen, H.; Li, D.; He, F.; Tu, Y. A novel method for detection of the transition between atrial fibrillation and sinus rhythm. IEEE Trans. Biomed. Eng. 2011, 58, 1113–1119. [Google Scholar] [CrossRef] [PubMed]
- Parvaresh, S.; Ayatollahi, A. Automatic atrial fibrillation detection using autoregressive modeling. In Proceedings of the 2011 International Conference on Biomedical Engineering and Technology, Kuala Lumpur, Malaysia, 4–5 June 2011; pp. 105–108. [Google Scholar]
- Dash, S.; Chon, K.; Lu, S.; Raeder, E. Automatic real time detection of atrial fibrillation. Ann. Biomed. Eng. 2009, 37, 1701–1709. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Nam, Y.; McManus, D.D.; Chon, K.H. Time-Varying Coherence Function for Atrial Fibrillation Detection. IEEE Trans. Biomed. Eng. 2013, 60, 2783–2793. [Google Scholar] [PubMed]
- Petrenase, A.; Marozas, V.; Sönmo, L. Low-complexity detection of atrial fibrillation in continuous long term monitoring. Comput. Biol. Med. 2015, 60, 2783–2793. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Ding, H.; Ung, B.; Pickwell-MacPherson, E.; Zhang, Y. Automatic Online Detection of Atrial Fibrillation Based on Symbolic Dynamics and Shannon Entropy. Biomed. Eng. Online 2014, 13, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Ding, H.; Wu, W.; Zhang, Y. A Real-Time Atrial Fibrillation Detection Algorithm Based on the Instantaneous State of Heart Rate. PLoS ONE 2015, 10, e0136544. [Google Scholar] [CrossRef] [PubMed]
- Lake, D.; Moorman, J. Accurate estimation of entropy in very short physiological time series: The problem of atrial fibrillation detection in implanted ventricular devices. Am. J. Physiol. Heart Circ. Physiol. 2011, 300, H319–H325. [Google Scholar] [CrossRef] [PubMed]
- Carrara, M.; Carozzi, L.; Moss, T.J.; de Pasquale, M.; Cerutti, S.; Lake, D.E.; Moorman, J.R.; Ferrario, M. Classification of cardiac rhythm using heart rate dynamical measures: Validation in MIT-BIH databases. J. Electrocardiol. 2015, 48, 943–946. [Google Scholar] [CrossRef] [PubMed]
- Carrara, M.; Carozzi, L.; Moss, T.J.; de Pasquale, M.; Cerutti, S.; Ferrario, M.; Lake, D.E.; Moorman, J.R. Heart rate dynamics distinguish among atrial fibrillation, normal sinus rhythm and sinus rhythm with frequent ectopy. Physiol. Meas. 2015, 36, 1873–1888. [Google Scholar] [CrossRef] [PubMed]
- Masè, M.; Disertori, M.; Marini, M.; Ravelli, F. Characterization of rate and regularity of ventricular response during atrial tachyarrhythmias. Insight on atrial and nodal determinants. Physiol. Meas. 2017, 38, 800–818. [Google Scholar] [CrossRef] [PubMed]
- Lian, J.; Mussig, D.; Lang, V. Computer modeling of ventricular rhythm during atrial fibrillation and ventricular pacing. IEEE Trans. Biomed. Eng. 2006, 53, 1512–1520. [Google Scholar] [CrossRef] [PubMed]
- Lerma, C.; Trine, K.M.; Guevara, M.; Glass, L. Stochastic aspects of cardiac arrhythmias. J. Stat. Phys. 2007, 128, 347–374. [Google Scholar] [CrossRef]
- Zeng, W.; Glass, L. Statistical properties of heartbeat intervals during atrial fibrillation. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1996, 54, 1779–1784. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Costa, M.; Goldberger, A.L.; Peng, C.-K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.-K.; Costa, M.; Goldberger, A.L. Adaptive data analysis of complex fluctuations in physiologic time series. Adv. Adapt. Data Anal. 2009, 1, 61–70. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.C.; Hseu, S.S.; Yien, H.W.; Goldberger, A.L.; Peng, C.K. Linguistic analysis of the human heartbeat using frequency and rank order statistics. Phys. Rev. Lett. 2003, 90, 108103. [Google Scholar] [CrossRef] [PubMed]
- Yang, A.C.; Goldberger, A.L.; Peng, C.K. Genomic classification using an information-based similarity index: application to the SARS coronavirus. J. Comput. Biol. 2005, 12, 1103–1116. [Google Scholar] [PubMed]
- Yang, A.C.; Peng, C.K.; Yien, H.W.; Goldberger, A.L. Information categorization approach to literary authorship disputes. Phys. A Stat. Mech. Appl. 2003, 329, 473–483. [Google Scholar] [CrossRef]
- Peng, C.K.; Yang, A.C.C.; Goldberger, A.L. Statistical physics approach to categorize biologic signals: From heart rate dynamics to DNA sequences. Chaos 2007, 17, 015115. [Google Scholar] [CrossRef] [PubMed]
- Christini, D.J.; Glass, L. Introduction: Mapping and control of complex cardiac arrhythmias. Chaos 2002, 12, 732–739. [Google Scholar] [CrossRef] [PubMed]
- Hall, K.; Christini, D.J.; Tremblay, M.; Collins, J.J.; Glass, L.; Billette, J. Dynamic control of cardiac alternans. Phys. Rev. Lett. 1997, 78, 4518–4521. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef] [PubMed]
- Moody, G.B.; Mark, R.G.; Goldberger, A.L. PhysioNet: A research resource for studies of complex physiologic and biomedical signals. Comput. Cardiol. 2000, 27, 179–182. [Google Scholar] [PubMed]
- Costa, M.; Moody, G.B.; Henry, I.; Goldberger, A.L. PhysioNet: An NIH research resource for complex signals. J. Electrocardiol. 2003, 36, 139–144. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Chang, E.Y. KBA: Kernel Boundary Alignment Considering Imbalanced Data Distribution. IEEE Trans. Knowl. Data Eng. 2005, 17, P786–P795. [Google Scholar] [CrossRef]
- Larburu, N.; Lopetegi, T.; Romero, I. Comparative study of algorithms for Atrial Fibrillation detection. In Proceedings of the Conference on Computing in Cardiology, Hangzhou China, 18–21 September 2011; Volume 38, pp. 265–268. [Google Scholar]
- Couceiro, R.; Carvalho, P.; Henriques, J.; Antunes, M.; Harris, M.; Habetha, J. Detection of atrial fibrillation using model-based ECG analysis. In Proceedings of the 19th International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008; pp. 1–5. [Google Scholar]
| m | Repeated Cross-Validation | Observation Window Size (n) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 | 100 | 150 | 200 | ||||||||||
| SEN | SPE | ACC | SEN | SPE | ACC | SEN | SPE | ACC | SEN | SPE | ACC | ||
| 4 | Dataset 1 | 86.34 | 86.46 | 86.44 | 93.06 | 93.49 | 93.43 | 94.74 | 94.14 | 94.21 | 96.62 | 96.28 | 96.32 |
| Dataset 2 | 85.71 | 87.09 | 86.15 | 91.17 | 92.00 | 91.66 | 94.12 | 93.63 | 93.90 | 95.02 | 95.11 | 95.08 | |
| Dataset 3 | 83.60 | 86.08 | 85.59 | 90.61 | 89.05 | 89.99 | 95.28 | 96.02 | 95.71 | 90.33 | 92.50 | 91.87 | |
| Dataset 4 | 86.49 | 86.03 | 86.55 | 92.67 | 93.02 | 92.80 | 93.06 | 93.22 | 93.19 | 92.49 | 93.44 | 93.06 | |
| Dataset 5 | 85.09 | 84.66 | 84.86 | 91.93 | 90.95 | 91.25 | 95.19 | 96.79 | 96.20 | 93.88 | 95.38 | 94.91 | |
| Average | 85.45 | 86.06 | 85.92 | 91.89 | 91.70 | 91.83 | 94.48 | 94.76 | 94.64 | 93.67 | 94.54 | 94.25 | |
| 5 | Dataset 1 | 86.34 | 85.15 | 85.34 | 93.06 | 93.06 | 93.06 | 95.32 | 94.73 | 94.81 | 96.62 | 95.92 | 96.01 |
| Dataset 2 | 86.45 | 87.85 | 87.09 | 89.85 | 90.70 | 90.11 | 94.49 | 94.05 | 94.20 | 91.38 | 92.12 | 92.03 | |
| Dataset 3 | 87.57 | 86.54 | 86.97 | 92.33 | 93.37 | 92.90 | 95.02 | 96.12 | 95.86 | 95.77 | 95.26 | 95.50 | |
| Dataset 4 | 85.23 | 84.83 | 85.01 | 92.28 | 92.55 | 92.44 | 93.66 | 94.52 | 94.20 | 96.13 | 94.94 | 95.36 | |
| Dataset 5 | 88.00 | 88.52 | 88.43 | 93.50 | 92.71 | 93.25 | 94.47 | 94.71 | 94.55 | 95.32 | 95.88 | 95.72 | |
| Average | 86.72 | 86.58 | 86.57 | 92.20 | 92.48 | 92.35 | 94.59 | 94.83 | 94.72 | 95.04 | 94.82 | 94.92 | |
| 6 | Dataset 1 | 87.39 | 88.11 | 88.00 | 93.27 | 93.31 | 93.30 | 96.49 | 95.16 | 95.32 | 96.14 | 96.99 | 96.88 |
| Dataset 2 | 87.33 | 86.40 | 86.94 | 95.44 | 96.04 | 95.81 | 94.81 | 95.29 | 95.15 | 94.65 | 95.08 | 94.89 | |
| Dataset 3 | 90.88 | 91.98 | 91.60 | 94.18 | 94.05 | 94.07 | 96.06 | 96.57 | 96.44 | 96.77 | 96.51 | 96.60 | |
| Dataset 4 | 86.47 | 85.90 | 86.07 | 91.46 | 92.69 | 92.50 | 95.90 | 96.47 | 96.39 | 95.02 | 96.33 | 96.19 | |
| Dataset 5 | 87.89 | 87.66 | 87.72 | 91.07 | 92.33 | 92.26 | 96.32 | 95.90 | 96.02 | 94.94 | 95.38 | 95.26 | |
| Average | 87.99 | 88.01 | 88.07 | 93.08 | 93.68 | 93.59 | 95.92 | 95.88 | 95.86 | 95.50 | 96.06 | 95.96 | |
| 7 | Dataset 1 | 89.59 | 89.47 | 89.49 | 94.69 | 94.03 | 94.13 | 96.78 | 95.65 | 95.79 | 97.10 | 97.06 | 97.07 |
| Dataset 2 | 88.04 | 87.23 | 87.40 | 91.56 | 92.86 | 92.42 | 96.13 | 96.60 | 96.41 | 94.44 | 93.95 | 94.10 | |
| Dataset 3 | 90.14 | 91.29 | 90.25 | 95.22 | 95.70 | 95.58 | 97.46 | 98.39 | 98.18 | 95.45 | 95.02 | 95.13 | |
| Dataset 4 | 87.37 | 87.05 | 87.10 | 94.31 | 94.57 | 94.51 | 95.08 | 95.23 | 95.17 | 95.48 | 95.66 | 95.62 | |
| Dataset 5 | 90.51 | 90.26 | 90.29 | 93.06 | 92.91 | 92.96 | 97.58 | 98.41 | 98.33 | 94.87 | 96.81 | 96.67 | |
| Average | 89.13 | 88.86 | 88.91 | 93.77 | 94.01 | 93.92 | 96.61 | 96.86 | 96.78 | 95.47 | 95.70 | 95.72 | |
| 8 | Dataset 1 | 90.54 | 89.69 | 89.83 | 95.51 | 95.36 | 95.38 | 97.08 | 97.10 | 97.08 | 97.10 | 97.92 | 97.82 |
| Dataset 2 | 89.64 | 89.22 | 89.30 | 95.08 | 95.27 | 95.22 | 95.20 | 99.04 | 97.27 | 97.15 | 98.58 | 98.40 | |
| Dataset 3 | 89.01 | 90.85 | 90.24 | 96.49 | 96.44 | 96.45 | 96.37 | 97.11 | 97.66 | 95.48 | 95.70 | 95.61 | |
| Dataset 4 | 88.46 | 90.80 | 90.03 | 95.68 | 96.02 | 95.97 | 96.68 | 98.00 | 97.38 | 95.20 | 96.49 | 96.33 | |
| Dataset 5 | 90.25 | 91.02 | 90.79 | 96.91 | 96.77 | 96.80 | 95.51 | 96.78 | 96.42 | 96.68 | 97.00 | 96.92 | |
| Average | 89.58 | 90.32 | 90.04 | 95.93 | 95.97 | 95.96 | 96.17 | 97.61 | 97.16 | 96.32 | 97.14 | 97.02 | |
| 9 | Dataset 1 | 90.35 | 89.2 | 89.38 | 95.71 | 95.18 | 95.26 | 98.25 | 97.96 | 98.01 | 97.58 | 97.85 | 97.82 |
| Dataset 2 | 92.09 | 88.25 | 89.06 | 97.47 | 97.18 | 97.01 | 97.36 | 97.79 | 97.70 | 93.92 | 95.06 | 94.77 | |
| Dataset 3 | 89.53 | 90.87 | 90.35 | 94.72 | 97.09 | 96.39 | 96.30 | 98.71 | 98.41 | 93.99 | 97.02 | 96.68 | |
| Dataset 4 | 87.60 | 89.33 | 89.02 | 94.76 | 98.10 | 97.06 | 96.95 | 97.28 | 97.11 | 95.05 | 96.44 | 96.11 | |
| Dataset 5 | 86.44 | 85.98 | 86.60 | 94.65 | 96.28 | 95.79 | 96.33 | 98.05 | 97.66 | 97.59 | 97.99 | 97.83 | |
| Average | 89.20 | 88.73 | 88.88 | 95.46 | 96.77 | 96.30 | 97.04 | 97.96 | 97.78 | 95.63 | 96.87 | 96.64 | |
| 10 | Dataset 1 | 89.11 | 89.73 | 89.63 | 96.33 | 95.11 | 95.29 | 97.95 | 96.77 | 96.94 | 97.58 | 97.99 | 97.94 |
| Dataset 2 | 89.45 | 90.92 | 90.84 | 95.73 | 95.88 | 95.84 | 94.69 | 95.66 | 95.28 | 95.95 | 97.93 | 96.64 | |
| Dataset 3 | 88.15 | 87.32 | 88.03 | 95.33 | 94.25 | 95.02 | 96.26 | 98.31 | 97.81 | 95.64 | 92.55 | 93.13 | |
| Dataset 4 | 85.06 | 87.28 | 86.37 | 96.85 | 96.20 | 96.46 | 96.64 | 97.53 | 97.19 | 97.26 | 95.05 | 95.81 | |
| Dataset 5 | 86.40 | 85.91 | 86.39 | 97.01 | 98.33 | 98.17 | 96.95 | 98.03 | 97.72 | 95.28 | 96.33 | 95.65 | |
| Average | 87.27 | 87.86 | 87.91 | 96.25 | 95.95 | 96.16 | 96.14 | 97.38 | 97.00 | 96.03 | 95.47 | 95.31 | |
| 11 | Dataset 1 | 88.78 | 88.45 | 88.66 | 95.51 | 94.75 | 94.86 | 97.66 | 97.53 | 97.55 | 97.58 | 97.78 | 97.88 |
| Dataset 2 | 84.54 | 83.97 | 84.12 | 93.77 | 93.92 | 93.89 | 97.80 | 97.12 | 97.25 | 95.55 | 96.78 | 96.42 | |
| Dataset 3 | 85.37 | 84.90 | 84.78 | 95.76 | 94.88 | 95.05 | 98.12 | 97.57 | 97.68 | 95.92 | 95.40 | 95.51 | |
| Dataset 4 | 87.77 | 87.93 | 87.87 | 95.15 | 94.79 | 94.90 | 98.04 | 97.60 | 97.81 | 97.99 | 97.29 | 97.45 | |
| Dataset 5 | 89.76 | 89.45 | 89.52 | 95.30 | 95.96 | 95.88 | 95.88 | 95.26 | 95.34 | 96.64 | 95.90 | 96.07 | |
| Average | 87.24 | 86.94 | 86.99 | 95.10 | 94.86 | 94.92 | 97.50 | 97.02 | 97.13 | 96.74 | 96.63 | 96.67 | |
| 12 | Dataset 1 | 87.93 | 85.78 | 86.61 | 93.67 | 94.57 | 94.44 | 96.78 | 97.04 | 96.99 | 97.10 | 96.92 | 96.94 |
| Dataset 2 | 86.10 | 86.82 | 86.67 | 96.36 | 95.33 | 95.45 | 95.45 | 96.23 | 96.06 | 97.13 | 97.64 | 97.55 | |
| Dataset 3 | 84.12 | 85.37 | 85.04 | 95.66 | 95.06 | 95.21 | 95.91 | 95.77 | 95.81 | 95.48 | 95.35 | 95.40 | |
| Dataset 4 | 84.87 | 83.52 | 83.66 | 92.50 | 93.02 | 92.91 | 96.86 | 95.98 | 96.30 | 95.52 | 96.06 | 96.13 | |
| Dataset 5 | 85.09 | 87.70 | 87.22 | 93.48 | 94.36 | 94.15 | 97.19 | 97.07 | 97.10 | 95.04 | 96.17 | 95.93 | |
| Average | 85.62 | 85.84 | 85.84 | 94.33 | 94.47 | 94.43 | 96.44 | 96.42 | 96.45 | 96.05 | 96.43 | 96.39 | |
| Tuning Parameter Δ | Detection Performance (%) | ||
|---|---|---|---|
| SEN | SPE | ACC | |
| 0.00 | 99.51 | 96.34 | 96.73 |
| 0.01 | 99.35 | 96.67 | 97.00 |
| 0.02 | 99.19 | 97.04 | 97.31 |
| 0.03 | 98.72 | 97.36 | 97.53 |
| 0.04 | 98.32 | 97.74 | 97.81 |
| 0.05 | 97.77 | 98.05 | 98.02 |
| 0.06 | 97.31 | 98.24 | 98.13 |
| 0.07 | 96.86 | 98.59 | 98.38 |
| 0.08 | 96.30 | 98.71 | 98.41 |
| 0.09 | 95.40 | 98.76 | 98.34 |
| 0.10 | 94.11 | 98.80 | 98.22 |
| 0.11 | 92.99 | 98.84 | 98.12 |
| 0.12 | 91.60 | 98.88 | 97.98 |
| 0.13 | 90.39 | 98.92 | 97.86 |
| 0.14 | 89.10 | 98.96 | 97.73 |
| 0.15 | 87.87 | 99.05 | 97.66 |
| 0.16 | 86.54 | 99.24 | 97.67 |
| 0.17 | 83.03 | 99.59 | 97.54 |
| 0.18 | 76.75 | 99.71 | 96.86 |
| 0.19 | 70.90 | 99.76 | 96.18 |
| Method | Year | Database | Length of Detected Episodes (Beats) | Best Performance (%) | |||
|---|---|---|---|---|---|---|---|
| Shortest | Best | SEN | SPE | ACC | |||
| Proposed method | 2017 | AFDB | 50 | 150 | 97.04 | 97.96 | 97.78 |
| Zhou, et al. [22] | 2015 | AFDB | 127 | 127 | 97.37 | 98.44 | 97.99 |
| Petrėnas, et al. [20] | 2015 | AFDB | 8 | 60 | 97.12 | 98.28 | - |
| Zhou, et al. [21] | 2014 | AFDB | 127 | 127 | 96.89 | 98.25 | 97.67 |
| Lee, et al. [19] | 2013 | AFDB * | 12 | 128 | 98.22 | 97.67 | 97.91 |
| Huang, et al. [16] | 2011 | AFDB | 128 | 128 | 96.1 | 98.1 | - |
| Lake, et al. [23] | 2011 | AFDB | 12 | 12 | 91 | 94 | - |
| Lian, et al. [15] | 2011 | AFDB | 32 | 128 | 95.9 | 95.4 | - |
| Parvaresh, et al. [17] | 2011 | AFDB * | 15 s | 15 s | 96.14 | 93.20 | - |
| Dash, et al. [18] | 2009 | AFDB ** | 128 | 128 | 94.4 | 95.1 | - |
| Babaeizadeh, et al. [14] | 2009 | AFDB * | - | - | 92 | - | - |
| Couceiro, et al. [44] | 2008 | AFDB * | 12 | 100 | 93.8 | 96.09 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, X.; Chang, E.; Yang, W.-H.; Jiang, B.C.; Yang, A.C.; Peng, C.-K. Automated Detection of Paroxysmal Atrial Fibrillation Using an Information-Based Similarity Approach. Entropy 2017, 19, 677. https://doi.org/10.3390/e19120677
Cui X, Chang E, Yang W-H, Jiang BC, Yang AC, Peng C-K. Automated Detection of Paroxysmal Atrial Fibrillation Using an Information-Based Similarity Approach. Entropy. 2017; 19(12):677. https://doi.org/10.3390/e19120677
Chicago/Turabian StyleCui, Xingran, Emily Chang, Wen-Hung Yang, Bernard C. Jiang, Albert C. Yang, and Chung-Kang Peng. 2017. "Automated Detection of Paroxysmal Atrial Fibrillation Using an Information-Based Similarity Approach" Entropy 19, no. 12: 677. https://doi.org/10.3390/e19120677
APA StyleCui, X., Chang, E., Yang, W.-H., Jiang, B. C., Yang, A. C., & Peng, C.-K. (2017). Automated Detection of Paroxysmal Atrial Fibrillation Using an Information-Based Similarity Approach. Entropy, 19(12), 677. https://doi.org/10.3390/e19120677





