1. Introduction
Using symbolizations to study observed data plays an important role in today’s time series analysis (see for instance the review papers of Daw et al. [
1], Zanin et al. [
2], Amigó et al. [
3], and the examples in biology, medicine, artificial intelligence and data mining, just to mention a few, given therein). Thereby, it is assumed that time series, given by measurements of a real-world time-dependent system, store information about the complexity of the underlying system, which can be accessed by symbolic dynamics. In this paper, we assume further that measurements provide
n-dimensional real-valued outcomes, that is a measuring process provides
n time series.
Knowing the complexity is a key to classify systems and to predict future developments. A data analyst can for instance quantify complexity by empirical entropy measures, in particular by estimating the well-defined Kolmogorov-Sinai entropy (KS entropy). In order to estimate the KS entropy, however, a data analyst is always faced with the problem of choosing an adequate symbolization scheme.
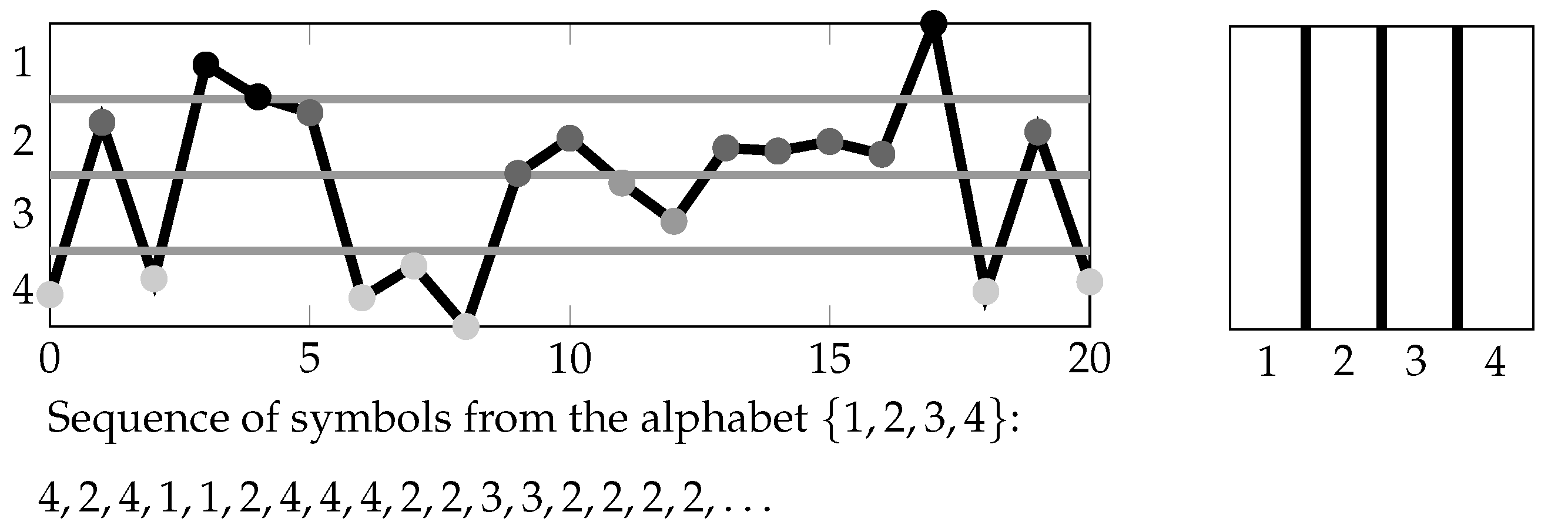
Symbolizing a time series could be done in a “classical” manner for example by subdividing the data range into a finite number of intervals (see
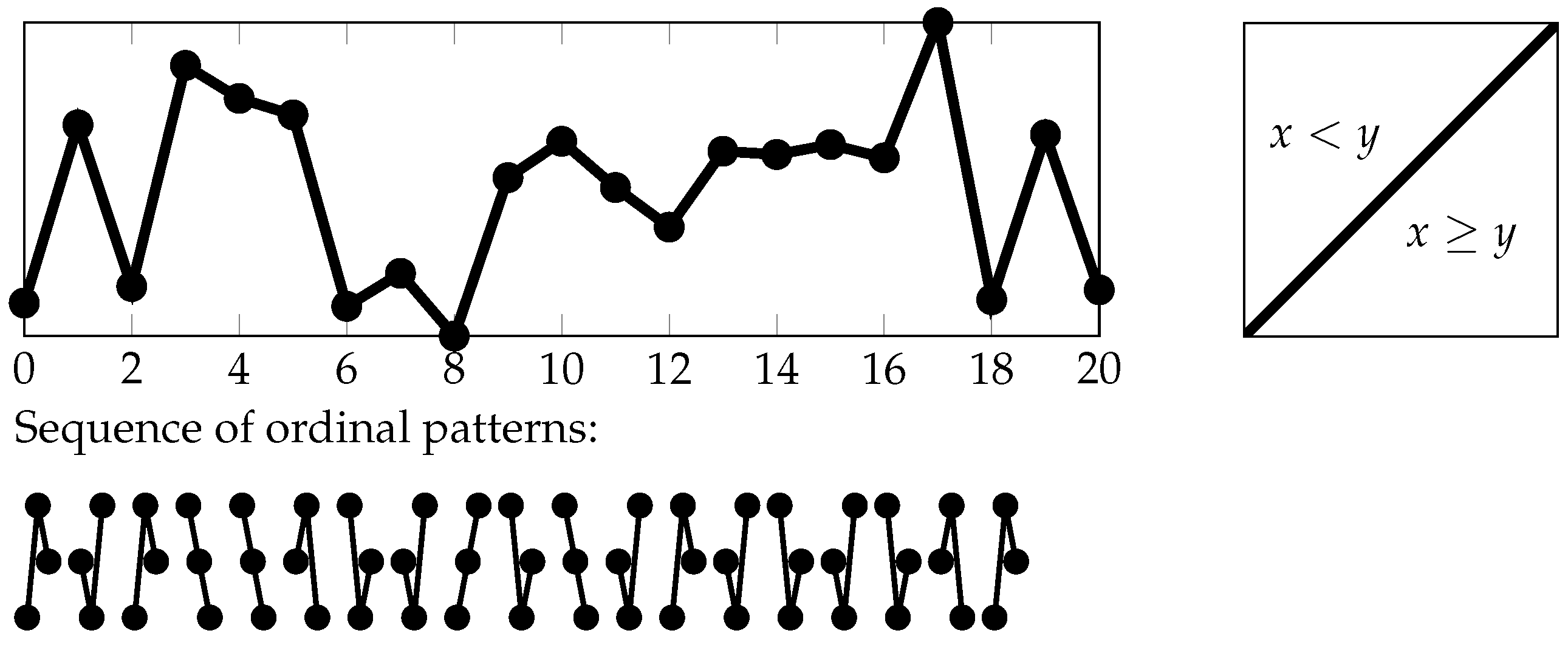
Section 2.1, often called the threshold crossing method in symbolic dynamics) or in an ordinal manner for example by considering the up and down behavior of subsequent measured values (see
Section 2.2). The most ideal, however unrealistic, case is given if the analyst knows the underlying dynamics and picks a generating (under the dynamics) partition (see
Section 1.1 and
Section 1.4 for the mathematical formulation of the general problem, as well as for instance Crutchfield and Packard [
4], Bollt et al. [
5] and Kennel and Buhl [
6]).
In the present paper, we show, by proposing a unifying approach to formalize symbolizations, that under relatively week assumptions, the search for a generating partition can be skipped if one chooses a symbolization scheme that regards a dependency between two measured values (see
Section 2.2). In fact, following some rules by picking such a symbolization scheme, a generating sequence of finite partitions (see
Section 1.1 and
Section 1.4) is provided by default and needs no further attention (see
Section 2.3 for an overview and
Section 3 and
Section 4.1, as well as the
Appendix for the mathematics behind this). Moreover, the unifying approach allows one to consider “classical” and the relatively new ordinal symbolic dynamics [
3] hand in hand and therefore to study respective assets and drawbacks.
In terms of the analyst, we propose a supplementing pool of complexity measures, which are in a certain sense approximations of the KS entropy and may be worth being compared in the finite setting of application (see Figure 7). Moreover, the relatively new ordinal approach could benefit from results achieved in “classical” symbolic dynamics, for instance to estimate a good symbolization scheme (see our ending remarks of the paper in
Section 5 and for instance Steuer et al. [
7], Letellier [
8] and, published most recently, Li and Ray [
9], as well as the references given therein). However, such topics exceed the scope of this paper.
1.1. Mathematical Formulation of the General Problem
Let us describe the central problems of determining KS entropy and give the main concepts of the paper without going into too much detail. The mathematical formulation is necessary at this point in order to state the results of the paper adequately.
We model a real-world time-dependent system by a state space , that is states of the system are taken from the set and events on the system from a -algebra on . We assume that the states are distributed according to a probability distribution on . Moreover, considering states of the system at times in , the dynamics of the system is described by a map T with the interpretation that the system is in state at time if it is in state at time t. For mathematical correctness, T is required to be measurable with respect to . We assume that the distribution of the states does not change in time, meaning T is -invariant, which is defined by for all sets .
The KS entropy is based on entropy rates of finite partitions of the state space. Given a finite partition
of
, the entropy rate
, roughly speaking, measures the complexity of possible symbolic paths (see
Section 4.1). A symbolic path is given by assigning to each state of the orbit:
a symbol
a when the state is contained in
. Here,
denotes the
t-th iterate of
under
T. We emphasize that starting with a partition
is equivalent to a start where to each state in
a symbol in
is assigned (in a measurable way). That is why we use the term symbolic approach.
In order to obtain a complexity measure that is independent of the discretization determined by a finite partition, one takes the supremum of the entropy rate
over all finite partitions
of
, that is the KS entropy
of
T:
Since usually there are uncountably many finite partitions, the determination of KS entropy on the basis of the definition is not feasible, so one is interested in finding natural partitions “carrying” the KS entropy.
In the case of a generating partition
under
T (see
Section 4.1), KS entropy is already characterized by this partition, meaning that:
(see, e.g., Walters [
10], Theorem 4.18). Finding such suitable partitions, however, is impossible in most cases. A more realistic way of approaching KS entropy is to look for a generating and increasing, i.e., refining (see
Section 4.1), sequence
of finite partitions
of
, where:
(see, e.g., Walters [
10], Theorem 4.22).
In the present paper, we discuss this countable increasing route to KS entropy in a framework where all partitions considered are derived from a natural real-valued “measuring process” and a symbolization scheme determined by a finite partition of the two-dimensional Euclidean space. The discussion includes and generalizes ideas from “classical” symbolic dynamics and from ordinal symbolic dynamics related to permutation entropy and sheds some new light on the latter one.
1.2. Observables and the Measuring Process
The modeling is completed by assuming that an n-dimensional outcome (here, ) of the system for each time is provided by observables , which mathematically are random variables on the probability space with values in the real numbers . It provides the link between the dynamical model and the given n-dimensional time series data.
Fixing some state
, we interpret the real numbers:
as the values measured by
at times
when the given system is in state
at the beginning.
Therefore, the random vector
for the time-developing system provides random vectors:
forming the measuring process:
with the
n time series
for
as outcomes. Note that the symbolizations we consider in the following are given at the observational level, i.e., with respect to the values of
; this complies with symbolizing a time series in real-world data analysis.
Let us regard , T, and as fixed in the following.
1.3. Information Contents in the Language of Event Systems
It is a central question of the given paper whether a description of a system, for instance by a measurement or by a symbolization, provides the same information as another one. In information theory, this is a matter of the richness of the event systems associated with the descriptions, more precisely a relation between sub-
-algebras
and
of
defined by (compare to Walters [
10], Definition 4.5):
The inclusion means that for each event in , there exists an event in being distinct from the first one with probability zero and that is interpreted as meaning that preserves all information contained in .
The
-algebra
on
consists of all events related to the given system, those events accessed by the given observables and the whole measuring process (
3) form the sub-
-algebras
and
of
, respectively. Mathematically,
is the smallest
-algebra built from all preimages of Borel sets in
for:
and
is the smallest
-algebra built from all preimages of Borel sets in
for:
In these definitions, it is enough to take only intervals I instead of Borel sets. Here, describes the event that the value of the i-th measurement at time t is in I.
The sub-
-algebra
, which is the smallest
-algebra built from all events contained in some of the partitions
for
, provides the events accessed by the corresponding symbolization (see
Section 4.1). Our goal is to construct an increasing sequence
of finite partitions, i.e.,
refines
(see
Section 4.1), which preserves the information given by the measuring process (
3), i.e.,
or weaker by the observables themselves, i.e.,
If (
4) holds and the measuring process preserves the information of the original system, i.e., if:
or if just (
5) holds, but the observables preserve already the information of the original system, i.e., if:
then:
meaning that
is generating (see
Section 4.1 and compare to Walters [
10]), which provides (
2).
Conditions (
6) and (
7) are not as artificial as they appear at first glance:
There is a very natural set of observables satisfying (
7), hence (
6). If
is a Borel subset of
, it is very plausible to assume that states and vectors of measured values are coinciding. This can be modeled by observables
;
with
being the
i-th coordinate projection, i.e.,
for
. Clearly, in this simplest variant of modeling measurements, observables basically are superfluous in the modeling.
In the case of only one observable, the separation of states is natural in a certain sense according to Takens’ theory (see Takens [
11] and Gutman [
12]).
1.4. A “Two-Dimensional” Way of Symbolizations
The partitions
with
that we want to study in the following are formed on the basis of a finite partition
of the two-dimensional Euclidean space
and finite sets
of time pairs:
i.e.,
is the coarsest partition refining all partitions:
for
(see
Section 4.1 for the definition of the join
of finite partitions
of
).
Here,
specifies the symbolization scheme for classifying the mutual position of measurements by
at two times
s and
t (see
Figure 1 and
Figure 2, as well as the next section). We call
the basic symbolization scheme in the following. Note that we display the two-dimensional Euclidean space
by a square for illustrative purposes.
Further, the choice of
complies with Definition 1, in particular in order to realize that
refines
(see
Section 4.1),
is finite (see Definition 1(i)), and each time point that is relevant for the symbolization is accessed (see Definition 1(ii)).
Definition 1. We call a sequence of sets with a timing if there exists a set with such that:
- (i)
for each , it holds , and
- (ii)
for each , there exists some such that or .
A timing is for instance given by the sets:
or by (
11) and (
17) (see below). It is suggestive to call the timing defined by (
9) full timing in the following.
Subsequently, we discuss the following two questions:
Section 2 is devoted to the first question. In the first part of
Section 3, we summarize our results to the second question and give some examples of basic symbolization schemes. Sufficient conditions that answer the second question including known results are presented for the interested reader in the second part of
Section 3 and proven in
Section 4 (see also the
Appendix). We close this paper with some remarks about further theoretical and practical scientific issues (see
Section 5).
3. Main Mathematical Results
Antoniouk et al. [
16] show that the search for a generating partition under
T can be bypassed by choosing ordinal symbolic dynamics. It namely provides, in the ergodic case and if
satisfies (
6) or weaker (
7), a generating sequence of finite partitions by default, that is the generating property is valid regardless of the properties of the original system considered (see Statement (
14) in
Section 2.2).
The question arises if other symbolic approaches deliver similar results. In fact, by generalizing the ideas and results of Antoniouk et al. [
16], we give sufficient conditions on
and
for (
14). This we present the interested reader in the next sections.
3.1. Preserving the Information of Observables
The following is quite technical, but shows under which conditions the information given by the observables is preserved if basic symbolization schemes
such as given by (
15), or finer, are considered. Hence, if Theorem 2 holds and
, then
is generating.
Theorem 2. Let T be ergodic, a random vector, a basic symbolization scheme, a timing and a sequence of finite partitions constructed from and (see Equation (
8)
). If further: - (i)
g is admissible with respect to for all ,
- (ii)
is admissible with respect to for all and
- (iii)
for all and ,
We call a function
admissible with respect to a random variable
Y on
if
this is for example the case if
is a one-to-one
-
measurable map (see the closing remarks of the
Appendix on one-to-one maps and Lemma A3 for general conditions on
such that
is admissible). Requiring that
has to be admissible with respect to
means that
g has to be constructed in such a way that:
holds (compare to the proof of Lemma A3 and subsequent remarks). This assumption is redundant if
is a Borel subset of
; each
;
is the
i-th coordinate projection (see the closing remarks of
Section 1.3); and
for all open subsets
A of
, because then,
is one-to-one (see the closing remarks of the
Appendix on one-to-one maps). Finally, note that symbolizations based on
as given by (
15), or finer, have the property (iii) of Theorem 2 (in particular, compare (iii) of Theorem 2 to the structure of (
15)). Summarizing, the assumptions of Theorem 2 are generalizations of the assumptions of Theorem 1, and thus, Theorem 1 follows by Theorem 2.
3.2. Preserving the Information of the Measuring Process
In this section, we state sufficient conditions such that the information given by the measuring process is preserved. Therefore, if these conditions are fulfilled and
, then
is generating. Define:
where
is an arbitrary random vector (compare to Equation (
8)), and consider the special case
for some
in the following.
Definition 2. Let be a basic symbolization scheme and be a timing. We call the tuple consistent if for all and , it holds: Compare to Keller et al. [
17], who regard the ordinal approach: observe that, in the consistent case, by applying (
16) repeatedly, one shows that:
for all
t,
. Consistency ensures that for all
, it holds:
In other words, if the information given by a measurement at a time is preserved by , then it also is preserved by (compare to the proof of Theorem 3).
Consistency depends on the interplay of the underlying system, the considered random vector
,
and
; however, a skillful choice of the timing guarantees that
is consistent independent of the system and
. This we discuss in
Section 4.3. Note here that
is always consistent if
is the full timing (see Equation (
9)); however, the tuple is not consistent in general if a timing given by:
is considered.
Theorem 3. Let be a random vector, a basic symbolization scheme, a timing and a sequence of finite partitions constructed by and (see Equation (
8))
. If further: - (i)
and
- (ii)
is consistent,
Recall that (i) of Theorem 3 particularly holds if Conditions (i)–(iii) of Theorem 2 are fulfilled.
5. Some Remarks
In proposing and studying our universal symbolic approach toward KS entropy, we have restricted ourselves to the kernel ideas. In particular, we have attached importance to point out that a “two-dimensional” symbolization, that is linking two observations, can provide a better basic symbolization scheme than symbolizing only on a one-dimensional observational level. The obtained results can be simply generalized in two directions:
On the one hand, infinitely many observables instead of finitely many ones can be considered. Here, the results obtained by Keller et al. [
18] (see also the references given in the paper) can directly be adapted, which leads to a description of the KS entropy by a double limit substituting the limit in (
2). On the other hand, some of our results remain true when relaxing ergodicity by some rather general conditions on the dynamics considered. For this, the ergodic decomposition theorem can be utilized. We refer to the discussion in Keller et al. [
18] and the references given therein.
Our study does not touch aspects as the speed of convergence in (
2), as a general comparison of basic symbolic schemes and as an entropy estimation, which are, incontestably, very interesting both from the theoretical and practical viewpoint. Our approach provides some theoretical framework within concrete methods for time series and system analysis and can be specified in accordance with requirements given in practice.
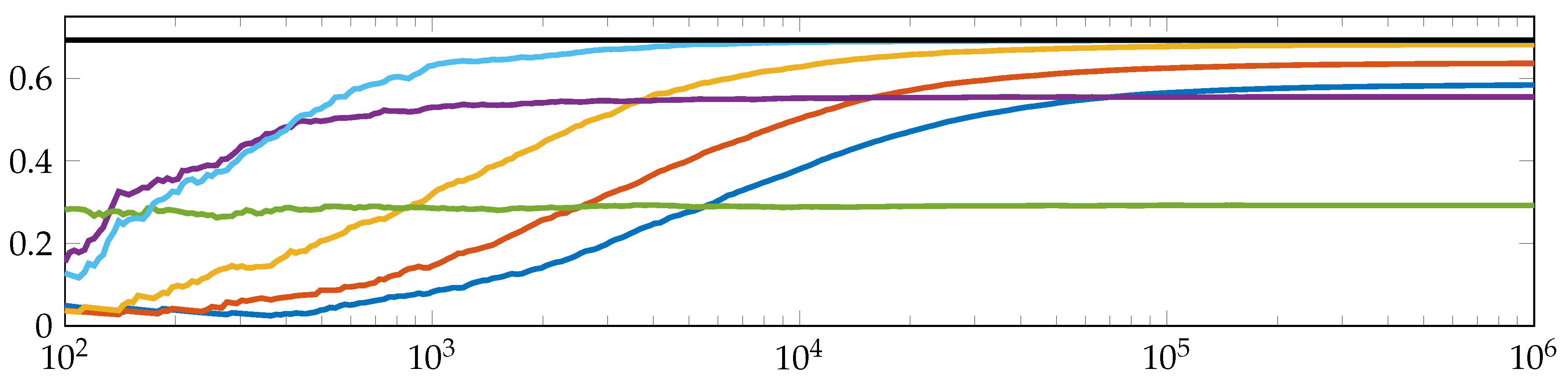
In order to give a brief perspective on the matter, we decoded a finite orbit
;
of the tent map (see
Section 2.1), that is:
for all
and
uniformly distributed, into a sequence of symbols, fixed a word length
and naively estimated the difference
by replacing the probabilities by relative frequencies of symbol word occurrences.
Figure 7 shows the results for different
and symbolization schemes in dependence of the orbit length
, here between
and
. We chose to take the difference because of (
19), i.e., the difference for fixed
t is a better approximation of the entropy rate
than
. For a fuller treatment, we refer the reader to Keller et al. [
19], in particular for more information of how to construct a symbol sequence with respect to ordinal symbolic dynamics with fixed order
and word length
.
Clearly,
Figure 7 emphasizes common problems of time series analysis, which have to be faced, as, for example, the trade-off between computational capacity and computation accuracy, which includes undersampling problems, the choice of parameters, stationarity assumptions, and so forth (see for instance Keller et al. [
19]). A discussion of all these aspects would be beyond the scope of this paper, but is planned for the future.