Assessment of Component Selection Strategies in Hyperspectral Imagery
Abstract
1. Introduction
2. Materials and Methods
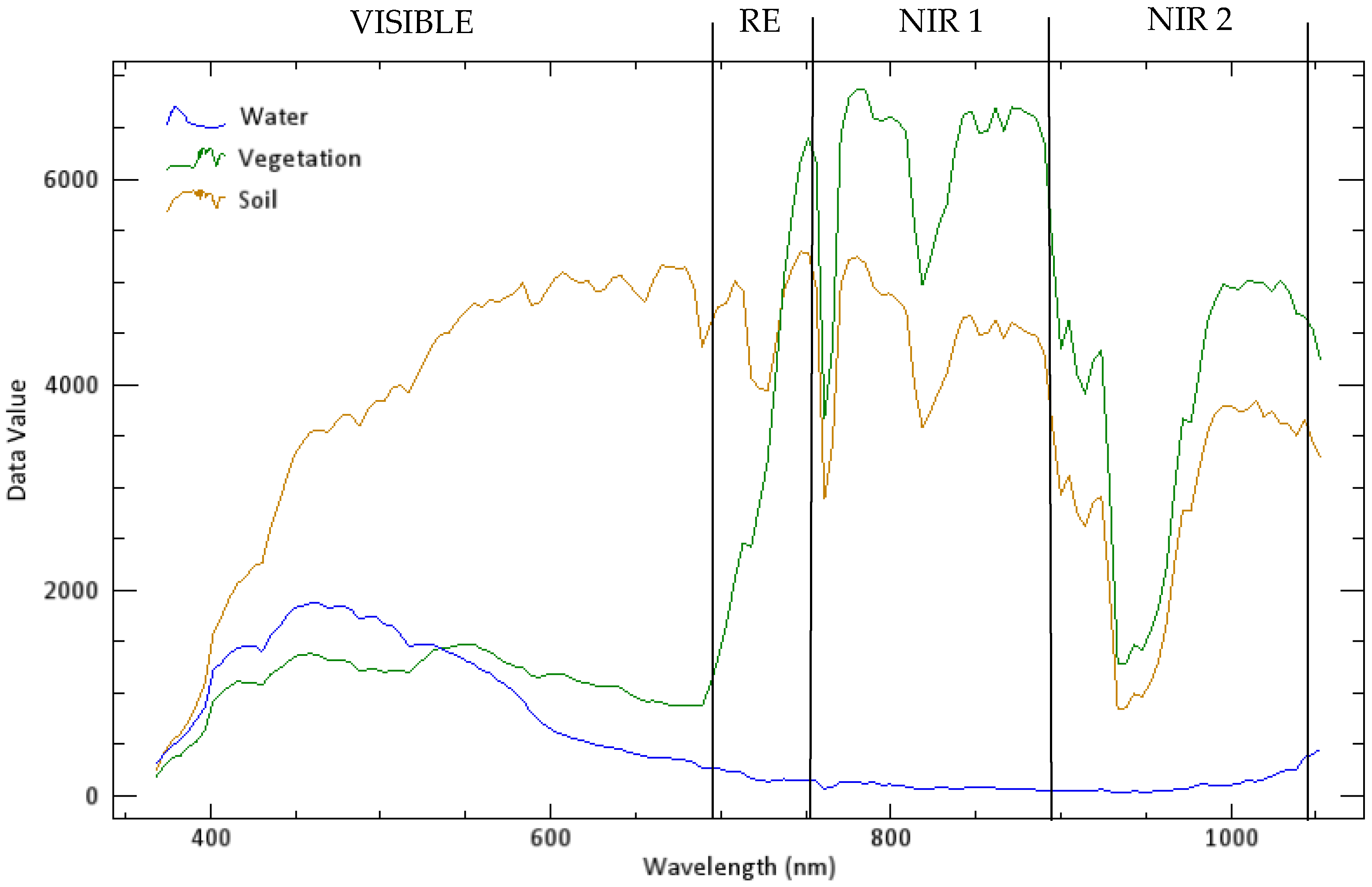
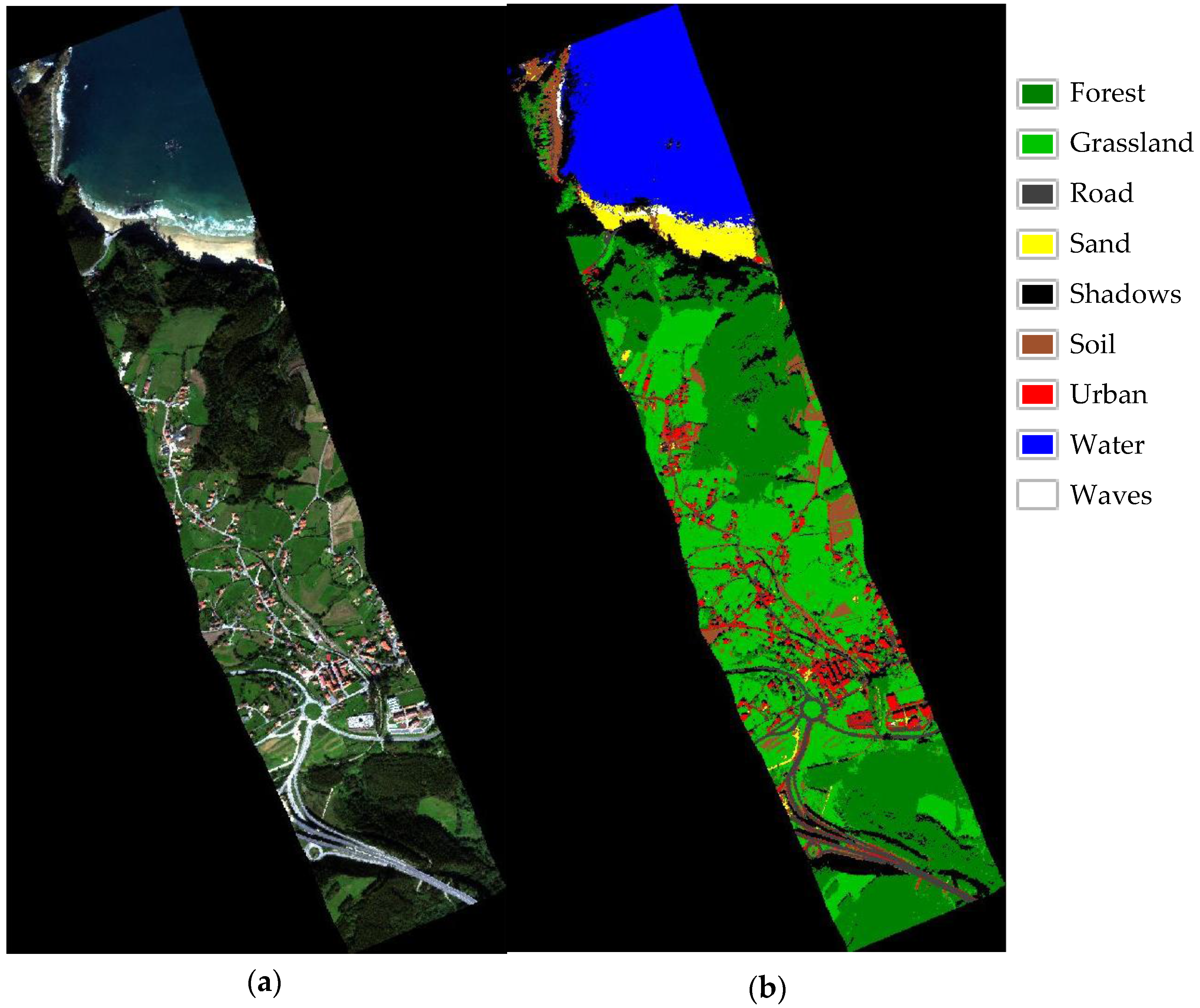
2.1. Study Area and Data Set
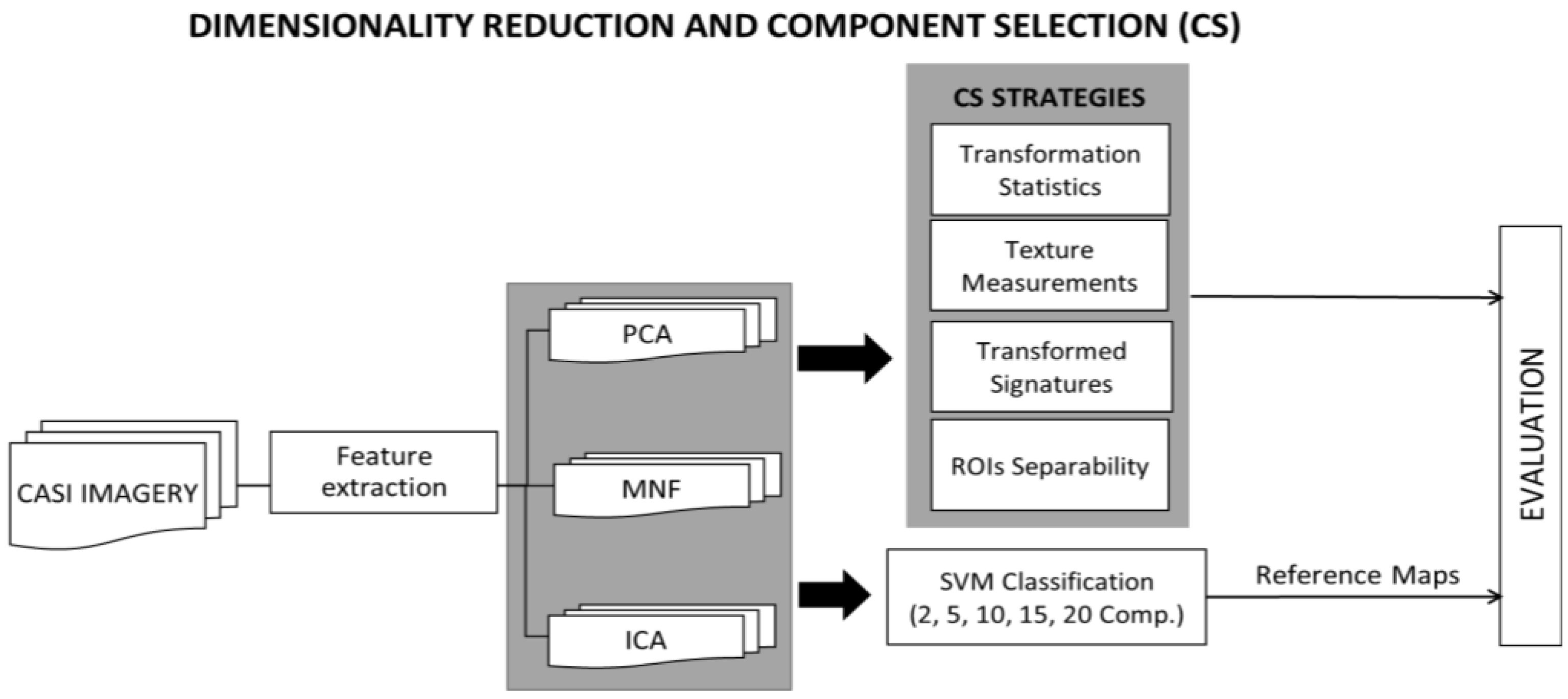
2.2. Dimensionality Reduction Methodology
2.2.1. Dimensionality Reduction Techniques
2.2.2. Component Selection Strategies
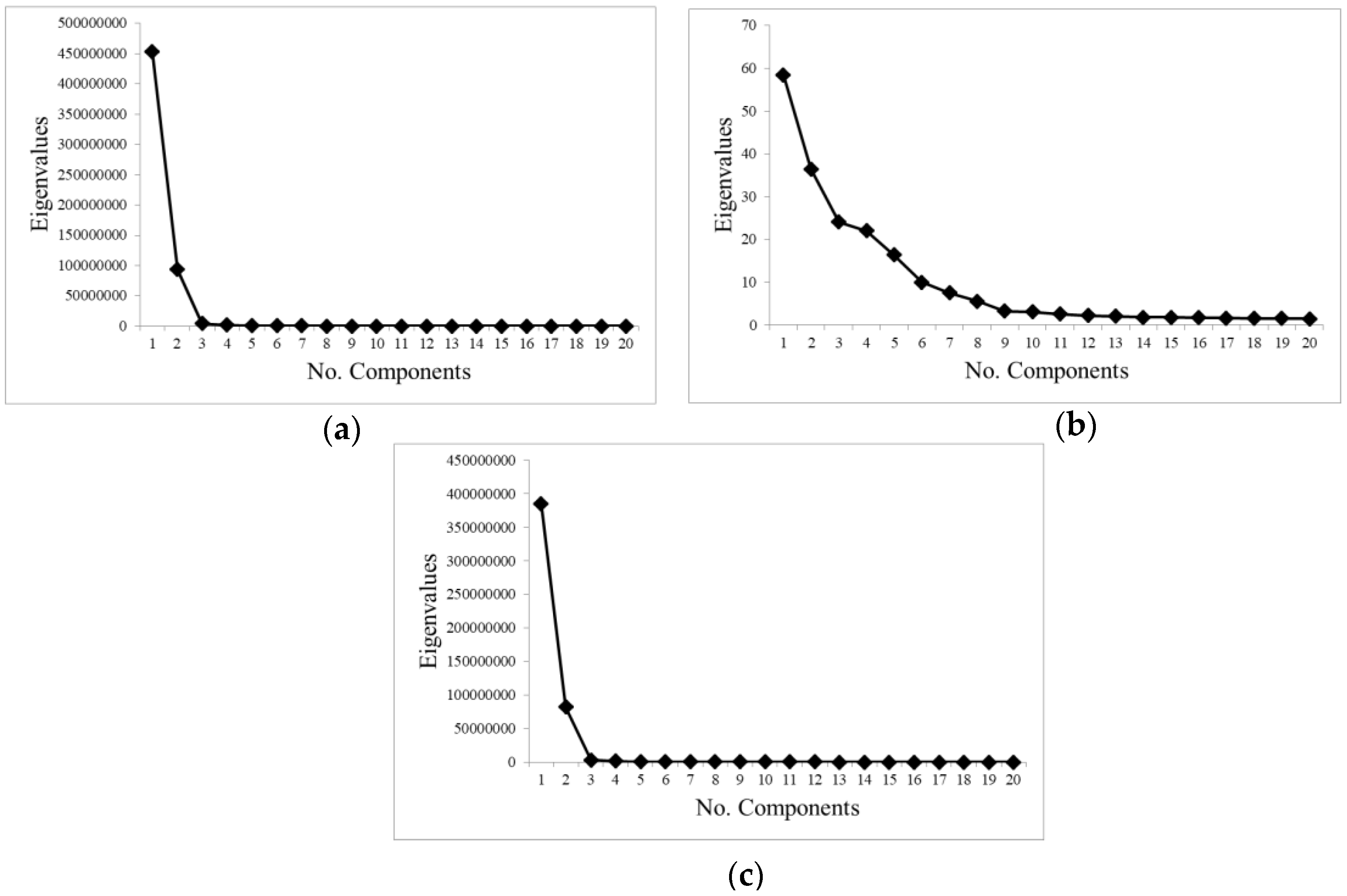
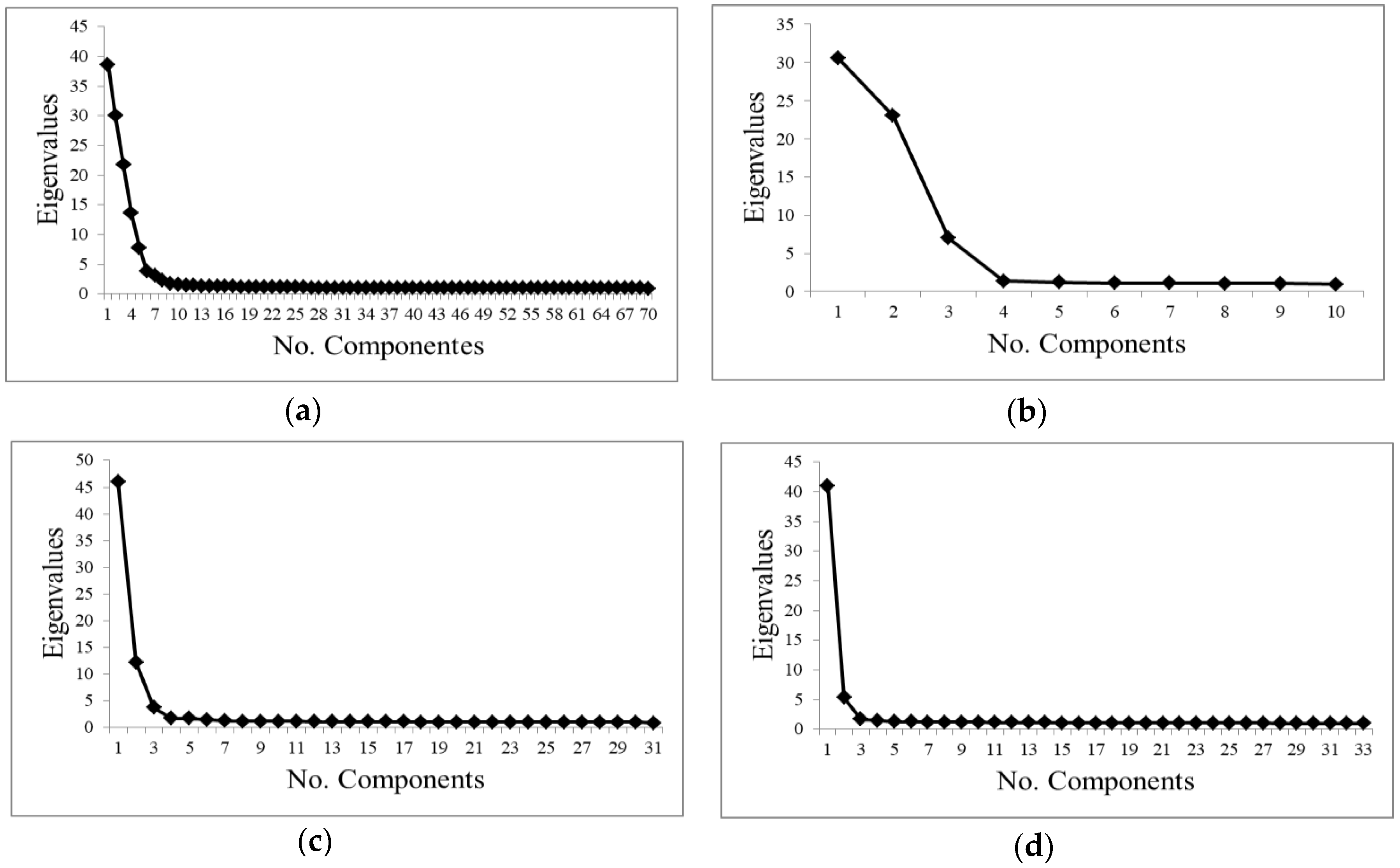
- Transformation statistics: it is the most common method used in the bibliography to select the suitable number of components. The eigenvalues of the obtained components were analyzed [34]. Components with large eigenvalues contain a higher amount of data variance, while components with lower eigenvalues contain less data information and more noise [31].
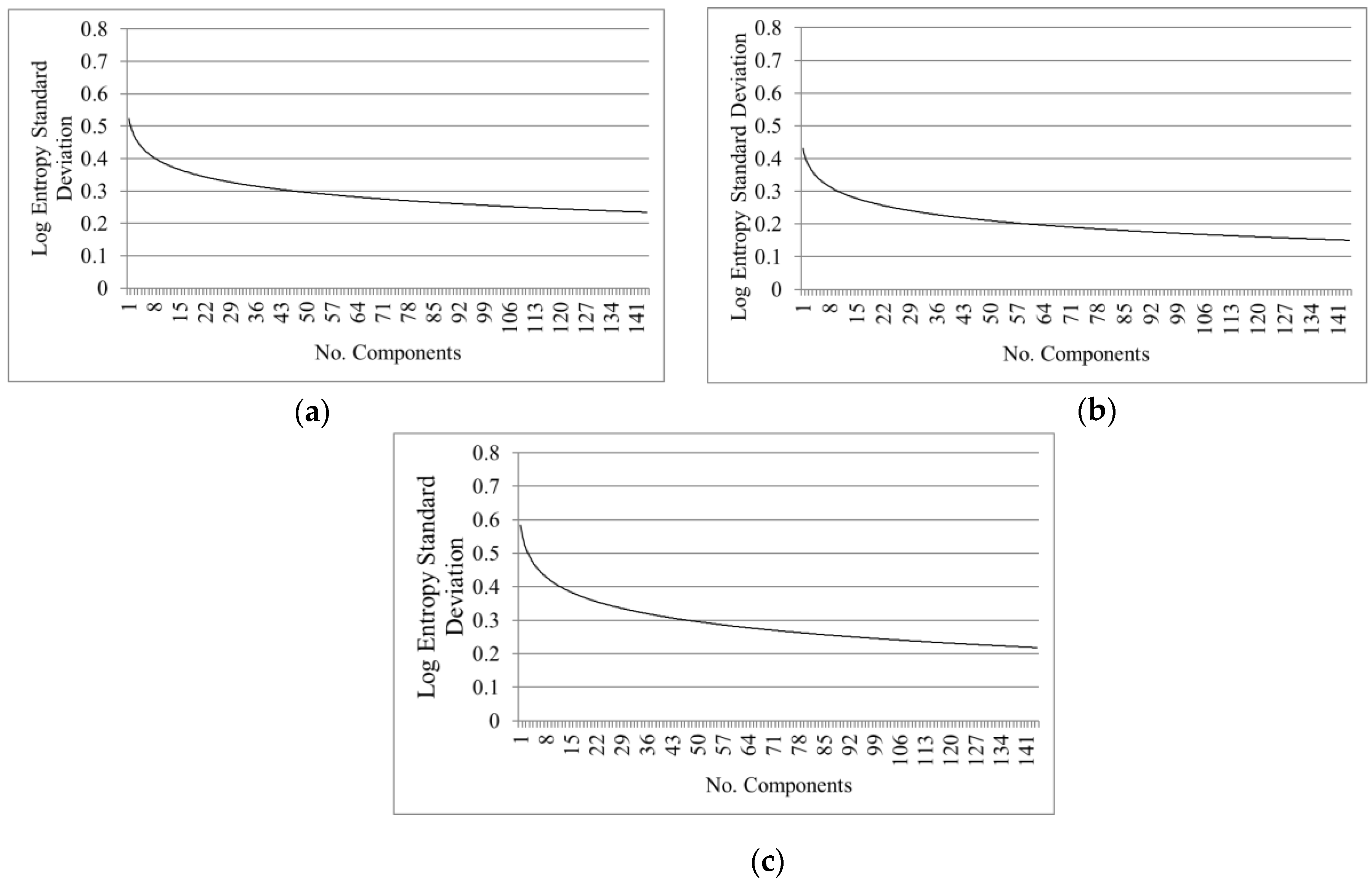
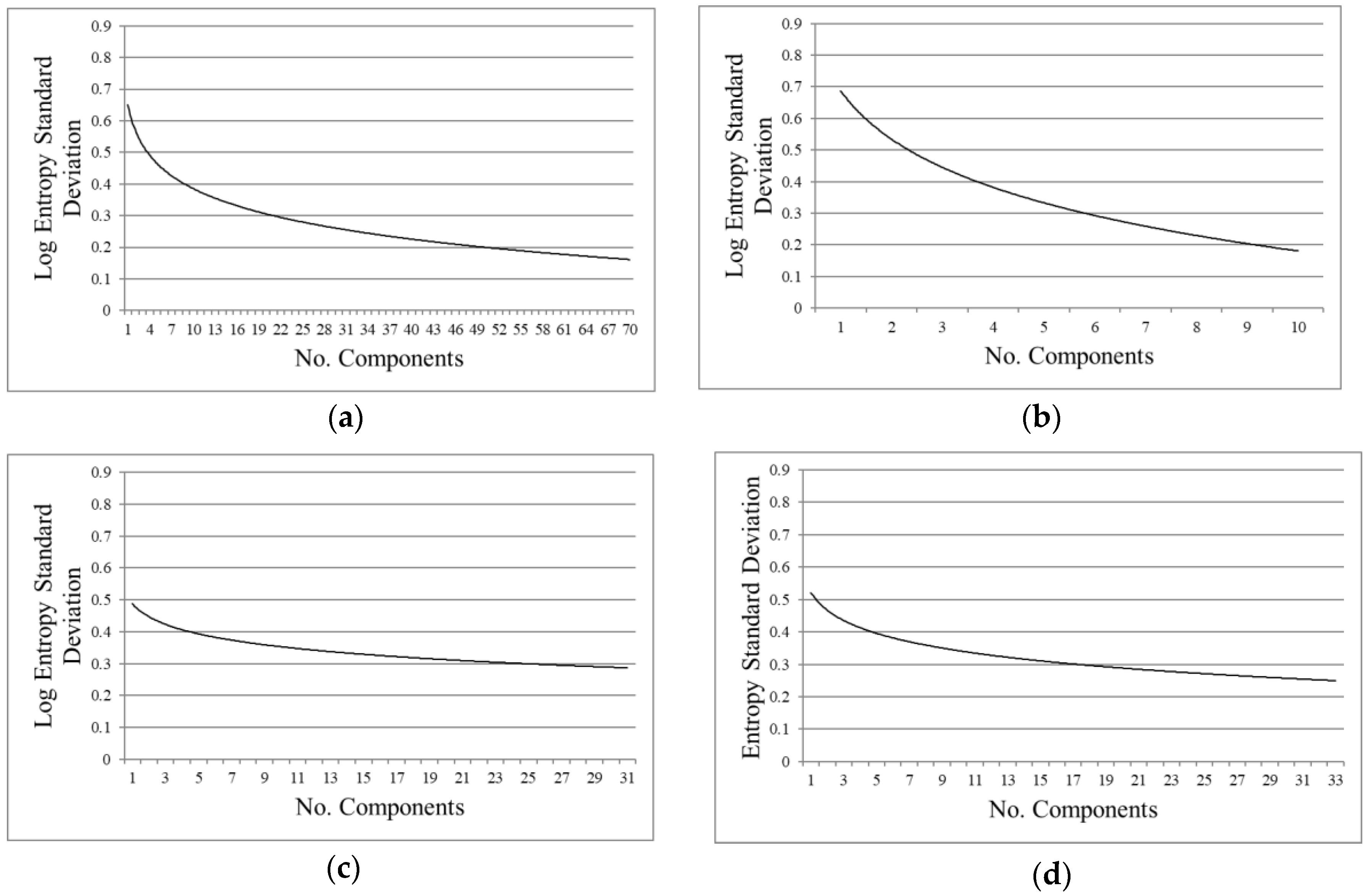
- Texture measurements: texture parameters, as entropy, are simple mathematical representations of image features. These features represent high-level information that can be used to describe the objects in and structure of images [10,35], and in consequence can be applied to select the components providing important information. An entropy first-order texture filter is applied based on a co-occurrence matrix [31]. The Equation (1) from Anys et al. [36] was used to compute the entropy using the pixel values in a kernel centered at the current pixel. Entropy is calculated based on the distribution of the pixel values in the kernel. It measures the disorder of the kernel values, where is the number of distinct grey levels in the image, and is the probability of each pixel value.
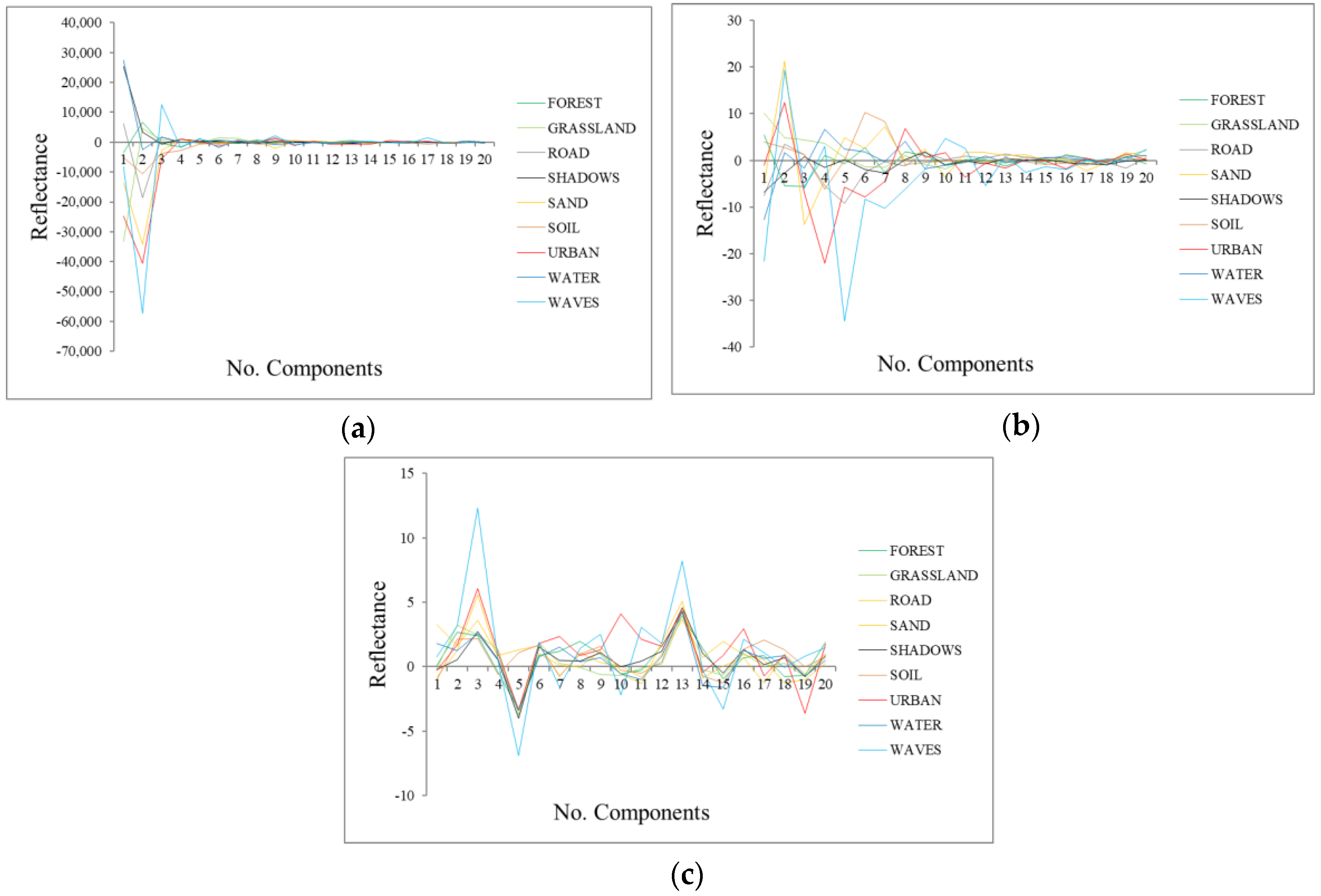
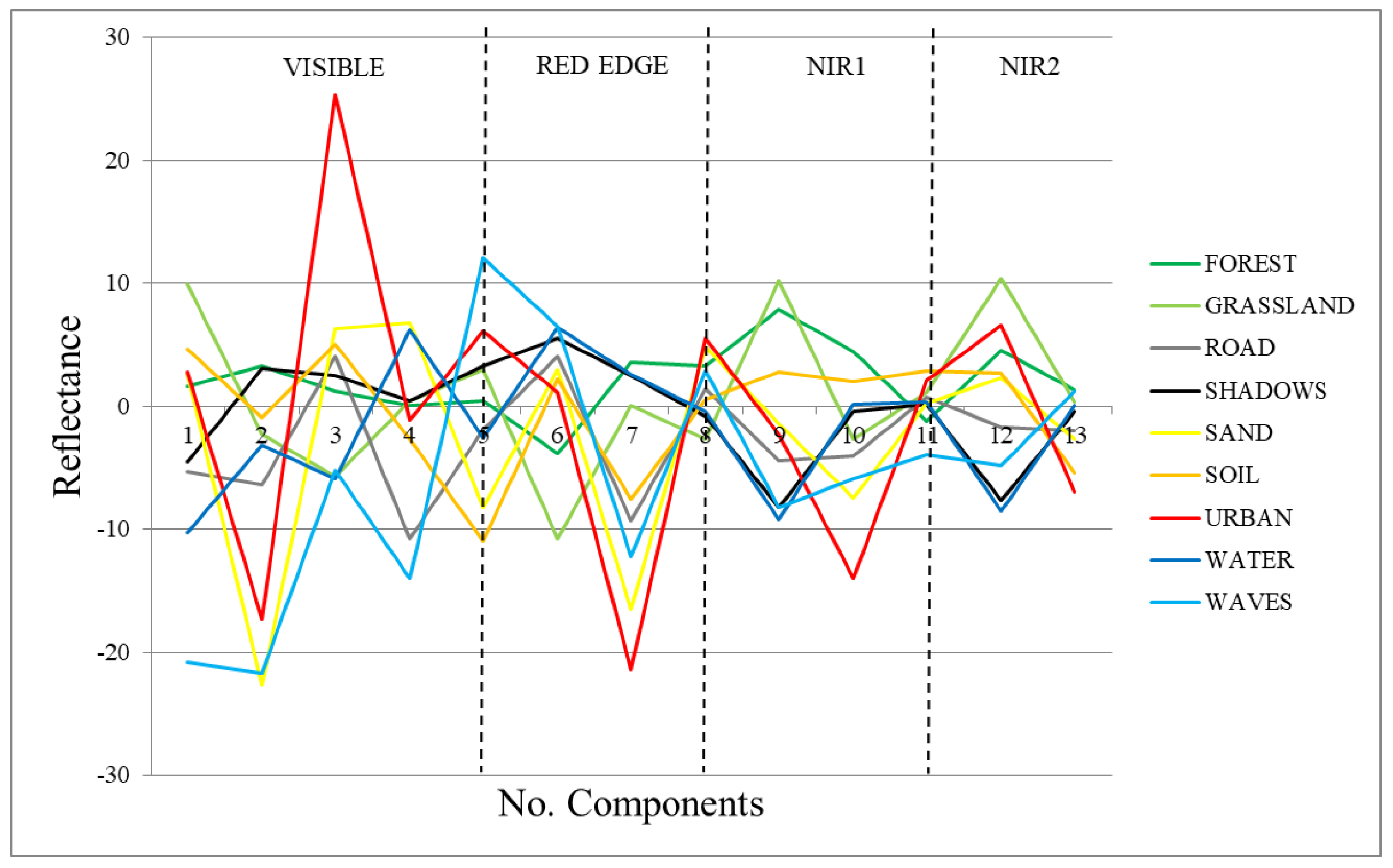
- Signatures of the classes in the transformed space (transformed signatures): the classes considered in the study will have values in the components with information, but they will not be distinguished within each other if the component is mainly noise. Moreover, spatially, in components without noise, objects’ shapes are recognizable, while in noisy components, only a “salt and pepper” effect appears. A visual assessment is used in order to determine from which components the classes cannot be distinguished within each other, being that those components are mainly noise. However, transformed signatures are dependent on the classes determined by each user as well as the type of image.
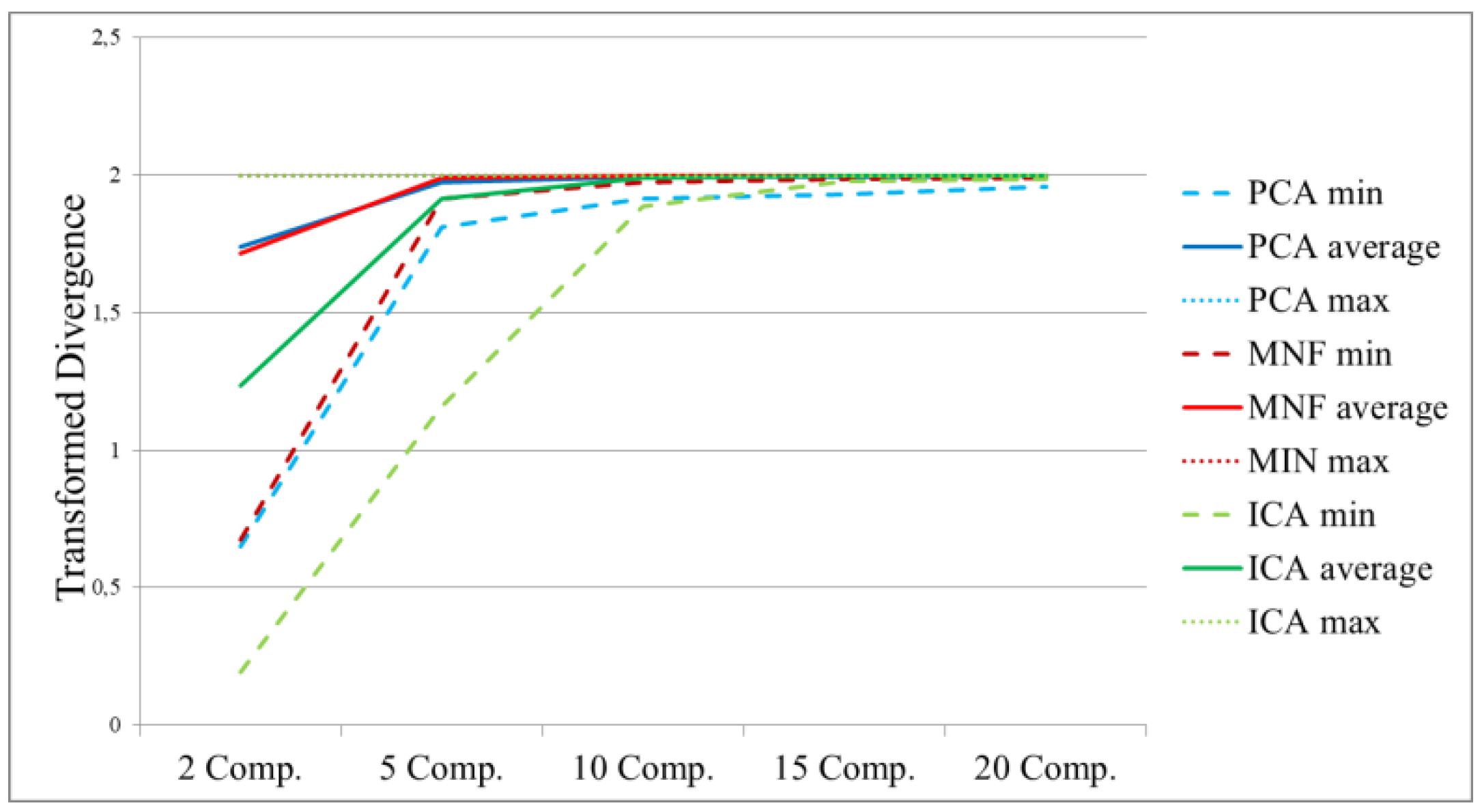
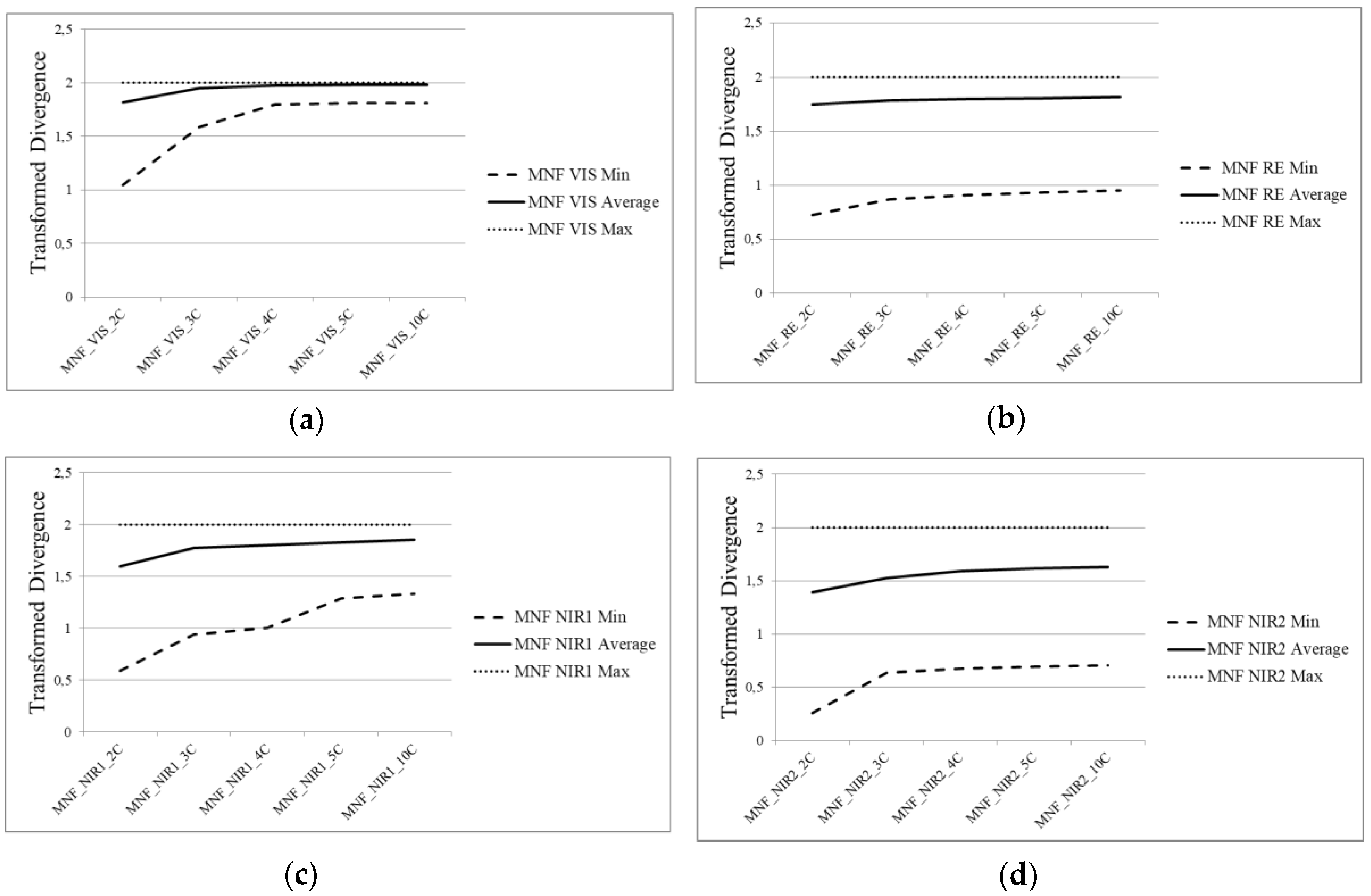
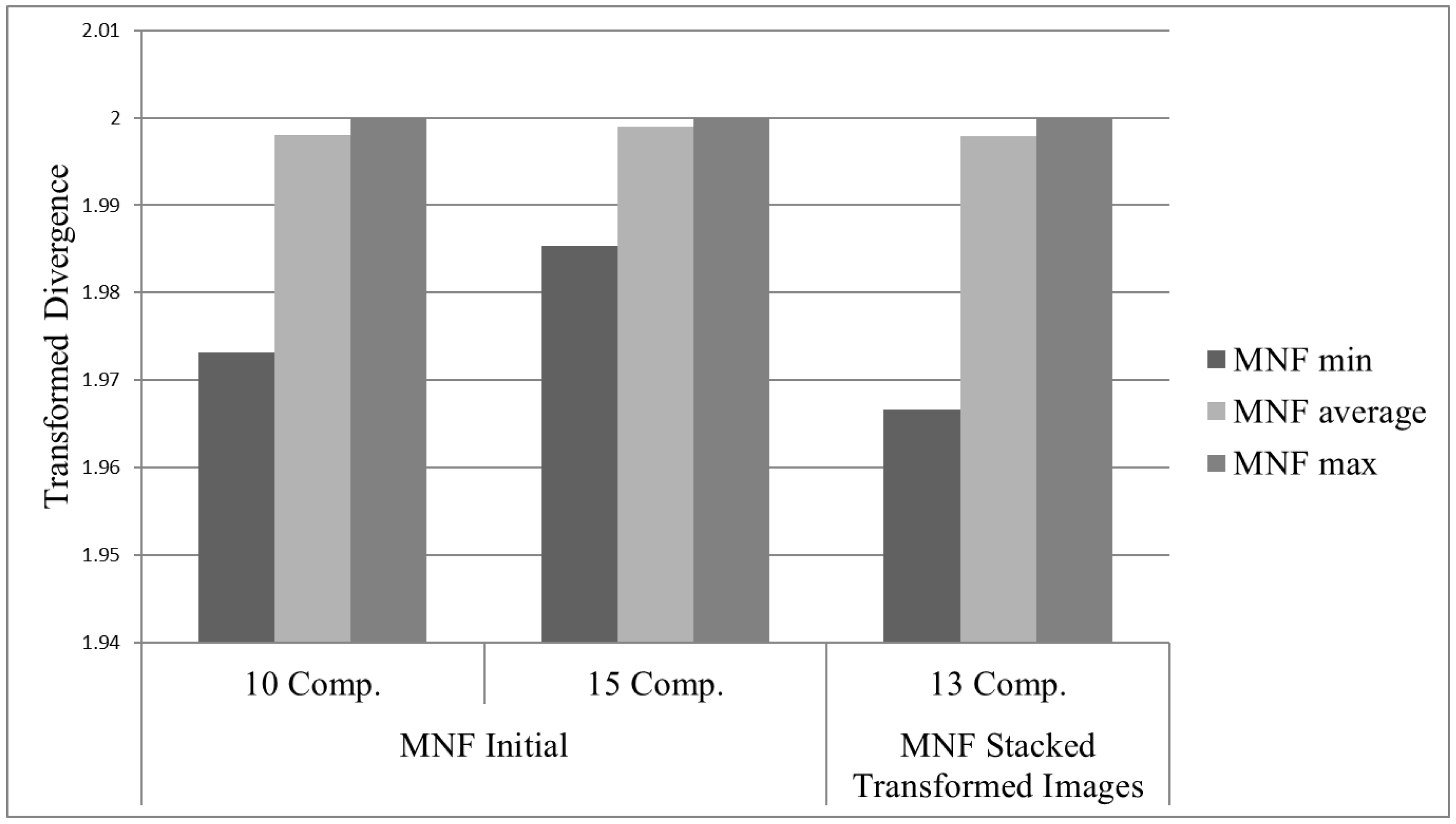
- ROIs separability in the transformed space: during the supervised classification procedure, training and testing regions were selected for each class of interest. The evaluation of the separability in different numbers of components could benefit the selection procedure. This strategy is class-dependent. An ROI’s separability was determined through the Transformed Divergence (TD) measure (2). This separability index exponentially takes into account the mean and the covariance, and its value ranges from 0 to 2 to indicate how well the selected ROI pairs are statistically separable. Values greater than 1.8 indicate that an ROI pair has good separability [31].
2.2.3. Spectral Division Analysis
3. Results and Discussion
3.1. Dimensionality Reduction Techniques
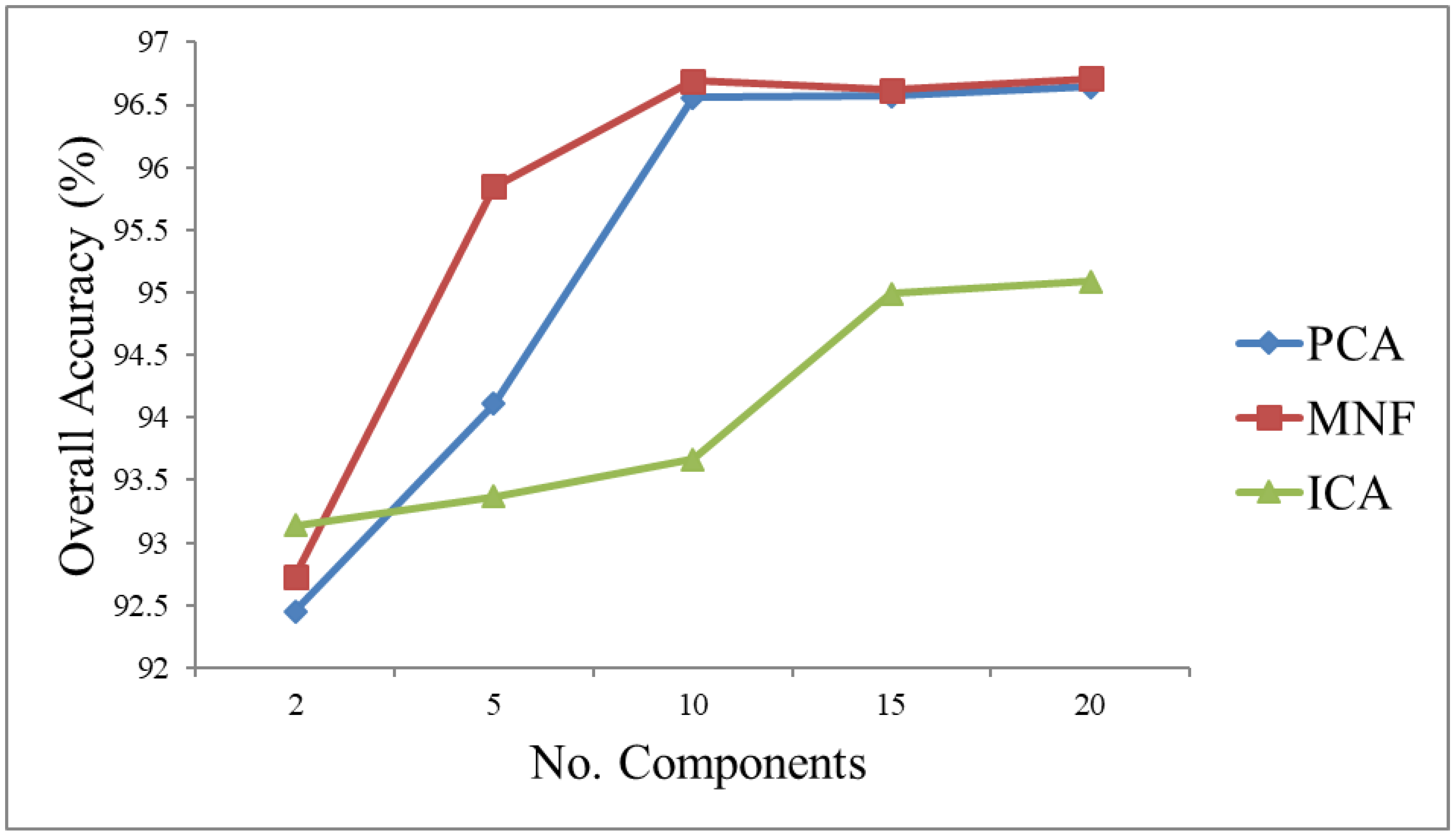
3.1.1. Classification Results for Each Technique
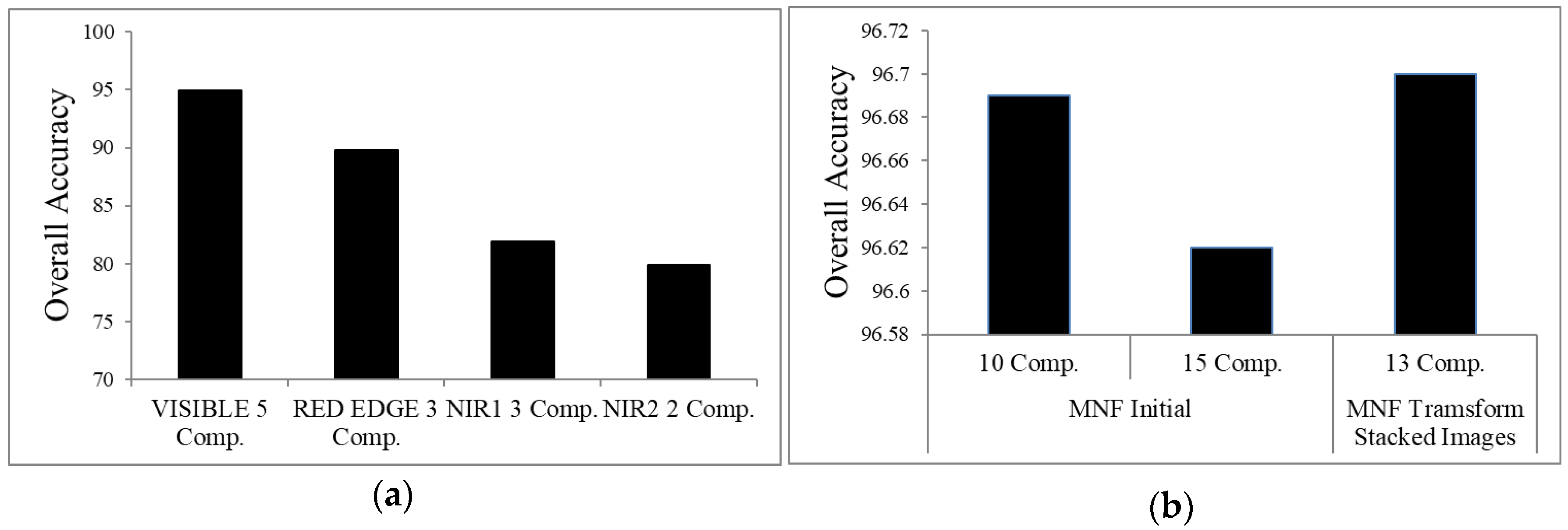
3.1.2. Results for the Component Selection Strategies
3.2. Spectral Division Analysis Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ren, J.; Zabalza, J.; Marshall, S.; Zheng, J. Effective feature extraction and data reduction in remote sensing using hyperspectral imaging. IEEE Signal Process. Mag. 2014, 31, 149–154. [Google Scholar] [CrossRef]
- Li, C.; Yin, J.; Zhao, J. Using improved ICA method for hyperspectral data classification. Arabian J. Sci. Eng. 2014, 39, 181–189. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Ghamisi, P. Spectral-Spatial Classification of Hyperspectral Remote Sensing Images; Artech House: Boston, MA, USA, 2015. [Google Scholar]
- Ballanti, L.; Blesius, L.; Hines, E.; Kruse, B. Tree species classification using hyperspectral imagery: A comparison of two classifiers. Remote Sens. 2016, 8, 445. [Google Scholar] [CrossRef]
- Villa, A.; Chanussot, J.; Jutten, C.; Benediktsson, J.A.; Moussaoui, S. On the use of ICA for hyperspectral image analysis. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Cape Town, South Africa, 12–17 July 2009; Volume 4, pp. 97–100. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Ghamisi, P.; Benediktsson, J.A.; Phinn, S. Land-cover classification using both hyperspectral and Lidar data. Int. J. Image Data Fusion 2015, 6, 189–215. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Neumann, C.; Förster, M.; Buddenbaum, H.; Ghosh, A.; Clasen, A.; Joshi, P.K.; Koch, B. Comparison of feature reduction algorithms for classifying tree species with hyperspectral data on three central European test sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2547–2561. [Google Scholar] [CrossRef]
- Ibrahim, R.W.; Moghaddasi, Z.; Jalab, H.A.; Noor, R.M. Fractional differential texture descriptors based on the Machado entropy for image splicing detection. Entropy 2015, 17, 4775–4785. [Google Scholar] [CrossRef]
- Licciardi, G.A.; Frate, F. In A comparison of feature extraction methodologies applied on hyperspectral data. In Proceedings of the 2010 Hyperspectral Workshop, Frascati, Italy, 17–19 March 2010; pp. 17–19. [Google Scholar]
- Wang, L.; Zhao, C. Hyperspectral Image Processing; Springer: Berlin, German, 2016. [Google Scholar]
- Luo, G.; Chen, G.; Tian, L.; Qin, K.; Qian, S.-E. Minimum noise fraction versus principal component analysis as a preprocessing step for hyperspectral imagery denoising. Can. J. Remote Sens. 2016, 42, 106–116. [Google Scholar] [CrossRef]
- Chang, C.-I.; Du, Q.; Sun, T.-L.; Althouse, M.L. A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef]
- Cheriyadat, A.; Bruce, L.M. Why principal component analysis is not an appropriate feature extraction method for hyperspectral data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, IGARSS, Toulouse, France, 21–25 July 2003; pp. 3420–3422. [Google Scholar]
- Du, H.; Qi, H.; Wang, X.; Ramanath, R.; Snyder, W.E. Band selection using independent component analysis for hyperspectral image processing. In Proceedings of the IEEE Applied Imagery Pattern Recognition Workshop, Washington, DC, USA, 15–17 October 2003; Volume 32, pp. 93–98. [Google Scholar]
- Lennon, M.; Mercier, G.; Mouchot, M.; Hubert-Moy, L. Independent component analysis as a tool for the dimensionality reduction and the representation of hyperspectral images. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Sydney, Australia, 9–13 July 2001; pp. 2893–2895. [Google Scholar]
- Wang, J.; Chang, C.-I. Independent component analysis-based dimensionality reduction with applications in hyperspectral image analysis. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1586–1600. [Google Scholar] [CrossRef]
- Liao, W.; Vancoillie, F.; Devriendt, F.; Gautama, S.; Pizurica, A.; Philips, W. Fusion of pixel-based and object-based features for classification of urban hyperspectral remote sensing data. In Proceedings of the 5th International Conference on Geographic Object-Based Image Analysis (GEOBIA), Thessaloniki, Greece, 21–24 May 2014; pp. 179–184. [Google Scholar]
- Mücher, C.A.; Kooistra, L.; Vermeulen, M.; Borre, J.V.; Haest, B.; Haveman, R. Quantifying structure of natura 2000 heathland habitats using spectral mixture analysis and segmentation techniques on hyperspectral imagery. Ecol. Indic. 2013, 33, 71–81. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support vector machine. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Rojas, M.; Dópido, I.; Plaza, A.; Gamba, P. Comparison of support vector machine-based processing chains for hyperspectral image classification. Proc. SPIE 2010, 78100B. [Google Scholar] [CrossRef]
- Denghui, Z.; Le, Y. Support vector machine based classification for hyperspectral remote sensing images after minimum noise fraction rotation transformation. In Proceedings of the IEEE International Conference Internet Computing & Information Services (ICICIS), Hong Kong, China, 17–18 September 2011; pp. 32–135. [Google Scholar]
- Rodarmel, C.; Shan, J. Principal component analysis for hyperspectral image classification. Surv. Land Inf. Sci. 2002, 62, 115. [Google Scholar]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Wiersma, D.J.; Landgrebe, D.A. Analytical design of multispectral sensors. IEEE Trans. Geosci. Remote Sens. 1980, GE-18, 180–189. [Google Scholar] [CrossRef]
- Drumetz, L.; Veganzones, M.A.; Gómez, R.M.; Tochon, G.; Dalla Mura, M.; Licciardi, G.A.; Jutten, C.; Chanussot, J. Hyperspectral local intrinsic dimensionality. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4063–4078. [Google Scholar] [CrossRef]
- Kaewpijit, S.; Le-Moige, J.; El-Ghazawi, T. Hyperspectral Imagery Dimension Reduction Using Principal Component Analysis on the HIVE. In Proceedings of the Science Data Processing Workshop, Greenbelt, MD, USA, 26–28 February 2002. [Google Scholar]
- Vidal, M.; Amigo, J.M. Pre-processing of hyperspectral images. Essential steps before image analysis. Chemom. Intell. Lab. Syst. 2012, 117, 138–148. [Google Scholar] [CrossRef]
- Richards, J.A. Remote Sensing Digital Image Analysis; Springer: Berlin, Germany, 1999; Volume 3. [Google Scholar]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Francis, J.G. The QR transformation—Part 2. Comput. J. 1962, 4, 332–345. [Google Scholar] [CrossRef]
- Padmanaban, R.; Bhowmik, A.K.; Cabral, P.; Zamyatin, A.; Almegdadi, O.; Wang, S. Modelling urban sprawl using remotely sensed data: A case study of Chennai city, Tamilnadu. Entropy 2017, 19, 163. [Google Scholar] [CrossRef]
- Anys, H.; Bannari, A.; He, D.; Morin, D. Texture analysis for the mapping of urban areas using airborne MEIS-II images. In Proceedings of the First International Airborne Remote Sensing Conference and Exhibition, Strasbourg, France, 12–15 September 1994; Environmental Research Institute of Michigan: Ann Arbor, MI, USA, 1994; pp. 231–245. [Google Scholar]
- Huang, X.; Zhang, L. An SVM ensemble approach combining spectral, structural, and semantic features for the classification of high-resolution remotely sensed imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 257–272. [Google Scholar] [CrossRef]
- Pal, M.; Mather, P.M. Assessment of the effectiveness of support vector machines for hyperspectral data. Future Gener. Comput. Syst. 2004, 20, 1215–1225. [Google Scholar] [CrossRef]
- Braun, A.C.; Weidner, U.; Hinz, S. Support vector machines for vegetation classification—A revision. Photogramm. Fernerkund. Geoinf. 2010, 2010, 273–281. [Google Scholar] [CrossRef]


| PCA | MNF | ICA | ||
|---|---|---|---|---|
| EVALUATION | SVM Classification | Good (10 comp.) | Best (10 comp.) | Medium (15 comp.) |
| COMPONENT SELECTION STRATEGIES | Eigenvalues | Wrong (2 comp.) | Good (9 comp.) | Wrong (2 comp.) |
| Entropy | Good (10 comp.) | Good (10 comp.) | Good (15 comp.) | |
| Signatures of the classes | Good (9 comp.) | Good (10 comp.) | Medium (11 comp.) | |
| ROIs separability | Good (10 comp.) | Good (10 comp.) | Good (15 comp.) | |
| REGIONS | EIGENVALUES | ENTROPY | SIGNATURES OF CLASSES | ROIS SEPARABILITY |
|---|---|---|---|---|
| Visible | 5 comp. | 5 comp. | 5 comp. | 4 comp. |
| Red Edge | 3 comp. | 3 comp. | 3 comp. | 3 comp. |
| NIR1 | 3 comp. | 3 comp. | 3 comp. | 3 comp. |
| NIR2 | 2 comp. | 3 comp. | 2 comp. | 3 comp. |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibarrola-Ulzurrun, E.; Marcello, J.; Gonzalo-Martin, C. Assessment of Component Selection Strategies in Hyperspectral Imagery. Entropy 2017, 19, 666. https://doi.org/10.3390/e19120666
Ibarrola-Ulzurrun E, Marcello J, Gonzalo-Martin C. Assessment of Component Selection Strategies in Hyperspectral Imagery. Entropy. 2017; 19(12):666. https://doi.org/10.3390/e19120666
Chicago/Turabian StyleIbarrola-Ulzurrun, Edurne, Javier Marcello, and Consuelo Gonzalo-Martin. 2017. "Assessment of Component Selection Strategies in Hyperspectral Imagery" Entropy 19, no. 12: 666. https://doi.org/10.3390/e19120666
APA StyleIbarrola-Ulzurrun, E., Marcello, J., & Gonzalo-Martin, C. (2017). Assessment of Component Selection Strategies in Hyperspectral Imagery. Entropy, 19(12), 666. https://doi.org/10.3390/e19120666







