Entropy Parameter M in Modeling a Flow Duration Curve
Abstract
:1. Introduction
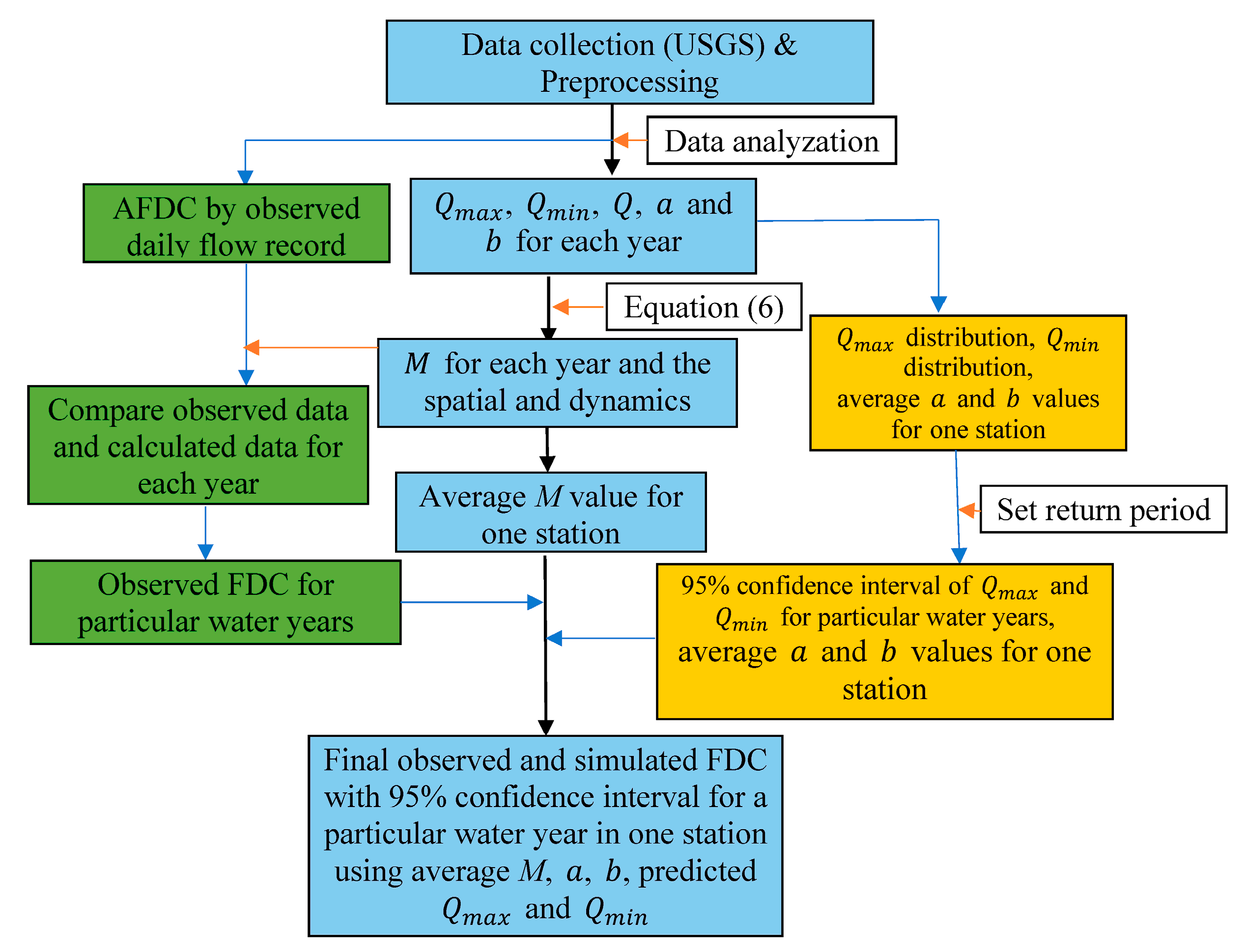
2. Materials and Methods
2.1. Derivation of FDC
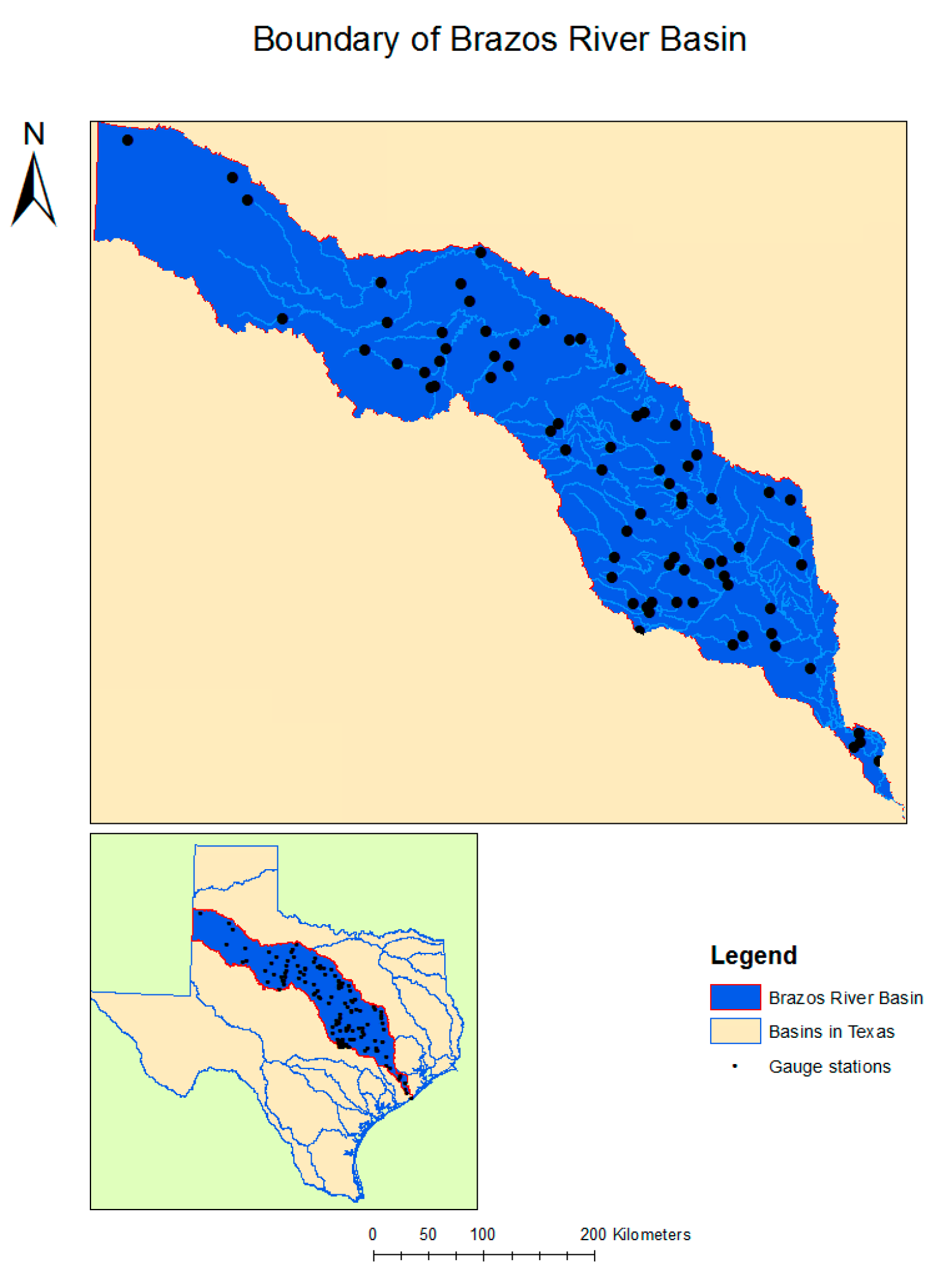
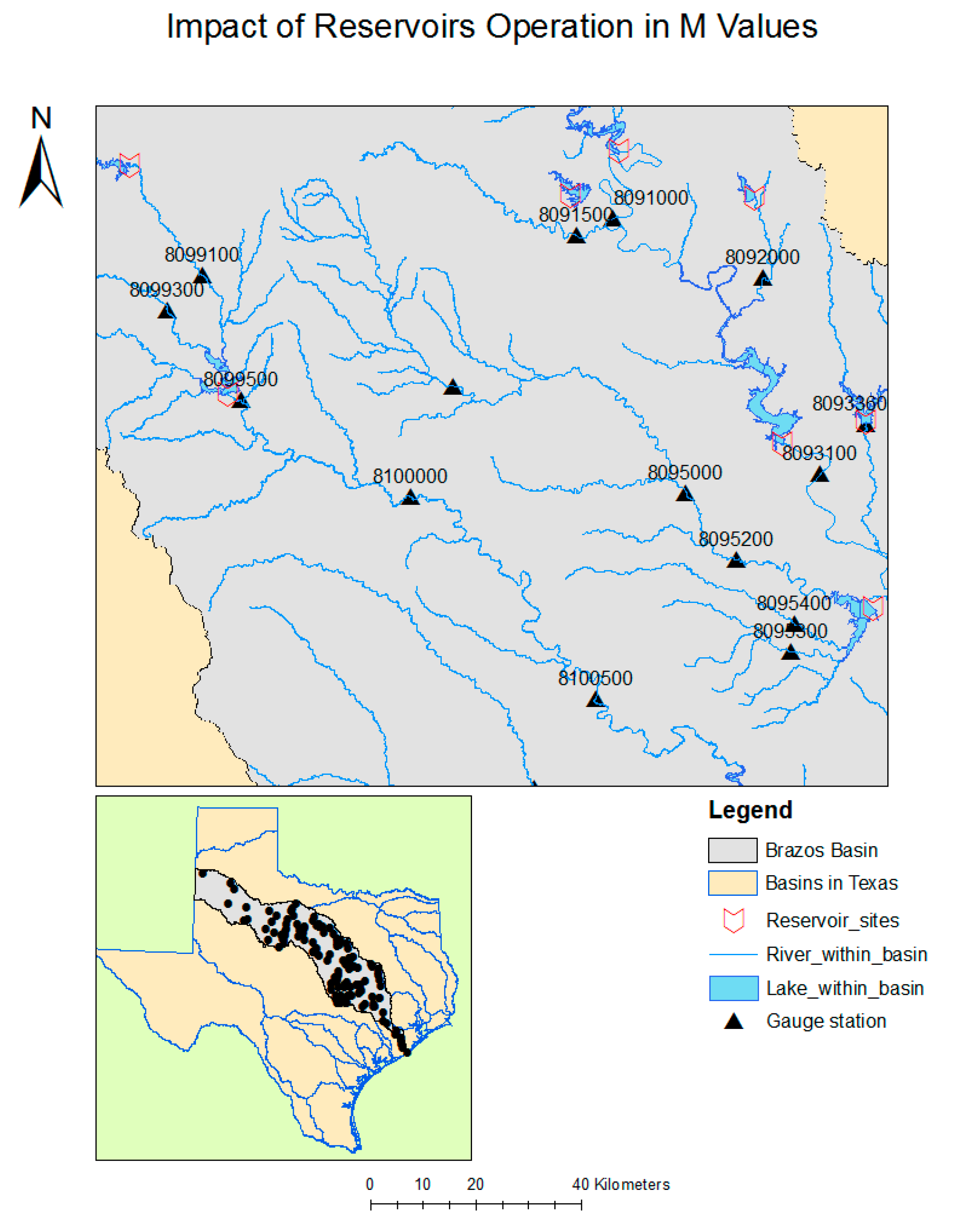
2.2. Study Area
3. Results and Discussion
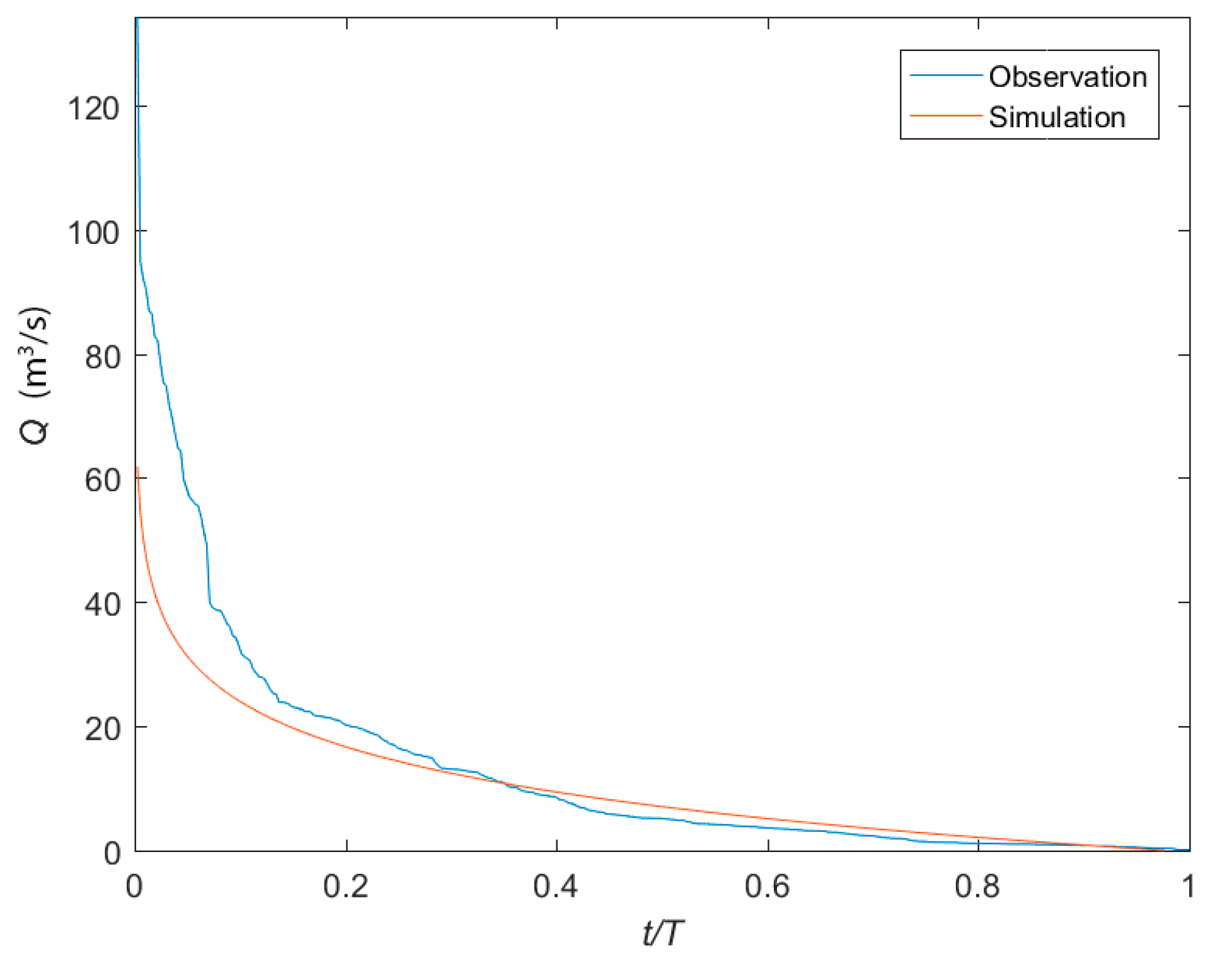
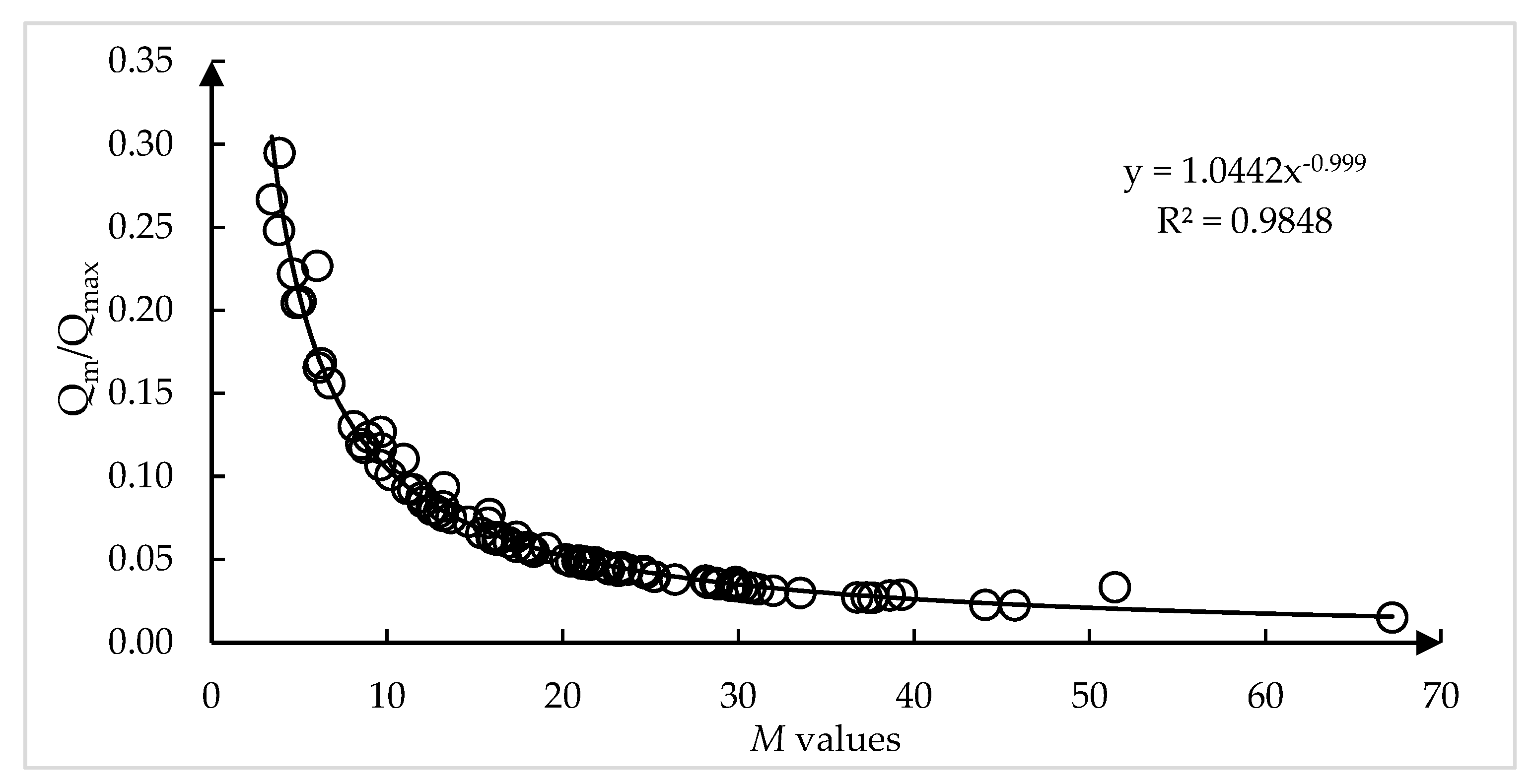
3.1. Flow Duration Curve Estimation
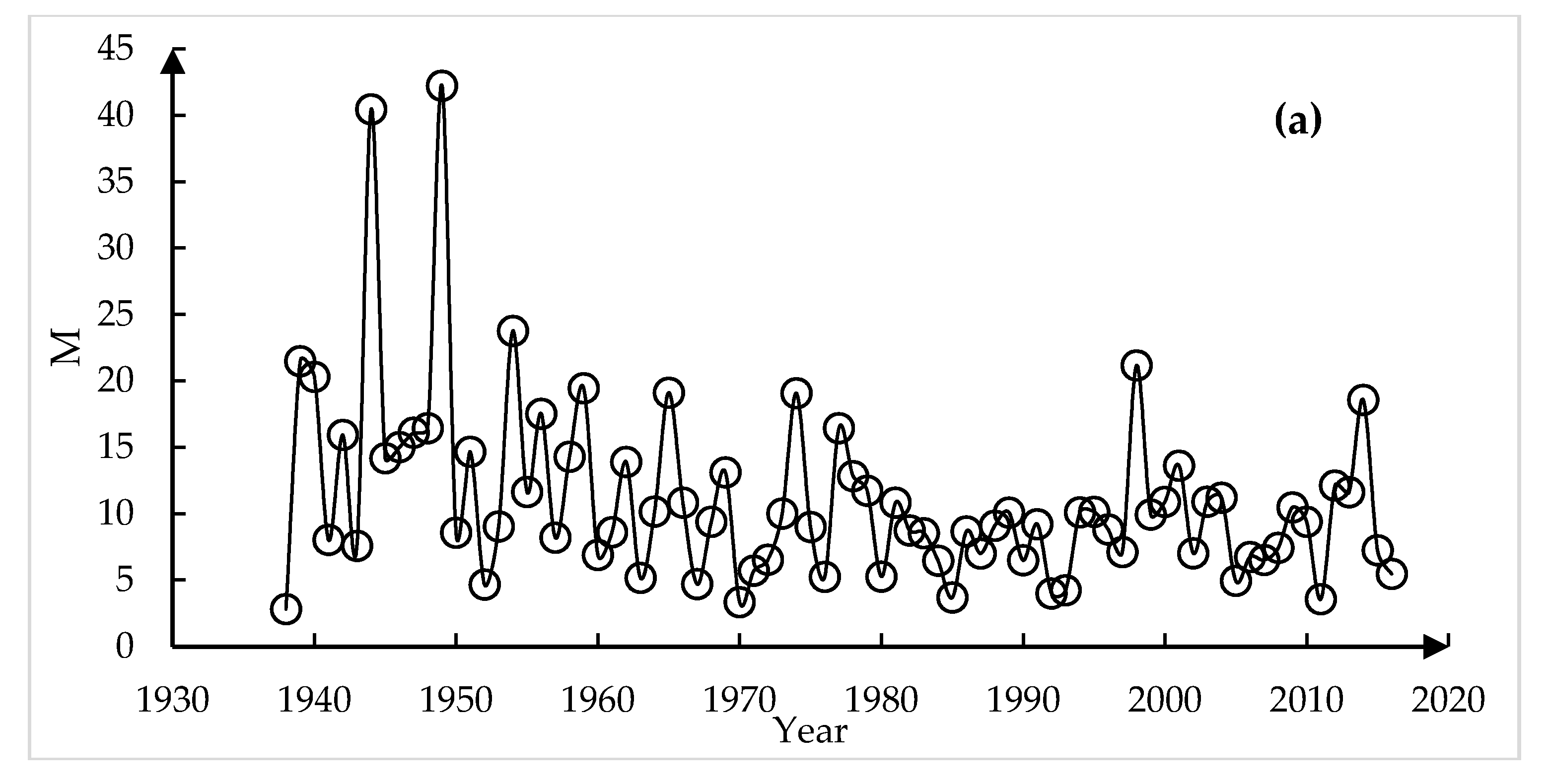
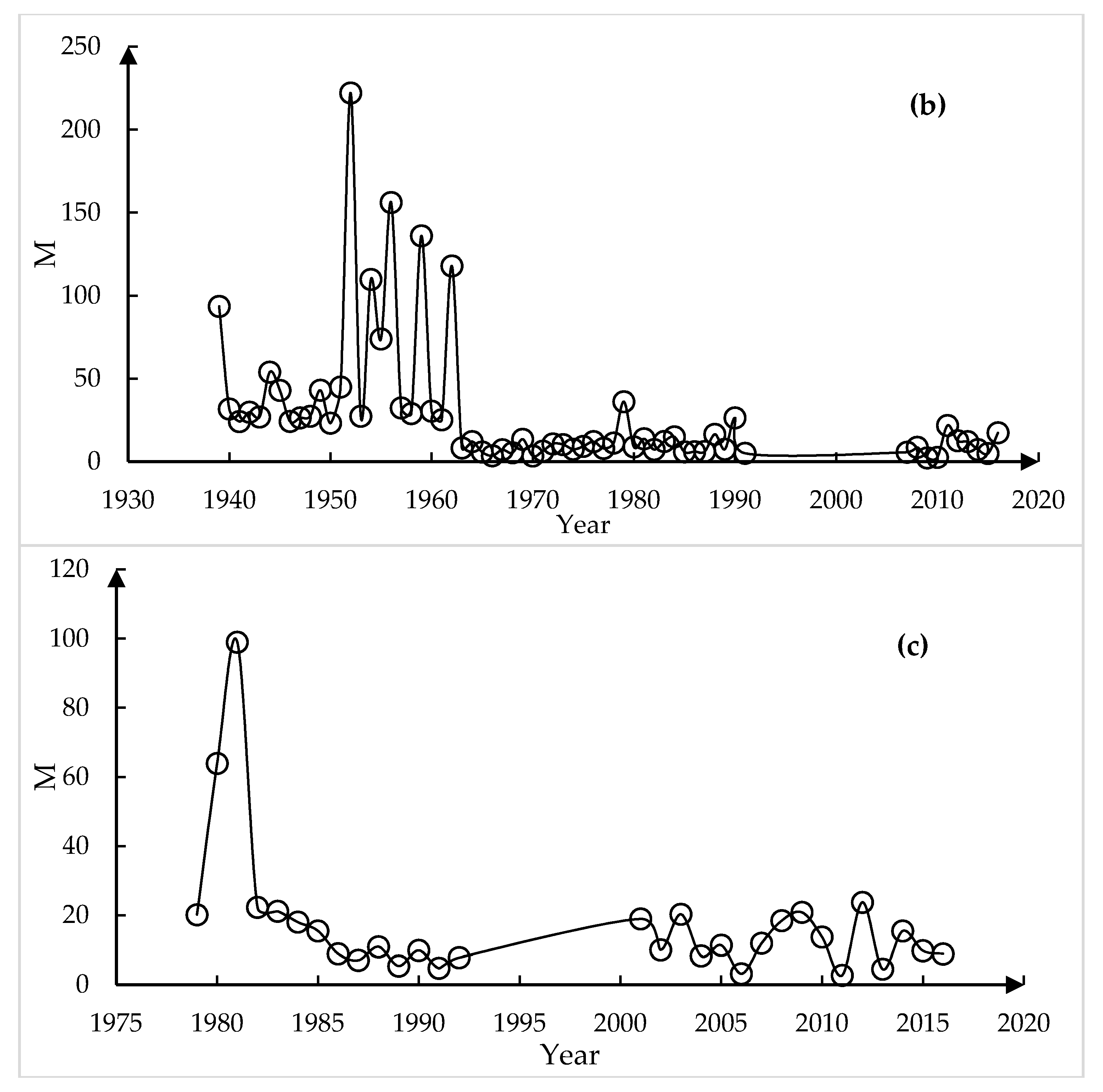
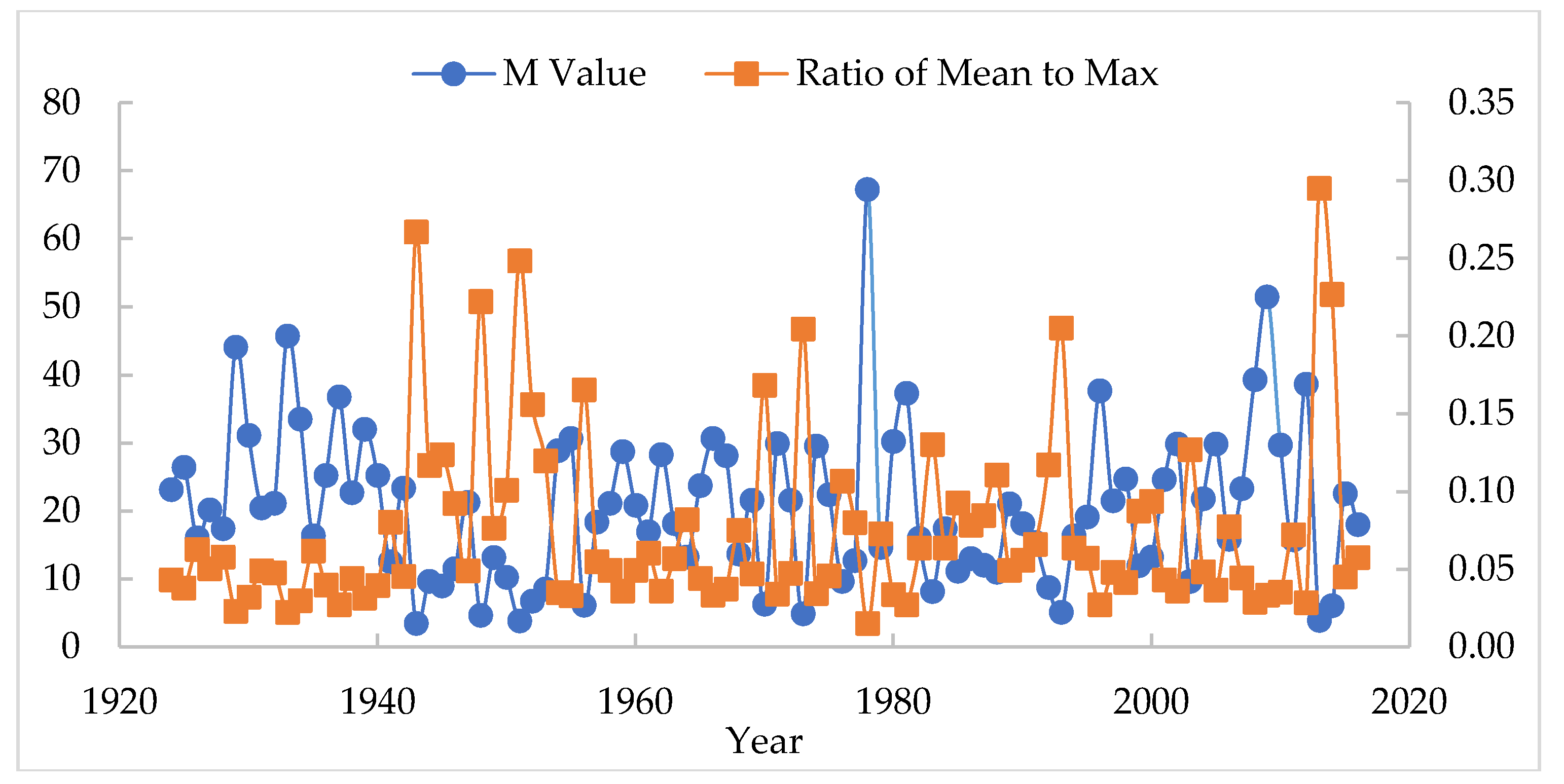
3.2. Time Variability of M
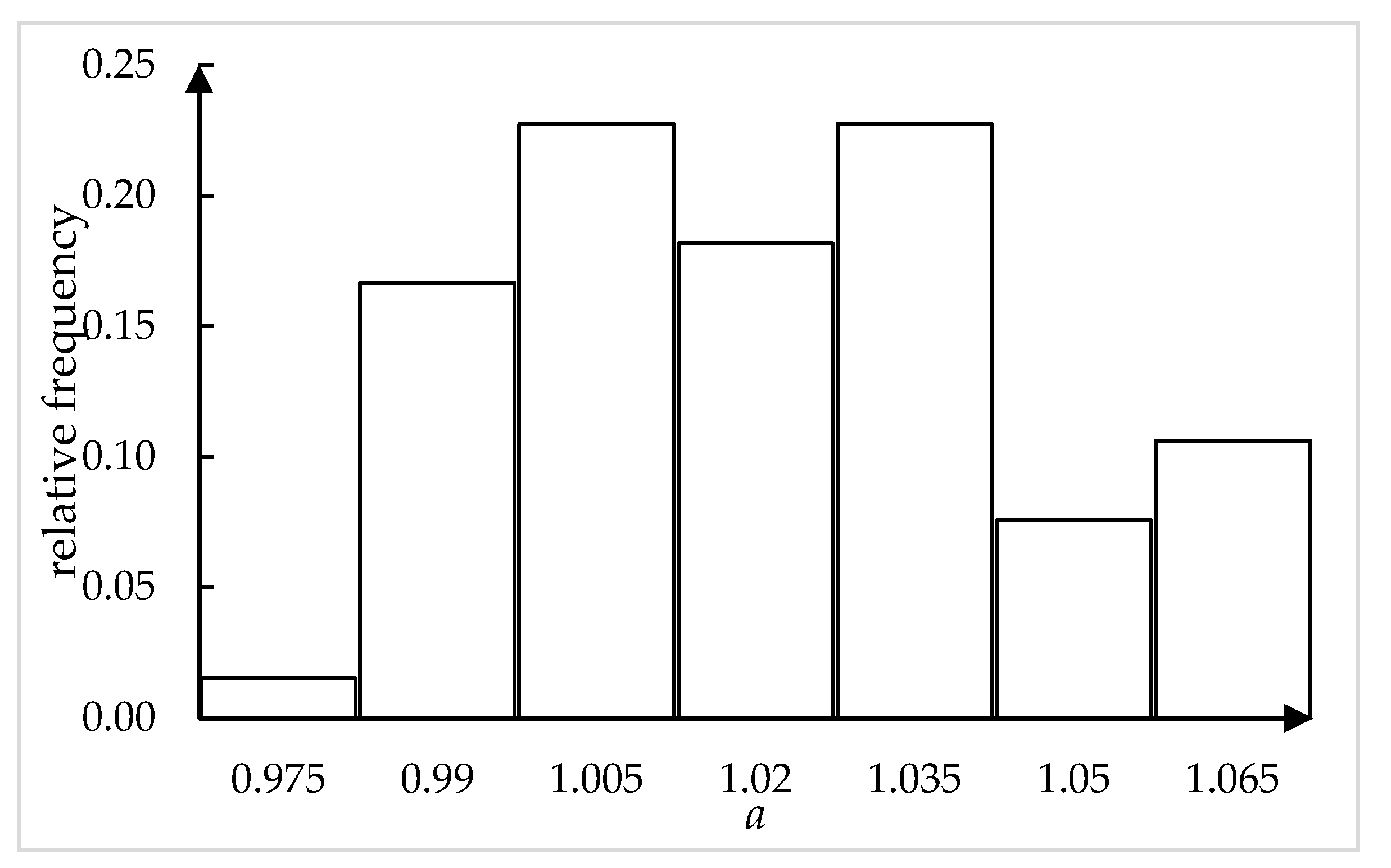
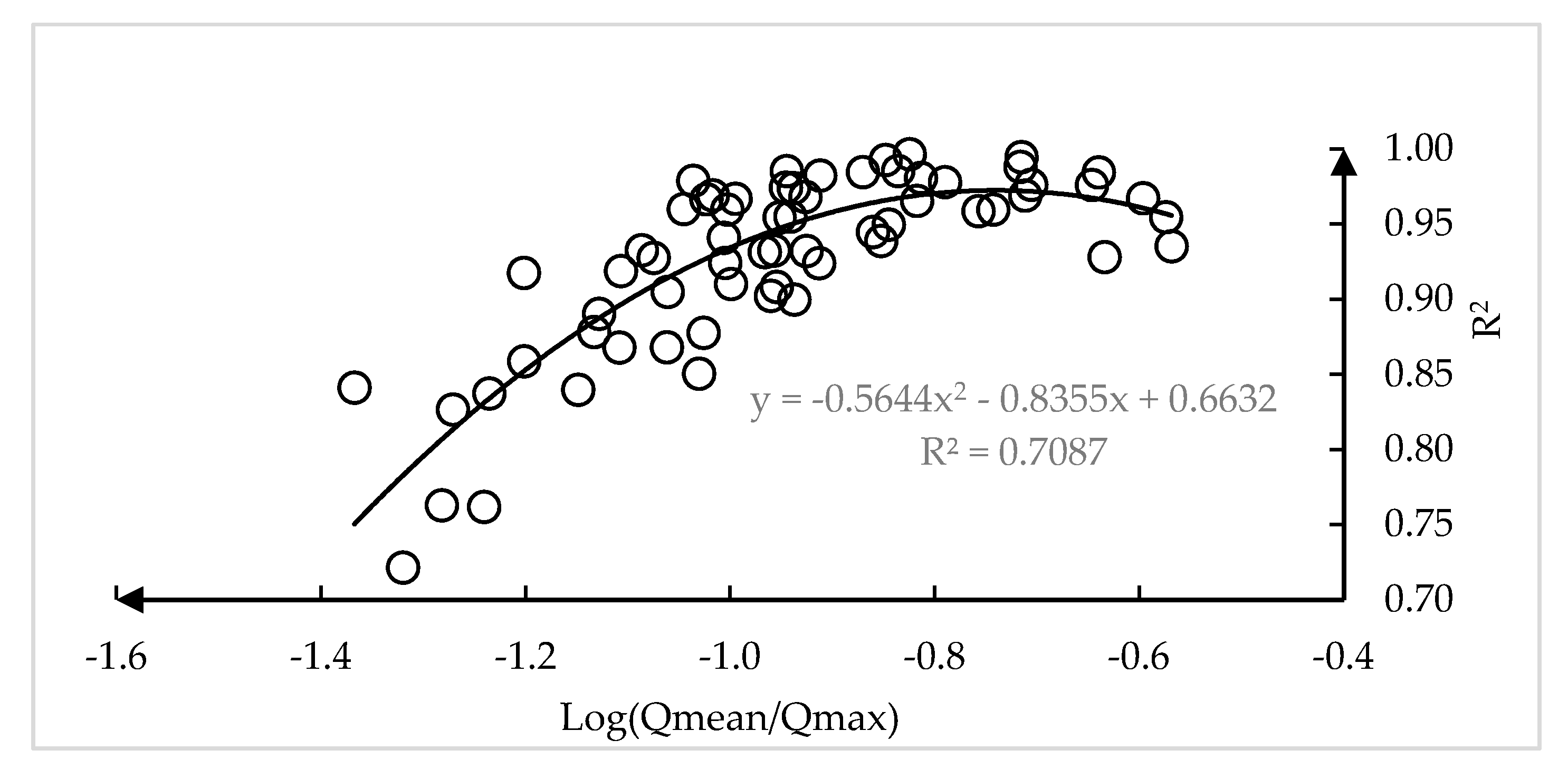
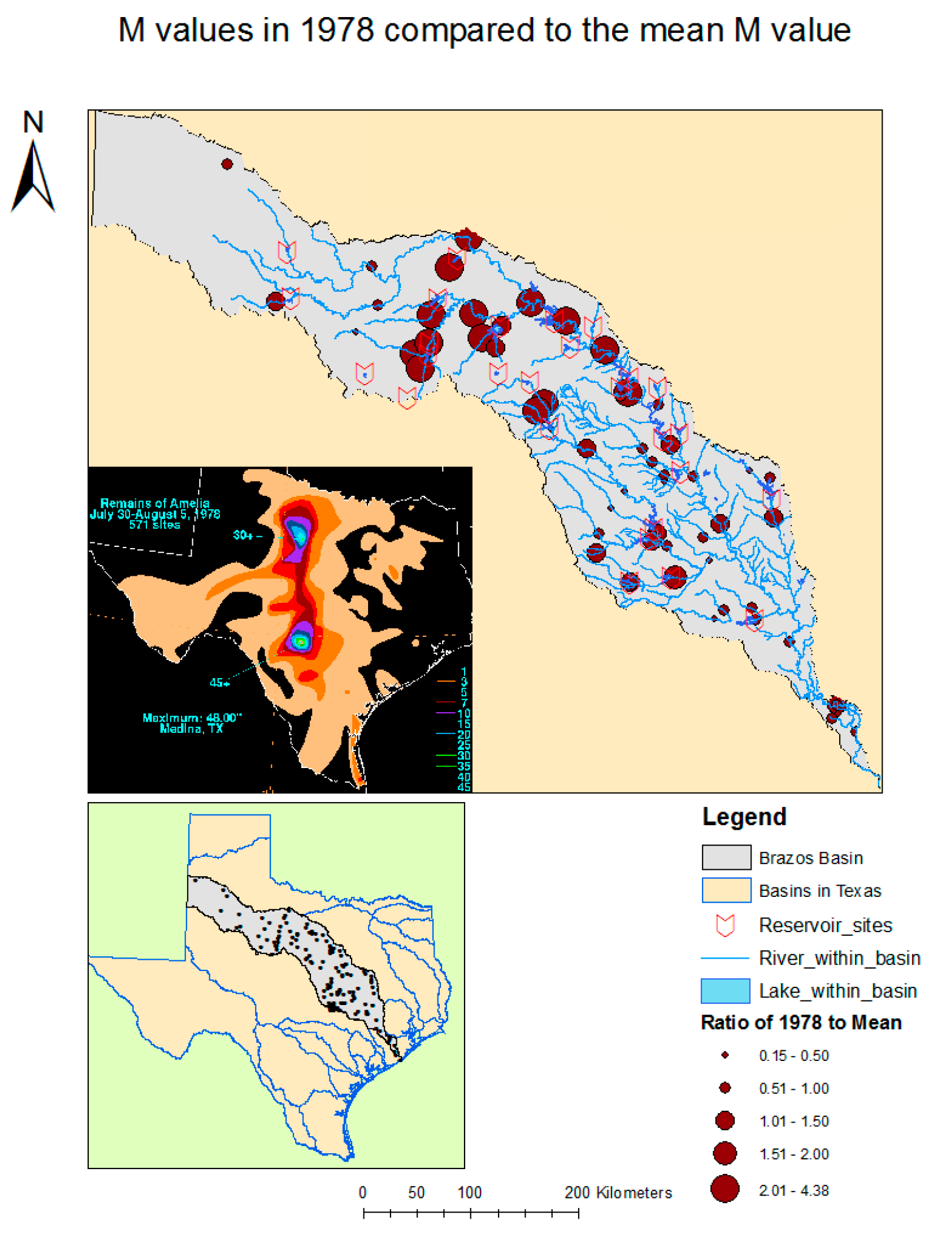
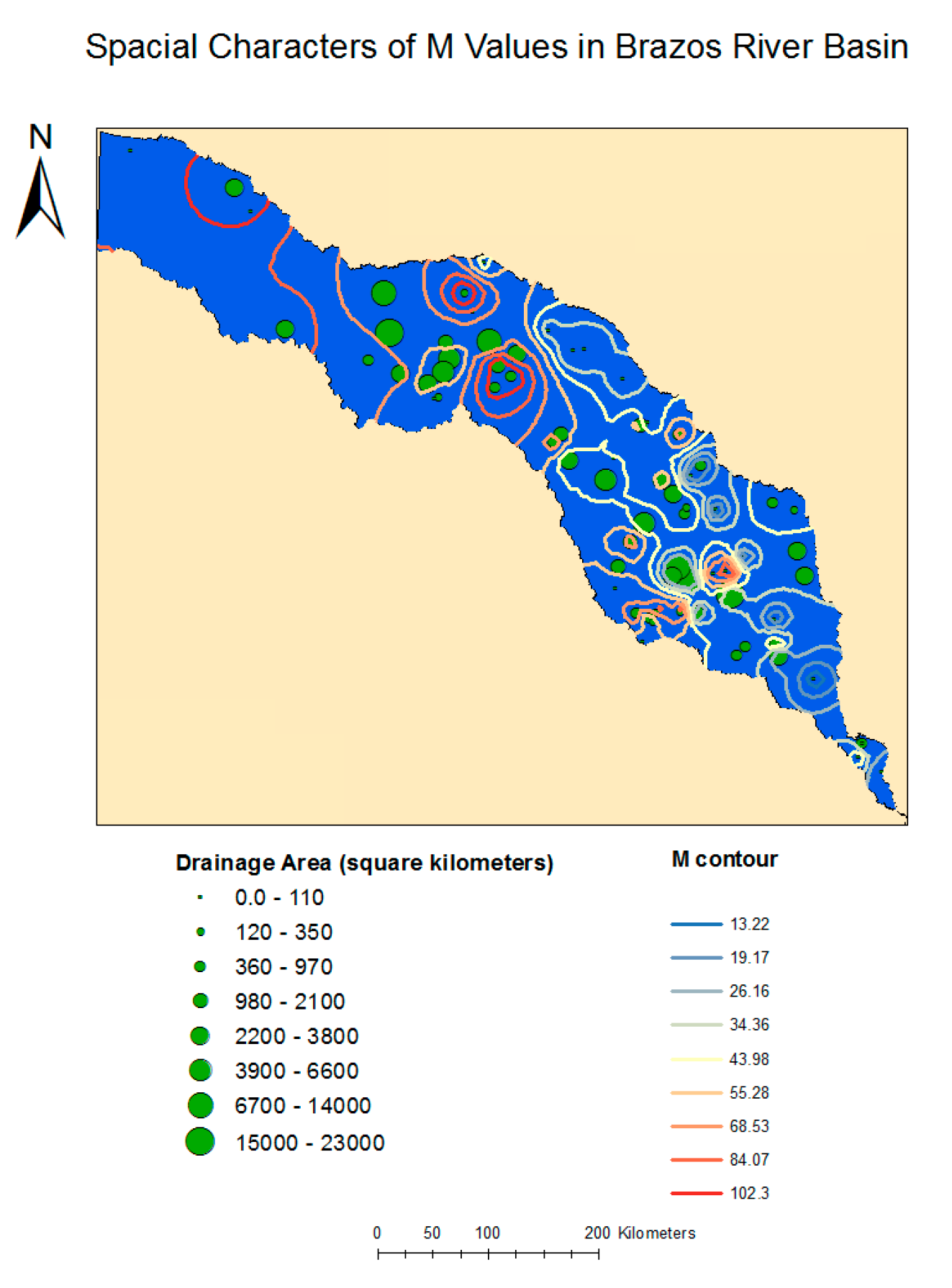
3.3. Spatial Variability
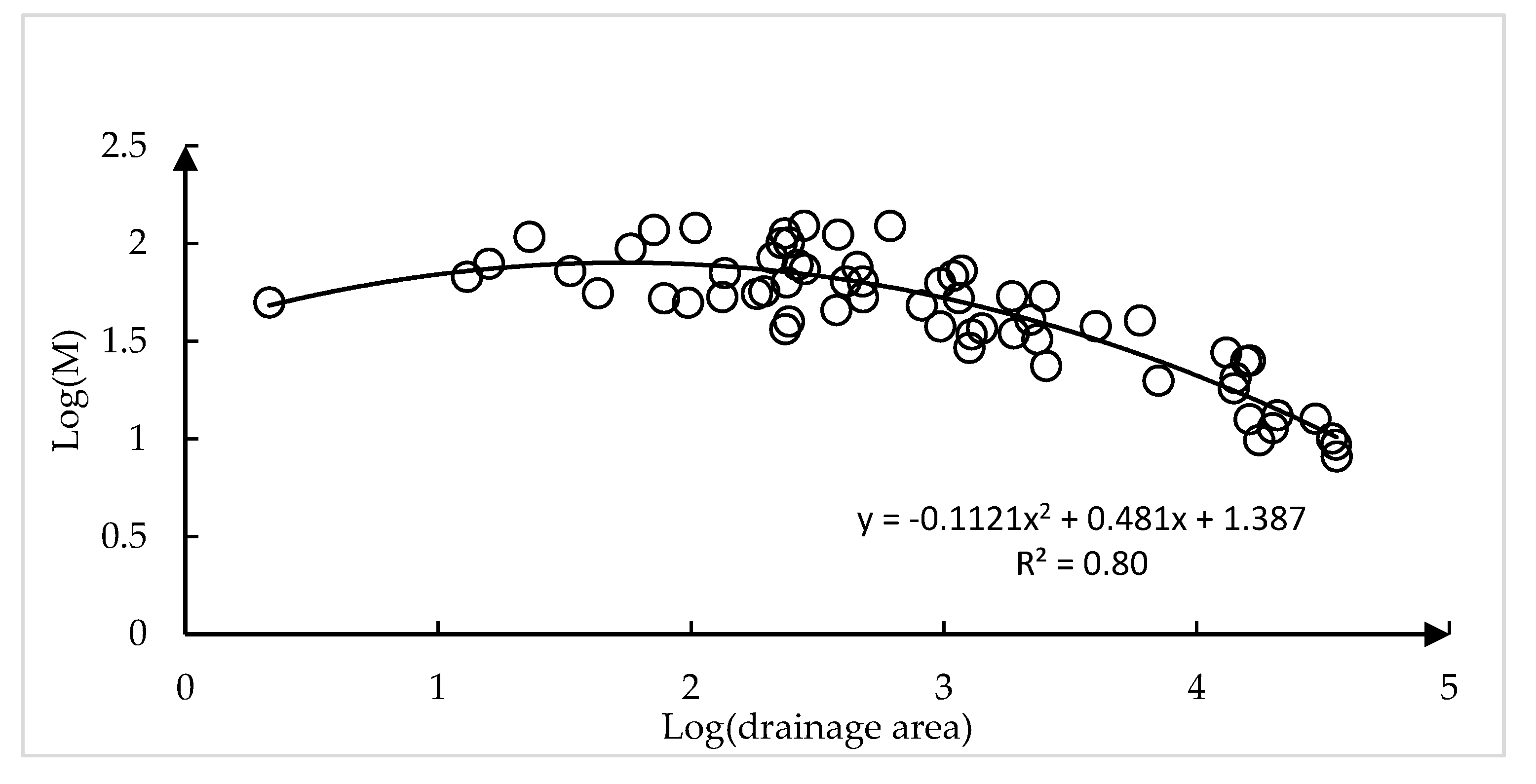
3.4. Test for Ungauged Stations
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Atieh, M.; Taylor, G.; Sattar, A.M.; Gharabaghi, B. Prediction of Flow Duration Curves for Ungauged Basins. J. Hydrol. 2017, 545, 383–394. [Google Scholar] [CrossRef]
- Atieh, M.; Gharabaghi, B.; Rudra, R. Entropy-Based Neural Networks Model for Flow Duration Curves at Ungauged Sites. J. Hydrol. 2015, 529, 1007–1020. [Google Scholar] [CrossRef]
- LeBoutillier, D.V.; Waylen, P.R. A stochastic model of flow duration curves. Water Resour. Res. 1993, 29, 3535–3541. [Google Scholar] [CrossRef]
- Vogel, R.M.; Fennessey, N.M. Flow-duration curves. I: New interpretation and confidence intervals. J. Water Resour. Plan. Manag. 1994, 120, 485–504. [Google Scholar]
- Singh, K.P. Model flow duration and streamflow variability. Water Resour. Res. 1971, 7, 1031–1036. [Google Scholar] [CrossRef]
- Cigizoglu, H.K.; Bayazit, M. A generalized seasonal model for flow duration curve. Hydrol. Process. 2000, 14, 1053–1067. [Google Scholar] [CrossRef]
- Castellarin, A.; Vogel, R.M.; Brath, A. A stochastic index flow model of flow duration curves. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Singh, V.P.; Byrd, A.; Cui, H. Flow duration curve using entropy theory. J. Hydrol. Eng. 2013, 19, 1340–1348. [Google Scholar] [CrossRef]
- Wurbs, R.A.; Bergman, C.E.; Carriere, P.E.; Walls, W.B. Hydrologic and Institutional Water Availability in the Brazos River Basin; Technical and Special Reports; Texas Water Resources Institute: College Station, TX, USA, 1988. [Google Scholar]
- Christensen, N.S.; Wood, A.W.; Voisin, N.; Lettenmaier, D.P.; Palmer, R.N. The effects of climate change on the hydrology and water resources of the Colorado River basin. Clim. Chang. 2004, 62, 337–363. [Google Scholar] [CrossRef]
- Tao, B.; Tian, H.; Ren, W.; Yang, J.; Yang, Q.; He, R.; Lohrenz, S.E. Increasing Mississippi river discharge throughout the twenty-first century influenced by changes in climate, land use and atmospheric CO2. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 15–19 December 2014. [Google Scholar]
- Roth, D. Texas Hurricane History; National Weather Service: Camp Springs, MD, USA, 2010.
- Fuller, W.E. Flood Flows; Transactions of the American Society of Civil Engineers: New York, NY, USA, 1914; Volume 77, pp. 564–617. [Google Scholar]

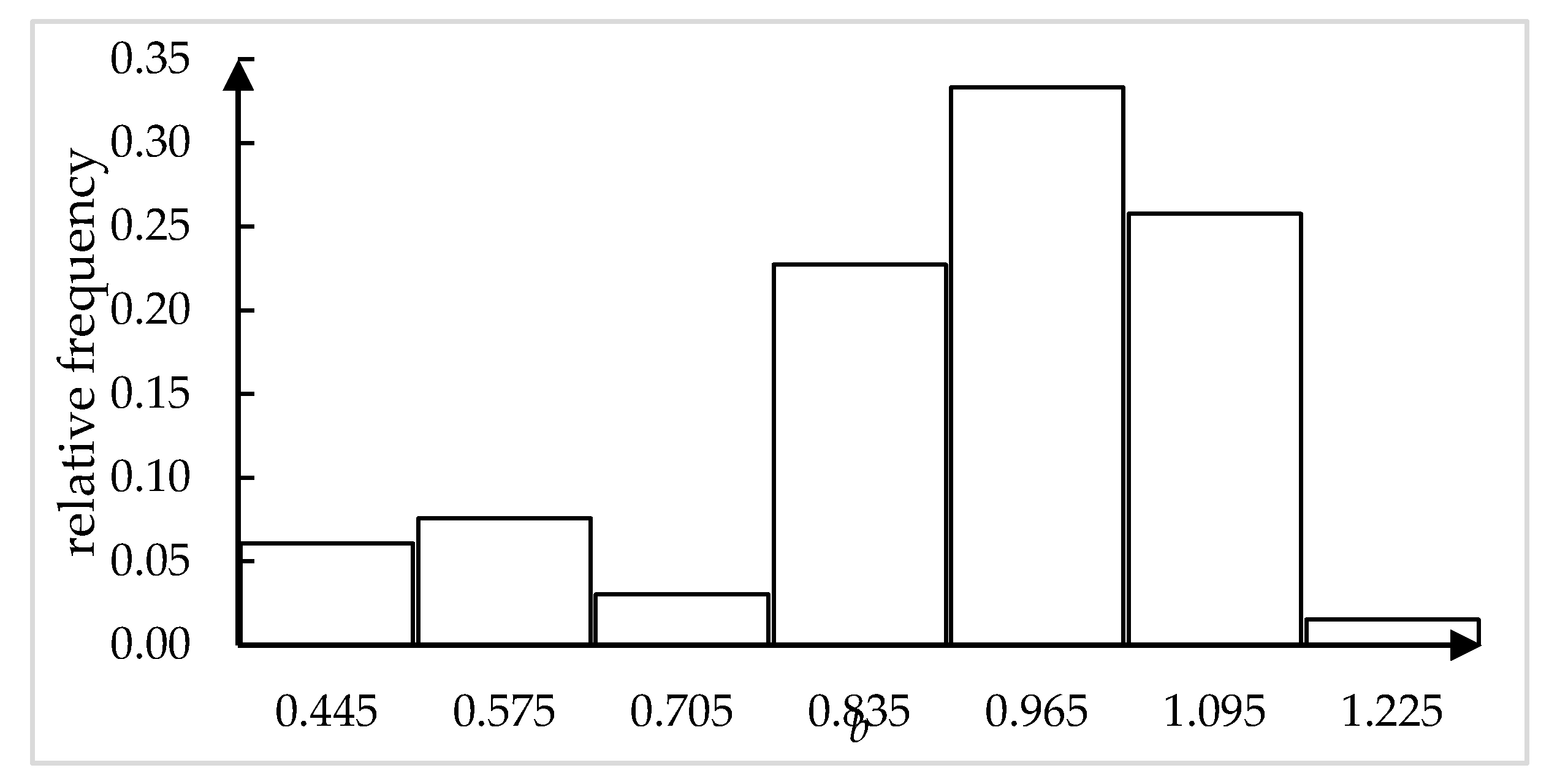
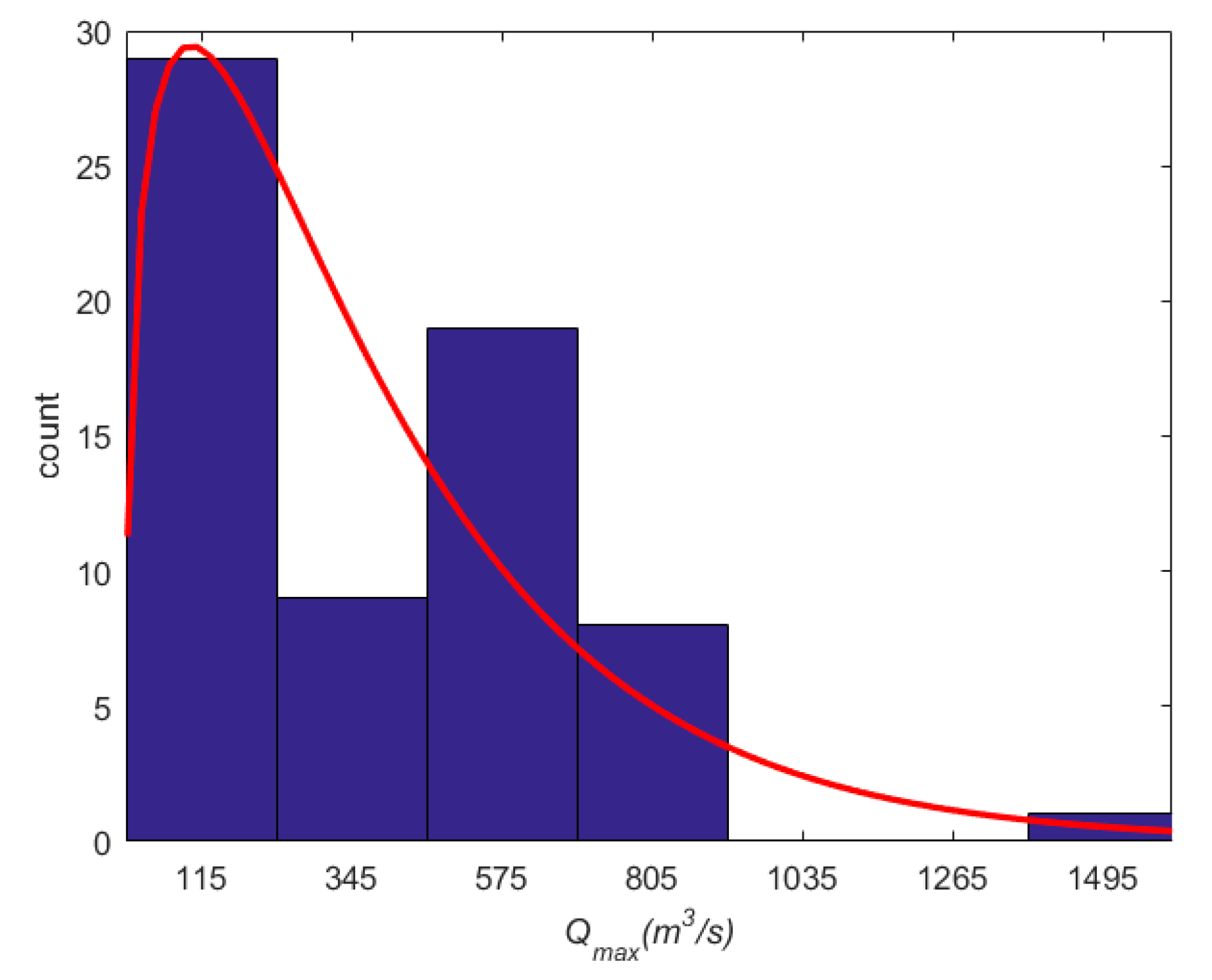
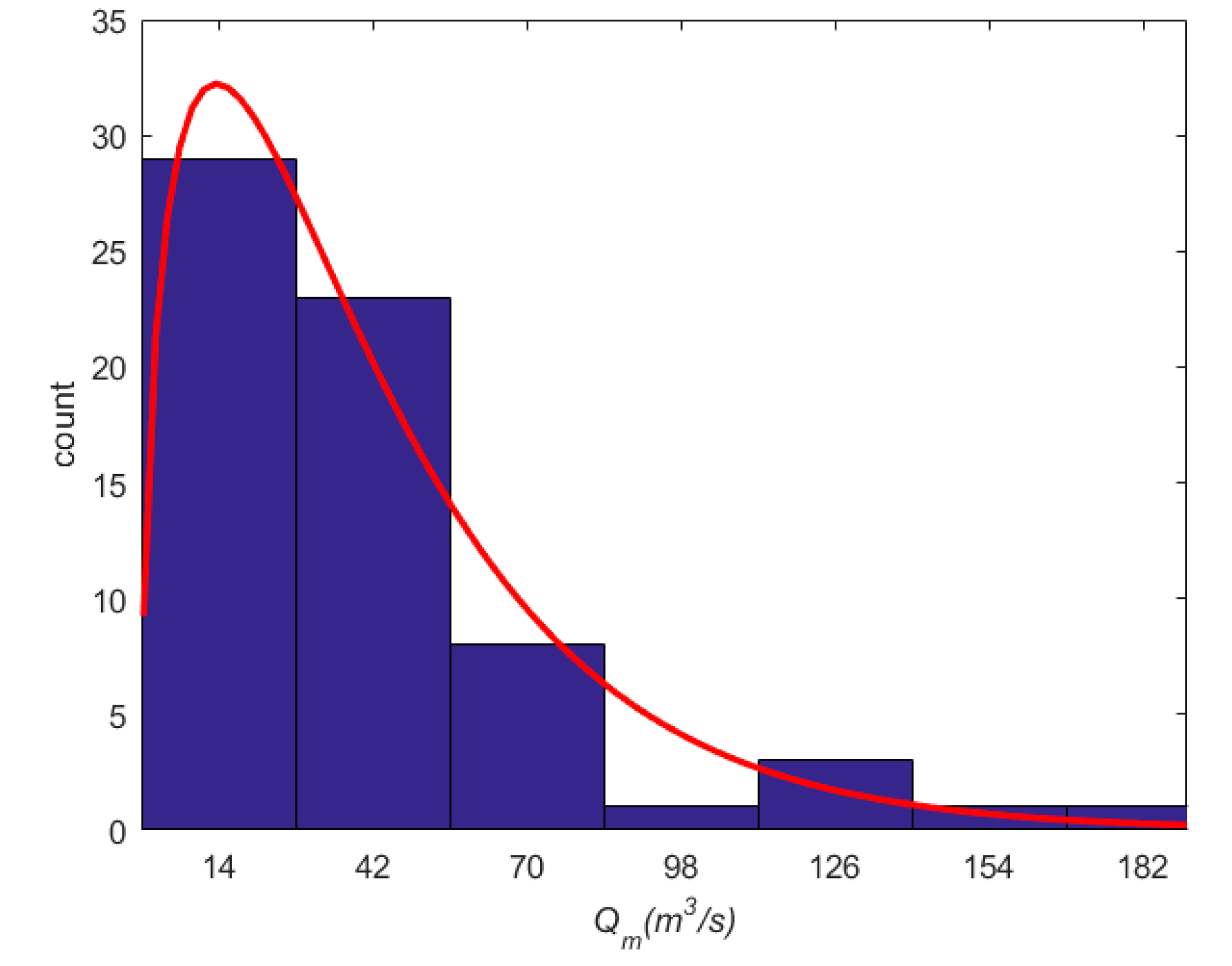
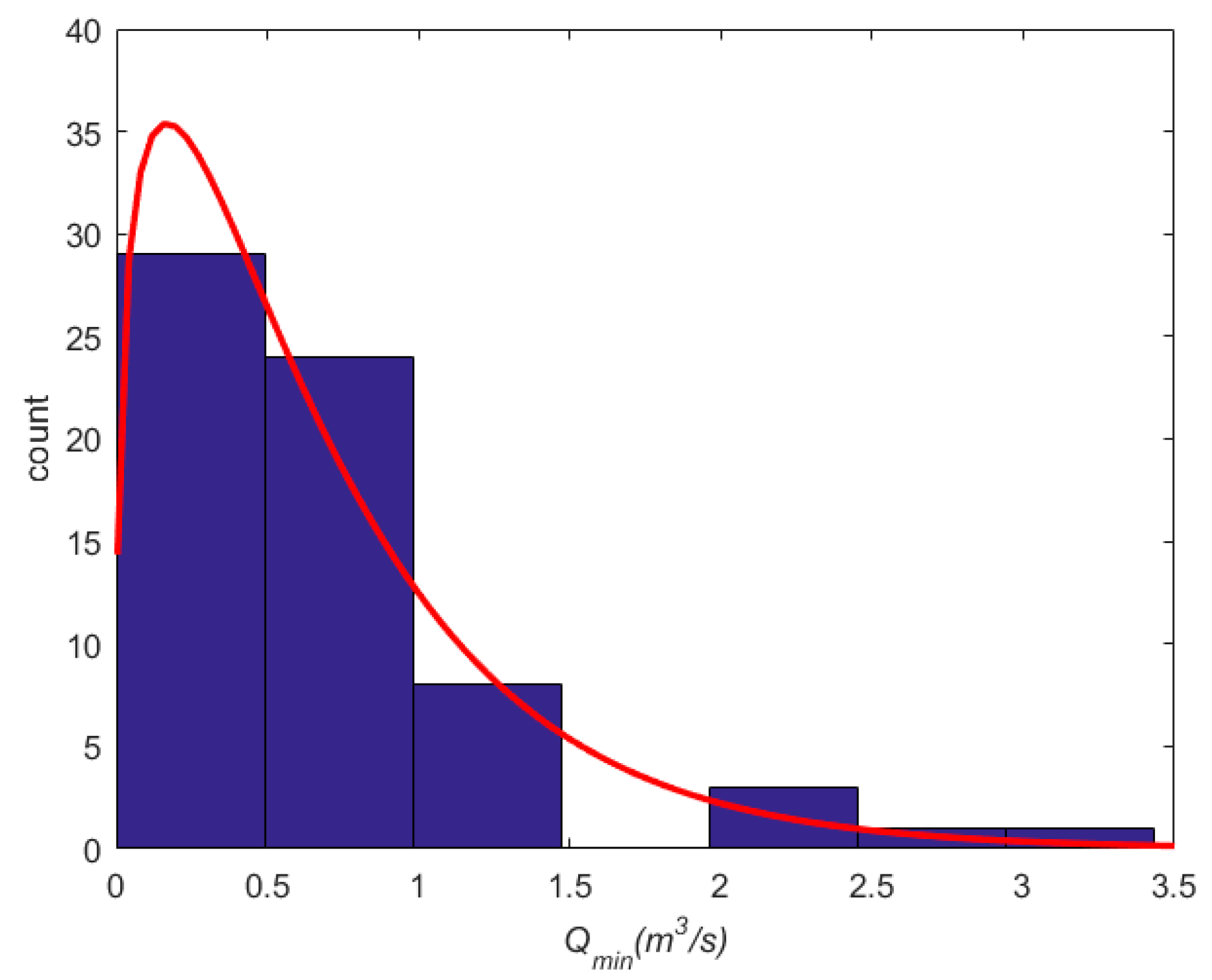
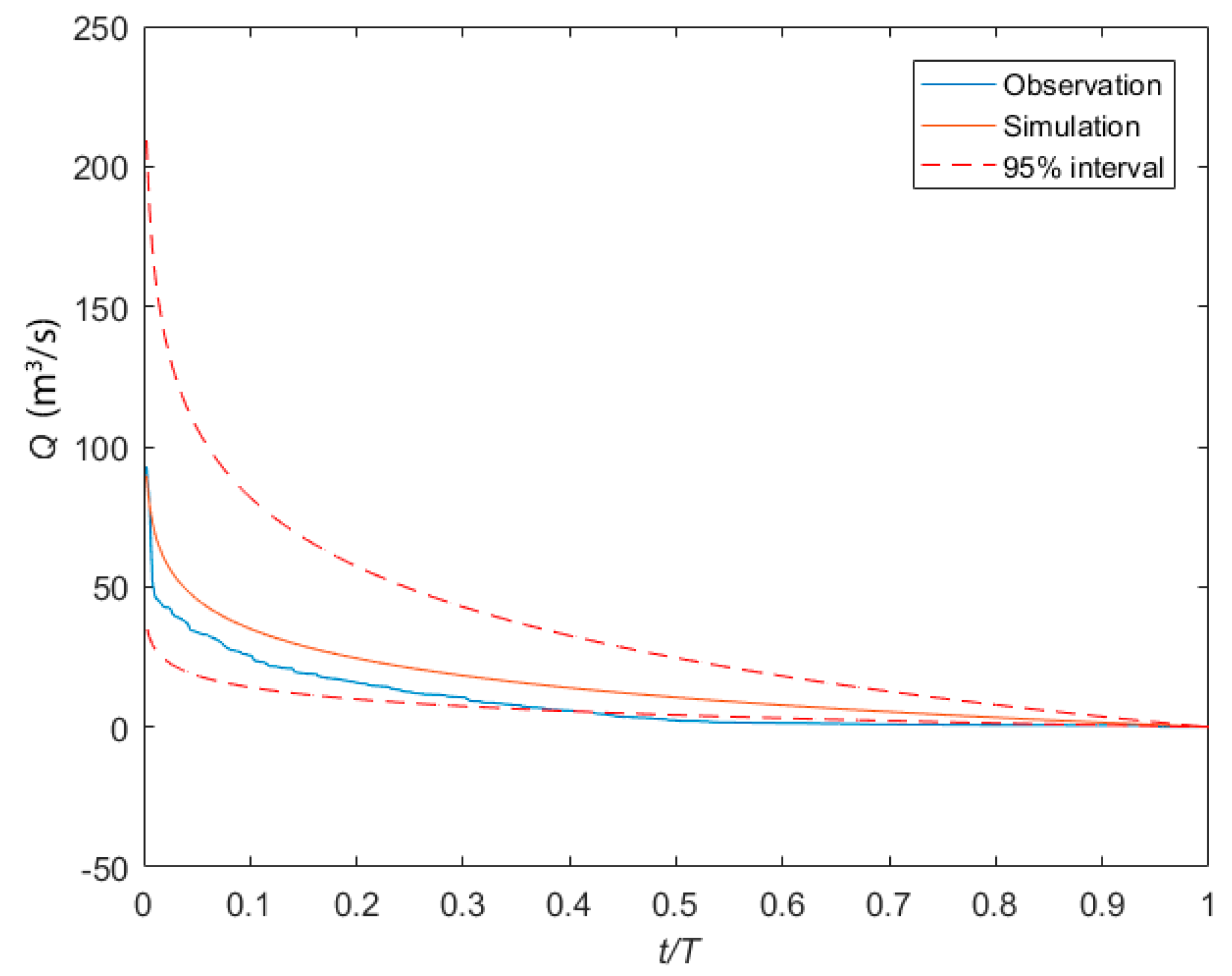
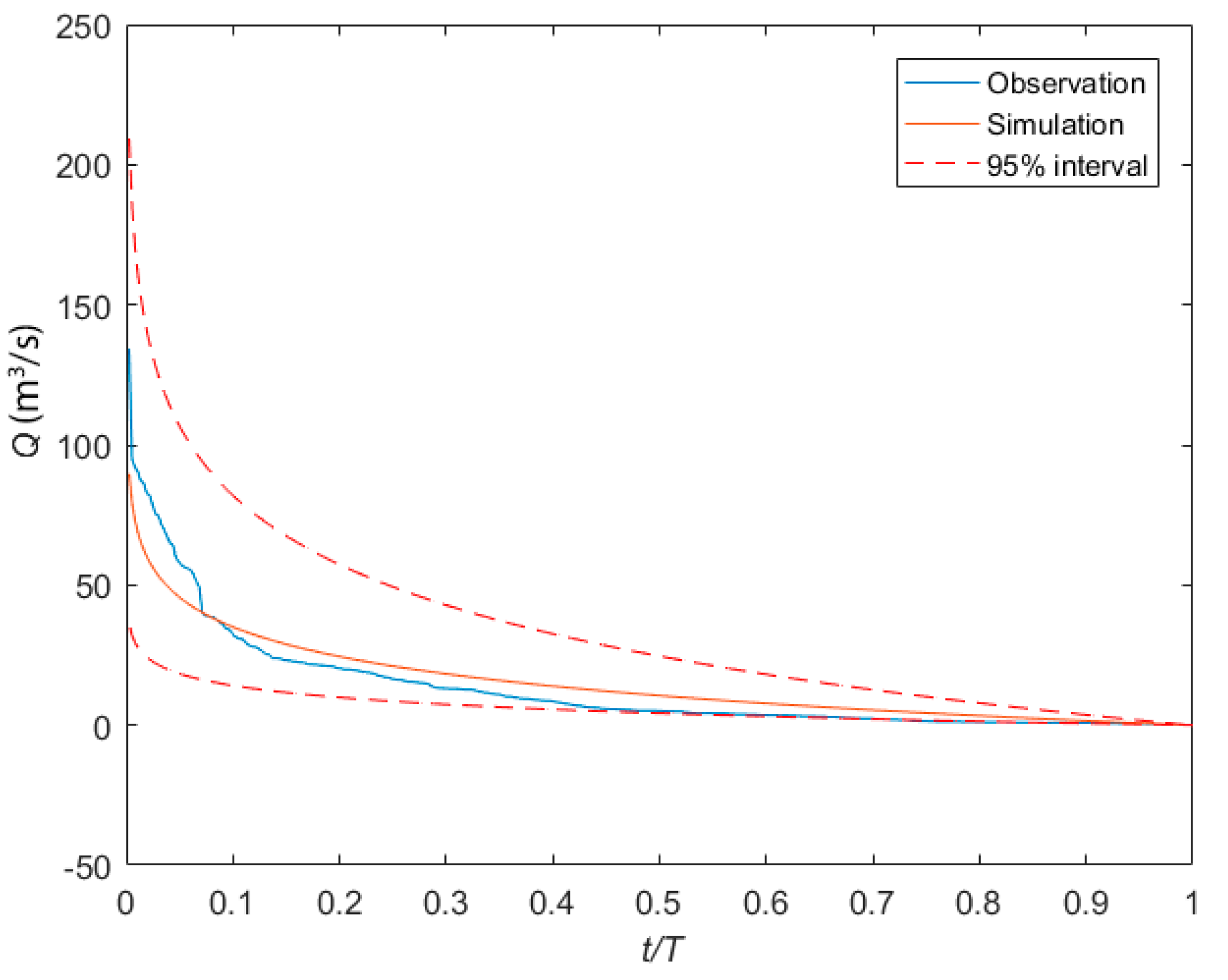
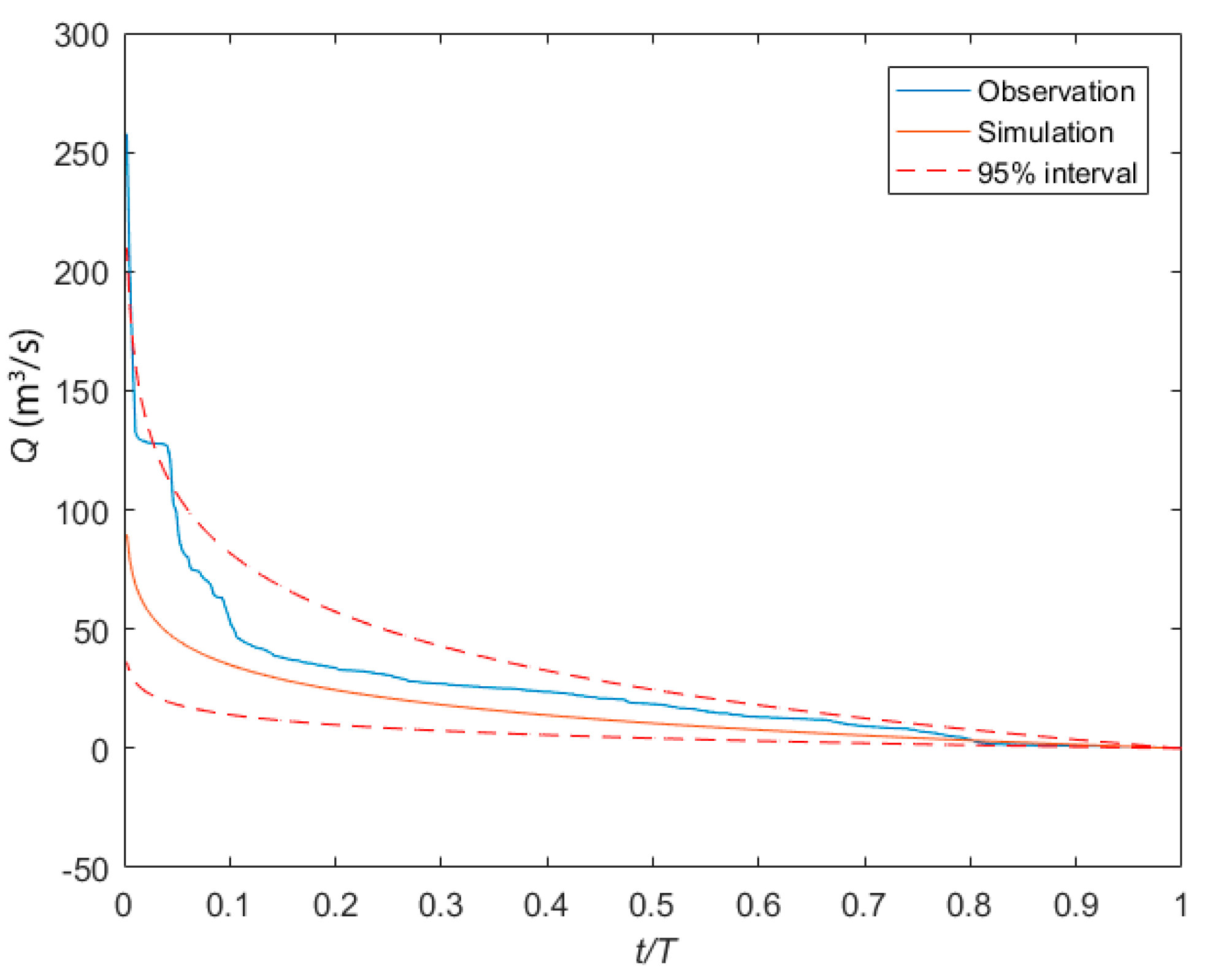
| Water Year | Year | Qmax | Qmin | LI Qmax | LI Qmin | UI Qmax | UI Qmin | a | b | M | R2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.3 | 2003 | 121.26 | 0.21 | 44.89 | 0.08 | 302.58 | 0.54 | 1.02 | 0.89 | 9.88 | 0.979 |
| 1.4 | 2009 | 169.09 | 0.3 | 68.16 | 0.12 | 395.75 | 0.7 | 0.969 | |||
| 1.8 | 1994 | 257.14 | 0.46 | 114.31 | 0.2 | 558.27 | 0.99 | 0.96 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Singh, V.P.; Byrd, A.R. Entropy Parameter M in Modeling a Flow Duration Curve. Entropy 2017, 19, 654. https://doi.org/10.3390/e19120654
Zhang Y, Singh VP, Byrd AR. Entropy Parameter M in Modeling a Flow Duration Curve. Entropy. 2017; 19(12):654. https://doi.org/10.3390/e19120654
Chicago/Turabian StyleZhang, Yu, Vijay P. Singh, and Aaron R. Byrd. 2017. "Entropy Parameter M in Modeling a Flow Duration Curve" Entropy 19, no. 12: 654. https://doi.org/10.3390/e19120654
APA StyleZhang, Y., Singh, V. P., & Byrd, A. R. (2017). Entropy Parameter M in Modeling a Flow Duration Curve. Entropy, 19(12), 654. https://doi.org/10.3390/e19120654





