Fault Diagnosis of Rolling Bearings Based on EWT and KDEC
Abstract
1. Introduction
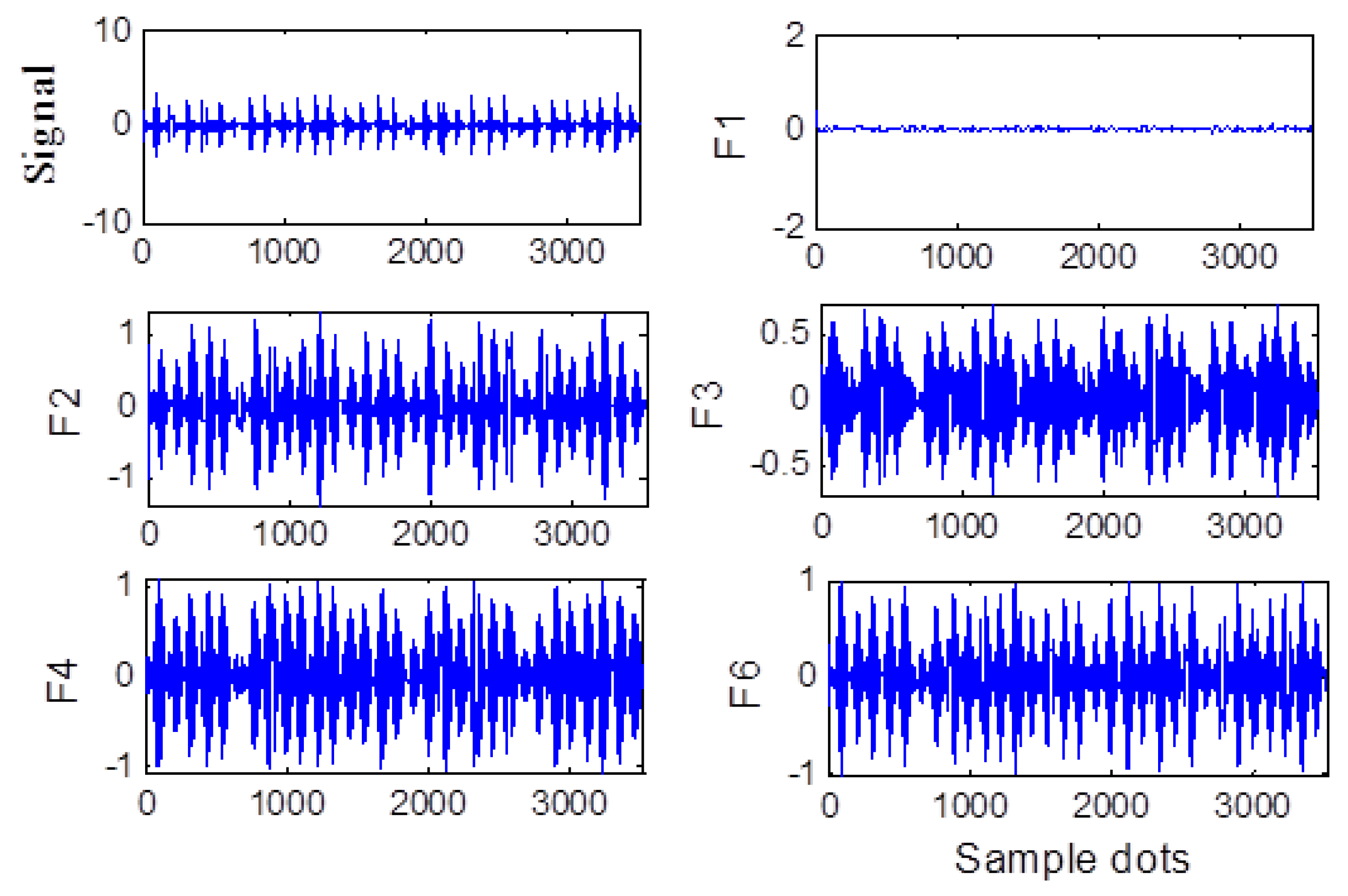
2. EWT Decomposition Method
2.1. EWT Principle
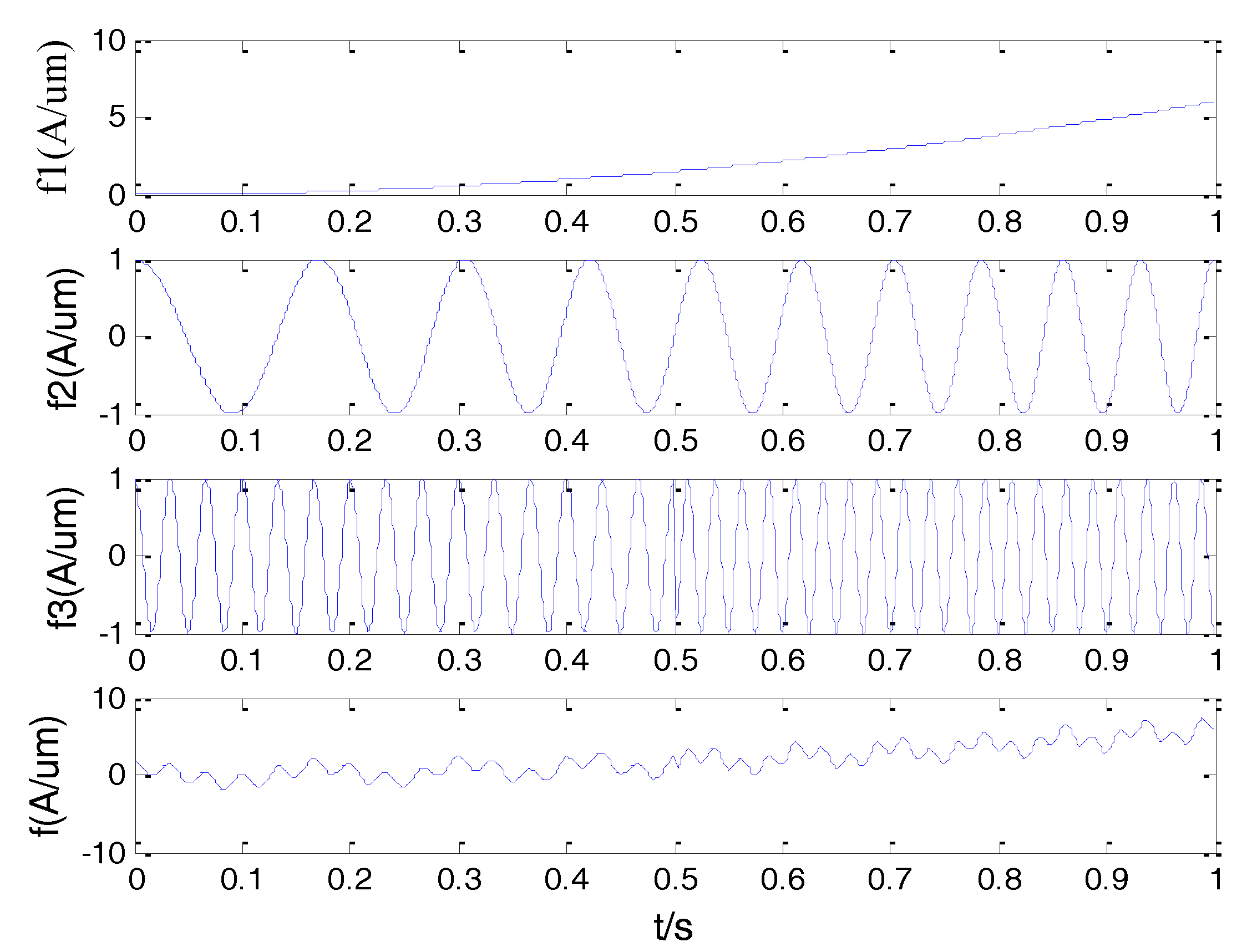
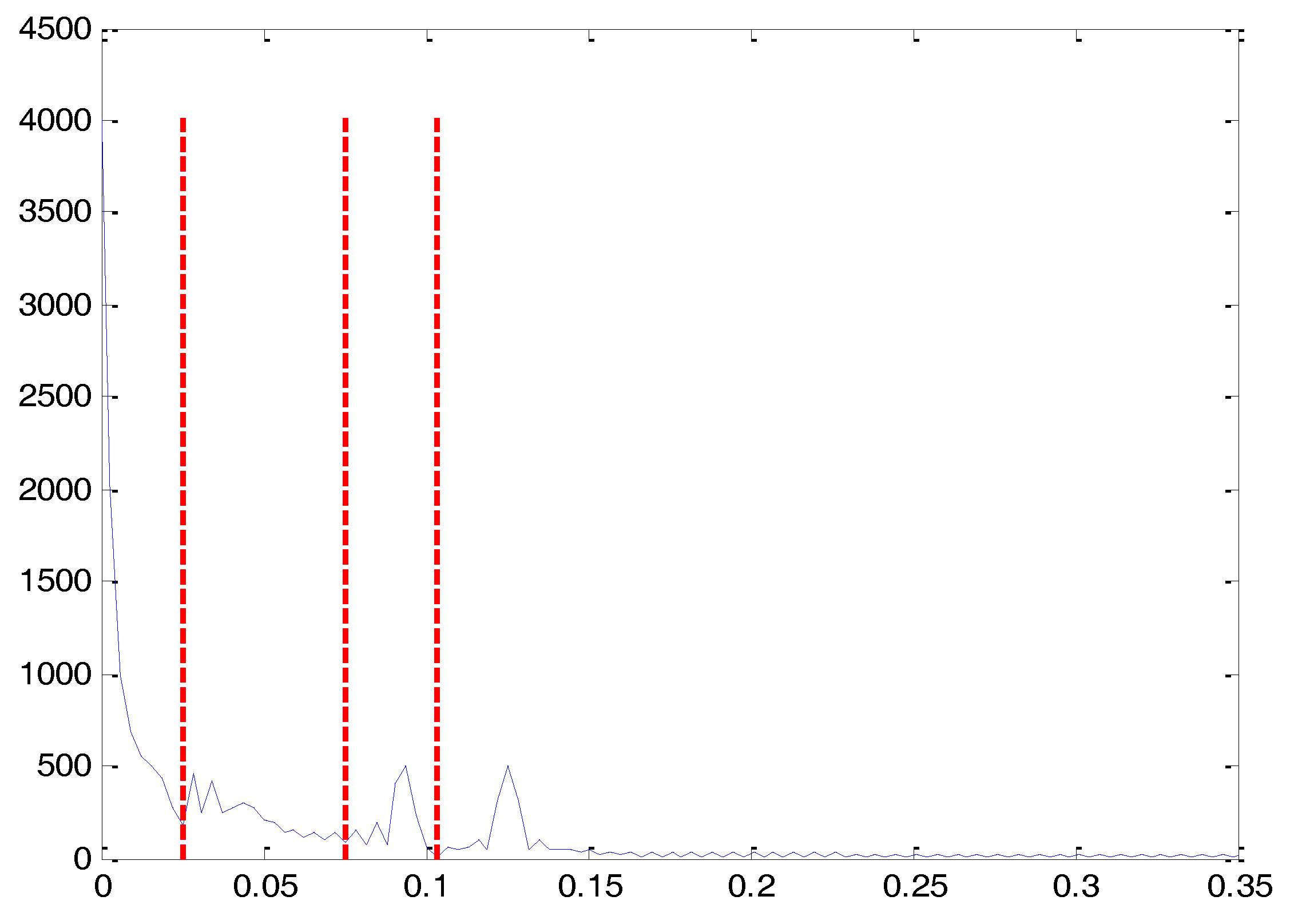
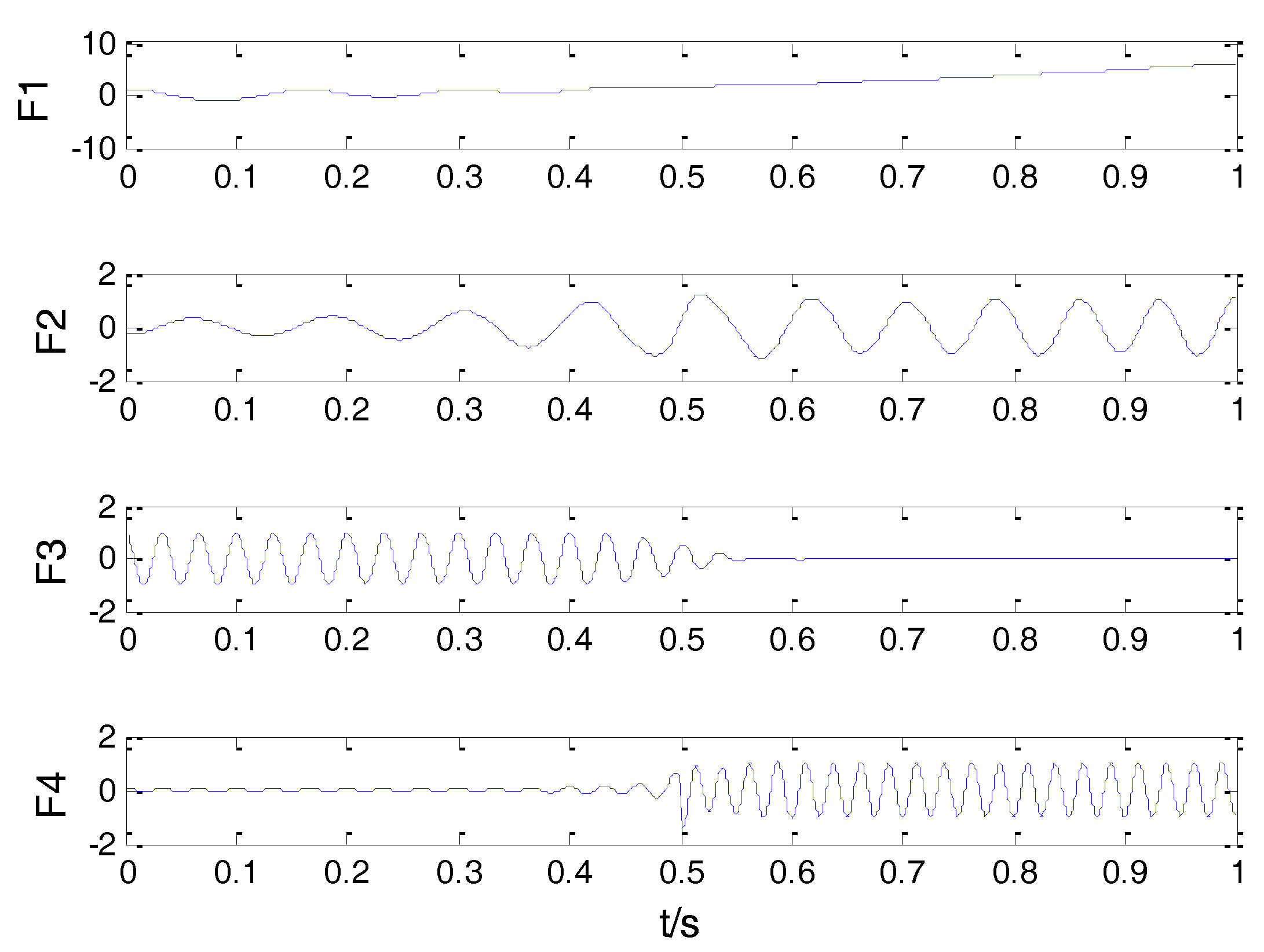
2.2. Analysis of the Simulation Signal
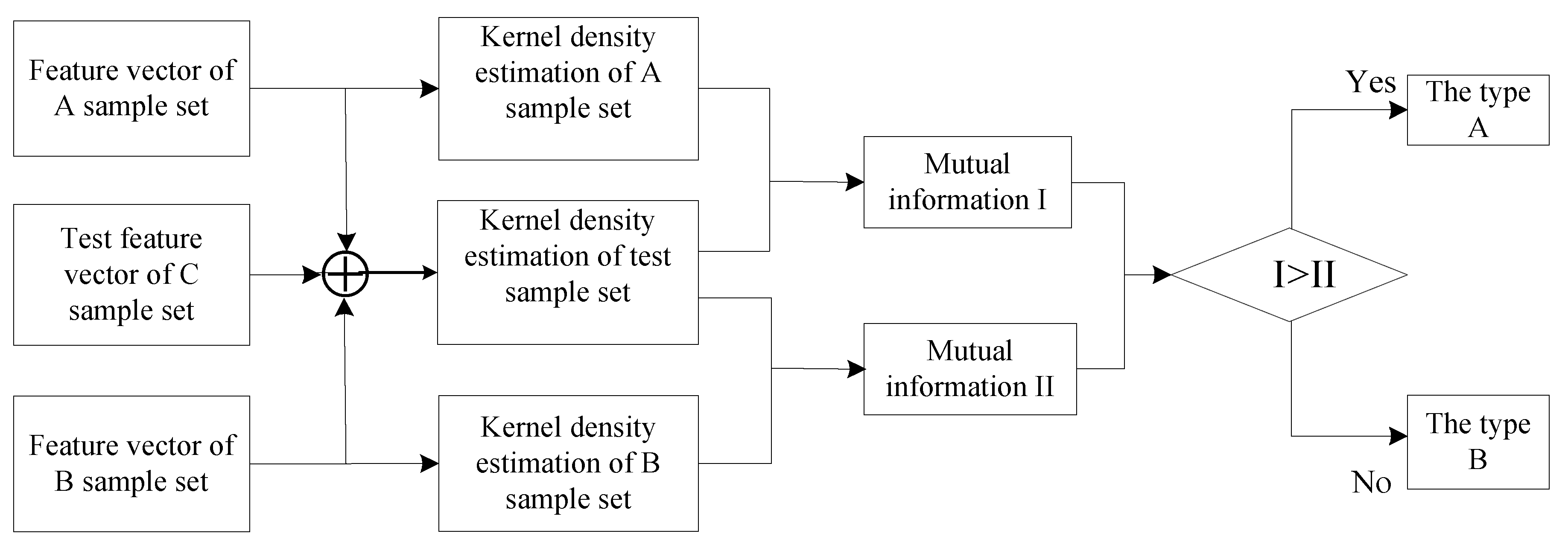
3. Classifier Based on the Kernel Density Estimation
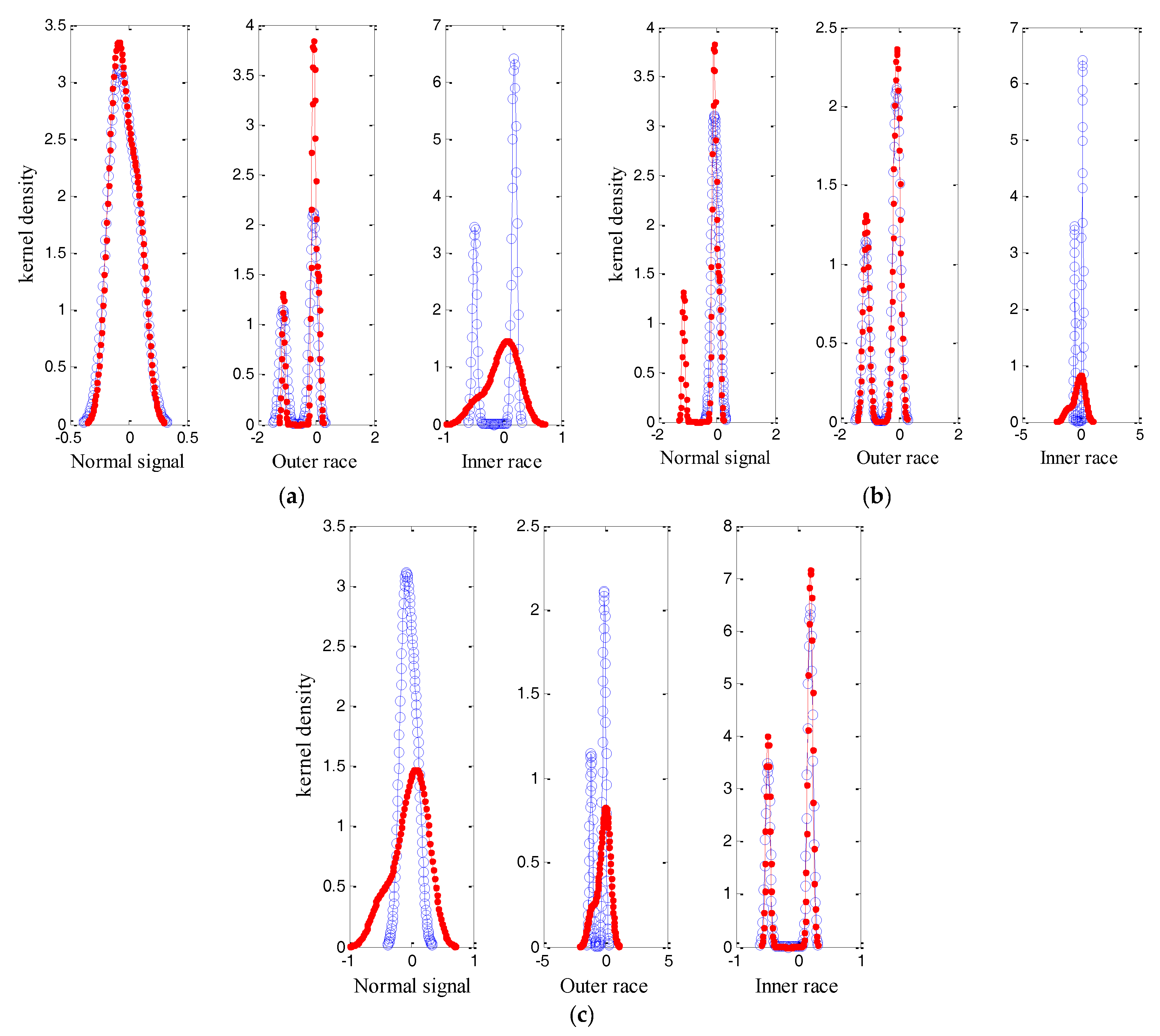
3.1. Kernel Density Estimation and Mutual Information
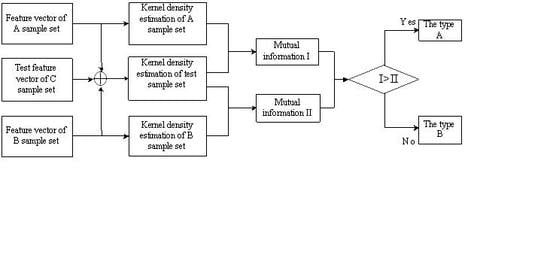
3.2. Basic Principle of Classifier
3.3. Fault Diagnosis Method of Rolling-Element Bearing
- (1)
- Decompose the vibration signal using EWT to obtain the F components; compute RMS, kurtosis (k), and skewness (Cw) of the first three F components to constitute the feature vector:where is the root mean square, and is kurtosis, is skewness.
- (2)
- Process multiple groups of vibration signal. Compute the feature vector according to the proposed method, and estimate the kernel density of the sample set.
- (3)
- Based on kernel density of the sample set, estimate the kernel density after the fusion of feature vector in an unknown state and the sample feature vector.
- (4)
- Compute the mutual information of fused kernel density estimation and the kernel density estimation for the sample set to identify the fault state of the rolling element bearings.
4. Experimental Results and Analysis
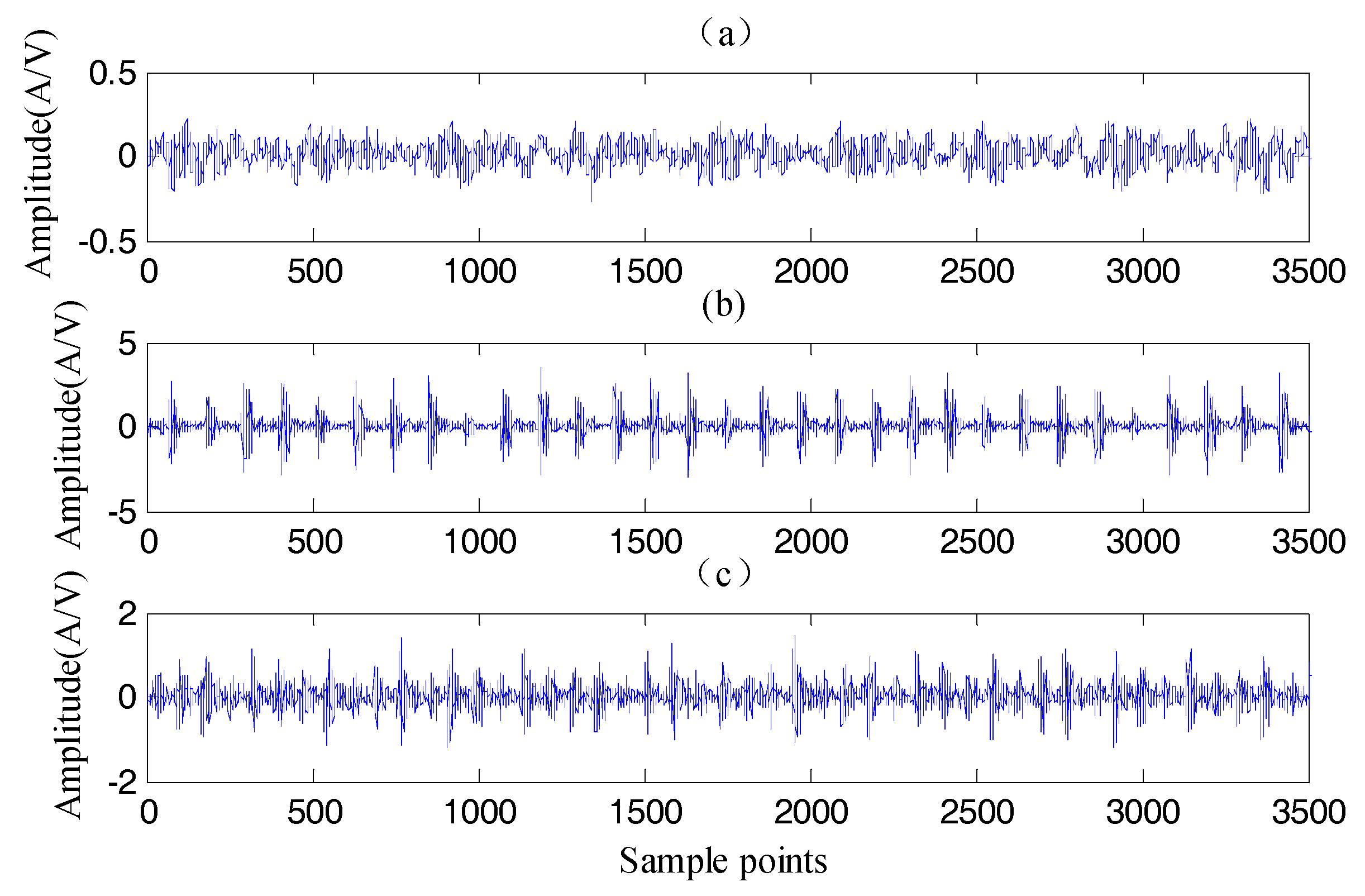
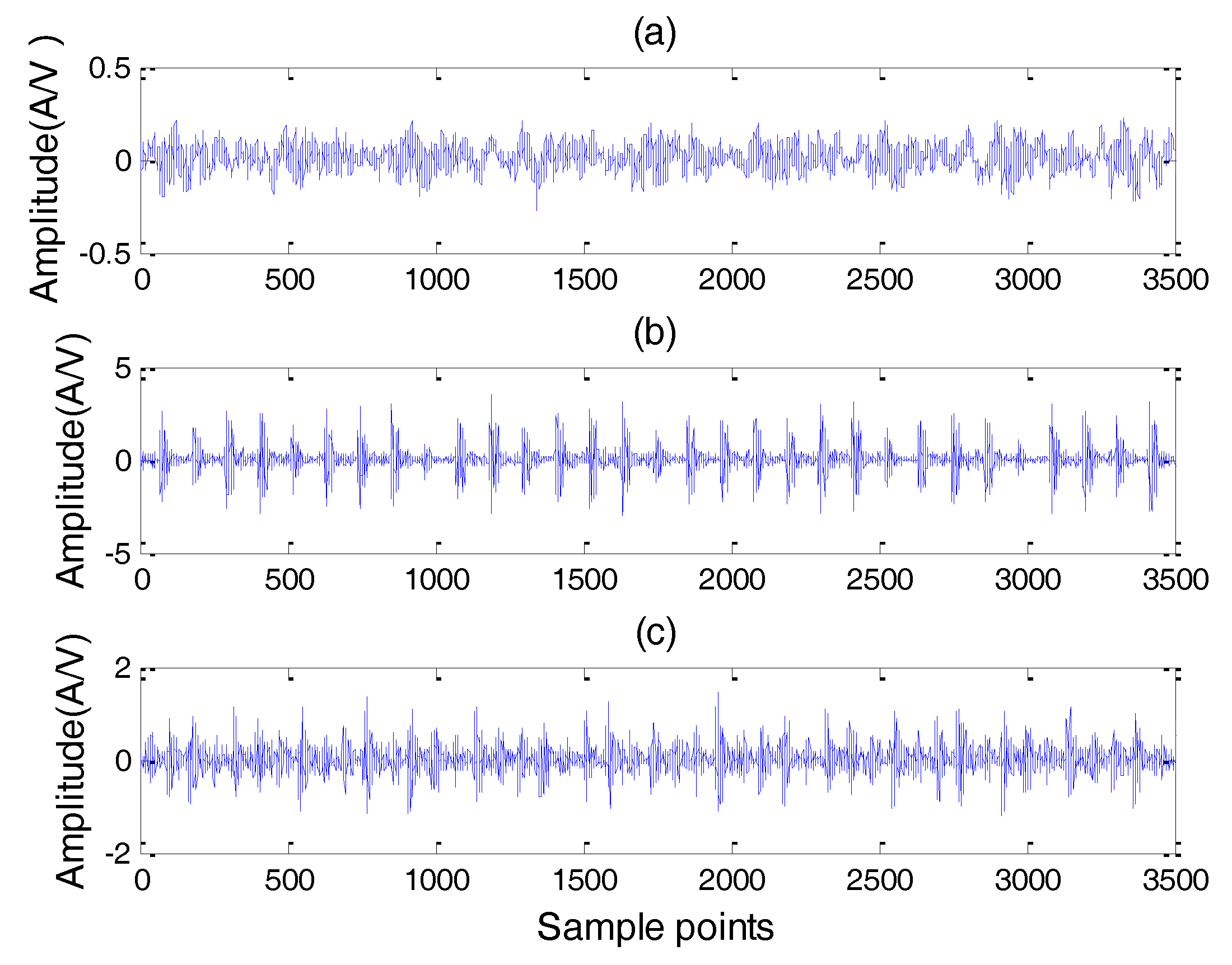
4.1. Experimental Apparatus and Instrumentations
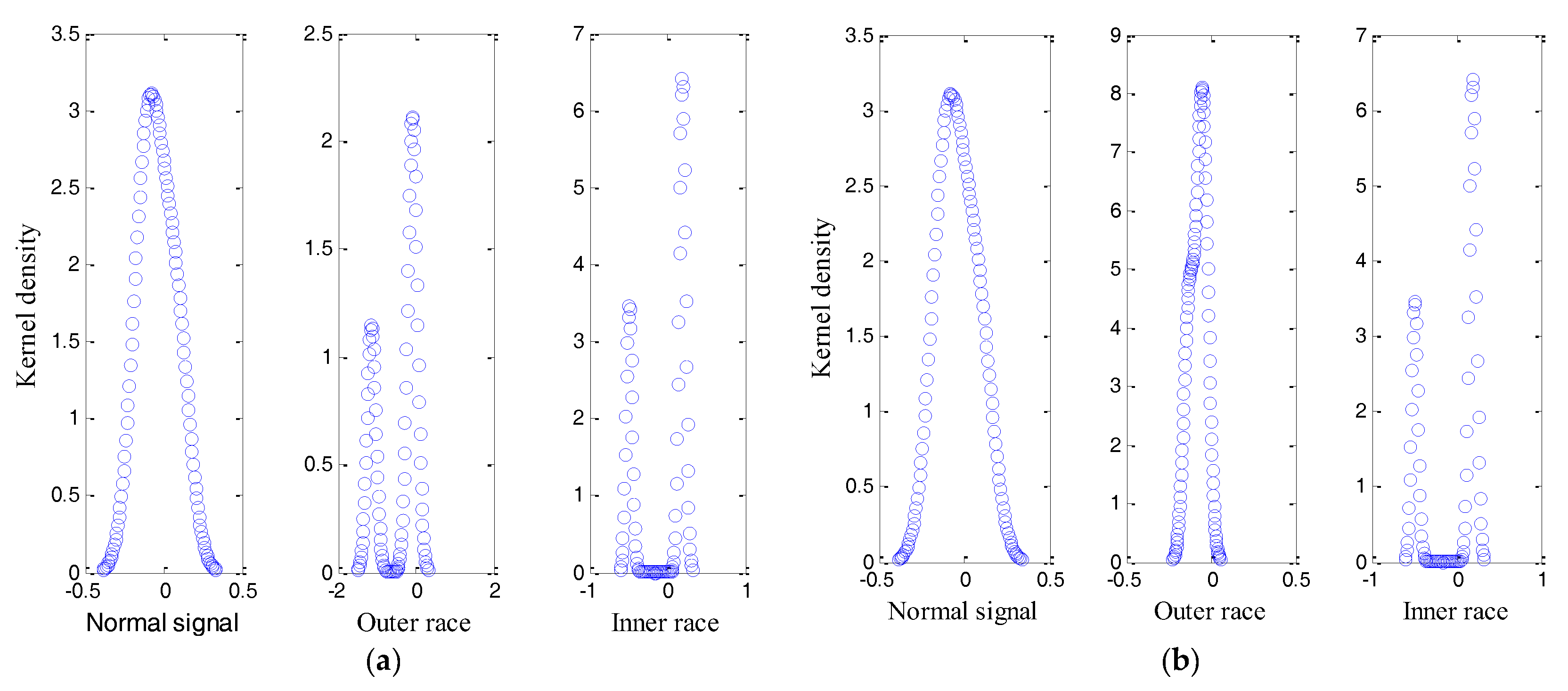
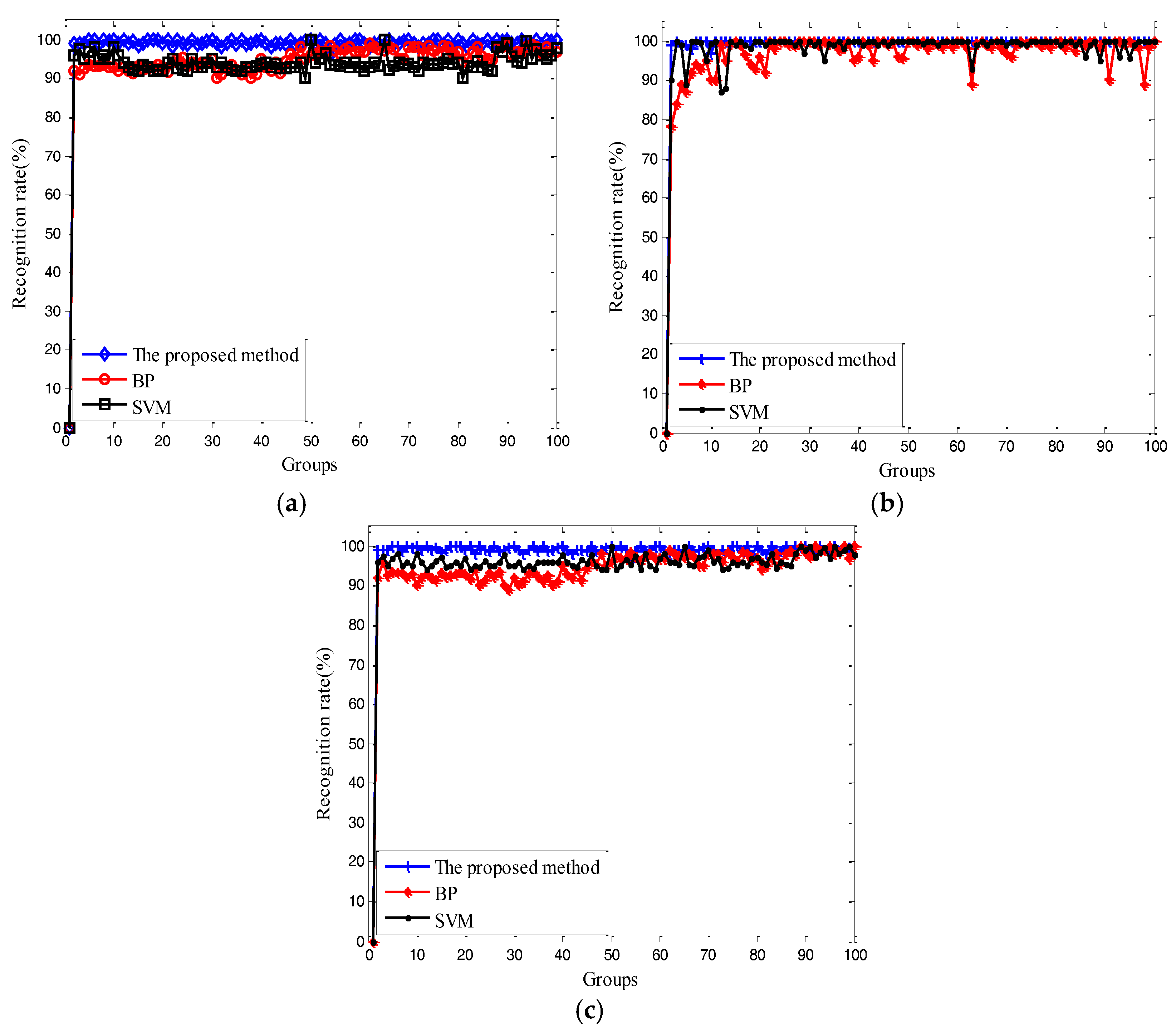
4.2. Analysis of Experimental Data
4.3. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vidal, Y.; Tutivén, C.; Rodellar, J.; Acho, L. Fault diagnosis and fault-tolerant control of wind turbines via a discrete time controller with a disturbance compensator. Energies 2015, 8, 4300–4316. [Google Scholar] [CrossRef]
- Rafiee, J.; Rafiee, M.A.; Tse, P.W. Application of mother wavelet functions for automatic gear and bearing fault diagnosis. Expert Syst. Appl. 2010, 37, 4568–4579. [Google Scholar] [CrossRef]
- Lei, Y.G.; Zuo, M.J. Fault diagnosis of rotating machinery using an improved HHT based on EEMD and sensitive IMFs. Meas. Sci. Technol. 2009, 20, 1–12. [Google Scholar] [CrossRef]
- Wardle, F.P. Vibration forces produced by waviness of the rolling surfaces of thrust loaded ball bearings Part 1: Theory. J. Mech. Eng. Sci. 1988, 202, 305–312. [Google Scholar] [CrossRef]
- Lynagh, N.; Rahnejat, H.; Ebrahimi, M.; Aini, R. Bearing induced vibration in precision high speed routing spindles. Int. J. Mach. Tools Manuf. 2000, 40, 561–577. [Google Scholar] [CrossRef]
- Vafaei, S.; Rahnejat, H.; Aini, R. Vibration monitoring of high speed spindles using spectral analysis techniques. Int. J. Mach. Tools Manuf. 2002, 42, 1223–1234. [Google Scholar] [CrossRef]
- Vafaei, S.; Rahnejat, H. Indicated repeatable runout with wavelet decomposition (IRR-WD) for effective determination of bearing-induced vibration. J. Sound Vib. 2003, 260, 67–82. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, Y.; Zhou, J.; Zang, Y. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM. Measurement 2015, 69, 164–179. [Google Scholar] [CrossRef]
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An Intelligent Fault Diagnosis Method Using Unsupervised Feature Learning Towards Mechanical Big Data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Xiao, Y.; Ding, E.; Chen, C.; Liu, X.; Li, L. A Novel Characteristic Frequency Bands Extraction Method for Automatic Bearing Fault Diagnosis Based on Hilbert Huang Transform. Sensors 2015, 15, 27869–27893. [Google Scholar]
- Nonetheless, S.V. Gearbox Fault Diagnosis Using Complementary Ensemble Empirical Mode Decomposition and Permutation Entropy. Shock Vib. 2016, 2016, 1–8. [Google Scholar]
- Chen, S.W.; Chen, Y.H. Hardware design and implementation of a wavelet de-noising procedure for medical signal processing. Sensors 2015, 15, 26396–26414. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.H.; Wong, P.K.; Yang, Z.X. Simultaneous-Fault Diagnosis of Gearboxes Using Probabilistic Committee Machine. Sensors 2016, 16, 185. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Q.; Li, J.; Bai, Z.; Sun, J.; Zhou, N.; Zeng, Z. A Small Leak Detection Method Based on VMD Adaptive De-Noising and Ambiguity Correlation Classification Intended for Natural Gas Pipelines. Sensors 2016, 16, 2116. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Zhang, M.; Yu, Q.; Zhang, H. Comparing the applications of EMD and EEMD on time-frequency analysis of seismic signal. J. Appl. Geophys. 2012, 83, 29–34. [Google Scholar] [CrossRef]
- Wang, W.; Chau, K.; Xu, D.; Chen, X.-Y. Improving forecasting accuracy of annual runoff time series using ARIMA based on EEMD decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Sun, J.; Xiao, Q.; Wen, J.; Wang, F. Natural gas pipeline small leakage feature extraction and recognition based on LMD envelope spectrum entropy and SVM. Measurement 2014, 55, 434–443. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transforms. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Yin, A.; Ren, H. A propagating mode extraction algorithm for microwave waveguide using variational mode decomposition. Meas. Sci. Technol. 2015, 26, 095009. [Google Scholar] [CrossRef]
- Yan, J.; Hong, H.; Zhao, H.; Li, Y.; Gu, C.; Zhu, X. Through-Wall Multiple Targets Vital Signs Tracking Basedon VMD algorithm. Sensors 2016, 16, 1293. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Markert, R.; Xiang, J.; Zheng, W. Research on variational mode decomposition and its applicationin detecting rub-impact fault of the rotor system. Mech. Syst. Signal Process. 2015, 60, 243–251. [Google Scholar] [CrossRef]
- Jovan, G.; Dragoljub, G.; Aleksandar, B.; Savic-Gajic, I.; Georgieva, O.; Di Gennaro, S. Online Condition Monitoring of Bearings to Support Total Productive Maintenance in the Packaging Materials Industry. Sensors 2016, 16, 316. [Google Scholar]
- Sharma, R.K.; Sugumaran, V.; Kumar, H.; Amarnath, M. A comparative study of naive Bayes classifier and Bayes net classifier for fault diagnosis of roller bearing using sound signal. Int. J. Decis. Support Syst. 2015, 1, 115. [Google Scholar] [CrossRef]
- Wang, Q.; Garrity, G.M.; Tiedje, J.M.; Cole, J.R. Naive Bayesian classifier for rapid assignment of rRNA sequences into the new bacterial taxonomy. Appl. Environ. Microbial. 2007, 73, 5261–5267. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Wu, L.; Ge, M. A Novel Faults Diagnosis Method for Rolling Element Bearings Based on EWT and Ambiguity Correlation Classifiers. Entropy 2017, 19, 231. [Google Scholar] [CrossRef]
- Lu, J.; Huang, J.; Lu, F. Sensor Fault Diagnosis for Aero Engine Based on Online Sequential Extreme Learning Machine with Memory Principle. Energies 2017, 10, 39. [Google Scholar] [CrossRef]
- Yang, B.S.; Han, T.; An, J.L. ART-KOHONEN neural network for fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2004, 18, 645–657. [Google Scholar] [CrossRef]
- Xiao, Y.; Kang, N.; Hong, Y.; Zhang, G. Misalignment Fault Diagnosis of DFWT Based on IEMD Energy Entropy and PSO-SVM. Entropy 2017, 19, 6. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, Y.; Chen, C.; Li, Y.-F.; Huang, H.-Z. Fault diagnosis of rotating machinery based on kernel density estimation and Kullback-Leibler divergence. J. Mech. Sci. Technol. 2014, 11, 4441–4454. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, C.; Liu, H. EMD self-adaptive selecting relevant modes algorithm for FBG spectrum signal. Opt. Fiber Technol. 2017, 36, 63–67. [Google Scholar] [CrossRef]
- Rezazadeh, A.S.; Koofigar, H.R.; Hosseinnia, S. Adaptive fault detection and isolation for a class of robot manipulators with time-varying perturbation. J. Mech. Sci. Technol. 2015, 29, 4901–4911. [Google Scholar] [CrossRef]
- Maes, F.; Collignon, A.; Vandermeulen, D.; Marchal, G.; Suetens, P. Multi-Modality Image Registration Maximization of Mutual Information. IEEE Trans. Med. Imaging 1996, 16, 14–22. [Google Scholar]

| Different Condition | Mutual Information | ||
|---|---|---|---|
| Normal Signal | Inner Race | Outer Race | |
| Normal signal | 0.8917 | 0.1397 | 0.1581 |
| Inner ring fault | 0.2717 | 0.8742 | 0.2015 |
| Outer ring fault | 0.2092 | 0.2941 | 0.7930 |
| Different Diagnosis Methods | Training Data | Testing Data | Accuracy (100%) | ||
|---|---|---|---|---|---|
| Normal Signal | Outer Race | Inner Race | |||
| EWT-KDEC | 20 | 5 | 98 | 100 | 97 |
| EMD-KDEC | 20 | 5 | 86 | 85 | 84 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, M.; Wang, J.; Ren, X. Fault Diagnosis of Rolling Bearings Based on EWT and KDEC. Entropy 2017, 19, 633. https://doi.org/10.3390/e19120633
Ge M, Wang J, Ren X. Fault Diagnosis of Rolling Bearings Based on EWT and KDEC. Entropy. 2017; 19(12):633. https://doi.org/10.3390/e19120633
Chicago/Turabian StyleGe, Mingtao, Jie Wang, and Xiangyang Ren. 2017. "Fault Diagnosis of Rolling Bearings Based on EWT and KDEC" Entropy 19, no. 12: 633. https://doi.org/10.3390/e19120633
APA StyleGe, M., Wang, J., & Ren, X. (2017). Fault Diagnosis of Rolling Bearings Based on EWT and KDEC. Entropy, 19(12), 633. https://doi.org/10.3390/e19120633