Digital Image Stabilization Method Based on Variational Mode Decomposition and Relative Entropy
Abstract
:1. Introduction
2. Related Work
2.1. Mathematic Model of Jitter Motion
2.2. VMD Theory
- (1)
- Initialize the modes , center pulsation , Lagrangian multiplier and the maximum iterations N (5000 in this paper). The cycle index is set to .
- (2)
- The cycle is started, .
- (3)
- The first inner loop is executed, and is updated according to following function:
- (4)
- The second inner loop is executed, and is updated according to the following function:
- (5)
- is updated according to the following:
- (6)
- Steps (2)–(5) are repeated until convergence, as follows:
2.3. RE Theroy
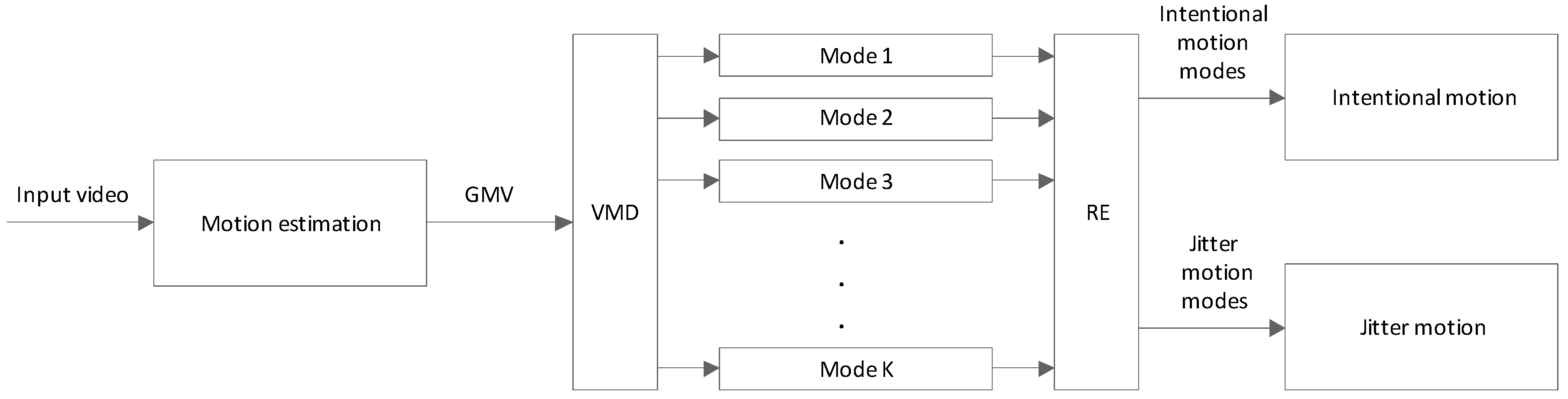
3. Proposed Digital Image Stabilization Framework
3.1. Motion Estimation
3.2. Motion Separation
3.3. Intentional Motion Vector Reconstruction
- (1)
- Calculate the GMV by SIFT point matching algorithm.
- (2)
- Decompose the GMV into modes via VMD.
- (3)
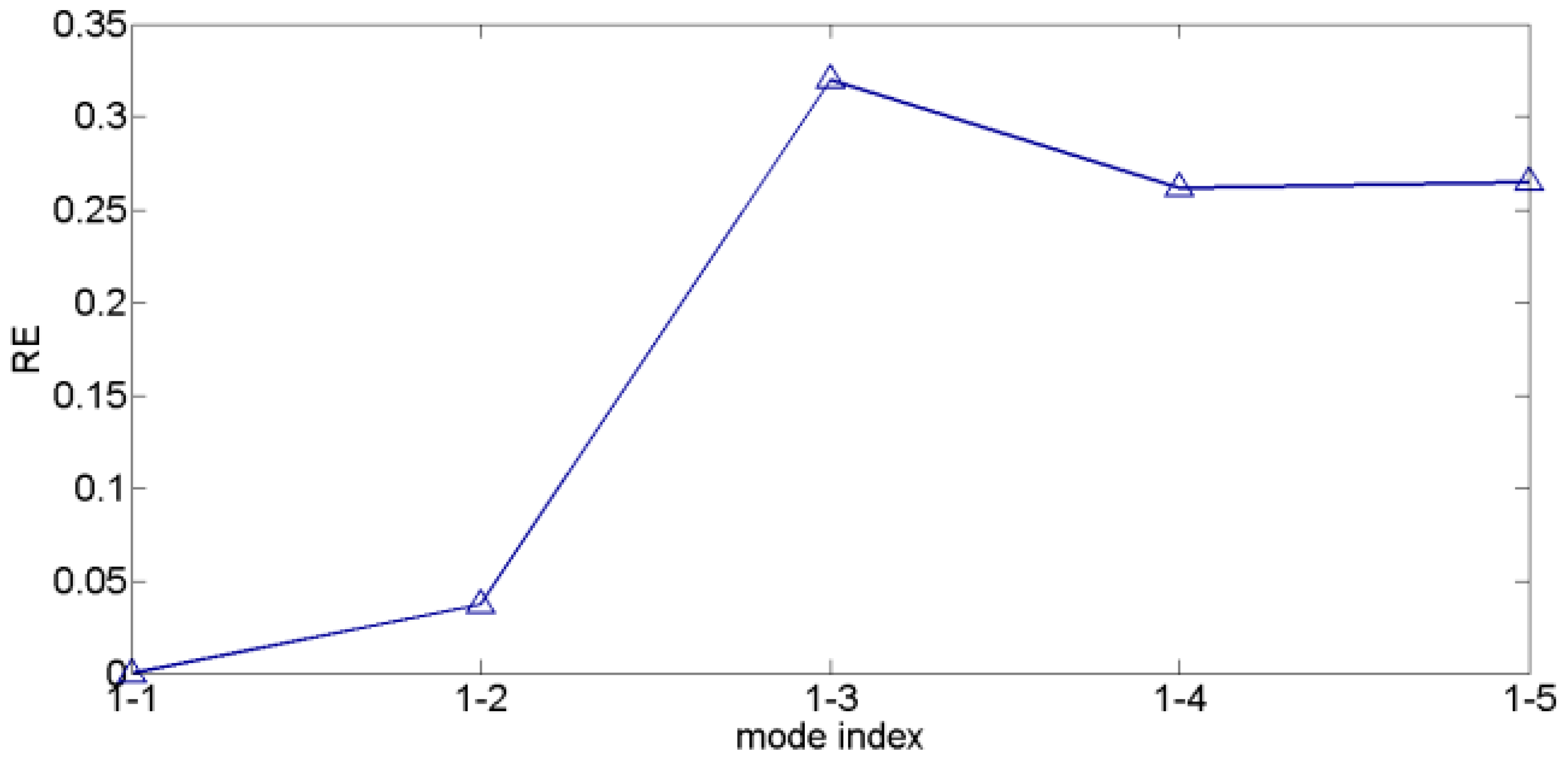
- Calculate the REs between the first mode and other modes.
- (4)
- If is smaller than a threshold (usually, can meet the demands of most situations), then the mode is considered an intentional motion mode.
- (5)
- Obtain the reconstructed intentional motion by summing the intentional motion modes as follows:
4. Experimental Results and Discussions
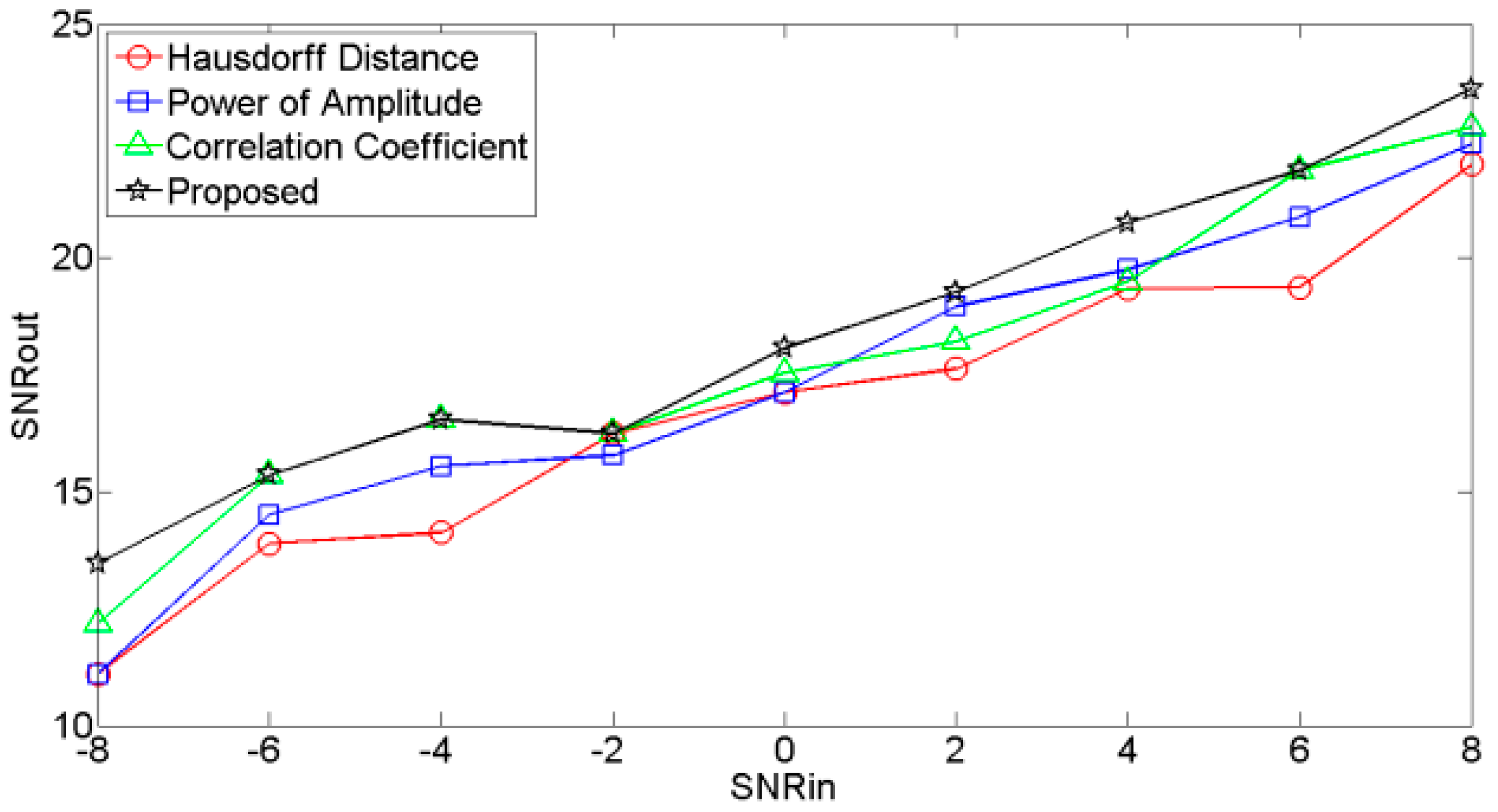
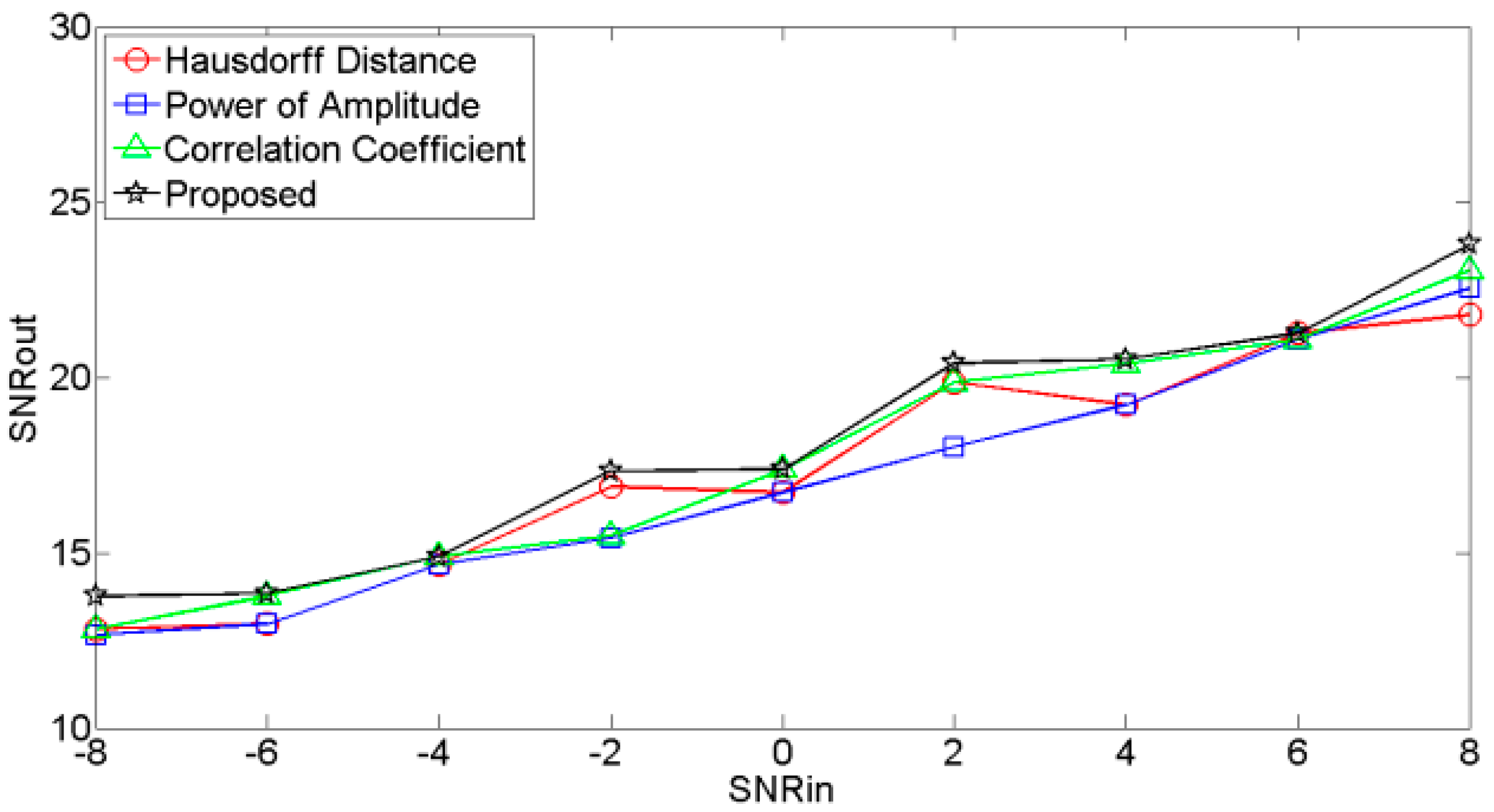
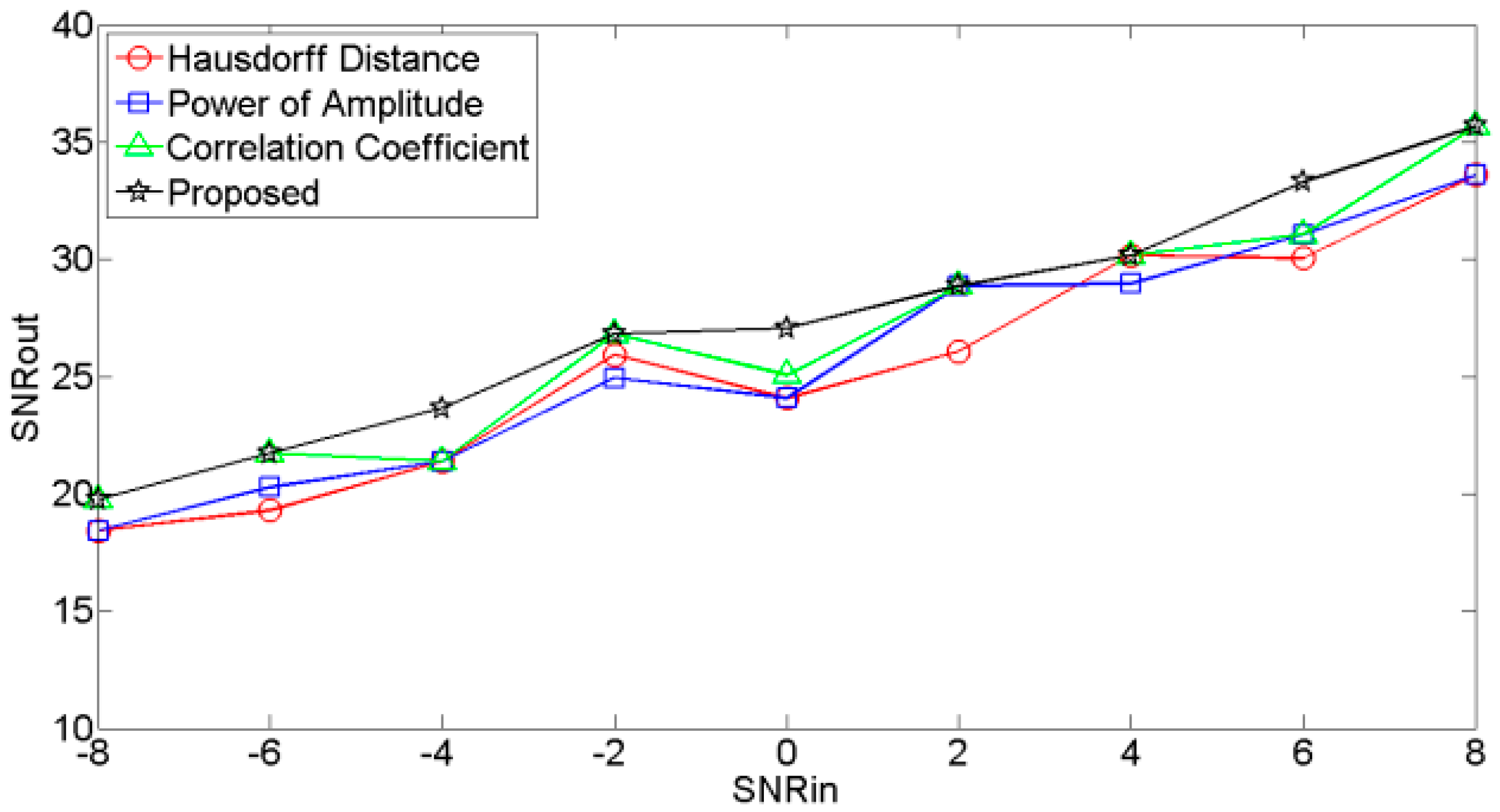
4.1. Performance of the RE
- (1)
- Noises are added to the original clean signal , and input SNR ranges from −8 dB to 8 dB with interval of 2 dB.
- (2)
- Noisy signals are decomposed into several modes via VMD.
- (3)
- According to different selection criteria, the modes are classified.
- (4)
- The reconstructed clean signals are calculated by summing the relevant modes.
- (5)
- Output SNRs are calculated for different reconstructed signals:
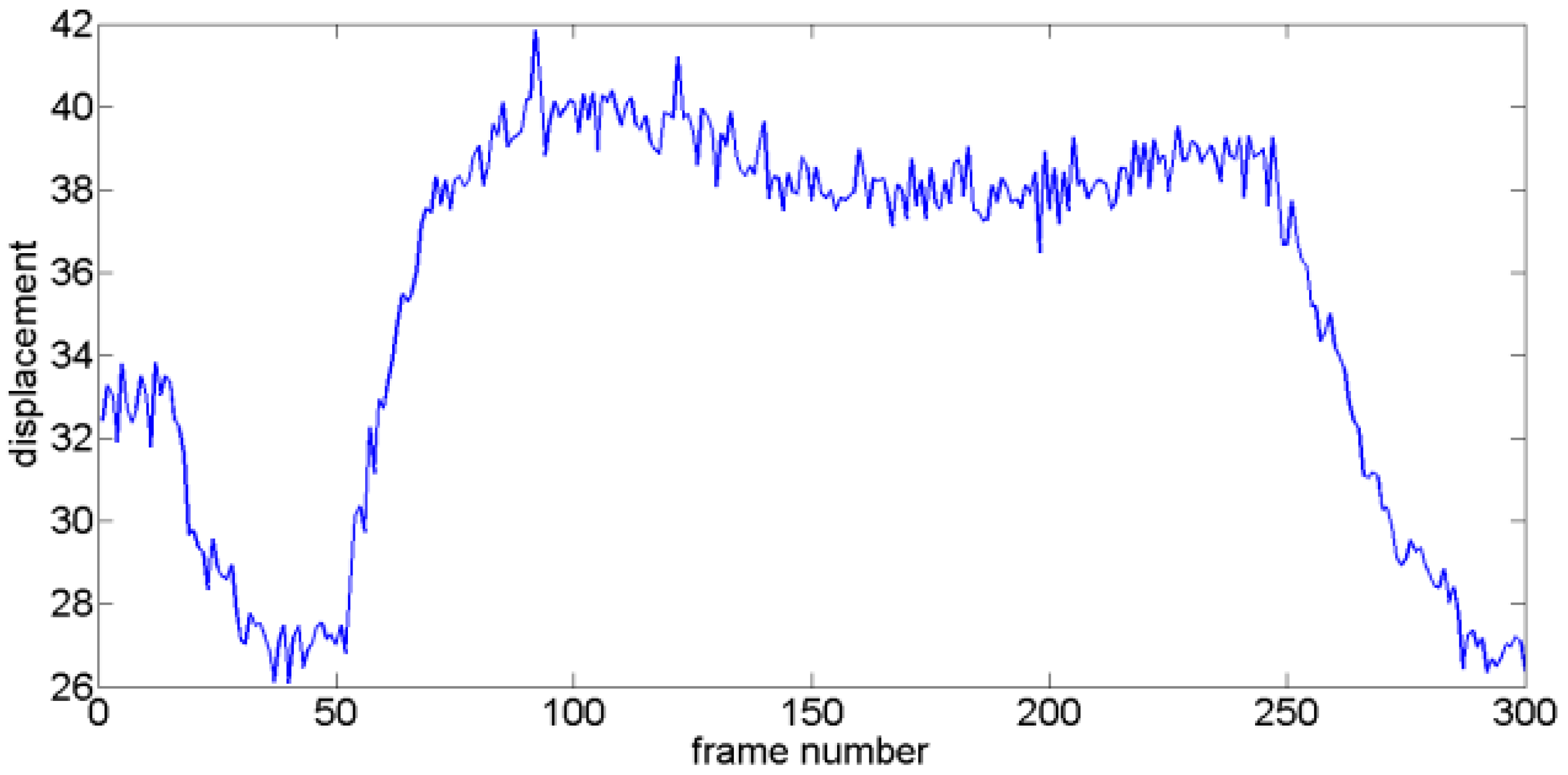
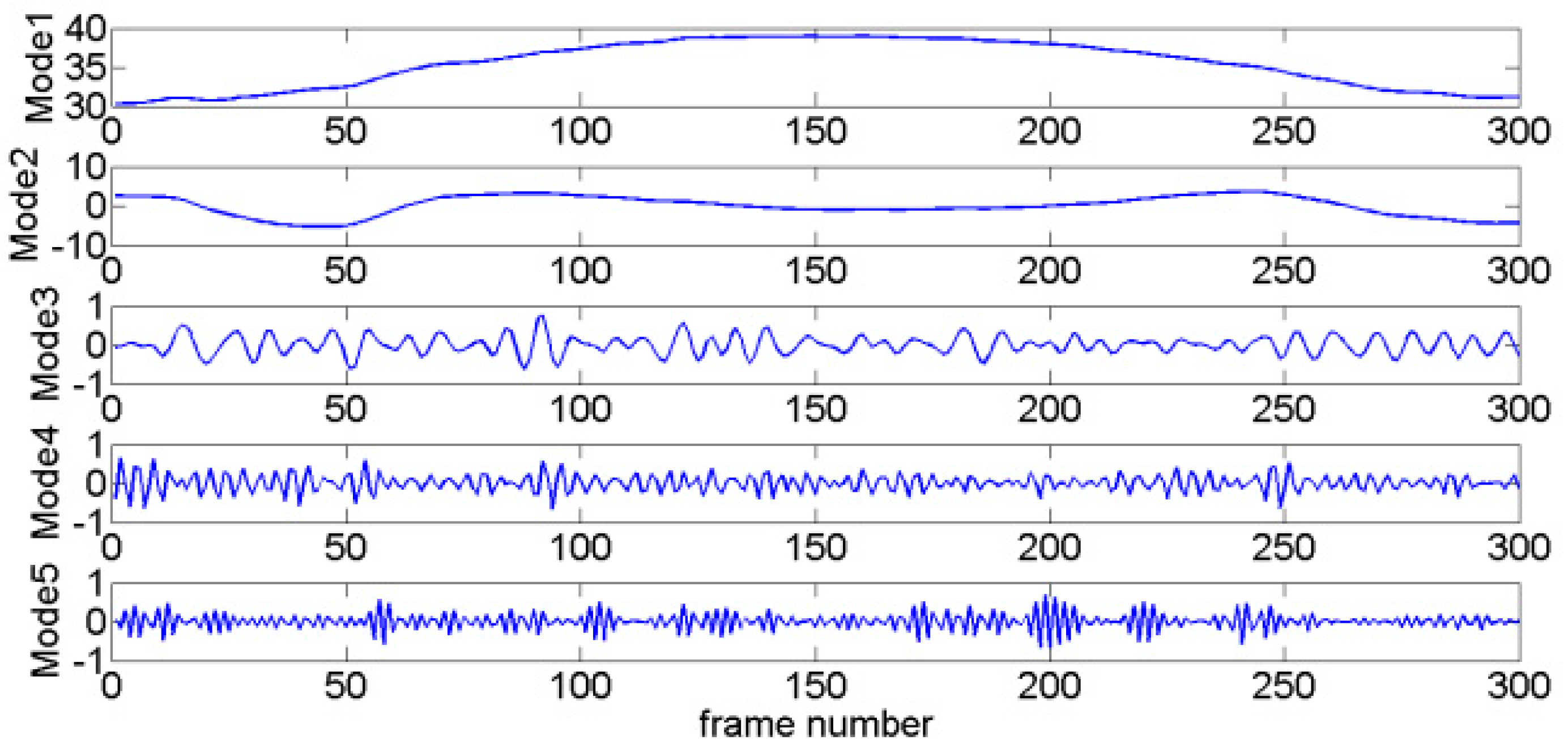
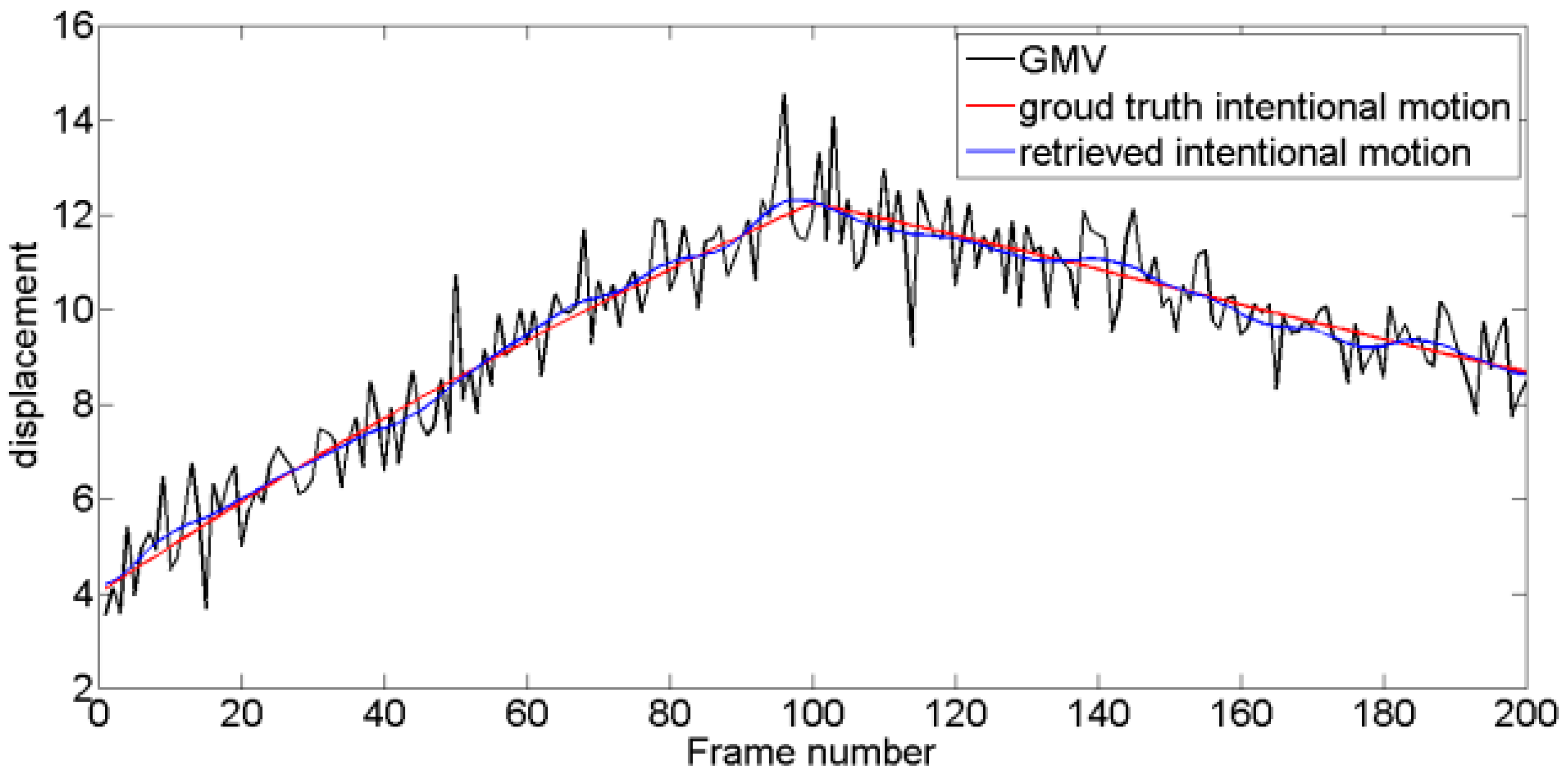
4.2. Performance of the VMD-RE Method in DIS
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Sato, K.; Ishizuka, S.; Nikami, A.; Sato, M. Control techniques for optical image stabilizing system. IEEE Trans. Consum. Electron. 1993, 39, 461–466. [Google Scholar] [CrossRef]
- Egusa, Y.; Akahori, H.; Morimura, A.; Wakami, N. An application of fuzzy set theory for an electronic video camera image stabilizer. IEEE Trans. Fuzzy Syst. 1995, 3, 351–356. [Google Scholar] [CrossRef]
- Tsytsulin, A.K.; Fakhmi, S.S. Stabilization of images on the basis of a measurement of their displacement, using a photodetector array and two linear photodetectors in combination. J. Opt. Technol. 2012, 79, 727–732. [Google Scholar] [CrossRef]
- Xu, L.; Lin, X. Digital Image Stabilization Based on Circular Block Matching. IEEE Trans. Consum. Electron. 2006, 52, 566–574. [Google Scholar]
- Jin, J.S.; Zhu, Z.; Xu, G. A stable vision system for moving vehicles. IEEE Trans. Intell. Transp. Syst. 2000, 1, 32–39. [Google Scholar] [CrossRef]
- Chiu, C.W.; Chao, P.C.P.; Wu, D.Y. Optimal design of magnetically actuated optical image stabilizer mechanism for cameras in mobile phones via genetic algorithm. IEEE Trans. Magn. 2007, 6, 2582–2584. [Google Scholar] [CrossRef]
- Qian, Y.; Li, Y.; Shao, J.; Miao, H. Real-time Image Stabilization for Arbitray Motion Blurred Image Based on Opto-Electronic Hybrid Joint Transform Correlator. Opt. Express 2011, 19, 10762–10768. [Google Scholar] [CrossRef] [PubMed]
- Kinugasa, T.; Yamamoto, N.; Komatsu, H.; Takase, S.; Imaide, T. Electronic image stabilizer for video camera use. IEEE Trans. Consum. Electron. 1900, 36, 520–525. [Google Scholar] [CrossRef]
- Burke, B.E.; Reich, R.K.; Savoye, E.D.; Tonry, J.L. An orthogonaltransfer CCD imager. IEEE Trans. Electron. Devices 1994, 41, 2482–2484. [Google Scholar] [CrossRef]
- Wang, C.T.; Kim, J.H.; Byun, K.Y.; Ko, S.J. Robust digital image stabilization using Kalman filter. IEEE Trans. Consum. Electron. 2009, 55, 6–14. [Google Scholar] [CrossRef]
- Zvantsev, S.P.; Merzlyutin, E.Y. Digital stabilization of images under conditions of planned movement. J. Opt. Technol. 2012, 79, 721–726. [Google Scholar] [CrossRef]
- Kumar, S.; Azartash, H.; Biswas, M.; Nguyen, T. Real-Time Affine Global Motion Estimation Using Phase Correlation and Its Application for Digital Image Stabilization. IEEE Trans. Image Process. 2011, 20, 3406–3418. [Google Scholar] [CrossRef] [PubMed]
- Ko, S.J.; Lee, S.H.; Lee, K.H. Digital image stabilizing algorithms based on bit-plane matching. IEEE Trans. Consum. Electron. 1998, 44, 617–622. [Google Scholar]
- Ko, S.J.; Lee, S.H.; Jeon, S.W.; Kang, E.S. Fast Digital Stabilizer Based on Gray-Coded Bit-Plane Matching. IEEE Trans. Consum. Electron. 1999, 45, 598–630. [Google Scholar]
- Kir, B.; Kurt, M.; Urhan, O. Local Binary Pattern Based Fast Digital Image Stabilization. IEEE Signal Process. Lett. 2015, 22, 341–345. [Google Scholar] [CrossRef]
- Yang, J.; Schonfeld, D.; Mohamed, M. Robust Video Stabilization Based on Particle Filter Tracking of Projected Camera Motion. IEEE Trans. Circuit Syst. Video Technol. 2009, 19, 945–954. [Google Scholar] [CrossRef]
- Ryu, Y.G.; Chung, M.J. Robust Online Digital Image Stabilization Based on Point-Feature Trajectory without Accumulative Global Motion Estimation. IEEE Signal Process. Lett. 2012, 19, 223–226. [Google Scholar] [CrossRef]
- Li, C.; Zhan, L.; Shen, L. Friction Signal Denoising Using Complete Ensemble EMD with Adaptive Noise and Mutual Information. Entropy 2015, 17, 5965–5979. [Google Scholar] [CrossRef]
- Xia, R.; Ke, M.; Feng, Q.; Wang, Z. Online wavelet denoising via a moving window. Acta Autom. Sin. 2007, 33, 897–901. [Google Scholar] [CrossRef]
- Ioannidis, K.; Andreadis, I. A Digital Image Stabilization Method Based on the Hilbert-Huang Transform. IEEE Trans. Instrum. Meas. 2012, 61, 2446–2457. [Google Scholar] [CrossRef]
- Hao, D.; Li, Q.; Li, C. Digital image stabilization in mountain areas using complete ensemble empirical mode decomposition with adaptive noise and structural similarity. J. Electron. Imaging 2016, 25, 33007. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009. [Google Scholar] [CrossRef]
- Komaty, A.; Boudraa, A.; Dare, D. Emd-based filtering using the Hausdorff distance. In Proceedings of the IEEE International Symposium on Signal Processing and Information Technology, Ho Chi Minh City, Vietnam, 12–15 December 2013; pp. 292–297. [Google Scholar]
- Zhang, S.Y.; Liu, Y.Y.; Yang, G.L. EMD interval thresholding denoising based on correlation coefficient to select relevant modes. In Proceedings of the 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 4801–4806. [Google Scholar]
- Zhao, Q.; Li, J.; Cui, N. Time field simulation of vibration performance for military automobile under road random input. China Sciencepap. 2012, 7, 862–875. [Google Scholar]
- Yang, Y.; Shen, Y.L.; Cao, Y.; Li, T.S. The exploiture of road simulation shaker table and control system. J. Syst. Simul. 2004, 16, 1044–1046. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Rockafellar, T. A Dual Approach to Sloving Nonlinear Programming Problems by Uncontrained Optimization. Math. Program. 1973, 5, 354–373. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Lowe, D.G.; Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. In Readings in Computer Vision: Issues, Problems, Principles, and Paradigms; Fischler, M.A., Ed.; Morgan Kaufmann: San Francisco, CA, USA, 1987; pp. 726–740. [Google Scholar]







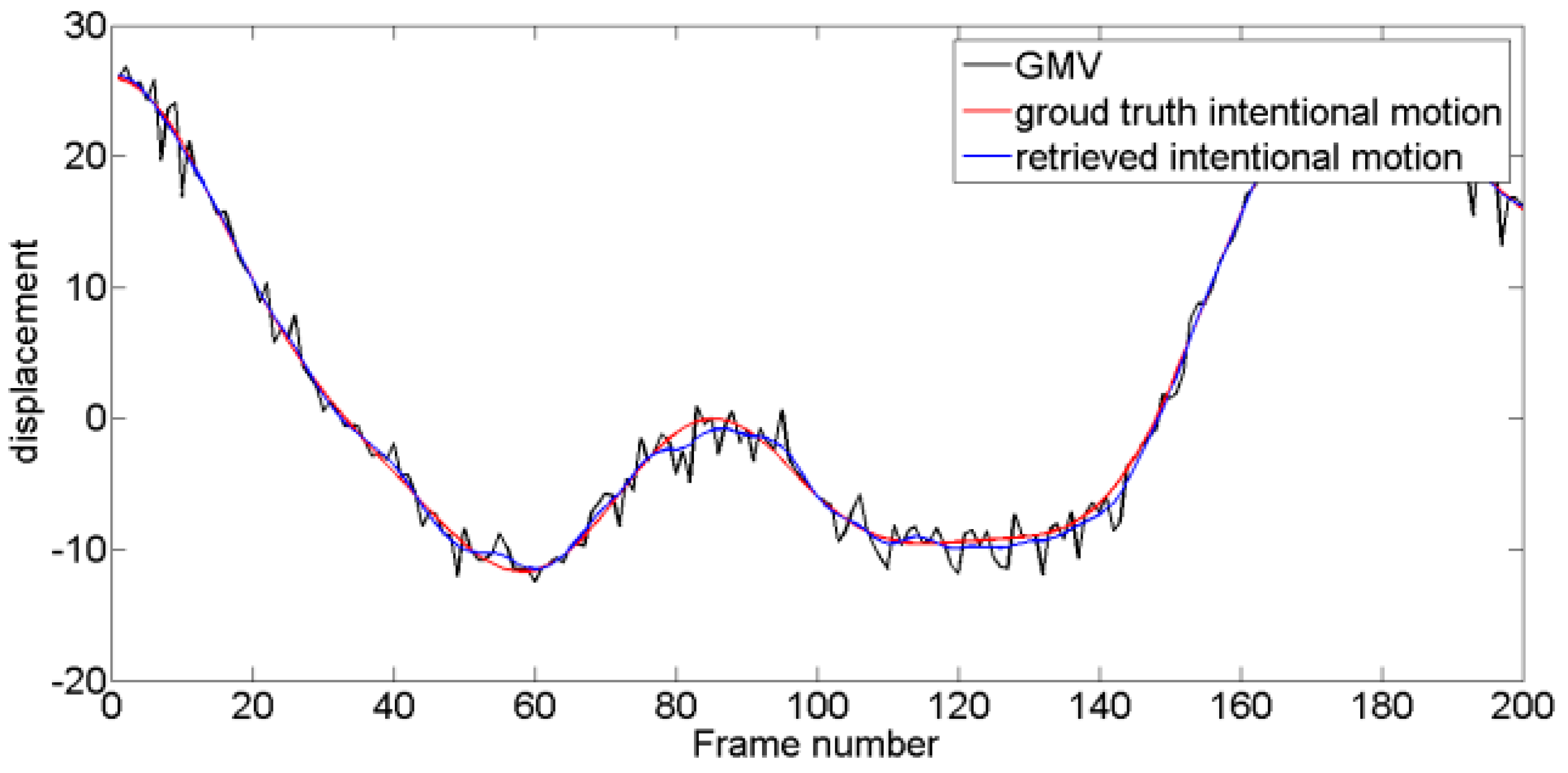
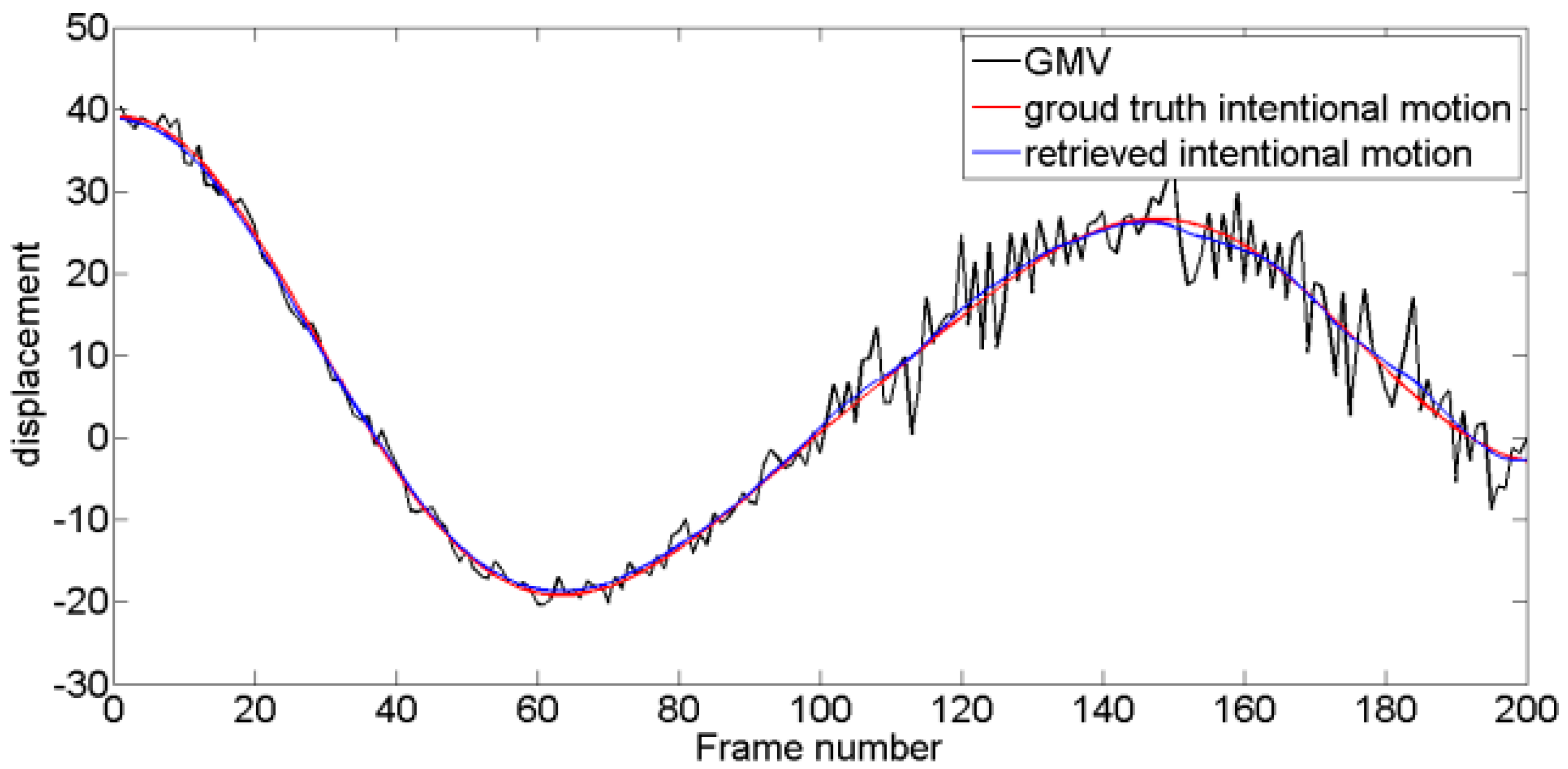
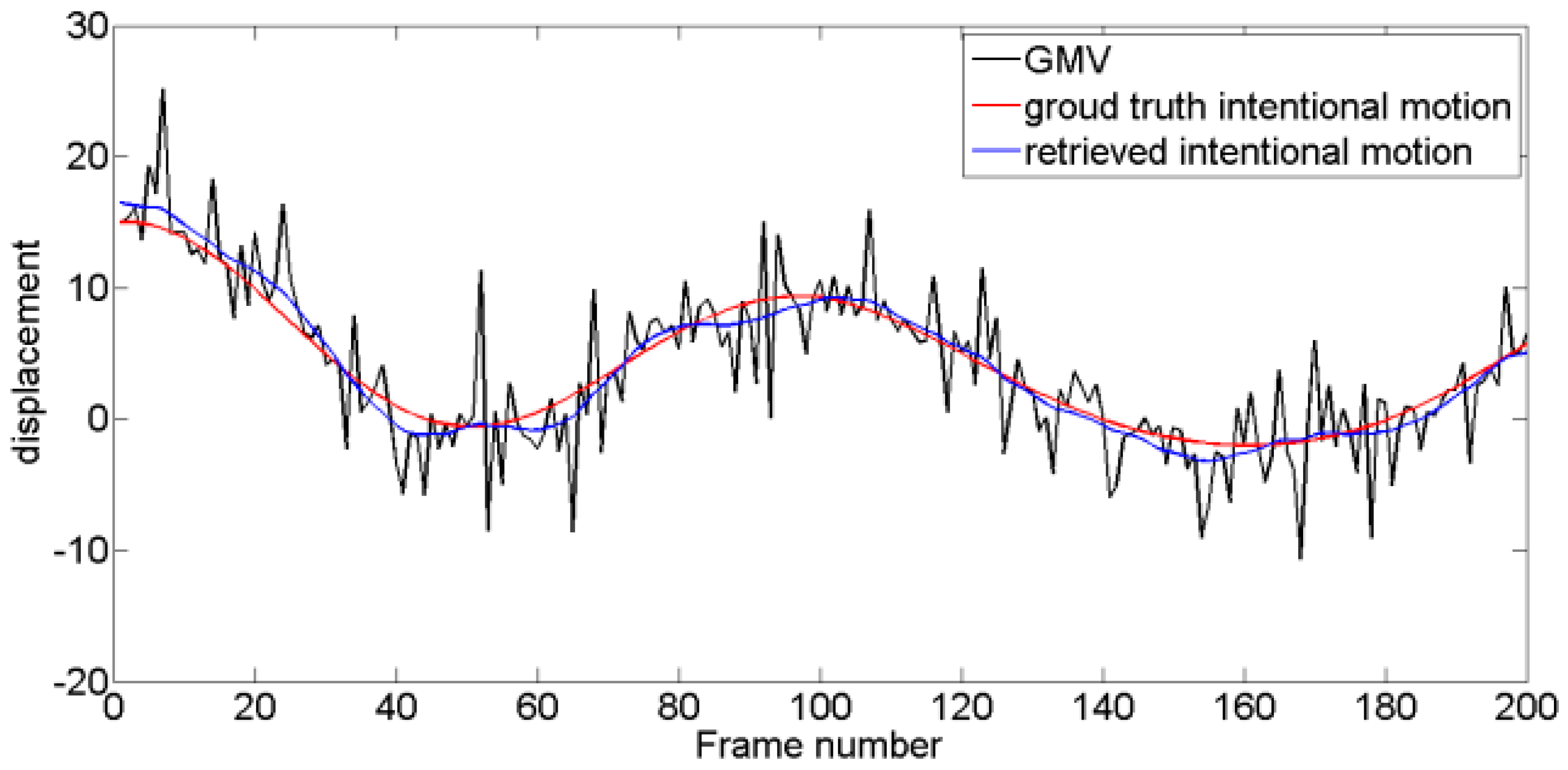
| Method | MF | KF | WD | EMD | E-EMD | VMD |
|---|---|---|---|---|---|---|
| Test 1 | 0.0188 | 0.0161 | 0.0110 | 0.0151 | 0.0120 | 0.0071 |
| Test 2 | 0.0384 | 0.0371 | 0.2125 | 0.0794 | 0.0337 | 0.0319 |
| Test 3 | 0.0927 | 0.1131 | 0.1646 | 0.0838 | 0.0547 | 0.0426 |
| Test 4 | 0.1038 | 0.1351 | 0.0815 | 0.0692 | 0.0670 | 0.0610 |
| Method | MF | KF | WD | EMD | E-EMD | VMD |
|---|---|---|---|---|---|---|
| Test 1 | 17.9043 | 19.5021 | 22.5678 | 19.8240 | 21.8030 | 26.3579 |
| Test 2 | 27.4209 | 27.9321 | 12.5721 | 21.1245 | 28.5721 | 29.0528 |
| Test 3 | 22.0902 | 20.3511 | 17.1060 | 22.9722 | 26.6741 | 28.8509 |
| Test 4 | 10.0575 | 8.0307 | 12.1508 | 13.5821 | 13.8527 | 14.6741 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, D.; Li, Q.; Li, C. Digital Image Stabilization Method Based on Variational Mode Decomposition and Relative Entropy. Entropy 2017, 19, 623. https://doi.org/10.3390/e19110623
Hao D, Li Q, Li C. Digital Image Stabilization Method Based on Variational Mode Decomposition and Relative Entropy. Entropy. 2017; 19(11):623. https://doi.org/10.3390/e19110623
Chicago/Turabian StyleHao, Duo, Qiuming Li, and Chengwei Li. 2017. "Digital Image Stabilization Method Based on Variational Mode Decomposition and Relative Entropy" Entropy 19, no. 11: 623. https://doi.org/10.3390/e19110623
APA StyleHao, D., Li, Q., & Li, C. (2017). Digital Image Stabilization Method Based on Variational Mode Decomposition and Relative Entropy. Entropy, 19(11), 623. https://doi.org/10.3390/e19110623




