1. Introduction
In quantum mechanics, the outcome of a measurement is subject to a probability distribution determined from the quantum state of the measured system and the measurement performed. The task of estimating the quantum state from the outcome of measurement is called the quantum estimation and it is a fundamental problem in quantum statistics [
1,
2,
3]. Tanaka and Komaki [
4] and Tanaka [
5] discussed quantum estimation using the framework of statistical decision theory and showed that Bayesian methods provide better estimation than the maximum likelihood method. In Bayesian methods, we need to specify a prior distribution on the unknown parameters of the quantum states. However, the problem of prior selection has not been fully discussed for quantum estimation [
6].
The quantum state estimation problem is related to the predictive density estimation problem in classical statistics [
7]. This is a problem of predicting the distribution of an unobserved variable
y based on an observed variable
x. Suppose
where
denotes an unknown parameter. Based on the observed
x, we predict the distribution
of
y using a predictive density
. The plug-in predictive density is defined as
, where
is some estimate of
from
x. The Bayesian predictive density with respect to a prior distribution
is defined as
where
is the posterior distribution. We compare predictive densities using the framework of statistical decision theory. Specifically, a loss function
is introduced that evaluates the difference between the true density
q and the predictive density
p. Then, the risk function
is defined as the average loss when the true value of the parameter is
:
A predictive density
is called minimax if it minimizes the maximum risk among all predictive densities:
We adopt the Kullback–Leibler divergence
as a loss function, since it satisfies many desirable properties compared to other loss functions such as the Hellinger distance and the total variation distance [
8]. Under this setting, Aitchison [
9] proved
where
is called the Bayes risk. Namely, the Bayesian predictive density
minimizes the Bayes risk. We provide the proof of Equation (
4) in the
Appendix A. Therefore, it is sufficient to consider only Bayesian predictive densities from the viewpoint of Kullback–Leibler risk, and the selection of the prior
becomes important.
For the predictive density estimation problem above, Komaki [
10] developed a class of priors called the latent information priors. The latent information prior
is defined as a prior that maximizes the conditional mutual information
between the parameter
and the unobserved variable
y given the observed variable
x. Namely,
where
is the conditional mutual information between
y and
given
x. Here,
are marginal densities. The Bayesian predictive densities based on the latent information priors are minimax under the Kullback–Leibler risk:
The latent information prior is a generalization of the reference prior [
11] that is a prior maximizing the unconditional mutual information
between
and
y.
Now, we consider the problem of estimating the quantum state of a system
based on the outcome of a measurement on a system
. Suppose the quantum state of the composed system
be
where
denotes an unknown parameter. We perform a measurement on the system
and obtain the outcome
x. Based on the measurement outcome
x, we estimate the state of the system
by a predictive density operator
. Similarly to the Bayesian predictive density (
1), the Bayesian predictive density operator with respect to the prior
is defined as
where
is the posterior distribution. Like the predictive density estimation problem discussed above, we compare predictive density operators using the framework of statistical decision theory. There are several possibilities for the loss function
in quantum estimation such as the fidelity and the trace norm [
12]. In this paper, we adopt the quantum relative entropy
as a loss function, since it is a quantum analogue of the Kullback–Leibler divergence (
3). Note that the fidelity and the trace norm correspond to the Hellinger distance and the total variation distance in the classical statistics, respectively. Under this setting, Tanaka and Komaki [
4] proved that the Bayesian predictive density operators minimize the Bayes risk:
This is a quantum version of Equation (
4).
From Tanaka and Komaki [
4], the selection of the prior becomes important also in quantum estimation. However, this problem has not been fully discussed [
6]. In this paper, we provide a quantum version of the latent information priors and prove that they provide minimax predictive density operators. Whereas the latent information prior in the classical case maximizes the conditional Shannon mutual information, the proposed prior maximizes the conditional Holevo mutual information. The Holevo mutual information, which is a quantum version of the Shannon mutual information, is a fundamental quantity in the classical-quantum communication [
13]. Our result shows that the conditional Holevo mutual information also has a natural meaning in terms of quantum estimation.
Unlike the classical statistics, the measurement is not unique in quantum statistics. Therefore, selection of the measurement also becomes important. From the viewpoint of minimax state estimation, measurements that minimize the minimax risk are considered to be optimal. We provide a class of optimal measurements for one qubit system. This class includes the symmetric informationally complete measurement [
14,
15]. These measurements and latent information priors provide robust quantum estimation.
3. Minimax Estimation of Quantum States
In this section, we develop the latent information prior for quantum state estimation and show that this prior provides a minimax predictive density operator.
In the following, we assume the following conditions:
is compact.
For every , .
For every , there exists such that .
The third assumption is achieved by adopting sufficiently small Hilbert space. Namely, if there exists such that for every , then we redefine the state space as the orthogonal complement of .
Let
be the set of all probability measures on
endowed with the weak convergence topology and the corresponding Borel algebra. By the Prohorov theorem [
18] and the first assumption,
is compact.
When
x is fixed, the function
is bounded and continuous. Thus, for every fixed
, the function
is continuous because
is endowed with the weak convergence topology and
. Let
be the eigenvalues and the normalized eigenvectors of the predictive density operator
. For every predictive density operator
, consider the function from
to
defined by
The last term in (
10) is lower semicontinuous under the definition
[
10], since each summand takes either zero or infinity and so the set of
such that this term takes zero is closed. In addition, the other terms in (
10) are continuous since the von Neumann entropy is continuous [
12]. Therefore, the function
in (
10) is lower-semicontinuous.
Now, we prove that the class of predictive density operators that are limits of Bayesian predictive density operators is an essentially complete class. We prepare three lemmas. Lemma 1 is useful for differentiation of quantum relative entropy (see Hiai and Petz [
19]). Lemmas 2 and 3 are from Komaki [
10].
Lemma 1. Let be n-dimensional self-adjoint matrices and t be a real number. Assume that is a continuously differentiable function defined on an interval and assume that the eigenvalues of are in if t is sufficiently close to . Then, Lemma 2 ([
10])
. Let μ be a probability measure on Θ.
Then,is a closed subset of for . Lemma 3 ([
10])
. Let be continuous, and let μ be a probability measure on Θ
such that for every . Then, there is a probability measure infor every n, such that . Furthermore, there exists a convergent subsequence of and the equality holds, where . By using these results, we obtain the following theorem, which is a quantum version of Theorem 1 of Komaki [
10].
Theorem 1. - (1)
Let be a predictive density operator. If there exists a prior such that and for every , then for every .
- (2)
For every predictive density operator ρ, there exists a convergent prior sequence such that , exists, and for every .
Next, we develop priors that provide minimax predictive density operators. Let
x be a random variable, which represents the outcome of the measurement, i.e.,
. Then, as a quantum analogue of the conditional mutual information (
5), we define the conditional Holevo mutual information [
13] between the quantum state
of
Y and the parameter
given the measurement outcome
x as
which is a function of
. Here, we used
and
The conditional Holevo mutual information provides an upper bound on the conditional mutual information as follows.
Proposition 1. Let be the state of the composed system . Suppose that a measurement is performed on X with the measurement outcome x and then another measurement is performed on Y with the measurement outcome y. Then, Proof. Since any measurement is a trace-preserving completely positive map, inequality (
12) follows from the monotonicity of the quantum relative entropy [
13]. ☐
Analogous with the latent information priors [
10] in classical statistics, we define latent information priors as priors that maximize the conditional Holevo mutual information. It is expected that the Bayesian predictive density operator
based on a latent information prior is a minimax predictive density operator. This is true from the following theorem, which is a quantum version of Theorem 2 of Komaki [
10].
Theorem 2. - (1)
Let be a prior maximizing . If for all ; then, is a minimax predictive density operator.
- (2)
There exists a convergent prior sequence such that is a minimax predictive density operator and the equality holds.
The proof of Theorems 1 and 2 are deferred to the
Appendix A.
We note that the minimax risk
depends on the measurement
E on
. Therefore, the measurement
E with minimum minimax risk is desirable from the viewpoint of minimaxity. We define a POVM
to be a minimax POVM if it satisfies
In the next section, we provide a class of minimax POVMs for one qubit system.
4. One Qubit System
In this section, we consider one qubit system and derive a class of minimax POVMs satisfying (
13).
Qubit is a quantum system with a two-dimensional Hilbert space. It is the fundamental system in the quantum information theory. A general state of one qubit system is described by a density matrix
where
. The parameter space
for pure states is called the Bloch sphere.
Let be a separable state. We consider the estimation of from the outcome of a measurement on . Here, we assume that the state is separable, since the state of Y changes according to the outcome of the measurement on X and so the estimation problem is not well-defined if the state is not separable.
Let
and
be Borel sets. From Haapasalo et al. [
20], it is sufficient to consider POVMs on
. For every probability measure
on
that satisfies
we define a POVM
by
In the following, we identify E with .
Let
be a class of POVMs on
represented by measures that satisfy the conditions
where
is the expectation with respect to a measure
. We provide two examples of POVMs in
.
Proposition 2. The POVM corresponding towhere is surface element, is in . Proof. From the symmetry of , . Moreover, from and the symmetry of , . ☐
Proposition 3. Suppose that satisfies . Let μ be a four point discrete measure on Ω
defined by Then, the POVM corresponding to μ belongs to .
Proof. Let
and
. From the assumption on
,
where
is the identity matrix and
is a matrix whose elements are all one. From (
16), we have
. Therefore,
and it implies
.
Therefore, . Since , it implies . Then, and . ☐
We note that the POVM (
15) is a special case of the SIC-POVM (symmetric, informationally complete, positive operator valued measure) [
14,
15].
Let
be a class of priors on
that satisfies the conditions
where
is the expectation with respect to a prior
.
Proposition 4. The uniform priorwhere is the surface element on the Bloch sphere, belongs to . Proof. Same as Proposition 2. ☐
Proposition 5. Suppose that satisfies . Then, the four point discrete priorbelongs to . Proof. Same as Proposition 3. ☐
We obtain the following result.
Lemma 4. Suppose . Then, for general measurement E, the risk function of the Bayesian predictive density operator is Proof. The distribution of the measurement outcome
is
Then, since
, the marginal distribution of the measurement outcome is
Therefore, the posterior distribution of
is
The posterior mean of and are and , respectively.
Thus, the Bayesian predictive density operator based on prior
is
and we have
Therefore, the quantum relative entropy loss is
Hence, the risk function is
☐
Theorem 3. For a measurement , every is a latent information prior: In addition, the risk of the Bayesian predictive density operator based on iswhere h is the binary entropy function . Proof. From Lemma 4 and
,
Therefore, the risk depends only on
and we have
Since
the function
is convex. In addition, we have
. Therefore,
takes the maximum at
.
In other words, takes maximum on the Bloch sphere. In addition, since , the support of is included in the Bloch sphere . Therefore, and it implies that is a latent information prior. ☐
We note that the Bayesian predictive density operator is identical for every
. In fact, every
also provides the minimax estimation of density operator
when there is no observation system
X.
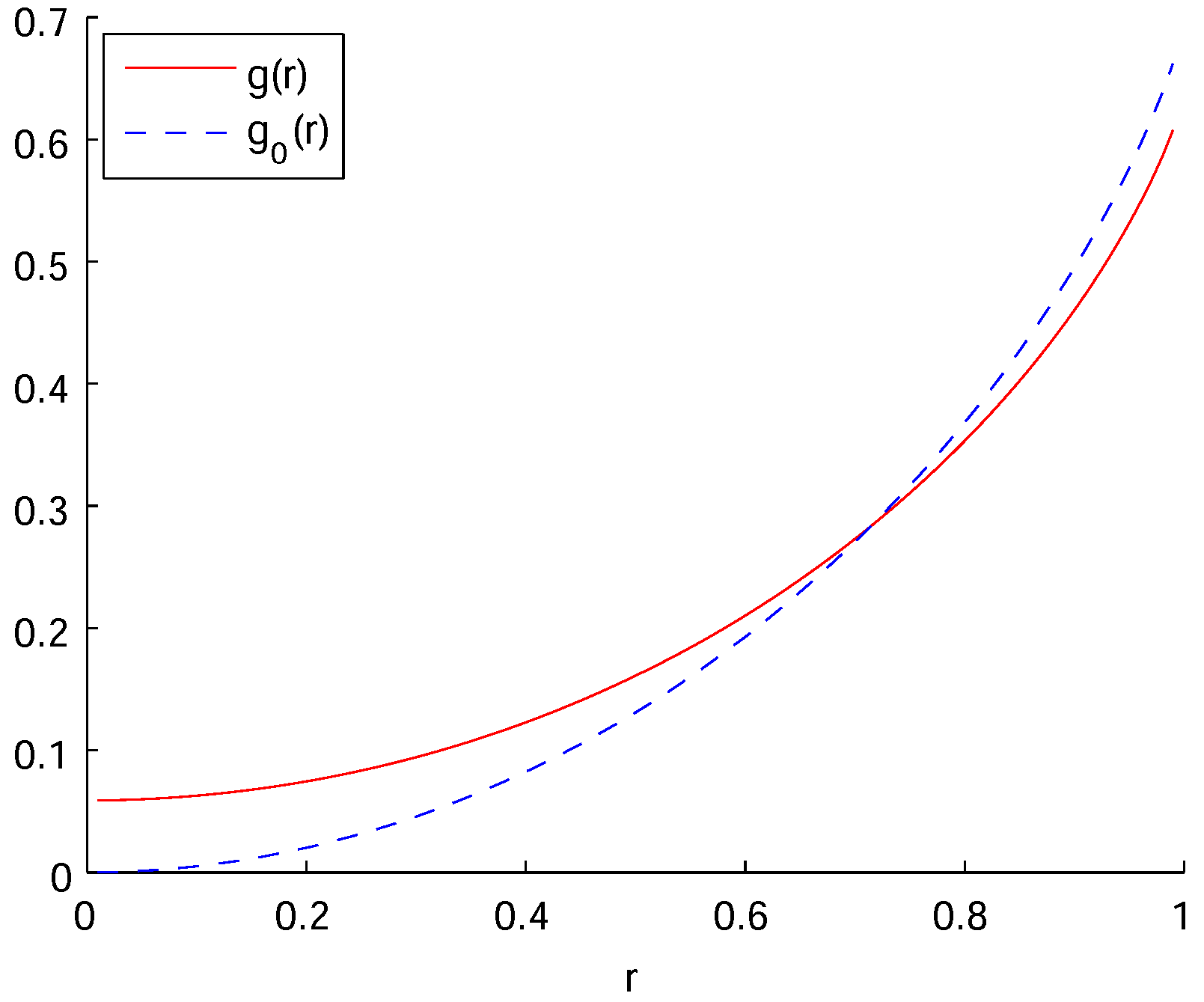
Figure 1 shows the risk function
in (
17) and also the minimax risk function
when there is no observation:
Whereas
around
, we can see that
around
. Both risk functions take the maximum at
and
The decrease in the maximum risk corresponds to the gain from the observation X.
Now, we consider the selection of the measurement
E. As we discussed in the previous section, we define a POVM
to be a minimax POVM if it satisfies (
13). We provide a sufficient condition on a POVM to be minimax. Let
be a minimax predictive density operator for the measurement
E.
Lemma 5. Suppose is a latent information prior for the measurement . Ifthen is a minimax POVM. Proof. For every
, we have
The last equality is from the minimaxity of . Therefore, is a minimax POVM. ☐
Theorem 4. Every is a minimax POVM.
Proof. Let . From Theorem 6, is a latent information prior for .
For general measurement
E, from Lemma 4, the risk function of the Bayesian predictive density operator
is
Hence, the Bayes risk of
with respect to
is
Now, since the Bayesian predictive density operator
minimizes the Bayes risk with respect to
among all predictive density operators [
4],
for every
E. Therefore,
On the other hand,
is obvious.
From Lemma 5, is minimax. ☐
Whereas Theorems 1 and 2 are valid even when is not separable, Theorems 3 and 4 assume the separability .
From Theorem 4, the POVM (
15) is a minimax POVM. Since this POVM is identical to the SIC-POVM [
14,
15], it is an interesting problem whether the SIC-POVM is a minimax POVM also in higher dimensions. This is a future work.