On the Uniqueness Theorem for Pseudo-Additive Entropies
Abstract
1. Introduction
2. Entropic (Pseudo-)Additivity Rules
2.1. Some (Pseudo-)Additivity Rules
2.2. Degeneracy in Solutions
2.3. Uniqueness Issue: Part I
- information theory, where it describes input-output information of the (quantum) communication channel and enters in the data processing inequality [28],
- non-equilibrium and complex dynamics, where it enters in the May–Wigner criterion for the stability of dynamical systems and helps to estimate the connectivity of the network of system exchanges [29],
- time series and data analysis, where it describes transfer entropies in bivariate time series and the degree of synchronization between two signals [12].
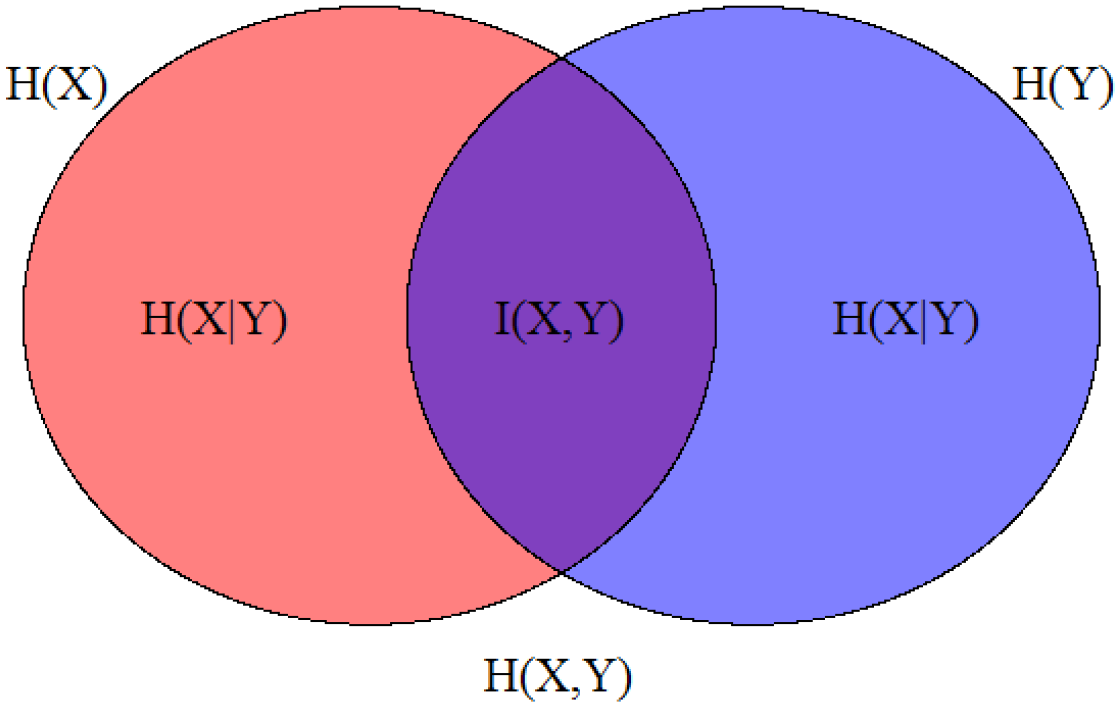
3. Entropic Chain Rule
Additive Entropic Chain Rule: Some Fundamentals
- continuity, i.e., when is a continuous function of all arguments,
- maximality, i.e., when for given n, is maximal for and
- expansibility, i.e., when ,
- iff Y is completely determined by X, e.g., (g is some function),
- entropic Bayes’ rule,
- “second law of thermodynamics”,
- if Y and X are independent (sometimes “if and only if” is required).
4. q-Additive Entropic Chain Rule
Uniqueness Issue: Part II
- iff Y is completely determined by X, e.g., ,
- q-entropic Bayes’ rule (The explicit form of the function depends on the type of q deformation. For instance, for q additivity, we have .),
- “second law of thermodynamics”,
- if Y and X are independent,
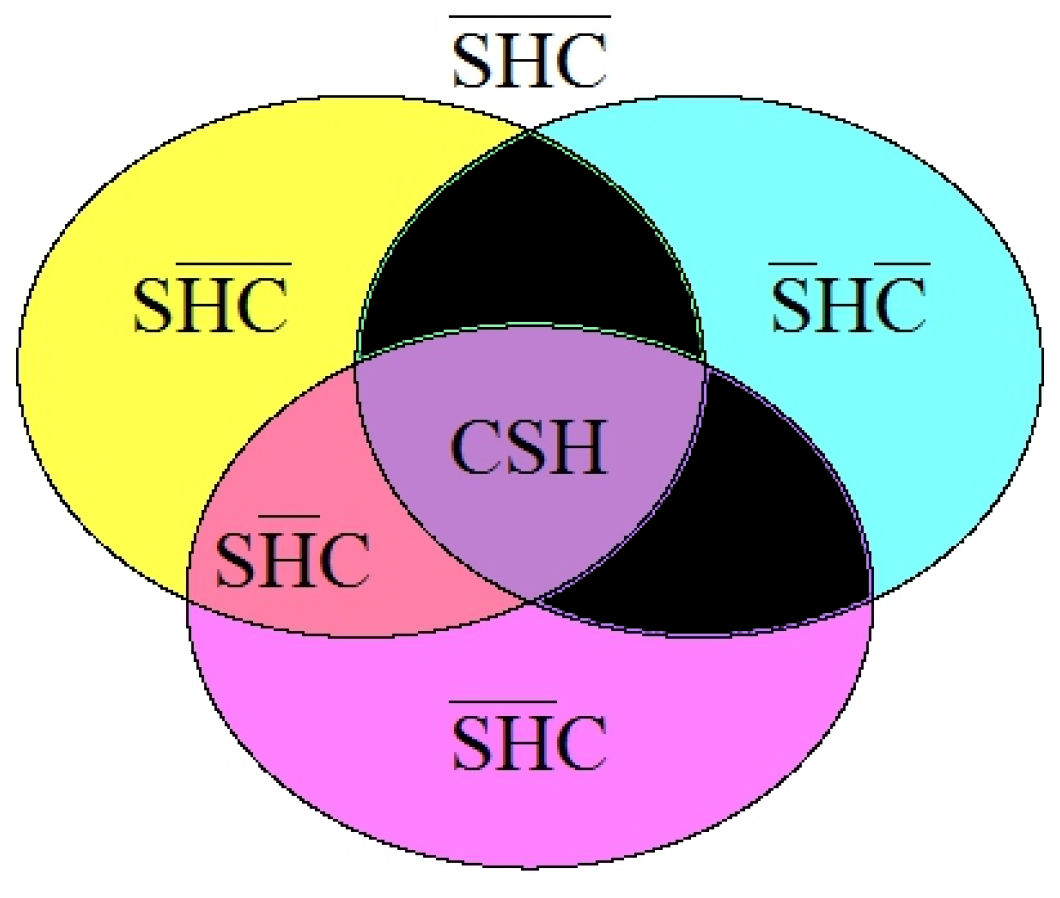
5. Theoretical Justification of Degeneracy
- Superadditivity, S: ,
- Homogeneity, H: ,
- Concavity, C: .
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| KN | Kolmogorov–Nagumo |
References
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics; Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Naudts, J. Generalised Thermostatistics; Springer: London, UK, 2011. [Google Scholar]
- Beck, C.; Cohen, E.G.D. Superstatistics. Phys. A 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Karmeshu, J. (Ed.) Entropy Measures, Maximum Entropy Principle and Emerging Applications; Springer: Berlin, Germany, 2003. [Google Scholar]
- Hanel, R.; Thurner, S. A comprehensive classification of complex statistical systems and an axiomatic derivation of their entropy and distribution functions. EPL Europhys. Lett. 2011, 93, 50006-p1–50006-p6. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S. When do generalized entropies apply? How phase space volume determines entropy. EPL Europhys. Lett. 2011, 96, 50003-p1–50005-p6. [Google Scholar] [CrossRef]
- Tempesta, P. Group entropies, correlation laws, and zeta functions. Phys. Rev. E 2011, 84, 021121-1–021121-10. [Google Scholar] [CrossRef] [PubMed]
- Biró, T.; Barnaföldi, G.; Ván, P. New entropy formula with fluctuating reservoir. Phys. A 2015, 417, 215–220. [Google Scholar] [CrossRef]
- Jizba, P.; Arimitsu, T. The world according to Rényi: Thermodynamics of multifractal systems. Ann. Phys. 2004, 312, 17–59. [Google Scholar] [CrossRef]
- Jizba, P.; Ma, Y.; Hayes, A.; Dunningham, J. One-parameter class of uncertainty relations based on entropy power. Phys. Rev. E 2016, 93, 060104(R)-1–060104(R)-5. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Jizba, P.; Kleinert, H.; Shefaat, M. Rényi’s information transfer between financial time series. Phys. A 2012, 391, 2971–2989. [Google Scholar] [CrossRef]
- Eom, Y.-H.; Jo, H.-H. Using friends to estimate heavy tails of degree distributions in large-scale complex networks. Sci. Rep. 2015, 5, 09752-1–09752-9. [Google Scholar] [CrossRef] [PubMed]
- Bercher, J.-F. Some properties of generalized Fisher information in the context of nonextensive thermostatistics. Phys. A 2013, 392, 3140–3154. [Google Scholar] [CrossRef]
- Short, A.J.; Wehner, S. Entropy in general physical theories. New J. Phys. 2010, 12, 033023. [Google Scholar] [CrossRef]
- Majhi, A. Non-extensive statistical mechanics and black hole entropy from quantum geometry. arXiv, 2017; arXiv:1703.09355. [Google Scholar] [CrossRef]
- Jizba, P.; Korbel, J. Remarks on “Comments on ’On q-non-extensive statistics with non-Tsallisian entropy” [Physica A 466 (2017) 160]. Phys. A 2017, 468, 238–243. [Google Scholar] [CrossRef]
- Schumacher, B.; Westmoreland, M. Quantum Processes, Systems, and Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Landsberg, P.T. Entropies Galore! Braz. J. Phys. 1999, 29, 46–49. [Google Scholar] [CrossRef]
- Vos, G. Generalized additivity in unitary conformal field theories. Nucl. Phys. B 2015, 899, 91–111. [Google Scholar] [CrossRef]
- Masi, M. A step beyond Tsallis and Renyi entropies. Phys. Lett. A 2005, 338, 217–224. [Google Scholar] [CrossRef]
- Korbel, J. Rescaling the nonadditivity parameter in Tsallis thermostatistics. Phys. Lett. A 2017, 381, 2588–2592. [Google Scholar] [CrossRef]
- Behara, M.; Chawla, J.S. Generalized gamma entropy. Sel. Stat. Can. 1974, 2, 15–38. [Google Scholar]
- Ochs, W.; Spohn, H.A. Characterization of the Segal entropy. Rep. Math. Phys. 1978, 14, 75–87. [Google Scholar] [CrossRef]
- Jizba, P.; Korbel, J. On q-non-extensive statistics with non-Tsallisian entropy. Phys. A 2016, 444, 808–827. [Google Scholar] [CrossRef]
- Lesche, B. Instabilities of Rényi entropies. J. Stat. Phys. 1982, 27, 419–422. [Google Scholar] [CrossRef]
- Hanel, R.; Thurner, S.; Tsallis, C. On the robustness of q-expectation values and Rényi entropy. EPL Europhys. Lett. 2009, 85, 20005-p1–20005-p6. [Google Scholar] [CrossRef]
- Campbell, L.L. A coding theorem and Rényi’s entropy. Inf. Control 1965, 8, 423–429. [Google Scholar] [CrossRef]
- Hastings, H.M. The May-Wigner stability theorem. J. Theor. Biol. 1982, 97, 155–166. [Google Scholar] [CrossRef]
- Nagumo, M. Über eine Classe der Mittelwerte. Jpn. J. Math. 1930, 7, 71–79. [Google Scholar] [CrossRef]
- Aczél, J. Lectures on Functional Equations an dtheir Applications; Academic Press: New York, NY, USA, 1966. [Google Scholar]
- Rényi, A. Selected Papers of Alfred Rényi; Akademia Kiado: Budapest, Hungary, 1976. [Google Scholar]
- Beck, C.; Schlögl, F. Thermodynamics of Chaotic Systems: An Introduction; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Abe, S. Axioms and uniqueness theorem for Tsallis entropy. Phys. Lett. A 2000, 271, 74–79. [Google Scholar] [CrossRef]
- Frank, T.D.; Daffertshofer, A. Exact time-dependent solutions of the Renyi Fokker-Planck equation and the Fokker-Planck equations related to the entropies proposed by Sharma and Mittal. Phys. A 2000, 285, 351–366. [Google Scholar] [CrossRef]
- Sharma, B.D.; Mittal, D.P. New non-additive measures of entropy for discrete probability distributions. J. Math. Sci. 1975, 10, 28–40. [Google Scholar]
- Aktürk, O.Ü.; Aktürk, E.; Tomak, M. Can Sobolev inequality be written for Sharma-Mittal entropy? Int. J. Theor. Phys. 2008, 47, 3310–3320. [Google Scholar] [CrossRef]
- Kosztołowicz, T.; Lewandowska, K.D. First-passage time for subd-diffusion: The nonadditive entropy approach versus the fractional model. Phys. Rev. E 2012, 86, 021108-1–021108-11. [Google Scholar] [CrossRef] [PubMed]
- Çankaya, M.N.; Korbel, J. On statistical properties of Jizba–Arimitsu hybrid entropy. Phys. A 2017, 474, 1–10. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jizba, P.; Korbel, J. On the Uniqueness Theorem for Pseudo-Additive Entropies. Entropy 2017, 19, 605. https://doi.org/10.3390/e19110605
Jizba P, Korbel J. On the Uniqueness Theorem for Pseudo-Additive Entropies. Entropy. 2017; 19(11):605. https://doi.org/10.3390/e19110605
Chicago/Turabian StyleJizba, Petr, and Jan Korbel. 2017. "On the Uniqueness Theorem for Pseudo-Additive Entropies" Entropy 19, no. 11: 605. https://doi.org/10.3390/e19110605
APA StyleJizba, P., & Korbel, J. (2017). On the Uniqueness Theorem for Pseudo-Additive Entropies. Entropy, 19(11), 605. https://doi.org/10.3390/e19110605





