Construction of New Fractional Repetition Codes from Relative Difference Sets with λ=1

Abstract

Fractional repetition (FR) codes are a class of distributed storage codes that replicate and distribute information data over several nodes for easy repair, as well as efficient reconstruction. In this paper, we propose three new constructions of FR codes based on relative difference sets (RDSs) with $\lambda =1$. Specifically, we propose new $(q^2-1,q,q)$ FR codes using cyclic RDS with parameters $(q+1,q-1,q,1)$ constructed from q-ary m-sequences of period $q^2-1$ for a prime power q, $(p^2,p,p)$ FR codes using non-cyclic RDS with parameters $(p,p,p,1)$ for an odd prime p or $p=4$ and $(4^l,2^l,2^l)$ FR codes using non-cyclic RDS with parameters $(2^l,2^l,2^l,1)$ constructed from the Galois ring for a positive integer l. They are differentiated from the existing FR codes with respect to the constructable code parameters. It turns out that the proposed FR codes are (near) optimal for some parameters in terms of the FR capacity bound. Especially, $(8,3,3)$ and $(9,3,3)$ FR codes are optimal, that is, they meet the FR capacity bound for all k. To support various code parameters, we modify the proposed $(q^2-1,q,q)$ FR codes using decimation by a factor of the code length $q^2-1$, which also gives us new good FR codes.

1. Introduction

As users of social media services and cloud services frequently upload large data files such as images and videos, huge storage space is required, which is implemented in the form of distributed storage systems (DSSs) [1,2]. DSSs manage a tremendous amount of storage nodes and a large number of failed nodes occur every day. Traditional solutions such as simple triplication and Reed–Solomon (RS) codes are no longer enough to efficiently maintain DSSs and enhance the reliability of stored data because, for node failure-handling, we have to consider the tremendous amount of data traffic over the network in DSS, the number of disk I/O (input/output) and the availability of local data processing, as well as the redundancy of stored data. Thus, it is necessary to find a new class of node failure-handling protocols that is well-fitted for the DSS environment, and for this reason, locally repairable codes [3,4,5,6,7] and regenerating codes [8] have recently attracted much attention.

Regenerating codes are proposed to minimize the total bandwidth of in-network data transfer required for repairing failed nodes, as well as to minimize the amount of stored data. Assume that each node stores $\alpha$ symbols, and it suffices to connect to any d other nodes and download $\beta$ symbols from each node to repair a failed node. It turns out [9] that there is a tradeoff between the amount of stored data $\alpha$ and the repair bandwidth $d\beta$, which is called the storage-bandwidth tradeoff. Minimum bandwidth regenerating (MBR) codes and minimum storage regenerating (MSR) codes are located at two extreme points of this tradeoff, respectively.

It is noted that the storage-bandwidth tradeoff was derived by allowing functional repair, where the repaired node may not have the same data as before, but it still plays the same role. The functional repair has some disadvantages against the exact repair in that all nodes may need to update the code information every time, and it is hard to maintain a systematic form of the code. Although it is proven that interior points on the tradeoff cannot be achieved with exact repair [10], many researches mainly focus on constructing exact regenerating codes and investigating the storage-bandwidth tradeoff for exact repair [11,12,13,14].

In general, DSSs handle an extremely large size of stored data, and thus, the data processing for node repairing requires a huge amount of computation. Thus, fractional repetition (FR) codes were firstly proposed in [15], which can be considered as a variant of MBR codes. FR codes enable repair-by-transfer to reduce computation in data processing for node repairing by relaxing the requirement of connecting to any d nodes. Instead, a repair is done by connecting to some d nodes based on a table. FR coding means that data symbols are replicated a few times and divided into several groups, each of which is stored at each node. Since no operations are used except for replication, computation for data processing becomes very small when repairing a failed node or collecting data symbol.

In designing DSSs, the system parameters can take arbitrary values based on the system environment, and this means many kinds of FR codes with various parameters need to be constructed. In [16], the existence of FR codes for each parameter set is shown by algorithm-based search, and some examples for each parameter set are provided. Many kinds of FR codes have been constructed mostly based on algebraic structures, combinatorial designs and graph theory [15,17,18,19,20,21,22]. In [15], Steiner systems are used as a class of $(v,(v-1)/(k-1),k)$ FR codes with $\beta =1$ under the existence of Steiner system $S(2,k,v)$. In [17], $((q^{n+2}-1)/(q-1),(q^{n+1}-1)/(q-1),q+1)$ FR codes are constructed for a prime power q and $n\ge 1$, which are based on the projective geometry and Latin squares. These FR codes are a subclass of the FR codes from Steiner systems in [15] and additionally designed to have a scalable property. In [18], various constructions of resolvable FR codes, especially net FR codes, are proposed by using grids, affine resolvable designs, Hadamard designs and mutually orthogonal Latin squares. The corresponding constructable parameters are $(2a,a,2)$ with $\beta =1$ from grids, $(q\rho ,q^{m-1},1\le \rho \le (q^m-1)/(q-1))$ with $\beta =q^{m-2}$ from affine resolvable designs, $(8a-2,2a,4a-1)$ with $\beta =a$ from Hadamard designs (where $4a-1\ge 7$ is an odd prime power) and $(\rho p^m,p^m,\rho \le p^m-1)$ or $(4a,a,4)$ with $\beta =1$ from mutually orthogonal Latin squares (for a prime p, positive integers m and an integer $a\ne 2,6$). Lastly, in [21], $(\rho \alpha ,\alpha ,\rho )$ FR codes with $\beta =1$ are constructed from transversal designs for $3\le \rho \le \alpha +1$. Furthermore, $\left(\right(s+1\left)\right(st+1),t+1,s+1)$ FR codes with $\beta =1$ are constructed from generalized quadrangles for $2\le s\le t$. These two classes of FR codes are optimal for selected parameters satisfying the conditions in [21].

The FR codes constructed from Steiner systems [15] support the number of data symbols equal to or slightly larger than the MBR capacity in (1). This means that the file size of the FR codes from Steiner systems shows a considerable gap from the upper bound of the FR capacity because any two rows of the incidence matrix of a Steiner system always have a collision [21]. On the other hand, in the incidence matrices of the proposed FR codes, there is no collision for some pairs of rows based on our analysis, and this property can make the proposed FR codes closer to optimal with respect to the FR capacity bound.

In this paper, we first propose new three constructions of $(q^2-1,q,q)$, $(p^2,p,p)$ and $(4^l,2^l,2^l)$ FR codes based on relative difference sets with parameters $(q+1,q-1,q,1)$, $(p,p,p,1)$ and $(2^l,2^l,2^l,1)$, respectively, where q is a prime power, p is an odd prime or $p=4$ and l is a positive integer. Especially, $(8,3,3)$ and $(9,3,3)$ FR codes are optimal, that is, they meet the FR capacity bound in [15] for all k. We show via theoretical derivations and numerical analysis that the proposed FR codes are (near) optimal for some parameters in terms of the FR capacity bound. Finally, for various numbers of nodes, we modify the proposed $(q^2-1,q,q)$ FR codes using decimation by a factor of the code length $q^2-1$, which also gives us new good FR codes. It is noted that some examples are already shown for small-valued parameter sets in [16], but we propose a systematic construction method of FR codes for the whole of the parameter sets based on well-organized mathematical structures unlike the algorithm-based search in [16]. It is also noted that the proposed FR codes can be seen as a part of the general class of FR code constructed from group divisible design (GDD) [19,20]. However, the contribution of this work is to explicitly provide three construction methods directly based on relative difference sets and m-sequences, propose a modification method from the three constructions to generate a new class of FR codes and analyze them in detail, while the basic idea and general framework are given in [19,20].

This paper is organized as follows. In Section 2, the basic definitions and notations are presented. The proposed FR codes are presented in Section 3. Additionally, we provide the characteristics of the proposed scheme and numerical results. In Section 4, we propose a modification method for Construction 1. Finally, we conclude this paper in Section 5.

2. Preliminaries

2.1. Regenerating Codes and Fractional Repetition Codes

In this paper, we assume that every node stores the same amount of data symbols. To clearly define regenerating codes and FR codes, we follow the notations in [21].

An ${(n,k,d,M,\alpha ,\beta )}_q$ regenerating code for $k\le d\le n-1$ and $\beta \le \alpha$ is defined as follows. The number of nodes and the number of information data symbols that need to be stored in DSS are denoted by n and M, respectively, and the symbols are in the finite field ${\mathbb{F}}_q$ of q elements. Each node stores $\alpha$ symbols. The parameter k is called the reconstruction degree, which means that a data collector can reconstruct all the stored information data by connecting to any k nodes and downloading $\alpha$ symbols from each node. A failed node is repaired by connecting to any d other nodes and downloading $\beta$ symbols from each node. With this notation, the repair bandwidth becomes $d\beta$. We assume $\beta =1$ for the code construction throughout paper as in [11], which can be simply expanded to the case of $\beta >1$. It is noted that this expansion does not cover all the FR codes for $\beta >1$ [18]. For MBR codes with $\beta =1$, d is equal to $\alpha$, and the number of data symbols to be stored in DSS is given as:

$$M=k\alpha -\left(\genfrac{}{}{0pt}{}{k}{2}\right),$$

(1)

which is called the MBR capacity.

In [18], the $\beta$-recoverability and FR codes are formally defined as follows.

Definition 1.

Let $\mathsf{\Omega }=\left[\theta \right]$ and $N_i$, $i=1,\dots ,d$ be subsets of Ω. Let $N=\{N_1,\dots ,N_d\}$, and consider $A\subset \mathsf{\Omega }$ with $\left|A\right|=d\beta$. We say that A is β-recoverable from N if there exist $B_i\subseteq N_i$ for each $i=1,\dots ,d$ such that $B_i\subset A$, $\left|B_i\right|=\beta$ and ${\cup }_{i=1}^d{B}_i=A$ [18].

Definition 2.

(FR codes [18]) An $(n,\alpha ,\rho )$ FR code $C=(\mathsf{\Omega },N)$ with repetition degree ρ and normalized repair bandwidth $\beta =\alpha /d$ (α and β are positive integers) is a set of n subsets $N=\{N_1,\dots ,N_n\}$ of a symbol set $\mathsf{\Omega }=\left[\theta \right]$ with the following properties.

1. 

The cardinality of each $N_i$ is α.

2. 

Each element of Ω is contained in exactly ρ sets in N.

3. 

Let $N^{surv}$ denote any $(n-\tau )$-sized subset of N and $N^{fail}=N\setminus N^{surv}$. Each $N_j\in N^{fail}$ is β-recoverable from some d-sized subset of $N^{surv}$. Let ${\rho }_{res}$ be the maximum value of τ such that this property holds.

Note that an $(n,\alpha ,\rho )$ FR code $\mathcal{C}$ satisfies $n\alpha =\rho \theta$. The parameter $\rho$ is called the repetition degree of $\mathcal{C}$. The incidence matrix of $\mathcal{C}$, denoted by $I\left(\mathcal{C}\right)$, is defined by the $n\times \theta$ binary matrix whose $(i,j)$ element is one if the set $N_i$ includes data symbol j or zero, otherwise. It is noted that the row and column weights of $I\left(\mathcal{C}\right)$ are $\alpha$ and $\rho$, respectively. An FR code can be used as an inner code together with an outer $(\theta ,M)$ maximum distance separable (MDS) code. This concatenated code is called distributed replication-based exact simple storage (DRESS) code with parameters $\left[\right(\theta ,M),k,(n,\alpha ,\rho \left)\right]$ [23]. According to an FR code $\mathcal{C}$, node i, $i=1,\dots ,n$, stores the data symbols in $N_i$. Figure 1 illustrates an example of a $\left[\right(\theta ,M),k,(n,\alpha ,\rho \left)\right]$ DRESS code.

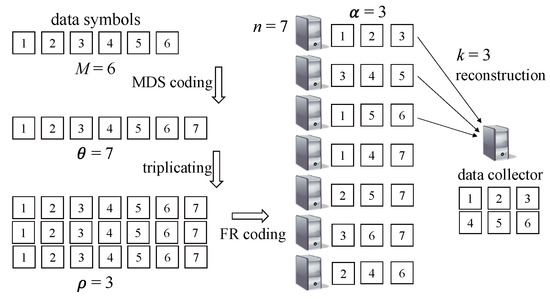
Figure 1. Structure of a $\left[\right(7,6),3,(7,3,3\left)\right]$ distributed replication-based exact simple storage (DRESS) code.

For a given FR code, the maximum number of information data symbols M to be stored in DSS is determined as a function of k as:

$$M\left(k\right)=\underset{\genfrac{}{}{0pt}{}{I\subset \{1,\dots ,n\}}{\left|I\right|=k}}{\min }\left|{\cup }_{i\in I}{N}_i\right|.$$

(2)

It is addressed in [15] that for a well-constructed FR code, $M\left(k\right)$ can be larger than the MBR capacity, that is,

$$M\left(k\right)\ge k\alpha -\left(\genfrac{}{}{0pt}{}{k}{2}\right)$$

holds for FR codes. For given parameters $(n,k,\alpha ,\rho )$, the FR capacity, denoted by $A(n,k,\alpha ,\rho )$, is defined as the maximum value of $M\left(k\right)$ among all FR codes with the parameters.

An upper bound for FR capacity was derived in [15] as:

$$A(n,k,\alpha ,\rho )\le \varphi \left(k\right)$$

where:

$$\varphi \left(1\right)=\alpha ,\varphi (k+1)=\varphi \left(k\right)+\alpha -⌈\frac{\rho \varphi \left(k\right)-k\alpha }{n-k}⌉.$$

(3)

Capacity-achieving FR codes were constructed for some parameters in [21], but the FR capacity is unknown in general. An FR code is called k-optimal if $M\left(k\right)=A(n,k,\alpha ,\rho )$. Furthermore, an FR code is called optimal if for any $k\le \alpha$, it is k-optimal [21].

2.2. Relative Difference Sets and q-Ary m-Sequences

Let G be a group of order $uv$ under an operation *, and let N be a normal subgroup of order u. Then, a $(v,u,w,\lambda )$ relative difference set (RDS) in G relative to N is defined as a subset D with w elements of the group G such that the multiset of $w(w-1)$ elements given by $\{d_1\ast d_2^{-1}|d_1,d_2\in D$ such that $d_1\ne d_2\}$ contains every element of $G\backslash N$ exactly $\lambda$ times and no element in N [24,25]. The parameters of RDSs satisfy the following equation:

$$w(w-1)=u(v-1)\lambda .$$

If G is a cyclic group, D is called a cyclic RDS. If $u=1$, D becomes a $(v,w,\lambda )$ difference set. That is, a $(v,w,\lambda )$ difference set is defined as a subset D with w elements of a group G with v elements such that the set of $w(w-1)$ elements given by $\{d_1\ast d_2^{-1}|d_1,d_2\in D$ such that $d_1\ne d_2\}$ contains every element of $G\backslash \left\{0\right\}$ exactly $\lambda$ times.

Let D be an RDS with parameters $(v,u,w,\lambda )$ given as $D=\{d_0,\cdots ,d_{w-1}\}$, where $d_0,\cdots ,d_{w-1}$ are elements in G. It is easy to check the following lemmas. Even though it is not difficult to derive it, we provide proofs for clear understanding.

Lemma 1.

If D is an RDS, then its right coset $D\ast b$ is also an RDS for $b\in G$.

Proof. 

Let $D\ast b=\{d_0\ast b,\cdots ,d_{w-1}\ast b\}$. By the definition, for $d_i,d_j\in D$, $i\ne j$, $d_i\ast d_j^{-1}=d_i\ast (b\ast b^{-1})\ast d_j^{-1}=(d_i\ast b)\ast {(d_j\ast b)}^{-1}$ becomes all elements in $G\backslash N$ exactly $\lambda$ times, when i and j vary for all elements in D. ☐

Lemma 2.

For cosets $D\ast b_1$ and $D\ast b_2$ of an RDS D, we have $|D\ast b_1\cap D\ast b_2|=\lambda$ if $b_1^{-1}\ast b_2$ is not in N. Otherwise, $|D\ast b_1\cap D\ast b_2|=0$.

Proof. 

Common elements of $D\ast b_1$ and $D\ast b_2$ are given as $d_i\ast b_1=d_j\ast b_2$ for some $i,j$. By the definition of RDS, $d_j^{-1}\ast d_i=b_2\ast b_1^{-1}$ covers all elements in $G\backslash N$. ☐

Let $F_q$ denote the finite field with $q=p^e$ elements, where p is a prime and e is a positive integer. The trace function from $F_{q^n}$ into $F_q$ is defined as:

$${\mathrm{tr}}_1^n\left(x\right)=\sum _{i=0}^{n-1}{x}^{q^i}.$$

(4)

Then, a q-ary m-sequence $s\left(t\right)$ of period $q^n-1$ is defined as:

$$s\left(t\right)={\mathrm{tr}}_1^n\left({\xi }^t\right),0\le t<q^n-1$$

(5)

where $\xi$ denotes a primitive element of $F_{q^n}$.

It is well-known that the q-ary m-sequence has the balance property, which means that zero appears $q^{n-1}-1$ times and each of the non-zero element in $F_q$ appears $q^{n-1}$ times in a period.

The $\delta$-homogeneous function from $F_{q^n}$ to $F_q$ is introduced by Klapper [26], which is defined as $H\left(xy\right)=y^{\delta }H\left(x\right)$ for any $x\in F_{q^n}$ and $y\in F_q$. Then, Kim et al. constructed an RDS from a $\delta$-homogeneous function on $F_{q^n}^{\ast }$ [27]. In addition, a function $f\left(x\right)$ is said to be difference-balanced if the difference function $f\left(xz\right)-f\left(x\right)$ is balanced for any $z\in F_{q^n}\backslash \{0,1\}$.

Theorem 1 ([27]).

Let q be a prime power and n a positive integer. If $f\left(x\right)$ is a δ-homogeneous function on $F_{q^n}^{*}$ over $F_q$ with difference-balanced property, where δ is relatively prime to $q^n-1$, then the set $D_f=\left\{x\right|f\left(x\right)=\zeta ,x\in F_{q^n}^{\ast },foragiven\zeta \in F_q^{\ast }\}$ is a cyclic RDS with parameters $(\frac{q^n-1}{q-1},q-1,q^{n-1},q^{n-2})$ in the multiplicative group $F_{q^n}^{\ast }$ relative to its normal subgroup $F_q^{\ast }$.

It is clear that for $n=2$, the trace function defined in (4) is a one-homogeneous function because we have ${\mathrm{tr}}_1^2\left(xy\right)=y{\mathrm{tr}}_1^2\left(x\right)$ for $y\in F_q$ and $x\in F_{q^2}$. Therefore, from a q-ary m-sequence of period $q^2-1$, we can construct a cyclic RDS with parameters $(q+1,q-1,q,1)$.

Example 1.

For $p=3$, let α be a primitive element of $F_{3^2}$. Then, a relative difference set with parameters $(4,2,3,1)$ is given as $D=\{1,\alpha ,{\alpha }^3\}$. It is easy to check that $d_1\ast d_2^{-1}$ for any two distinct elements $d_1,d_2\in D$ can cover only once all elements in $F_{3^2}\backslash F_3$.

3. The Proposed FR Codes

In this section, we construct new classes of FR codes with parameters $(q^2-1,q,q)$, $(p^2,p,p)$ and $(4^l,2^l,2^l)$ based on the cyclic RDS with parameters $(q+1,q-1,q,1)$ constructed from the q-ary m-sequences, the non-cyclic RDS with parameters $(p,p,p,1)$ and the non-cyclic RDS with parameters $(2^l,2^l,2^l,1)$, respectively, for a prime power q, an odd prime p or $p=4$ and a positive integer l. Furthermore, it is demonstrated that these codes are (near) optimal for some parameters with respect to the FR capacity bound in (3).

3.1. Construction of FR Codes from RDSs

First, we propose a general construction method of FR codes based on the RDSs with parameters $(v,u,w,1)$. Since the relative difference sets with $\lambda =1$ are equivalent to a class of group divisible design (GDD), the proposed FR codes can be seen to originate from the common framework, which exploits the incidence matrix of a combinatorial design to construct an FR code. Particularly, the incidence matrix of a balanced incomplete block design (BIBD) or a GDD can be directly used as the incidence matrix of the corresponding FR code. Thus, the incidence matrix of an FR code can be directly constructed from a given RDS, and the general construction method is a result of this process.

Let $G=\{g_0,g_1,\dots ,g_{uv-1}\}$ be a group of order $uv$ under an operation ∗, and let N be a normal subgroup of order u. Furthermore, let D be an RDS with parameters $(v,u,w,1)$ in G relative to N. Then, an incidence matrix of FR code is constructed from D as:

$$I\left(\mathcal{C}\right)={\left[\begin{array}{c}{c}_{i,j}\end{array}\right]}_{0\le i,j<uv}$$

(6)

whose $(i,j)$ element is given as:

$$c_{i,j}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{g}_j\in D\ast g_i\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

This is our basic method to construct three classes of FR codes from RDSs, which will be explicitly given as follows. It is noted that the GDDs corresponding to the proposed FR codes are symmetric, and more general parameter sets of the symmetric GDDs are found in [28]. Suppose that the i-th row of $I\left(\mathcal{C}\right)$ is denoted by $c_i=(c_{i,0},\cdots ,$$c_{i,uv-1})$ for $0\le i<uv$. For any pair of rows $c_{i_1}$ and $c_{i_2}$ in $I\left(\mathcal{C}\right)$, we will say that there is a collision if $c_{i_1,j}=c_{i_2,j}=1$ for some j, $0\le j<uv$.

Construction 1.

Define a map ${\mu }_{\zeta }(·)$ from $F_q$ to $F_2$ for $\zeta \in F_q^{\ast }$ as:

$${\mu }_{\zeta }\left(l\right)=\left\{\begin{array}{cc}1,\hfill & l=\zeta \hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

(7)

Furthermore, we define a binary sequence $b_{\zeta }\left(t\right)={\mu }_{\zeta }\left(s\left(t\right)\right)$ for the q-ary m-sequence $s\left(t\right)$ of period $q^2-1$. Then, a cyclic RDS with parameters $(q+1,q-1,q,1)$ in $Z_{q^2-1}=\{0,1,\dots ,q^2-2\}$ relative to $N=\{0,1(q+1),\dots ,(q-2\left)\right(q+1\left)\right\}$ is obtained as $D=\left\{t\right|b_{\zeta }\left(t\right)=1,0\le t<q^2-1\}$. According to the general construction method, we propose new $(q^2-1,q,q)$ FR codes $\mathcal{C}$ whose incidence matrices $I\left(\mathcal{C}\right)$ have the form:

$$I\left(\mathcal{C}\right)={\left[\begin{array}{c}{c}_{i,j}\end{array}\right]}_{0\le i,j<q^2-1}$$

(8)

where:

$$c_{i,j}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}j\in D+i\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

and $D+i=\{t+i|t\in D\}$ for $0\le i<q^2-1$.

Note that the cyclic RDS with parameters $(q+1,q-1,q,1)$ in Construction 1 is equivalent to the RDS with the same parameters from Theorem 1. The first row corresponds to the binary sequence $\mu$-mapped from the q-ary m-sequence of period $q^2-1$ in (5). We call this sequence the characteristic sequence of the corresponding RDS. Each of the other rows is cyclically shifted to the right by one position from the row above it. The size of $I\left(\mathcal{C}\right)$ is $(q^2-1)\times (q^2-1)$, which means that the length of the FR code $\mathcal{C}$ is $n=q^2-1$ and the parameter $\theta$ is also $q^2-1$. It is easily shown from the balance property of the q-ary m-sequence that the row and column weights are q, that is, $\alpha =\rho =q$.

Example 2.

A ternary m-sequence $s\left(t\right)$ of period eight is generated as

$$\left(s\right(0\left)s\right(1\left)s\right(2)\cdots s(7\left)\right)=\left(11012202\right).$$

For $\zeta =1$, we have an RDS with parameters $(4,2,3,1)$ as $D=\{0,1,3\}$, and its characteristic sequence is given as:

$$(b_1\left(0\right)b_1\left(1\right)b_1\left(2\right)\cdots b_1\left(7\right))=\left(11010000\right).$$

Then, the incidence matrix of the $(8,3,3)$ FR code $\mathcal{C}$ is given as:

$$I\left(\mathcal{C}\right)=\left[\begin{array}{c}11010000\\ 01101000\\ 00110100\\ 00011010\\ 00001101\\ 10000110\\ 01000011\\ 10100001\end{array}\right].$$

(9)

We can see that the row and column weights are $q=3$.

Example 3.

A 5-ary m-sequence of period 24 is generated as:

$$\left(s\right(0\left)s\right(1)\cdots s(23\left)\right)=\left(131033212011424022343044\right).$$

For $\zeta =1$, we have an RDS with parameters $(6,4,5,1)$ as $D=\{0,2,7,10,11\}$, and its characteristic sequence is given as:

$$(b_1\left(0\right)b_1\left(1\right)\cdots b_1\left(23\right))=\left(101000010011000000000000\right).$$

In the same way as the ternary case, the $24\times 24$ incidence matrix of the corresponding $(24,5,5)$ FR code is constructed using cyclic shift, and its row and column weights are $q=5$.

Example 4.

A 4-ary m-sequence of period 15 is generated as:

$$(s\left(0\right)\cdots s\left(14\right))=\left(10\gamma \gamma 1\gamma 0{\gamma }^2{\gamma }^2\gamma {\gamma }^{2}011{\gamma }^2\right)$$

where γ is a primitive element of $F_4$ with the primitive polynomial $x^2+x+1$ and $F_{16}$ is an extended field of $F_4$ by $x^2+x+\gamma$. For $\zeta =1$, we have:

$$(b_1\left(0\right)\cdots b_1\left(14\right))=\left(100010000000110\right).$$

Then, the incidence matrix of the $(15,4,4)$ FR code $\mathcal{C}$ is given as:

$$I\left(\mathcal{C}\right)=\left[\begin{array}{c}100010000000110\\ 010001000000011\\ ⋮\\ 000100000001101\end{array}\right]$$

(10)

where the row and column weights are $q=4$.

Remark 1.

In [18], the resolvable FR code is defined as follows. Let $\mathcal{C}=(\mathsf{\Omega },V)$ where $V=\{V_1,\dots ,V_n\}$ is an FR code. A subset $P\subset V$ is said to be a parallel class if for $V_i\in P$ and $V_j\in P$ with $i\ne j$, we have $V_i\cap V_j=\varnothing$ and ${\cup }_{\{j:V_j\in P\}}{V}_j=\mathsf{\Omega }$. A partition of V into r parallel classes is a resolution. If there exists at least one resolution, then the code is called a resolvable FR code. It is clear that the FR codes from the first construction are not resolvable because q is not a factor of $q^2-1$, while the FR codes from the net in [18] are always resolvable. This is evidence that the proposed construction is not a proper subset of the constructions in [18].

In 1966, Elliott and Butson [25] constructed non-cyclic RDSs with parameters $(p^n,p,p^n,p^{n-1})$ and $(4,4,4,1)$, where p is an odd prime. Using those RDSs, we can construct FR codes with parameters $(p^2,p,p)$ and $(16,4,4)$, respectively.

In the following description, the symbol ⊕ means the direct sum, and $Z_p$ denotes the additive group of integers modulo p. Let $G_n$ be the elementary Abelian p-group of order $p^n$ with identity zero, whose elements are expressed as n-tuples of elements of $Z_p$. Then, the RDS can be constructed as in the following theorem.

Theorem 2 ([25]).

Let $G=Z_p\oplus G_n$, and let $N=Z_p\oplus \left\{\mathbf{0}\right\}$. For $a_i\not\equiv 0\left(\mathrm{mod}p\right)$, $i=1,\cdots ,n$,

$$D=\left\{(f\left(m\right),m)\right|m=(m_1,m_2,\cdots ,m_n)\in G_n\}$$

is an RDS with parameters $(p^n,p,p^n,p^{n-1})$ of G relative to N, where $f\left(m\right)={\sum }_{i=1}^n{a}_i{m}_i^2\left(\mathrm{mod}p\right)$.

Since we are interested in the case of $\lambda =1$, we only use the RDSs in Theorem 2 for the case of $n=1$. In this case, we can simplify $f\left(m\right)$ as $f\left(m\right)=a_1{m}^2\left(\mathrm{mod}p\right)$ for $m\in Z_p$, and we have the RDS D with parameters $(p,p,p,1)$, whose elements are given as $\left(f\right(m),m)$.

Note that there is no explicit ordering among elements in the RDS D. However, for the construction of FR codes, we will use the arbitrary order of elements in D, for example, a lexicographic order i defined as $i=f\left(m\right)\times p+m$ for $m\in Z_p$, which is in the range between zero and $p^2-1$. Thus, construction of new FR codes by using the RDSs in Theorem 2 is given as follows.

Construction 2.

Let D be a non-cyclic RDS with parameters $(p,p,p,1)$, where p is an odd prime or four. For $(i_1,i_2),(j_1,j_2)\in G$, we have lexicographic orders $i=p\times i_1+i_2$ and $j=p\times j_1+j_2$. According to the general construction method, we propose new $(p^2,p,p)$ FR codes $\mathcal{C}$ whose incidence matrices $I\left(\mathcal{C}\right)$ have the form given by:

$$I\left(\mathcal{C}\right)={\left[\begin{array}{c}{c}_{i,j}\end{array}\right]}_{0\le i,j<p^2}$$

(11)

whose $(i,j)$ element is given as:

$$c_{i,j}=\left\{\begin{array}{cc}1,\hfill & if(j_1,j_2)\in D+(i_1,i_2)\hfill \\ 0,\hfill & otherwise\hfill \end{array}\right.$$

where $D+(i_1,i_2)=\left\{(d_1+i_1,d_2+i_2)\right|(d_1,d_2)\in D\}$.

In the following examples, we provide incidence matrices for FR codes with parameters $(9,3,3)$, $(16,4,4)$ and $(25,5,5)$.

Example 5.

Let $p=3$, $n=1$ and $a_1=1$. Then, we have $Z_3=\{0,1,2\}$ and $G=Z_3\oplus Z_3$. The RDS D with parameters $(3,3,3,1)$ is given as $D=\left\{\right(f\left(m\right),m\left)\right|m\in \{0,1,2\}\}$, where $f\left(m\right)=m^2\left(\mathrm{mod}3\right)$. That is, we have $D=\left\{\right(0,0),(1,1),(1,2\left)\right\}$. Then, we have the following cosets of D for all elements in $G=Z_3\oplus Z_3$ as:

$$\begin{array}{cc}\hfill D+(0,0)& =\left\{\right(0,0),(1,1),(1,2\left)\right\}\hfill \\ \hfill D+(0,1)& =\left\{\right(0,1),(1,2),(1,0\left)\right\}\hfill \\ \hfill D+(0,2)& =\left\{\right(0,2),(1,0),(1,1\left)\right\}\hfill \\ \hfill D+(1,0)& =\left\{\right(1,0),(2,1),(2,2\left)\right\}\hfill \\ \hfill D+(1,1)& =\left\{\right(1,1),(2,2),(2,0\left)\right\}\hfill \\ \hfill D+(1,2)& =\left\{\right(1,2),(2,0),(2,1\left)\right\}\hfill \\ \hfill D+(2,0)& =\left\{\right(2,0),(0,1),(0,2\left)\right\}\hfill \\ \hfill D+(2,1)& =\left\{\right(2,1),(0,2),(0,0\left)\right\}\hfill \\ \hfill D+(2,2)& =\left\{\right(2,2),(0,0),(0,1\left)\right\}.\hfill \end{array}$$

By using a lexicographic order, we can obtain the following incidence matrix for a $(9,3,3)$ FR code as:

$$I\left(\mathcal{C}\right)=\left[\begin{array}{c}100011000\\ 010101000\\ 001110000\\ 000100011\\ 000010101\\ 000001110\\ 011000100\\ 101000010\\ 110000001\end{array}\right].$$

Note that the proposed $(9,3,3)$ FR code meets the FR capacity bound in (3), that is, it is an optimal FR code with parameters $(9,3,3)$.

Example 6.

An RDS with parameters $(4,4,4,1)$ can be obtained as $D=\left\{\right(0,0),(0,1),(1,3),(3,0\left)\right\}$ of $G=Z_4\oplus Z_4$ and the forbidden normal subgroup $2Z_4\oplus 2Z_4$ [29]. By using a lexicographic order, we can similarly obtain the following incidence matrix for a $(16,4,4)$ FR code as:

$$I\left(\mathcal{C}\right)=\left[\begin{array}{c}1001100000000100\\ 1100010000000010\\ 0110001000000001\\ 0011000100001000\\ 0100100110000000\\ 0010110001000000\\ 0001011000100000\\ 1000001100010000\\ 0000010010011000\\ 0000001011000100\\ 0000000101100010\\ 0000100000110001\\ 1000000001001001\\ 0100000000101100\\ 0010000000010110\\ 0001000010000011\end{array}\right].$$

Example 7.

Let $p=5$, $n=1$ and $a_1=1$. Then, we have $Z_5=G_1=\{0,1,2,3,4\}$. Then, the RDS D with parameters $(5,5,5,1)$ is given as $D=\left\{\right(0,0),(1,1),(4,2),(4,3),(1,4\left)\right\}$, which corresponds to the first row of the proposed incidence matrix when we use a lexicographic order. The remaining rows can be obtained by adding all elements in $G=Z_5\oplus Z_5$ just as in the previous examples. Then, a $(25,5,5)$ FR code is obtained by using a lexicographic order.

In the third construction, we utilize the Galois ring $GR(4,l)$, which is a local ring with maximum ideal $2GR(4,l)$. Hou and Sehgal proposed a semi-regular RDS from the Galois ring [30], where the semi-regular RDSs satisfy $k=\lambda v$. It is known that $GR{(4,l)}^{\ast }$, the group of units, contains a unique cyclic subgroup $T^{\ast }$ of order $2^l-1$, and $T=T^{\ast }\cup \left\{0\right\}$ is called the Teichmuller set of $GR(4,l)$. Then, each element $a\in GR(4,l)$ has a unique two-adic representation $a=x_0+2x_1$, where $x_0,x_1\in T$. The Frobenius map $\sigma :GR(4,l)\to GR(4,l):x_0+2x_1\to x_0^2+2x_1^2(x_0,x_1\in T)$ is an automorphism of $GR(4,l)$ of order l. The relative trace of $GR(4,l)$ is the map $Tr:GR(4,l)\to Z_4$ defined by $Tr\left(a\right)={\sum }_{i=0}^{l-1}{\sigma }^i\left(a\right)$. Let W be a finite Abelian group and $h:W\to T$ any function with $\left|W\right|=r$. Let $G=GR(4,l)\times W$ and:

$$D={\cup }_{w\in W}((1+2h\left(w\right))T,w)\subset G.$$

Then, R is a semi-regular RDS in G relative to $N=2GR(4,l)\times \left\{0\right\}$. It should be noted that the cardinality of W is related to $\lambda$. Thus, to construct RDS with $\lambda =1$, we only consider the case of $G=GR(4,l)$ and $N=2GR(4,l)$. Then,

$$D=(1+2h)T$$

(12)

is a non-cyclic RDS with parameters $(2^l,2^l,2^l,1)$, where h is an element in T and l is a positive integer.

To assign the proper order to each element in $GR(4,l)$, we denote $T=\{0,1,\beta ,{\beta }^2,\cdots ,{\beta }^{2^l-2}\}=\{T_0,T_1,T_2,\cdots ,T_{2^l-1}\}$, where each element in each set has component-wise correspondence. Then, an element of $GR(4,l)$ is indexed as $a_{i\times 2^l+j}=T_j+2T_i$ for $T_i,T_j\in T$.

Construction 3.

Let D be a non-cyclic RDS with parameters $(2^l,2^l,2^l,1)$, where l is a positive integer. According to the general construction method, we propose new $(4^l,2^l,2^l)$ FR codes C whose incidence matrices $I\left(C\right)$ have the form given by:

$$I\left(\mathcal{C}\right)={\left[\begin{array}{c}{c}_{i,j}\end{array}\right]}_{0\le i,j<4^{l}r}$$

(13)

where:

$$c_{i,j}=\left\{\begin{array}{cc}1,\hfill & if{a}_j\in D+a_i\hfill \\ 0,\hfill & otherwise\hfill \end{array}\right.$$

and $D+a_i=\{a_t+a_i|a_t\in D\}$.

In the following examples, we provide the incidence matrix for FR codes with parameters (16,4,4).

Example 8.

For $GR(4,2)$, the Teichmuller set is given as:

$$T=\{0,1,\beta ,{\beta }^2\}$$

where β is a root of $g\left(x\right)=x^2+x+1$. Then, all elements of $GR(4,2)$ are given as:

$$\begin{array}{cc}\hfill GR(4,2)& =\{0,1,\beta ,{\beta }^2,2,3,\beta +2,{\beta }^2+2,2\beta ,1+2\beta ,3\beta ,{\beta }^2+2\beta ,2{\beta }^2,1+2{\beta }^2,\beta +2{\beta }^2,3{\beta }^2\}\hfill \\ & =\{a_0,a_1,a_2,a_3,a_4,a_5,a_6,a_7,a_8,a_9,a_{10},a_{11},a_{12},a_{13},a_{14},a_{15}\}\hfill \end{array}$$

and $2GR(4,2)=\{0,2,2\beta ,2{\beta }^2\}$.

Therefore, $\left|N\right|=\left|2GR\right(4,2\left)\right|=4$ and $\left|G\right|=vu=4^2$, i.e., $v=2^2$. Since it is a semi-regular RDS ($k=\lambda v$), we have $k=v=2^{2}r$ for the case of $\lambda =1$. Because h in (12) is an arbitrary element in T, we set $h=\beta$. Thus, a semi-regular RDS D is given as $D=(1+2\beta )T=\{0,1+2\beta ,\beta +2{\beta }^2,{\beta }^2+2\}$, which is a $(4,4,4,1)$ RDS. We can apply the proposed ordering to construct a $(16,4,4)$ FR code as follows:

$$I\left(\mathcal{C}\right)=\left[\begin{array}{c}1000000101000010\\ 0101000000001010\\ 0110100100000000\\ 0011000011000000\\ 0001100000100100\\ 0000010110100000\\ 1001011000000000\\ 0000001100001100\\ 0100001010000001\\ 0000101001010000\\ 0000000001101001\\ 1100000000110000\\ 0010010000011000\\ 1010000000000101\\ 0000000010010110\\ 0000110000000011\end{array}\right].$$

3.2. Properties of the Proposed FR Codes

In this subsection, we will investigate how good the number of data symbols $M\left(k\right)$ to be stored in DSS is in terms of the upper bound of the FR capacity in (3) for the proposed FR codes. To this end, some properties of the incidence matrices of the proposed FR codes are given in the following theorems. From Lemma 2, it is easy to prove the following property of $(q^2-1,q,q)$ FR codes from Construction 1.

Theorem 3.

Let $c_{i_1}$ and $c_{i_2}$ be the $i_1$-th and $i_2$-th rows in $I\left(\mathcal{C}\right)$ of the proposed FR codes from Construction 1, where $i_1\ne i_2$ and $0\le i_1,i_2<q^2-1$. Then, the inner product of $c_{i_1}$ and $c_{i_2}$ is given as:

$$\begin{array}{c}\hfill c_{i_1}·c_{i_2}=\left\{\begin{array}{cc}0,\hfill & if{i}_2-i_1\equiv 0(\mathrm{mod}q+1)\hfill \\ 1,\hfill & otherwise.\hfill \end{array}\right.\end{array}$$

Proof. 

Let $G=Z_{q^2-1}$ and $N=\{0,1(q+1),\dots ,(q-2\left)\right(q+1\left)\right\}$ denote the corresponding cyclic group and the normal subgroup, respectively. From Lemma 2, since $|(D+i_1)\cap (D+i_2)|=0$ for $i_2-i_1\equiv 0(\mathrm{mod}q+1)$, two rows $c_{i_1}$ and $c_{i_2}$ are orthogonal to each other. Otherwise, from $|D{g}^{i_1}\cap D{g}^{i_2}|=1$, we have $c_{i_1}·c_{i_2}=1$. ☐

That is, for any pair of two rows in $I\left(\mathcal{C}\right)$, there is no collision or only one collision.

Similarly, we have the property of FR codes from Construction 2 as follows.

Theorem 4.

Let $c_i$ and $c_j$ be the i-th and j-th rows in $I\left(\mathcal{C}\right)$ of the proposed FR codes from Construction 2, where i and j are the lexicographic orders of $(i_1,i_2)$ and $(j_1,j_2)$, respectively, for $i\ne j$, $0\le i,j<p-1$. Then, the inner product of $c_i$ and $c_j$ is given as:

$$c_i·c_j=\left\{\begin{array}{cc}0,\hfill & if{i}_2=j_2\hfill \\ 1,\hfill & otherwise.\hfill \end{array}\right.$$

Proof. 

From Lemma 2, since $|[D+(i_1,i_2)]\cap [D+(j_1,j_2)]|=0$ for $i_2-j_2=0$, two rows $c_i$ and $c_j$ are orthogonal to each other. Otherwise, from $|[D+(i_1,i_2)]\cap [D+(j_1,j_2)]|=1$, we have $c_i·c_j=1$. ☐

That is, for any pair of two rows in $I\left(\mathcal{C}\right)$, there is no collision or only one collision. Actually, $M\left(k\right)$ of the proposed FR codes is very close to the FR capacity bound and greater than or equal to the MBR bound, which are shown via the following theorem and numerical analysis as below.

Theorem 5.

The number of data symbols to be stored in the proposed FR codes satisfies $M\left(k\right)\ge kq-\left(\genfrac{}{}{0pt}{}{k}{2}\right)$.

Proof. 

The MBR capacity $M\left(k\right)=kq-\left(\genfrac{}{}{0pt}{}{k}{2}\right)$ is found when every pair of rows among k rows chosen from the incidence matrix of an FR code has exactly one collision. Equation (2) says that $M\left(k\right)$ can be strictly larger than the MBR capacity if some pairs of rows have no collision and the other pairs have one collision. The incidence matrices of the proposed FR codes satisfy the above condition for a given k, and thus, $M\left(k\right)$ of the proposed FR codes is larger than or equal to the MBR capacity. ☐

Figure 2 demonstrates the number of data symbols $M\left(k\right)$ of the proposed FR codes with parameters $(8,3,3)$, $(9,3,3)$, $(15,4,4)$, $(16,4,4)$, $(24,5,5)$ and $(25,5,5)$. We cannot find any existing FR code whose parameters are the same as the proposed ones, and thus, we plot the MBR capacity and the FR capacity bound $\varphi \left(k\right)$ in (3). We can see that the $(8,3,3)$ and $(9,3,3)$ FR codes are optimal because they achieve the FR capacity bound for all k. The $(15,4,4)$, $(16,4,4)$, $(24,5,5)$ and $(25,5,5)$ FR codes do not exactly achieve the FR capacity bound, but the gaps become smaller; thus, it deserves to be called FR capacity-approaching.

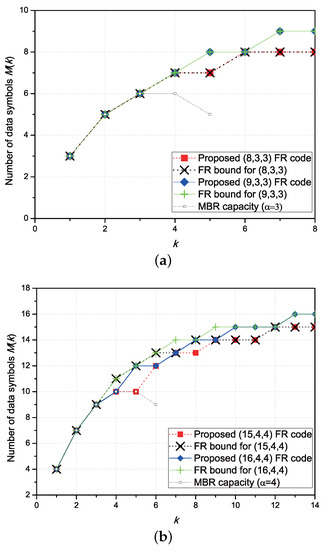
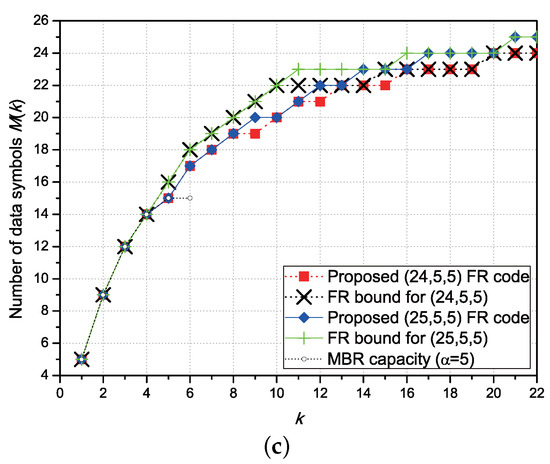
Figure 2. Comparison of the number of data symbols to be stored in the proposed fractional repetition (FR) codes with the minimum bandwidth regenerating (MBR) capacity and the FR capacity bound. (a) $(8,3,3)$ and $(9,3,3)$ FR codes; (b) $(15,4,4)$ and $(16,4,4)$ FR codes; (c) $(24,5,5)$ and $(25,5,5)$ FR codes.

4. Modification of the Proposed FR Codes

In this section, we propose a modification method for the proposed FR codes from Construction 1 to support various numbers of storage nodes. It is trivial to obtain irregular incidence matrices from the regular ones by selecting some of the rows in the matrices, where “regular” means that all the rows in the incidence matrix have a constant Hamming weight and so do all the columns; otherwise, it is called “irregular”. Thus, we propose a method to obtain regular incidence matrices from larger regular incidence matrices.

Thus, by decimating an incidence matrix of Construction 1 in (13) by a decimation factor r, we have r$(n/r)\times (n/r)$ matrices as follows.

Construction 4.

The $(n/r)\times (n/r)$ incidence matrix for FR codes can be derived by decimating rows and columns of the original $n\times n$ incidence matrix in Construction 1 by a factor r of $q+1$ as:

$$I(\mathcal{C},r,h)=\left[\begin{array}{c}{c}_{i,j}^{\left(h\right)}\end{array}\right]$$

(14)

where $c_{i,j}^{\left(h\right)}=b_{\zeta }(r(i+j)+h\mathrm{mod}{q}^2-1)$ for $0\le i,j\le n/r-1$ and $0\le h\le r-1$.

Then, for the sub-incidence matrices in (14), we can determine parameters $\alpha =\rho$ as in the following theorem.

Theorem 6.

In Construction 4, for $r\left|\right(q+1)$, there are $(r-1)$ sub-incidence matrices of size $n/r\times n/r$ with Hamming weights of rows and columns $(q+1)/r$ and a sub-incidence matrix of the same size with Hamming weights of rows and columns $(q+1)/r-1$.

Proof. 

Let $t=t_{1}T+t_2$, where $T=q+1$, $0\le t_1<q-1$ and $0\le t_2<q+1$. Then, we have:

$$\begin{array}{cc}\hfill {\mathrm{tr}}_1^2\left({\xi }^t\right)& ={\mathrm{tr}}_1^2\left({\xi }^{t_{1}T+t_2}\right)\hfill \\ & ={\xi }^{t_{1}T}{\mathrm{tr}}_1^2\left({\xi }^{t_2}\right)\hfill \end{array}$$

(15)

where $\xi$ is a primitive element of $F_{q^2}$. From (15), an m-sequence $s\left(t\right)$ can be two-dimensionally represented as:

$$\left[\begin{array}{cccc}{\xi }^{0·T}{\mathrm{tr}}_1^2\left({\xi }^0\right)& {\xi }^0{\mathrm{tr}}_1^2\left({\xi }^1\right)& \cdots & {\xi }^0{\mathrm{tr}}_1^2\left({\xi }^q\right)\\ {\xi }^T{\mathrm{tr}}_1^2\left({\xi }^0\right)& {\xi }^T{\mathrm{tr}}_1^2\left({\xi }^1\right)& \cdots & {\xi }^T{\mathrm{tr}}_1^2\left({\xi }^q\right)\\ ⋮& ⋮& \ddots & ⋮\\ {\xi }^{(q-2)T}{\mathrm{tr}}_1^2\left({\xi }^0\right)& {\xi }^{(q-2)T}{\mathrm{tr}}_1^2\left({\xi }^1\right)& \cdots & {\xi }^{(q-2)T}{\mathrm{tr}}_1^2\left({\xi }^q\right)\end{array}\right].$$

(16)

Note that each column in (16) contains all non-zero elements in $F_q$ since ${\xi }^T$ is a primitive element of $F_q$ except for one zero column such that ${\mathrm{tr}}_1^2\left({\xi }^{t_2}\right)=0$. Therefore, when applying the binary mapping $\mu$ in (7), there is only one “1” in each column except for the zero column. Note that the zero column occurs at $t_2=(q+1)/2$ since ${\mathrm{tr}}_1^2\left({\xi }^{t_2}\right)={\xi }^{t_2}+{\xi }^{q{t}_2}=0$, that is, ${\xi }^{(q-1)t_2}=-1$.

Decimating by r, where $r\left|\right(q+1)$, we only select some columns in (16) with $t_2\equiv h\left(\mathrm{mod}r\right)$ for a sub-sequence $b_{\zeta }(rt+h)$. Then, among r sub-sequences, only a sub-matrix for $h\equiv (q+1)/2\left(\mathrm{mod}r\right)=h^{\prime }$ has the all-zero column, and the others do not have the zero element. Since each element of $F_q^{\ast }$ occurs once and if we select $n/r$ columns, the decimated sub-sequences have $(q+1)/r$ ones (i.e., $\alpha =(q+1)/r$) except for one sub-sequence, which contains the zero column with $(q+1)/r-1$ ones (i.e., $\alpha =(q+1)/r-1$). Since we will construct each row of $I(\mathcal{C},r,h)$ by cyclically shifting $b_{\zeta }\left(t\right)$, we have $\rho =(q+1)/r$ for $r-1$ sub-incidence matrices and $\rho =(q+1)/r-1$ for $I(\mathcal{C},r,h^{\prime })$. ☐

In addition, it is easy to see that the decimated incidence matrices inherit the same property in Theorem 3 as the original incidence matrices as follows.

Theorem 7.

The decimated incidence matrices $I(\mathcal{C},r,h)$ of the proposed FR codes have the following properties. Let $c_{i_1}$ and $c_{i_2}$ be two distinct rows in $I(\mathcal{C},r,h)$, where $i_1\ne i_2$ and $0\le i_1,i_2<q^2-1$. Then, the inner product of $c_{i_1}$ and $c_{i_2}$ is given as:

$$c_{i_1}·c_{i_2}=\left\{\begin{array}{cc}0,\hfill & if{i}_2-i_1\equiv 0(\mathrm{mod}(q+1)/r)\hfill \\ 1,\hfill & otherwise.\hfill \end{array}\right.$$

Proof. 

Since the decimated incidence matrices $I(\mathcal{C},r,h)$ are generated from the original $I\left(\mathcal{C}\right)$, it is not possible to have more than one collision in any pair of two rows in $I(\mathcal{C},r,h)$. In addition, the decimation factor r is a factor of $q+1$, and two rows $c_{i_1}$ and $c_{i_2}$ with $i_2-i_1\equiv 0(\mathrm{mod}q+1)$ in the original $I\left(\mathcal{C}\right)$ are always included in the same $I(\mathcal{C},r,h)$. ☐

From Theorem 7, the following property straightforwardly holds.

Corollary 1.

The number of data symbols to be stored in the proposed FR codes satisfies $M\left(k\right)\ge k(q+1)/r-\left(\genfrac{}{}{0pt}{}{k}{2}\right)$.

As an example, we present the incidence matrix of the $(24,4,4)$ FR code as follows.

Example 9.

A seven-ary m-sequence of period 48 is generated as:

$$\left(s\right(0\left)s\right(1)\cdots s(47\left)\right)=\left(104366463052445420165515603411314025332350612262\right).$$

For $\zeta =1$, we have an RDS with parameters $(8,6,7,1)$ as $D=\{0,18,22,28,29,31,43\}$, and its characteristic sequence is given as:

$$\begin{array}{c}\hfill (b_1\left(0\right)b_1\left(1\right)\cdots b_1\left(47\right))=\left(100000000000000000100010000011010000000000010000\right).\end{array}$$

Decimating $b_1\left(t\right)$ by a factor $r=2$, we have:

$$(b_1^{\prime }\left(0\right)b_1^{\prime }\left(1\right)\cdots b_1^{\prime }\left(23\right))=\left(100000000101001000000000\right).$$

In the same way as the previous examples, the $24\times 24$ incidence matrix of the corresponding $(24,4,4)$ FR codes is constructed using cyclic shift and its row and column weights are $\alpha =\rho =4$.

The number of data symbols $M\left(k\right)$ of the $(24,4,4)$ FR code in Example 9 is presented with respect to k in Figure 3. Note that in this example, we can obtain another FR code with the same code length of 24 given in Figure 2c. However, they have different $\rho$ and $\alpha$ such as $\alpha =\rho =4$ and $\alpha =\rho =5$, respectively. Note that there is some deviation between the upper bound in (3) and $M\left(k\right)$ of the proposed one in Figure 3. Remember that since (3) is the upper bound, there is no guarantee that the bound is the same as the actual capacity of FR codes. However, for the low k’s, which are less than $\rho$ or $\alpha$, we can see that the proposed FR code can achieve the capacity as in Figure 2a–c and Figure 3.

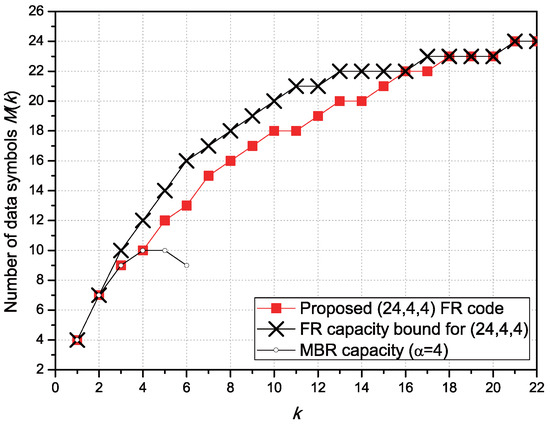
Figure 3. Comparison of the number of data symbols to be stored in the proposed (24, 4, 4) FR codes with the MBR capacity and the FR capacity bound with the same size.

In Table 1, we list possible parameters from Constructions 1–4. As you can see, there are the same parameters from the distinct original m-sequences. However, even though they have the same parameters $(n,\alpha ,\rho )$, this does not mean that the incidence matrices are equivalent. For example, we can obtain the same parameters $(12,2,2)$ from $(24,5,5)$ for $q=5$ and from $(48,7,7)$ for $q=7$. However, the former has the binary sequence $\left(000101000000\right)$, and the later has the binary sequence $\left(100000010000\right)$ by decimation. It is easy to see that we cannot obtain the later binary sequence by cyclically shifting the former binary sequence. That is, they are distinct instances with the same parameters.

Table 1. Possible parameters obtained from the proposed constructions in Constructions 1–4 (decimation).

q or l	Original $(\mathit{n},\mathit{\alpha },\mathit{\rho })$	Decimated $(\mathit{n},\mathit{\alpha },\mathit{\rho })$	Construction
$l=1$	$(4,2,2)$		3
$q=3$	$(8,3,3)$	$(4,2,2)$	1
	$(9,3,3)$	-	2
$q=4$	$(15,4,4)$	−	1
	$(16,4,4)$	-	2
$l=2$	$(16,4,4)$		3
$q=5$	$(24,5,5)$	$(12,3,3)$, $(12,2,2)$, $(8,2,2)$	1
	$(25,5,5)$	-	2
$q=7$	$(48,7,7)$	$(24,4,4)$, $(24,3,3)$, $(12,2,2)$	1
	$(49,7,7)$	-	2
$l=3$	$(64,8,8)$		3
$q=8$	$(63,8,8)$	$(21,3,3)$	1
$q=9$	$(80,9,9)$	$(40,5,5)$, $(40,4,4)$, $(16,2,2)$	1
$q=11$	$(120,11,11)$	$(60,6,6)$, $(60,5,5)$, $(40,4,4)$, $(40,3,3)$, $(20,2,2)$	1
	$(121,11,11)$	-	2

5. Concluding Remarks

In this paper, new constructions of FR codes with parameters $(q^2-1,q,q)$, $(p^2,p,p)$ and $(16,4,4)$ are proposed, where q is a prime power and p is an odd prime. The proposed FR codes are constructed from RDSs with $\lambda =1$. It turns out that the proposed FR codes are near optimal with respect to the FR capacity bound, and especially, the proposed $(8,3,3)$ and $(9,3,3)$ FR codes are optimal with respect to the FR capacity bound. It is noted that there is no conventional FR codes whose parameters are the same as the proposed ones, and thus, the proposed construction enriches choices of parameters for FR code design. Finally, we also provide a modification method for the proposed incidence matrices to adapt various requirement of the number of storage nodes.