EXONEST: The Bayesian Exoplanetary Explorer
Abstract
:1. Introduction
2. EXONEST
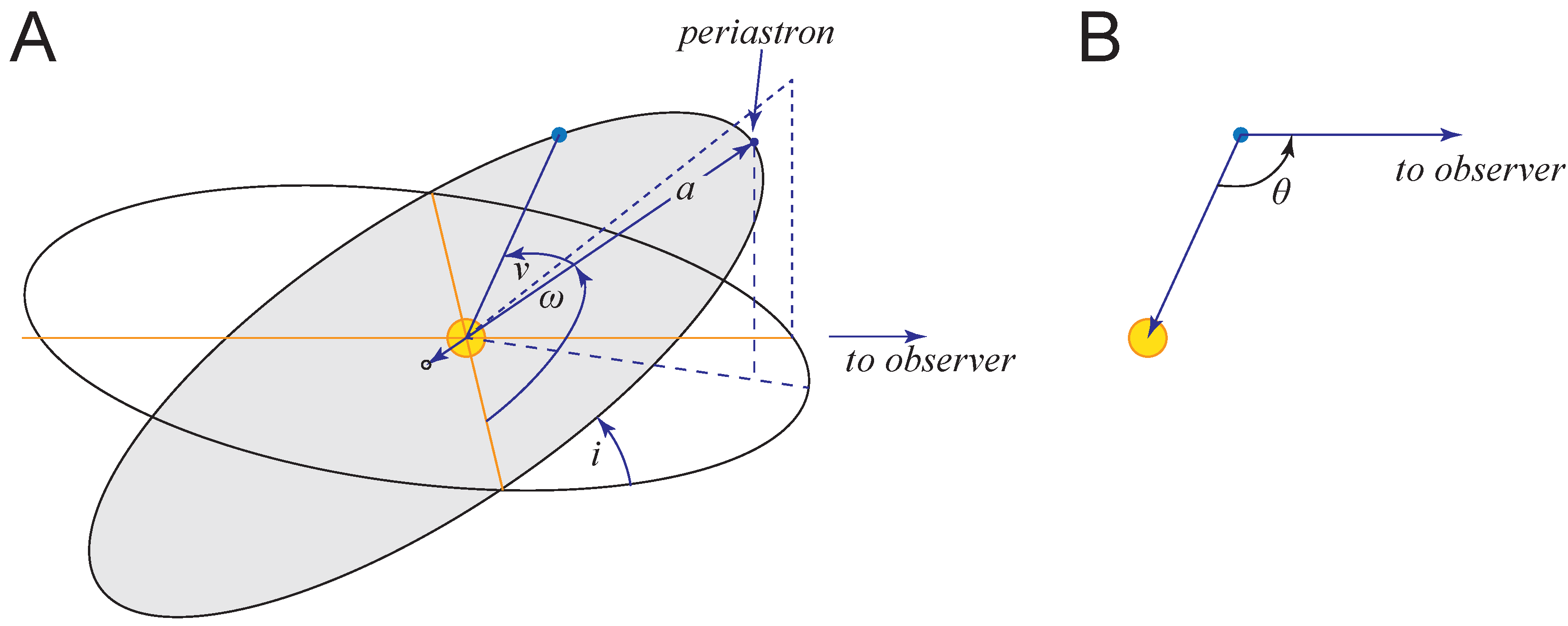
3. Orbital Models
4. Photometric Effects
4.1. Transits and Eclipses
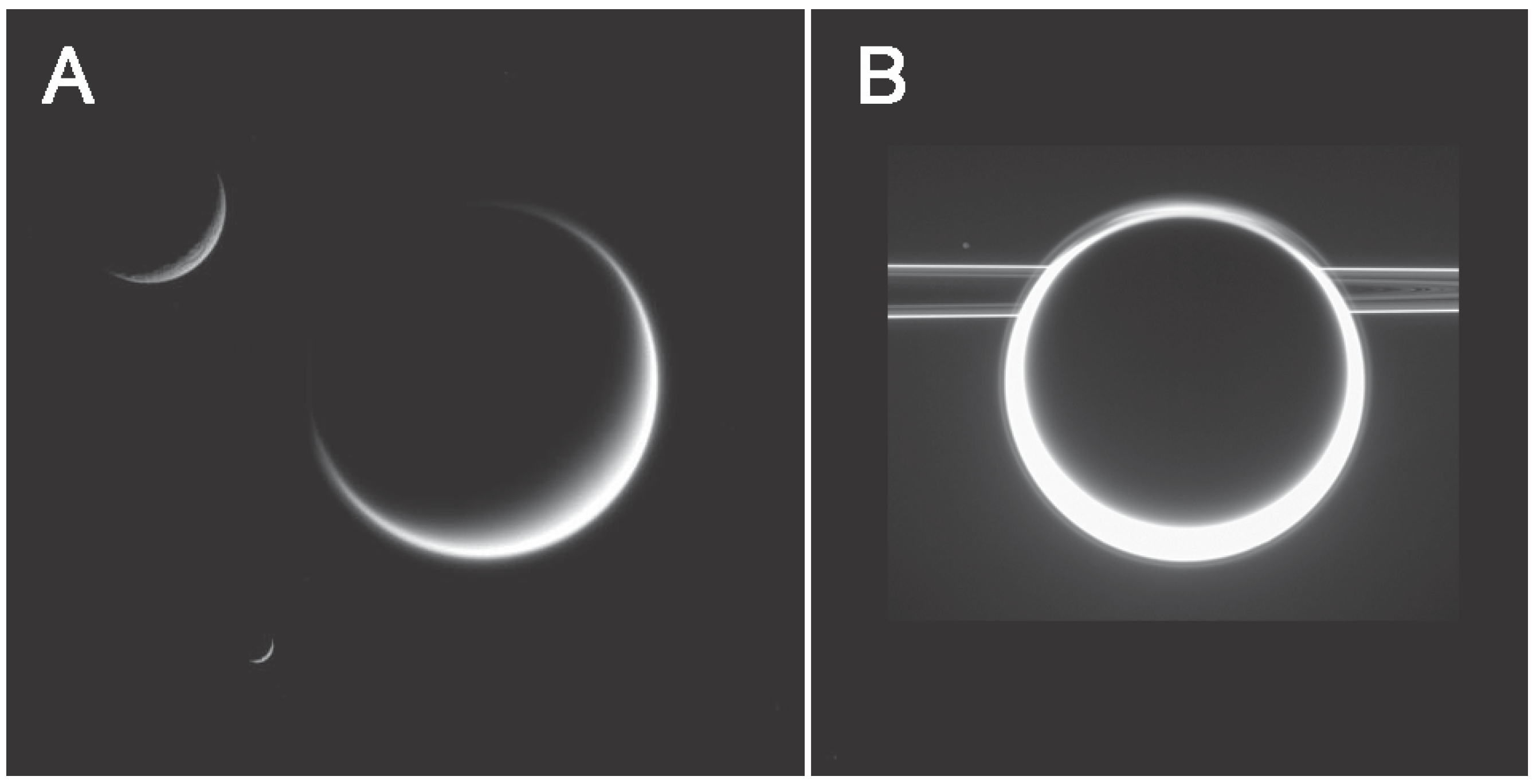
4.2. Reflected Light
New Efforts to Properly Model Reflected Light
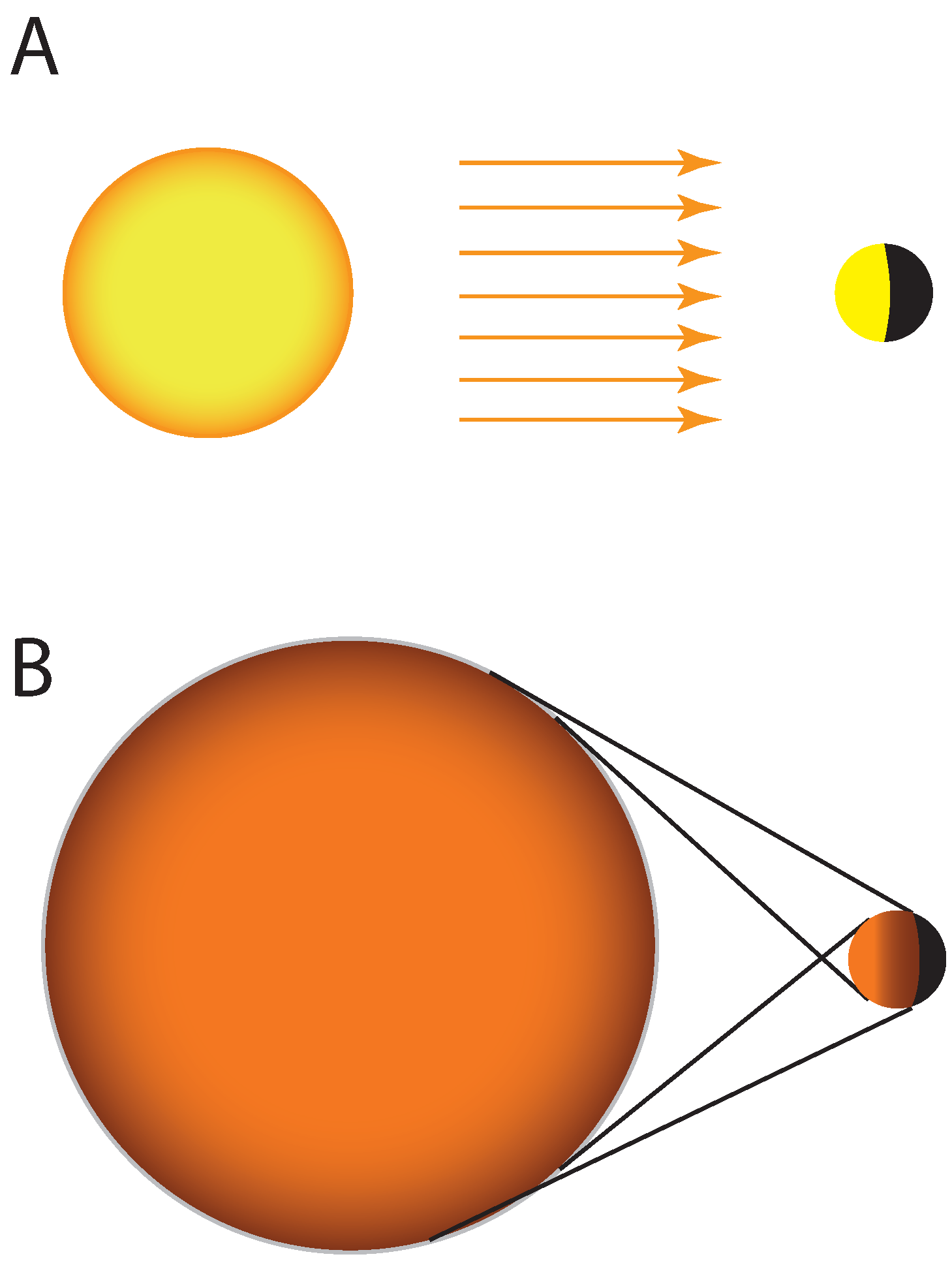
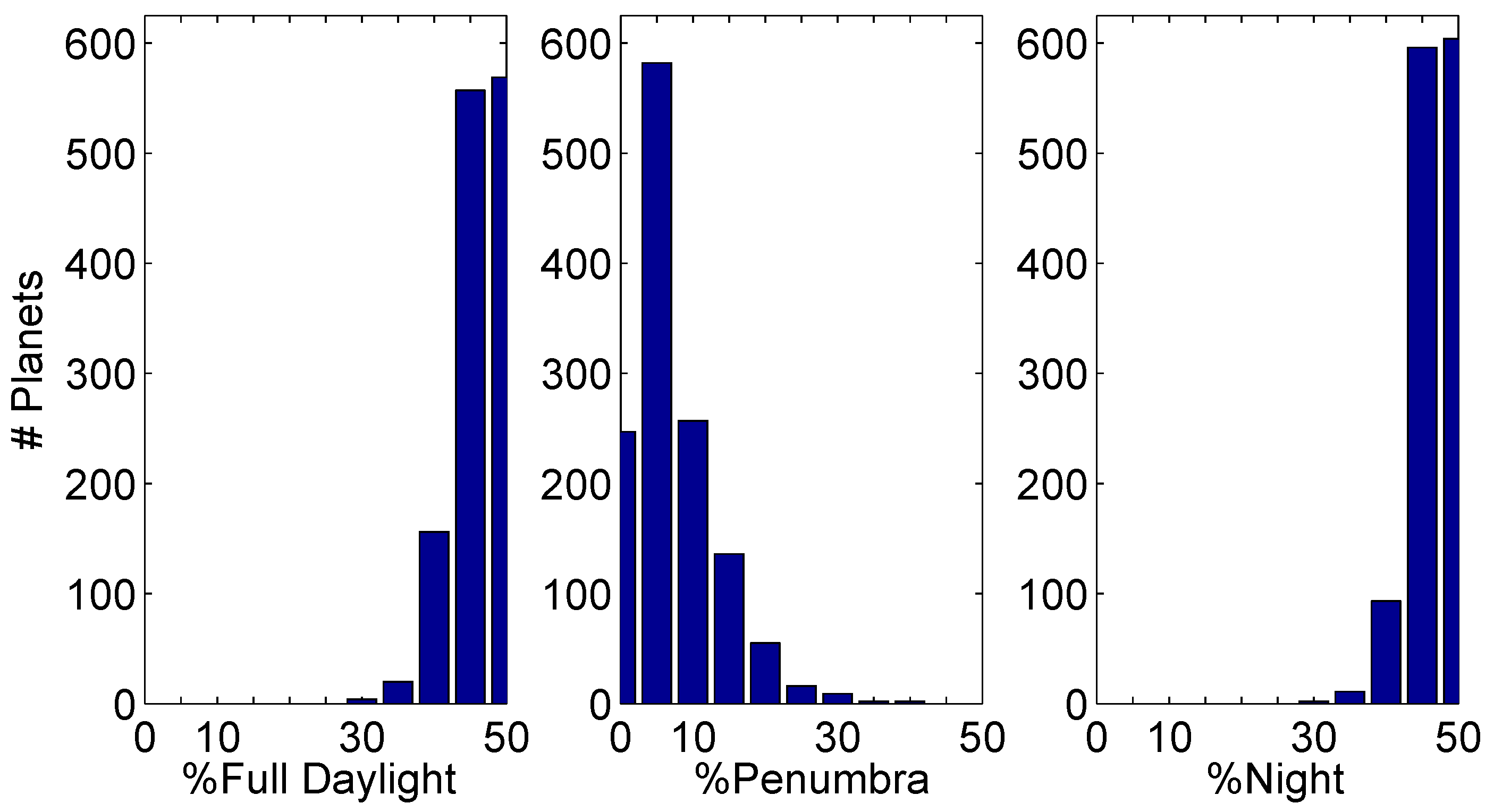
4.3. Thermal Emissions
4.4. New Efforts to Model Refracted and Forward Scattered Light
4.5. New Efforts to Model Atmospheric Effects
4.6. Doppler Boosting/Beaming
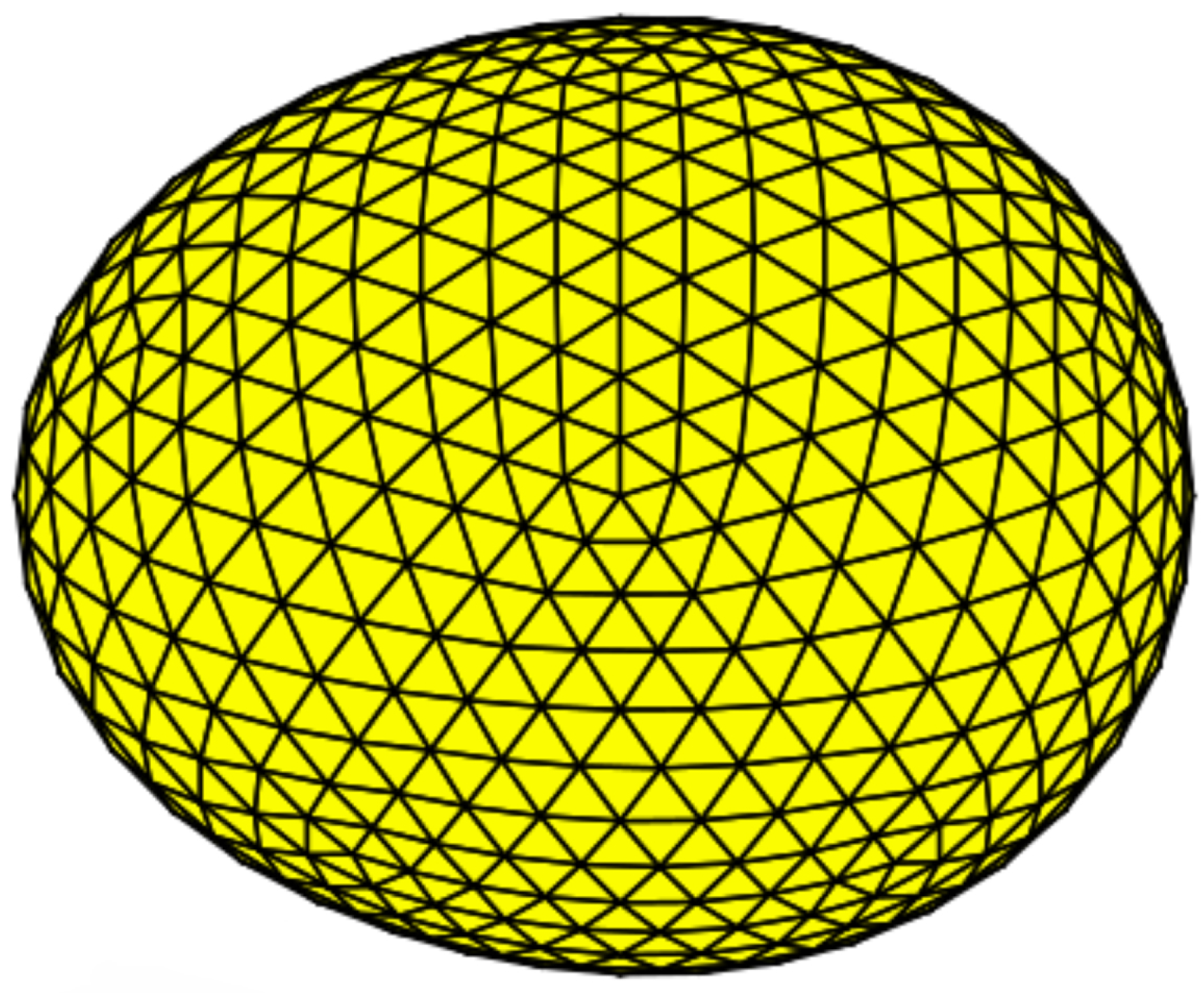
4.7. Tidal Forces and Ellipsoidal Variations
4.7.1. Trigonometric Models
4.7.2. Direct Modeling: EVIL-MC
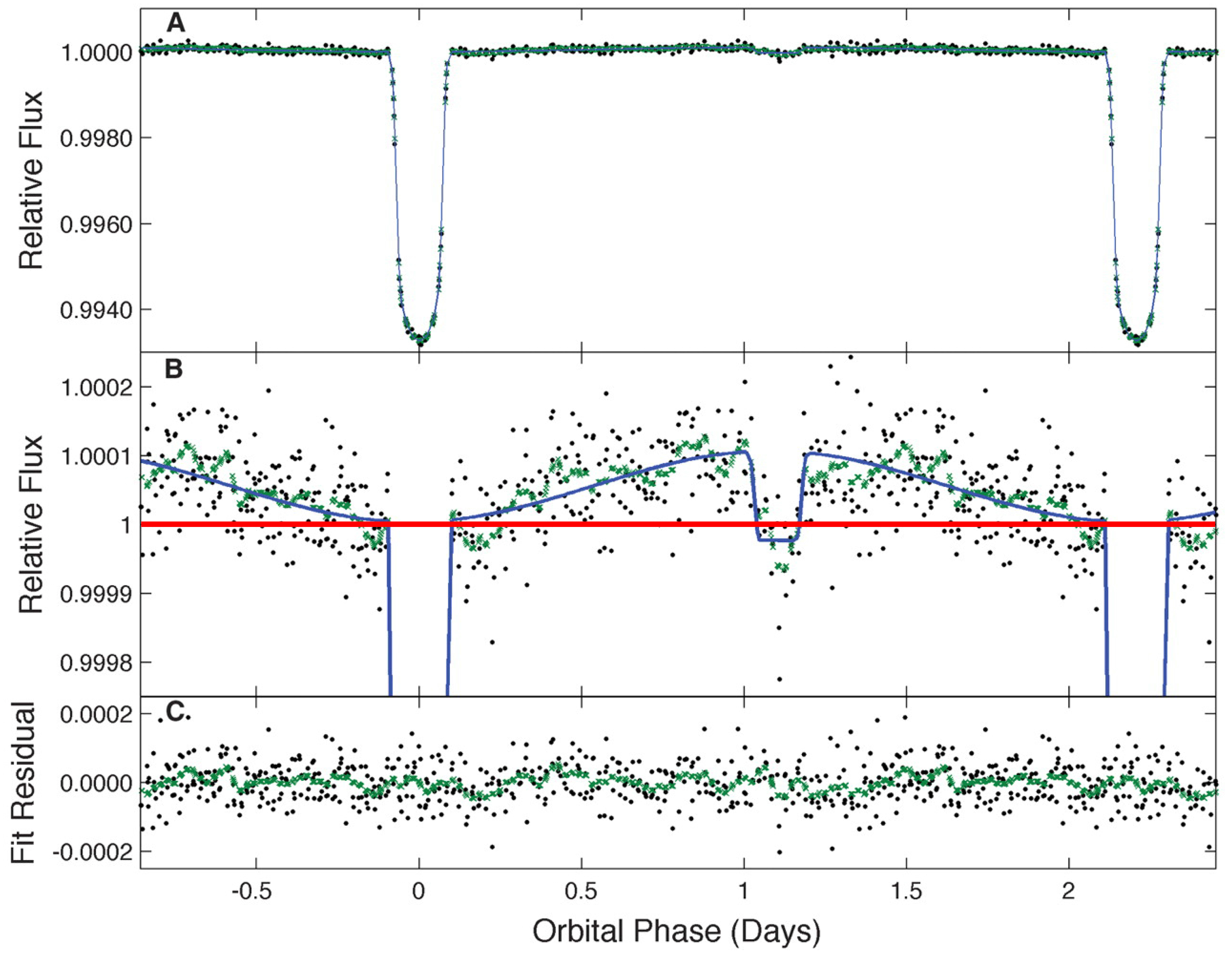
4.7.3. Model Testing
5. Bayesian Inference Engine
Priors and Likelihoods
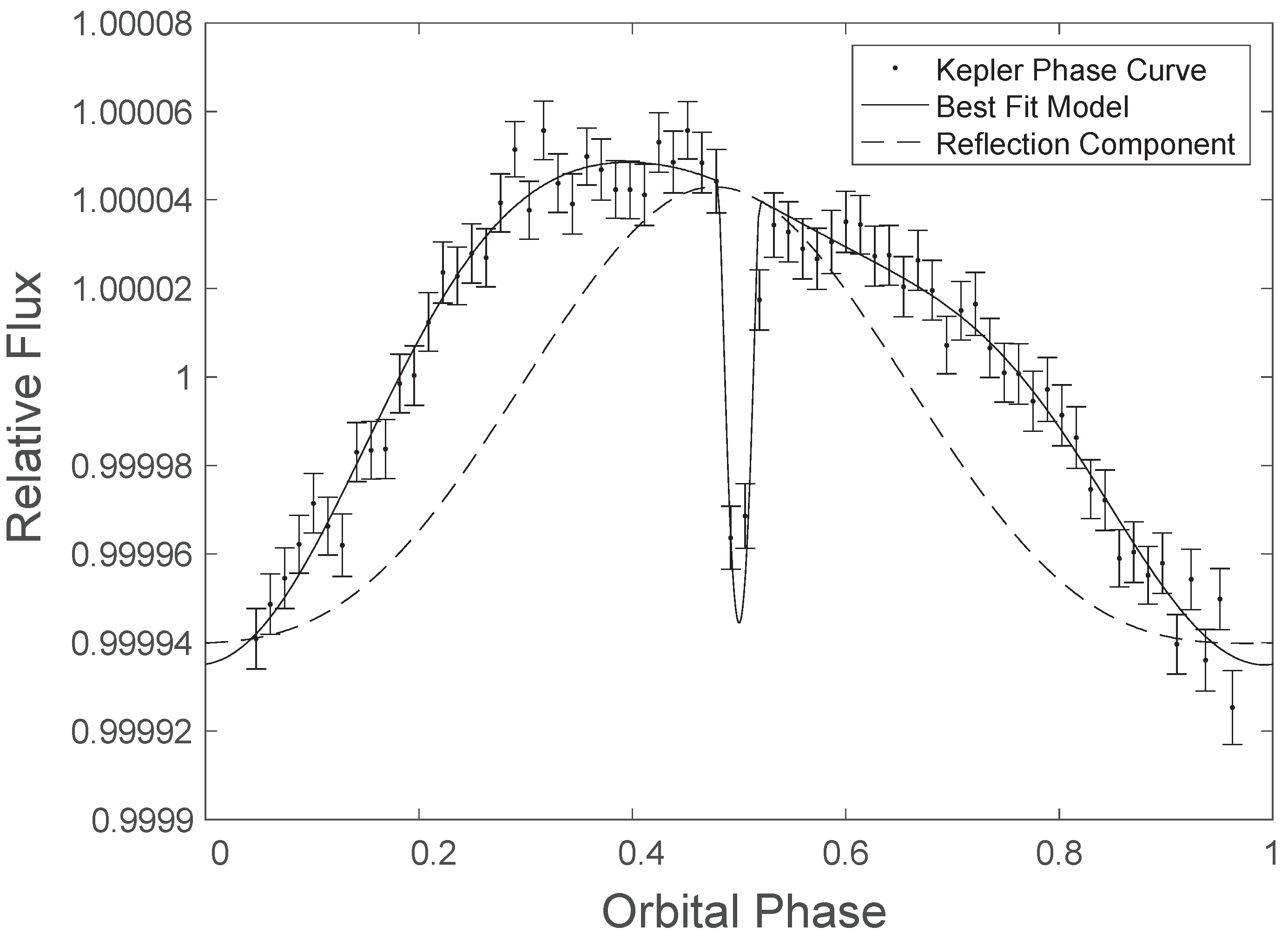
6. Application: Kepler-76b
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- NASA. NASA Strategic Plan 2014; The National Aeronautics and Space Administration: Washington, DC, USA, 2014.
- Caltech. NASA Exoplanet Archive. Available online: https://exoplanetarchive.ipac.caltech.edu/ (accessed on 1 August 2017).
- Borucki, W.J.; Koch, D.; Basri, G.; Batalha, N.; Brown, T.; Caldwell, D.; Caldwell, J.; Christensen-Dalsgaard, J.; Cochran, W.D.; DeVore, E.; et al. Kepler Planet-Detection Mission: Introduction and First Results. Science 2010, 327, 977–980. [Google Scholar] [CrossRef] [PubMed]
- Ricker, G.R.; Latham, D.W.; Vanderspek, R.K.; Ennico, K.A.; Bakos, G.; Brown, T.M.; Burgasser, A.J.; Charbonneau, D.; Clampin, M.; Deming, L.D.; et al. Transiting Exoplanet Survey Satellite (TESS). Bull. Am. Astron. Soc. 2010, 42, 459. [Google Scholar]
- Placek, B.; Knuth, K.H.; Angerhausen, D. Combining photometry from Kepler and TESS to improve short-period exoplanet characterization. Publ. Astron. Soc. Pac. 2016, 128, 074503. [Google Scholar] [CrossRef]
- Beichman, C.; Benneke, B.; Knutson, H.; Smith, R.; Lagage, P.O.; Dressing, C.; Latham, D.; Lunine, J.; Birkmann, S.; Ferruit, P.; et al. Observations of transiting exoplanets with the James Webb Space Telescope (JWST). Publ. Astron. Soc. Pac. 2014, 126, 1134. [Google Scholar] [CrossRef]
- Placek, B.; Angerhausen, D.; Knuth, K.H. Optimizing Observing Strategies for Exoplanet Secondary Eclipses and Phase Curves. Astrophys. J. 2017, in press. [Google Scholar]
- ESA. Science and Technology: CHEOPS. Available online: http://sci.esa.int/cheops/ (accessed on 30 September 2016).
- CHEOPS Science Team—University of Bern. CHEOPS Mission Homepage. Available online: http://cheops.unibe.ch/ (accessed on 28 March 2017).
- Broeg, C.; Fortier, A.; Ehrenreich, D.; Alibert, Y.; Baumjohann, W.; Benz, W.; Deleuil, M.; Gillon, M.; Ivanov, A.; Liseau, R.; et al. CHEOPS A Transit Photometry Mission for ESA’s Small Mission Programme. EPJ Web Conf. 2013, 47. [Google Scholar] [CrossRef]
- ESA. Science and Technology: PLATO. Available online: http://sci.esa.int/plato/ (accessed on 30 September 2016).
- ESA Study Team; PLATO Science Study Team. PLATO Science Study Team. PLATO Science Requirements Document. In ESA Public Documents; ESA Study Team; PLATO Science Study Team, 2010. [Google Scholar]
- Hippke, M.; Angerhausen, D. Photometry’s Bright Future: Detecting Solar System Analogs with Future Space Telescopes. Astrophys. J. 2015, 810, 29. [Google Scholar] [CrossRef]
- NASA. Wide Field Infrared Survey Telescope. Available online: https://wfirst.gsfc.nasa.gov/index.html (accessed on 29 October 2016).
- Placek, B.; Knuth, K.H.; Angerhausen, D. EXONEST: Bayesian model selection applied to the detection and characterization of exoplanets via photometric variations. Astrophys. J. 2014, 795, 112. [Google Scholar] [CrossRef]
- Placek, B. Bayesian Detection and Characterization of Extra-Solar Planets via Photometric Variations. Ph.D. Thesis, University at Albany (SUNY), Albany, NY, USA, 2014. [Google Scholar]
- Skilling, J. Nested sampling. In Bayesian Inference and Maximum Entropy Methods in Science and Engineering, Garching, Germany 2004; Fischer, R., Dose, V., Preuss, R., von Toussaint, U., Eds.; American Institute of Physics (AIP): New York, NY, USA, 2004; pp. 395–405. [Google Scholar]
- Skilling, J. Nested sampling for general Bayesian computation. Bayesian Anal. 2006, 1, 833–859. [Google Scholar] [CrossRef]
- Sivia, D.S.; Skilling, J. Data Analysis. A Bayesian Tutorial, 2nd ed.; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Feroz, F.; Hobson, M.P.; Bridges, M. MultiNest: An efficient and robust Bayesian inference tool for cosmology and particle physics. Mon. Not. R. Astron. Soc. 2009, 398, 1601–1614. [Google Scholar] [CrossRef]
- Feroz, F.; Balan, S.T.; Hobson, M.P. Detecting extrasolar planets from stellar radial velocities using Bayesian evidence. Mon. Not. R. Astron. Soc. 2011, 415, 3462–3472. [Google Scholar] [CrossRef]
- Feroz, F.; Hobson, M.P.; Cameron, E.; Pettitt, A.N. Importance nested sampling and the MultiNest algorithm. arXiv, 2013; arXiv:1306.2144. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equations of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Brown, R.A. Photometric orbits of extrasolar planets. Astrophys. J. 2009, 702, 1237. [Google Scholar] [CrossRef]
- Borucki, W.J.; Koch, D.; Jenkins, J.; Sasselov, D.; Gilliland, R.; Batalha, N.; Latham, D.W.; Caldwell, D.; Basri, G.; Brown, T.; et al. Kepler’s Optical Phase Curve of the Exoplanet HAT-P-7b. Science 2009, 325, 709. [Google Scholar] [CrossRef] [PubMed]
- Seager, S.; Mallěn-Ornelas, G. A unique solution of planet and star parameters from an extrasolar planet transit light curve. Astrophys. J. 2003, 585, 1038. [Google Scholar] [CrossRef]
- Mandel, K.; Agol, E. Analytic light curves for planetary transit searches. Astrophys. J. Lett. 2002, 580, L171. [Google Scholar] [CrossRef]
- Borucki, W.J.; Summers, A.L. The photometric method of detecting other planetary systems. Icarus 1984, 58, 121–134. [Google Scholar] [CrossRef]
- Barnes, J.W. Effects of Orbital Eccentricity on Extrasolar Planet Transit Detectability and Light Curves. Publ. Astron. Soc. Pac. 2007, 119, 986. [Google Scholar] [CrossRef]
- Jaynes, E.T. Probability Theory: The Logic of Science; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Gregersen, E. The Milky Way and Beyond: Stars, Nebulae, and Other Galaxies; The Rosen Publishing Group: New York, NY, USA, 2010. [Google Scholar]
- Heller, R.; Pudritz, R.E. The search for extraterrestrial intelligence in Earth’s solar transit zone. Astrobiology 2016, 16, 259–270. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, J.M.; Doyle, L.R. Detecting reflected light from close-in extrasolar giant planets with the Kepler photometer. Astrophys. J. 2003, 595, 429–445. [Google Scholar] [CrossRef]
- Seager, S. Exoplanet Atmospheres: Physical Processes; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Perryman, M. The Exoplanet Handbook; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Sobolev, V.V. Light Scattering in Planetary Atmospheres; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- Carter, J. Estimation of Planetary Photometric Emissions for Extremely Close-in Exoplanets. Ph.D. Thesis, University at Albany, Albany, NY, USA, 2017. in progress. [Google Scholar]
- Ḱopal, Z. Photometric Effects of Reflection in Close Binary Systems. Mon. Not. R. Astron. Soc. 1954, 114, 101–117. [Google Scholar] [CrossRef]
- Ḱopal, Z. Close Binary Systems; John Wiley and Sons Inc.: New York, NY, USA, 1959. [Google Scholar]
- Placek, B.; Knuth, K.; Angerhausen, D.; Jenkins, J. Characterization of Kepler-91b and the investigation of a potential Trojan companion using EXONEST. Astrophys. J. 2015, 814, 147. [Google Scholar] [CrossRef]
- Esteves, L.; De Mooij, E.; Jayawardhana, R. Changing phases of alien worlds: Probing atmospheres of Kepler planets with high-precision photometry. Astrophys. J. 2015, 804, 150. [Google Scholar] [CrossRef]
- Esteves, L.J.; De Mooij, E.J.W.; Jayawardhana, R. Optical phase curves of Kepler exoplanets. Astrophys. J. 2013, 772, 51. [Google Scholar] [CrossRef]
- Sliski, D.H.; Kipping, D.M. A high false positive rate for Kepler planetary candidates of giant stars using asterodensity profiling. Astrophys. J. 2014, 788, 148. [Google Scholar] [CrossRef]
- Charbonneau, D.; Allen, L.E.; Megeath, S.T.; Torres, G.; Alonso, R.; Brown, T.M.; Gilliland, R.L.; Latham, D.W.; Mandushev, G.; O’Donovan, F.T.; et al. Detection of thermal emission from an extrasolar planet. Astrophys. J. 2005, 626, 523. [Google Scholar] [CrossRef]
- Van Cleve, J.E.; Caldwell, D.A. Kepler Instrument Handbook; NASA/Ames Research Center: Moffett Field, CA, USA, 2009.
- Léger, A.; Grasset, O.; Fegley, B.; Codron, F.; Albarede, A.F.; Barge, P.; Barnes, R.; Cance, P.; Carpy, S.; Catalano, F.; et al. The extreme physical properties of the CoRoT-7b super-Earth. Icarus 2011, 213, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Maurin, A.S.; Selsis, F.; Hersant, F.; Belu, A. Thermal phase curves of nontransiting terrestrial exoplanets-II. Characterizing airless planets. Astron. Astrophys. 2012, 538, A95. [Google Scholar] [CrossRef]
- Sidis, O. Transits of transparent planets Atmospheric lensing effects. Astrophys. J. 2010, 720, 904. [Google Scholar] [CrossRef]
- Misra, A. The Effects of Refraction and Forward Scattering on Exoplanet Transit Transmission Spectroscopy. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2015. [Google Scholar]
- Misra, A.; Meadows, V.; Crisp, D. The effects of refraction on transit transmission spectroscopy: Application to Earth-like exoplanets. Astrophys. J. 2014, 792, 61. [Google Scholar] [CrossRef]
- Bétrémieux, Y.; Kaltenegger, L. Refraction in planetary atmospheres: Improved analytical expressions and comparison with a new ray-tracing algorithm. Mon. Not. R. Astron. Soc. 2015, 451, 1268–1283. [Google Scholar] [CrossRef]
- Muñoz, A.G.; Cabrera, J. Exoplanet phase curves at large phase angles. Diagnostics for extended hazy atmospheres. Mon. Not. R. Astron. Soc. 2017, in press. [Google Scholar]
- Muñoz, A.G.; Lavvas, P.; West, R.A. Titan brighter at twilight than in daylight. Nat. Astron. 2017, 1. [Google Scholar] [CrossRef]
- Showman, A.P.; Polvani, L.M. Equatorial superrotation on tidally locked exoplanets. Astrophys. J. 2011, 738, 71. [Google Scholar] [CrossRef]
- Faigler, S.; Mazeh, T. BEER Analysis of Kepler and CoRoT Lightcurves. II. Evidence for Superrotation in the Phase Curves of Three Kepler Hot Jupiters. Astrophys. J. 2015, 800, 73. [Google Scholar] [CrossRef]
- Heng, K. On the existence of shocks in irradiated exoplanetary atmospheres. Astrophys. J. Lett. 2012, 761, L1. [Google Scholar] [CrossRef]
- Batygin, K.; Stanley, S.; Stevenson, D.J. Magnetically Controlled Circulation on Hot Extrasolar Planets. Astrophys. J. 2013, 776, 53. [Google Scholar] [CrossRef]
- Menou, K. Magnetic scaling laws for the atmospheres of hot giant exoplanets. Astrophys. J. 2012, 745, 138. [Google Scholar] [CrossRef]
- Rauscher, E.; Menou, K. Three-dimensional Atmospheric Circulation Models of HD 189733b and HD 209458b with Consistent Magnetic Drag and Ohmic Dissipation. Astrophys. J. 2013, 764, 103. [Google Scholar] [CrossRef]
- Demory, B.O.; De Wit, J.; Lewis, N.; Fortney, J.; Zsom, A.; Seager, S.; Knutson, H.; Heng, K.; Madhusudhan, N.; Gillon, M.; et al. Inference of inhomogeneous clouds in an exoplanet atmosphere. Astrophys. J. Lett. 2013, 776, L25. [Google Scholar] [CrossRef]
- Heng, K.; Demory, B.O. Understanding Trends Associated with Clouds in Irradiated Exoplanets. Astrophys. J. 2013, 777, 100. [Google Scholar] [CrossRef]
- Armstrong, D.J.; de Mooij, E.; Barstow, J.; Osborn, H.P.; Blake, J.; Saniee, N.F. Variability in the atmosphere of the hot giant planet HAT-P-7 b. Nat. Astron. 2016, 1. [Google Scholar] [CrossRef]
- Pallé, E.; Ford, E.B.; Seager, S.; Montañés-Rodríguez, P.; Vazquez, M. Identifying the rotation rate and the presence of dynamic weather on extrasolar Earth-like planets from photometric observations. Astrophys. J. 2008, 676, 1319. [Google Scholar] [CrossRef]
- Artigau, É.; Bouchard, S.; Doyon, R.; Lafrenière, D. Photometric variability of the T2. 5 brown dwarf SIMP J013656. 5+ 093347: Evidence for evolving weather patterns. Astrophys. J. 2009, 701, 1534. [Google Scholar] [CrossRef]
- Gillon, M.; Triaud, A.H.M.J.; Jehin, E.; Delrez, L.; Opitom, C.; Magain, P.; Lendl, M.; Queloz, D. Fast-evolving weather for the coolest of our two new substellar neighbours. Astron. Astrophys. 2013, 555, L5. [Google Scholar] [CrossRef]
- Ford, E.B.; Seager, S.; Turner, E.L. Characterization of extrasolar terrestrial planets from diurnal photometric variability. Nature 2001, 412, 885–887. [Google Scholar] [CrossRef] [PubMed]
- Van Eylen, V.; Nielsen, M.L.; Hinrup, B.; Tingley, B.; Kjeldsen, H. Investigation of systematic effects in Kepler data: Seasonal variations in the light curve of HAT-P-7b. Astrophys. J. Lett. 2013, 774, L19. [Google Scholar] [CrossRef]
- Rybicki, G.B.; Lightman, A.P. Radiative Processes in Astrophysics; John Wiley and Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Faigler, S.; Mazeh, T. Photometric Detection of non-transiting Short-Period Low-Mass companions through the beaming, ellipsoidal, and reflection effects in Kepler and CoRoT light curves. Mon. Not. R. Astron. Soc. 2011, 415, 3921–3928. [Google Scholar] [CrossRef]
- Morris, S.L. The Ellipsoidal Variable Stars. Astrophys. J. 1985, 295, 143–152. [Google Scholar] [CrossRef]
- Heyrovský, D. Computing Limb-Darkening Coefficients from Stellar Atmosphere Models. Astrophys. J. 2007, 656, 483–492. [Google Scholar] [CrossRef]
- Sing, D. Stellar Limb-Darkening Coefficients for CoRoT and Kepler. Astron. Astrophys. 2010, 510, A21. [Google Scholar] [CrossRef]
- Kane, S.R.; Gelino, D.M. Distinguishing Between Stellar and Planetary Companions with Phase Monitoring. Mon. Not. R. Astron. Soc. 2012, 424, 779–788. [Google Scholar] [CrossRef]
- Jackson, B.K.; Lewis, N.; Barnes, J.; Deming, L.; Showman, A.; Fortney, J. The EVIL-MC Model for Ellipsoidal Variations of Planet-Hosting Stars and Applications to the HAT-P-7 System. Astrophys. J. 2012, 751, 112. [Google Scholar] [CrossRef]
- Gai, A. Bayesian Model Testing of Models for Ellipsoidal Variation on Stars Due to Hot Jupiters. Master’s Thesis, University at Albany, Albany, NY, USA, 2016. [Google Scholar]
- Gai, A.; Knuth, K.H. Bayesian Model Testing of Ellipsoidal Variations on Stars Due to Hot Jupiters; Anthony Gai (Univeraity at Albany): Albany, NY, USA, 2017; in press. [Google Scholar]
- Ford, E.B. Improving the Efficiency of Markov Chain Monte Carlo for Analyzing the Orbits of Extrasolar Planets. Astrophys. J. 2006, 642, 505. [Google Scholar] [CrossRef]
- Knuth, K.H.; Habeck, M.; Malakar, N.K.; Mubeen, A.M.; Placek, B. Bayesian evidence and model selection. Digit. Signal Process. 2015, 47, 50–67. [Google Scholar] [CrossRef]
- Faigler, S.; Tal-Or, L.; Mazeh, T.; Latham, D.W.; Buchhave, L.A. BEER Analysis of Kepler and CoRoT Light Curves. I. Discovery of Kepler-76b: A Hot Jupiter with Evidence for Superrotation. Astrophys. J. 2013, 771, 26. [Google Scholar] [CrossRef]
- Angerhausen, D.; DeLarme, E.; Morse, J.A. A Comprehensive Study of Kepler Phase Curves and Secondary Eclipses: Temperatures and Albedos of Confirmed Kepler Giant Planets. Publ. Astron. Soc. Pac. 2015, 127, 1113–1130. [Google Scholar] [CrossRef]
- Abraham, R.H.; Shaw, C.D. Dynamics-The Geometry of Behavior: Vol.: 2: Chaotic Behavior; Aerial Press, Incorporated: Santa Cruz, CA, USA, 1983. [Google Scholar]
- Lock, S.J.; Stewart, S.T. The structure of terrestrial bodies: Impact heating, corotation limits, and synestias. J. Geophys. Res. Planets 2017, 122, 950–982. [Google Scholar] [CrossRef]

| Planet | Semi-Major Axis (AU) | Transit Probability |
|---|---|---|
| Mercury | 0.39 | 1.18% |
| Venus | 0.72 | 0.64% |
| Earth | 1.00 | 0.46% |
| Mars | 1.53 | 0.30% |
| Jupiter | 5.20 | 0.09% |
| Saturn | 9.54 | 0.05% |
| Solar Radius | 0.0046 AU |
| Model | Log (Evidence) | EVIL-MC’s Bayes’ Factor |
|---|---|---|
| EVIL-MC | 14,256.91 ± 0.91 | 1 |
| Kane and Gelino (Mod) | 14,256.71 ± 0.73 | 2.20 |
| BEER | 14,256.26 ± 0.74 | 2.65 |
| Kane and Gelino (2012) | 14,253.66 ± 0.72 | 5.25 |
| Model | log Z (×10) | log |
|---|---|---|
| R | −9.5987 | −9.5987 |
| RE | −9.5822 | −9.5822 |
| REB | −9.5685 | −9.5684 |
| REB + SR | −9.5676 | −9.5676 |
| Kepler-76b Parameter Estimates (REB + SR Model) | ||
|---|---|---|
| Model Parameters | REB + SR Parameter Estimates | Literature Values |
| 1.35 ± 0.05 | 1.25 ± 0.08 | |
| 1.97 ± 0.12 | 2.0 ± 0.26 | |
| i | 77.9 ± 0.03 | 78.0 ± 0.2 |
| 0.31 ± 0.22 | 0.23 ± 0.02, 0.22 ± 0.02 | |
| Modeled Effect | EXONEST | Under Study |
|---|---|---|
| Circular Orbits | X | |
| Elliptical Orbits | X | |
| Primary Transit | X | |
| Secondary Eclipse | X | |
| Limb Darkening | X | M |
| Reflected Light | X | R |
| Refracted Light | S | |
| Thermal Emissions | X | R |
| Doppler Beaming | X | |
| Ellipsoidal Variations | X | M |
| Atmospheric Effects | S | |
| Multiple Planets | D | |
| Planetary Shapes | S |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Knuth, K.H.; Placek, B.; Angerhausen, D.; Carter, J.L.; D’Angelo, B.; Gai, A.D.; Carado, B. EXONEST: The Bayesian Exoplanetary Explorer. Entropy 2017, 19, 559. https://doi.org/10.3390/e19100559
Knuth KH, Placek B, Angerhausen D, Carter JL, D’Angelo B, Gai AD, Carado B. EXONEST: The Bayesian Exoplanetary Explorer. Entropy. 2017; 19(10):559. https://doi.org/10.3390/e19100559
Chicago/Turabian StyleKnuth, Kevin H., Ben Placek, Daniel Angerhausen, Jennifer L. Carter, Bryan D’Angelo, Anthony D. Gai, and Bertrand Carado. 2017. "EXONEST: The Bayesian Exoplanetary Explorer" Entropy 19, no. 10: 559. https://doi.org/10.3390/e19100559
APA StyleKnuth, K. H., Placek, B., Angerhausen, D., Carter, J. L., D’Angelo, B., Gai, A. D., & Carado, B. (2017). EXONEST: The Bayesian Exoplanetary Explorer. Entropy, 19(10), 559. https://doi.org/10.3390/e19100559






