In this section, we investigate the nonlinear complex behaviors of the proposed compound financial price dynamics. To obtain a robust result, actual market datasets (Shanghai Stock Exchange (SSE) composite index and Hang Seng Index (HSI)) are comparatively considered with the simulation ones, the selected daily closing prices for the period from 28 June 1995 to 31 May 2017 with 5320 data points (some slight differences exist for different non-trading days between the two markets, and some one-day missing values are supplemented by linear interpolation). The time series are available on the Yahoo Finance website (
https://finance.yahoo.com). For simplicity, the corresponding empirical experiment is performed by computer simulation for different infection rates
in contact process, and different intensity
in compound Poisson process. In the following, we set the time length of analysis to 5320 and initial probability
to
(namely, each individual is independently infected with probability
) in contact process to gain simulation datasets.
4.1. Basic Statistical Properties of Returns
The statistical analysis of the financial returns and the corresponding absolute return series has attracted the interest of many researchers for their wide application in asset allocation, asset pricing, risk management, stock return volatility forecasting, etc. [
2,
10,
12,
13,
14,
15]. Recent empirical works have reported that the empirical probability distributions of financial returns are believed to deviate from a Gaussian distribution, and they usually exhibit more leptokurtic and fatter tails than the Gaussian case, which is usually called “fat-tail” distribution, and may be explained as the result of the herd effect of investors in the security markets or illiquidity. A highly leptokurtic distribution is characterized by a narrower and larger maximum, and by fatter tails than a Gaussian one [
10]. The kurtosis, which is one of the most important statistics to describe leptokurtic, is exhibited in
Table 1. When the kurtosis of a series is larger than 3, which is the kurtosis of a Gaussian distribution, there exist fat tails in the probability distribution. Moreover, the descriptive statistics, the Kolmogorov-Smirnov (K-S) test and Anderson-Darling (A-D) test of normalized returns of the actual marketdatasets and the simulation ones are also exhibited in
Table 1 [
42]. In the K-S test of the corresponding normalized returns, the signification level is 5%, and the lengths of returns are 5320, the critical values are the same at
. The K-S test returns the logical value
if it rejects the null hypothesis that the distribution of normalized returns follows the standard normal distribution at the given significance level, while
if it cannot. In the A-D test of the returns, the hypothesized distribution is normal distribution in this paper, the signification level is also 5%, and the corresponding critical values are
. The A-D test returns the logical value
if it rejects the null hypothesis that the distribution of returns follows a given probability distribution (here, normal distribution) at the given significance level, while
if it cannot [
42].
According to the empirical results in
Table 1, we can find that the tail distributions of the simulative datasets and the actual ones are deviating from the Gaussian case, the kurtosis are larger than 3. Moreover, in K-S test and A-D test, all the logical values are 1, and all the stats are larger than the corresponding critical value, so the null hypothesis that the distribution of the simulative datasets and the actual ones follow the normal distribution can be rejected at the significance level 5%. It is obvious that the actual datasets and the simulation ones display similar fat-tail and leptokurtic attributes. We also find that the kurtosis isincreasing steadily from
to
with
increasing from
to
and fixed
, which imply that the fat-tail behavior is more significantly as
increases. The reason of this increasing is that the rate
represents the rate of attitude spread in the price dynamics, and the increasing of
implies the interaction among the investors becomes more and more active, which is supposed to bring the herd behavior of the security market, and usually results in the fat-tail distribution for the returns. There are similar patterns for
and
, but larger kurtosis than the case of
, which may be explained that
represents the rate of Poisson jumps; that is, a larger
shows more large fluctuations and directly leads to fat-tail phenomenon of the returns.
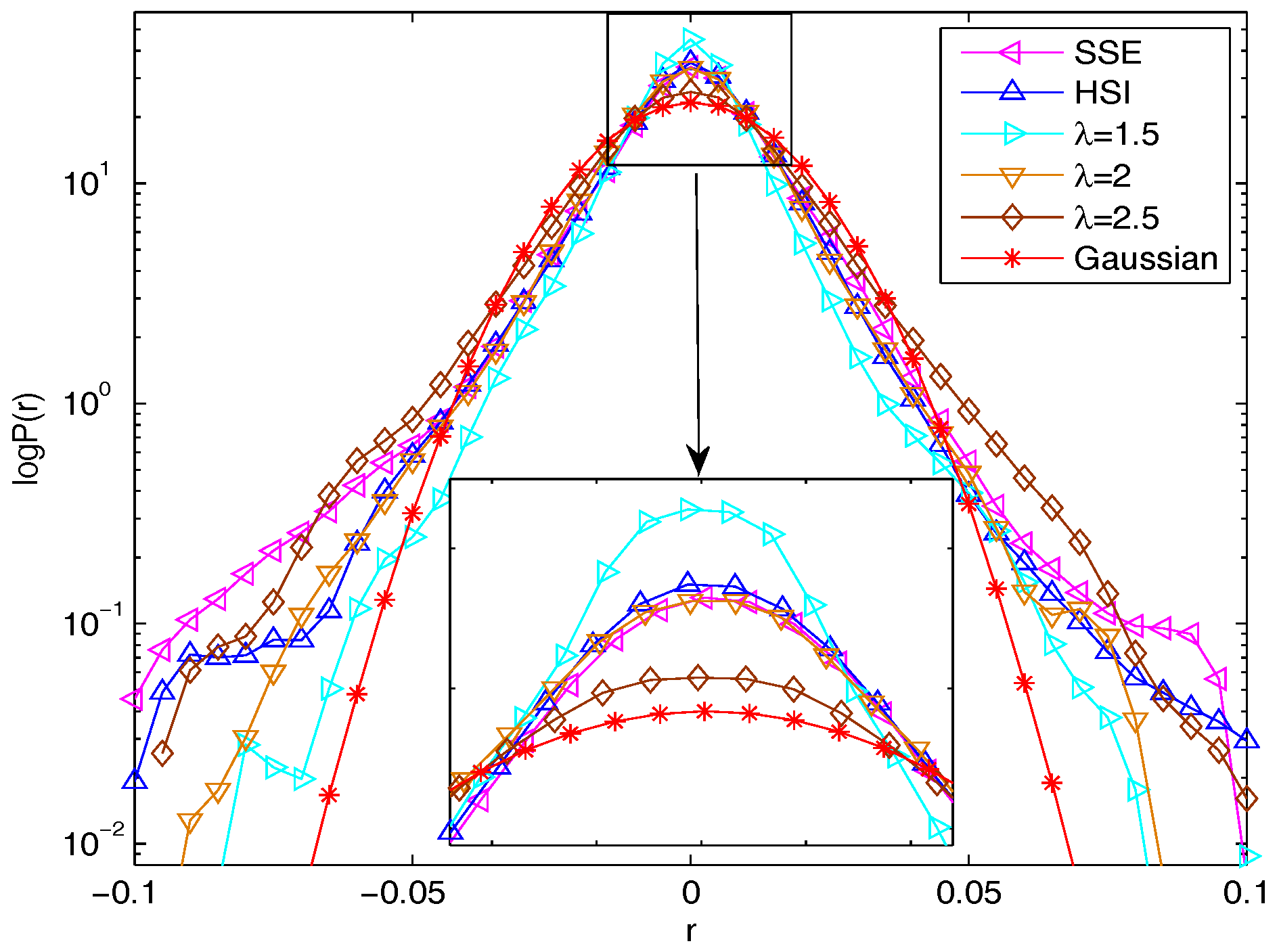
Moreover, the empirical probability density distributions of the simulation datasets with
are presented in
Figure 1 with comparison to a Gaussian distribution. The patterns of these curves also show that the actual datasets and the simulated ones deviate from the Gaussian. It is transparent that the simulation datasets exhibit the similar fat-tail and peak distributions to the actual ones.
4.2. Fractional Permutation Entropy
Permutation entropy, proposed by Bandt and Pompe, is a complex measure for arbitrary time series based on analysis of order patterns [
29]. Consider a time series
, comparing
n-dimension vector
, suppose it has permutation
, and all
n! permutations
of order
n which are considered as possible order types of
n different numbers. For each permutation
, the relative frequency is determined as
where
n and
denote the embedding dimension and the time delay, respectively. The permutation entropy of order
is defined as
where the sum runs over all
permutations
of order
n. The permutation entropy
is between 0 and
for
, when all the permutations have same frequency,
reaches its maximum.
Permutation entropy of returns
and absolute returns
for
of simulation datasets and actual datasets with
are exhibited in
Table 2. We can find that all the permutation entropy values are close, the permutation entropy of returns
is slightly increasing from
to
with
increasing from
to
and fixed
and
, which means that the behavior of returns is more complex as
increases. The reason for this increase is that the rate
represents the rate of attitude spread, and the increasing of
implies that the interaction among the investors becomes more frequent, which is supposed to bring more random order patterns and temporal information, and hence lead to more complex dynamics. There are similar patterns for
and
, but with larger permutation entropy than the case of
. This may be explained as a larger
shows more frequent violent fluctuation to the stock price. Additionally, the permutation entropy values of absolute returns
are slightly smaller than those of returns
, which represents that the absolute return series exhibit less order permutation patterns, larger correlation, and hence are easier to predict than the return series.
A generalized expression of permutation entropy is brought with approaches in fractional calculus by References [
43,
44]. Fractional permutation entropy (FPE), a modified permutation entropy, is proposed to detect fractional order characteristics for complex system.
where
,
is the probability that the system is in state
i, and
i runs over all possible states in the system,
leads to the permutation entropy as
, where
is the gamma function, and
is digamma function, which has the form
. The FPE of returns
with fractional exponent
from
to
with step size of
for
and
of simulation datasets and actual datasets are exhibited in
Table 3. For every fixed parameter set, as
value increases, the FPE firstly increases and then decreases. For a fixed
, the FPE values for larger
are larger than the corresponding FPE values for smaller
, which shows that a larger
leads to more complex dynamics. Comparing the FPE for
with
, we find that the FPE for
are slightly less than the corresponding FPE values for
, which means that high frequency of jumps leads to the increasing of complexity.
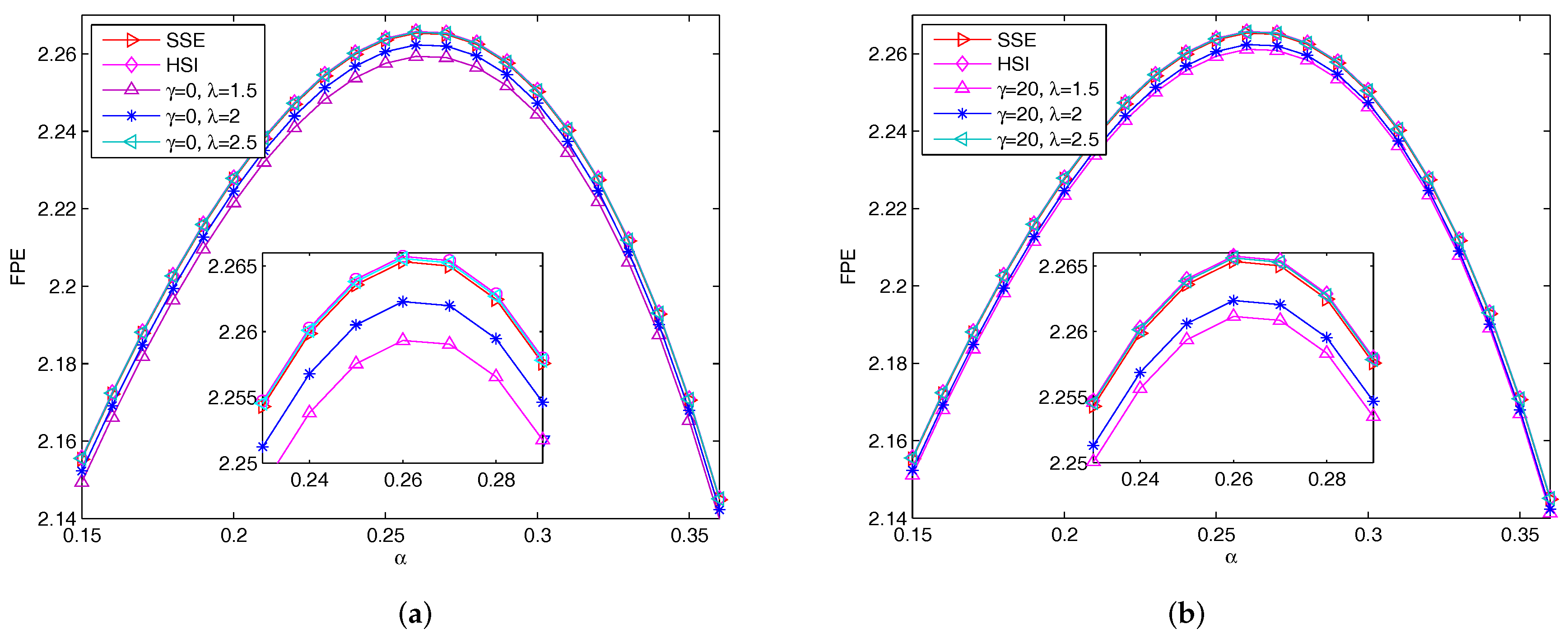
Figure 2 depicts FPE curves versus
from
to
with step size of
for the actual market datasets and the simulation ones with
and
((a) for
and (b) for
). We can find that all curves evolve along similar shape. In
Figure 2, the FPE values track with larger
lie above the ones with smaller
. It indicates that, when
increases, the FPE increases, which means that the dynamics of system become more complex as
increases. Because the rate
relates to the speed of investors react to the security market, as
increases, the market will become more swarming and the investors are more likely to group together which lead to large fluctuations as a result.
4.3. Fractional Sample Entropy
Sample entropy proposed by Richman and Moorman [
30], which is independent of data length and exhibits relative consistency, is a complex statistics method of time series through comparing of vector pairs in template vectors of two adjacent embedding dimension. Considering a time series
, the state vector
is defined as
(
), where
,
represents the time delay (set
in the following for simplicity) and
m represents the embedding dimension, respectively. The underlying dynamics of time series
are fully embedded in the
m-dimensional phase space
. The embedding theorem [
45] guarantees a full knowledge of a system contained in the time series of any one measurement and a proxy for the full multivariate phase space that can be constructed from the time series. Two vectors,
and
, are considered as close if their distance
is smaller than a given tolerance level
. Let
represents the number of vectors
(where
to exclude self-matches) that are close to the vector
. Then, the probability that any vector
is close to the vector
within a tolerance level
is defined as
The average of the
is given as
which represents the frequency that any two vectors are within
of each other. Then, the sample entropy of time series
is given as
Although
m and
are vital in calculating the sample entropy, no guidelines exist for optimizing their values. The rule accepted widely is that
and values of
m of 1 or 2. We calculate the fractional sample entropy for all datasets with parameters
and
,
represents the standard deviation of the considered time series, which is the usually chosen parameters combination [
31].
Sample entropies of returns
and absolute returns
of simulation datasets and actual datasets with
are exhibited in
Table 4. For every fixed parameter set, as
value increases, the sample entropy increases, which means that the sample entropy values for larger
are larger than those for smaller
, which shows that a larger
leads to larger fluctuation, larger difference in number of vector pairs in template vectors of two adjacent embedding dimension, less self-similarity in data series, hence leads to more complex dynamics. We also find that sample entropies for
and
are slightly less than those for
, which means that higher frequency of jumps leads to more diversified template vectors. Meanwhile, the sample entropies of absolute returns
are slightly smaller than those of returns
, which displays that the absolute return series exhibit more self-similarity, lower complex dynamics than the return series.
The fractional sample entropy, a modified sample entropy approximation based on the methods in References [
30,
43], is developed to detect characteristics of fractional order information for complex dynamics [
31]. The fractional sample entropy (FSE) of time series
is then defined as Reference [
31]
The FSE method is applied to study the complex behaviors of the actual datasets, the simulation ones, the empirical results with Gaussian are exhibited in
Table 5 and
Table 6 and
Figure 2.
Table 5 displays the FSE of returns
with fractional exponent
form
to
with step size of
for different values of
and
. For every fixed parameter set, as
value increases, the FSE firstly increases and then decreases. All the FSE values of simulation datasets and actual ones are less than the corresponding FSE values of Gaussian, which displays that they are deviating from the Gaussian series. Meanwhile, for every fixed parameter set, as
value increases, the FSE increases, which means that the FSE for larger
are larger than those for smaller
, which shows that a larger
leads to more complex dynamics. We also find that the FSE for
and
are slightly less than those for
, which means that higher frequency of jumps leads to more complex behaviors. Additionally, comparing
Table 6 with
Table 5, we find that the FSE values of absolute returns
are observably less than the corresponding FSE values of returns
(except for Gaussian), which means that the absolute return series exhibit lower complexity than the return series.
Figure 3 depicts FSE curves versus
for the actual market datasets and the simulation ones,
ranges from
to
with step size of
.
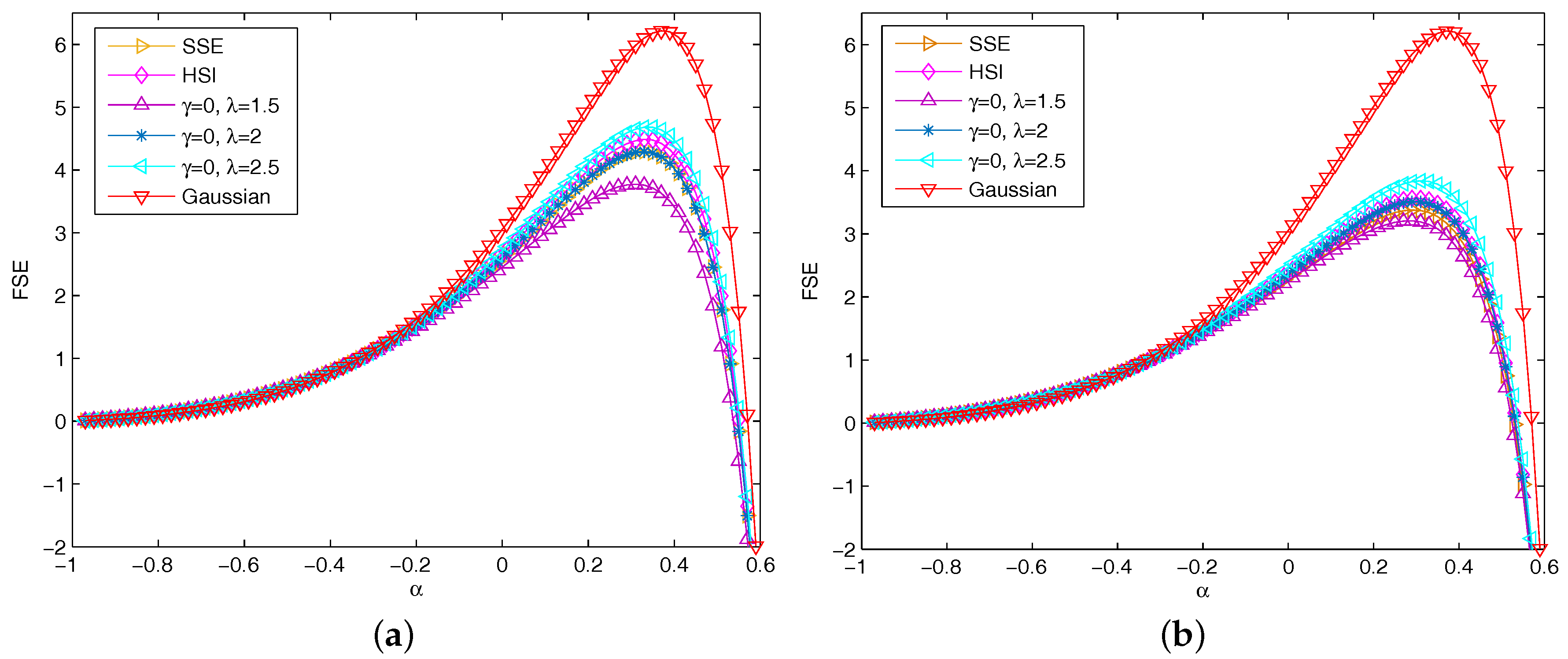
Figure 3a depicts the FSE curves of returns of the SSE, the HSI, and the financial price model for
,
and
with fixed
. All curves evolve along similar shape, as
value increases, the FSE firstly increases and then decreases. The FSE values of Gaussian lies above others, and, as can be seen, all datasets are deviating from the Gaussian. In
Figure 3a, the FSE track with larger
lies above the ones with smaller
. It indicates that, when
increases, the FSE increases, which means that the dynamics of system become more complex as
increases. Because the rate
relates to the speed of investors react to the security market, as
increases, the market will become more swarming and the investors are more likely to group together which lead to large fluctuations as a result.
Figure 3b depicts the FSE curves of absolute returns of the actual datasets and simulation ones. Being compared with
Figure 3a,b has similar dynamics behaviors.
Figure 3b illustrates that except for Gaussian series, the FSE of absolute return series of actual datasets and simulation ones significantly decrease, which means that absolute return series exhibit lower complexity than return series.
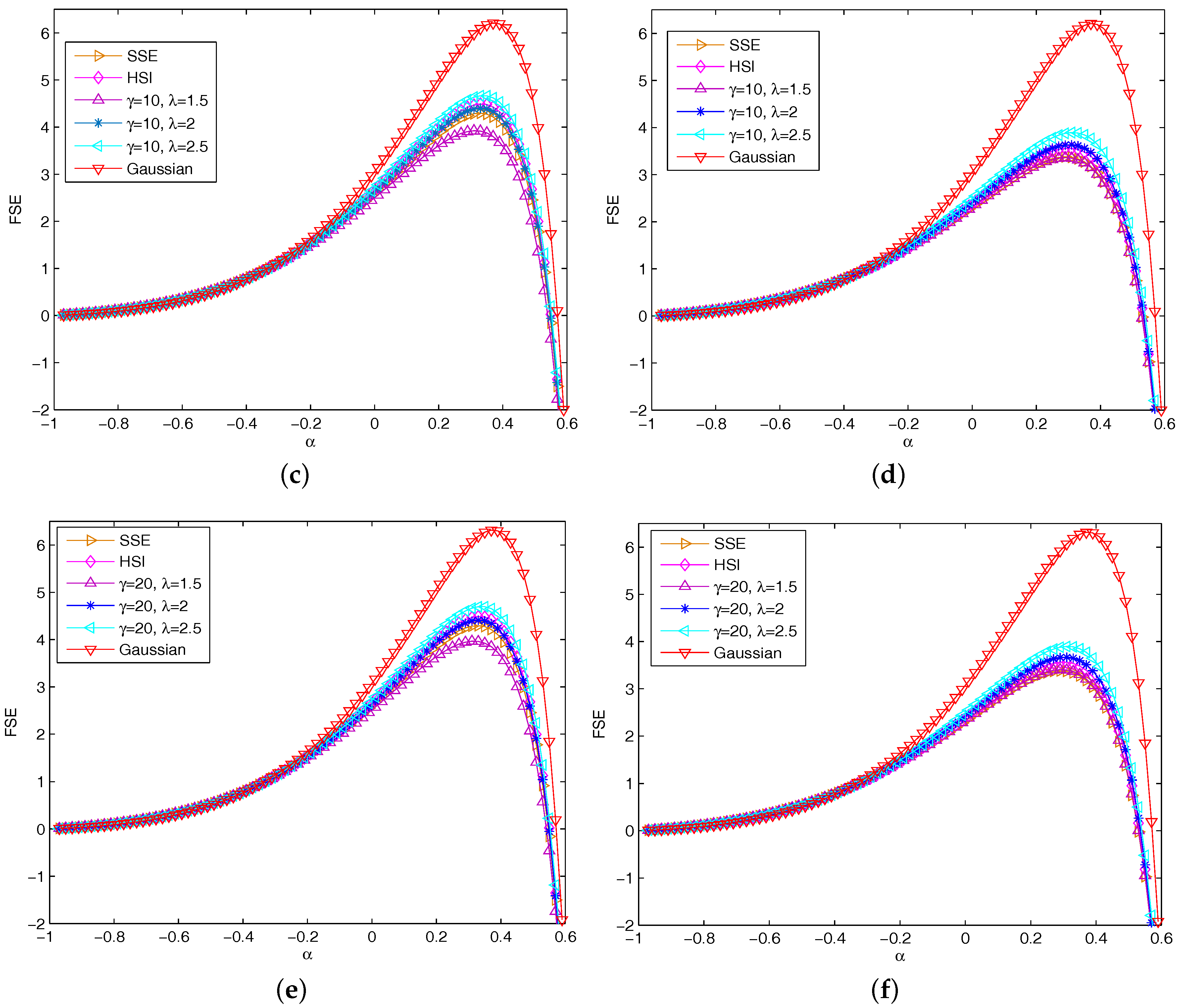
Figure 3c,d and
Figure 3e,f depict the FSE curves of returns and absolute return series with
and
, and have similar patterns with
Figure 3a,b.