Distributed Rateless Codes with Unequal Error Protection Property for Space Information Networks
Abstract
:1. Introduction
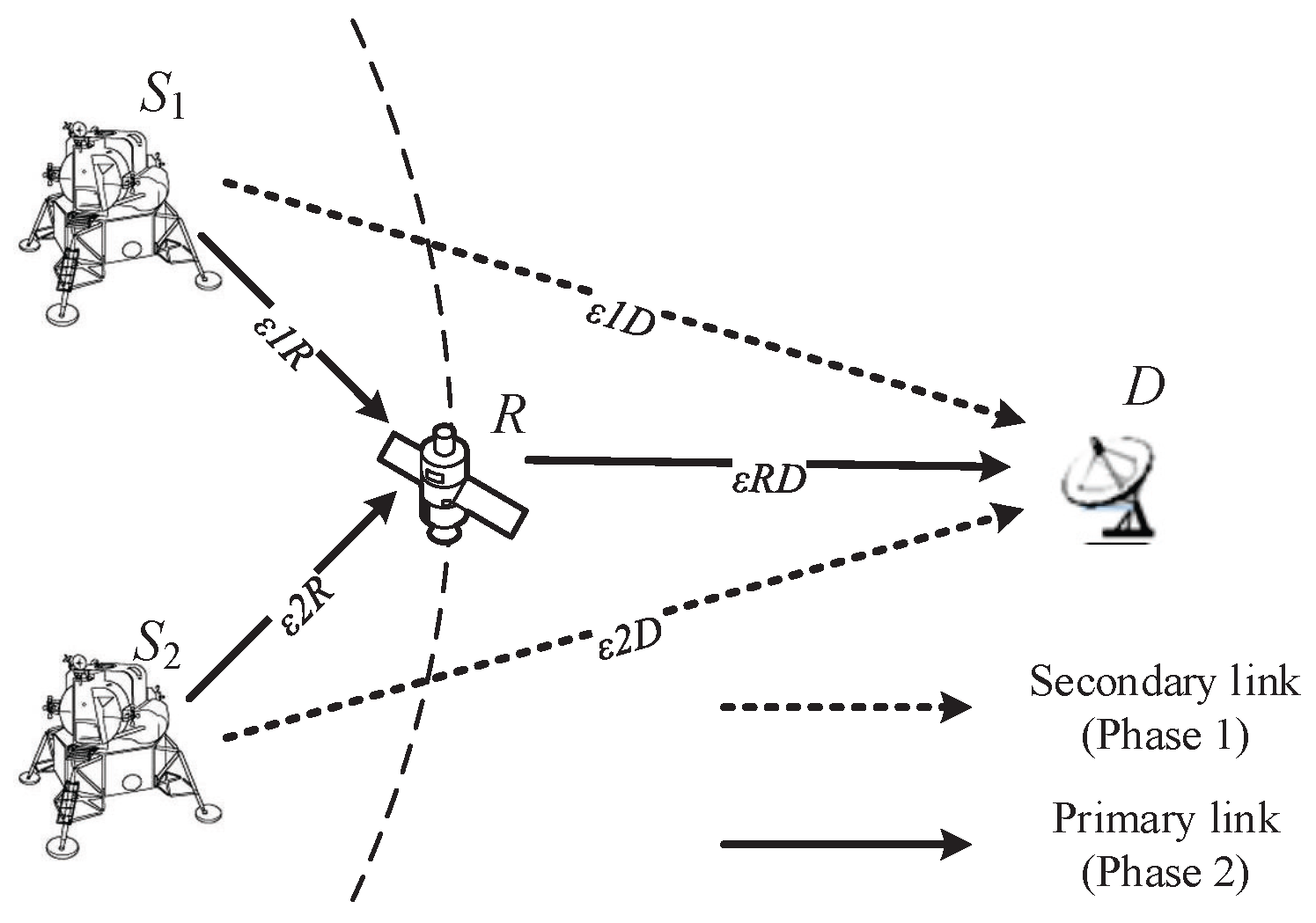
2. System Model
- Initialization Suppose that the information symbol lengths of and are and , respectively. The () symbols are divided into n subsets according to their importance levels, expressed as and , the fraction of the information symbols in is and . selects the i-th importance level from subset with probability , which is called symbol-selection weight [21]. employs an LT-coding degree distribution in Phase 1, and in Phase 2, where denotes a pre-selected maximum value of .
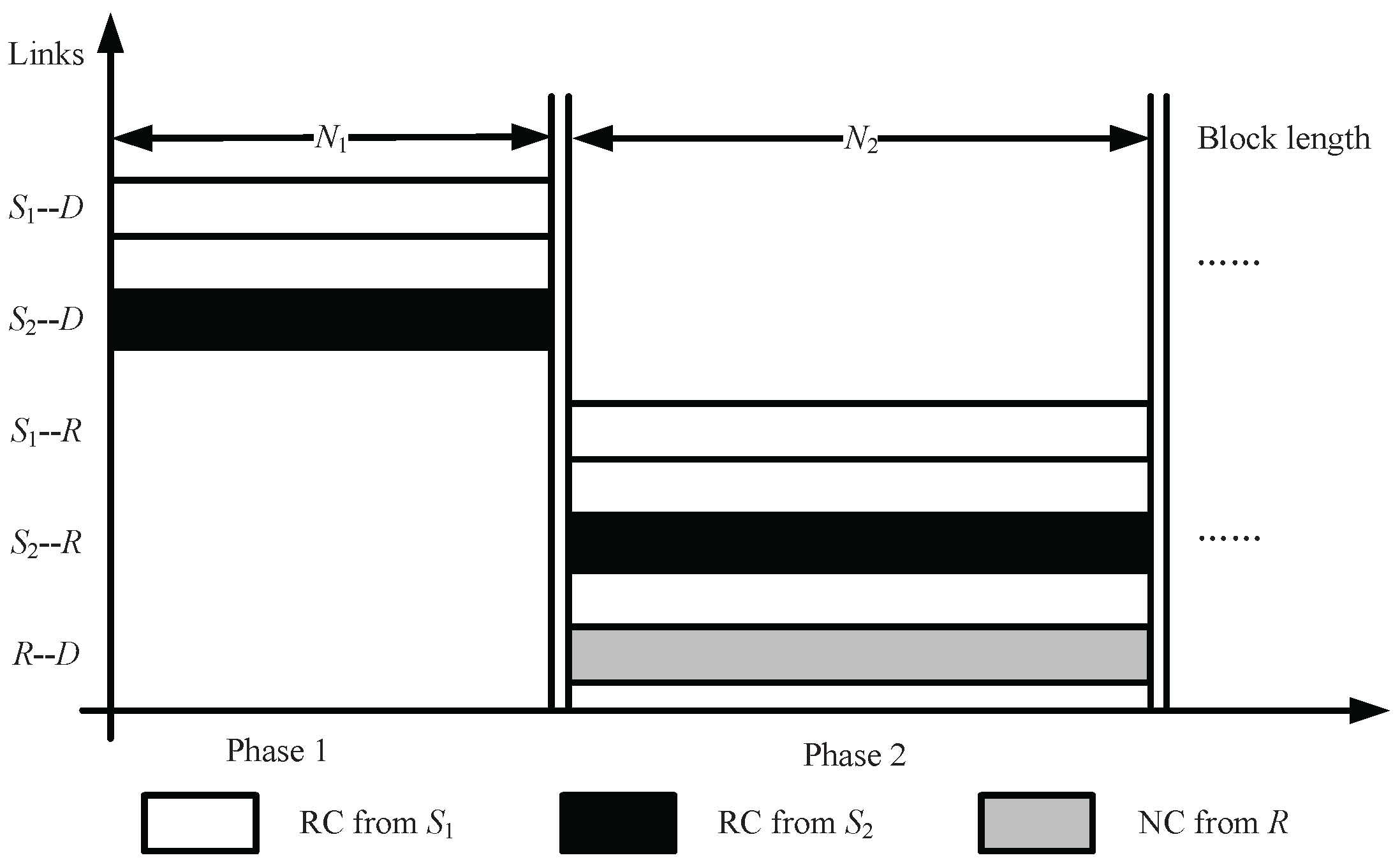
- Phase 1 R is invisible, and and generate distributed rateless coded symbols from information symbols using LT-coding degree distribution , and transmit coded symbols to D by secondary links. In an encoding process at , if a degree is randomly selected with probability using the degree distribution , then information symbols are selected uniformly at random and are bitwise XORed to form the coded symbol.
- Phase 2.1 R is visible, and and generate distributed UEP rateless coded symbols from information symbols using LT-coding degree distribution , and transmit coded symbols to R by primary links. In an encoding process at , if a degree is randomly selected with probability using the degree distribution , then information symbols are selected with probability in and are bitwise XORed to form the coded symbol.
- Phase 2.2 The coded symbols are transmitted to relay R from and , and based on the network coding rule and , R generates three types of network coded symbols and forwards them to the destination D. R forwards ’s output symbol directly with the probability , while forwarding ’s output symbol directly with the probability , and XORs the two incoming symbols with the probability and then forwards to D .
- Decoding After receiving enough coded symbols from , and R, a joint decoding is performed on D to recover the information symbols of and .
3. Design of Distributed Unequal Error Protection Rateless Codes
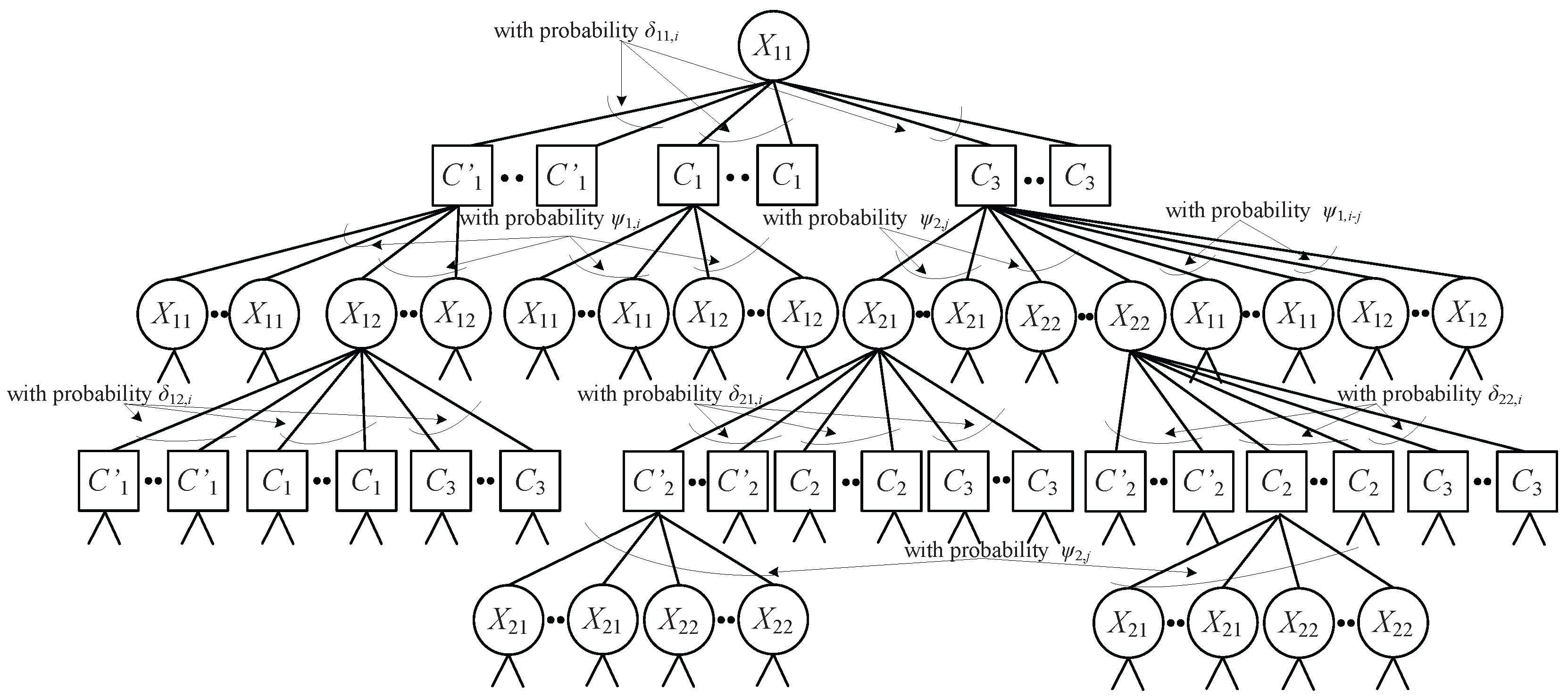
3.1. Analysis of RC and NC Degree Distributions by the And-Or Tree Technique
3.2. Analysis of System Throughput
3.3. Optimizations of Rateless Coding Scheme and Network Coding Rule
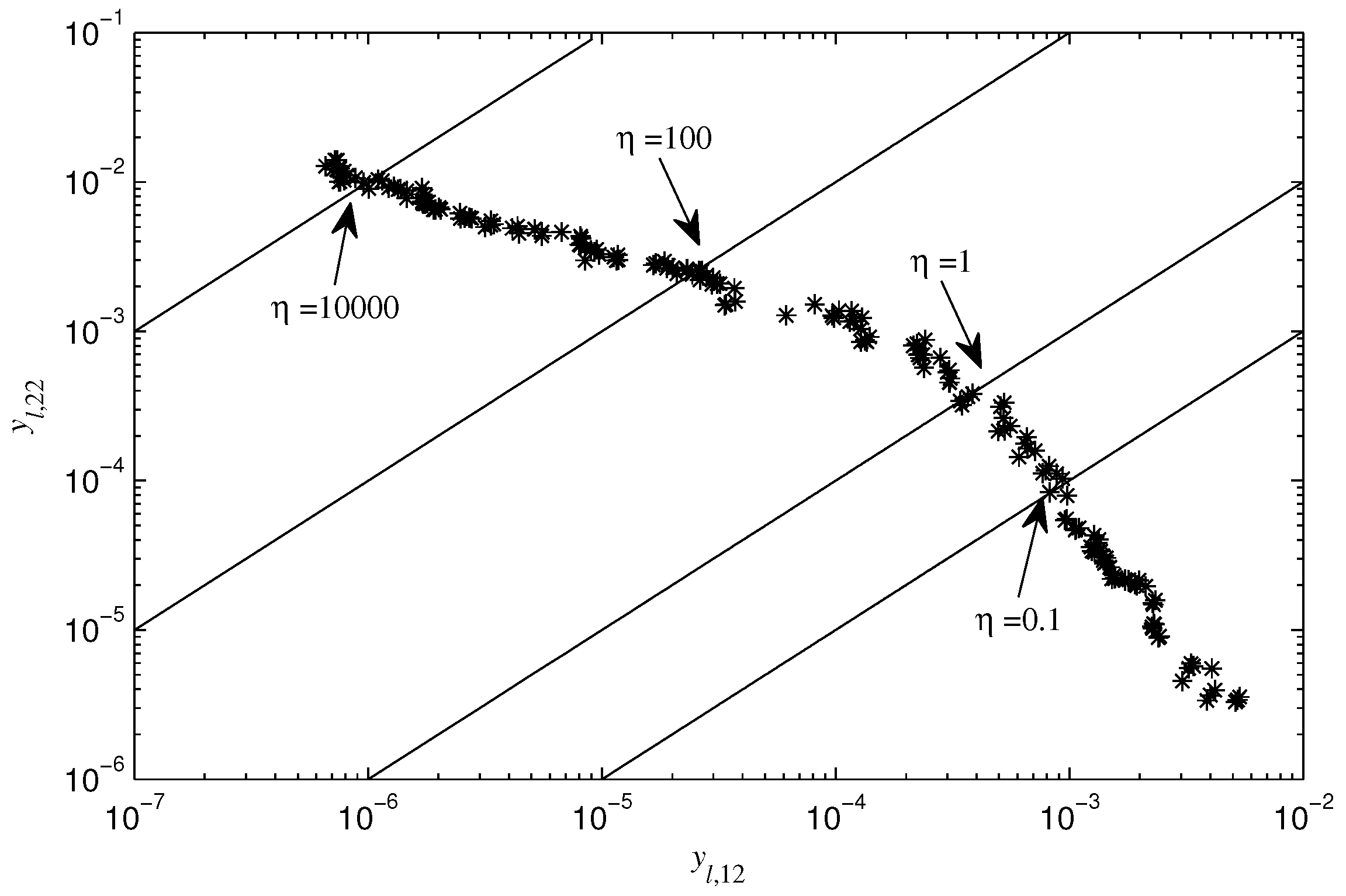
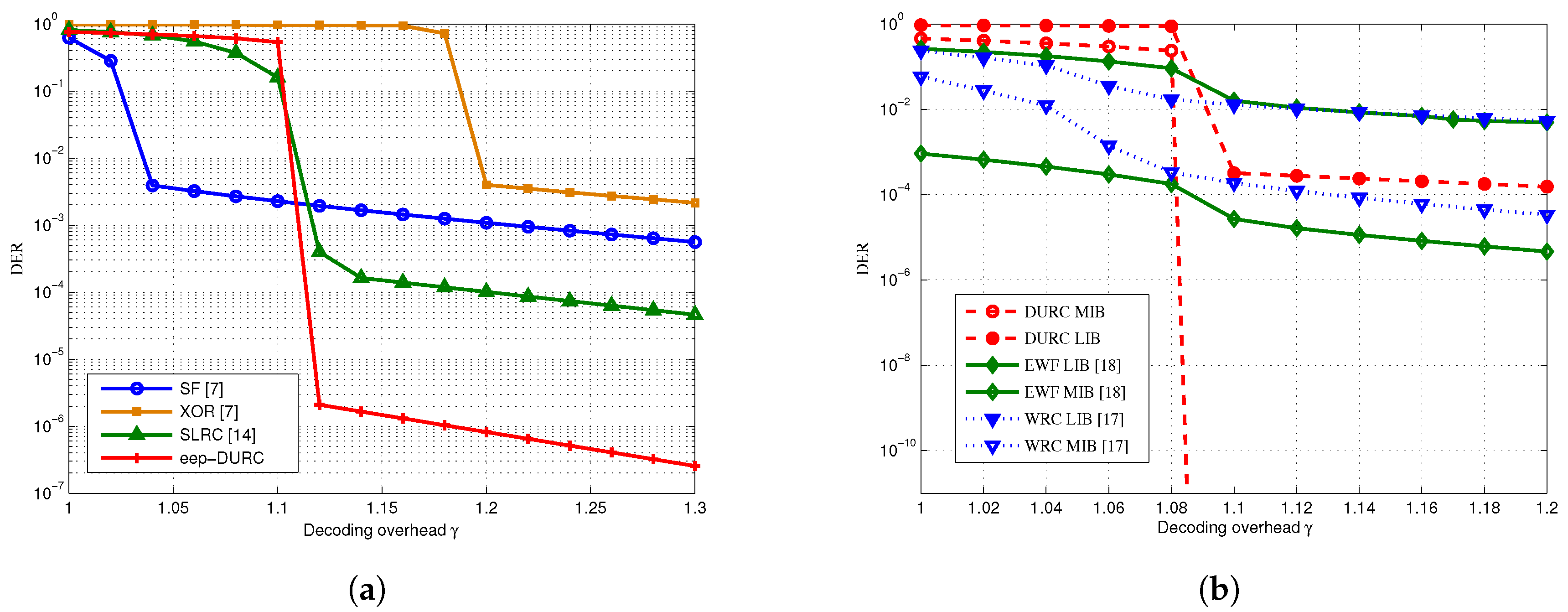
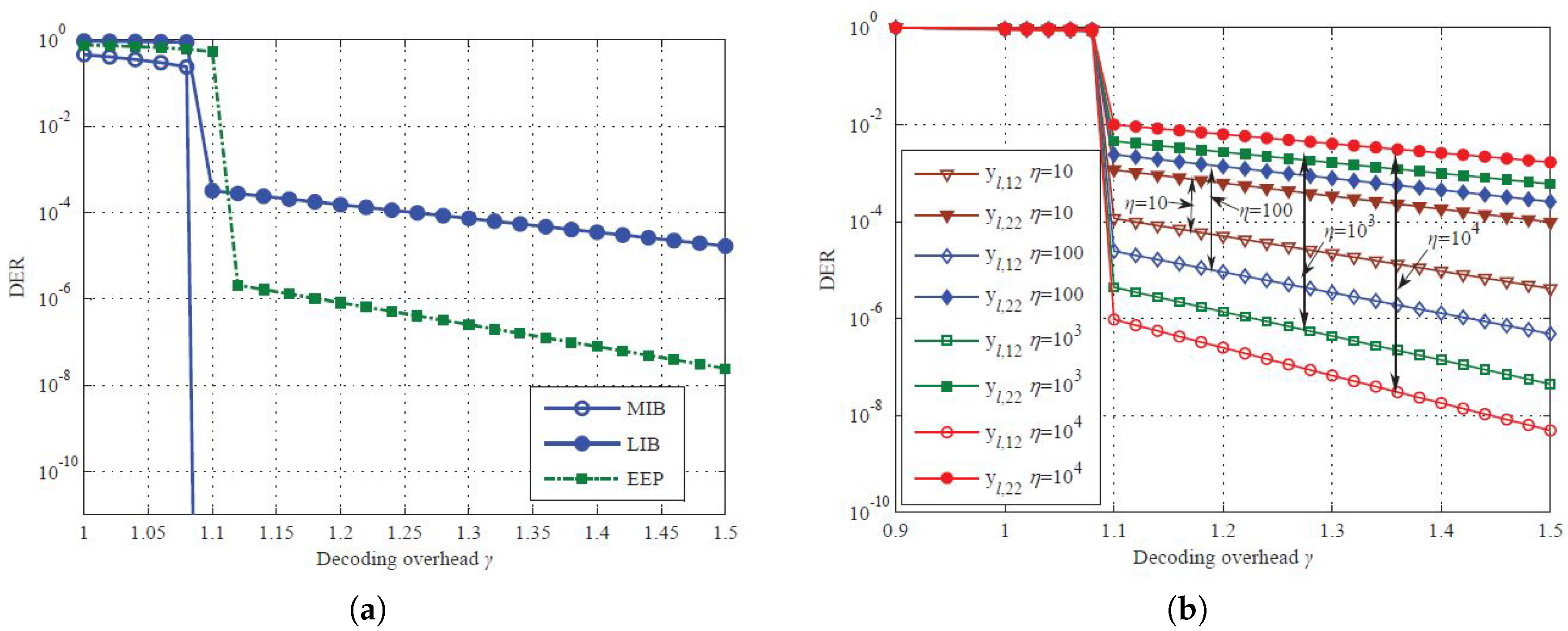
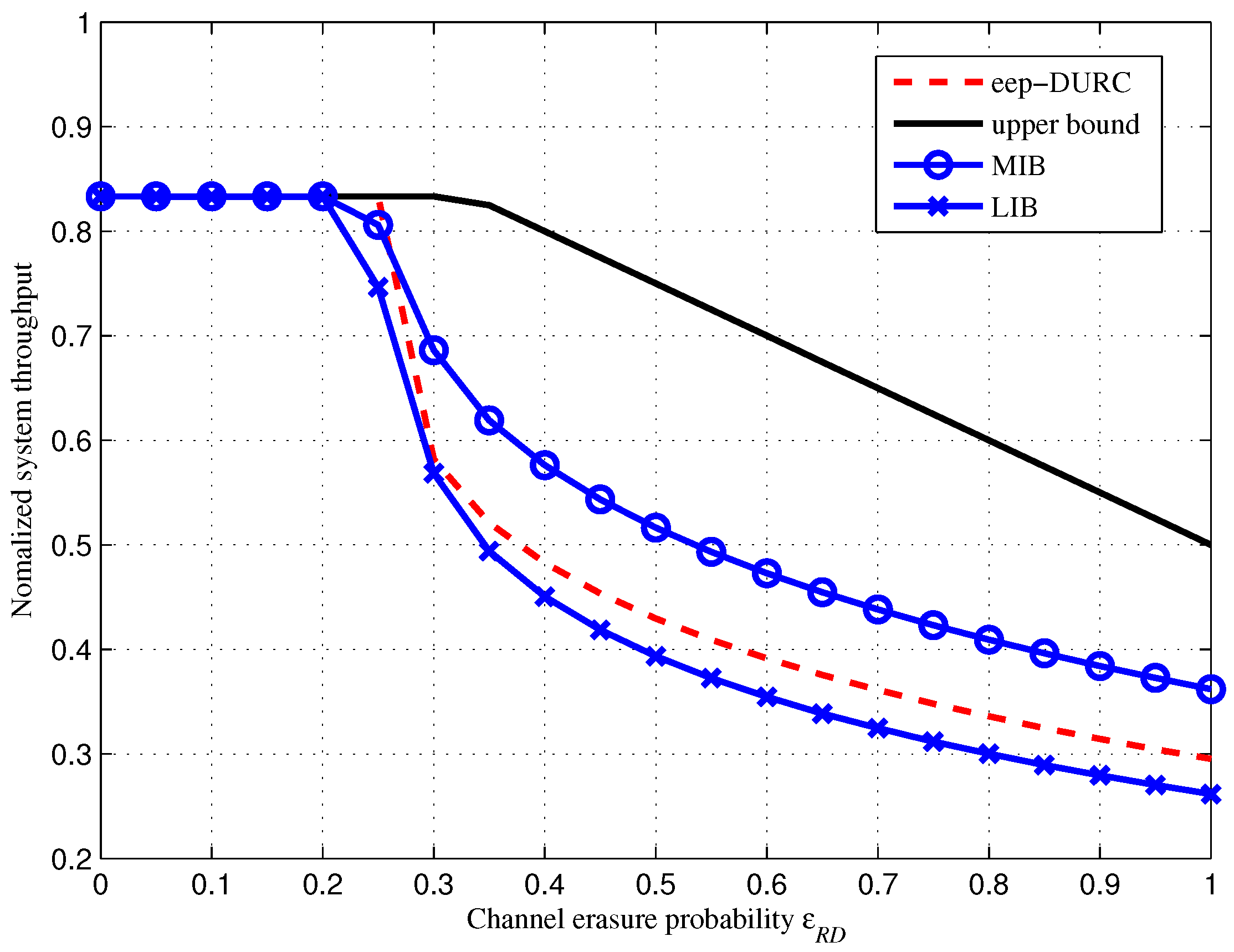
4. Simulation and Comparison
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- De Cola, T.; Paolini, E.; Liva, G.; Calzolari, G.P. Reliability options for data communications in the future deep-space missions. Proc. IEEE 2011, 99, 2056–2074. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, R.-H.; Zhao, K.-L.; Li, W.-F.; Sun, X.; Hu, J.-L.; Ji, X.-Y. Modeling RTT for DTN protocol over asymmetric cislunar space channels. IEEE Syst. J. 2016, 10, 556–567. [Google Scholar] [CrossRef]
- Consultative Committee for Space Data Systems (CCSDS). Erasure Correcting Codes for Use in Nearearth and Deep-Space Communications; National Aeronautics and Space Administration: Washington, DC, USA, November 2014. [Google Scholar]
- De Cola, T.; Marchese, M. Reliable data delivery over deep space networks: Benefits of long erasure codes over ARQ strategies. IEEE Wirel. Commun. 2010, 17, 57–65. [Google Scholar] [CrossRef]
- Paolini, E.; Liva, G.; Matuz, B.; Chiani, M. Maximum likelihood erasure decoding of LDPC codes: Pivoting algorithms and code design. IEEE Trans. Commun. 2012, 60, 3209–3220. [Google Scholar] [CrossRef]
- Liva, G.; Pulini, P.; Chiani, M. On-line construction of irregular repeat accumulate codes for packet erasure channels. IEEE Trans. Wirel. Commun. 2013, 12, 680–689. [Google Scholar] [CrossRef]
- Garrammone, G.; De Cola, T.; Matuz, B.; Liva, G. Recent findings on erasure codes for space communications. Int. J. Satell. Commun. Netw. 2014, 32, 201–211. [Google Scholar] [CrossRef]
- Luby, M. LT codes. In Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, Vancouver, BC, Canada, 16–19 November 2002; pp. 271–280.
- Shokrollahi, A. Raptor codes. IEEE Trans. Inf. Theory 2006, 52, 2551–2567. [Google Scholar] [CrossRef]
- Jiao, J.; Guo, Q.; Zhang, Q.-Y. Packets interleaving ccsds file delivery protocol in deep space communication. IEEE Aerosp. Electron. Syst. Mag. 2011, 26, 5–11. [Google Scholar] [CrossRef]
- Li, H.; Luo, H. An erasure coding-based loss-tolerant file delivery protocol for deep space communications. Acta Astronaut. 2011, 68, 1409–1416. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, J.; Sui, X.-D.; Wu, S.-H.; Li, Y.-H.; Zhang, Q.-Y. Rateless coding scheme for time-varying dying channels. In Proceedings of the 8th Wireless Communications & Signal Processing, Yangzhou, China, 13–15 October 2016; pp. 1–6.
- Niephaus, C.; Kretschmer, M.; Ghinea, G. QoS provisioning in converged satellite and terrestrial networks: A survey of the state-of-the-art. IEEE Commun. Surv. Tutor. 2016, 19, 1–27. [Google Scholar] [CrossRef]
- Gu, S.-S.; Yang, Y.; Jiao, J.; Xiang, W.; Zhang, Q.-Y. Distributed rateless coded collaboration for satellite relay networks. In Proceedings of the Wireless Communications & Signal Processing, Nanjing, China, 15–17 October 2015; pp. 1–6.
- Muhammad, M.; Giambene, G.; De Cola, T. QoS Support in SGD-based High Throughput Satellite Networks. IEEE Trans. Wirel. Commun. 2016, 15, 1–15. [Google Scholar] [CrossRef]
- Puducheri, S.; Kliewer, J.; Fuja, T. The design and performance of distributed LT codes. IEEE Trans. Inf. Theory 2007, 53, 3740–3754. [Google Scholar] [CrossRef]
- Sejdinovic, D.; Piechocki, R.; Doufexi, A. AND-OR tree analysis of distributed LT codes. In Proceedings of the IEEE Infromation Theory Workshop, Taormina, Italy, 12–10 June 2009; pp. 261–265.
- Liau, A.; Yousefi, S.; Kim, I.-M. Binary soliton-like rateless coding for the Y-network. IEEE Trans. Commun. 2011, 59, 3217–3222. [Google Scholar] [CrossRef]
- Liau, A.; Kim, I.-M.; Yousefi, S. Improved low-complexity soliton-like network coding for a resource-limited relay. IEEE Trans. Commun. 2013, 61, 3327–3335. [Google Scholar] [CrossRef]
- Gu, S.-S.; Jiao, J.; Yang, Z.-H.; Zhang, Q.-Y.; Xiang, W.; Cao, B. Network-coded rateless coding scheme in erasure multiple-access relay enabled communications. IET Commun. 2014, 8, 537–545. [Google Scholar] [CrossRef]
- Rahnavard, N.; Vellambi, B.N.; Fekri, F. Rateless codes with unequal error protection property. IEEE Trans. Inf. Theory 2007, 53, 1521–1532. [Google Scholar] [CrossRef]
- Sejdinovic, D.; Vukobratovic, D.; Doufexi, A. Expanding window fountain codes for unequal error protection. IEEE Trans. Commun. 2009, 57, 2510–2516. [Google Scholar] [CrossRef]
- Talari, A.; Rahnavard, N. Distributed unequal error protection rateless codes over erasure channels: A two-source scenario. IEEE Trans. Commun. 2012, 60, 2084–2090. [Google Scholar] [CrossRef]
- Baik, J.; Suh, Y.; Rahnavard, N.; Heo, J. Generalized unequal error protection rateless codes for distributed wireless relay networks. IEEE Trans. Commun. 2015, 63, 4630–4650. [Google Scholar] [CrossRef]
- Talari, A.; Rahnavard, N. On the intermediate symbol recovery rate of rateless codes. IEEE Trans. Commun. 2012, 60, 1237–1242. [Google Scholar] [CrossRef]
- Luby, M.; Mitzenmacher, M.; Shokrollahi, A. Analysis of random processes via and/or tree evaluations. In Proceedings of the 9th Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, CA, USA, 25–27 January 1998; pp. 364–373.
- Sanghavi, S. Intermediate performance of rateless codes. In Proceedings of the IEEE Infromation Theory Workshop, Bergen, Norway, 2–6 September 2007; pp. 478–482.
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
| Importance Levels | Network Coding Rule | Selection Weights | Degree Distributions |
|---|---|---|---|
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, J.; Yang, Y.; Feng, B.; Wu, S.; Li, Y.; Zhang, Q. Distributed Rateless Codes with Unequal Error Protection Property for Space Information Networks. Entropy 2017, 19, 38. https://doi.org/10.3390/e19010038
Jiao J, Yang Y, Feng B, Wu S, Li Y, Zhang Q. Distributed Rateless Codes with Unequal Error Protection Property for Space Information Networks. Entropy. 2017; 19(1):38. https://doi.org/10.3390/e19010038
Chicago/Turabian StyleJiao, Jian, Yi Yang, Bowen Feng, Shaohua Wu, Yonghui Li, and Qinyu Zhang. 2017. "Distributed Rateless Codes with Unequal Error Protection Property for Space Information Networks" Entropy 19, no. 1: 38. https://doi.org/10.3390/e19010038
APA StyleJiao, J., Yang, Y., Feng, B., Wu, S., Li, Y., & Zhang, Q. (2017). Distributed Rateless Codes with Unequal Error Protection Property for Space Information Networks. Entropy, 19(1), 38. https://doi.org/10.3390/e19010038






